ms计算磁矩

MS 4。

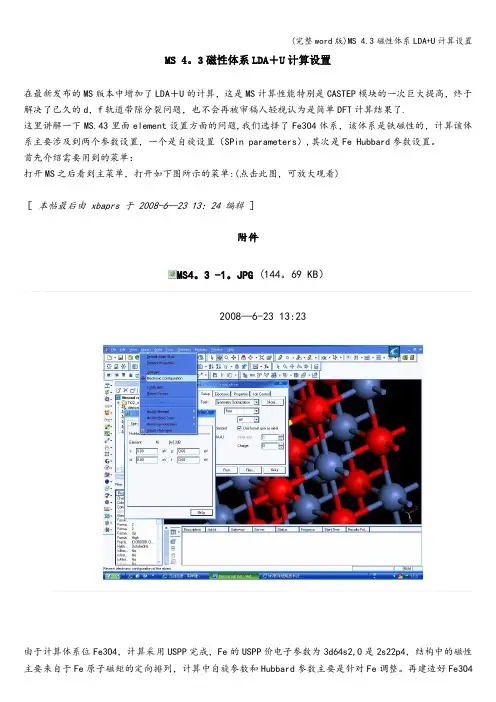
3磁性体系LDA＋U计算设置在最新发布的MS版本中增加了LDA＋U的计算，这是MS计算性能特别是CASTEP模块的一次巨大提高，终于解决了已久的d，f轨道带隙分裂问题，也不会再被审稿人轻视认为是简单DFT计算结果了.这里讲解一下MS.43里面element设置方面的问题,我们选择了Fe3O4体系，该体系是铁磁性的，计算该体系主要涉及到两个参数设置，一个是自旋设置（SPin parameters）,其次是Fe Hubbard参数设置。

首先介绍需要用到的菜单：打开MS之后看到主菜单，打开如下图所示的菜单:(点击此图，可放大观看)［本帖最后由 xbaprs 于 2008-6—23 13：24 编辑］附件MS4。

3 -1。

JPG (144。

69 KB）2008—6-23 13:23由于计算体系位Fe3O4，计算采用USPP完成，Fe的USPP价电子参数为3d64s2,O是2s22p4，结构中的磁性主要来自于Fe原子磁矩的定向排列，计算中自旋参数和Hubbard参数主要是针对Fe调整。

再建造好Fe3O4结构之后（注MS结构库中包含此结构），为一个面心立方晶格,一个惯用晶胞包含8个Fe3O4单位，因此整个结构有24个Fe原子，32个O。

计算可以采用FCC结构的初级晶胞结构，也可以采用惯用晶胞。

我们计算采用后者。

打开Modify－electronic configuration菜单，看到Spin和Hubbard U两个子菜单如图：SPin主要是自旋控制参数，由于再铁磁性结构中Fe自旋是高度极化的，因此这个地方设置为High spin state，即3d6结构为4个自旋平行同向电子.自旋方向不管是Up还是Down当然不会改变Fe原子自旋极化的性质,但会改变总的磁矩(自旋电子数目，这点会再CASTEP计算参数Spin设置中体现出来，可以尝试把部分Fe原子自旋改成High,SPin up，部分为High，Down，然后查看CASTEP计算控制面板的SPin数值)。

磁学中的磁矩计算在磁学领域，磁矩是一个至关重要的概念，它对于理解物质的磁性行为起着关键作用。

磁矩的计算不仅在理论研究中具有重要意义，在实际应用中也有着广泛的用途，比如在电磁设备的设计、磁性材料的研究等方面。

要理解磁矩的计算，首先得明确磁矩的定义。

磁矩可以简单地理解为描述磁体磁性强弱和方向的物理量。

就好像一个力有大小和方向一样，磁矩也有其大小和方向。

在微观层面，原子中的电子绕核运动以及电子自身的自旋都会产生磁矩。

对于单个电子来说，其轨道磁矩和自旋磁矩是磁矩的两个重要组成部分。

轨道磁矩的大小与电子绕核运动的轨道半径、角动量等因素有关。

而自旋磁矩则是电子固有的一种磁性属性。

在计算单个电子的磁矩时，我们可以使用一些量子力学的公式和原理。

例如，对于电子的轨道磁矩，其大小可以表示为μl ＝（e/2m)L ，其中 e 是电子电荷，m 是电子质量，L 是电子的轨道角动量。

而电子的自旋磁矩大小为μs ＝ ge(e/2m)S ，这里的 g 是一个称为朗德 g 因子的常数，S 是电子的自旋角动量。

当我们考虑多个电子组成的原子时，情况就变得稍微复杂一些。

由于电子之间存在相互作用和排布规则，总的原子磁矩并不是各个电子磁矩的简单相加。

在原子中，电子按照一定的规则填充不同的能级和轨道。

根据洪德法则，在基态时，电子会尽可能以自旋平行的方式排布，以使得原子的总磁矩最大。

对于一些常见的磁性物质，比如铁磁性材料，其磁性来源于大量原子磁矩的协同作用。

在铁磁性材料中，相邻原子的磁矩会相互影响，形成磁畴。

磁畴内的原子磁矩方向基本一致，从而表现出宏观的强磁性。

在计算宏观物体的磁矩时，通常需要考虑物体的形状、磁化状态等因素。

对于一个均匀磁化的圆柱体，其磁矩可以通过磁化强度 M 与圆柱体的体积 V 的乘积来计算，即磁矩μ ＝ M × V 。

如果是一个环形电流，其磁矩可以表示为μ ＝ I × A ，其中 I 是电流强度，A 是电流所围成的面积。

磁铁磁矩计算公式
1. 磁矩的基本概念。

- 磁矩是磁铁磁性大小的一种物理量表示。

对于一个载流线圈，磁矩μ = NIS，其中N是线圈匝数，I是电流强度，S是线圈面积，磁矩的方向由右手螺旋定则确定（四指指向电流方向，大拇指为磁矩方向）。

- 在磁铁中，磁矩可以看作是由许多微观的磁偶极子组成的宏观表现。

2. 条形磁铁磁矩的近似计算（基于磁荷观点）
- 假设条形磁铁的两极有磁荷+q_m和-q_m，两极之间的距离为l，则磁矩μ = q_ml。

这里的磁荷是一种类比于电荷的概念，在实际的微观物理中并不存在真正意义上的磁荷，但这种模型在某些情况下可以方便地对磁铁的磁性进行计算和分析。

3. 基于安培分子环流假说的磁矩计算（微观角度）
- 根据安培分子环流假说，物质的磁性来源于分子电流。

对于一个磁性物质中的小单元（可以看作是小的磁矩单元），如果分子电流为I_m，小单元的面积为
S_m，则这个小单元的磁矩μ_m = I_mS_m。

对于一块磁铁，其总的磁矩就是这些微观磁矩的矢量和。

不过在实际计算中，由于微观结构的复杂性，这种计算往往非常困难，更多的是从宏观的等效磁荷或者通过测量来确定磁矩。

需要注意的是，在高中人教版教材中并没有直接给出磁铁磁矩的计算公式，以上内容是基于物理概念的拓展，在大学物理相关知识中有更深入的讲解。

磁学现象与物质的磁性人们很早就发现磁性材料具有特殊的功能特性。

公元前3世纪，《吕氏春秋·精通篇》中就出现“石，铁之母也。

以有磁石，故能引其子；石之不慈者，亦不能引也”的记载，叙述了磁性材料可以吸引特定的物质，如铁等。

在战国末期韩非所著的《有度篇》中已出现“故先王以立司南以端前夕”的记载；而在东汉王充的《论衡·是应篇》中出现了“司南之勺，投之于地，其柢指南”的记载，叙述了磁性材料具有南北极，可以指示南北方向的特性。

北宋沈括所著的《梦溪笔谈》中已有制作指南针的详尽描述，明朝《萍洲可谈》中出现船舶在苏门答腊海中航行时应用指南针的详细记载，叙述了磁性材料的应用。

在欧洲，人们在小亚细亚的Magnesia 地区发现了磁铁矿，因而人们把磁石叫做Magnet 。

人们虽然很早就发现了磁性的存在，但对磁性现象本质的认识却经历了相当长的时间。

1820年，奥斯特发现了电流的磁效应，1831年法拉第发现了电磁感应定律以及楞次发现的楞次定律，人们才逐渐揭开了磁性的奥秘。

随着原子结构的被揭露，尤其是量子力学的成就，人们对目前磁性的物理本质才有了一个大体满意的解释。

一、磁及磁现象的根源是电荷的运动1.1 一些基本的磁现象当电流通过一条导线，生成一个方向由右手定则指示的磁场。

如果大拇指指示正向电流I 的方向，四指就指示磁场B 的方向。

如果一条载流的长导线被卷成圆筒形，环绕圆筒线圈可观察到一个磁场；磁场的形状具有环环相叠的圆柱对称性，它的方向由右手定则规定。

此时，四指指示电流方向，拇指给出线圈内部的磁场方向。

外部的磁场具有圆环对称性。

而地球磁场源自地球熔融铁核的流动。

这种流动才使图中罗盘针的黑端指示出地理北极的方向。

假定一根棒状磁体按图1-3从一个线圈内部向外移开，在线圈绕组的两端可检测到一个电压脉冲。

电压源自线圈内磁力线的变化。

感生电压遵从Lenz 定律—如果线圈内的磁力线发生变化，由此在线圈内感生的电压是这样的．由它产生的电流决定的磁场与初始的变化方向相反。

1.磁化强度及磁偶极矩饱和磁化强度是单位体积内部磁矩的总和。

面磁矩的计算公式是电流乘以面积（A·m2）饱和磁化强度是在外磁场下，随着激发磁场的变化，磁场达到最大值的磁化强度叫做饱和磁化强度。

单位是（A·m/kg或者G），有的文献标注的是Ms，有的文献标注的是4πM，这是由于采用的单位制不同造成的。

磁偶极矩是磁常数（μ。

）和磁矩的乘积，j=μ。

·m，磁偶极矩的国际制单位为T·m3，高斯单位制为磁偶极矩CGSM单位，磁常数（真空磁导率）在国际单位制中的数值为4πx10-7H/m。

使用高斯为单位的话饱和磁化强度前面都要乘以4π。

磁极化强度是一个与材料体积相关联的矢量，它等于次提及内的磁偶极矩与该体积之比。

磁极化强度的国际单位制单位为T，高斯单位制单位为Gs。

对于磁极化强度，单位换算公式为1T=104/4πGs。

磁谱是指在磁场很弱的情况下，磁性物质的起始磁导率与磁场频率的关系，通常在磁性材料在交变磁场作用下的磁导率表示为μ=μ-iμ涡流损耗是指磁性材料在交变磁场中时，其内部产生的感生电流而引起的能量损耗，其与电阻率和薄膜的厚度有关。

在材料中加入铝元素和氧元素，会增加材料的铁磁共振频率表和矫顽力。

同时材料的各向异性能也会发生改变。

单轴的各向异性能。

[1]FeCo 基软磁薄膜的制备及其微波软磁特性研究，青岛大学[2]关于纯Ni、纯Co及WC-Co硬质合金比饱和磁化强度值的讨论[3]关于纯Ni、纯Co及WC-Co硬质合金比饱和磁化强度值的讨论Ⅱ2.磁致伸缩系数：铁磁性物质在磁化时，沿着磁化方向会发生长度的伸长或缩短的现象，这种效应可以用磁致伸缩系数λ来表示。

而且λ的大小等于沿着磁化方向的伸长量与总长度的比值，单位一般取ppm。

Λ大于0表示沿着磁化方向的尺寸伸长，称为正磁致伸缩，例如铁；反之称为负磁致伸缩，例如镍。

MS 4.3磁性体系LDA＋U计算设置在最新发布的MS版本中增加了LDA＋U的计算，这是MS计算性能特别是CASTEP模块的一次巨大提高，终于解决了已久的d，f轨道带隙分裂问题，也不会再被审稿人轻视认为是简单DFT计算结果了。

这里讲解一下MS.43里面element设置方面的问题，我们选择了Fe3O4体系，该体系是铁磁性的，计算该体系主要涉及到两个参数设置，一个是自旋设置（SPin parameters），其次是Fe Hubbard参数设置。

首先介绍需要用到的菜单：打开MS之后看到主菜单，打开如下图所示的菜单：（点击此图，可放大观看）[本帖最后由 xbaprs 于 2008-6-23 13:24 编辑]附件MS4.3 -1.JPG由于计算体系位Fe3O4，计算采用USPP完成，Fe的USPP价电子参数为3d64s2，O是2s22p4，结构中的磁性主要来自于Fe原子磁矩的定向排列，计算中自旋参数和Hubbard参数主要是针对Fe调整。

再建造好Fe3O4结构之后（注MS结构库中包含此结构），为一个面心立方晶格，一个惯用晶胞包含8个Fe3O4单位，因此整个结构有24个Fe原子，32个O。

计算可以采用FCC结构的初级晶胞结构，也可以采用惯用晶胞。

我们计算采用后者。

打开Modify－electronic configuration菜单，看到Spin和Hubbard U两个子菜单如图：SPin主要是自旋控制参数，由于再铁磁性结构中Fe自旋是高度极化的，因此这个地方设置为High spin state，即3d6结构为4个自旋平行同向电子。

自旋方向不管是Up还是Down当然不会改变Fe原子自旋极化的性质，但会改变总的磁矩（自旋电子数目，这点会再CASTEP计算参数Spin设置中体现出来，可以尝试把部分Fe原子自旋改成High，SPin up，部分为High，Down，然后查看CASTEP计算控制面板的SPin数值）。

MS 4.3磁性体系LDA＋U计算设置（系列一）在最新发布的MS版本中增加了LDA＋U的计算，这是MS计算性能特别是CASTEP模块的一次巨大提高，终于解决了已久的d，f轨道带隙分裂问题，也不会再被审稿人轻视认为是简单DFT计算结果了。

这里讲解一下MS.43里面element设置方面的问题，我们选择了Fe3O4体系，该体系是铁磁性的，计算该体系主要涉及到两个参数设置，一个是自旋设置（SPin parameters），其次是Fe Hubbard参数设置。

首先介绍需要用到的菜单：打开MS之后看到主菜单，打开如下图所示的菜单：（点击此图，可放大观看）附件1: 1.JPG (2009-05-16 14:46:46, 144.69 K)由于计算体系位Fe3O4，计算采用USPP完成，Fe的USPP价电子参数为3d64s2，O是2s22p6，结构中的磁性主要来自于Fe原子磁矩的定向排列，计算中自旋参数和Hubbard参数主要是针对Fe调整。

再建造好Fe3O4结构之后（注MS结构库中包含此结构），为一个面心立方晶格，一个惯用晶胞包含8个Fe3O4单位，因此整个结构有24个Fe原子，32个O。

计算可以采用FCC结构的初级晶胞结构，也可以采用惯用晶胞。

我们计算采用后者。

打开Modify－electronic configuration菜单，看到Spin和Hubbard U两个子菜单如图：SPin主要是自旋控制参数，由于再铁磁性结构中Fe自旋是高度极化的，因此这个地方设置为High spin state，即3d6结构为4个自旋平行同向电子。

自旋方向不管是Up还是Down 当然不会改变Fe原子自旋极化的性质，但会改变总的磁矩（自旋电子数目，这点会再CASTEP计算参数Spin设置中体现出来，可以尝试把部分Fe原子自旋改成High，SPin up，部分为High，Down，然后查看CASTEP计算控制面板的SPin数值）。

磁流体磁化强度计算公式磁流体磁化强度计算公式 磁流体是一种特殊的材料，具有高度可调的磁性和流动性质。

它在许多领域中得到了广泛应用，如电力传输、声波控制和医学成像等。

磁化强度是磁流体的一个重要物理量，它描述了磁性材料受到磁场激励后的响应程度。

本文将介绍磁化强度的计算公式。

磁化强度（M）是磁流体中磁矩（m）与单位体积（V）的比值。

其计算公式可以表示为：M = m / V 其中，磁矩是单位截面内磁流体所具有的总磁矩。

磁矩的计算需要考虑材料中每个微元体积的磁矩大小和方向，并对整个体积进行积分。

通常，磁矩可以通过以下公式计算：m = ∫ J dV其中，J是磁流体的磁化强度矢量。

磁化强度矢量（J）可以通过磁场强度（H）与磁导率（μ）之间的关系进行计算。

根据安培定律和磁流体的特性，磁化强度矢量在空间中的分布可以用以下公式表示：J = χH 其中，χ是磁流体的磁化率。

磁化率是衡量磁流体对磁场激励响应的物理量，其值可以通过实验测量或理论计算得到。

磁化率受到温度、外加磁场和材料特性等因素的影响。

在实际应用中，磁化强度的计算需要结合具体的实验或仿真数据，并考虑材料的非线性效应。

对于线性材料，磁化率与磁场强度之间的关系可以通过以下公式描述：χ = χ0 + χ1H 其中，χ0是材料的初始磁化率，χ1是材料的磁化率与磁场强度之间的线性关系系数。

这个公式可以帮助我们预测磁化强度随磁场强度变化的趋势。

在磁流体的非线性材料中，磁化强度的计算将更加复杂。

此时，需要引入更多的参数和公式来描述磁性材料的特性。

例如，饱和磁化强度（Ms）是一个重要的参数，描述了在饱和磁场下材料的最大磁化强度。

根据实验或仿真数据，可以得到不同磁场强度下的磁化强度-磁场强度曲线。

通过对这些数据的拟合，可以得到磁化强度与磁场强度和材料特性之间的更为准确的关系。

总结起来，磁流体磁化强度的计算公式涉及到磁矩、磁化强度矢量和磁化率等物理量的计算。

对于线性材料，磁化强度与磁场强度成正比，可以通过磁化率与磁场强度之间的线性关系来描述。

磁量子数ml自旋磁量子数ms的解释与应用磁量子数ml和自旋磁量子数ms是量子力学中的两个重要概念，它们的物理意义和应用在很多领域都有着重要的作用。

下面就让我们来详细了解一下这两个概念。

一、磁量子数ml的解释磁量子数ml是描述原子轨道磁矩方向的量子数，它的取值范围是- l ~ + l，其中l为轨道量子数。

磁量子数ml的正负号表示磁矩方向的相对位置，当ml为正数时，磁矩方向与外磁场方向相同；当ml为负数时，磁矩方向与外磁场方向相反。

磁量子数ml的大小表示磁矩在空间中的方向，而不是磁矩的大小。

例如，当l=1时，磁量子数ml的取值范围为-1、0、1。

其中，当ml=1时，磁矩方向与外磁场方向相同；当ml=0时，磁矩方向垂直于外磁场方向；当ml=-1时，磁矩方向与外磁场方向相反。

二、自旋磁量子数ms的解释自旋磁量子数ms是描述电子自旋磁矩方向的量子数，它的取值范围是-1/2 ~ +1/2。

自旋磁量子数ms的正负号表示自旋磁矩方向的相对位置，当ms为正数时，自旋磁矩方向与外磁场方向相同；当ms为负数时，自旋磁矩方向与外磁场方向相反。

自旋磁量子数ms的大小表示自旋磁矩在空间中的方向，而不是自旋磁矩的大小。

例如，当电子自旋量子数为1/2时，自旋磁量子数ms的取值范围为-1/2、+1/2。

其中，当ms =1/2时，自旋磁矩方向与外磁场方向相同；当ms=-1/2时，自旋磁矩方向与外磁场方向相反。

三、磁量子数ml和自旋磁量子数ms的应用磁量子数ml和自旋磁量子数ms的物理意义和应用在很多领域都有着重要的作用。

例如，在核磁共振成像技术中，利用外磁场对原子核的磁矩进行激发，通过测量不同磁量子数ml和自旋磁量子数ms的原子核反应信号，可以得到不同位置的图像信息。

在电子自旋共振技术中，通过测量电子自旋磁矩的方向和大小，可以得到物质的结构和性质信息。

此外，在化学反应中，通过磁量子数ml和自旋磁量子数ms的变化，可以得到反应物和产物之间的相互作用信息。

原子磁矩的计算子磁矩（AtomicMagneticMoment），是物理学中非常重要的物理量，它反映了原子本身电子轨道中电子环境对原子空间结构的影响。

原子磁矩的大小取决于原子的结构，也是化学性质的重要参量，是探究物质结构、性质的重要物理量之一。

原子磁矩的计算是一个非常重要的物理学研究课题，它包括原子磁矩的理论计算、实验测量和数值模拟计算等，因此，原子磁矩的计算的方法也有很多种。

理论计算原子磁矩是一种比较常见的原子磁矩计算方法，它包括基于程序的理论计算和量子原子磁矩理论（QMOM）。

基于程序的理论计算是用特定的计算程序来去建模原子磁矩，然后使用可用于任何原子计算的计算机程序来计算原子磁矩。

量子原子磁矩理论（QMOM）则是基于量子力学的理论来计算原子磁矩，它需要简化的量子力学模型，以找到给定原子结构的原子磁矩。

实验测量原子磁矩是另一种常见的原子磁矩计算方法，它包括Boltzmann散射测量技术，Kohn-Sham自洽场理论测量，核磁共振（NMR）测量，物理质量测量，电子双重转动差测量等。

Boltzmann散射测量技术是一种直接测量原子磁矩的方法，它基于基态原子的Boltzmann 散射来获取原子磁矩，通过同步辐射照射原子并观察由此引起的散射的强度和其他特性来测量原子磁矩。

Kohn-Sham理论测量是一种利用基于电子云的自洽场理论来计算原子磁矩的方法，结合多态微观理论，能够比较准确地测量原子磁矩。

核磁共振（NMR）测量，是用核磁共振方法来直接测量原子磁矩的方法，它利用电子轨道及其相关能级变化，测量原子磁矩。

物理质量测量是一种比较简单的原子磁矩测量方法，它利用物理质量比（PMB）去测量原子磁矩。

最后，电子双重转动差测量也是一种常用的原子磁矩测量方法，它是利用电子轨道中双重转动差来测量原子磁矩的方法。

最后，数值模拟计算也是一种常用的原子磁矩计算方法，它是利用数值模拟技术来计算原子磁矩的方法。

数值模拟技术是一种利用数值模型来模拟物理和化学系统的技术，可以用来测量原子磁矩。

ms计算功函数在物理学中，功是指力在物体上所做的功率乘以时间的积分。

在机械系统中，功函数是描述系统的能量变化的重要工具之一。

而在磁学中，我们也可以利用磁场的力来计算系统的功函数。

本文将讨论如何以ms计算磁场中的功函数。

在磁学中，我们经常会遇到磁场对磁性物质施加力的情况。

当一个磁性物质在磁场中移动时，磁场会对其施加一个力，这个力可以用磁矩和磁场的叉乘来表示。

根据力的定义，力乘以物体的位移即为做功，而功函数则是描述系统在力的作用下能量的变化。

假设一个磁矩为m的磁性物质在磁感应强度为B的磁场中移动一个位移为ds，那么磁场对其做的功可以表示为：dW = m·B·ds。

这里，dW表示磁场对磁性物质在ds位移上所做的功。

如果我们想要计算整个移动过程中的总功，可以通过对这个微小功的积分来实现。

假设磁性物质从位置A移动到位置B，整个过程中受到的磁场力是变化的，那么我们可以将整个路径分为许多微小的位移，然后对每个微小位移上的功进行积分，即可得到整个路径上的总功。

这个积分过程可以表示为：W = ∫m·B·ds。

通过计算这个积分，我们可以得到磁场对磁性物质在整个路径上所做的功函数。

这个功函数可以帮助我们了解磁场对系统能量的影响，进而研究系统的稳定性和运动规律。

除了磁场对磁性物质的功函数，我们还可以利用磁场的力来计算其他系统的功函数。

例如，当一个电流在磁场中运动时，磁场会对电流产生一个力，这个力乘以电流的位移即为磁场对电流所做的功。

通过对这个功进行积分，我们可以得到系统的总功函数，从而了解系统在磁场中的能量变化情况。

总的来说，以ms计算磁场中的功函数是研究磁学中重要的一部分。

通过计算磁场对磁性物质或电流所做的功，我们可以了解系统在磁场中的能量变化和运动规律，进而深入研究磁学中的各种现象和问题。

希望本文能够帮助读者更好地理解磁场中的功函数计算方法，进一步探索磁学的奥秘。