轴向受载铁木辛柯梁的弯曲研究
- 格式:docx
- 大小:40.82 KB
- 文档页数:7

铁木辛柯梁理论
简称为“六理”的铁木辛柯梁理论是20世纪著名哲学家和历史
学家铁木辛柯、梁公开提出的一种“系统性社会理论”,旨在实施
“自由、平等、法治”的人权概念,以及在未来实现民主社会和新型
国家的建立。
铁木辛柯梁理论的一个关键思想是,一个强大的国家可以通过保
障人权来获得发展与繁荣,因此,铁木辛柯和梁提出,在未来的社会
发展中保护人权应成为国家最重要的任务。
此外,国家只有保护宪法
中规定的权利,改善人民的物质生活和持续发展,才能实现所谓的自
权安全。
此外,铁木辛柯梁理论还详细说明了每一个国家社会发展的未来
蓝图,把成长和发展过程定位到国家对民众权力的责任上。
理论的核
心就是人的自由、平等和尊严的维护,因为,只有当国民获得自由和
平等待遇时,会有社会新进展,把人类带到自由平等的社会。
另外,铁木辛柯梁理论还认为,法治的实施是社会发展不可或缺
的前提,它使国家能够有效管理国家和社会关系,并将国家的行动和
价值观以及国家标准配备于一身。
将法治作为社会进步的神经,它能
够完美融合社会所有组成部分,形成一个完整而和谐的国家机构系统。
从上述,我们可以明确看到,“铁木辛柯梁理论”作为一个“系
统性社会理论”,它提供了一种以自由、平等和法治为核心的社会理论,确保每个国家実施人权和法治的统一主体,有利于建立一个安全
而平等的社会。
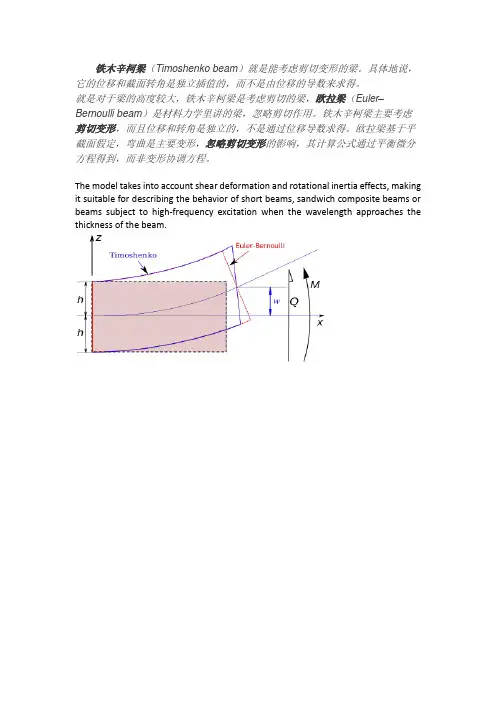
铁木辛柯梁(Timoshenko beam)就是能考虑剪切变形的梁。
具体地说,它的位移和截面转角是独立插值的,而不是由位移的导数来求得。
就是对于梁的高度较大,铁木辛柯梁是考虑剪切的梁,欧拉梁(Euler–Bernoulli beam)是材料力学里讲的梁,忽略剪切作用。
铁木辛柯梁主要考虑剪切变形,而且位移和转角是独立的,不是通过位移导数求得。
欧拉梁基于平截面假定,弯曲是主要变形,忽略剪切变形的影响,其计算公式通过平衡微分方程得到,而非变形协调方程。
The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behavior of short beams, sandwich composite beams or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam.Example of simply support beam in Timoshenko beam theoryand the free end is at . If a point load is applied to the middle of beam in the positive direction there are some equation:Therefore, from the expressions for the bending moment and shear force, we haveIntegration of the first equation, and application of the boundarycondition at , leads toThe second equation can then be written asIntegration and application of the boundary condition at givesThe axial stress is given by。

沿轴向指数分布的功能梯度Timoshenko梁的频率精确解邓昊;程伟【摘要】Based on the state space variable replacement,the transfer matrix equation of a Timoshenko beam with axially exponential distributed functional gradation was derived.The exact solution of natural frequencies of the structure with multiple boundary conditions was obtained by the transfer matrix method and compared with the available analytical solution.The results show that the relation curve between the frequency and the gradient of the material is continuous and smooth,and there is no jumping phenomenon.Meanwhile the finite element method was used to verify the results.The effects of shear stiffness and moment of inertia on the natural frequencies of the structure were analyzed by comparing the results according to different beam theories.The calculation results show that the method presented is clear in physical concept and can reduce the computational complexity and the amount of computation.%通过对状态空间变量进行变量替换,求得了沿轴向指数分布的功能梯度Timoshenko梁的状态空间传递矩阵方程.通过传递矩阵法计算了多种边界条件下结构固有频率的精确解,并与解析解进行对比.通过分析梯度参数对结构固有频率与模态振型的影响,该计算结果表明频率与材料梯度变量之间的关系曲线是连续光滑的,并未出现部分文献中的跳跃现象,并且采用有限元法该计算结果进行验证.通过对比不同梁理论的计算结果,定量的分析了剪切刚度和转动惯量对结构固有频率的影响.计算结果表明,该方法物理概念清晰,降低问题求解难度的同时可以减少计算量.【期刊名称】《振动与冲击》【年(卷),期】2017(036)006【总页数】7页(P91-96,113)【关键词】状态空间变量;传递矩阵法;固有频率;功能梯度材料;指数梯度【作者】邓昊;程伟【作者单位】北京航空航天大学航空科学与工程学院,北京100191;北京航空航天大学航空科学与工程学院,北京100191【正文语种】中文【中图分类】TV312工程中存在着大量的多相材料,为了使材料的性质从一相过渡到另一相,通常在两相材料之间使用沿轴向变化的功能梯度材料。

铁木辛柯材料力学铁木辛柯(Tm1-xCoxFe2)是一种具有潜在应用前景的磁性材料,其具有优异的磁性能和力学性能,因此在磁记录、传感器、磁存储器件等领域具有广泛的应用前景。
本文将对铁木辛柯材料的力学性能进行详细介绍和分析。
首先,铁木辛柯材料的力学性能主要包括硬度、弹性模量、屈服强度、断裂韧性等指标。
硬度是材料抵抗外界压力的能力,通常用洛氏硬度或维氏硬度来表示;弹性模量是材料在弹性阶段内的应力和应变关系的斜率,是衡量材料抗弹性变形能力的重要参数;屈服强度是材料在拉伸或压缩过程中开始发生塑性变形的应力值;断裂韧性是材料抗断裂能力的指标,通常用冲击韧性和断裂韧性来表示。
这些力学性能指标对于铁木辛柯材料的工程应用具有重要意义。
其次,铁木辛柯材料的力学性能受多种因素影响,包括晶体结构、晶粒大小、杂质含量、热处理工艺等。
晶体结构是决定材料硬度和弹性模量的重要因素,晶粒大小对材料的塑性变形和断裂韧性具有显著影响,杂质含量会影响材料的强度和韧性,热处理工艺可以改善材料的力学性能。
因此,通过合理设计材料的组织结构和优化工艺参数,可以有效提高铁木辛柯材料的力学性能。
最后,针对铁木辛柯材料的力学性能优化,可以采取一系列方法进行改进。
例如,可以通过合金化、晶粒细化、热处理强化等手段来提高材料的硬度和强度;可以通过合理设计材料的组织结构和形貌,来提高材料的断裂韧性和抗疲劳性能;还可以通过表面处理、涂层改性等手段来改善材料的耐磨性和耐蚀性能。
这些方法可以有效地提高铁木辛柯材料的力学性能,拓展其在工程领域的应用范围。
综上所述,铁木辛柯材料具有优异的磁性能和力学性能,在磁记录、传感器、磁存储器件等领域具有广泛的应用前景。
通过对其力学性能的深入研究和优化,可以进一步提高其在工程应用中的性能表现,推动其在材料科学和工程技术领域的发展和应用。
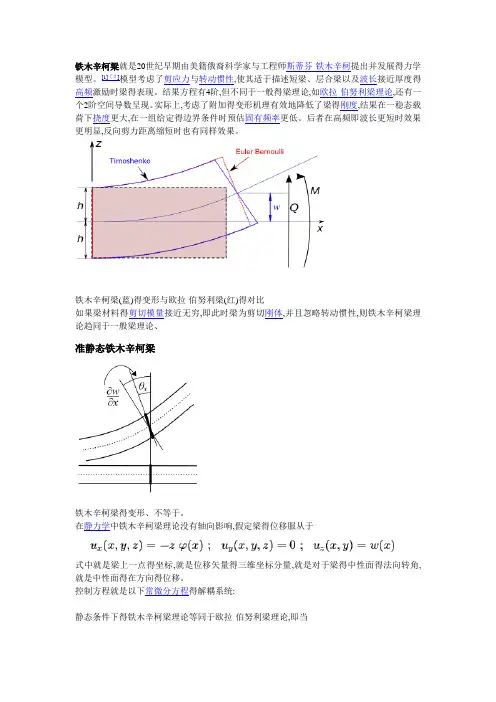
铁木辛柯梁就是20世纪早期由美籍俄裔科学家与工程师斯蒂芬·铁木辛柯提出并发展得力学模型。
[1][2]模型考虑了剪应力与转动惯性,使其适于描述短梁、层合梁以及波长接近厚度得高频激励时梁得表现。
结果方程有4阶,但不同于一般得梁理论,如欧拉-伯努利梁理论,还有一个2阶空间导数呈现。
实际上,考虑了附加得变形机理有效地降低了梁得刚度,结果在一稳态载荷下挠度更大,在一组给定得边界条件时预估固有频率更低。
后者在高频即波长更短时效果更明显,反向剪力距离缩短时也有同样效果。
铁木辛柯梁(蓝)得变形与欧拉-伯努利梁(红)得对比如果梁材料得剪切模量接近无穷,即此时梁为剪切刚体,并且忽略转动惯性,则铁木辛柯梁理论趋同于一般梁理论、准静态铁木辛柯梁铁木辛柯梁得变形、不等于。
在静力学中铁木辛柯梁理论没有轴向影响,假定梁得位移服从于式中就是梁上一点得坐标,就是位移矢量得三维坐标分量,就是对于梁得中性面得法向转角,就是中性面得在方向得位移。
控制方程就是以下常微分方程得解耦系统:静态条件下得铁木辛柯梁理论等同于欧拉-伯努利梁理论,即当可忽略上面控制方程得最后一项,得到有效得近似,式中就是梁得长度。
对于等截面均匀梁,合并以上两个方程,动态铁木辛柯梁在铁木辛柯梁理论中若不考虑轴向影响,则给出梁得位移式中就是梁内一点得坐标,就是位移矢量得三维坐标分量,就是对于梁得中性面得法向转角,就是中性面方向得位移。
从以上假设,铁木辛柯梁,考虑到振动,要用线性耦合偏微分方程描述:[3]其中因变量就是梁得平移位移与转角位移。
注意不同于欧拉-伯努利梁理论,转角位移就是另一个变量而非挠度斜率得近似。
此外,•就是梁材料得密度(而非线密度);•就是截面面积;•就是弹性模量;•就是剪切模量;•就是轴惯性矩;•,称作铁木辛柯剪切系数,由形状确定,通常矩形截面;•就是载荷分布(单位长度上得力);••这些参数不一定就是常数。
对于各向同性得线弹性均匀等截面梁,以上两个方程可合并成[4][5]轴向影响如果梁得位移由下式给出其中就是方向得附加位移,则铁木辛柯梁得控制方程成为其中,就是外加轴向力。


曲线梁桥的受力特点和分析方法摘要:由于在经济和审美上的优势,曲线梁桥被广泛应用于现代公路立交系统。
曲线梁的竖曲和扭转耦合,由于结构上的特点,相对于直梁桥而言,曲线梁的分析更为复杂。
本文对弯道梁桥的受力特点进行了介绍,并总结了分析弯道梁桥的有关理论。
关键词:曲线梁桥;弯扭耦合;支承体系;有限元法引言曲线梁桥是指主梁本身为弧形的弯曲桥梁。
由于其独特的线形,曲线梁桥突破了多种地形的限制,同时在高速公路、山地公路、城市桥梁等方面,由于其优美的曲线造型而得到了更快的发展。
曲线梁桥具有现实意义,发展前景非常看好,无论从几何角度、美学角度,还是从经济角度,都是如此。
1曲线桥梁受力特性1.1弯扭耦合作用由于受弯曲率的影响,当竖向弯曲时,曲线梁截面必然会产生扭转,而这种扭转又会导致梁的挠曲变形,这种挠曲变形被称为“弯扭耦合作用”。
对于弯道梁桥的设计,相对于直线型梁桥来说,要特别注意,因为弯道扭力耦合作用所产生的附加扭力,会使梁体结构产生较不利的受力条件,从而增加结构的挠曲变形。
值得注意的是,由于自重在使用荷载下占绝大多数,对于混凝土曲线箱梁桥而言,也会导致更明显的弯扭耦合。
由于弯道梁桥沿弯梁的线形布置支承不成直线,因此由于弯道外侧较重,导致桥体恒载重心相对于形心向外偏移。
曲线梁在自重的作用下,也会产生扭转和扭曲的变形,从而使曲线桥发生翻转,出现匍匐的现象,这就是曲线梁在自重的作用下产生的变形[1]。
1.2曲线梁内外侧受力不均匀曲线桥因弯曲和扭动耦合作用,变形大于同跨径的直线桥,且曲率半径越小、桥越宽,因此其简支曲线梁外缘的挠度比内缘大,这种变化趋势是显而易见的。
曲线梁桥体具有向外扭转的较大扭力、弯曲扭力耦合和偏载作用的可能。
扭转作用会越来越明显,曲率半径越小、跨度越大的曲线梁桥甚至会引起抗扭支座内侧支座产生空心现象,这种情况在抗扭转支座的内部支座上会产生空心现象,这种情况的发生曲线桥的支点反力与直线桥相比,有一种倾向,它的外侧会变大、内侧会变小,甚至在内侧产生负反力。


铁木辛柯梁振动偏微分方程推导过程示例文章篇一:《探索铁木辛柯梁振动偏微分方程的推导过程》哎呀,一提到铁木辛柯梁振动偏微分方程的推导过程,可能好多小伙伴就觉得头疼,觉得这是超级难的东西。
可我呀,就想试着跟大家讲讲,说不定讲着讲着大家就懂了呢!咱们先来说说铁木辛柯梁是啥。
想象一下,有一根长长的梁,就像咱们学校操场旁边的那个长长的栏杆一样。
不过这个梁可不是普通的梁哦,它有好多特性呢。
铁木辛柯梁考虑了梁的剪切变形和转动惯量,这就像是我们在玩搭积木的时候,不但要考虑积木块的形状(类似梁的形状),还要考虑它们的重量(类似转动惯量)和它们之间可能滑动变形的情况(类似剪切变形)。
那怎么开始推导这个方程呢?咱们得从最基本的东西开始想。
比如说力和变形的关系。
就好比我们拉一个弹簧,用力越大,弹簧拉得越长,这里面就有个关系对吧?对于铁木辛柯梁也一样。
我们先假设梁在振动呢。
这时候梁上的每个小部分都在动来动去。
我就想象我自己是梁上的一个小粒子,哎呀,那感觉可奇怪了。
周围的小伙伴们有的也在想象,他们就说:“你这小粒子,在梁上晃悠啥呢?”我就回答:“我这不是在感受梁振动嘛,这样才能更好地理解这个方程推导呀。
”我们要考虑梁的弯矩、剪力这些东西。
弯矩就像是一个大力士在梁的一端使劲拧梁,让梁有弯曲的趋势。
剪力呢,就像是有一把大剪刀在梁上想要把梁剪开一样。
这两个力在梁振动的时候可重要啦。
那怎么把这些力和梁的振动联系起来呢?这就需要用到一些物理的知识啦。
我们知道加速度和力是有关系的,就像我们跑步的时候,用力跑就有加速度,跑得就越来越快。
梁上的小粒子也有加速度呢。
我就跟小伙伴们讨论:“你们说这个小粒子的加速度该怎么算呀?”有个聪明的小伙伴说:“肯定和梁的变形有关系呀。
”他说得对极了。
我们假设梁在x方向上,然后我们看梁的一个小段。
这个小段的长度很小很小,就像我们铅笔尖那么小。
在这个小段上,弯矩的变化、剪力的变化都和梁的振动有关系。
我就像是个小侦探一样,在这个小段上找线索。

铁木辛柯Stephen Prokofievitch Timoshenko,СтепанПроко-фьевичТимошенко(1878~1972)美籍俄罗斯力学家。
1878年12月23日生于乌克兰的什波托夫卡,1972年5月29日卒于联邦德国。
生平铁木辛柯1901年毕业于俄国彼得堡交通道路学院。
服军役一年后,1902年回母校任实验讲师,次年到彼得堡工学院任讲师。
1903~1906年开始了他的创造性工作,每年夏天都去德国格丁根大学,在著名学者 F.克莱因、A.弗普尔和L.普朗特等人的指导下从事研究工作。
1907~1911年任基辅工学院教授。
1912~1917年在彼得格勒一些学院任教授。
1920年7月到南斯拉夫任教。
1922年受聘于美国费城振动专业公司,次年到匹兹堡的威斯汀豪斯(Westinghouse)电气公司,从事力学研究工作,设计成光弹性设备和电气火车头。
1928年,他建立了“美国机械工程师学会力学部”。
同年秋天到密歇根大学任教授,他先后组织了“每周力学讨论会”和“夏季应用力学讨论会”,后者有著名学者普朗特等人参加。
1936年起,铁木辛柯到斯坦福大学任教授达二十年之久。
1938年到苏联旅行,受到隆重接待,并写了《俄国工程教育》一书。
他在密歇根大学和斯坦福大学培养了不少研究生,其中也有中国研究生。
1965年迁居联邦德国,直至逝世。
著述铁木辛柯在应用力学方面著述甚多。
1904年他发表第一篇论文《各种强度理论》,次年发表《轴的共振现象》,首次考虑到质量分布的影响,并把瑞利方法应用于结构工程问题。
1905年,他得出开口剖面薄壁杆扭转问题中扭矩T和转角嗞的关系:T=Cφ′-Dφ″(C为抗扭刚度,D 为附加刚度)。
1906年,他解决了用板的挠度微分方程去求板受压的临界值问题。
以后又发表了关于弹性体稳定性问题的论文多篇,对船舶制造和飞机设计有指导意义。
他最早把瑞利-里兹法应用到弹性稳定问题,从而获得十年一次的“茹拉夫斯基奖”。

典型梁理论的学习对比摘要:经典梁理论也叫Bernoulli-Euler梁理论,它是建立在最基本的初等假设基础上的,因此它的结果只有当细长梁在低频时才与理论值接近,当在高阶模态或梁为短粗梁时,其结果与真实情况相差很大。
铁木辛柯在1921-1922年提出了Timoshenko梁理论,这个理论同时考虑了梁的弯曲变形引起的转动惯量和梁的剪切变形,这个理论大大地改善了以往的梁的动力学理论。
它使得梁在模态阶数不是很高时,在即使不是细长的情况下,它的动力参数的精度也得到了很好的改善,因此Timoshenko梁理论也被广泛的运用到很多实际工程上。
本文介绍了贝努里-欧拉梁和铁木辛柯梁,讨论了他们的基本假设,推导了两者的运动方程.。
分析了贝努里-欧拉梁和铁木辛柯梁的不同之处,并通过具体算例,计算了细长梁和短梁分别用贝努里-欧拉梁和铁木辛柯梁模拟的挠度,对两者的不同之处进行验证[1]。
关键词:贝努里-欧拉梁;铁木辛柯梁;基本假设Comparative study on theories of typical beamsAbstract:Classical beam theory is also called Bernoulli-Euler beam theory, it is built on the basic assumption based on the primary, so it's only when the results of slender beam at low frequencies close to the theoretical value, and when at the higher modes or beam is shorter rough beams, its results with the real situation vary greatly. Timoshenko put forward the Timoshenko beam theory in 1921-1922, taking into account the theory of inertia caused by the beam bending and shear deformation of the beam, this theory has greatly improved the previous kinetic theory of the beam. It makes the accuracy of dynamic parameters of the beam, which not slender or at the number of modes is not very high , has also been a good improvement, so Timoshenko beam theory has been widely applied to many practical engineering. Introduce the basic assumptions of Bernoulli-Euler beam and Timoshenko beam, motion equation of the two beams is derived. Analyze the difference of Bernoulli-Euler beam and Timoshenko beam, through an example, calculate the deflection of the slender beam and short beam with the Bernoulli-Euler beam and the Timoshenko beam, verify the difference between the two beams.Key words: Bernoulli-Euler beam; Timoshenko beam; basic assumptions1引言现今应用中梁理论主要有:(1)精确的弹性方程;(2)Euler-Bernoulli梁理论;(3)Timoshenko梁理论。
铁木辛柯梁轴向应变
铁木辛柯梁轴向应变是指铁木辛柯梁在轴向受力下产生的变形情况。
铁木辛柯梁是一种传统的建筑材料,由铁木辛柯这种特殊的木材制成,具有较高的强度和耐久性。
在建筑结构中,铁木辛柯梁常常承受着巨大的轴向力,因此轴向应变的研究对于确保结构的稳定性和安全性具有重要意义。
铁木辛柯梁轴向应变的大小与轴向受力的大小有直接关系。
当外力作用于铁木辛柯梁上时,梁体会发生弯曲和拉伸等变形。
这种变形会导致梁体内部产生轴向应变,即单位长度的变形量。
轴向应变是一个标量,用来描述梁体在轴向方向上的变形程度。
铁木辛柯梁轴向应变的计算通常采用应变-位移关系来进行。
应变与位移之间存在着一定的比例关系,可以通过测量位移来计算出轴向应变。
在实际工程中,我们可以使用应变计等专门的仪器来测量轴向应变,从而评估结构的变形情况。
铁木辛柯梁轴向应变的大小对结构的安全性和稳定性有着重要影响。
如果轴向应变过大,可能会导致铁木辛柯梁的破坏或失效,从而引发严重的安全事故。
因此,在设计和施工过程中,需要合理控制轴向力的大小,以保证铁木辛柯梁的正常使用和寿命。
铁木辛柯梁轴向应变是一个重要的工程问题,对于确保结构的安全性和稳定性至关重要。
通过合理的设计和施工,可以有效控制轴向
应变的大小,从而保证铁木辛柯梁的正常使用和寿命。
这对于建筑结构的可靠性和稳定性具有重要意义,也是工程师们在实践中需要重视的问题。
力学大师S.P.铁木辛柯郭日修【摘要】S.P.铁木辛柯,20世纪活跃在工程力学领域约60年,培养了几代优秀的工程师和力学家,取得了丰硕的研究成果,推动了工程力学的进展,人们尊之为力学大师.本文从学术生涯、研究成果、学术著作、学术贡献几方面简介铁木辛柯.【期刊名称】《力学与实践》【年(卷),期】2016(038)004【总页数】3页(P462-464)【关键词】力学史;工程力学;铁木辛柯【作者】郭日修【作者单位】海军工程大学舰船工程系,武汉 430033【正文语种】中文【中图分类】O3铁木辛柯(S.P.Timoshenko)1878年12月出生于乌克兰.1896年9月进入“交通道路工程学院”,这是俄罗斯铁路系统唯一培养工程师的高等学校,铁木辛柯向往成为一名从事铁路工程实践的工程师.1900年暑假他赴巴黎参加国际博览会,发现很多欧洲国家如德国、比利时、法国等在文化和工业发展方面都胜过俄罗斯.他认识到,要使俄罗斯进步,必须开展创新性的学术工作,推动科学技术发展.因此,他决定大学毕业后留在彼得堡的高等学校工作,这有利于他从事学术工作.1901年,铁木辛柯在交通道路工程学院毕业,第二年回到学院任机械实验室工程师,从事材料试验工作,同时在学院学习一些高级的数学、力学课程.1903年春,他获得彼得堡工学院讲师席位,配合教授的讲课,给学生上习题课.他为此花费大量时间准备习题和作业.这些习题后来大部分纳入他编著的应用力学和材料力学教科书.这期间,他还阅读了A.E.H.乐甫的《弹性理论》和瑞利的《声学理论》两本经典著作,这对他此后的学术工作有重要影响,他还通过这两本书的阅读,学习、掌握了英语.1904年夏,他获得机会去欧洲,大部分时间在慕尼黑工学院,在著名力学家 A.弗普尔指导下从事强度理论的实验研究.这年秋,铁木辛柯回到彼得堡,他以极大的热情和创意,写出了他的第一篇论文《各种强度理论》,并发表.1905年 4月—1905年秋和 1906年夏,铁木辛柯先后两次到哥廷根大学应用数学与应用力学研究所游学,在F.克菜因和L.普朗特指导下,从事弹性稳定性问题的研究,并选学一些高级数学课程.哥廷根大学应用数学与应用力学研究所是在数学家克莱因倡议下于1904—1905年组建,聘请普朗特主持,其目的在于力促数学、力学和其他基础学科在工程技术中的应用.哥廷根的学风深深影响了铁木辛柯,使他此后致力于应用数学和力学理论解决工程技术问题.1906年1月,铁木辛柯任基辅工学院材料力学课程教授.他一反此前大学讲授材料力学的方法,从最简单的问题——杆的拉伸/压缩讲起,然后讲三维应力状态,这使他的讲课易于理解,深受学生欢迎.1908年秋,铁木辛柯给工程师讲授“弹性理论”,当时,“弹性理论”是理论物理的一部分,只对理科学生开课,铁木辛柯考虑到工程师的兴趣在于应用弹性理论解决工程问题,因此,他讲课着重阐释课程内容的物理意义及其应用,并以一些光弹性实验来验证理论,讲课深受工程师欢迎.在基辅工学院的授课,显示了铁木辛柯讲课的才华.1911年秋,铁木辛柯抵彼得堡.有一段时间,他曾任俄罗斯海军顾问工程师,他有关板的弯曲和稳定性的研究成果,在军舰结构设计中得到应用.1913年,铁木辛柯获交通道路学院教授席位.这一年,他出版了两卷本的《弹性理论》,并出版了《弹性系统的稳定性》文集.1920年,铁木辛柯离开俄罗斯,3月抵达南斯拉夫,在新成立的萨格勒布工学院任力学教授.1922年,铁木辛柯受聘于费城“振动专业公司”. 1923年任职于匹兹堡威斯汀豪斯电气公司力学部,从事力学研究工作.1926年他受公司派遣到欧洲考察欧洲一些大公司的研究工作,并代表美国参加在瑞士苏黎士举行的“国际应用力学大会”,在会上宣读了关于《平板开孔和填角的应力集中》以及《铁路钢轨的应力》论文,当时美国只有三人参加这个国际会议.1927年他在G.M.伊登(威斯汀豪斯公司首席机械工程师)的支持下,组织成立美国机械工程师学会应用力学学部,后来,这个学部是该学会中最大、最活跃的学部,出版了力学领域具领先地位的期刊《应用力学学报》.1927年,他应密歇根大学邀请,到该大学研究生院任力学教授,指导研究生.他开出一系列应用力学方面的研究生课程,吸引了大批相关专业研究生来听课.他讲课深入浅出,解析精辟,清晰易懂,即使很艰深的理论,经他讲解,学生也感到易于接受.他作为俄罗斯人却用英语讲课,发音正确,语言流畅,学生、尤其是外国留学生听起来,比很多美国教授用“美国话”(美式英语)讲课更容易听懂.由于铁木辛柯的声誉,密歇根大学的应用力学研究生数量增加很快,尤其是博士生,铁木辛柯的负担很重.尽管如此,每一个博士生都能得到他的耐心指导,博士生鲜有攻读学位失败者.他组织了每周一次的“应用力学讨论会”,每年夏天还组织“夏季应用力学讨论会”,吸引了国际上很多著名力学家参加,如L.普朗特,R.V.苏斯威尔,H.M.威斯特嘉德等等,讨论会成为应用力学界的盛事.铁木辛柯在密歇根执教九年,是他著作多产的一段时间,出版了《工程振动》等7本著作.1934—1935年冬,铁木辛柯曾应邀到柏克莱大学作系列讲课.1936年秋,铁木辛柯应聘到斯坦福大学任工程力学教授,主持一个授“工程师”学位的二年制研究生专业,研究生人数很多,铁木辛柯对指导大批“工程师”学位研究生甚感兴趣.在斯坦福大学,铁木辛柯还主动帮助改进本科力学课程的教学,使之更具活力,他甚至有时还亲自上讲台讲一节静力学或材料力学课,这对教授本人和听课的学生都是一种享受,因为铁木辛柯讲授基础力学课,更显示其讲课艺术的高超.铁木辛柯虽于1944年退休,但他仍作为工程力学“荣誉教授”继续在斯坦福大学执教,并积极参予斯坦福大学于1949年组建的“工程力学学部”的活动;继续修订、出版他此前出版的著作,1953年他出版了两本新著.为表彰铁木辛柯对工程力学的贡献,斯坦福大学建立了一个以他个人命名的“铁木辛柯工程力学实验室”,内有新添置的实验设施,并作为“工程力学学部”教师和研究生聚会、开展“应用力学讨论会”和学术活动的场所.1965年铁木辛柯迁居联邦德国,直到1972年逝世.铁木辛柯在工程力学领域辛勤耕耘约60年,取得了多方面的研究成果,推动了工程力学的发展.其研究成果主要有[1]:在A.弗普尔指导下,开展强度理论研究,1904年发表他的第一篇论文《各种强度理论》;在轴的扭振问题中,首次考虑质量分布的影响,发表论文《轴的扭转振动》(1905),并把瑞利方法应用于结构工程问题;研究了工字梁的侧向屈曲,发表论文《梁的侧向屈曲》(1905);是成功研究开口薄壁等截面直杆扭转的第一人,发现扭矩T和扭转角Φ之间的关系T=Cφ′-Dφ′′[2],式中 C为抗扭刚度,D为附加刚度.1905年—1906年发表相关论文.用板的弯曲微分方程求得受压板的临界载荷,发表论文《受压矩形板的稳定性》(1907).此后又发表多篇有关稳定性的论文,对船舶和飞机结构设计有重要指导意义.最早应用瑞里--利兹方法求解弹性系统稳定性问题,发表论文《弹性系统稳定性问题的近似求解方法》(1910),这项研究成果于1911年获茹拉夫斯基奖,此奖项十年颁发一次.成功地应用能量原理求解梁和板的弯曲问题和梁的受迫振动问题.解决了半圆剖面梁承受弯曲的剪力中心,对称剖面悬臂梁自由端承受横载荷的剪应力分布等问题.建立了考虑旋转惯性和剪力影响的梁横向振动微分方程(1912),这种计算模型被称为“铁木辛柯梁”.解决了平板上圆孔周围的应力集中问题,发表论文《平板开圆孔的应力集中》(1907),后又研究解决了采用环形加强的圆孔周围的应力分布问题,发表论文《关于平板开圆孔的应力》(1924).研究桥梁振动问题,发表论文《桥梁振动》(1927—1928).研究悬索桥的应力分析问题,先后发表论文《悬索桥刚度》(1930)和《悬索桥理论》(1943).铁木辛柯可能是20世纪工程力学领域著作最多的力学家,大部分著作是教科书,都是基于他授课的讲义编著的.铁木辛柯在俄罗斯出版的书籍主要有[1]:《材料力学》(1911),《弹性理论》两卷本(1913),这两本书是他此后在美国出版的《弹性理论》、《弹性稳定性理论》、《板壳理论》的蓝本.此外,还出版了一本文集《弹性系统的稳定性——铁木辛柯教授文集》(1913);俄罗斯力学家И.Г.布勃诺夫为这本书写了《书评》.[3]1922年以后,铁木辛柯在美国出版了大量英文著作,按出书的时间先后列出如下.《应用弹性力学》(1925),与J.M.莱塞尔合作;《工程振动问题》(1928);《材料力学》卷I(初等),卷II(高等)(1930);《弹性理论》(1933);《弹性稳定性理论》(1936);《材料力学》(1936),与G.H.马克柯乐夫合作;《工程力学》(1936),与D.H.杨合作;《板壳理论》(1940);《结构理论》(1945),与杨合作;《高等动力学》(1948),与杨合作;《材料力学史》(1953).1953年,由E.L.爱律克生等人编辑出版了《铁木辛柯论文集》,编者在“前言”中指出:“此书实际上涵盖了铁木辛柯全部重要的科学论文”,书中并附有铁木辛柯俄文写作的论文目录.铁木辛柯的英文著作,大部份是教科书,《弹性理论》、《弹性稳定性理论》,《板壳理论》等几本书是专著,列入美国“工程师学会”专著集,也被广泛采用作为研究生教学用书.铁木辛柯在工程力学领域辛勤耕耘约60年,致力于将数学、力学理论应用于工程技术,促使工程技术现代化.他一生主要在大学执教,讲授基础力学课程(本科工程力学课程)和高等工程力学课程(研究生力学课程),指导研究生.他培养了几代优秀工程师和工程力学学者.他在授课的基础上,编写了大量工程力学教科书和专著,这些著作被高等工程院校广泛采用作教材,被广大工程师们学习参考,惠及的学子和工程师难以胜数.铁木辛柯在工程力学领域的贡献,第一位的,是他培养建立了一支庞大的工程力学人才队伍,他们或工作在工程实践第一线,或工作在工程力学教学、研究领域.在铁木辛柯引领下,他们共同推动工程力学发展,促使工程技术现代化.铁木辛柯致力于应用数学力学理论解决工程实践中的技术难题,他活跃在工程力学领域的那一段时间,正是20世纪飞机、钢船等工程结构迅速发展的几十年.他的研究工作,都有一定的工程背景,他的研究成果,都有一定的工程应用.如“弹性稳定性理论”、“板壳理论”、“工程振动理论”等方面的研究成果,与飞机、钢船等“薄壁结构”设计关联密切,有力地推动了20世纪飞机、钢船等工程结构设计的进展,铁木辛柯是20世纪在工程力学领域研究成果最丰硕的力学家.铁木辛柯对中国工程力学的发展,也作出了重要贡献,主要是在人才培养方面.在铁木辛柯的众多研究生中,有不少中国留学生,他们在铁木辛柯指导下攻读研究生学位,在治学和为人方面,他们深受导师的影响,他们学成后回国,大多选择在高校执教并从事研究工作.他们以很高的学术造诣和对教学工作的热情而深受学生欢迎,很多人成为名师,为国家培养了大批工程力学领域的人才.如王俊奎教授,在铁木辛柯指导下于 1940年取得博士学位,回国后在大学任教,他在国内首先开设“板壳理论”课,并将铁木辛柯的《板壳理论》一书翻译成中文出版;自1952年起,他在北京航空航天大学任教授,是我国第一批(1981年)为数不多的固体力学博士生导师之一.另一方面,铁木辛柯的著作曾在中国被广泛采用作为教材或重要参考书,如《工程力学》、《材料力学》(初等)在20世纪40年代至50年代初被我国高校工科广泛采用作为本科的教科书,《弹性理论》、《弹性稳定性理论》、《板壳理论》在中国被广泛采用作为相关专业研究生的教学用书,并被工程师广泛参考.出人才、出成果,20世纪的工程力学(固体力学)家无出其右者,人们尊铁木辛柯为力学大师.【相关文献】1 Young DH.Biographical Sketch//Eriksen EL.Collected Papers—S.P.Timoshenko.New York:McGraw-Hill,19532 王俊奎.铁木辛柯S.P.中国大百科全书总编辑委员会//中国大百科全书:力学卷.北京:中国大百科全书出版社,1985.4713 郭日修.布勃诺夫--伽辽金方法溯源.//王希诚等:科学殿堂的力学之光,大连:大连理工大学出版社,2011.81-84。
基于铁木辛柯梁理论的工字梁剪切变形计算方法研究辛育霞,王勇,付佳豪,倪天琦,齐贺阳(航空工业北京长城计量测试技术研究所,北京 100095)摘要:飞机机翼通常采用工字梁作为支撑结构,然而由于工字梁的几何参数改变,理论计算会受到影响,梁理论的选择会直接影响计算结果。
目前,现有的工字梁挠度计算主要基于欧拉-伯努利梁理论,未充分考虑梁弯曲时存在的剪切变形。
因此,本文提出了一种基于铁木辛柯梁理论的考虑剪切作用的工字梁计算方法,用于针对受集中力影响的工字梁进行计算。
通过表征剪切变形对梁变形的影响,获得了剪切变形对梁的作用规律,并解释了剪切变形在梁中的变形机制。
研究表明,当工字悬臂梁靠近固定端一定范围内以及梁的跨高比小于5时,计算时应考虑剪切变形的影响。
该计算方法得出的内力计算理论结果与仿真及电测法结果基本一致,可以应用于实际工程计算中。
关键词:工字梁;剪切变形;铁木辛柯梁理论;电测法中图分类号:TB9;V224 文献标志码:A 文章编号:1674-5795(2023)05-0031-08Research on calculation method of shear deformation of I⁃beam based onTimoshenko beam theoryXIN Yuxia, WANG Yong, FU Jiahao, NI Tianqi, QI Heyang(Changcheng Institute of Metrology & Measurement, Beijing 100095, China)Abstract: Aircraft wings usually use I⁃beams as support structures. However, due to changes of the geometric param⁃eters of the I⁃beams, theoretical calculations will be affected, and the choice of beam theory will directly affect the calcula⁃tion results. At present, the existing deflection calculation of I⁃beams is mainly based on the Euler Bernoulli beam theory, without fully considering the shear deformation during beam bending. Therefore, this article proposes a calculation method for I⁃beams considering shear effects based on the Timoshenko beam theory, which is used to calculate I⁃beams af⁃fected by concentrated forces. By characterizing the effect of shear deformation on beam deformation, the law of action of shear deformation on the beam was obtained, and the deformation mechanism of shear deformation in the beam was ex⁃plained. Research has shown that when the I⁃shaped cantilever beam is within a certain range near the fixed end and the span to height ratio of the beam is less than 5, the influence of shear deformation should be considered in the calculation. The theoretical results of internal force calculation obtained by this method are basically consistent with the results of simulation and electrical measurement method, and can be applied to practical engineering calculation.Key words: I⁃beam; shear deformation; Timoshenko beam theory; electrometric methoddoi:10.11823/j.issn.1674-5795.2023.05.05收稿日期:2023-03-17;修回日期:2023-04-12基金项目:航空创新基金项目(ZC02102280)引用格式:辛育霞,王勇,付佳豪,等.基于铁木辛柯梁理论的工字梁剪切变形计算方法研究[J].计测技术,2023,43(5):31-38.Citation:XIN Y X,WANG Y,FU J H,et al.Research on calculation method of shear deformation of I⁃beam based on Timoshenko beam theory[J].Metrology & Measurement Technology,2023,43(5):31-38.0 引言工字梁是一种空腹式杆件,这种截面设计主要通过离形心最远的翼缘抵抗弯曲,利用腹板抵抗剪切,具有强度高、重量轻的优点,是飞机机翼的理想支撑结构[1],针对工字梁的研究是研究机翼变形的基础。
铁木辛柯《弹性理论》中的一个问题
蒋平
【期刊名称】《西南石油大学学报》
【年(卷),期】1992(000)003
【摘要】铁木辛柯、古地尔所著《弹性理论》(1)是一本权威性著作,在我国及世界上均有较大影响。
但是该书中有一处明显的错误,即认为在作为空间问题处理的梁的纯弯曲问题中,材料力学的平截面假设仍然成立。
这个论断,在该书1960年英文第三版中仍未改正。
在国内外一些弹性力学书籍中,也存在着同样的问题。
因此,在这里指出这一问
【总页数】2页(P127-128)
【作者】蒋平
【作者单位】西南石油学院石油机械系
【正文语种】中文
【中图分类】TE-55
【相关文献】
1.弹性支持的无限铁木辛柯梁对移动振动质量的响应 [J], 翁雪涛;胡安
2.黏弹性胶合铁木辛柯梁的力学性能分析 [J], 王林;吴鹏;周叮;张建东
3.铁木辛柯弹性稳定理论在深水桩自由站立分析中的应用 [J], 侯涛;张孝卫;刘洪涛;袁玉杰
4.基于铁木辛柯梁理论解的装配式预应力锚索框架梁受力特征分析 [J], 魏少伟;包
秀明;姚建平;吕宋
5.基于铁木辛柯梁理论建立高层简化分析模型的实用方法 [J], 鹿磊
因版权原因,仅展示原文概要,查看原文内容请购买。
铁木辛柯材料力学铁木辛柯是一种具有优异性能的材料,广泛应用于航空航天、汽车制造、建筑结构等领域。
在材料力学中,铁木辛柯材料的特性和性能对于工程设计和应用具有重要意义。
本文将就铁木辛柯材料的力学性能进行介绍和分析。
首先,铁木辛柯材料的强度和硬度是其最突出的特点之一。
由于其具有高强度和硬度,铁木辛柯材料可以承受较大的载荷和压力,因此在工程设计中具有重要的应用价值。
同时,铁木辛柯材料的耐磨性和耐腐蚀性也非常优秀,能够在恶劣环境下保持稳定的性能,这使得其在航空航天和汽车制造领域得到广泛应用。
其次,铁木辛柯材料的弹性模量和塑性变形特性也是工程设计中需要考虑的重要因素。
弹性模量是衡量材料抵抗变形能力的指标,铁木辛柯材料具有较高的弹性模量,能够在受力后恢复原状,这对于工程结构的稳定性和耐久性具有重要意义。
而在塑性变形方面,铁木辛柯材料的塑性变形能力较强,能够在一定范围内发生塑性变形而不破裂,这对于工程结构的安全性和可靠性具有重要意义。
此外,铁木辛柯材料的断裂韧性和疲劳性能也是工程设计中需要重点考虑的因素。
断裂韧性是材料抵抗断裂的能力,铁木辛柯材料具有较高的断裂韧性,能够在受到冲击载荷时不易发生断裂,这对于工程结构的安全性具有重要意义。
而在疲劳性能方面,铁木辛柯材料能够在长期交变载荷作用下保持稳定的性能,不易发生疲劳断裂,这对于工程结构的使用寿命具有重要意义。
综上所述,铁木辛柯材料具有优异的力学性能,对于工程设计和应用具有重要意义。
在实际工程中,需要充分考虑铁木辛柯材料的各项力学性能,合理设计和选择材料,以确保工程结构的稳定性、安全性和可靠性。
希望本文的介绍和分析能够对铁木辛柯材料的力学性能有所了解,并为工程设计和应用提供参考和指导。
轴向受载铁木辛柯梁的弯曲研究WANG Xuhong;LI Xiangyu【摘要】轴向受载的铁木辛柯梁的弯曲问题.在新近提出的一种铁木辛柯梁模型中,引入了一个反映变形过程中轴力方向的跃迁系数,基于此模型,解析地获得了多种边界条件下梁挠度的封闭形式的表达式.此外,采用数值计算验证当前结果的正确性,并探讨了跃迁系数对梁弯曲行为的影响.【期刊名称】《成都大学学报(自然科学版)》【年(卷),期】2019(038)002【总页数】4页(P187-189,205)【关键词】跃迁系数;铁木辛柯梁;弯曲行为【作者】WANG Xuhong;LI Xiangyu【作者单位】;【正文语种】中文【中图分类】TB123;TU3110 引言轴向受载的梁由于其能够提升抗拉和抗弯强度而被广泛应用于工程建设中.例如,在宏观尺度上,轴向受载梁经常被用在桥梁、铁路和隧道等基础设施建设和航空工业中的关键部位[1-2];而在微纳米尺度,轴向受到压力的纳米线常被埋在PDMS 基体中构成结构的一部分[3-5].因此,轴向受载的梁的变形行为是一个很重要的研究课题.例如,Simsek等[6-7]基于铁木辛柯梁理论,采用修正的偶应力理论和高阶梁理论研究了功能梯度纳米梁的弯曲问题;Ansari等[8]为了修正铁木辛柯梁理论,采用应力梯度弹性理论考察了横向剪切变形的影响;Li等[9]采用拉格朗日运动关系研究了考虑摩擦影响的棱柱铁木辛柯梁的大变形问题;Tuna等[10]基于初始积分模型,研究了欧拉—伯努利梁和铁木辛柯梁的静力弯曲行为并得到了解析解.事实上,对于铁木辛柯梁轴向力在变形时的方向有两种不同的假设:一种认为,轴力的方向沿着中性轴的方向[11-13],另一种认为,轴力的方向垂直于变形后的横截面[14-15].对此,Chen等[16]通过引入跃迁系数建立了一个统一的铁木辛柯梁模型,并研究了梁的强迫振动.但随着跃迁系数的引入,有许多典型的问题需要解决,比如新近提出的梁模型的静态响应问题.对此,本研究主要分析了跃迁系数对轴向受载铁木辛柯梁弯曲行为的影响:首先,推导出了控制方程,再通过拉普拉斯变换对其进行处理,得到了方程的解析解;其次,展开数值计算验证当前解的正确性并考察了跃迁系数对铁木辛柯梁弯曲行为的影响.1 问题描述和解决1.1 问题描述在笛卡尔坐标系Oxy中,考虑一个长为L、高为h,在轴向和横向分别受力为T 和P的梁(见图2).梁的材料参数为:杨氏模量为E,剪切模量为G,密度为ρ,横截面面积为A,惯性矩为I.图1 铁木辛柯梁模型示意图由文献[16]可得轴向受载铁木辛柯梁的控制方程为,EIφ″+(κGA+αT)(w′-φ)=0(κGA+αT)(w″-φ′)-Tw″=P(1)式中,w和φ分别表示挠度和转角,α表示轴力方向的跃迁系数.在本研究中,α在0到1之间变化,当α=0时,对应轴力的方向沿着中性轴的方向,当α=1时,对应轴力的方向垂直于变形后的横截面,压力(或拉力)被假定为正(或负).将(1)式表述为挠度的方程,可以得到,w″″+a2w″=f(x)(2)其中,(3)a1=κGA-(1-α)T,a2=κGA+αT(4)式中,κ为剪切修正系数.假定在梁上任意点x0处受到一个大小为P的集中力,则方程为,(5)式中,δ()为狄拉克函数.式(5)的解是数学上的格林函数解,对于解决很多相关的问题十分重要.例如,在梁上施加一个分布力P(x),可通过叠加原理得到相应的挠度,W(x)=P(x0)w(x;x0)dx0(6)1.2 拉普拉斯变换根据已经给出的控制方程,对式(5)关于坐标x进行拉普拉斯变换,可以得到,(7)式中,w(0)、w′(0)、w″(0)、w‴(0)是待定常数,s是拉普拉斯复数.对式(7)进行拉普拉斯逆变换可以得到,w(x;x0)=H(x-x0)Ψ1(x-x0)+w(0)Ψ2(x)+w′(0)Ψ3(x)+w″(0)Ψ4(x)+w‴(0)Ψ5(x)(8)式中,H(x)是单位阶跃函数.方程Ψi(x)的定义如下,(9)通过拉普拉斯变换可得到式(5)的通解,而式(8)中的待定常数可以通过边界条件进行确定.1.3 待定常数的确定通过边界条件可确定相应条件下显式表达式所需的待定常数.在确定这些常数之前,先得到转角φ、弯矩M和剪力V确切的表达式如下所示,(10)由式(8)可得,(11)本研究中考虑4种常见的边界条件,即简支梁、固支梁、悬臂梁、一端简支一段固支的梁.其中,对于简支梁,w(0)=0,M(0)=0,w(L)=0,m(L)=0;对于固支—简支,w(0)=0,φ(0)=0,w(L)=0,M(L)=0;对于固支梁,w(0)=0,φ(0)=0,w(L)=0,φ(L)=0;对于悬臂梁,w(0)=0,φ(0)=0,M(L)=0,V(L)=0.如此,可以通过边界条件确定相应的待定常数,将其代回(8)式中,便可以得到多种边界条件下挠度的显式表达式.2 数值分析考虑两种类型的力,即集中力和分布力,将其施加在一个特定参数的铁木辛柯梁上.材料具体参数如下,E=7.0×1010N/m2,G=2.61×1010 N/m2,L=0.5m,κ=0.87,ρ=2 778 kg/m3,横截面是高为h的正方形.为了方便计算,引入以下的无量纲参数,式中,nH和nC为无量纲化的轴向压力,η表示高跨比.简支梁和固支梁的临界屈曲力分别是,(12)2.1 解的有效性为了验证当前结果的有效性,本研究对解析解和有限元(FEM)结果进行对比,考虑以下两种情形:其一,在梁的中点处施加单位大小的集中力;其二,在梁表面施加集度为单位力的分布力.这两种情形下,梁的高跨比均为0.2,且都在轴向受到一个单位大小的力.在数值模拟计算中,采用商业有限元软件ANSYS 15.0,并用BEAM 188梁单元划分网格.在模拟中,设有1 000个单元和2 002个节点.无量纲化挠度随无量纲化坐标x/L变化的曲线如图2所示,其中是简支梁在梁中点处受到集中力P时的最大挠度,为PL3/(48EI).由图2可以看出,解析结果和有限元结果较为吻合,这在一定程度上证明了结果的有效性.2.2 跃迁系数对挠度的影响在梁的中点处施加一个单位大小的集中力,并在轴向施加不同等级的轴力,来观察梁挠度的变化.图2 高跨比为0.2,简支梁和固支梁无量纲化挠度随无量纲化坐标x/L的变化为了量化跃迁系数α对静挠度的影响,定义相对误差为,式中,和分别表示当α=0和α=1时发生在简支梁和固支梁中点处的最大挠度.为了符合工程中梁的实际情况,高跨比的取值不大于0.3.相对误差随高跨比和轴向压力的变化趋势如图3所示.图3 简支梁和固支梁相对误差随高跨比和轴向压力的变化由图3可以看出,相对误差RDdef随着高跨比和轴向压力的增大而增大.当轴力为高跨比为0.3时,α对梁挠度的影响接近50%,表明跃迁系数α对梁挠度具有重要的影响.3 结论本研究基于统一铁木辛柯梁模型分析了梁的弯曲问题,并通过拉普拉斯变换得到了多种边界条件下梁挠度和转角的解析表达式.首先,通过理论推导和数值分析验证了结果的有效性.其次,相比简支梁,跃迁系数α对固支梁的影响随着高跨比的增大而增大,当轴力为高跨比为0.3时,跃迁系数对梁挠度的影响接近50%,此证明了跃迁系数对工程实际的重要性.参考文献:【相关文献】[1]Lin T Y,Burns N H.Design of prestressed concrete structures[M].New York,NY,USA:John Wiley Sons Inc,1981.[2]Aslam M,Shafigh P,Jumaat M Z,et al.Strengthening of RC beams using prestressed fiber reinforced polymers:A review[J].Constr Build Mater,2015,82(1):235-256.[3]Ahn J H,Je J H.Stretchable electronics:Materials,architectures and integrations[J].J PhysD Appl Phys,2012,45(10):103001.[4]Xu F,Lu W,Zhu Y.Controlled 3D buckling of silicon nanowires for stretchable electronics[J].ACS Nano,2010,5(1):672-678.[5]Ryu S Y,Xiao J,Park W I,et teral buckling mechanics in silicon nanowires on elastomeric substrates[J].Nano Lett,2009,9(9):3214-3219.[6]Simsek M,Yurtcu H H.Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory[J].Compos Struct,2013,97(1):378-386.[7]Simsek M,Reddy J N.Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory[J].Int J Eng Sci,2013,64(1):37-53.[8]Ansari R,Gholami R,Shojaei MF,et al.Size-dependent bending,buckling and free vibration of functionally graded Timoshenko microbeams based on the most general strain gradient theory[J].Compos Struct,2013,100(1):385-397.[9]Li D K,Li X rge deflection and rotation of Timoshenko beams with frictional end supports under three-point bending[J].CR Mécan,2016,344(8):556-568.[10]Tuna M,Kirca M.Exact solution of Eringen’s nonlocal integral model for bending of Euler-Bernoulli and Timoshenko beams[J].Int J Eng Sci,2016,105(1):80-92.[11]Viola E,Ricci P,Aliabadi M H.Free vibration analysis of axially loaded cracked Timoshenko beam structures using the dynamics tiffness method[J].J Sound Vib,2007,304(1/2):124-53.[12]Mei C,Karpenko Y,Moody S,et al.Analytical approach to free and forced vibrations of axially loaded cracked Timoshenko beams[J].J Sound Vib,2006,291(3/5):1041-1060. [13] P.Forced transverse vibration of rayleigh and Timoshenko double-beam system with effect of compressive axial load[J].Int J Mech Sci,2012,60(1):59-71.[14]Saito H,Otomi K.Vibration and stability of elastically supported beams carrying an attached mass under axial and tangential loads[J].J Sound Vib,1979,62(2):257-266. [15]Kounadis A,Katsikadelis J T.Shear and ro tatory inertia effect on Beck’s column[J].J Sound Vib,1976,49(2):171-178.[16]Chen T,Su G Y,Shen Y S,et al.Unified Green’s functions of forced vibration of axially loaded Timoshenko beam:Transition parameter[J].Int J Mech Sci,2016,113(1):211-220.。