§5 从力做的功到向量的数量积(一)
- 格式:ppt
- 大小:689.50 KB
- 文档页数:10
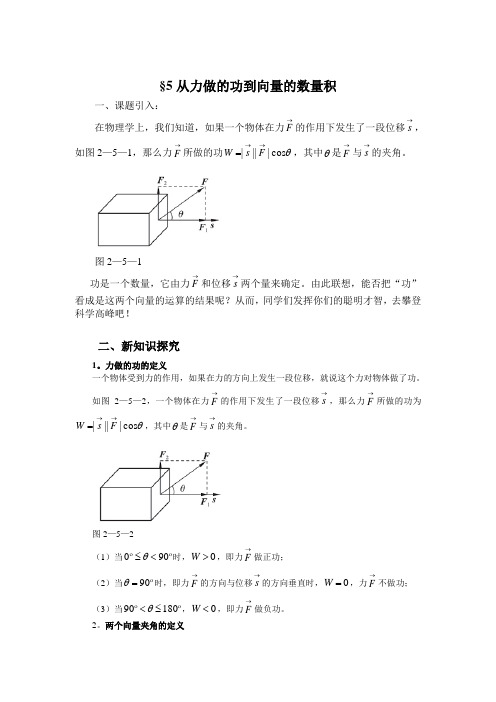
§5从力做的功到向量的数量积一、课题引入:在物理学上,我们知道,如果一个物体在力→F 的作用下发生了一段位移→s ,如图2—5—1,那么力→F 所做的功θcos ||||→→=F s W ,其中θ是→F 与→s 的夹角。
图2—5—1功是一个数量,它由力→F 和位移→s 两个量来确定。
由此联想,能否把“功”看成是这两个向量的运算的结果呢?从而,同学们发挥你们的聪明才智,去攀登科学高峰吧!二、新知识探究1。
力做的功的定义一个物体受到力的作用,如果在力的方向上发生一段位移,就说这个力对物体做了功。
如图2—5—2,一个物体在力→F 的作用下发生了一段位移→s ,那么力→F 所做的功为θcos ||||→→=F s W ,其中θ是→F 与→s 的夹角。
图2—5—2(1)当900<≤θ时,0>W ,即力→F 做正功;(2)当90=θ时,即力→F 的方向与位移→s 的方向垂直时,0=W ,力→F 不做功; (3)当18090≤<θ,0<W ,即力→F 做负功。
2。
两个向量夹角的定义已知如图2—5—3(1)两个非零向量→a 、→b ,如图2—5—2(2)作→=a , →=b ,则∠AOB=θ()1800︒≤≤︒θ叫作向量→a 与→b 的夹角。
图2—5—3(1)当0=θ时,→a 与→b 同向; (2)当180=θ时,→a 与→b 反向;(3)当90=θ时,→a 与→b 垂直,记→a ⊥→b ;注意:(1)在两向量的夹角定义,两向量必须是同起点的,如图2—5-4所示:图2—5—4(2)规定→0与任意向量垂直。
3、向量→b 在→a 方向上的射影|→b |θcos 叫作向量→b 在→a 方向上的射影,它是一个实数,与向量→a 的方向与→b 所成的角有关,与向量→a 的位置无关。
已知向量→a 和→b ,如图2—5—5,→=a , →=b ,过点B 作1BB ⊥OA 于1B ,则θcos ||1→=b OB 。

主备:安伟 辅备:高一数学组 审核:张永辉 日期:2011-11-21§5 从力做的功到向量的数量积班级 姓名【学习目标】 1.向量数量积的定义及其几何意义;2. 向量的数量积的性质;3. 向量数量积的运算律;4.向量数量积坐标表示【重点难点】 重点:向量数量积的定义及坐标表示 难点:几何意义【学法指导】 自主探索与合作交流相结合一、知识梳理1.平面向量数量积(内积)的定义:已知两个非零向量a 与b ,我们把数量 叫做a 与b 的数量积(或内积),记作 ,即 ,其中θ是a 与b 的夹角. 规定:零向量与任一向量的数量积均为 .2.向量的数量积的性质:设a 与b 都是非零向量,θ为a 与b的夹角. (1)a b ⊥⇔ ;(2)当a 与b 同向时,a b ∙ = ,当a 与b 反向时,a b ∙ = .(3)a a ∙ = 或2a a a a =∙= ;(4)cos θ= ;(5)ab ∙ a b .(填“=”、“≥”“≤”)4.向量数量积的运算律:已知向量a ,b ,c 和实数λ,则(1)a b ∙ = ;(交换律)(2)()a b λ∙ = = ;(与数乘的结合律)(3)()a b c +∙ = .(分配律)预习自测1.若a b ∙ <0,则a 与b 的夹角θ的取值范围是2. (1) 22a a = (2) 2a b a ∙ =b a (3) ()2a b ∙ = 22a b ∙ (4)()2a b + =222a a b b +∙+(5)c b a c b a ⋅⋅=⋅⋅)()( 上列等式中,其中正确的是3.若已知向量a 与b ,且a = 2,b = 3,a b ∙ =-3,求向量a 与b 的夹角为_____课内探究考点1.平面向量数量积的基本运算例1:已知正三角形ABC 的边长为1,求:(1) AB AC ∙ (2) AB BC ∙ (3) BC AC ∙变式:已知a = 5,b = 2,a 与b 的夹角为 120,求()()23a b a b +∙- 、b a +的值考点2.平面向量的垂直问题例2、已知非零向量a 和b 满足2a b = ,且a b + 与2a b - 垂直,求证:a b ⊥ .考点3.利用平面向量的数量积解决夹角问题例3.设两个向量1e 、2e ,满足2||1=e ,1||2=e ,1e 、2e 的夹角为60°,若向量2172e e t + 与向量21e t e+的夹角为钝角,求实数t 的取值范围.达标检测1. 已知向量a 与b 共线,求a b ∙ =2. 已知向量a 与b 的夹角为60°,且a = 3,b = 2,求a b ∙ =3. 已知非零向量a ,b ,满足a = b = a b - ,则a 与a b + 的夹角为_________.小结反思。


§5 从力做的功到向量的数量积知识梳理1.两个向量的夹角(1)定义:已知两个非零向量a ,b ,如图2-5-1所示,作OA =a ,OB =b ,则∠AOB 称为a 与b 的夹角,记作〈a ,b 〉.图2-5-1(2)范围:[0,π],〈a ,b 〉=〈b ,a 〉.(3)当〈a ,b 〉=2π时,称向量a 与b 互相垂直,记作a ⊥b .规定零向量与任一向量垂直. (4)当〈a ,b 〉=0时,a 与b 同向;当〈a ,b 〉=π时,a 与b 反向.2.向量的射影图2-5-2已知向量a 和b ,如图2-5-2所示,作=a ,=b ,过点B 作的垂线,垂足为B 1,则OB 1的数量|b |cosθ 叫做向量b 在向量a 方向上的正射影(简称射影).3.向量的数量积(内积)(1)定义:|a ||b |cosθ叫做向量a 与b 的数量积(或内积),记作a ·b ,即a ·b =|a ||b |cosθ.(2)理解:两向量的数量积不是向量而是数量,它可以为正数、为零、为负数.(3)几何意义:向量a 与向量b 的数量积等于a 的长度|a |与b 在a 方向上的射影|b |cosθ的乘积,或看作是b 的长度|b |与a 在b 方向上的射影|a |cosθ的乘积.4.向量数量积的性质设a 、b 为两个非零向量,e 是与b 同向的单位向量.(1)e ·a =a ·e =|a |cos 〈a ,e 〉.(2)a ·b ⇔a ·b =0.(3)当a 与b 同向时,a ·b =|a ||b |;当a 与b 反向时,a ·b =-|a ||b |;特别地:a ·a =|a |2或|a |=a a •.(4)cos 〈a ,b 〉=||||b a b a •. (5)|a ·b |≤|a ||b |.5.向量数量积的运算律交换律:a ·b =b ·a ;结合律:(λa )·b =λ(a ·b )=a ·(λb )(λ∈R );分配律:(a +b )·c =a ·c +b ·c .知识导学1.学好本节,需复习平行向量基本定理、平面向量基本定理、平面向量的坐标表示、平面向量的坐标运算.2.本节的重点是向量数量积的坐标运算、度量公式及其应用,特别是向量垂直的坐标运算的应用;难点是向量数量积的理解,以及灵活应用度量公式解决问题. 疑难突破1.向量的数量积、向量的数乘和实数的乘法,这三种运算有什么区别和联系? 剖析:难点是对这三种运算分不清.其突破的途径主要是从运算的定义、表示方法、性质、结果和几何意义上来分析对比.①从定义上看:两个向量数量积的结果是一个实数,而不是向量,符号由夹角的大小决定;向量的数乘的结果是一个向量,其长度是原向量长度的倍数,其方向由这个实数的符号所决定;两个实数的积也是一个实数,符号由这两个实数的符号所决定.②从运算的表示方法上看:两个向量a 、b 的数量积称为内积,写成a ·b ;大学里还要学到两个向量的外积a ×b ,而a ·b 是两个向量的数量的积,因此书写时要严格区分.符号“·”在向量运算中不是乘号,既不能省略,也不能用“×”代替;向量的数乘的写法同单项式的写法;实数的乘法的写法我们就非常熟悉了.③从运算的性质上看:在向量的数量积中,若a ·b =0,则a =0或b =0或〈a ,b 〉=2π;在向量的数乘中,若λa =0,则λ=0或a =0;在实数的乘法中,若a ·b =0,则a =0或b =0.在向量的数量积中:a ·b =b ·c ⇒b =0或a =c 或〈b ,(a -c )〉=2π;在向量的数乘中,λa =λb (λ∈R )⇒a =b 或a ≠b ;在实数的乘法中,ab =bc ⇒a =c 或b =0.在向量的数量积中:(a ·b )c ≠a ·(b ·c );在向量的数乘中,(λm)a =λ(ma )(λ∈R ,m ∈R );在实数的乘法中,有(a ·b )c =a ·(b ·c ).④从几何意义上来看:在向量的数量积中,a ·b 的几何意义是a 的长度|a |与b 在a 方向上的射影|b |cosθ的乘积;在向量的数乘中,λa 的几何意义就是把向量a 沿向量a 的方向或反方向放大或缩小|λ|倍.2.如何应用|a |=a a •来求平面内两点间的距离?剖析:难点是知道这个等式成立,但不会用来求平面内两点间的距离.其突破口是建立平面向量基底,再代入等式即可.例如:如图2-5-3所示,已知平行四边形ABCD 中,AB=3,AD=1,∠DAB=3π,求对角线AC 和BD 的长.图2-5-3解:设=a ,=b .则|a |=3,|b |=1,〈a ,b 〉=3π. ∴a ·b =|a ||b |cos 〈a ,b 〉=23. 又∵AC =a +b ,=a -b ,∴|AC |=132)(222=+•+=+=b b a a b a ,|DB 72)(222=+•-=-=b b a a b a ,∴AC=13,DB=7.由此可见向量法求平面内两点间的距离的步骤是:①建立平面向量基底或建立平面直角坐标系,将平面内两点间距离转化为向量的长度; ②应用公式|a |=a a •,通过向量运算求出向量的长度;③把向量的长度还原成平面内两点间的距离.。


§5 从力做的功到向量的数量积(第一课时)(陕西省西安中学焦宇 710021)【教材版本】北师大版【设计理念】《数学课程标准》中强调:“数学课程要实现:人人学有价值的数学;人人都获得必需的数学;不同的人在数学上得到不同的发展。
”同时,她倡导的“关注过程”“强调本质”“体现数学的文化价值”“发展数学的应用意识”等都向我们昭示出高中数学课程的价值取向。
为使《数学课程标准》得以顺利实施,教师理应不断更新教学观念,努力成为数学学习活动的组织者、引导者、合作者。
通过精心设计、实践与反思,不断改进教学方法和教学手段……以优化课堂教学,提高课堂教学的效率。
课程设计必须从学生的角度出发,要与学生的经历和经验相联系,关注学生的体验、感悟和实践过程。
基于以上认识,对于“平面向量数量积及运算律”引入,我进行了这样的教学设计:首先演示一个外力作功的实验:W=|F| |S|cosθ,并揭示这个物理模型的实质,即:力与位移的数量积。
其次,具体分析平面向量的夹角,向量的数量积、重要性质等概念,并巩固练习。
再者,基本概念均简明有效的给出,为之后学生深入学习、探究提供了时间上的保证,从定义出发推导运算律也变得简单易行。
随后,从特殊到一般,得出数量积的几何表示。
在教师为主导、学生为主体的教学模式中,学习活动进展顺利,学生们都显得游刃有余。
在教学过程中,学生对平面向量数量积的定义及运算律的理解有些难度,总的感觉是:在核心问题上的处理不太容易把握,学生需要较多的时间去探究和体验。
结合多年教学发现学生对数量积的结果是数量重视不够,解题中往往忽略,导致出错,因此教学中应重点强调;性质中≤学生容易忽略;书写中符号“⋅”学生容易省略不写,教学和作业中发现问题教师应时常提醒学生及时纠正,避免重复错误;运算律中消去律和结合律不能乱用,要给学生讲清楚一定不能与实数的运算律混淆,这些地方应反复给学生强调。
最后,在有效落实教学目标的同时,如何让学生的“学”更轻松些,让教师的“教”更顺畅些,使“数量积”的概念形成更具一般性,更能揭示“数量积”的本质内含就显得尤为重要。
课题从力做的功到向量的数量积(1)授课时间 3教学目标1正确理解平面向量的数量积的概念,能够运用这一概念求两个向量的数量积,并能根据条件逆用等式求向量的夹角;2掌握平面向量的数量积的5条重要性质及运算律,并能运用这些性质解决有关问题;3通过平面向量的数量积的概念,几何意义,重要性质及运算律的应用,培养学生的应用意识.教学重点两个向量的数量积的概念、数量积的运算律的理解,数量积处理长度、角度和垂直的问题.教学难点向量数量积运算律的理解及灵活运用,向量数量积的几何意义及数量积的重要性质的灵活应用.教学方法课型新授课从实际的物理问题出发,经过观察、分析、归纳、概括出力对物体做功时力的大小和方向与所做的功的关系,从而引出两个向量数量积的概念.教学中教师为主导,学生为主体,让学生从实例到数学实质的过度中掌握向量数量积的概念.实例 在物理学中,一个物体受到力的作用,如果在力的方向上发生了一段位移,我们就说这个力对物体做了功.如果力的方向跟物体运动的方向相同,功就等于力的大小和位移大小的乘积.如果当力F 的方向与物体运动的方向成θ角时,将力F 进行分解:与位移方向平行的分力1F 满足1||||cos θ=F F ,物体在1F 的方向上产生了位移s ,因而对物体做的功为||cos ||θ⋅F s ;与位移方向垂直的分力2F ,由于没有使物体在该分力的方向上发生位移,因而对物体不做功.可见,力F 对物体做的功为||||cos W θ=F s .当00090θ≤<时,0W >,即力F 做正功;当090θ=时,0W =,即力F 不做功;当0090180θ<<时,0W <,即力F 做负功.力对物体所做的功,可以看作力F 和位移s 这两个向量的某种运算的结果.教学内容两个向量夹角的定义已知两个非零向量a 和b ,如图,作OA =a ,OB =b ,00(0180)AOB θθ∠=≤≤叫做向量a 与b 的夹角.当00θ=时,a 与b 同向; 当0180θ=时,a 与b 反向; 当090θ=时,a 与b 垂直.规定:由于零向量的方向是不确定的,为今后方便起见,我们规定零向量与任一向量垂直.注意:零向量与任一向量垂直是我们对夹角定义的一种补充,目的只是使定义完备. 两个向量数量积的定义已知两个向量a 和b ,它们的夹角为θ,我们把||||cos θa b 叫做向量a 与b 的数量积(或内积).记作⋅a b (如图)F1F 2F ababOAB θθabOa bOBA1B θa b OABθ1Bab1()O B ABθ即||||cos θ⋅=a b a b由此可以看出,两个向量的数量积是这两个向量的长度的乘积与它们夹角的余弦值的乘积. 二、学生活动,猜想讨论问题1 讨论向量数量积与实数与向量乘积的区别.问题2 如图,讨论向量数量积的几何意义.(A ) (B) (C) 问题3 结合向量数量积的定义及其几何意义,讨论当力F 与位移s 的夹角0090θ≤<、090θ=、090180θ<<时力F 对物体所做的功W 的情况.向量数量积的几何意义:向量a 和b 的数量积等于a 的长度||a 与b 在a 的方向上的射影||cos θb 的乘积,或b 的长度||b 与a 在b 的方向上的射影||cos θa 的乘积.例题及练习例1 已知||3=a ,||4=b ,且a 与b 的夹角150θ=︒,求⋅a b .例2 已知16⋅=-a b ,||2||=a b ,||4=b ,求a 与b 的夹角θ.引入问题 设,,a b c 是任意的非零平面向量,且它们相互不共线,下列命题中正确的是( ) ①()()0⋅-⋅=a b c c a b ; ②||||||+<+a b a b ; ③⋅=⋅a b a c ,则=b c ;④22(3)(3)9||||+⋅-=-a b a b a b . 向量的数量积的性质由向量数量积的定义和几何意义,我们可以得到如下性质: (1) 若e 是单位向量,则||cos θ⋅=⋅=e a a e a .(2) 若⊥a b ,则0⊥=a b ,反之,若0⊥=a b ,则⊥a b ,即0⊥⇔⋅=a b a b .(3) ||=⋅a a a .(4) cos (||||0)||||θ⋅=≠a ba b a b . (5) 对于两个向量a ,b ,有||||||⋅≤a b a b .当且仅当//a b 时,等号成立.注:以上性质是向量数量积的一些重要性质,与向量数量积的定义及其几何意义有很大关系. 向量的数量积的运算律(1)如果向量a 和b ,它们的夹角为θ,则||||cos θ⋅=⋅=a b b a a b .(2)根据实数与向量的积的意义, a 与λa 的关系为: 当a 为非零向量,λa 表示与a 共线的向量,当0λ>时, λa 与a 同向,其长度为||||λa ;当0λ<时,λa 与a 反向,其长度为||||λa ;当0λ=时, λa 为零向量,其长度为0.当a 为零向量时,λa 也为零向量.所以,如果向量a 和b ,它们的夹角为θ.当0λ≥时,()()()||||cos λλλλθ⋅=⋅=⋅=a b a b a b a b ; 当0λ<时,()()()||||cos λλλλθ⋅=⋅=⋅=-a b a b a b a b ; (3)如图,OA =a ,AB =b ,OC =c ,则OB +=a b . ∵ 1111OB OA A B =+,∴ +a b 在c 方向上的射影等于a ,b 在c 方向上的射影的和,∴ ()⋅+=⋅+⋅a b c a b a c .⋅=⋅a b b a ;()()()λλλ⋅=⋅=⋅a b a b a b ; ()⋅+=⋅+⋅a b c a b a c .我们回到引入的问题中,用向量数量积的一些知识来解决问题.问题 设,,a b c 是任意的非零平面向量,且它们相互不共线,下列命题中正确的是( ) ①()()0⋅-⋅=a b c c a b ; ②||||||+<+a b a b ; ③⋅=⋅a b a c ,则=b c ;④22(3)(3)9||||+⋅-=-a b a b a b .解: ①()⋅a b c 表示与c 共线的向量,()⋅c a b 表示与b 共线的向量,故()()⋅-⋅a b c c a b 不一定为零向量,故不正确; ②由于,a bAOB1A 1B C 1θ2θθabc+a b不共线,由向量加法的三角形法则,两边之和大于第三边,||||||+<+a b a b 正确;③由向量数量积的几何意义,⋅=⋅a b a c ,说明向量,b c 在a 方向上的射影是相等的,但=b c 不一定成立,故说法不正确;④由向量数量积的运算律知22(3)(3)9||||+⋅-=-a b a b a b 正确.例题及练习例4 在ABC ∆中,设边BC ,CA ,AB 的长度分别为,,a b c ,证明:2222cos a b c bc A =+-;2222cos b c a ca B =+-; 2222cos c a b ab C =+-.例5 证明菱形的两条对角线互相垂直. 例6 已知单位向量1e ,2e 的夹角为60︒,求向量12=+a e e ,212=-b e e 的夹角.课后作业问题1 已知||||5==a b ,向量a 与b 的夹角为3π,求||+a b ,||-a b 。