2018届人教A版 立体几何 单元测试

【备战2017高考高三数学全国各地一模试卷分项精品】专题八立体几何一、选择题【2017湖南衡阳上学期期末】一个四面体的三视图如图所示，则该四面体的外接球的表面积为（）A. B. C. D.【答案】B【点睛】本题考查了由三视图求几何体外接球的表面积，解题的关键是根据三视图判断几何体的性质，求得外接球的半径．【2017荆、荆、襄、宜四地七校联考】已知在四面体中，分别是的中点，若，则与所成角的度数是( )A. B. C. D.【答案】D 【解析】 取中点，则，与所成角等于与所成角，又，所以，因此与所成角的度数是，选D.【2017荆、荆、襄、宜四地七校联考】某几何体的三视图如图所示，则该几何体的体积为( )A. B. C. D.【答案】B【2017山西五校联考】某几何体的三视图如图所示，则该几何体的表面积为（ ）A. B.C. D.【答案】A【解析】该几何体为长方体挖去了一个圆锥，圆锥的底面半径为1，母线长为2，几何体的表面积为，故选A.【2017云南师大附中月考】某几何体的三视图如图所示，则该几何体的体积为（）A. 8B.C.D. 4【答案】A【2017云南师大附中月考】四面体的四个顶点都在球的球面上，，且平面平面，则球的表面积为（）A. B. C. D.【答案】B【解析】如图，分别为的中点，易知球心点在线段上，因为，则．又∵平面平面，平面平面=BC，∴平面ABC，∴，∴．因为点是的中点，∴，且．设球心的半径为，，则，在中，有，在中，有，解得，所以，故选B．【点睛】本题主要考查球内接多面体，球的表面积，属于中档题，其中依据题意分析出球心必位于两垂直平面的交线上，然后再利用勾股定理，即可求出球的半径，进而可求出球的表面积，此类题目主要灵活运用线面垂直的判定及性质，面面垂直的判定及性质是解题的关键.【2017江西上饶一模】设某几何体的三视图如图所示，则该几何体的体积为（）A. 8B. 4C. 2D.【答案】B【点睛】关于三视图的考察是高考中的必考点，一般考试形式为给出三视图，求解该几何体的体积或表面积.三视图问题首先观察俯视图确定几何体的底面形状，再结合正视图，侧视图确定几何体的准确形状，如本题中俯视图为梯形，所以该几何体底面为梯形，结合正视图中的顶点可知该几何体为四棱锥，结合底面梯形中的对角线可知四棱锥中有一条侧棱垂直于底面，由此可确定该棱锥的几何特征.【2017江西上饶一模】在正方体中，过点作平面平行平面，平面与平面交于直线，平面与平面交于直线，则直线与直线所成的角为（）A. B. C. D.【答案】C【2017江西赣州上学期期末】如图是一个正方体被切掉部分后所得几何体的三视图，则该几何体的体积为（）A. B. C. D.【答案】B【解析】如图所，该几何体是将一个正方体切掉一个三棱柱和一个三棱锥得到的，所以该几何体的体积.【2017广东深圳一模】已知棱长为2的正方体，球与该正方体的各个面相切，则平面截此球所得的截面的面积为（）A. B. C. D.【答案】D二、填空题【2017江西赣州上学期期末】在四面体中，平面，，，，则该四面体的外接球的表面积为__________．【答案】【解析】四面体可看成如上图长方体的一部分，则四面体的外接球的球心为的中点，.【2017湖北武汉武昌区调研】在矩形中，，现将沿矩形的对角线所在的直线进行翻折，在翻折的过程中，给出下列结论：①存在某个位置，使得直线与直线垂直；②存在某个位置，使得直线与直线垂直；③存在某个位置，使得直线与直线垂直.其中正确结论的序号是__________．（写出所有正确结论的序号）【答案】②【2017河北衡水六调】一个直六棱柱的底面是边长为2的正六边形，侧棱长为3，则它的外接球的表面积为__________．【答案】【解析】直六棱柱的外接球的直径为直六棱柱中最长的对角线，∵一个直六棱柱的底面是边长为2的正六边形，侧棱长为3，∴直六棱柱的外接球的直径为，∴外接球的半径为，∴外接球的表面积为．三、解答题【2017湖南衡阳上学期期末】如图所示，在直三棱柱中，底面是等腰三角形，且斜边，侧棱，点为的中点，点在线段上，（1）求证：不论取何值时，恒有；（2）当为何值时，面.【答案】（1）见解析；（2）（2）由（1）得，故只需保证即可故当即当为的中点时，面.【2017山西五校联考】在四棱锥中，平面，底面为矩形，点分别为棱的中点，为线段的中点，且为上一点，且平面（1）确定的位置，并求线段的长；（2）平面与交于点，求三棱锥的体积．【答案】（1）见解析；（2）.【解析】（1）设与交于点，连接，则为的中点，1分证明如下：因为平面，且平面平面，所以，又为线段的中点，则为的中点，3分因为为棱的中点，所以，又底面，所以底面，4分则，因为，，所以，6分（2）延长交的延长线于点，由，且，得为的中点，7分连接，则但为与的交点，8分易得，则，所以，10分因为的面积为，所以. 12分【2017云南师大附中月考】如图，三棱锥中，平面，，，是的中点，是的中点，点在上，.（1）证明：平面；（2）若，求点到平面的距离.【答案】（Ⅰ）证明过程见解析；（Ⅱ）.（Ⅱ）∵平面ABC，∴．又∴平面PAB．又∴，∴．记点P到平面BCD的距离为d，则∴，∴，所以，点P到平面BCD的距离为．【2017江西赣州上学期期末】如图甲所示，是梯形的高，，，，现将等腰梯形沿折起如图乙所示的四棱锥，且，点是线段的中点.（1）证明：；（2）在图中作出平面与交点，并求线段的长度.【答案】（1）详见解析；（2）.【2017湖南长沙一模】如图，以、、、、为顶点的六面体中，和均为等边三角形，且平面平面，平面，．(Ⅰ)求证: 平面；(Ⅱ)求此六面体的体积．【答案】(1)证明见解析；(2) 2．(Ⅱ) 因为是等边三角形，所以是中点，而是等边三角形，因此，由平面，知，从而平面，又因为，所以平面，因此四面体的体积为，四面体的体积为，而六面体的体积=四面体的体积+四面体的体积故所求六面体的体积为2【2017湖北武汉武昌区调研】如图，四棱锥中，，，侧面为等边三角形，，.（Ⅰ）证明：平面；（Ⅱ）求四棱锥的高.【答案】（Ⅰ）证明见解析；（Ⅱ）.（Ⅱ）设四棱锥的高为，则也是三棱锥的高，由（Ⅰ）知，平面，由，得，又，，，故四棱锥的高为.另解：连结，过作于，则为所求的高.【2017河北衡水六调】如图，在四棱锥中，平面，底面是菱形，为与的交点，为棱上一点.（1）证明：平面平面；（2）若平面，求三棱锥的体积.【答案】（1）详见解析；（2）.（2）连接，∵平面，平面平面，∴．∵是的中点，∴是的中点．取的中点，连接，∵四边形是菱形，，∴，又，∴平面，且，故．【2017四川资阳上学期期末】如图，矩形和等边三角形中，，平面平面．是线段上的一个动点．（1）若，确定的位置，并说明理由；（2）求三棱锥的体积．【答案】（1）证明过程见解析；（2）.（2）由题，由（1）和三角形为等边三角形得为的中点，∴为三棱锥的高，于是，又∵无论是上的何点，到的距离不变，即为三角形底边的高，∴，∴．【2017广东深圳一模】如图，四边形为菱形，四边形为平行四边形，设与相交于点，．（1）证明：平面平面；（2）若，求三棱锥的体积．【答案】（1）证明见解析；（2）.【解析】（1）证明：连接，∵四边形为菱形，∵，在和中，，，∴，∴，∴，∵，∴平面，∵平面，∴平面平面；解法二：∵，∴点到平面的距离为点到平面的距离的两倍，所以，作，∵平面平面平面， ∴，∴三棱锥的体积为．【2017江西上饶一模】如图所示，在正方体1111ABCD A B C D -中，棱长为2，E 、F 分别是棱1DD 、11C D 的中点．（1）求三棱锥11B A BE -的体积；（2）试判断直线1B F 与平面1A BE 是否平行，如果平行，请在平面1A BE 上作出与1B F 平行的直线，并说明理由． 【答案】（1）（2）平面-中，底面ABCD是正方【2017荆、荆、襄、宜四地七校联考】如图，在四棱锥S ABCD形，SA⊥底面ABCD，==，点M是SD的中点，AN SC⊥，且交SC于点N．SA AB2SB平面ACM；(Ⅰ) 求证://(Ⅱ) 求点C到平面AMN的距离．（Ⅱ）由条件有,,DC SA DC DA ⊥⊥∴ DC ⊥平面SAD ，∴.AM DC ⊥ 又∵ ,SA AD M =是SD 的中点，∴.AM SD ⊥∴AM ⊥平面.SDC ∴.SC AM ⊥ ………………………8分由已知SC AN ⊥，∴SC ⊥平面.AMN于是CN ⊥面AMN ，则CN 为点C 到平面AMN 的距离 ………………………9分在Rt SAC ∆中，2,SA AC SC ====，于是2AC CN SC CN =⋅⇒=，∴点C 到平面AMN 的距离为． ……………12分。

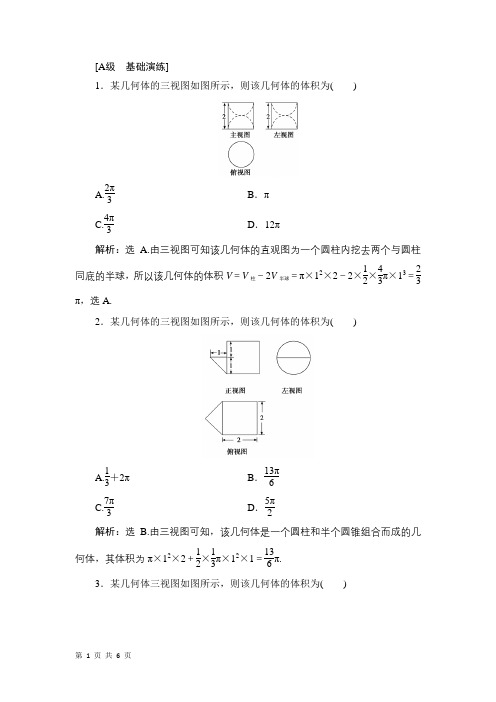
[A 级 基础演练]1．某几何体的三视图如图所示，则该几何体的体积为( )A.2π3 B ．π C.4π3D ．12π解析：选 A.由三视图可知该几何体的直观图为一个圆柱内挖去两个与圆柱同底的半球，所以该几何体的体积V ＝V 柱－2V 半球＝π×12×2－2×12×43π×13＝23π，选A.2．某几何体的三视图如图所示，则该几何体的体积为( )A.13＋2π B ．13π6 C.7π3D ．5π2解析：选 B.由三视图可知，该几何体是一个圆柱和半个圆锥组合而成的几何体，其体积为π×12×2＋12×13π×12×1＝136π.3．某几何体三视图如图所示，则该几何体的体积为( )A ．8－2πB ．8－πC ．8－π2D ．8－π4解析：选B.这是一个正方体切掉两个14圆柱后得到的几何体，如图，几何体的高为2，V ＝23－14×π×12×2×2＝8－π. 4．一个四面体的三视图如图所示，则该四面体的表面积是( )A ．1＋ 3B ．1＋2 2C ．2＋ 3D ．2 2解析：选C.如图，该四面体有两个面为等腰直角三角形，另外两个面为正三角形．故该四面体的表面积S ＝2×12×2×2＋2×12×2×2×32＝2＋ 3.5．(2017·沈阳质检)四面体A -BCD 的四个顶点都在球O 的球面上，AB ⊥平面BCD ，△BCD 是边长为3的等边三角形．若AB ＝2，则球O 的表面积为( )A.32π3 B ．12π C ．16πD ．32π解析：选C.将四面体A -BCD 补形成正三棱柱，则其外接球的球心为上、下底面的中心连线的中点，底面△BCD 的外接圆半径为3，所以外接球的半径R ＝（3）2＋⎝ ⎛⎭⎪⎫AB 22＝2，球O 的表面积S ＝4πR 2＝16π，故选C.6．某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为( )A ．1B ． 2 C. 3D ．2解析：选C.根据三视图，可知几何体的直观图为如图所示的四棱锥V -ABCD ，其中VB ⊥平面ABCD ，且底面ABCD 是边长为1的正方形，VB ＝1.所以四棱锥中最长棱为VD .连接BD ，易知BD ＝2，在Rt △VBD 中，VD ＝VB 2＋BD 2＝ 3.7．一个多面体的三视图如图所示，则该多面体的体积为( )A.233 B ．476 C ．6D ．7解析：选A.由三视图画出几何体的直观图如图所示．该几何体是正方体去掉两个角所形成的多面体．其体积为V ＝2×2×2－2×13×12×1×1×1＝233.8.某一容器的三视图如图所示，则该几何体的体积为 ．解析：依题意，题中的几何体是从一个棱长为2的正方体中挖去一个圆锥，其中该圆锥的底面半径是1、高是2，因此题中的几何体的体积等于23－13π×12×2＝8－2π3.答案：8－2π39．(2016·高考天津卷)已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示(单位：m)，则该四棱锥的体积为 m 3.解析：根据三视图可知该四棱锥的底面是底边长为2 m 、高为1 m 的平行四边形，四棱锥的高为3 m ，故其体积为13×2×1×3＝2(m 3)．答案：210．(2017·大连模拟)直三棱柱ABC -A 1B 1C 1的六个顶点都在球O 的球面上．若AB ＝BC ＝2，∠ABC ＝90°，AA 1＝22，则球O 的表面积为 ．解析：由题设可知，直三棱柱可以补成一个球的内接长方体，所以球的直径为长方体的体对角线长，即22＋22＋（22）2＝4，故球O 的表面积S ＝4πR 2＝16π.答案：16π[B 级 能力突破]1．如图，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，则该多面体的体积为( )A.23 B ．33 C.43D ．32解析：选A.如图，分别过点A ，B 作EF 的垂线，垂足分别为G ，H ，连接DG ，CH ，容易求得EG ＝HF ＝12，AG ＝GD＝BH ＝HC ＝32，则△BHC 中BC 边的高h ＝22.∴S △AGD ＝S △BHC ＝12×22×1＝24，∴V ＝V E ­ADG ＋V F ­BHC ＋V AGD ­BHC ＝2V E ­ADG ＋V AGD ­BHC ＝13×24×12×2＋24×1＝23.2．如图是一几何体的三视图，则该几何体的表面积是( )A ．5＋ 3B ．5＋2 3C ．4＋2 2D ．4＋2 3解析：选A.由三视图可知该几何体的直观图如图所示，该图是一个六面体ABCDEFG ，其中底面ABCD 为正方形，AF ∥CG ，且AF ＝CG ＝1，DE ∥AF ，且DE ＝2AF ，易计算出EF ＝BF ＝BG ＝EG ＝2，所以四边形EFBG 为菱形，其对角线长分别为2和6，故该几何体的表面积S ＝1×1＋12×1×1×2＋12×(1＋2)×1×2＋12×6×2＝5＋3，故选A.3．(2017·广西三市联考)三棱锥P -ABC 中，P A ⊥AB ，P A ⊥AC ，∠BAC ＝120°，P A ＝AB ＝AC ＝2，则此三棱锥外接球的体积为 ．解析：设△ABC 外接圆的半径为r ，三棱锥外接球的半径为R ，∵AB ＝AC ＝2，∠BAC ＝120°，∴BC ＝AB 2＋AC 2－2AB ·AC cos ∠BAC ＝4＋4－2×2×2×⎝ ⎛⎭⎪⎫－12＝23，∴2r ＝2332＝4，∴r ＝2，由题意知P A ⊥平面ABC ，则将三棱锥补成三棱柱可得R ＝⎝ ⎛⎭⎪⎫P A 22＋r 2＝5，∴此三棱锥外接球的体积为43π·(5)3＝2053π. 答案：2053π4．若一个几何体的表面积和体积相同，则称这个几何体为“同积几何体”．已知某几何体为“同积几何体”，其三视图如图所示，则a 的值为 ．解析：根据几何体的三视图可知该几何体是一个四棱柱，如图所示，可得其体积为12(a ＋2a )·a ·a ＝32a 3，其表面积为12·(2a ＋a )·a ·2＋a 2＋a 2＋2a ·a ＋2a ·a ＝7a 2＋2a 2，所以7a 2＋2a 2＝32a 3，解得a ＝14＋223.答案：14＋223。

高一数学必修第二册第八章《立体几何初步》单元练习题卷6（共22题）一、选择题（共10题） 1. 已知 4+(a−2)ii为纯虚数，则实数 a 的值为 ( )A ． 4B ． 2C ． 1D ． −22. 如图，在矩形 OACB 中，E 和 F 分别是边 AC 和 BC 上的点，且满足 AC =3AE ，BC =3BF ，若 OC⃗⃗⃗⃗⃗ =λOE ⃗⃗⃗⃗⃗ +μOF ⃗⃗⃗⃗⃗ ，其中 λ,μ∈R ，则 λ+μ 是A ．83B ．32C ．53D ．13. 棱锥的侧面和底面可以都是 ( ) A ．三角形B ．四边形C ．五边形D ．六边形4. 有下列三个说法：① 两个互相平行的面是正方形，其余各面都是四边形的几何体一定是棱台； ②有两个面平行且相似，其余各面都是梯形的多面体是棱台； ③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台． 其中正确的有 ( ) A ． 0 个B ． 1 个C ． 2 个D ． 3 个5. 某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图： 则下面结论中不正确的是 ( )A．新农村建设后，种植收入减少B．新农村建设后，其他收入增加了一倍以上C．新农村建设后，养殖收入增加了一倍D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半6.根据下面给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是( )A．逐年比较，2008年减少二氧化硫排放量的效果最显著B．2007年我国治理二氧化硫排放显现成效C．2006年以来我国二氧化硫年排放量呈减少趋势D．2006年以来我国二氧化硫年排放量与年份正相关7.已知i为虚数单位，下列各式的运算结果为纯虚数的是( )A．i(1+i)B．i(1−i)2C．i2(1+i)2D．i+i2+i3+i48.在下列结论中，正确的是( )A．若两个向量相等，则它们的起点和终点分别重合B．模相等的两个平行向量是相等向量C．若a和b⃗都是单位向量，则a=b⃗D．两个相等向量的模相等9.某书店新进了一批书籍，如表是某月中连续6天的销售情况记录：日期6日7日8日9日10日11日根据上表估计该书店该月（按31天计当日销售量(本)304028443842算）的销售总量是 ( ) A ． 1147 本 B ． 1110 本 C ． 1340 本 D ． 1278 本10. 在 △ABC 中，内角 A ，B ，C 的对边分别为 a ，b ，c ，且 bsin (π−C )−√2ccos (π+B )=0，则tanB = ( ) A ．√22B ． √2C ． −√22D ． −√2二、填空题（共6题）11. A ，B 两种品牌各三种车型 2017 年 7 月的销量环比（与 2017 年 6 月比较）增长率如下表：A 品牌车型A 1A 2A 3环比增长率−7.29%10.47%14.70%B 品牌车型B 1B 2B 3环比增长率−8.49%−28.06%13.25%根据此表中的数据，有如下四个结论：① A 1 车型销量比 B 1 车型销量多；② A 品牌三种车型总销量环比增长率可能大于 14.70%； ③ B 品牌三种车型车总销量环比增长率可能为正；④ A 品牌三种车型总销量环比增长率可能小于B 品牌三种车型总销量环比增长率．其中正确的结论个数是 ．12. 设复数 z 1=x +2i ，z 2=3−yi （x,y ∈R ），若 z 1+z 2=5−6i ，则 z 1−z 2= ．13. 如果两个球的体积之比为 8:27，那么两个球的表面积之比为 ．14. 在复平面内，点 A (−2,1) 对应的复数 z ，则 ∣z +1∣= ．15. 已知点 A (−2,0)，设 B ，C 是圆 O ：x 2+y 2=1 上的两个不同的动点，且向量 OB⃗⃗⃗⃗⃗ =tOA ⃗⃗⃗⃗⃗ +(1−t )OC ⃗⃗⃗⃗⃗ （其中 t 为实数），则 AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ = ．16. 如图，在平面四边形 ABCD 中，AB ⊥BC ，AB =√3，BC =1，△ACD 是等边三角形，则 AC⃗⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ 的值为 ．三、解答题（共6题）17. 某鱼苗实验场进行某种淡水鱼的人工孵化试验，按在同一条件下的试验结果，10000 个鱼卵能孵出 8520 尾鱼苗．(1) 求这种鱼卵孵化的频率（经验概率）；(2) 估计 30000 个这种鱼苗能孵化出多少尾鱼苗？ (3) 若要孵出 5000 尾鱼苗，估计需要准备多少个鱼卵？18. 在数学考试中，小明的成绩在 90 分以上的概率是 0.18，在 80∼89 分的概率是 0.51，在70∼79 分的概率是 0.15，在 60∼69 分的概率是 0.09，60 分以下的概率是 0.07，计算： (1) 小明在数学考试中取得 80 分以上成绩的概率； (2) 小明考试及格的概率．19. 从① B =π3，② a =2，③ bcosA +acosB =√3+1 这三个条件中任选一个，补充在下面问题中，并解决相应问题．已知在锐角 △ABC 中，角 A ，B ，C 的对边分别为 a ，b ，c ，△ABC 的面积为 S ，若 4S =b 2+c 2−a 2，b =√6，且 ，求 △ABC 的面积 S 的大小．20. 现有一个底面是菱形的直四棱柱，它的体对角线长为 9 和 15，高是 5，求该直四棱柱的侧面积、表面积．21. 某班抽取 20 名学生周测物理考试成绩（单位：分）的频率分布直方图如下．(1) 求频率分布直方图中 a 的值，并写出众数；(2) 分别求出成绩落在 [50,60) 与 [60,70) 中的学生人数；(3) 从成绩在 [50,70) 的学生中任选 2 人，求这 2 人的成绩都在 [60,70) 中的概率．22. 已知点 O (0,0)，A (1,2)，B (4,5)，且 OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +tAB⃗⃗⃗⃗⃗ ． (1) t 为何值时，P 在 x 轴上？P 在 y 轴上？P 在第二象限？(2) 四边形 OABP 能否成为平行四边形？若能，求出相应的 t 值；若不能，说明理由．答案一、选择题（共10题）1. 【答案】B【解析】4+(a−2)ii =−i[4+(a−2)i]−i⋅i=a−2−4i为纯虚数，则实数a满足：a−2=0，解得a=2．【知识点】复数的乘除运算2. 【答案】B【解析】以O为原点，OA为x轴、OB为y轴建立平面直角坐标系．设OA=a，OB=b，则E(a,b3)，F(a3,b)，C(a,b)．由已知，得(a,b)=λ(a,b3)+μ(a3,b)，则有{a=λa+μa3,b=λb3+bμ,解得λ=μ=34，因此λ+μ=32．【知识点】平面向量的分解、平面向量的坐标运算3. 【答案】A【解析】三棱锥的侧面和底面都是三角形．故选A．【知识点】棱锥的结构特征4. 【答案】A【解析】当两个互相平行的正方形全等时，不是棱台，故①中说法错误；②③可用反例去检验，如图（1）（2）所示，故②③中说法错误．故选A．【知识点】棱台的结构特征5. 【答案】A【解析】设建设前经济收入为a，则建设后经济收入为2a，由题图可知：种植收入第三产业收入养殖收入其他收入建设前经济收入0.6a0.06a0.3a0.04a建设后经济收入0.74a0.56a0.6a0.1a据如表可知B，C，D中结论均正确，A中论不正确．【知识点】频率分布直方图6. 【答案】D【解析】由柱形图可知：A，B，C均正确，2006年以来我国二氧化硫年排放量在逐渐减少，所以排放量与年份负相关，所以D不正确．【知识点】频率分布直方图7. 【答案】C【解析】对于A，i(1+i)=i−1不是纯虚数；对于B，i(1−i)2=−2i2=2是实数；对于C，i2(1+i)2=−2i为纯虚数；对于D，i+i2+i3+i4=i−1−i+1=0不是纯虚数．【知识点】复数的乘除运算8. 【答案】D【解析】由平面向量的基本概念可得，D是正确的．【知识点】平面向量的概念与表示9. 【答案】A=37（本）,【解析】从表中6天的销售情况可得，一天的平均销售量为30+40+28+44+38+426该月共31天，故该月的销售总量约为37×31=1147（本）．【知识点】样本数据的数字特征10. 【答案】D【解析】由已知得bsinC+√2ccosB=0，即sinBsinC+√2sinCcosB=0，因为sinC≠0，所以sinB+√2cosB=0，故tanB=−√2．【知识点】正弦定理二、填空题（共6题）11. 【答案】2【知识点】概率的应用12. 【答案】 −1+10i【解析】因为 z 1+z 2=x +2i +(3−yi )=(x +3)+(2−y )i =5−6i (x,y ∈R )， 所以 x =2 且 y =8，所以 z 1−z 2=2+2i −(3−8i )=−1+10i ． 【知识点】复数的加减运算13. 【答案】 4:9【解析】因为 V 1:V 2=8:27=R 13:R 23，所以 R 1:R 2=2:3，所以 S 1:S 2=R 12:R 22=4:9．【知识点】球的表面积与体积14. 【答案】 √2【知识点】复数的几何意义15. 【答案】 3【解析】 OB⃗⃗⃗⃗⃗ =tOA ⃗⃗⃗⃗⃗ +(1−t )OC ⃗⃗⃗⃗⃗ ⇒CB ⃗⃗⃗⃗⃗ =tCA ⃗⃗⃗⃗⃗ ， 所以 A ，B ，C 三点共线，所以设直线 BC ：y =k (x +2)．{x 2+y 2=1,y =k (x +2)⇒(1+k 2)x 2+4k 2x +4k 2−1=0， 设 B (x 1,y 1)，C (x 2,y 2)， 所以 x 1+x 2=−4k 21+k 2，x 1x 2=4k 2−11+k 2．所以AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =(x 1+2,y 1)(x 2+2,y 2)=(x 1+2)(x 2+2)+k 2(x 1+2)(x 2+2)=(1+k 2)[x 1x 2+2(x 1+x 2)+4]=(1+k2)⋅(4k 2−11+k 2−8k 21+k 2+4)=3.【知识点】平面向量数量积的坐标运算16. 【答案】 −1【解析】 AB ⊥BC ，AB =√3，BC =1， 所以 AC =2，∠BCA =60∘； 又 △ACD 是等边三角形， 所以 AD =AC =2，AD ⊥AB ， 所以AC ⃗⃗⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )⋅(BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )=AB ⃗⃗⃗⃗⃗ ⋅BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗ =−√3×√3+1×2=−1.【知识点】平面向量的数量积与垂直三、解答题（共6题） 17. 【答案】(1) 0.852．(2) 25560 尾．(3) 约 5869 个．【知识点】频率与概率18. 【答案】(1) 分别记小明的成绩“在 90 分以上”“在 80∼89 分”“在 70∼79 分”“在 60∼69 分”为事件 B ，C ，D ，E ，这四个事件彼此互斥．小明的成绩在 80 分以上的概率是 P (B ∪C )=P (B )+P (C )=0.18+0.51=0.69． (2) 法一：小明考试及格的概率是P (B ∪C ∪D ∪E )=P (B )+P (C )+P (D )+P (E )=0.18+0.51+0.15+0.09=0.93.法二：小明考试不及格的概率是 0.07，又小明考试不及格与及格互为对立事件，故小明考试及格的概率 P =1−0.07=0.93． 【知识点】事件的关系与运算19. 【答案】因为 4S =b 2+c 2−a 2，cosA =b 2+c 2−a 22bc，S =12bcsinA ，所以 2bcsinA =2bccosA ，显然 cosA ≠0， 所以 tanA =1， 又 A ∈(0,π)， 所以 A =π4．若选择① B =π3，由 asinA =bsinB ，得a=bsinAsinB =√6×√22√32=2．又sinC=sin[π−(A+B)]=sin(A+B)=sinAcosB+cosAsinB=√22×12+√22×√32=√6+√24,所以S=12absinC=3+√32．若选择② a=2，由asinA =bsinB，得sinB=bsinAa=√32，B∈(0,π2)，所以cosB=12．sinC=sin[π−(A+B)]=sin(A+B)=sinAcosB+cosAsinB=√6+√24.所以S=12absinC=3+√32．若选择③ bcosA+acosB=√3+1，所以acosB=1，即a⋅a 2+c2−62ac=1，所以a2=6+2c−c2，又a2=6+c2−2√6c⋅√22=6+c2−2√3c，所以6+2c−c2=6+c2−2√3c，解得c=√3+1，所以S=12bcsinA=3+√32．【知识点】正弦定理、余弦定理20. 【答案】如图，设底面对角线AC=a，BD=b，交点为O，体对角线A1C=15，B1D=9，所以a2+52=152，b2+52=92，所以a2=200，b2=56．因为该直四棱柱的底面是菱形，所以AB2=(AC2)2+(BD2)2=a2+b24=200+564=64，所以AB=8．所以直四棱柱的侧面积 S 侧=4×8×5=160． 所以直四棱柱的底面积 S 底=12AC ⋅BD =20√7．所以直四棱柱的表面积 S 表=160+2×20√7=160+40√7． 【知识点】棱柱的表面积与体积21. 【答案】(1) 据直方图知组距 =10，由 (2a +3a +6a +7a +2a )×10=1，解得 a =1200=0.005， 众数：75．(2) 成绩落在 [50,60) 中的学生人数为 2×0.005×10×20=2， 成绩落在 [60,70) 中的学生人数为 3×0.005×10×20=3．(3) 记成绩落在 [50,60) 中的 2 人为 A 1，A 2，成绩落在 [60,70) 中的 3 人为 B 1，B 2，B 3， 则从成绩在 [50,70) 的学生中任选 2 人的基本事件共有 10 个：(A 1,A 2)，(A 1,B 1)，(A 1,B 2)，(A 1,B 3)，(A 2,B 1)，(A 2,B 2)，(A 2,B 3)，(B 1,B 2)，(B 1,B 3)，(B 2,B 3)， 记“两人成绩都落在 [60,70)”为事件 C ，则事件 C 包含的基本事件有 3 个：(B 1,B 2)，(B 1,B 3)，(B 2,B 3)， P (C )=310．【知识点】样本数据的数字特征、频率分布直方图、古典概型22. 【答案】(1) OA⃗⃗⃗⃗⃗ =(1,2)，OB ⃗⃗⃗⃗⃗ =(4,5)，OP ⃗⃗⃗⃗⃗ =(1+3t,2+3t )． 若 P 在 x 轴上，则 t =−23． 若 P 在 y 轴上，则 t =−13． 若 P 在第二象限，则 −23<t <−13．(2) OA⃗⃗⃗⃗⃗ =(1,2)，PB ⃗⃗⃗⃗⃗ =(3−3t,3−3t )． 若 OABP 成平行四边形，则 OA ⃗⃗⃗⃗⃗ =PB⃗⃗⃗⃗⃗ ，即 {3−3t =1,3−3t =2, 此方程无解．故不能． 【知识点】平面向量的坐标运算、平面向量数乘的坐标运算。

【2017年高三数学优质试卷分项精品】专题九立体几何一、选择题1.【2016年湖北八校高三联考】如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为( )A．8πB．252πC．12πD．414π【答案】DBSD2.【2016年安徽安庆高三一模】一个几何体的三视图如图所示,其体积为（）A．116B C．32D．12【答案】A【解析】该几何体是一个直三棱柱截去一个小三棱锥,如图 所示,则其体积为：611111213121221=⨯⨯⨯⨯-⨯⨯⨯=V .故选A.3.【2016年江西四校高三联考】棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是（ ）A.314 B.4 C.310D.3 【答案】B【解析】如图，红色虚线表示截面，可见这个截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半，122242V =⨯⨯⨯=. 4.【2016年安徽淮北一中高三检测】《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L 与高h ，计算其体积V 的近似公式2136V L h ≈，它实际上是将圆锥体积公式中的圆周率π近似取为3，那么近似公式2275V L h ≈，相当于将圆锥体积公式中的π近似取为（ ） A ．227 B ．258 C ．15750 D ．355113【答案】B 【解析】2211312V πr h L h π==，若2275V L h ≈，则121275π=，258π=．故选B ． 5.【2016年江西南昌高三统考】如图网格纸上小正方形的边长为l ，粗实线画出的是某几何体的三视图，则这个几何体的体积为(A)1 (B)2 (C)3 (D)4【答案】D【解析】由题意，得该几何体是由两个三棱锥组合而成（如图所示），其中⊥AD 面ABC ，⊥CE 面ABC , BCAC ⊥,4,2====CE AD BC AC ，则4)4221(312)2221(3121=⨯⨯⨯+⨯⨯⨯⨯=+=V V V ；故选D ．6. 【2016年河南八市高三联考】已知直线l 与平面α相交但不垂直，m 为空间内一条直线，则下列结论可能成立的是（ ）A ．//,m l m α⊥B ．,m l m α⊥⊥C ．,//m l m α⊥D ．//,//m l m α 【答案】C7. 【2016年福建厦门一中高三模考】某几何体的三视图如图所示，则该几何体的体积为（ ）A B C D 【答案】C【解析】根据三视图画出直观图如图所示，即为三棱柱中截去一个三棱锥，其体积为111-2212232B EFD V V V -==⨯-⨯⨯=-=三棱柱 8. 【2016年湖南师大附中高三三模】如图，若Ω是长方体ABCD －A 1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体，其中E 为线段A 1B 1上异于B 1的点，F 为线段BB 1上异于B 1的点，且EH ∥A 1D 1，则下列结论中不正确的是（ ）A ．EH ∥FGB ．四边形EFGH 是矩形C ．Ω是棱柱D ．四边形EFGH 可能为梯形【答案】D9. 【2016年山西四校高三联考】已知一个几何体的三视图如右图所示，则该几何体的体积为（ ）A.7B.173C. 273D.8正视图【答案】A10.【2016年河北石家庄高三模考】如图，已知平面l =⊥βαβα ,，B A 、是直线l 上的两点，D C 、是平面β内的两点，且6,6,3,,===⊥⊥CB AB AD l CB l DA .P 是平面α上的一动点，且直线PC PD ,与平面α所成角相等，则二面角D BC P --的余弦值的最小值是（ ） A．51 B ．21C ．23D ．1【答案】C【解析】因为βα⊥⊥,AB AD ,所以而建立空间坐标系，以B 为原点，BC 为y 轴正向，BA 为x 轴负方向，过点B 且垂直于l 在平面β内向上的轴为z 轴正方向，则)036()060(),000(),006(，，，，，，，，--D C B A ,设点),0,(z x P ，),6,(),,3,6(z x PC z x PD --=---=直线PC PD ,与平面α所成角相等，则16)8(6)(3)6(222222=++⇒+-=+--z x z x z x 即点P 的轨迹为圆。

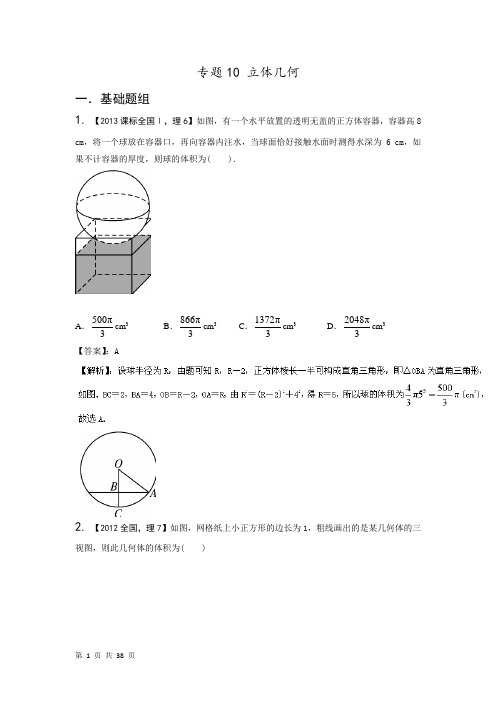
专题10 立体几何一．基础题组1.【2013课标全国Ⅰ，理6】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为 6 cm，如果不计容器的厚度，则球的体积为( )．A．500π3cm3B．866π3cm3C．1372π3cm3D．2048π3cm3【答案】：A2.【2012全国，理7】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )A．6 B．9 C．12 D．18【答案】B3.【2011全国新课标，理6】在一个几何体的三视图中，正视图和俯视图如下图所示，则相应的侧视图可以为( )【答案】D4. 【2006全国，理7】已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（ ）（A ）16π （B ）20π （C ）24π （D ）32π 【答案】C5. 【2005全国1，理2】一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为（ ）A ．8π2B ．8πC ．4π2D ．4π 【答案】B6. 【2005全国1，理4】如图，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE 、△BCF 均为正三角形，EF//AB ，EF=2，则该多面体的体积为（ ）A ．32 B ．33 C ．34 D ．23【答案】A7. 【2010新课标，理14】正视图为一个三角形的几何体可以是__________．(写出三种)答案：三棱锥、圆锥、四棱锥(答案不唯一)8. 【2014课标Ⅰ，理19】(本小题满分12分)如图，三棱柱111C B A ABC -中，侧面C C BB 11为菱形，C B AB 1⊥.（Ⅰ）证明：1AB AC =;（Ⅱ）若1AC AB ⊥，︒=∠601CBB ,BC AB =,求二面角111C B A A --的余弦值.AA 1B1CC 1【答案】（Ⅰ）详见解析；（Ⅱ）17z yOAA 1BB 1CC 19. 【2013课标全国Ⅰ，理18】如图，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°.(1)证明：AB ⊥A 1C ；(2)若平面ABC ⊥平面AA 1B 1B ，AB ＝CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值．10. 【2008全国1，理18】（本小题满分12分）四棱锥A BCDE -中，底面BCDE 为矩形，侧面ABC ⊥底面BCDE ，2BC =，CD =AB AC =．（Ⅰ）证明：AD CE ⊥；（Ⅱ）设CE 与平面ABE 所成的角为45 ，求二面角C AD E --的大小．11.【2015高考新课标1，理6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

高一数学必修第二册第八章《立体几何初步》单元练习题卷9（共22题）一、选择题（共10题）1.用斜二测画法作出一个三角形的直观图，则原三角形面积是直观图面积的( )A．12倍B．2√2倍C．2倍D．√24倍2.若长方体三个面的面积分别为√2，√3，√6，则长方体的体积等于( )A．√6B．6C．6√6D．363.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为( )A．9πB．22π3C．28π3D．34π34.在下列命题中：①存在一个平面与正方体的12条棱所成的角都相等；②存在一个平面与正方体的6个面所成较小的二面角都相等；③存在一条直线与正方体的12条棱所成的角都相等；④存在一条直线与正方体的6个面所成的角都相等．其中真命题的个数为( )A．1B．2C．3D．4 5.已知底面半径为1的圆锥侧面展开图是一个半圆，则该圆锥的体积是( )A．√33πB．2√33πC．√3πD．4√33π6.如图，正方体ABCD−A1B1C1D1的棱长为a，M，N分别为A1B和AC上的点，A1M=AN=√23a，则MN与平面BB1C1C的位置关系是( )A．相交但不垂直B．平行C．垂直D．不能确定7.体积为√3的三棱锥P−ABC的顶点都在球O的球面上，PA⊥平面ABC，PA=2，∠ABC= 120∘，则球O的体积的最小值为( )A．7√73πB．28√73πC．19√193πD．76√193π8.已知矩形ABCD中，AB=2，BC=1，F为线段CD上一动点（不含端点），现将△ADF沿直线AF进行翻折，在翻折过程中不可能成立的是( )A．存在某个位置，使直线AF与BD垂直B．存在某个位置，使直线AD与BF垂直C．存在某个位置，使直线CF与DA垂直D．存在某个位置，使直线AB与DF垂直9.如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则( )A．BM=EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM=EN，且直线BM，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线10.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A．14斛B．22斛C．36斛D．66斛二、填空题（共6题）11.若圆柱的轴截面为正方形，且此正方形面积为4，则该圆柱的体积为．12.设一个圆锥的侧面展开图是半径为2的半圆，则此圆锥的体积等于．13.若两条直线a，b无公共点，则两直线的位置关系是．14.棱长为1的正方体ABCD−A1B1C1D1及其内部一动点P，集合Q={P∣∣ PA∣ ≤1}，则集合Q构成的几何体表面积为．15.如图所示，已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成，则该多面体的体积是．16.在三棱椎P­−ABC中，底面ABC是等边三角形，侧面PAB是直角三角形，且PA=PB=2，PA⊥AC，则该三棱椎外接球的表面积为．三、解答题（共6题）17.已知圆柱的底面直径与高都等于球的直径．求证：(1) 球的表面积等于圆柱的侧面积；．(2) 球的表面积等于圆柱全面积的2318.侧面都是等腰直角三角形的正三棱锥，底面边长为a时，求该棱锥的表面积．19.已知四棱锥P−ABCD中，底面ABCD为等腰梯形，AD∥BC，PA=AD=AB=CD=1，BC=2，PB=PD=√2．(1) 证明：AC⊥平面PAB；(2) 过PA的平面交BC于点E，若平面PAE把四棱锥P−ABCD分成体积相等的两部分，求此时三棱锥E−PBD的体积．20.画出如图所示水平放置的直角梯形的直观图．21.如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD为正方形，F为对角线AC与BD的交点，E为棱PD的中点．(1) 证明：EF∥平面PBC；(2) 证明：AC⊥PB．22.如图，在正方体ABCD−A1B1C1D1中，点M，N，E，F分别是棱CD，AB，DD1，AA1上的点，若MN与EF交于点Q，求证：D，A，Q三点共线．答案一、选择题（共10题） 1. 【答案】B【解析】设原三角形的底边长为 a ，高为 ℎ，则直观图中底边长仍为 a ，高为 ℎ2⋅sin45∘=√2ℎ4，所以原三角形面积与直观图面积的比值为 12aℎ12a⋅√2ℎ4=√2=2√2，即原三角形面积是直观图面积的2√2 倍． 【知识点】直观图2. 【答案】A【解析】如图，设长方体 ABCD −A 1B 1C 1D 1 的侧面 AA 1B 的面积为 √2，侧面 AA 1D 的侧面积为 √3，侧面ABD 的侧面积为 √6．再设侧棱 AA 1=a ，AD =b ，AB =c ． 则 {ac =√2,ab =√3,bc =√6, 三式作积得：a 2b 2c 2=6．所以 abc =√6．所以长方体的体积等于 √6．【知识点】棱柱的表面积与体积3. 【答案】D【解析】根据几何体的三视图可得直观图为：该几何体为上面为一个半径为 2 的半球，下面为底面半径为 2，高为 3 的半圆柱体． 如图所示：故 V =12×π×22×3+23×π×23=34π3．【知识点】球的表面积与体积、由三视图还原空间几何体、圆柱的表面积与体积4. 【答案】D【解析】①存在一个平面AB1D1与正方体的12条棱所成的角都相等，故①正确；②存在一个平面AB1D1与正方体的6个面所成较小的二面角都相等，故②正确；③存在一条直线AC1与正方体的12条棱所成的角都相等，故③正确；④存在一条直线AC1与正方体的6个面所成的角都相等，故④正确．故选：D．【知识点】棱柱的结构特征5. 【答案】A【解析】设圆锥的母线长为l，则πl=2π×1，所以l=2，设圆锥的高为ℎ，所以ℎ=√22−1=√3，所以圆锥的体积V=13π⋅l2⋅√3=√3π3．【知识点】圆锥的表面积与体积6. 【答案】B【解析】如图，过点M作MP∥A1B1交BB1于点P，过点N作NQ∥AB交BC于点Q，连接PQ，因为A1M=AN=√23a，且A1B=AC=√2a，所以MP=23A1B1，NQ=23AB，所以四边形MNQP为平行四边形，所以MN∥PQ．又因为MN⊄平面BB1C1C，PQ⊂平面BB1C1C，所以MN∥平面BB1C1C．【知识点】直线与平面平行关系的判定7. 【答案】B【解析】因为V P−ABC=13S△ABC⋅PA=13×12×AB×BC×sin120∘×2=√3，所以AB⋅BC=6．因为PA⊥平面ABC，PA=2，所以O到平面ABC的距离为d=12PA=1．设△ABC的外接圆半径为r，球O的半径为R，R=√r2+d2=√r2+1．由余弦定理可知AC2=AB2+BC2−2AB⋅BC⋅cos120∘=AB2+BC2+6≥2AB⋅BC+6=18,当且仅当AB=BC=√6时取等号，所以AC≥3√2．由正弦定理可得2r=ACsin∠ABC ≥√2√32=2√6，所以r≥√6，所以R≥√7．所以当R=√7时，球O的体积取得最小值V=43πR3=28√7π3．【知识点】球的表面积与体积8. 【答案】C【解析】对于A，连接DB，作AF⊥BD于O，交DC与F（如图），此时DO⊥AF，BO⊥AF，将△ADF沿直线AF进行翻折过程中，AF⊥面DOB，可得AF⊥DB．对于B，因为AD⊥DF始终成立，要使直线AD与BF垂直，只需AD⊥DB即可，只需DB=√3即可，显然存在存在某个位置，使DB=√3，对于C，因为AD⊥DF始终成立，要使直线AD与CF垂直，只需AD⊥DC即可，根据勾股定理可得只需DC=2即可，显然不存在存在某个位置，使DC=2，对于D，如图∠DFA<90∘，在翻折过程中，一定存在某个位置使得DF⊥DC，即DF⊥AB．综上，在翻折过程中不可能成立的是C．【知识点】直线与直线的位置关系9. 【答案】B【解析】如图，连接BD，BE．因为N为正方形ABCD的中心，所以N∈BD．又因为M是ED的中点，所以M∈ED．所以M,N∈平面BED．所以由图知BM与EN相交，设ED=DC=a，则BD=√2a，EB=√2a．在△EBD中，由中线定理得EN2=14[2(ED2+EB2)−BD2]=a2，所以EN=a．又因为BM=√72a，所以BM≠EN．【知识点】直线与平面垂直关系的性质10. 【答案】B【解析】设圆锥底面的半径为R尺，由14×2πR=8得R=16π，从而米堆的体积V=1 4×13πR2×5=3203π（立方尺），因此堆放的米约有3203×1.62π≈22（斛）．【知识点】圆锥的表面积与体积二、填空题（共6题）11. 【答案】2π【解析】因为圆柱的轴截面是正方形，且面积为4，所以圆柱的底面半径r=1，高ℎ=2，所以圆柱的体积V=πr2h=π×12×2=2π．【知识点】圆柱的表面积与体积12. 【答案】√33π【解析】设圆锥的底面半径为r，则2πr=2π，所以r=1．所以圆锥的高ℎ=√22−12=√3．所以圆锥的体积V=13πr2h=√33π．【知识点】圆锥的表面积与体积13. 【答案】平行或异面【知识点】直线与直线的位置关系14. 【答案】5π4【知识点】球的表面积与体积15. 【答案】√26【解析】由题知该多面体为正四棱锥，底面边长为1，侧棱长为1，斜高为√32，连接顶点和底面中心即为高，可求得高为√22，所以体积V=13×1×1×√22=√26．【知识点】棱锥的表面积与体积16. 【答案】12π【解析】由于PA=PB，CA=CB，PA⊥AC，则PB⊥CB，因此取PC中点O，则有OP=OC=OA=OB，即O为三棱锥P−­ABC外接球球心，又由PA=PB=2，得AC=AB=2√2，所以PC=√22+(2√2)2=2√3，所以S=4π×(√3)2=12π．【知识点】球的表面积与体积三、解答题（共6题）17. 【答案】(1) 略．(2) 略．【知识点】圆柱的表面积与体积、球的表面积与体积18. 【答案】因为正三棱锥的侧面都是等腰直角三角形，所以侧棱长等于√22a，所以该棱锥的表面积S=√34a2+3×12×(√22a)2=3+√34a2．【知识点】棱锥的表面积与体积19. 【答案】(1) 在等腰梯形ABCD，AD∥BC，AD=AB=CD=1，BC=2，由题意得：∠ABC=60∘，在△ABC中，AC2=AB2+BC2−2AB⋅BCcos∠ABC=3，则有AB2+AC2=BC2，所以AC⊥AB，在△PAB中，因为PA=AB=1，PB=√2，所以PA⊥AB，同理，在△PAD中，所以PA⊥AD，所以AB∩AD=A，所以PA⊥平面ABCD，又因为PA⊥平面ABCDAC⊂平面ABCD}⇒PA⊥AC，即AC⊥ABAC⊥PAAB∩PA=A}⇒AC⊥平面PAB．(2) 在梯形ABCD中，设BE=a，所以V三棱锥P−ABE =12V四棱锥P−ABCD，所以S△ABE=12S梯形ABCD，所以12×AB×BEsin∠ABE=(BC+AD)×ℎ4，而ℎ=ABsin60∘=√32，所以a=32，所以V三棱锥E−PBD =V三棱锥P−BED=13S△BED⋅PA=13×12×32×√32×1=√38.故三棱锥E−PBD的体积为√38．【知识点】直线与平面垂直关系的判定、棱锥的表面积与体积20. 【答案】（1）在已知的直角梯形OBCD中，以底边OB所在直线为x轴，垂直于OB的腰OD所在直线为y轴建立平面直角坐标系．画相应的xʹ轴和yʹ轴，使∠xʹOʹyʹ=45∘，如图①②所示．（2）在xʹ轴上截取OʹBʹ=OB，在yʹ轴上截取OʹDʹ=12OD，过点Dʹ作xʹ轴的平行线l，在l上沿xʹ轴正方向取点Cʹ，使得DʹCʹ=DC．连接BʹCʹ，如图②．（3）所得四边形OʹBʹCʹDʹ就是直角梯形OBCD的直观图，如图③．【知识点】直观图21. 【答案】(1) 因为四边形ABCD是正方形，F为对角线AC与BD的交点，所以F是BD的中点，又E是PD的中点，所以EF∥PB，又EF⊄平面PBC，PB⊂平面PBC，所以EF∥平面PBC．(2) 因为四边形ABCD是正方形，所以AC⊥BD，因为PD⊥平面ABCD，AC⊂平面ABCD，所以AC⊥PD，又BD⊂平面PBD，PD⊂平面PBD，BD∩PD＝D，所以AC⊥平面PBD，又PB⊂平面PBD，所以AC⊥PB．【知识点】直线与平面平行关系的判定、直线与平面垂直关系的性质22. 【答案】因为MN∩EF=Q，所以Q∈直线MN，Q∈直线EF，又因为M∈直线CD，N∈直线AB，CD⊂平面ABCD，AB⊂平面ABCD，所以M,N∈平面ABCD，所以MN⊂平面ABCD，所以Q∈平面ABCD．同理，可得EF⊂平面ADD1A1，所以Q∈平面ADD1A1，又因为平面ABCD∩平面ADD1A1=AD，所以Q∈直线AD，即D，A，Q三点共线．【知识点】平面的概念与基本性质。

【2017年高三数学优质试卷分项精品】专题九 立体几何一、选择题1.【2016全国大联考2（课标I 卷）】我国数学史上有一部堪与欧几里得《几何原本》媲美的书，这就是历来被尊为算经之首的《九章算术》，其中卷第五《商功》有一道关于圆柱体的体积试题：今有圆堡，周四丈八尺，高一丈一尺，问积几何？其意思是：含有圆柱形的土筑小城堡，底面周长是4丈8尺，高1丈1尺，问它的体积是多少？若π取3，估算小城堡的体积为（ ）A ．1998立方尺B ．2012立方尺C ．2112立方尺D ．2324立方尺 【答案】C【解析】设圆柱体的底面半径为R ，则由题意，得2348R ⨯=，得8R =，所以小城堡的体积238112112V S h ==⨯⨯=底（立方尺），故选C ．2.[2016年全国大联考3(课标Ⅱ卷)】如图所示，网格纸上每个小格都是边长为1的正方形，粗线画出的是一个几何体的三视图，记该几何体的各棱长度构成的集合为A ，则（ ） AA B ．3A ∈ C．A D．A【答案】C【解析】由三视图知该几何体的直观图为图中所示的三棱锥A BCD -，AB AC BC ===，1BD =，故选C ．DCBA3.[2016全国大联考4(山东卷)】某三棱锥的三视图如图所示,则该三棱锥的外接球的体积是（ ）A ．43π B ．83πC D【答案】C.4.【2016全国大联考2(山东卷)】如图为某几何体的三视图，则其体积为（ ）A.243π+ B.243π+ C.43π+ D.43π+【答案】D【解析】由三视图可知，该几何体是一个半圆柱（所在圆柱1OO ）与四棱锥的组合体，其中四棱锥的底面ABCD 为圆柱的轴截面，顶点P 在半圆柱所在圆柱的底面圆上（如图所示），且P 在AB 上的射影为底面的圆心O .由三视图数据可得，半圆柱所在圆柱的底面半径1r =，高2h =， 故其体积221111222V r h πππ==⨯⨯=； 四棱锥的底面ABCD 为边长为2的正方形，PO ⊥底面ABCD ，且1PO r ==.故其体积2211421333ABCD V S PO =⨯=⨯⨯=正方形. 故该几何体的体积1243V V V π=+=+.5.【2016押题卷1（课标1卷）】某几何体的三视图如图所示，则该几何体的体积为（ ）A ．16163π-B ．32163π-C ．1683π-D ．3283π-【答案】D6.【2016全国大联考3（课标I 卷）】已知20sin 12cos d 2x a x xπ⎛⎫=-+ ⎪⎝⎭⎰，如图，若三棱锥P ABC -的最长的棱PA a =，且PB BA ⊥，PC AC ⊥，则此三棱锥的外接球的体积为（ ） A.163πB.43πC. πD.3π【答案】B 【解析】()200sin 12cos d sin cos d (cos sin )202x a x x x x x x x πππ⎛⎫=-+=+=-+= ⎪⎝⎭⎰⎰，由于PB BA ⊥，PC AC ⊥，则三棱锥的外接球的直径为2PA a ==，因此外接球的体积是3441=33ππ⨯. 7.【2016全国大联考4（课标Ⅰ卷）】在三棱锥BCD A -中，△ABC 与△BCD 都是边长为6的正三角形，平面ABC ⊥平面BCD ，则该三棱锥的外接球的体积为 （ ）A.π155B.π60C.π1560D.π1520【答案】D8.【2016押题卷1（课标1卷）】四棱锥P ABCD -的底面ABCD 为正方形，PA ⊥底面ABCD ，2AB =，若该四棱锥的所有顶点都在体积为24316π同一球面上，则PA =（ ）A ．3B ．72C ．D ．92【答案】B【解析】连结,AC BD 交于点E ，取PC 的中点O ，连结OE ，则OE PA ，所以OE ⊥底面ABCD ，则O 到四棱锥的所有顶点的距离相等，即O球心，均为12PC ==34243316ππ=，解得72PA =，故选B ．9.【2016全国大联考1（课标I 卷）】直三棱柱111ABC A B C -中，底面是正三角形，三棱柱P 是111A B C ∆中心，且三棱柱的体积为94，则PA 与平面ABC 所成的角大小是（ ） A.6πB.4πC.3πD.23π 【答案】C【解析】由题意可设底面三角形的边长为a ，过点P 作平面ABC 的垂线，垂足为O ，则点O 为底面ABC 的中心，故PAO ∠即为PA与平面ABC所成的角，由于23OA ==，而，又因为三棱柱的体积为94，由棱柱体积公式得)294V ==，解得a =tan POPAO AO∠===，得，故PA 与平面ABC 所成的角大小是3π，故正确答案为C.10.【2016押题卷1（课标2卷）】在正方体1111ABCD A B C D -中，M 是线段11A C 的中点，若四面体M ABD -的外接球体积为36p ，则正方体棱长为（ ）B 1AA ．2B ．3C ．4D ．5 【答案】C【解析】设正方体棱长为a ，因为ABD D 是等腰直角三角形，且MA MB MD ==，设'O 是BD 中点，连接'O M ，则'O M ^面ABD ，所以球心O 必在'O M 上，可求得外接球半径为3，可得2223(3))a =-+，解得4a =，故正方体棱长为4． 11.【2016押题卷3（课标1卷）】已知H 是球O 的直径AB 上一点，2:1:=HB AH ，⊥AB 平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的体积为（ ） A.π9 B. π43C. π829D.π34 【答案】C【解析】如图，易知点H 为截面圆的圆心，取截面圆上一点M ，连接HM ，OM .设球O 的半径为R ，则由2:1:=HB AH ，得R AH 32=， 所以R OH 31=. 因为截面面积为ππ=⋅2HM ， 所以1=HM .在Rt △HMO 中，222HM OH OM +=， 所以191912222+=+=R HM R R ， 所以423=R . 所以ππ829)423(343=⋅=球V . 二、填空题12.【2016全国大联考3（课标Ⅱ卷）】在正四棱锥V ABCD -内有一半球，其底面与正四棱锥的底面重合，且与正四棱锥的四个侧面相切，若半球的半径为2，则当正四棱锥的体积最小时，其高等于_____________．【答案】【解析】如图所示，设顶点V 在底面ABCD 的射影为点O ，并设正四棱锥的高VO 的长为x ，底面正方形的边长为2a ，过点O 作平行于AB 的直线交BC 于点F ，作OM ⊥VF 于点M ，则OM =2，VF =.在Rt △VOF中，有ax =，得22244x a x =-.所以正四棱锥V ABCD -的体积为322116()4334x V x a x x =⋅=⨯-（2x >），222216(12)()3(4)x x V x x -'=⨯-.令()0V x '=，得x =当x ∈时，()0V x '<；当)x ∈+∞时，()0V x '>，故当x =F x22aOD CBAVM三、解答题13.【2016押题卷2（课标I 卷）】在三棱锥ACD P -中，CD AD ⊥，CD AD ==2，△PAD 为正三角形，点F 是棱PD 的中点，且平面PAD ⊥平面ACD ． （Ⅰ）求证：AF ⊥平面PCD ；（Ⅱ）求二面角F AC P --的平面角的余弦值.【解析】（Ⅰ）因为PA AD =,F 是PD 的中点， 所以AF ⊥PD ，又因为平面PAD ⊥平面ACD ，CD AD ⊥， 所以⊥CD 平面PAD ， 因为⊂AF 平面PAD ， 所以AF CD ⊥. 因为D CD PD =⋂，所以AF ⊥平面PCD . ……………………6分设平面CAF 的法向量为),,(222z y x =m，则222220302AC x y x AF ⎧⋅=-+=⎪⎨⋅=-=⎪⎩m m ，取2x =1，则3122==z y ，，则m =（1,1,3）， ……………10分所以537111,cos ⨯++=∙>=<||||n m n m n m，所以二面角F AC P --的平面角的余. .……………12分14.【2016押题卷2（课标Ⅱ卷）】在四棱柱1111D C B A ABCD -中，底面ABCD 是菱形，且1AA AB =， 6011=∠=∠AD A AB A .（1）求证：平面⊥BD A 1平面AC A 1； （2）若221==D A BD ，求平面BD A 1与平面BD B 1所成角的大小.（2）由DA B A 11=及221==D A BD 知DA B A 11⊥，又由,,,11BD BD AB B A AD D A ===得BD A 1∆≌ABD ∆，故 90=∠BAD ，于是112221AA BD O A AO ===， 从而O A AO 1⊥，结合BD O A ⊥1，得⊥O A 1底面ABCD ，如图，建立空间直角坐标系，则),1,0,0(),0,1,0(),0,1,0(),0,0,1(1A D B A -(1,0,0)C -,),1,0,1(11-==AA BB (0,2,0),DB =uu u r设平面BD B 1的一个法向量为),,(z y x n =，由⎪⎩⎪⎨⎧=⋅=⋅001BB n BD n 得⎩⎨⎧=+-=00z x y ，令1=x ，得)1,0,1(=n ，平面BD A 1的一个法向量为)0,0,2(=CA ， 设平面BD A 1与平面BD B 1所成角为θ，则22cos ==θ，故 45=θ.（12分）15.【2016押题卷2（山东卷）】棱锥P ABCD -的三视图如图所示，（I）求证：平面PBD⊥平面PAC（II）在线段PD上是否存在一点Q，使CQ与平面PBD，若存在，指出点Q的位置，若不存在，说明理由.2，【解析】（Ⅰ）由三视图可知在Rt△BAD中，AD=2，BD=2∴AB=2，ABCD为正方形，因此BD⊥AC. …………2分BD平面ABCD，∴BD⊥PA .∵PA⊥平面ABCD，⊂又∵PA∩AC=A,∴BD⊥平面PAC.BD平面PBD, ∴平面PBD⊥平面PAC…………6分∵⊂16.【2016押题卷1（山东卷）】在如图所示的几何体中，四边形ABCD 为矩形，直线⊥AF 平面ABCD ，AB EF //，12,2====EF AF AB AD ，点P 在棱DF 上. （1）求证：BF AD ⊥；（2）若P 是DF 的中点，求异面直线BE 与CP 所成角的余弦值；（3）若FP =C APD --的余弦值.【解析】（1）证明：因为⊥AF 平面ABCD ，所以⊥AF AB ，又⊥AD AB,所以⊥AD 平面ABEF ，又⊂BF 平面ABEF ，故BF AD ⊥.…………3分（2）因为 90=∠BAF ，所以AB AF ⊥，又由（1）得AF AD ⊥，AB AD ⊥，所以以A 为坐标原点，AB ，AD ，AF 所在直线分别为z y x ,,轴，建立如图所示空间直角坐标系xyz A -，则)0,0,1(B ，)1,0,21(E ，)21,1,0(P ，)0,2,1(C .………………4分 所以)1,0,21(-=BE ，)21,1,1(--=CP ，所以1554||||,cos =>=<CP BE CP BE ， 所以异面直线BE 与CP 所成角的余弦值为1554.………………8分（3）因为⊥AB 平面ADF ，所以平面ADF 的一个法向量)0,0,1(1=n .由FP =P 为FD 的三等分点且此时)32,32,0(P .在平面APC 中，)32,32,0(=AP ，)0,2,1(=AC .所以平面APC 的一个法向量)1,1,2(2--=n .……………………10分 所以36|||||,cos |2121==><n n n n ，又因为二面角C AP D --的大小为锐角，所以该二面角的余弦值为36.……………………………………………………………………12分 17.【2016全国大联考1（课标Ⅱ卷）】已知四棱锥ABCD P -中，⊥PA 平面ABCD ，底面ABCD 是菱形，0120=∠BAD ，对角线AC 与BD 交于点O ，M 为OC 中点．（Ⅰ）求证：⊥BD PM ；（Ⅱ）若二面角D PM O --的正切值为62，求PAAD的值．【解析】（Ⅰ） 因为⊥PA 平面ABCD ，所以PA BD ⊥又ABCD 为菱形，所以AC BD ⊥,又因为PA AC A = ，所以BD ⊥平面PAC ，又因为PM AC P ⊂面，所以⊥BD PM ．……5分（Ⅱ）如图,以A 为原点,,AD AP 所在直线为y 轴,z 轴建立空间直角坐标系，设PA a =，1AD =，则(0,0,)P a ，(0,1,0)D ，,3,0)8M,1,0)4O 从而(0,1,)PD a =-，3,)8PM a =-，3(,0)4OD =因为BD ⊥平面PAC ,所以平面PMO的一个法向量为3(,0)4OD = ．设平面PMD 的法向量为(,,)n x y z = ,由,PD n PM n ⊥⊥得0308y az x y az -=⎧+-=取,,1x y a z ===，即,,1)n a = ……10分设OD 与n的夹角为θ，则二面角O PM D --大小与θ相等从而tan θ=，得cos 15θ=，1cos 5θ==，，解得34a =，故34PA AD =．……12分18.【2016全国大联考1（山东卷）】如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF 且BE ＜CF ，∠BCF=2π，AD=3，EF=2.（1）求证： AE ∥平面DCF ；（2）若1BE =-，且λ=BEAB，当λ取何值时，直线AE 与BF 所成角的大小为060？ 【解析】（1）过E 作EG ∥BC 交FC 于G ，连结DG ， 因为BE ∥CF ， 所以四边形BCGE 是平行四边形 ， 因此EG ∥BC ∥AD ，--------------------------2分且EG=BC=AD ， 所以四边形ADGE 也是平行四边形 ， 于是AE ∥DG .又AE ⊄平面DCF ，DG ⊂平面DCF ， 故AE ∥平面 DCF ． ---------------------------5分（2）过E 作GE ⊥CF 交CF 于G ，由已知 EG ∥BC ∥AD ，且EG=BC=AD ，所以EG=AD ＝3，又EF=2， 所以GF=1 ．因为四边形ABCD 是矩形， 所以DC ⊥BC ． 因为∠BCF=2π， 所以FC ⊥BC ，又平面AC ⊥平面BF ，平面AC∩平面BF=BC ，于是FC ⊥平面AC ， 所以FC ⊥CD .分别以CB 、CD 、CF 为轴建立空间直角坐标系． ---------------------------7分 由λ=BEAB，得AB=1)λ. 所以 A （3，1)λ-，0），B ，E(3，01-)，F(0，0)，， 所以→AE=(0，(1λ-，1)，(BF =.------------------------9分依题意有0cos 60||||AE BF AE BF ⋅=⋅，ABCDEFG即12=，解得1λ=.----------------------------11分 故当1λ=时，直线AE 与BF 所成角的大小为060.----------------------------12分19.【2016全国大联考2（课标I 卷）】如图，在直三棱柱111ABC A B C -（侧棱垂直于底面的棱柱为直棱柱）中，11,2BC CC AC ===，=90ABC ∠︒． （1）求证：平面1ABC ⊥平面11A B C ；（2）设D 为AC 的中点，求平面1ABC 与平面1C D B 所成锐角的余弦值．【解析】（1）∵=90ABC ∠︒，∴AB BC ⊥．又由条件知1BB ⊥平面ABC ，AB ⊂平面ABC ，∴1BB AB ⊥．……………2分 又∵1BB BC B = ，∴AB ⊥平面11BB C C ，∴1AB B C ⊥．由11BC CC ==，知四边形11BB C C 为正方形，∴11B C BC ⊥．……………4分 又1=AB BC B ，则1B C ⊥平面1ABC ．又∵1B C ⊂平面11A B C ，∴平面1ABC ⊥平面11A B C ．……………6分20.【2016全国大联考2（山东卷）】如图，四棱锥P ABCD -中，底面ABCD 是平行四边形，且PA ⊥平面ABCD ，2PA AB AD ===，60BAD ∠= . （Ⅰ）证明：平面PBD ⊥平面PAC ；（Ⅱ）求平面APD 与平面PBC 所成二面角（锐角）的余弦值.CBP（Ⅱ）设AC 与BD 的交点为O ，取PC 的中点Q ，连结OQ . 在APC ∆中，AO OC =，CQ QP =， ∴//OQ PA ， ∵PA ⊥平面ABCD ，∴OQ ⊥平面ABCD . ………………………6分如图，以OA 、OB 、OQ 所在直线分别为x 轴、y 轴、z轴，建立空间直角坐标系，则(0,1,0),(A B C ，(0,1,0),2)D P -. ………………………7分设平面PBC 的一个法向量为(,,)n x y z =r，而(1,0)BC =-uu u r，(2)PB =-uu r，由n BC n PB⎧⊥⎪⎨⊥⎪⎩r uu u r r uu r，得020y y z ⎧-=⎪⎨+-=⎪⎩ ，∴cos ,||||m n m n m n <>===⨯u r ru r r g u r r . 设所求二面角为θ，由题意可得(0,)2πθ∈，所以cos |cos ,|m n θ=<>= . …………………12分C。

一、选择题：本大题共小题，每小题分，共分．在每小题给出的四个选项中，只有一项是符合题目要求的．．已知互相垂直的平面α，β交于直线.若直线，满足∥α，⊥β，则( )．∥ ．∥ ．⊥．⊥解：因为⊥β，⊂β，所以⊥.故选.．()某几何体的三视图如图所示(单位：)，则该几何体的体积是()．．解：该几何体为一个正方体和一个正四棱锥的组合体，其体积＝＋×××＝()．故选.．一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是( )．球．三棱锥 ．正方体．圆柱解：球的三视图是三个相同的圆，三棱锥的三视图可以是三个全等的三角形，正方体的三视图可能是三个相同的正方形，而当圆柱的底面放置在水平面上时，其俯视图是圆，正视图是矩形．故选.．()如图，在正方体­中，，分别为，的中点，则下列直线中与直线相交的是( )．直线．直线 ．直线．直线解：在同一个平面内不平行的两条直线或有公共交点的两条直线为相交直线，可判断选项正确．故选. ．如图，在正方体­中，，分别是棱，的中点，则与平面的位置关系是( )．∥平面．与平面相交 ．在平面内．与平面的位置关系无法判断解：正方体­中，，分别是棱，的中点，取的中点，连接，，则∥，∥，所以∥平面，∥平面，又因为∩＝，所以平面∥平面，从而可得∥平面.故选.．一个四面体的顶点在空间直角坐标系­中的坐标分别是(，，)，(，，)，(，，)，(，，)，画该四面体三视图中的正视图时，以平面为投影面，则得到的正视图可以为( )解：如图所示，点(，，)，(，，)，(，，)，(，，)，此四点恰为正方体­上四个点，且构成一个棱长为的正四面体，该正四面体在投影面上的正视图为正方形.故选.．已知正四棱柱­中，＝，为中点，则异面直线与所成角的余弦值为( )解：取的中点，连接，则∠为所求的角，设＝，∠＝＋×)＝＝＝.故选.．()已知四棱锥的三视图如图所示，则四棱锥的四个侧面中面积最大的是( )．．．．解：由三视图知，该几何体是四棱锥，其直观图如图，四个侧面中面积最大的是△，由题设知＝，＝，＝＝，所以＝，取中点，连接，，则⊥，所以⊥，＝＝，所以△＝·＝.故选.．()已知等腰直角三角形的直角边的长为，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )．π．π解：将等腰直角三角形绕其斜边所在直线旋转一周，可得到两个同底的圆锥，因此＝π·()·＝π.故选.．半球内有一个内接正方体，则这个半球的体积与正方体的体积之比为( )π∶π∶．π∶．π∶解：将半球补成整个球，同时把原半球的内接正方体再补接一个同样的正方体，构成的长方体恰好是球的内接长方体，那么这个长方体的体对角线就是它的外接球的直径．设正方体的棱长为，球的半径为，则()＝＋＋()，即＝.所以半球＝×π＝π＝π，正方体＝.所以半球∶正方体＝π∶＝π∶.故选.．已知正四棱柱­中，＝，＝，为的中点，则直线与平面的距离为( )．．解：如图，连接，交于，连接，在△中，易证∥.从而∥平面，所以直线到平面的距离即为点到平面的距离，设为.由等体积法，得­＝△×＝­＝△×＝××××＝.又因为在△中，＝，＝＝，。

第八章《立体几何初步》章末检测一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、列说法中，正确的是()B.若棱柱有两个侧面是矩形，则该棱柱的其他侧面也是矩形2、一平面四边形OABC的直观图O′A′B′C′如图所示，其中O′C′⊥x′轴，A′B′⊥x′轴，B′C′∥y′轴，则四边形OABC的面积为()A．322B．32C．3 D．323、如图，在三棱柱ABC－A1B1C1中，AA1⊥底面ABC，AB⊥BC，AA1＝AC＝2，直线A1C与侧面AA1B1B所成的角为30°，则该三棱柱的侧面积为()A．4＋42B．4＋43C．12 D．8＋4 2 4、已知三棱台ABC－A1B1C1中，三棱锥A－A1B1C1的体积为4，三棱锥A1－ABC 的体积为8，则该三棱台的体积为()A．12＋3 3 B．12＋4 2C．12＋4 3 D．12＋475、如图1，正方形SG1G2G3中，E、F分别是G1G2、G2G3的中点，D是EF的中点，如图2，沿SE、SF、EF将正方形折成一个四面体，使G1、G2、G3重合，重合后的点记为G，则在四面体S－EGF中()A．SG⊥平面EFG B．SD⊥平面EFGC．GF⊥平面SEF D．GD⊥平面SEF6、设m，n是两条不同的直线，α，β是两个不同的平面，p：m⊥n，若p是q 的必要条件，则q可能是()A．q：m⊥α，n∥β，α⊥βB．q：m⊂α，n⊥β，α∥βC．q：m⊥α，n⊥β，α∥βD．q：m⊂α，n∥β，α⊥β7、如图，在三棱锥P－ABC中，点D，E分别为棱PB，BC的中点．若点F在线段AC上，且满足AD∥平面PEF，则AFFC的值为()A．1 B．2C．12D．238、棱长为1的正方体ABCD－A1B1C1D1中，E，F，G分别是AB，BC，B1C1不正确的是()A.P点在直线BC1上运动时，三棱锥A－D1PC体积不变B.Q点在直线EF上运动时，直线GQ始终与平面AA1C1C平行B1BD⊥平面ACD1D－EFG的体积为3 8二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9、设有不同的直线a，b和不同的平面α，β，给出下列四个命题中，其中正确的是()A．若a∥α，b∥α，则a∥b B．若a∥α，a∥β，则α∥βC．若a⊥α，b⊥α，则a∥b D．若a⊥α，a⊥β，则α∥β10、如图，在正方体ABCD－A1B1C1D1中，M，N，P分别是C1D1，BC，A1D1的中点，下列结论正确的是()A.AP与CM是异面直线B.AP，CM，DD1相交于一点C.MN∥BD1D.MN∥平面BB1D1D11、“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共截去八个三棱锥，得到的半正多面体的表面积为12＋43，则关于该半正多面体的下列说法中正确的是()A．AB＝ 2B．该半正多面体的外接球的表面积为6πC．AB与平面BCD所成的角为π4D．与AB所成的角是π3的棱共有16条12、如图，正方体ABCD－A1B1C1D1的棱长为3，线段B1D1上有两个动点E，F，且EF＝1，则当E，F移动时，下列结论正确的是( )A.AE ∥平面C 1BD ACEF 的体积不为定值 A －BEF 的体积为定值 D.四面体ACDF 的体积为定值三、填空题：本题共4小题，每小题5分，共20分.13、一个圆台上、下底面的半径分别为3 cm 和8 cm ，若两底面圆心的连线长为12 cm ，则这个圆台的母线长为________cm.14、在正四棱柱ABCD －A 1B 1C 1D 1中，O 为底面ABCD 的中心，P 是DD 1的中点，设Q 是CC 1上的点，则点Q 满足条件________时，有平面D 1BQ ∥平面P AO . 15、已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上，若球O 的表面积为16π，则O 到平面ABC 的距离为________．16、如图所示，在四棱锥P －ABCD 中，底面ABCD 是菱形，∠DAB ＝π3，侧面P AD 是等边三角形，且平面P AD ⊥平面ABCD ，E 为棱PC 上一点，若平面EBD ⊥平面ABCD ，则PEEC ＝ .四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17、（1）已知圆锥的顶点为A ，过母线AB ，AC 的截面面积是2 3.若AB ，AC 的夹角是60°，且AC 与圆锥底面所成的角是30°，求该圆锥的表面积； （2）已知三棱锥S －ABC 中，∠SAB ＝∠ABC ＝π2，SB ＝4，SC ＝213，AB ＝2，BC ＝6，求三棱锥S －ABC 的体积.18、如图，在四棱锥P－ABCD中，底面ABCD是矩形，点E在棱PC上(异于点P，C)，平面ABE与棱PD交于点F.(1)求证：AB∥EF；(2)若AF⊥EF，求证：平面P AD⊥平面ABCD.19、如图，在四棱锥C－ABED中，四边形ABED是正方形，点G，F分别是线段EC，BD的中点．(1)求证：GF∥平面ABC；(2)线段BC上是否存在一点H，使得平面GFH∥平面ACD？若存在，请找出点H并证明；若不存在，请说明理由．20、在四棱锥P－ABCD中，平面P AD⊥平面ABCD，P A＝PD＝2，四边形ABCD 是边长为2的菱形，∠DAB＝60°，E是AD的中点．(1)求证：BE⊥平面P AD；(2)求点E到平面P AB的距离．21、如图，在四棱锥P－ABCD中，四边形ABCD是边长为2的正方形，△PBC为正三角形，M，N分别为PD，BC的中点，PN⊥AB.(1)求三棱锥P－AMN的体积；(2)求二面角M－AN－D的正切值.22、在四棱锥P-ABCD中，△P AD是等边三角形，且平面P AD⊥平面ABCD，AD＝2AB＝2BC，∠BAD＝∠ABC＝90°.(1)AD上是否存在一点M，使得平面PCM⊥平面ABCD，若存在，请证明；若不存在，请说明理由；(2)若△PCD的面积为87，求四棱锥P-ABCD的体积．。

人教A版高一数学必修第二册第八章《立体几何初步》章末练习题卷（共22题）一、选择题（共10题）1.棱锥的侧面和底面可以都是( )A．三角形B．四边形C．五边形D．六边形2.分别在两个平面内的两条直线间的位置关系是( )A．异面B．平行C．相交D．以上都有可能3.一个建筑物上部为四棱锥，下部为长方体，且四棱锥的底面与长方体的上底面尺寸一样，已知长方体的长、宽、高分别为20m，5m，10m，四棱锥的高为8m，若按1:500的比例画出它的直观图，那么直观图中，长方体的长、宽、高和棱锥的高应分别为( )A．4cm,1cm,2cm,1.6cm B．4cm,0.5cm,2cm,0.8cmC．4cm,0.5cm,2cm,1.6cm D．2cm,0.5cm,1cm,0.8cm4.一个棱柱是正四棱柱的条件是( )A．底面是正方形，有两个侧面是矩形B．底面是正方形，有两个侧面垂直于底面C．底面是菱形，且有一个顶点处的三条棱两两垂直D．每个侧面都是全等矩形的四棱柱5.下列三个命题中错误的个数是( )①经过球面上任意两点，可以作且只可以作一个球的大圆；②球面积是它大圆面积的四倍；③球面上两点的球面距离，是这两点所在截面圆上以这两点为端点的劣弧的长．A．0B．1C．2D．36.已知圆柱的侧面展开图是一个边长为4π的正方形，则这个圆柱的表面积是( )A．8π+16π2B．2π+4π2C．4π+16π2D．8π+4π27.某几何体的三视图如图所示，其中俯视图是正方形，那么该几何体的表面积是( )A．32B．24C．4+12√2D．12√28.如图，下列表示该平面错误的是( )A．平面αB．平面AB C．平面AC D．平面ABCD9.半径为2的球的表面积为( )A．4πB．8πC．12πD．16π10.下面空间图形的画法中错误的是( )A．B．C．D．二、填空题（共6题）11.棱柱的概念12.平面的概念几何中所说的“平面”，是从课桌面、黑板面、平静的水面等，这样的一些物体中抽象出来的．类似于直线向两端无限延伸，几何中的平面是向四周的．13.若圆锥的母线长l=5(cm)，高ℎ=4(cm)，则这个圆锥的体积等于(cm3)．14.空间两个平面的位置关系有．15.判断正误．两两相交的三条直线最多可以确定三个平面．( )16.思考辨析，判断正误．在几何体的直观图中，原来平行的直线仍然平行．( )三、解答题（共6题）17.如图，正方体ABCD−A1B1C1D1的棱长为2．(1) 求证：AC⊥B1D；(2) 求三棱锥C−BDB1的体积．18.几何中的“平面”有边界吗？用什么图形表示平面？19.请回答下列问题：(1) 已知：l⫋α，D∈α，A∈l，B∈l，C∈l，D∉l．求证：直线AD，BD，CD共面于α．(2) 将一个苹果切3刀，最多可以切成x块，最少可切成y块，求x+y的值．20.如图，在四棱锥P−ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，DC=6，AD=8，BC=10，PD=9，E为PA的中点．(1) 求证：DE∥平面BPC．(2) 在线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出此时三棱锥B−PCF的体积；若不存在，请说明理由．21.若两个平面平行，那么两个平面内的所有直线都相互平行吗？22.观察（1），（2），（3）三个图形，说明它们的位置关系有什么不同，并用字母表示各个平面．答案一、选择题（共10题） 1. 【答案】A【解析】三棱锥的侧面和底面都是三角形．故选A ． 【知识点】棱锥的结构特征2. 【答案】D【解析】分别在两个平面的两条直线平行、相交、异面都可能，可将两条直线放在长方体里进行研究．【知识点】直线与直线的位置关系3. 【答案】C【解析】由比例尺可知长方体的长、宽、高和四棱锥的高分别为 4cm ，1cm ，2cm 和 1.6cm ，再结合斜二测画法，可知直观图的相应尺寸应分别为 4cm ，0.5cm ，2cm ，1.6cm ． 【知识点】直观图4. 【答案】C【知识点】棱柱的结构特征5. 【答案】C【知识点】球面距离、球的结构特征6. 【答案】A【解析】设圆柱的底面半径为 r ，母线长为 l ， 因为侧面展开图是一个边长为 4π 的正方形， 所以 2πr =l =4π，可得 r =2，l =4π，所以圆柱的表面积为 S =2πr 2+2πrl =8π+16π2． 【知识点】圆柱的表面积与体积7. 【答案】C【解析】由三视图可知，该几何体是一个底面为正方形的长方体， 长方体的底面正方形的对角线长为 2，长方体的高是 3； 所以，底面正方形的边长为 √12+12=√2，该长方体的表面积为 2×(√2)2+4×3×√2=4+12√2． 【知识点】棱柱的表面积与体积、由三视图还原空间几何体8. 【答案】B【解析】该平面可用希腊字母 α，β，γ 表示，故A 正确；该平面可用平行四边形的对角线表示，故C正确；该平面可用平行四边形的四个顶点表示，故D正确；该平面不可用平行四边形的某条边表示，故B不正确．【知识点】平面的概念与基本性质9. 【答案】D【解析】因为球的半径为r=2，所以该球的表面积为S=4πr2=16π．【知识点】球的表面积与体积10. 【答案】D【解析】遮住的地方应该画成虚线或不画，故选项D中的图形画法有误．【知识点】平面的概念与基本性质二、填空题（共6题）11. 【答案】平行；四边形；平行；平行；公共边；公共顶点【知识点】棱柱的结构特征12. 【答案】无限延展【知识点】平面的概念与基本性质13. 【答案】12π【解析】设圆锥底面的半径为r，则r=√52−42=3，×π×9×4=12π，填12π．故V=13【知识点】圆锥的表面积与体积14. 【答案】平行、相交、重合【知识点】平面与平面的位置关系15. 【答案】√【知识点】平面的概念与基本性质16. 【答案】√【知识点】直观图三、解答题（共6题）17. 【答案】(1) 因为四棱柱ABCD−A1B1C1D1为正方体，所以BB1⊥平面ABCD．因为AC⊂平面ABCD，所以BB1⊥AC．因为底面ABCD为正方形，所以AC⊥BD．因为BB1∩BD=B，BB1,BD⊂平面BB1D，所以AC⊥平面BB1D．因为B1D⊂平面BB1D，所以AC⊥B1D．(2) 易知V C−BDB1=V B1−BDC．因为B1B⊥平面ABCD，所以B1B是三棱锥B1−BDC的高．因为V B1−BDC =13S△BDC⋅BB1=13×12×2×2×2=43，所以三棱锥C−BDB1的体积为43．【知识点】直线与平面垂直关系的判定、棱锥的表面积与体积18. 【答案】没有，平行四边形．【知识点】平面的概念与基本性质19. 【答案】(1) 因为l⫋α，A∈l，B∈l，C∈l，所以A,B,C∈α又D∈α，D∉l，所以AD⫋α，BD⫋α，CD⫋α，则直线AD，BD，CD共面．(2) x=8，y=3，x+y=11．【知识点】平面的概念与基本性质20. 【答案】(1) 取PB的中点M，连接EM，CM，过点C作CN⊥AB，垂足为N，如图所示．因为CN⊥AB，DA⊥AB，所以CN∥DA，又AB∥CD，所以四边形CDAN为矩形，所以CN=AD=8，DC=AN=6．在Rt△BNC中，BN=√BC2−CN2=√102−82=6，所以AB=12．因为E，M分别为PA，PB的中点，所以EM∥AB且EM=6，又DC∥AB，且CD=6，所以 EM ∥CD 且 EM =CD ， 则四边形 CDEM 为平行四边形， 所以 DE ∥CM ．因为 CM ⊂平面BPC ，DE ⊄平面BPC ，所以 DE ∥平面BPC ．(2) 存在．理由如下：由题意可得 DA ，DC ，DP 两两互相垂直，故以 D 为原点，DA ，DC ，DP 所在直线分别为 x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系 Dxyz ． 则 D (0,0,0)，B (8,12,0)，C (0,6,0)，所以 DB⃗⃗⃗⃗⃗⃗ =(8,12,0)． 假设 AB 上存在一点 F 使 CF ⊥BD ，设点 F 坐标为 (8,t,0)(0≤t ≤12)， 则 CF⃗⃗⃗⃗⃗ =(8,t −6,0)， 由 CF ⃗⃗⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0，得 64+12(t −6)=12t −8=0， 所以 t =23，即 AF =23，故 BF =12−23=343．又 PD =9，所以 V 三棱锥B−PCF =V 三棱锥P−BCF =13×12×343×8×9=136．【知识点】直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题21. 【答案】不是．【知识点】平面与平面平行关系的性质22. 【答案】图（1）表示两个相交的半平面；图（2）表示开口向里的两个相交的半平面；图（3）表示开口向外的两个相交的半平面． 【知识点】平面的概念与基本性质。