当前位置：文档之家 › 数字信号处理 第五章04

数字信号处理 第五章04

  • 格式：pdf
  • 大小：324.65 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

数字信号处理-第五章

数字信号处理-第五章

系 统 函 数
：
H (z) n M 0h (n )z n Y X ( (z z ) ) b 0 b 1 z 1 b 2 z 2 b M z M
单位脉冲响应的值等于差分方程系数：
h
h(n)=bn
n=0,1,·····,M
33
FIR数字滤波器的特点：
系统函数：
N1
H(z) h(n)zn n0
有N-1个零点分布于z平面 z=0处 是N-1阶极点
h
26
还可以如下式这样进行分解： H (z)1 1 0 0..6 4z z 1 11 1 0 0..5 3z z 1 1H 3(z)H 4(z)
h
27
级联型结构的特点：
调整某一路的分子系数能单独调整滤波器的一组 零点，而不影响其它零极点； 调整某一路的分母系数能单独调整滤波器的一组 极点，而不影响其它零极点；便于调整滤波器频 率响应性能
直接型
h
38
将H(z)进行因式分解，得到： H(z)=(0.6+0.5z-1)(1.6+2z-1+3z-2) 按照上式画出它的级联型结构如图所示。
级联型
h
39
5.5 线性相位网络结构
FIR滤波器单位抽样响应h(n)为实数，0 n N 1 且满足：
偶对称： h (n ) h (N 1 n ) 或奇对称 h (n ) h (N 1 n ) ： 即对称中心在 (N-1) / 2处 则这种FIR滤波器具有严格线性相位。
bi zi
i0 N 1 ak zk
k 1
基本运算：加法，乘法（乘以常数），移位（时延）
h
3
信号流图由基本支路构成
1.基本支路箭头表示信号流向，两个圆点表示输入输出节点，箭头旁边的 符号表示增益（缺省为1）

数字信号处理,第5章课后习题答案

数字信号处理,第5章课后习题答案

第五章习题与上机题5.1 已知序列12()(),0 1 , ()()()nx n a u n a x n u n u n N =<<=--，分别求它们的自相关函数，并证明二者都是偶对称的实序列。

解：111()()()()()nn mx n n r m x n x n m a u n au n m ∞∞-=-∞=-∞=-=-∑∑当0m ≥时，122()1mmnx n ma r m aaa∞-===-∑ 当0m <时，122()1m mnx n a r m aaa -∞-===-∑ 所以，12()1mx ar m a =-2 ()()()()N x n u n u n N R n =--=22210121()()()()()1,0 =1,00, =()(1)x NN n n N mn N n m N r m x n x n m Rn R n m N m N m N m m Nm N m R m N ∞∞=-∞=-∞--=-=-=-=-⎧=--<<⎪⎪⎪⎪=-≤<⎨⎪⎪⎪⎪⎩-+-∑∑∑∑其他从1()x r m 和2()x r m 的表达式可以看出二者都是偶对称的实序列。

5.2 设()e()nTx n u n -=，T 为采样间隔。

求()x n 的自相关函数()x r m 。

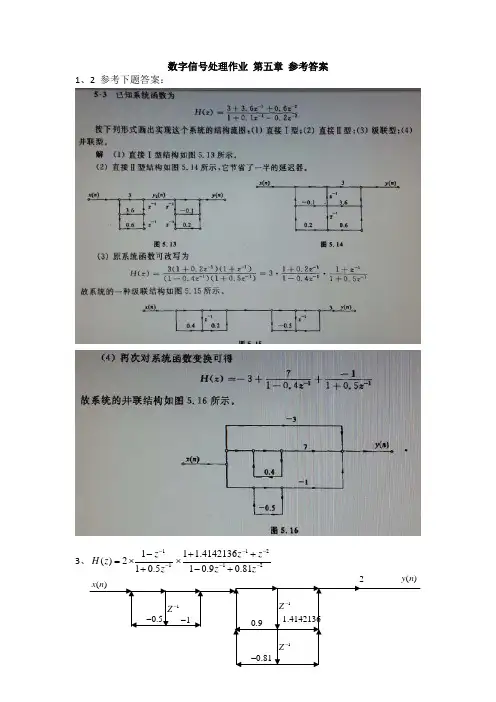
解：解：()()()()e()e ()nTn m T x n n r m x n x n m u n u n m ∞∞---=-∞=-∞=-=-∑∑用5.1题计算1()x r m 的相同方法可得2e()1e m Tx Tr m --=-5.3 已知12()sin(2)sin(2)s s x n A f nT B f nT ππ=+，其中12,,,A B f f 均为常数。

求()x n 的自相关函数()x r m 。

解：解：()x n 可表为)()()(n v n u n x +=的形式，其中)2sin()(11s nT f A n u π=，=)(n v 22sin(2)s A f nT π，)(),(n v n u 的周期分别为 s T f N 111=，sT f N 221=，()x n 的周期N 则是21,N N 的最小公倍数。

高西全版数字信号处理 第五章+课后答案

高西全版数字信号处理 第五章+课后答案

ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
Байду номын сангаас
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答
co
m
ww kh
课
w. da w.
案 网 后 答

数字信号处理 第五章

数字信号处理 第五章

+ a2 z-1
数字信号处理—第五章
6
举例：二阶数字滤波器
y ( n ) a 1 y ( n 1) a 2 y ( n 2 ) b 0 x ( n )
x(n) b0 +
-1 a1 z
y(n)
+ a2 z-1
数字信号处理—第五章
7
举例：二阶数字滤波器
y ( n ) a 1 y ( n 1) a 2 y ( n 2 ) b 0 x ( n )
z z
2 2
H (z)
1 1k z 1 1k z
1 1
x(n)
H 1(z)
y (n )
H 2(z)
H k (z)
数字信号处理—第五章
22
数字信号处理—第五章
23
IIR数字滤波器的级联型结构优点
1) 每个二阶或一阶子系统单独控制零、极点。 2）级联顺序可交换，零、极点对搭配任意，因此级联 结构不唯一。有限字长对各结构的影响是不一样的， 可通过计算机仿真确定子系统的组合及排序。 3）级联各节之间要有电平的放大和缩小，以使变量值 不会太大或太小。太大可能导致运算溢出；太小可 能导致信噪比太小。 4）级联系统也属于最少延时单元实现，需要最少的存 储器，但乘法次数明显比直接型要多。 4）级联结构中后面的网络输出不会再流到前面，运算 误差积累比直接型小。

数字信号处理—第五章
4
基本单元(数字滤波器结构）有两种表 示方法
数字信号处理—第五章
5
举例：二阶数字滤波器
y ( n ) a 1 y ( n 1) a 2 y ( n 2 ) b 0 x ( n )
x(n) b0 +

《数字信号处理导论_第5章》

《数字信号处理导论_第5章》

1 H ( ) b(n )cos n 2 n 1
N /2
1 时 cos n 0 2
则 H ( ) 0 z 1是零点
H ( )对 0, 2 呈偶对称 H ( )对 呈奇对称
0
10
20
y2 ( n )
0
-2 -10
0
10
20
定义：
d ( ) g ( ) d
为系统的群延迟 (Group Delay, GD)
显然，若系统具有线性相位，则其GD为
常数。
GD可作为相频响应是否线性的一种度量，同 时，它也表示了系统输出的延迟。
若： 则：
x(n) xa (n) cos( 0 n), c 0 x(n) : Narrowband Signal
z e j
j N21 N 1 N 1 " " h(n)cos 2 n e n 0 N 1 N 1 j je 2 h ( n )sin N 1 n " " 2 n 0
为第一类线性相位
N 1 2
2）h(n)奇对称

h( n) h( N 1 n)
j N 1 N 1 2
频率响应：
j
N 1 H (e ) H ( z ) z e j je h(n)sin 2 n n 0 N 1 j j N 1 N 1 2 2 e h(n)sin 2 n n 0
z 1为零点 故不能设计成高通、带阻滤波器
3）h(n)奇对称，N为奇数

数字信号处理_第5章4

数字信号处理_第5章4

FIR优化设计
问题的提出
设计的物理可实现FIR滤波器H (ejW )与理想滤波 器Hd (ejW )的逼近程度?
只有矩形窗函数法设计出的FIR滤波器是积分平 方误差最小意义下的最优FIR滤波器。 解决方法：采用优化设计！
FIR数字滤波器优化设计的基本思想：
在一定的误差准则下，设计线性相位FIR滤波器 H(z)，使得H(z)所对应的幅度函数A(W)和理想滤波器 的幅度函数D(W)的误差在区间上达到最小。
~
~
-6
FIR优化设计
优化设计的MATLAB实现
等波纹FIR滤波器设计 估计滤波器阶数M，并获得调用remez函数的参数 [M,fo,ao,w] = remezord(f,a,dev)
f：需设计的FIR数字滤波器的频带(B个)构成的向量 a：B个元素的向量,分别表示FIR滤波器在B个频带 中的幅度值。一般对通带取值为1，阻带取值为0。 dev：B个元素的向量,分别表示FIR滤波器在B个频 带中的波动值
FIR优化设计
等波纹FIR滤波器设计
等波纹线性相位FIR滤波器的设计步骤：
(5) 寻找新的极值点 { W k }，并求出最大误差值
~
~
(6) 如果 T (如 T=10 )，执行(7)。 否则用 { W k } 交换 { W k } 回到(3)。
(7) 解方程获得g[k]。 (8) 由g[k]求出h[k]。
上例的设计结果
（设计指标为Wp=0.5p，Ws=0.6p, p=s=0.0017）
0
M=59
20 G a in, dB 55 80 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Normalized frequency 0.9 1

数字信号处理第三版(姚天任、江太辉) 答案 第五章-unprotected

E[x(i)x( j)] −
2
N −1 N −1
E[x(i)x( j)]
N n=0
N2 i=0 j=0
N2 i=0 j=0
∑ ∑∑ =
1 N
N −1
E[x2 (n)] −
n=0
1 N2
N −1 N −1
E[x(i)x( j)]
i=0 j=0
∑ ∑ ∑∑ =
1
N −1
E[x2 (n)] −
1
N −1
N −1 N −1
∫ = 1
q
0 −q
xdx
=
1 2q
x2
|0−q =
−
q 2
∞
∫ mx2 = E[x2 ] = −∞ xpx2 (x)dx
∫ = 1
q
q/2 −q/2
xdx
=
1 2q
x2
|−q
/2 q/
2
=
0
∞
∫ mx3 = E[x3 ] = −∞ xpx3 (x)dx
∫ = 1
2π
2π 0
xdx =
1 4π
x2
|02π = π
∞ −∞
(x
−
mx2
)2
px2
( x)dx
∫ = 1 q
q/2 −q / 2
x2dx
=
1 3q
x3
|q / 2
−q/
2
=
q2 12
∫ σ 2 x3
=
E[( x3
− mx3 )2 ] =
∞ −∞
(x
−
mx3
)2
px3
( x)dx
∫ = 1
2π
2π 0

精品文档-数字信号处理(吴瑛)-第5章


第5章 数字滤波器概论
5.3 实际滤波器的设计指标
5.3.1 图5.3.1是理想低通滤波器的幅频响应，该理想低通滤波
器具有截止频率ωd。可以看出，理想滤波器在通带内幅度为常 数(非零)，在阻带内幅度为零。另外，一般理想滤波器 要求具有线性相位(在第8章讨论)，这里假设相频响应 θ(ω)=0
h(n) sin(nd )
第5章 数字滤波器概论
1. 根据H(ejω) 一般数字滤波器从滤波功能上分类，和模拟滤波器一样， 可以分成低通、高通、带通和带阻等滤波器。它们的理想幅频 响应如图5.2.2
第5章 数字滤波器概论
图5.2.2 (a) 低通; (b) 高通; (c) 带通; (d) 带阻
第5章 数字滤波器概论
需要注意的是，数字滤波器的频率响应H(ejω)都是以2π 为周期的，滤波器的低通频带处于2π的整数倍处，而高通频 带处于π
5.3.2 当滤波器形状为非理想时，要用一些参数指标来描述其关
键特性。图5.3.5表示低通滤波器的幅频响应。滤波器的通带 定义了滤波器允许通过的频率范围。在阻带内，滤波器对 信号严重衰减。ωp和ωs分别称为通带截止频率(或通带上限频 率)和阻带截止频率(或阻带下限频率)。参数δ1定义了通带波 纹(Pass Band Ripple)，即滤波器通带内偏离单位增 益的最大值。参数δ2定义了阻带波纹(Stop Band Ripple)，即 滤波器阻带内偏离零增益的最大值。
截短脉冲响应自然会对频率响应产生影响。截短后，滤波 器幅频响应曲线不再是理想矩形，通带不再平坦，有过渡带， 同时阻带衰减不再为零。图5.3.4给出了因果脉冲响应 的幅频响应。当然，脉冲响应保留的采样点越多，即滤波器阶
第5章 数字滤波器概论 图5.3.4 非理想低通滤波器因果脉冲响应的幅频响应

数字信号处理作业 第五章 参考答案

为得到 H ( z ) ，
(1) 由极点构成 H a ( s ) 的分母多项式，分子为分母多项式的常数。 (2) H a ( s ) 展成部分分式。 (3) 据有理分式变换得到对应的 H ( z ) 各分式，整理得到最后的 H ( z ) 。 22、 取 T=1， 预畸， 由已知列出对模拟滤波器的衰减要求， 解出 N=6.04， 取 N=7， 得到
−0.5
Z −1
−1
0.9
−0.81
4、 H ( z ) = −4.9383 +
2.1572 4.7811 − 1.5959 z −1 + 1 + 0.5 z −1 1 − 0.9 z −1 + 0.81z −2
−4.9383
x ( n) y ( n)
2.1572 −0.5
Z −1
4.7811
Z
0.9 −0.81
= H 2 ( z)
α 02 + α12 z -1 -3.1986 + 0.2591z -1 = 1 +z 2 1 + 1.618 z - 4π 2 2 1 + r z 1 - 2rz -cos 5
频率取样型实现流程图：
−10.125
Z −1
18.3236
x ( n)
Z −1
x ( n)
Z −1
Z −1
+
Z −1
− 7 4
+
Z −1
− 69 8
+
y ( n) 4） 频率取样型：取 r=1，N=5，得到 DFT{h(n)}为：
{-10.1250 9.1618 + 6.6564i -1.5993 - 4.9221i -1.5993 + 4.9221i 9.1618 - 6.6564i}

数字信号处理_吴镇扬_第二版_第五章习题答案


5.7 （1）由于h2(n)是h1(n)圆周移位的序列，根据DFT的 2π 性质有： −j 4k − jπ k
H 2 (k ) = e
8
H 1 (k ) = e
H 1 (k )
~ ~ H1 ( k ) = H 2 ( k ) 成立 所以
(2)由于h1 (n ) 和h2 (n ) 均为偶对称序列，以其构成的低通滤波器
(3)若采用海明窗设计，则
⎡ ⎛ 2πn ⎞⎤ wHam ( n) = ⎢0.54 − 0.46 cos ⎜ ⎟ ⎥ RN ( n ) ⎝ N − 1 ⎠⎦ ⎣ 2 h( n) = sin[(n − α )ωc ]cos[(n − α )ω0 ]wHam (n) N 为奇数时， (n − α )π
h( n N 为偶数时， ) =
0 −ωc
e − jωα e jω nd ω
可见h(n)关于(N-1)/2偶对称，即 h( n) = h( N − 1 − n)
(1)当 N 为奇数时，为第一类滤波器。 (2)当N为偶数时，为第二类滤波器
⎧hd ( n) h( n) = hd ( n) ⋅ R(n ) = ⎨ ⎩0 0 ≤ n ≤ N −1
解：由经验公式可知若 不小于 At 40dB , 则
β = 0.5842 At - 21)0.4 + 0.07886(At - 21) ≈ 3.3953 （ At − 8 40 − 8 N= = ≈ 22.28 2.286∆ω 2.286× 0.2π ωc + ωr ωc′ = = 0.2π 2 ′ ⎧ωc ′ ⎪ π Sa[ωc (n − α )] n ≠ α ′ 1 ωc − jωα jωn ⎪ hd (n) = ∫ ′ e e dω = ⎨ ′ 2π −ωc ωc ⎪ n =α ⎪ ⎩ π
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

H (e j )
1 1 j Ha Ha j T T T
Ha(j)

T-1
h (n ) Tha (nT ) H (z )
i 1 N

1 s i z 1
sT Ha j T j 2 T
TAi
H (e )
s1,2 = −0.18 ± j 0.70;
, k = 1, 2,L , N
s3,4 = −0.50 ± j 0.50;
s5,6 = −0.70 ± j 0.18 K = 0.12 ( H a ( s ) s =0 = 1)
K ; 2 2 2 ( s + 0.36 s + 0.49)( s + 0.99 s + 0.49)( s + 1.36 s + 0.49)
2、IIR数字低通滤波器 的频率变换（高通、带 通、带阻数字滤波器的 设计 1、IIR数字低通滤波器 的频域直接设计方法 2、IIR数字低通滤波器 的时域直接设计方法
IIR数字滤波 器设计
二、直接设计IIR数 字滤波器
三、IIR数字滤波器 的优化设计方法
1、最小均方误差方法 2、最小p误差方法 3、最小平方逆设计法 4、线性规划设计方法
√
解：(1)由已知条件列出对模拟 滤波器的衰减要求 20 lg H a ( jΩp ) ≥ −1dB ⇒ 20 lg H a ( jΩs ) ≤ −15dB ω H (e jω ) = H a ( j ) = H a ( jΩ), ω ≤ π T ω = ΩT , T = 1 ωp ω ⇒ Ωp = = 0.2π , Ωs = s = 0.3π , T T 20 lg H a ( j 0.2π ) ≥ −1dB ⇒ 20 lg H a ( j 0.3π ) ≤ −15dB 1 2 A2 ( Ω ) = H a ( j Ω ) = 2N Ω 1+ Ωc
Ω 2 N ⇒ 20 lg H a ( jΩ) = −10 lg 1 + Ω c 0.2π 2 N −10 lg 1 + ≥ −1dB Ω c ⇒ 0.3π 2 N −10 lg 1 + ≤ −15dB Ω c 0.2π 1 + Ωc 取等号 0.3π 1 + Ωc
2、IIR数字低通滤波器 的频率变换（高通、带 通、带阻数字滤波器的 设计 1、IIR数字低通滤波器 的频域直接设计方法 2、IIR数字低通滤波器 的时域直接设计方法
IIR数字滤波 器设计
二、直接设计IIR数 字滤波器
三、IIR数字滤波器 的优化设计方法
1、最小均方误差方法 2、最小p误差方法 3、最小平方逆设计法 4、线性规划设计方法
脉冲响应不变法--变换原理
ha(t) Ha()
t h(n)=ha(nT)
W H(T)--H(ejw)

n h1(n)=ha(nT1)
…
W 2/T
…
H1(T1) --H(ejw1)

n
…
W 2/T1
…

Time domain
Frequency domain
脉冲响应不变法--变换原理
ha(t) ) ha (t ) ha (t ) h(n ) H (z ) ˆ (s ) H a (s ) H a
sit i 1
n
s si
Ai
并联，部分分式
N N siTn i 1
u(nT )
z
1
H (z )
Ai lim
i 1
n N
h(n )z


N i 1 sT | z ||e i | N
1 (e z ) 1 e i z 1 Ai
sT siT
n i 1 siT 1 N
数字信号处理
周治国
2016.11
第五章 数字滤波器
IIR数字滤波器 脉冲响应不变变换法
1、从模拟低通滤波器 设计数字低通滤波器 一、从模拟滤波器 设计数字滤波器
（1）脉冲/阶跃响应不 变法 （2）双线性变换法 （1）直接由模拟原型 到各种类型数字滤波器 的转换 （2）从数字低通滤波 器到各种类型数字滤 波器的转换 （1）零、极点位置累 试法（点阻滤波器） （2）幅度平方函数法 （1）帕德逼近法 （2）波形形成滤波器 设计

H (z )
?
n
h(n )z

n
) ha (t )
) ) t H h (t ) s L ( ) a a ) H (z ) H a (s ) ) 1 H a (s ) T
n
h (nT )e
a
sTn
h(n)=ha(nT)
2 Ha sj m H a (s ) T m n 1 2 j H (e ) H (z ) |z e j j j m Ha H T T m a T T T 1 1 H (e j ) H a j H j T T a T n
03A(05-06)
提示： (1)所有小数均计算到小数点后两位 (2)假设取样间隔T = 1 (3)双线性变换的频率变换关系为： Ω = 2 Ttg (ω 2) (4)模拟巴特沃斯低通滤波器H a ( s )的极点为： sk = Ωc e jπ [1 2+ (2 k −1)/(2 N )] , k = 1, 2,L , N (4)模拟巴特沃斯低通滤波器平方函数为： A2 (Ω) = 1 [1 + (Ω Ωc ) 2 N ]
⇒ H ( z) =
IIR滤波器设计2--往年真题
如果所要设计的数字低通滤波器满足下列条件： (a)在ω ≤ π / 8的通带范围内幅度变化不大于3dB， (b)在π / 2 ≤ ω ≤ π 的阻带范围内幅度衰减不小于20dB， 试用脉冲响应不变变换法，设计相应的数字巴特沃斯 低通滤波器， (1)确定滤波器的阶数N (2)确定滤波器的系统函数H ( z ) (3)确定滤波器的频率响应H (e jω ) (4)给出滤波器的直接I型结构实现形式
模拟原型滤波器数字化设计方法
原理（Principle） 首先按一定指标设计出满足要求的模拟原型滤波器，再将 其通过某种方式数字化 转换方法（Conversion methods） — 将微分方程转换为差分方程 — 脉冲响应不变变换法 — 双线性变换法 — 匹配Z变换 要求（Requirement） ① s-平面的左半平面应映射至z-平面的单位圆内，即系统 稳定性要在转换中能够保持； ② 保形要求（频率选择能力）
1、从模拟低通滤波器 设计数字低通滤波器 一、从模拟滤波器 设计数字滤波器
（1）脉冲/阶跃响应不 变法 （2）双线性变换法 （1）直接由模拟原型 到各种类型数字滤波器 的转换 （2）从数字低通滤波 器到各种类型数字滤 波器的转换 （1）零、极点位置累 试法（点阻滤波器） （2）幅度平方函数法 （1）帕德逼近法 （2）波形形成滤波器 设计
Ω 2 N ⇒ 20 lg H a ( jΩ) = −10 lg 1 + Ω c π / 8 2 N −10 lg 1 + ≥ −3dB Ω c ⇒ 2N π /2 −10 lg 1 + ≤ −20dB Ω c π / 8 2 N 0.3 1 + = 10 (a ) Ωc 取等号 2N π / 2 2 1 + = 10 (b) Ωc Ωc = π / 8 = 0.39 解出：N = 1.66，取N = 2
或直接由表5-1 Ωc 6 H a (s) = 6 s + 3.863Ωc s 5 + 7.464Ωc 2 s 4 + 9.141Ωc 3 s 3 + 7.464Ωc 4 s 2 + 3.863Ωc 5 s + Ωc 6 展成部分分式 A B C D H a (s) = + + + s − (−0.18 + j 0.70) s − ( −0.18 − j 0.70) s − ( −0.50 + j 0.50) s − ( −0.50 − j 0.50) E F + + s − ( − 0.70 + j 0.18) s − ( − 0.70 − j 0.18) 解得： A =; B =; C =; D =; E =; F = 由 1 1 z ⇔ = s − si 1 − e siT z −1 z − e siT
2N
= 100.1 (a )
2N
1.5 = 10 (b) 解出：N = 5.89，Ωc = 0.7047取N = 6
代入( a), Ωc = 0.7032 代入(b), Ωc = 0.7080
(2)由巴特沃斯滤波器极点公式得到 sk = Ωc e H a (s) =
1 2 k −1 jπ [ + ] 2 2N
A (e
i

N
siT n
) z u(n )
n
A e
N i 1 i n 0
siT

n
1e
Ai
z 1
此处把课本（5-23）和 （5-43）（5-46）统一起来 Ai Ai z
s si

1 e z
siT
1
z e i
sT
优缺点
1、增益过高（T-1）
H(ejω)