数字信号处理第5章习题答案完整版

H α ( s ) = H αN (
ω c = 2πf c T = 2π × 400 HZ / 6000 HZ =
Ωc = 2 ωc 2 π 2 tg = tg ( ) = 0.2 × T T 2 T 15
2π 15
s=
2 1 − z −1 , T 1 + z −1
s = Ωc
1 − z −1 −1 π tg ( ) 1 + z 15 1 1
=
1 + 3z −1 + 3z −2 + z −3 0.005376(1 + 3z −1 + 3z −2 + z −3 ) = 186 − 412 z −1 + 318 z − 2 − 84 z −3 1 − 2.215 z −1 + 1.71z − 2 − 0.4516 z −3
5.24 用双线性变换设计一个三阶巴特沃思数字高通滤波器，采样频率为 f s = 6 KHZ ，截止 频率为 f c = 1.5 KHZ （不计 3KHZ 以上的频率分量） 。 解法 1：三阶巴特沃思低通模拟滤波器的原型函数：
按照冲激不变条件，可以写出
因此系统函数为
H ( z ) = ∑ h(n) z − n
n =0
∞
1 1 2 2 = + 1 − e − aT e − jbT z −1 1 − e −aT e jbT z −1 = 1 − (e − aT cos bT ) z −1 (1 − e − aT e − jbT z −1 )(1 − e −aT e jbT z −1 )
所以
ω1 + ω 2
H BP ( z ) = H αN ( s )
s=
1 1+ z − 2 3 1− z − 2

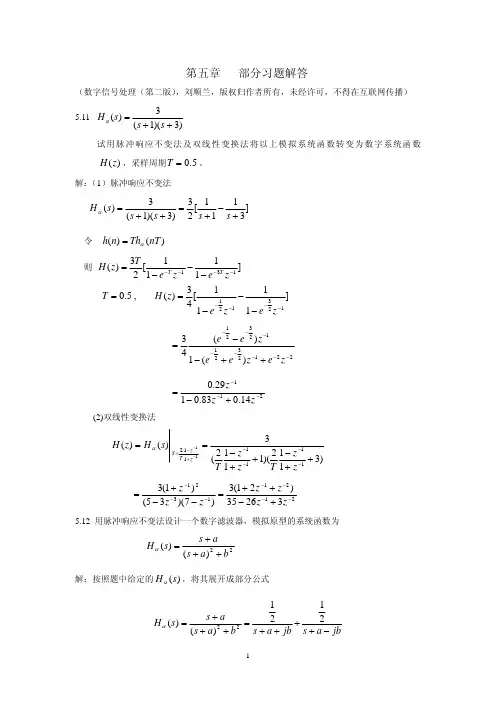
数字信号处理第5章答案史林赵树杰编著第五章练习题答案%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%5.8 已知复序列()()()f n x n jy n =+的8点DFT 为()[()](07)F k DFTf n k =≤≤，其值为(0)13,(1)24,(2)37,(3)45,(4)25,(5)12,(6)48,(7)6,F j F j F j F j F j F j F j F j =-=-+=+=--=+=--=-=不计算()F k 的离散傅里叶逆变换（IFFT ），试求实序列()x n 和()y n 的8点DFT ()X k 和()Y k 。

解：利用DFT 的共轭对称性()()()f n x n jy n =+[]()()()()F k DFT f n X k jY k ==+[]Re ()()()f n Fep k x n ??[]Im ()()()j f n Fop k y n ??所以[][]*()()R e ()()1(())(())()2N N N X k D FT x n D FT f n Fep k F k F N k R k ??====+-?[][]*1()()Im ()()1(())(())()2N N N Y k D FT y n D FT f n Fep k j F k F N k R k j ??====--?%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%5.9 设()x n 和()y n 是长度为N 的两个实序列。

已知()[()](01)X k DFT x n k N =≤≤-，()[()](01)Y k DFT y n k N =≤≤-。

现在希望根据()X k 和()Y k 求()x n 和()y n ，为了提高运算效率，试设计一种算法，用一次N 点IFFT 来完成。

第五章习题与上机题5.1 已知序列12()(),0 1 , ()()()nx n a u n a x n u n u n N =<<=--，分别求它们的自相关函数，并证明二者都是偶对称的实序列。

解：111()()()()()nn mx n n r m x n x n m a u n au n m ∞∞-=-∞=-∞=-=-∑∑当0m ≥时，122()1mmnx n ma r m aaa∞-===-∑ 当0m <时，122()1m mnx n a r m aaa -∞-===-∑ 所以，12()1mx ar m a =-2 ()()()()N x n u n u n N R n =--=22210121()()()()()1,0 =1,00, =()(1)x NN n n N mn N n m N r m x n x n m Rn R n m N m N m N m m Nm N m R m N ∞∞=-∞=-∞--=-=-=-=-⎧=--<<⎪⎪⎪⎪=-≤<⎨⎪⎪⎪⎪⎩-+-∑∑∑∑其他从1()x r m 和2()x r m 的表达式可以看出二者都是偶对称的实序列。

5.2 设()e()nTx n u n -=，T 为采样间隔。

求()x n 的自相关函数()x r m 。

解：解：()()()()e()e ()nTn m T x n n r m x n x n m u n u n m ∞∞---=-∞=-∞=-=-∑∑用5.1题计算1()x r m 的相同方法可得2e()1e m Tx Tr m --=-5.3 已知12()sin(2)sin(2)s s x n A f nT B f nT ππ=+，其中12,,,A B f f 均为常数。

求()x n 的自相关函数()x r m 。

解：解：()x n 可表为)()()(n v n u n x +=的形式，其中)2sin()(11s nT f A n u π=，=)(n v 22sin(2)s A f nT π，)(),(n v n u 的周期分别为 s T f N 111=，sT f N 221=，()x n 的周期N 则是21,N N 的最小公倍数。

第五章 数字滤波器一、数字滤波器结构填空题:1．FIR 滤波器是否一定为线性相位系统？（ ）.解：不一定计算题：2．设某FIR 数字滤波器的冲激响应，,3)6()1(,1)7()0(====h h h h6)4()3(,5)5()2(====h h h h ，其他n 值时0)(=n h 。

试求)(ωj e H 的幅频响应和相频响应的表示式,并画出该滤波器流图的线性相位结构形式。

解： {}70,1,3,5,6,6,5,3,1)(≤≤=n n h ∑-=-=10)()(N n nj j e n h e H ωω⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+=+++++++=---------------ωωωωωωωωωωωωωωωωωωω2121272323272525272727277654326533566531j j j j j j j j j j j j j j j j j j j e e e e e e e e e e e ee e e e e e e )(27)(27cos 225cos 623cos 102cos 12ωφωωωωωωj j e H e=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=- 所以)(ωj e H 的幅频响应为ωωωωωω2727cos 225cos 623cos 102cos 12)(j eH -⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛= )(ωj e H 的相频响应为ωωφ27)(-=作图题:3．有人设计了一只数字滤波器，得到其系统函数为：2112113699.00691.111455.11428.26949.02971.114466.02871.0)(------+-+-++--=z z z z z z z H 2112570.09972.016303.08557.1---+--+z z z请采用并联型结构实现该系统。

(c) 若用周期图平滑法，为获得与(b)中的 Bartlett 法差不多的分辨率，要用多少时滞的自相 关值？若要求估计的方差与四分段的 Bartlett 估计的方差不相上下，需要多长的数据？
《现代数字信号处理》习题参考答案
解：(a)
级联的系统函数是：
H
(
Z
)
=
1
+
aZ
−1
1 +
0.99Z
−2
×
1
−
法的品质因子是 QB
=
1 VB
=
K
。
因此，若要 QB Qper ≥ 5 ，必须要求 K ≥ 5 。由于 M = 178 （对 Δf = 0.005 ），因此必须使 数点数满足： N = KM ≥ 5×178 = 890 点。
5.4 设随机过程 x(n) 是单位方差白噪声 w(n) 激励如下的系统而产生的。
《现代数字信号处理》习题参考答案
第五章习题参考答案
5.1 给定随机过程 x(n)的 N=10000 个样本点，要计算其周期图，但由于存储单元有限，你最 多只能计算 1024 点的 DFT，试说明如何利用这 10000 个样本值计算其周期图，并使其 分辨率为：
Δω = 0.89 2π 10000
解：（提示：试分析时间抽取 FFT 算法是如何工作的）
( ) [ ] 因此在 0,π 区间内，功率谱 Px e jω 每针对 Px ( z) 的一对共轭复极点及其镜像共轭对都有
一个峰值，位置对应于极点的相角。共有两个峰值，其频率满足：
2 cosω1 =
a 0.98
； 2 cosω2
=
−a 0.99
因此：
ω1 = cos−1 2

为得到 H ( z ) ，
(1) 由极点构成 H a ( s ) 的分母多项式，分子为分母多项式的常数。 (2) H a ( s ) 展成部分分式。 (3) 据有理分式变换得到对应的 H ( z ) 各分式，整理得到最后的 H ( z ) 。 22、 取 T=1， 预畸， 由已知列出对模拟滤波器的衰减要求， 解出 N=6.04， 取 N=7， 得到
−0.5
Z −1
−1
0.9
−0.81
4、 H ( z ) = −4.9383 +
2.1572 4.7811 − 1.5959 z −1 + 1 + 0.5 z −1 1 − 0.9 z −1 + 0.81z −2
−4.9383
x ( n) y ( n)
2.1572 −0.5
Z −1
4.7811
Z
0.9 −0.81
= H 2 ( z)
α 02 + α12 z -1 -3.1986 + 0.2591z -1 = 1 +z 2 1 + 1.618 z - 4π 2 2 1 + r z 1 - 2rz -cos 5
频率取样型实现流程图：
−10.125
Z −1
18.3236
x ( n)
Z −1
x ( n)
Z −1
Z −1
+
Z −1
− 7 4
+
Z −1
− 69 8
+
y ( n) 4） 频率取样型：取 r=1，N=5，得到 DFT{h(n)}为：
{-10.1250 9.1618 + 6.6564i -1.5993 - 4.9221i -1.5993 + 4.9221i 9.1618 - 6.6564i}

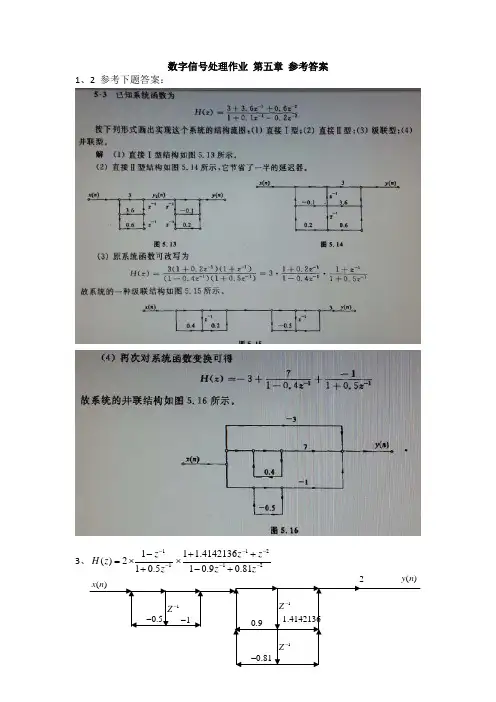
FIR 数字滤波器设计本章知识点：对于一个离散时间系统∑∑=-=--=M 1n nn 1-N 0n nnz a 1z bz H )(,若分母多项式中系数0a a a M 21====Λ，则此系统就变成一个FIR 系统∑-=-=1N 0n nn z b z H )(，其中系数1-N 10b ,.b ,b Λ即为该系统的单位取样响应h ( 0 ) , h ( 1 ) ,… h ( N-1 ),且当n > N-1时，h ( n ) = 0。

FIR 系统函数H(z) 在Z 平面上有N-1个零点，在原点z=0处有N-1个重极点。

这类系统不容易取得较好的通带和阻带特性，要想得到与IIR 系统类似的衰减特性，则要求较高的H(z)阶次。

相比于IIR 系统来说，FIR 系统主要有三大突出优点：1）系统永远稳定；2）易于实现线性相位系统；3）易于实现多通带（或多组带）系统。

线性相位FIR 滤波器实现的充要条件是：对于任意给定的数值N （奇数或偶数），冲激响应h[n] 相对其中心轴21-N 必须成偶对称或奇对称，此时滤波器的相位特性是线性的，且群延时均为常数 21-=N τ。

由于h(n) 有奇对称和偶对称两种情况，h(n)的点数N 有奇数、偶数之分。

因此，h （n ）可以有4种不同的类型，分别对应于4种线性相位FIR 数字滤波器：h[n] 偶对称N 为奇数、h[n] 偶对称N 为偶数、h[n] 奇对称N 为奇数、h[n] 奇对称N 为偶数。

四种线性相位FIR 滤波器的特性归纳对比于表5.１中。

一．FIR DF 设计方法FIR DF 的设计实现不能像IIR DF 设计那样借助于模拟滤波器的设计方法来实现，其设计方法主要是建立在对理想滤波器频率特性进行不同程度逼近的基础上，主要的逼近方法有三种：窗函数法；频率抽样法；最佳一致逼近法。

1． 窗函数法窗函数法是设计FIR 滤波器的最直接方法，它通过采用不同时宽的窗函数，对理想滤波器的无限长冲激响应h d (n)进行截短，从而得到系统的有限长冲激响应 h (n)，这一过程可用式5－1来描述：,021-N ||,(n)h )()()(d ⎪⎩⎪⎨⎧≤=其它＝ n n w n h n h R d （5.1）其中W R (n)是时宽为N 的窗函数。

FIR 数字滤波器设计本章知识点：对于一个离散时间系统∑∑=-=--=M 1n nn 1-N 0n nnz a 1z bz H )(,若分母多项式中系数0a a a M 21==== ，则此系统就变成一个FIR 系统∑-=-=1N 0n n nz bz H )(，其中系数1-N 10b ,.b ,b 即为该系统的单位取样响应h ( 0 ) , h ( 1 ) ,… h ( N-1 ),且当n > N-1时，h ( n ) = 0。

FIR 系统函数H(z) 在Z 平面上有N-1个零点，在原点z=0处有N-1个重极点。

这类系统不容易取得较好的通带和阻带特性，要想得到与IIR 系统类似的衰减特性，则要求较高的H(z)阶次。

相比于IIR 系统来说，FIR 系统主要有三大突出优点：1）系统永远稳定；2）易于实现线性相位系统；3）易于实现多通带（或多组带）系统。

线性相位FIR 滤波器实现的充要条件是：对于任意给定的数值N （奇数或偶数），冲激响应h[n] 相对其中心轴21-N 必须成偶对称或奇对称，此时滤波器的相位特性是线性的，且群延时均为常数 21-=N τ。

由于h(n) 有奇对称和偶对称两种情况，h(n)的点数N 有奇数、偶数之分。

因此，h （n ）可以有4种不同的类型，分别对应于4种线性相位FIR 数字滤波器：h[n] 偶对称N 为奇数、h[n] 偶对称N 为偶数、h[n] 奇对称N 为奇数、h[n] 奇对称N 为偶数。

四种线性相位FIR 滤波器的特性归纳对比于表5.１中。

一．FIR DF 设计方法FIR DF 的设计实现不能像IIR DF 设计那样借助于模拟滤波器的设计方法来实现，其设计方法主要是建立在对理想滤波器频率特性进行不同程度逼近的基础上，主要的逼近方法有三种：窗函数法；频率抽样法；最佳一致逼近法。

1． 窗函数法窗函数法是设计FIR 滤波器的最直接方法，它通过采用不同时宽的窗函数，对理想滤波器的无限长冲激响应h d (n)进行截短，从而得到系统的有限长冲激响应 h (n)，这一过程可用式5－1来描述：,021-N ||,(n)h )()()(d ⎪⎩⎪⎨⎧≤=其它＝ nn w n h n h R d （5.1）其中W R (n)是时宽为N 的窗函数。

5.7 （1）由于h2(n)是h1(n)圆周移位的序列，根据DFT的 2π 性质有： −j 4k − jπ k
H 2 (k ) = e
8
H 1 (k ) = e
H 1 (k )
~ ~ H1 ( k ) = H 2 ( k ) 成立 所以
(2)由于h1 (n ) 和h2 (n ) 均为偶对称序列，以其构成的低通滤波器
(3)若采用海明窗设计，则
⎡ ⎛ 2πn ⎞⎤ wHam ( n) = ⎢0.54 − 0.46 cos ⎜ ⎟ ⎥ RN ( n ) ⎝ N − 1 ⎠⎦ ⎣ 2 h( n) = sin[(n − α )ωc ]cos[(n − α )ω0 ]wHam (n) N 为奇数时， (n − α )π
h( n N 为偶数时， ) =
0 −ωc
e − jωα e jω nd ω
可见h(n)关于(N-1)/2偶对称，即 h( n) = h( N − 1 − n)
(1)当 N 为奇数时，为第一类滤波器。 (2)当N为偶数时，为第二类滤波器
⎧hd ( n) h( n) = hd ( n) ⋅ R(n ) = ⎨ ⎩0 0 ≤ n ≤ N −1
解：由经验公式可知若 不小于 At 40dB , 则
β = 0.5842 At - 21)0.4 + 0.07886(At - 21) ≈ 3.3953 （ At − 8 40 − 8 N= = ≈ 22.28 2.286∆ω 2.286× 0.2π ωc + ωr ωc′ = = 0.2π 2 ′ ⎧ωc ′ ⎪ π Sa[ωc (n − α )] n ≠ α ′ 1 ωc − jωα jωn ⎪ hd (n) = ∫ ′ e e dω = ⎨ ′ 2π −ωc ωc ⎪ n =α ⎪ ⎩ π

最小， 而既非通带波纹最小， 又非阻带波动最小。 所以， 用这种优化程序设计的滤波器的阻带最小衰减和通带波纹可能 不满足要求。
第５章 无限脉冲响应(IIR)数字滤波器的设
计
特别是以理想滤波器特性作为Hd(ejω)时， 为了使ε2最小，
优化过程尽可能逼近Hd(ejω)的间断特性（即使过渡带最窄）， 而使通带出现较大过冲、 阻带最小衰减过小， 不能满足工
H(ejω)=|H(ejω)|ejθ(ω) 其中， |H(ejω)|称为幅频特性函数， θ(ω)称为相频特性函数。
常用的典型滤波器|H(ejω)|是归一化的， 即|H(ejω)|max=1， 下 的讨论一般就是针对归一化情况的。 对IIR数字滤波器， 通
常用幅频响应函数|H(ejω)|来描述设计指标， 而对线性相位特 性的滤波器， 一般用FIR数字滤波器设计实现。
计
图5.1.6
第５章 无限脉冲响应(IIR)数字滤波器的设
计
5.1.4 IIR-DF的直接设计法
所谓直接设计法， 就是直接在数字域设计IIR[CD*2]DF 的方法。 相对而言， 因为从AF入手设计DF是先设计相应的 AF， 然后再通过s-z平面映射， 将Ha(s)转换成H(z)， 所以 这属于间接设计法。 该设计法只能设计与几种典型AF相对 应的幅频特性的DF。 而需要设计任意形状幅频特性的DF时， 只能用直接设计法。 直接设计法一般都要借助于计算机进行 设计， 即计算机辅助设计（CAD）。 现在已有多种DF优化 设计程序。 优化准则不同， 所设计的滤波器特点亦不同。所 以最主要的是建立优化设计的概念， 了解各种优化准则的 特点， 并根据设计要求， 选择合适的优化程序设计DF。
≤≤
(5.1.1)
≤
(5.1.2)

《数字信号处理》朱金秀第五章习题及参考答案第五章习题及参考答案一、习题1、求下列序列的Z变换及收敛域：（1）3?nu(n) （2）?4?nu(?n?1) （3）3?nu(?n) （4）?(n?1) （5）?(n)（6）5?n[u(n)?u(n?10)]2、求下列序列的Z变换及其收敛域，并求出零、极点：（1）x(n)?R3(n)（2）x(n)??rncos(?0n??)u(n),式中?、r、?0、?均为常数3、已知X(z)?31?0.5z?1?21?3z?1，求X(z)的反变换x(n)。

4、求下列X(z)的反变换：（1）1-1z?1X(z)?6,|z|?11?1z?22 4（2）)?1-6z?1X(z,|z|?11?1?22 4z15、求下列序列的Z变换及收敛域：（1）x(n)?b|n|,（2）x(n)?|b|?11u(n) n31（3）x(n)??nu(?n?1)3（4）x(n)?nsin(?n),6、已知x1(n)?n?0且?为常数111nu(n)，x(n)?u(n)，且当|z|?|a|时，Z[au(n)]?, 23n4n1?az?1令y(n)?x1(n?3)?x2(?n?1)，请利用Z变换性质求y(n)的Z变换Y(z)。

7、一个线性移不变因果系统由下列差分方程描述：y(n)?3y(n?1)?2y(n?2)?x(n?1)（1）求该系统的系统函数，并指出其收敛域；（2）求该系统的单位脉冲响应。

8、设系统由下列差分方程描述： y(n)?y(n?1)?y(n?2)?x(n)（1）求系统函数H(z)，并求出零、极点；（2）若限定系统是因果的，写出H(z)的收敛域，并求出单位脉冲响应h(n);（3）若限定系统是稳定的，写出H(z)的收敛域，并求出单位脉冲响应h(n)。

2529、用MATLAB实现长除法，计算下列X(z)的Z反变换（取10个点）：1?1z12（1）X(z)?,|z|?121?z?1411?z?13（2）X(z)?,|z|?3 ?1?21?6z?9z1?10、已知X(z)?11、已知X(z)?换。

————第五章————数字滤波网络5.1 学 习 要 点本章主要介绍数字滤波器的系统函数()z H 与其网络结构流图之间的相互转换方法，二者之间的转换关系用Masson 公式描述。

由于信号流图的基本概念及Masson 公式已在信号与系统分析课程中讲过，所以下面归纳IIR 系统和FIR 系统的各种网络结构及其特点。

5.1.1 IIR 系统的基本网络结构1. 直接型结构如果将系统函数()z H 化为标准形式(5.1)式：()∑∑=-=--=Nk kkMk kkz az bz H 11 (5.1) 则可根据Masson 公式直接画出()z H 的直接II 型网络结构流图如图5.1所示（取N=4，M=3）。

二阶直接II 型网络结构最有用，它是级联型和并联型网络结构的基本网络单元。

优点：可直接由标准形式(5.1)或差分方程()()()∑∑==-+-=Mk kN k kk n x b k n y a n y 01画出网络结构流图，简单直观。

缺点：对于高阶系统：（1）调整零、极点困难；（2）对系数量化效应敏感度高；（3）乘法运算量化误差在系统输出端的噪声功率最大。

2. 级联型结构将(5.1)式描述的系统函数()z H 分解成多个二阶子系统函数的乘积形式()()()()z H z H z H z H m 21⋅= (5.2) (),1221122110------++=zzzzz H i i i i i i ααβββ m i ,,2,1 = (5.3)画出的级联型方框图如图5.2所示。

图中每一个子系统均为二阶直接型结构，根据()z H 的具体表达式确定()z H i 的系数i i i i 1210,,,αβββ和i 2α后，可画出()z H i 的网络结构流图如图5.3所示。

优点：（1）系统结构组成灵活；（2）调整零、极点容易，因为每一级二阶子系统()z H i 独立地确定一对共轭零点和一对共轭极点；（3）对系数量化效应敏感度低。

第五章 数字滤波器的基本结构1。

用直接I 型及典范型结构实现以下系统函数21214.06.028.02.43)(-----+++=z z z z z H分析:①注意系统函数H(z)分母的 0z 项的系数应该化简为1。

②分母), 2 , 1( ••••••=-i z i 的系数取负号，即为反馈链的系数。

解：21212.03.014.01.25.1)(-----+++=z z z z z H )2.03.0(14.01.25.12121----+--++=z z z z ∵)()(1)(1z X z Y z a zb z H Nn nn Mm mn=-=∑∑=-=- ∴3.01-=a ，2.02=a5.10=b ，1.21=b ，4.02=b2。

用级联型结构实现以下系统函数)8.09.0)(5.0()14.1)(1(4)(22++-+-+=z z z z z z z H 试问一共能构成几种级联型网络。

分析：用二阶基本节的级联来表达（某些节可能是一阶的)。

解： ∏------++=k k k k k z zz z A z H 2211221111)(ααββ )8.09.01)(5.01()4.11)(1(4211211------++-+-+=z z z z z z ∴ 4=A8.0 ,9.0 , 0,5.0 1,4.1 , 0 ,1 2212211122122111-=-====-===ααααββββ由此可得：采用二阶节实现，还考虑分子分母组合成二阶（一阶）基本节的方式,则有四种实现形式.3。

给出以下系统函数的并联型实现。

)8.09.01)(5.01(6.141.158.12.5)(211321------++--++=z z z z z z z H 分析：注意并联的基本二阶节和级联的基本二阶节是不一样的,这是因为系统函数化为部分分式之和,分子的1-z 的最高阶数比分母1-z 的最高阶数要低一阶，如果分子、分母多项式的1-z 的最高阶数相同，则必然会分解出一个常数项的相加（并联）因子。

1.计算以下诸序列的N点DFT,在变换区间 内,序列定义为
（2） ；
（4） ；
（6） ；
（8） ；
（10） 。
解：
（2）
（4）
（6）
（8）解法1直接计算
解法2由DFT的共轭对称性求解
因为
所以
即
结果与解法1所得结果相同。此题验证了共轭对称性。
（10）解法1
上式直接计算较难，可根据循环移位性质来求解X(k)。
画出级联型结构如题3解图（b）所示。
4.图中画出了四个系统，试用各子系统的单位脉冲响应分别表示各总系统的单位脉冲响应，并求其总系统函数。图d
解：
(d)
5.写出图中流图的系统函数及差分方程。图d
解：
(d)
6.写出图中流图的系统函数。图f
解：
(f)
8．已知FIR滤波器的单位脉冲响应为 ，试用频率采样结构实现该滤波器。设采样点数N=5，要求画出频率采样网络结构，写出滤波器参数的计算公式。
总结以上x(n)是实、偶函数时，对应的傅里叶变换 是实、偶函数。
（2）x(n)是实、奇函数。
上面已推出，由于x(n)是实序列， 具有共轭对称性质，即
由于x(n)是奇函数，上式中 是奇函数，那么
因此
这说明 是纯虚数，且是w的奇函数。
10.若序列 是实因果序列，其傅里叶变换的实部如下式:
求序列 及其傅里叶变换 。
因为
所以
将x(n)的表达式代入上式，得到
8.设线性时不变系统的单位取样响应 和输入 分别有以下三种情况，分别求出输出 。
（1） ；
（2） ；
（3） 。
解：
（1）
先确定求和域，由 和 确定对于m的非零区间如下：

所以 T［ax1(n)+bx2(n)］=aT［x1(n)］+bT［x2(n)］
第 1 章 时域离散信号和时域离散系统
（2） 令输入为
输出为
x(n－n0)
y′(n)=2x(n－n0)+3 y(n－n0)=2x(n－n0)+3=y′(n) 故该系统是非时变的。 由于
T［ax1(n)+bx2(n)］=2ax1(n)+2bx2(n)+3 T［ax1(n)］=2ax1(n)+3 T［bx2(n)］=2bx2(n)+3 T［ax1(n)+bx2(n)］≠aT［x1(n)］+bT［x2(n)］ 故该系统是非线性系统。
T［ax1(n)+bx2(n)］=ax1(n) sin(ωn)+bx2(n) sin(ωn) =aT［x1(n)］+bT［x2(n)］
故系统是线性系统。
第 1 章 时域离散信号和时域离散系统
6． 给定下述系统的差分方程， 试判定系统是否是因果稳定系统， 并说明 理由。
（1） y(n)=
1 x(Nn－1 k)
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器， 延时器是线性非时变系统， 下面证明。 令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
（6） y(n)=x(n2)

5-1 An AM broadcast transmitter is tested by feeding the RF output into a 50-Ω (dummy) load. Tone modulation is applied. The carrier frequency is 850 kHz and the FCC licensed power output is 5,000 W. The sinusoidal tone of 1,000 Hz is set for 90% modulation.(a) Evaluate the FCC power in dBk (dB above 1 kW) units.(b) Write an equation for the voltage that appears across the 50-Ω load, giving numerical values for all constants.(c) Sketch the spectrum of this voltage as it would appear on a calibrated spectrum analyzer.(d) What is the average power that is being dissipated in the dummy load? (e) What is the peak envelope power? Solution ：(a) FCC power:500010lg 6.99()1000dBK ⎛⎫= ⎪⎝⎭()()()():c o s 20001000900.9501cos m m m c c b Let m t A t f H z A s t A m t tπω==→=∴Ω=+⎡⎤⎣⎦是％调制负载上通过的电压为：()707[10.9 cos (2000)]cos[2850,000]s t t t ππ=+(c)])cos[(2)707(9.0])cos[(2)707(9.0cos 707)(t t t t s m c m c c ωωωωω++-+=212500050c A =707c A V=(d)50Ω负载上的平均功率：()222A V G real 210.921505020.95000170252c A st P w<>⎡⎤==+⎢⎥⎣⎦⎡⎤=+=⎢⎥⎣⎦(e) (){}[]222PEP P 1max 500010.918050250cA m t w =+=⨯+=⎡⎤⎣⎦⨯5-2 An AM transmitter is modulated with an audio testing signal given by()120.2sin 0.5cos m t t t ωω=+, where 1500f Hz =,2f =,and 100c A =.Assume that the AM signal is fed into a 50Ω load. (a) Sketch the AM waveform. (b) What is the modulation percentage?(c) Evaluate and sketch the spectrum of the AM waveform. Solution: ()()12100(10.2sin 0.5cos )cos c a s t t t t ωωω=++2222221110.9()()12222c c cs t A A m t A ⎡⎤<>=+<>=+⎢⎥⎣⎦5-4 Assume that an AM transmitter is modulated with a video testing signal given by ()10.20.6sin m t t ω=-+,where f 1=3.57MHz. Let A c =100. (a) Sketch the AM waveform.(b) What are the percentages of positive and negative modulation? (c) Evaluate and sketch the spectrum of the AM waveform about f c .Solution:()()()()()()1110.20.6sin 3.57;1001001cos 1000.80.6sin cos m c c c a m t t f f M H zA s t m t t t tωωωω=-+====+=+()m ax m in140100%pos.m od.40%10010020%neg.m od.80%100ccc cA A b A A A A --===--===()()()()()04015c c m c m c f Sff f j f f f f f f δδδ>=------+⎡⎤⎣⎦5-5 A 50,000-W AM broadcast transmitter is being evaluated by means of a two-tonetest.The transmitteris connected to a 50-Ω load, and()1111cos cos 2m t A t A t ωω=+, where f 1=500 Hz. Assume that a perfect AMsignal is generated.(a) Evaluate the complex envelope for the AM signal in terms of A 1 and ω1. (b) Determine the value of A 1 for 90% modulation.(c) Find the values for the peak current and average current into the 50-Ω load for the 90% modulation case. Solution:(a))]2cos (cos 1[2236)](1[)(V2236)50(2000,501112t t A t m A t g A A C c cωω++=+==⇒=(b)()1111111cos 2c c os 2os []cos A t t m t A t A t ωωωω=++=to find [m (t )]min : x (θ) = cos θ +cos2θ()sin 2sin 20dx d θθθθ=--=sin 4sin cos θθθ-=125.1)5.104(5.104-=︒︒=x θ()()()111min 104.51.12min 0.905.8om t A m A x At -=→=⎡==-⎡⎤⎣⎤⎣⎦⎦m ax 1M I N 1m ax m in112236[12]2236[1 1.125]3.1250.900.57622cA A A A A A A A A =+=--==⇒=另解：(c)m ax m ax m ax m ps1112236[12(0.8)]5813.6volts116.272 50()2236[10.8(cos cos 2)]cos 0 Av c c A A I A I s t t t tfor ωωωωω=+=====++⋅=>>m ax m ax m ax m ps1112236[12(0.576)]4811.9volts96.238 50()2236[10.576(cos cos 2)]cos 0 c c A A I A s t t t tfor ωωωωω=+====++⋅=>>另解：∴ mps A 0I Av =5-12 SSB signals can be generated by the phasing method shown in Fig. 5-5a, by the filter method, of Fig. 5-5b, or by the use of Weaver ’s method [Weaver, 1956], as shown in Fig. P5-12. For Weaver ’s method (Fig. P5-12), where B is the bandwidth of m (t ),(a) Find a mathematical expression that describes the waveform out of each block on the block diagram.(b) Show that s (t) is an SSB signal.Figure P5-12 Weaver ’s method for generating SSB.Solution:)cos(212cos )(1Bt t B t V ππ=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡++-=↔==)21()21(21)()cos()()()()(313B f M B f M f V Bt t m t V t m t V π⎥⎦⎤⎢⎣⎡++--=↔==)21()21(21)()sin()()()()(424B f M B f M j f V Bt t m t V t m t V π⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<⎥⎦⎤⎢⎣⎡++-=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<=elsewhere ,021||,)21()21(21elsewhere f ,021|| ),()(45f Bf B f M B f M B f f V f VLikewise ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<⎥⎦⎤⎢⎣⎡++--=elsewhere ,021||,)21()21(21)(6f B f B f M B f M f V ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=t B f t v t V c 212cos )()(59π⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<++⎥⎦⎤⎢⎣⎡++++-++<--⎥⎦⎤⎢⎣⎡+--+---=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛--=⇒elsewhere 21|21|,0,)2121()2121(21|21|,)2121()2121(41 212121)(559f B B f f B B f f M B B f f M B B f f B B f f M B B f f M B f f V B f f V f V c c c c c c c ccc c c c c c c c c f f B f B B f f B f f f B B f f B B f BB f f B B B f f -<<--⇒<+++<<⇒++<<-+⇒<--<-⇒<--21|21| Likemise 21212121 21212121|21:|AsideThus,[][]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-<<--+++++<<-+--=elsewhere ,0,)()(41,)()(41)(9f f f B f B f f M f f M B f f f f f M B f f M f V c c c c c c c cLikewise⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧<++⎥⎦⎤⎢⎣⎡+++--++<--⎥⎦⎤⎢⎣⎡+--+----=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛---=elsewhere 21|21|,0,)2121()2121(4121|21|,)2121()2121(41212121)(6610f BB f f B B f f M B B f f M B B f f B B f f M B B f f M B f f V B f f V j f V c c c c c c c c[][]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-<<--++-++<<-+---⇒elsewhere ,0,)()(41,)()(41)(10f f f B f B f f M f f M B f f f f f M B f f M f V c c c c c c c cputout=s(t) = v 9(t)+v 10(t ))()()(109f V f V f s +=⇒5-13 An SSB-AM transmitter is modulated with a sinusoid ()15cos m t t ω=, where1112,500,and 1c f f Hz A ωπ===. (a) Evaluate ()ˆmt . (b) Find the expression for a lower SSB signal.cc c f c -S(t) is a USSB signal⇒ USSBf f f B f f f M B f f f f f M f S c c c c c c =⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-<<--++<<-=⇒elsewhere ,0),(21),(21)((c) Find the rms value of the SSB signal. (d) Find the peak value of the SSB signal.(e) Find the n ormalized average power of the SSB signal. (e) Find the normalized PEP of the SSB signal. Solution:()()1ˆ5sin a mt t ω= ()()()()()111ˆcos sin 5cos cos 5sin sin 5cos c c c c c b s t m t t mt t t t t t tωωωωωωωω=+=+=-()()15cos c s t t ωω=-()()22552rms c st V <>=→==()5P d V V =()()2252e st w <>=()252P E P f P w =5-18 A phasing-type SSB-AM detector is shown in Fig. P5-18. This circuit is attached to the IF out-put of a conventional superheterodyne receiver to provide SSB reception.(a) Determine whether the detector is sensitive to LSSB or USSB signals. How would the detector be changed to receive SSB signals with the opposite type of sidebands?(b) Assume that the signal at point A is a USSB signal with f c = 455 kHz. Find the mathematical expressions for the signals at points B through I . (c) Repeat part (b) for the case of an LSSB-AM signal at point A .(d) Discuss the IF and LP filter requirements if the SSB signal at point A has a3-kHz bandwidth.Figure P5-18Solution: (a)ˆ()()cos ()sin ''''A c c s t m t t m t t U SSBL SSBωω=-→+→()cos D c s t t ω=2ˆ()()()()cos ()sin cos ˆ()()(1cos 2)sin 222B A D c c c c c s t s t s t m t t mt t t m t m t t tωωωωω===+()()2c m t s t =()sin E c s t t ω=2()()()ˆ()sin cos ()sin ˆ()()sin 2(1cos 2)22F A E c c c c c s t s t s t m t t t m t t m t m t t t ωωωωω===-ˆ()()2G m t s t =()()()2H m t s t =-I :()()()()()()22,(),I c H m t m t s t s t s t U SSB m t LSSB=-=+⎧=⎨⎩To receive USSB signals, Additive V H (t ) from V C (t) at the summer.CHI(b) see part (a.) (c) see part (a.)(d) IF should be cantered atf c ±1.5 kH z,LSSBU SSBhave 3kHz BW and as small aroll-off factor as is economically feasible. LPF should have 3 kHz BW and as small a roll-off factor as is feasible, also.5-20 A modulated signal is described by the equations (t )=10 cos[(2π⨯108)t+10 cos (2π⨯103t )] Find each of the following: (a) Percentage of AM.(b) Normalized power of the modulated signal. (c) Maximum phase deviation. (d) Maximum frequency deviation. Solution: (a) ma xm i nc A AA ==0% A M∴ (b) W 502/10/2/22norm ===c A P()()()()()()310cos 2102210101502j tj t c org t e A eg t st g t wπθ===∴<>=<>=(c) m ax 10 radions θ∆=(d)kHz10102)2000(102)2000sin()2000(10)()(4===∆=∆-==πππωππθωd d F t dt t d t5-23 A MF signal has sinusoidal modulation with a frequency of f m =15KHzand modulation index of 2.0β=.(a) Find the transmission bandwidth by using carson ’s rule.(b)What percentage of the total FM signal power lies within the carson rule bandwidth?Solution:().cos 22(1)231590m m T m a m t A f tB f KHzπβ==+=⨯⨯=()()()()012320.223920.576720.352820.1289J J J J ====在卡森带宽内取了三次边频：()()()()()()()()2222222201232222201231111222222222.122222299.75%c c c c c A J A J A J A J b A J J J J ⎡⎤+⨯++⎢⎥⎣⎦∴⎡⎤=+⨯++=⎣⎦5-26 A modulated RF waveform is given by []1500cos 20cos c t t ωω+, where1112,1,100c f f K H z and f M H z ωπ===.(a) If the phase deviation constant is 100 rad/V , find the mathematical expression for the corresponding phase modulation voltage ()m t . What is the peak value and its frequency?(b) If the frequency deviation constant is 6110/rad V s ⨯⋅, find the mathematical expression for the corresponding FM voltage ()m t . What is the peak value and its frequency?(c)If the RF waveform appears across a 50Ω load, determine the average powerand the PEP.Solution:.:a PM.:b FM()22150012522s c RF P A KW ===波形的规一化功率：()12500025005050s real PEP P P W P Ω====通过50负载后：5-46 A digital baseband signal consisting of rectangular binary pulses occurring at a rate of 24 kbits/s is to be transmitted over a bandpass channel.(a) Evaluate the magnitude spectrum for OOK signaling that is keyed by a baseband digital test pattern consisting of alternating 1’s and 0’s.(b) Sketch the magnitude spectrum and indicate the value of the first null-to-null bandwidth . Assume a carrier frequency of 150 MHz.(c) For a random data pattern, find the PSD and plot the result. Compare this1()cos[()]500cos[20cos ]100()20cos 210001()cos 210005c c c P S t A t D m t t t m t tm t tωωωππ=+=+∴==[]()166()cos[()]500cos[20cos ]10()20cos 2100020()sin 2100021000104sin 21000100t c c c f t S t A t D m t dt t t m t dt t m t t tωωωπππππ-∞-∞=+=+∴==-=-⎰⎰result with that obtained in parts (a) and (b) for alternating data. Solution:(a) Evaluate the magnitude spectrum for OOK signaling that is keyed by a baseband digital test pattern consisting of alternating 1’s and 0’s.()()cos c c s t A m t t ω= , m (t )为单极性 OOK : ()()c g t A m t =0000000/4/4/4/4/2/20000()1sin(/2)2/2/2sin(/2)()()() 2/211 w here:22jn tn n T jn tT jn tc n c T T jn jn c c cn n n bg t C eA eC A edt T T jn A A e en T jn T n A n G f C f nf f nf n R f T T ωωωππωππππδδπ∞=-∞-----∞∞=-∞=-∞===⋅--==-⎡⎤=-=-⎢⎥⎣⎦===∑⎰∑∑*1()[()()]2c c S f G f f G f f =-+--(b) Sketch the magnitude spectrum and indicate the value of the first null-to-null bandwidth. Assume a carrier frequency of 150 MHz.48null B K H z =(c) For a random data pattern, find the PSD and plot the result. Compare this result with that obtained in parts (a) and (b) for alternating data.48null B K H z =The null-to-null bandwidth is the same for both (b) and (c). Both have sinx/x type spectral envelope.5-47 对于BPSK 调制，重做5.46的(a)(b)(c)()()U nipolar N R Zc g t A m t =→22sin ()()4cb g b b A fT P f f T fT πδπ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦1()[()()]4s g g c c P f P f f P f f =-+--()()cos c c s t A m t t ω= ,(a)(b)()/2/2b b b b t T t T p t T T ⎡⎤⎡⎤+-=-⎢⎥⎢⎥⎣⎦⎣⎦∏∏ ()()()0nm t p t t nT δ=*-∑()()()()()2/22/22sin b b bbj fT j fT b b b b j fT j fT b b b b bP f T Sa fT eT Sa fT eT Sa fT e ej T Sa fT fT πππππππππ--=-⎡⎤=-⎣⎦=()()()()12sin()22sin()2/2sin(/2)2b b b nb b b b n b n b n Mf j T Sa fT fT f T T n jSa fT fT f T n j Sa n n f T ππδππδππδ⎛⎫=⋅- ⎪⎝⎭⎛⎫=- ⎪⎝⎭⎛⎫=- ⎪⎝⎭∑∑∑()()[()()]2c c c A S f Mf f f f f δδ=*-++(c) ()()cos c c s t A m t t ω= m(t)为极性NRZ()()c g t A m t =()()22sin b gc b b fT P f A T fT ππ⎛⎫= ⎪⎝⎭()()()14sgc g c P fP f f P f f ⎡⎤=-+--⎣⎦5-49 Evaluate the magnitude spectrum for an FSK signal with alternating 1 and 0 data. Assume that the mark frequency is 50 kHz, the space frequency is 55 kHz, and the bit rate is 2,400 bits/s. Find the first null-to-null bandwidth. Solution:The result if given by (5-86).f 1: : =50KHz f 2 : =55KHz R : = 2.4 Kbit/s where f2>f121f f h R-=A C := 1122c f f f +=Solution:By problem 5.46:0000*sin(/2)()()() 2/211w here:221()[()()]2c n bc c A n G f C f nf f nf n R f T T S f G f f G f f πδδπ∞∞-∞-∞⎡⎤=-=-⎢⎥⎣⎦====-+--∑∑()()1122()cos()cos()FSK n b c n n b c n s t a p t nT A t a p t nT A t ωθωθ⎡⎤=-⋅+⎢⎥⎣⎦⎡⎤+-⋅+⎢⎥⎣⎦∑∑()()nbnm t a p t nT =-∑null (5550)2 2.49.8kH zB =-+⨯=b.()()c g t A m t =22sin ()()4c b g b b A fT P f f T fT πδπ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦1()[()()]4s g g c c P f P f f P f f =-+--null (5550)2 2.49.8kH zB =-+⨯=5.53 A binary baseband signal is pass through a raised cosine-rolloff filter with a 50% rolloff factor and is then modulated onto a carrier. The data rate is 64 kbits/s. Evaluate(a) The absolute bandwidth of a resulting OOK signal.(b) The approximate bandwidth of a resulting FSK s ignal when the mark freqwency is 150KHz and the space freqwency is 155KHz.(Note: It is interesting to compare these bandwidths with those obtained in probs. 5-46 and 5-49) Solution:()0643222R f K H z ===()()010.5321.548B f K H z =+=⨯= a. OOK()()0210.548296OOK B f KHz =+=⨯=b. FSK()()()212155150248101FSK B f f B KHz =-+=-+⨯=5-58 Assume that a QPSK signal is used to send data at a rate of 30 Mbits/s over asatellite transponder. The transponder has a bandwidth of 24 MHz.(a) If the satellite signal is equalized to have an equivalent raised cosine filter characteristic, what is the rolloff factor r required?(b) Could a rolloff factor r be found so that a 50-Mbit/s data rate could be supported?Solution:for QPSK M=4, l=2(a) If the satellite signal is equalized to have an equivalent raised cosine filtercharacteristic, what is the rolloff factor r required?0.6 6.130)24(2)1(230)1(24===+⇒+=⇒r or r r(b) Could a rolloff factor r be found so that a 50-Mbit/s data rate could besupported?()r f B +=10()021T B f r =+()021T B f r =+502424(1)(1)225r r ⇒=+⇒+=A rolloff factor ,r could not be found support 50Mb/s QPSK signaling5.62 Assume that a telephone line channel is equalized to allow bandpass data transmission over a frequency range of 400 to 3100Hz so that the available channel bandwidth is 2700Hz and the midchannel frequency is 1750Hz. Design a 16-symbol QAM signaling scheme that will allow a data rate of 9600 bits/s to be transferred over the channel. In you design, choose an appropriate rolloff factor r and indicate the absolute and 6-dB QAM signal bandwidth. Discuss why you selected the particular value of r that you used. 5.62 Solution:31004002700Q AM B H z =-= 49600162424004M l D Bd ==→=→==()()131004002400127000.125D r r r +=-→+=→=62400dB B D Hz ==习题：5.69 5.715.69 Plot the MSK Type I modulation waveforms x(t) and y(t).5.71 Plot the MSK TypeⅡmodulation waveforms x(t) and y(t).5.67 For π/4 QPSK signal,(a) Caculate the carrier phase shifts when the input data stream is 10110100101010 , where the leftmost bits are first applied to the transmitter.(b) Find the absolute bandwidth of the signal if r=0.5 raised cosine-rolloff filtering is used and the data rate is 1.5Mbits/s.Solution:For π/4 QPSK signal, M=4 ,l=2 0 1.52(1)(1)(1)(10.5) 1.1322T R B f r D r r M H z =+=+=+=+=。

2011/4/10
3
Notice: Skipped Sections

5.7 5.8 (all) 5.9 (all) 5.10 5.11
2011/4/10
4
5.1
Introduction
2011/4/10
5
5.1 Introduction
Digital processing of a real-world continuous-time signal involves the following basic steps:
The multiplication operation yields an impulse train
Note: Analog Filters are very important for digital systems. Since both the anti-aliasing filter and the reconstruction filter are analog lowpass filters, we review first the theory behind the design of such filters Also, the most widely used IIR digital filter design method is based on the conversion of an analog lowpass prototype
g[n ] = ga (nT ), -¥ <n < ¥
(5.1)
With T being the sampling period. The reciprocal of T is called the sampling frequency , i.e., 1⁄ . It is known that the frequency-domain of the analog signal is given by its FT: