垂直于弦的直径课件

5
分析：∵OC⊥AB，OC 过圆心 O，∴CA＝12AB．∵AB＝4，∴AC＝2.在 Rt△AOC
中，由勾股定理，得 OA＝ AC2＋OC2＝ 22＋12＝ 5，即⊙O 的半径为 5. 答案：B
第五页，共二十四页。
6
基础过关
1．下列结论正确的是( A ) A．经过圆心的直线是圆的对称轴 B．直径是圆的对称轴 C．与圆相交的直线是圆的对称轴 D．与直径相交的直线是圆的对称轴
人教版九年级数学上册 《垂直于弦的直径》圆PPT教学课件
科 目：数学 适用版本：人教版 适用范围：【教师教学】
垂直于弦的直径
第一页，共二十四页。2以练Fra bibliotek学名师点睛
知识点 1 圆的轴对称性 圆是轴对称图形，任何一条直径所在直线都是圆的对称轴．
知识点 2 垂径定理及其推论 垂直于弦的直径平分弦，并且平分弦所对的两条弧．
由勾股定理，得 OA2＝OD2＋AD2，即 r2＝(r－10)2＋302，解得 r＝50.即这个车轮 的外圆半径为 50 cm.
第十八页，共二十四页。
19
13．如图，在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C、D． (1)求证：AC＝BD； (2)若大圆的半径R＝10，小圆的半径r＝8，且点O到直线AB的距离为6，求AC的 长．
第六页，共二十四页。
7
2．如图，⊙O 的直径 AB⊥弦 CD 于点 E，则下列结论中一定正确的是( B )
A．AE＝OE C．OE＝12CE
B．CE＝DE D．∠AOC＝60°
第七页，共二十四页。
8
3．【教材 P83 练习 T1 变式】如图，在半径为 5 的⊙O 中，弦 AB＝6，OP⊥AB， 垂足为点 P，则 OP 的长为( C )

（√ ） （√ ） （×）
轴
经过圆心
中心
圆心
垂直于弦的 直径平分弦，并且平分弦所对的两条弧
垂直
弦所对的两条弧
问题：你知道赵州桥吗?它是1300多年前我国隋代建 造的石拱桥，是我国古代人民勤劳与智慧的结晶．它的主 桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4m, 拱高（弧的中点到弦的距离）为7.2m，你能求出赵州桥主 桥拱的半径吗？
∵AB∥CD，∴ON⊥CD于N
在RtAOM中，AM 5cm,OM OA2 AM2 12cm. 在RtOCN中，CN 12cm,ON OC2 CN 2 5cm.
∵MN=OM-ON，∴MN=7cm. (2)当AB、CD在O点异侧时，如图②所示，
由（1）可知OM=12cm,ON=5cm，MN=OM+ON，
（并2且）平A分M=A（BBM及，AA（DCB=．BC，AD=BD，即直径CD平分弦AB，
这样，我们就得到下面的定理：垂直于弦的直径平分弦， 并且平分弦所对的两条弧。进一步，我们还可以得到结论：平 分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧 。
知识点一 垂径定理及其推论
C
知识点一 垂径定理及其推论
通过本节课的学习,我们就会很容易解决这一问题．
探究：1．圆是轴对称图形吗？如果是，它的对称轴是什 么？你能找到多少条对称轴？
分析讨论：圆是轴对称图形,它的对称轴是直径，我能找到 无数多条直径．
探究： 2．你是用什么方法解决上述问题的？与同伴进行 交流．
分析讨论我：是利用沿着圆的任意一条直径折叠的方法解决 圆的对称轴问题的．
.2垂直于弦的直径
判断：
（１）直径是弦．（ √ ）
（２）弦是直径． （ × ）

24.1.2 垂直于弦的直径
———（垂径定理）
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
赵州石拱桥
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧 形,它的跨度(弧所对是弦的长)为37m,拱高(弧的中点到弦的距 离,也叫弓形高)为7.23m,求桥拱的半径(精确到0.1m).
OA2 AD2 OD2
即 解R得2分： 1R析8.：722 7O.A9(2Rm=A)D72.2+O2D2
其中OD=OC-CD
因此，赵州桥的主拱桥的半径约为27.9m。
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
E
B
｛（3）平分弦
D
（4）平分弦所对的优弧
（5）平分弦所对的劣弧
① CD是直径 可推得 ② CD⊥AB
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
③AE=BE,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
平分弦（不是直径）的直径垂直于弦,并且
D 平分弦所对的两条弧.（垂径定理推论）
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
判断下列图形，能否使用垂径定理？

。
04
垂直于弦的直径与勾股定理 的关系
勾股定理的表述
勾股定理
在一个直角三角形中，直角边的平方 和等于斜边的平方。
勾股定理的证明方法
利用相似三角形的性质、四边形面积 的计算、代数方法等。
垂直于弦的直径与勾股定理的联系
垂直于弦的直径是直角三角形斜 边的中线。
根据勾股定理，直角三角形斜边 的中线长度等于斜边的一半。
在航海学中，勾股定理用于确定 船只的位置和航向，例如确定船
只与陆地之间的距离和角度。
05
垂直于弦的直径在现实生活 中的应用
工程设计中的应用
桥梁设计
在桥梁设计中，垂直于弦的直径 可以用于确定桥梁的承重能力和 稳定性，确保桥梁的安全性和可
靠性。
建筑设计
在建筑设计中，垂直于弦的直径可 以用于确定建筑物的结构强度和稳 定性，保证建筑物的安全和耐久性 。
答案
$( - frac{sqrt{3}}{3},frac{sqrt{3}}{3})$
题目
已知圆C：$(x - a)^{2} + (y - b)^{2} = r^{2}$，直线l过 点$(a,b)$且与圆C交于A，B两点，$angle AOB = 120^{circ}$（O为坐标原点），则实数r的取值范围是 ____．
感谢您的观看
THANKS
弦
连接圆上任意两点的线段 。
直径
经过圆心，并且两端点都 在圆上的线段。
性质
弦的中垂线经过圆心
垂直于弦并且经过圆心的线段称为弦 的中垂线，它也经过圆心。
弦被直径平分
垂直于弦的直径将弦分为两段相等的 部分。
弦与直径形成的角为直角
垂直于弦的直径与弦形成的角为直角 ，即弦与直径垂直。

·O
或作弦心距构造直角三角形，利用垂径定理和勾股
定理求解.
A
C
B
垂径定理 圆是轴对称图形
知识小结 内容
推论
垂直于弦的直径平分弦, 并且平分弦所对的两条弧
一条直线满足:①过圆心;②垂直于弦; ③平 分弦（不是直径）; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.满足其中两个条件就 可以推出其他三个结论（“知二推三”）
第二十四章 圆 24.1 圆的有关性质
垂直于弦的直径
1
理解圆的轴对称性及垂径定理的推 导.(难点)
学
习 目
2
能初步应用垂径定理进行计算和证明. （重点）
标
3
通过圆的对称性，培养学生对数学的 审美观，并激发学生对数学的热爱.
观察思考 把一个圆沿着它的任意一条直径对折，重复几次，
你发现了什么？由此你能得到什么结论？
1.半径为4cm的⊙O 中，弦AB=2 cm,
那么圆心O 到弦AB 的距离是
.
O
4
A1E B
2.⊙O 的直径为10 cm，圆心O 到弦AB的距离OE=4cm，
则弦AB 的长是 6cm .
O
54
A EB
达标练习
3.如图，⊙M 与x轴交于A，B 两点，与y轴交于C，D 两点，
(0, 若M(2,0)，B(5,0)，则C点的坐标是
a 2
2
例题变式
如图，在⊙O中，弦AB的长为 6 cm，圆心O到AB的距离（弦心距）为 4 cm，
求⊙O的半径．
解： 过圆心O 作OE⊥AB于E， A
,(垂径定理）
3E B
4
O
在Rt △ AOE 中 ,
方法总结

OC=8cm，则AB=
；
O
45
┌
A
D
8
30°
B
C
第7页，共16页。
巩固训练
一弓形弦长为 4 c6m，弓形所在的圆的半径为7cm，则 弓形的高为＿＿＿＿.
C
C
A
D
B
O
O
A
D
B
第8页，共16页。
4、如图，点A、B是⊙O上两点，AB=8,点P 是⊙O上的动点（P与A、B不重合）,连接AP 、BP,过点O分别作OE⊥AP于E,OF⊥BP于
O
A
D
B
如图，⊙O的直径为10，弦AB=8,P为AB上
的一个动点，那么OP长的取值范围是
。 3cm≤OP≤5cm
第12页，共16页。
5
3
4C
1.已知P为⊙O内一点，且OP＝2cm， 如果⊙O的半径是3cm,那么过P点的最
短的弦等于 2 5 c m .
2.过⊙O内一点M的最长弦长为4厘米，最短 弦长为2厘米，则OM的长是多少？
垂径定理
垂直于弦的直径平分弦,并且平分弦 所对的两条弧。
C
·O
AE D
第1页，共16页。
∵ CD是直径， CD⊥AB
∴ AE=BE, A⌒C ⌒ A⌒D ⌒
B
=BC, =BD.
垂径定理推论
平分弦（不是直径）的直径垂直于弦, 并且平分弦所对的两条弧。
C
·O AE
D
第2页，共16页。
∵ CD是直径， AE=BE
∴ CD⊥AB,A⌒C ⌒ A⌒D ⌒
B
=BC, =BD.
垂径定理的本质是
满足其中任两条，必定 同时满足另三条

年的历史，是我国古代人民勤劳与智慧的结晶.它的主
桥拱是圆弧形，它的跨度（弧所对的弦的长）为 37
m，拱高（弧的中点到弦的距离）为 7.23 m，求赵州
桥主桥拱的半径（结果保留小数点后一位）.
解：如图，过桥拱所在圆的圆心 O 作 AB 的垂线，交 AB
于点 C，交弦 AB 于点 D，则 CD = 7.23.
赵州桥中，弦长 a，弦心距 d，弓形高 h，半径 r 之间有
以下关系：
指圆心 O 到弦的距离
C
d+h=r
h
a
A
B 数量关系
D
2
r d
O
总结
垂径定理往往转化成应用勾股定理解直角三角形
课堂练习
1. 如图 a、b，一弓形弦长为
cm，弓形所在的圆的
半径为 7 cm，则弓形的高为＿_＿＿____cm.
2 或 12
问题2：不借助任何工具，你能找到圆形纸片的圆心吗？
由此你得到了什么结论？你能证明你的结论吗？
●O
结论：圆是轴对称图形，任何一条直径所在的直
线都是圆的对称轴.
问题3：如何证明圆是轴对称图形？
圆上任意一点关于直径所在直线 (对称轴) 的对称
点也在圆上.
同学们在自己作的圆中按照如下步骤作图，并
写出已知和证明：
基本图形及
变式图形
构造直角三角形，利用勾股定理
计算或建立方程.
OC ＝2，则☉ O 的半径长为

.
⁠
3. （2023·宜昌中考）如图， OA ， OB ， OC 都是☉
O 的半径， AC ， OB 交于点 D . 若 AD ＝ CD ＝8，
OD ＝6，则 BD 的长为 4 .

应用
利用垂直于弦的直径来证 明平面图形中的一些定理 和性质
实例
利用垂直于弦的直径来计 算平面图形的面积和周长
03
CHAPTER
垂直于弦的直径在实际问题 中的应用
在建筑设计中的应用
建筑结构分析
垂直于弦的直径在建筑设计中可用于分析结构的稳定性。通过计算直径上的应 力分布，可以评估结构的承载能力和安全性。
案例三
总结词
日常生活用品中的垂直于弦的直径应用主要 体现在工具和家居用品的设计上。
详细描述
在日常生活中，许多工具和家居用品都利用 了垂直于弦的直径原理。例如，剪刀、餐具 等工具的设计中，通过垂直于弦的直径实现 受力点的优化，提高使用舒适度和效率。在 家居用品中，如椅子、桌子等，垂直于弦的 直径有助于提高家具的稳定性和承重能力， 保证使用的安全性和舒适性。
交通工具设计
在交通工具设计中，垂直于弦的直径也有广泛应用。例如， 在汽车、火车等交通工具的车身和部件设计中，通过分析直 径上的应力分布，可以优化车身结构和材料选择，提高其安 全பைடு நூலகம்和经济性。
04
CHAPTER
垂直于弦的直径的应用案例 分析
案例一：建筑设计中的垂直于弦的直径应用
总结词
建筑设计中的垂直于弦的直径应用主要 体现在空间布局和结构稳定性方面。
实例
利用直径和垂直于直径的弦来计算圆的面积和周 长
在三角形中的应用
01
02
03
定理
垂直于弦的直径平分弦， 并且平分弦所对的两条弧
应用
利用垂直于弦的直径来证 明三角形的中线定理和平 行四边形定理
实例
利用垂直于弦的直径来计 算三角形的面积和周长
在其他图形中的应用

AB=8cm， ∴AE=4cm. 在RtAOE中，有OA= OE2 AE2 = 32 42 =5（cm）. ∴⊙O的半径为5cm.
垂直于弦的直径
【例2】已知：如图1，在以O为圆心的两个同心圆中，大圆的 弦AB交小圆于CD两点.求证：AC=BD.
【解析】此题可用三角形全等来证明， 构造△AOC与△BOD即可；但是若利用垂 径定理来证明 会更简单.
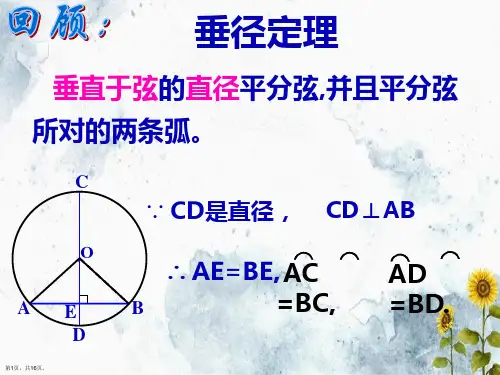
垂直于弦的直径
5.如图1,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长的 取值范围____3_≤__O_P_≤__5_________.
C
C
O
A
B
DOE
A
PB
A
D
B
图1
图2
图3
6.已知:如图2,有一圆弧形拱桥,拱的跨度AB=16cm,拱高CD=4cm,那么
拱形的半径____1_0_____m.
7.如图3,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA,CE⊥OB, CD=CE, 则 »AC 与B»C 的大小关系是____相__等_________.
垂直于弦的直径
8．圆中两弦CD与AB互相垂直,垂足为E, 若DE=3厘米, EC=7厘米,则圆心到AB的距离OF是___2____厘米． 9. P为⊙O内一点, PO=3cm, 过P的最短弦为8cm, 则过P 的最长弦的长等于__1_0_c_m__． 10. AB⊥CD,垂足为E， CD为⊙O直径, 且AB=20, CE=4, 那么⊙O的半径是_1_4_._5_．
ห้องสมุดไป่ตู้
问题： 1300 多年前，我国隋代建造的赵州石拱桥的桥拱是圆弧 形，它的跨度（弧所对的弦长）为37.4米，拱高（弧的中点到弦 的距离，也叫拱形高）为7.2米，求桥拱的半径.（精确到0.1米）

垂直于弦的直径公开 课版课件
• 垂直于弦的直径的基本概念 • 垂直于弦的直径的性质证明 • 垂直于弦的直径定理的应用 • 垂直于弦的直径定理的推论 • 垂直于弦的直径定理的证明方法
目录
Part
01
垂直于弦的直径的基本概念
定义与性质
定义
垂直于弦的直径是一条线段，它 过圆心并与给定的弦垂直。
性质
推论二：经过圆心，平分弦的线段垂直于该弦
总结词
此推论说明，如果一条线段经过圆心并平分弦，那么这条线段垂直于该弦。
详细描述
由于线段经过圆心，它必然与圆相交于两点。由于它平分弦，这两点将与弦形成两个相等的部分。根 据垂径定理，经过圆心的线段与弦垂直。
推论三：平分弦的直径垂直于该弦
总结词
这个推论表明，如果一条直径平分弦，那么这条直径垂直于该弦。
利用圆的性质证明
总结词：逻辑周密
详细描述：根据圆的性质，直径是圆中最长的弦，因此它必然平分与之垂直的任何其他弦。
利用反证法证明
总结词：反向思考
详细描述：第一假设与弦垂直的直径不平分该弦，然后通过一系列逻辑推理，最终得出矛盾，从而证 明垂直于弦的直径必然平分该弦。
THANKS
感谢您的观看
总结词
垂直于弦的直径将弦分为两段相等的线 段，这是垂直于弦的直径的基本性质之 一。
VS
详细描述
由于直径是弦的中垂线，它必然将弦分为 两段相等的线段。这是基于几何学的基本 定理，即任何经过圆心并垂直于弦的线段 都将弦平分，并将弦分为两段相等的线段 。这个性质在解决几何问题时非常有用， 因为它可以帮助我们快速找到弦的中点， 从而简化问题。
Part
03
垂直于弦的直径定理的应用
在几何证明题中的应用