九上数学每日一练：弧长的计算练习题及答案_2020年解答题版

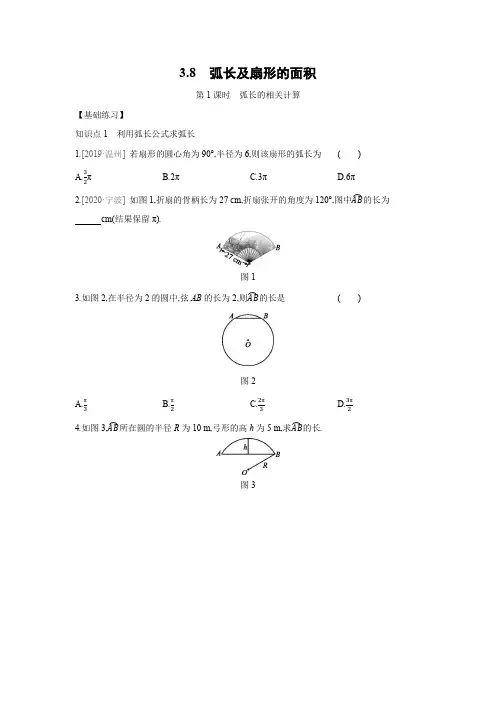
3.8弧长及扇形的面积第1课时弧长的相关计算【基础练习】知识点1利用弧长公式求弧长1.[2019·温州]若扇形的圆心角为90°,半径为6,则该扇形的弧长为()A.32πB.2πC.3πD.6π2.[2020·宁波]如图1,折扇的骨柄长为27 cm,折扇张开的角度为120°,图中AB⏜的长为cm(结果保留π).图13.如图2,在半径为2的圆中,弦AB的长为2,则AB⏜的长是()图2A.π3B.π2C.2π3D.3π24.如图3,AB⏜所在圆的半径R为10 m,弓形的高h为5 m,求AB⏜的长.图3⏜的长.5.如图4,四边形ABCD是☉O的内接四边形,☉O的半径为2,∠B=135°,求AC图46.一段圆弧形的公路弯道,圆弧的半径为2 km,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20 s,弯道上有一块限速警示牌,限速为40 km/h,则这辆汽车经过弯道时有没有超速?(π取3)知识点2利用弧长公式求圆心角或半径7已知弧长等于3π,弧所在圆的半径为6,则该弧所对的圆心角的度数是.,则该扇形的半径是.8.已知扇形的圆心角为45°,弧长等于π29.若半径为 5 cm的一段弧长等于半径为 2 cm的圆的周长,则这段弧所对的圆心角为.10.(1)直径为100 cm的圆弧的度数为40°,求这条弧的长;(2)圆弧的圆心角为300°,它所对的弧长等于半径为6 cm的圆的周长,求该弧所在圆的半径.【能力提升】11.如图5,△ABC内接于☉O,∠A=60°,BC=6√3,则BC⏜的长为()图5A.2πB.4πC.8πD.12π12.如图6,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则AP⏜与QB⏜的长度之和为()图6A.2π3B.4π3C.5π3D.π13.如图7,公园内有一块半径为20 m的圆形草坪,A,B是圆上的点,点O为圆心,∠AOB=120°,从点A到点B的路只有劣弧AB,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5 m,结果保留整数,参考数据:√3≈1.732,π取3.142).图714.[2020·潍坊]如图8,四边形ABCD是正方形,曲线DA1B1C1D1A2…是由一段段90度的弧组成的.其中:DA 1⏜的圆心为点A ,半径为AD ; A 1B 1⏜的圆心为点B ,半径为BA 1; B 1C 1⏜的圆心为点C ,半径为CB 1; C 1D 1⏜的圆心为点D ,半径为DC 1;…DA 1⏜,A 1B 1⏜,B 1C 1⏜,C 1D 1⏜,…的圆心依次按点A ,B ,C ,D 循环.若正方形ABCD 的边长为1,则的长是 .图815.如图9,在菱形ABCD 中,AB=2,∠C=60°,我们把菱形ABCD 的对称中心称作菱形的中心.菱形ABCD 在直线l 上向右做无滑动地翻滚,每绕着一个顶点旋转60°叫一次操作,则: (1)经过1次这样的操作,菱形中心O 所经过的路径长为多少? (2)经过18次这样的操作,菱形中心O 所经过的路径总长为多少?(3)经过3n (n 为正整数)次这样的操作,菱形中心O 所经过的路径总长为 .(结果都保留π)图9答案1.C [解析] 该扇形的弧长=90×π×6180=3π.故选C . 2.18π3.C [解析] 连结OA ,OB.∵OA=OB=AB=2,∴△AOB 是等边三角形,∴∠AOB=60°, ∴AB⏜的长为60×π×2180=2π3.故选C .4.解:如图,连结OA ,OC ,则O ,C ,D 共线,且OC ⊥AB.∵OD=R=10 m,CD=h=5 m, ∴OC=5 m,∴∠CBO=30°, ∴∠BOC=60°.∵OC ⊥AB ,∴∠AOB=2∠BOC=120°, ∴AB⏜的长=120×π×10180=203π(m).5.解:如图,连结OA ,OC.∵∠B=135°,∴∠D=180°-135°=45°,∴∠AOC=90°,则AC⏜的长为90π×2180=π. 6.解:∵l=nπr 180=10π×2180=π9(km),∴汽车的速度为π9÷203600≈60(km/h).∵60 km/h >40 km/h,∴这辆汽车经过弯道时超速了.7.90° [解析] 设该弧所对的圆心角为n °.由题意得nπ·6180=3π,解得n=90,∴该弧所对的圆心角的度数是90°. 故答案为90°. 8.29.144° [解析] 依题意得 2π×2=nπ×5180,解得 n=144.10.解:(1)l=40π×50180=100π9(cm).(2)∵n=300,l=2×6π=12π(cm),l=nπR180, ∴R=180l nπ=180×12π300π=7.2(cm).11.B [解析] 连结OB ,OC. ∵∠A=60°, ∴∠BOC=120°.∵BC=6√3,∴R=OB=6,则BC⏜的长=nπR 180=120π×6180=4π.故选B . 12.B [解析] 如图,连结OP ,OQ ,则OP=OQ=2. ∵OP=OQ=PQ=2, ∴△OPQ 为等边三角形, ∴∠POQ=60°,∴∠AOP+∠BOQ=120°, 则AP ⏜与QB ⏜的长度之和为120×π×2180=4π3.故选B .13.15 [解析] 过点O 作OC ⊥AB 于点C ,则AC=BC. ∵∠AOB=120°,OA=OB , ∴∠A=30°,∴OC=12OA=10 m,∴AC=√OA 2-OC 2=10√3 m, ∴AB=20√3 m . 又∵劣弧AB 的长=120π×20180=403π(m),∴403π-20√3≈7.25(m)≈15步. 14.4039π15.解:(1)如图,连结AC ,BD 交于点O.在菱形ABCD 中,AB=2,∠BCD=60°,∴AB=AD ,∠BAD=∠BCD=60°,AC ⊥BD ,BO=DO , ∴△ABD 是等边三角形,∴BD=AB=2, ∴BO=DO=1, ∴AO=√AD 2-DO 2=√3,∴经过1次这样的操作,菱形中心O 所经过的路径长为60π×√3180=√33π. (2)由(1)可得:第一次旋转点O 所经过的路径长为√33π, 第二次旋转点O 所经过的路径长为√33π, 第三次旋转点O 所经过的路径长为60π×1180=π3.∵18÷3=6,∴经过18次这样的操作,菱形中心O 所经过的路径总长为6×√33π+√33π+π3=(4√3+2)π.(3)经过3n (n 为正整数)次这样的操作,菱形中心O 所经过的路径总长为n ×2√33π+π3=2√3+13n π.。

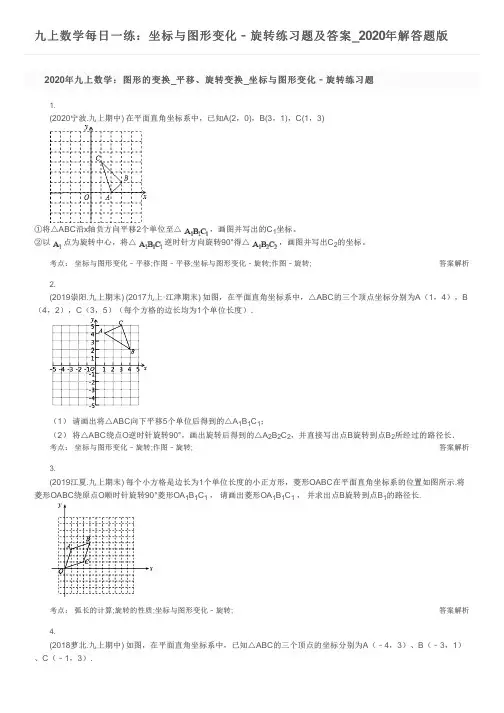
九上数学每日一练：坐标与图形变化﹣旋转练习题及答案_2020年解答题版答案解析答案解析答案解析2020年九上数学：图形的变换_平移、旋转变换_坐标与图形变化﹣旋转练习题1.(2020宁波.九上期中) 在平面直角坐标系中，已知A(2，0)，B(3，1)，C(1，3)①将△ABC沿x轴负方向平移2个单位至△ ，画图并写出的C坐标。②以 点为旋转中心，将△ 逆时针方向旋转90°得△ ，画图并写出C的坐标。考点： 坐标与图形变化﹣平移;作图﹣平移;坐标与图形变化﹣旋转;作图﹣旋转;2.(2019崇阳.九上期末) (2017九上·江津期末) 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．

（1） 请画出将△ABC向下平移5个单位后得到的△ABC；（2） 将△ABC绕点O逆时针旋转90°，画出旋转后得到的△ABC，并直接写出点B旋转到点B所经过的路径长．考点： 坐标与图形变化﹣旋转;作图﹣旋转;

3.(2019江夏.九上期末) 每个小方格是边长为1个单位长度的小正方形，菱形OABC在平面直角坐标系的位置如图所示.将

菱形OABC绕原点O顺时针旋转90°菱形OABC ， 请画出菱形OABC ， 并求出点B旋转到点B的路径长.

考点： 弧长的计算;旋转的性质;坐标与图形变化﹣旋转;4.(2018萝北.九上期中) 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）

、C（﹣1，3）．

12

1112222

1111111答案解析答案解析（1） 请按下列要求画图：①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△ABC，画出△ABC；②△ABC与△ABC关于原点O成中心对称，画出△ABC．（2） 在（1）中所得的△ABC和△ABC关于点M成中心对称，请直接写出对称中心M点的坐标．考点： 作图﹣平移;坐标与图形变化﹣旋转;作图﹣旋转;5.(2017济宁.九上期中) 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1）

3.8 弧长及扇形的面积（1）（巩固练习）姓名班级第一部分1、圆弧的圆心角为300°，它所对的弧长等于半径为6cm的圆的周长，求该弧所在的圆的半径.2、在半径为8的圆中，一条弧的长为2 ，求这条弧所对有圆心角的度数.3、一个滑轮起重装置如图所示，滑轮的半径是10cm，当重物上升10cm时，滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度约为（假设绳索与滑轮之间没有滑动，л取3.14 ，结果精确到1°)4、弯制管道时，先按中心线计算“展开长度”，再下料. 如图，求管道的展开长度.（单位：毫米，精确到1毫米）.5、如图，两个同心圆，大圆半径OC ，OD 分别交小圆于A ，B. 已知AB 的长为8π，CD 的长为12π，AC=12cm. 求：(1) ∠COD 的度数n ；(2) 小圆的半径r 和大圆的半径R 的长.第二部分1. 圆心角是1°的弧长等于圆周长的…………………………………………………（ ）A.190 B. 1180 C. 1270 D. 13602. 已知扇形的圆心角不变，则弧长与半径之间的函数关系式………………………（ ）A. 正比例函数B. 一次函数C. 反比例函数D. 二次函数 3. 已知半径为4的⊙O 中，直径所对的弧长= .OR 210100︒180ODCBAC4. 已知⊙O 的半径为10cm ，则60°的圆心角所对的弧长= .5.如图所示为一弯形管道，其中心线上一段圆弧AB. 已知半径OA=60㎝，∠AOB=108°，则管道的长度（即弧AB 的长）为 cm （结果保留π）6. 已知圆上的一段弧长为30 cm ，圆的半径是15cm ，则这段弧的度数是 .7. 长是1.44лcm 的弧所对的圆周角是36°，则该弧所在圆的直径是 cm .8. 如图，在Rt △ABC 中，∠C=90°，∠A=60°， AC=3cm , 将△ABC 绕点B 旋转至△A'B'C'的位置，且使 A ，B (B')，C'三点在同一直线上，则点A 经过的最短路线长是 .9. 一段铁路弯道成圆弧形，圆弧的半径是0.3km , 一列火车以每小时36km 的速度经10秒钟通过弯道，求弯道所对圆心角的度数（л取3.14，结果精确到0.1°） .10. 如图，AB 的半径长为40，弓形的高为20，求AB 的长.参考答案第一部分【分析】由于AB 的长与n ，r 有关，CD 的长与n ，R 有关，未知元素有n ，r ，R 三个，所以只要列出关于n ，r ，R 的三个关系式，便可解方程组求得.【解】(1) 由弧长公式，得8180n r ππ=……① 12180n Rππ=……②②-①，得()4180n R rππ-=. ∵R-r=AC=4，∴n=60°.(2) 把n=60分别代入①，②，得r=24cm，R=36cm.第二部分1. 圆心角是1°的弧长等于圆周长的…………………………………………………（）A. 190B. 1180C. 1270D. 1360答案：D2. 已知扇形的圆心角不变，则弧长与半径之间的函数关系式………………………（）A. 正比例函数B. 一次函数C. 反比例函数D. 二次函数答案：A3. 已知半径为4的⊙O中，直径所对的弧长= .答案：4π4. 已知⊙O的半径为10cm，则60°的圆心角所对的弧长= .答案：103πcm5.如图所示为一弯形管道，其中心线上一段圆弧AB. 已知半径OA=60㎝，∠AOB=108°，则管道的长度（即弧AB的长）为cm（结果保留π）答案：36πcm6. 已知圆上的一段弧长为30πcm，圆的半径是15cm，则这段弧的度数是 .答案：360°7. 长是1.44лcm的弧所对的圆周角是36°，则该弧所在圆的直径是cm .答案：7.2C8. 如图，在Rt △ABC 中，∠C=90°，∠A=60°， AC=3cm , 将△ABC 绕点B 旋转至△A'B'C'的位置，且使 A ，B (B')，C'三点在同一直线上，则点A 经过的最短路线长是 . 答案：53π9. 一段铁路弯道成圆弧形，圆弧的半径是0.3km , 一列火车以每小时36km 的速度经10秒钟通过弯道，求弯道所对圆心角的度数（л取3.14，结果精确到0.1°） . 解：∵36100.13600l =⨯=km ，R=0.3km ，180n R l π=，∴1801800.16019.10.3l n R πππ⨯===≈⨯°.10. 如图，AB 的半径长为40，弓形的高为20，求AB 的长.解：∵OC=40-20=20，OB=40，∠OCB=90°，∴∠OBC=30°. ∴∠BOC=60°，即n=120°. ∴12040801801803n R l πππ⨯⨯===.。

苏科版九年级数学上册 《弧长及扇形的面积》课时练习一、选择题1.若扇形的半径为6，圆心角为120°，则此扇形的弧长是( )A.3πB.4πC.5πD.6π2.如图，PA 、PB 是⊙O 切线,切点分别为A 、B,若OA=2,∠P=60°,则长为（ ）A.πB.πC.D.3.如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型.若圆的半径为r ，扇形的半径为R ，扇形的圆心角等于90°，则R 与r 之间的关系是( ).A.R=2rB.r R 3=C.R=3rD.R=4r4.钟表的轴心到分针针端的长为5cm ，那么经过40分钟，分针针端转过的弧长是( ) A.103πcm B.203πcm C.253πcm D.503πcm 5.如图,AB 为⊙O 的直径,AB=6,AB ⊥弦CD,垂足为G,EF 切⊙O 于点B,∠A=30°,连接AD 、OC 、BC,下列结论不正确的是（ ）A.EFA.EF ∥CDB.△COB 是等边三角形C.CG=DGD.的长为π6.一个扇形的弧长是10π cm ，面积是60π cm 2，则此扇形的圆心角的度数是( )A.300°B.150°C.120°D.75°7.如图，这是中央电视台“曲苑杂谈”中的一副图案，它是一扇形图形，其中∠AOB 为120°，OC 长为8cm ，CA 长为12cm ，则贴纸部分的面积为( )A.64πcm 2B.112πcm 2C.144πcm 2D.152πcm 28.如图，AB 为半圆的直径，且AB=4，半圆绕点B 顺时针旋转45°，点A 旋转到点A ′的位置，则图中阴影部分的面积为( ) A.π B.2π C.π2D.4π 9.如图,将△ABC 绕点C 按顺时针旋转60°得到△A ′B ′C,已知AC=6,BC=4,则线段AB 扫过图形面积为（ ）A.πB.πC.6πD.π10.如图，△ABC 中，BC=4，以点A 为圆心，2为半径的⊙A 与BC 相切于点D ，交AB 于E ，交AC 于F ，点P 是⊙A 上一点，且∠EPF=40°，则圆中阴影部分的面积是( ).A.π49-B.8π49-C.4π89-D.8π89-二、填空题11.已知弧所对的圆心角为90°，半径是4，则弧长为 .12.已知一条弧的半径为9，弧长为8π，那么这条弧所对的圆心角为 .13.如图，点A、B、C在半径为9的⊙O上，弧AB的长为2π，则∠ACB的大小是．14.已知扇形的圆心角为120°，半径为2，则这个扇形的面积S扇形= .15.如图，⊙O的半径为2，点A，B在⊙O上，∠AOB=90°，则阴影部分面积为_______.16.如图，在Rt△OAB中，∠AOB=45°，AB=2，将Rt△OAB绕点O顺时针旋转90°得到Rt △OCD，则AB扫过的面积(图中阴影部分面积)为________.三、解答题17.如图，在△ABC中，∠ACB=90°，∠B=15°，以点C为圆心，CA长为半径的圆交AB于点D.若AC=6，求弧AD的长.18.如图，已知以线段AB为直径作半圆O1，以线段AO1为直径作半圆O2，半径O1C交半圆O2于D点.试比较与的长.19.如图，一扇形纸扇完全打开后，AB和AC的夹角为120°，AB长为25 cm，贴纸部分的宽BD为15 cm，求纸扇上贴纸部分的面积.20.如图，正方形ABCD的边长为2 cm，以边BC为直径作半圆O，点E在AB上，且AE=1.5 cm，连接DE.(1)DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由.(2)求阴影部分的面积.答案1.B2.C3.D4.B5.D6.B7.B8.B.9.D10.B11.2π12.160°13.20°． 14.4315.π－216.π17.解：连接CD.∵AC=CD ，∴∠CAD=∠CDA.∵∠ACB=90°，∠B=15°，∴∠CAD=75°，∴∠ACD=30°. ∵AC=6，∴错误!的长度为错误!=π.18.解：的长等于的长. 19.解：∵AB=25 cm ，BD=15 cm ，∴AD=25－15=10(cm).∵S 扇形ABC =120π×252360=625π3(cm 2)， S 扇形ADE =120π×102360=100π3(cm 2)，∴贴纸部分的面积=625π3－100π3=175π(cm 2). 20.解：(1)DE 与半圆O 相切.证明：过点O 作OF ⊥DE ，垂足为F.在Rt △ADE 中，AD=2 cm ，AE=1.5 cm ，∴DE=2.5 cm.连接OE ，OD.由题意，知OB=OC=1 cm ，BE=AB －AE=0.5 cm.∵S 四边形BCDE =S △DOE ＋S △BOE ＋S △CDO ，∴12×(0.5＋2)×2=12×2.5·OF ＋12×1×0.5＋12×1×2， ∴OF=1 cm ，即OF 的长等于半圆O 的半径.又∵OF ⊥DE ，∴DE 与半圆O 相切.(2)阴影部分的面积=正方形ABCD 的面积－△ADE 的面积－半圆的面积=2×2－12×32×2－12×π×12=5－π2(cm 2). 即阴影部分的面积为5－π2cm 2.。

3.8 弧长及扇形的面积(二)1.如图，已知扇形OAB的半径为10，圆心角为54°，则此扇形的面积为(C)(第1题)A. 100πB. 20πC. 15πD. 5π2.钟面上的分针长度是6 cm，经过25 min，分针在钟面上扫过的面积为(B)A. 7.5π cm2B. 15π cm2C. 22.5π cm2D. 30π cm23.如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，OC＝2，则阴影部分的面积为(D)(第3题)A. 2πB. πC. π3 D.2π34.如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB长为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18 .(第4题)5.如图，扇形OAB的圆心角为90°，分别以OA，OB为直径在扇形内作半圆，P 和Q分别表示两个阴影部分的面积，那么P和Q的大小关系是P＝Q .(第5题)6.如图，AB是半圆O的直径，C，D是半圆O的三等分点.若弦CD＝2，求图中阴影部分的面积.(第6题)【解】如解图，连结OC，OD，OD与BC交于点E.(第6题解)∵C，D是半圆O的三等分点，∴∠BOD＝∠COD＝60°.又∵OC＝OD，∴△OCD为等边三角形，∴半圆O 的半径OD ＝CD ＝2. 易证得△CDE≌△BOE，∴S 阴影＝S 扇形OBD ＝60×π×22360＝23π.7.如图，在Rt△ABC 中，AC ＝BC ，以点A 为圆心画DF ︵，交AB 于点D ，交AC 的延长线于点F ，交BC 于点E.若图中两个阴影部分的面积相等，求AC 与AF 的长度之比.(第7题)【解】 ∵图中两个阴影部分的面积相等， ∴S △ABC ＝S 扇形ADF .在Rt△ABC 中，∵AC ＝BC ，∴∠A ＝45°.∴12AC 2＝45π·AF 2360，∴AC AF ＝π2.8.如图，在扇形OAB 中，∠AOB ＝90°，以点A 为圆心，OA 长为半径作OC ︵交AB ︵于点C.若OA ＝2，则阴影部分的面积为3－13π .(第8题)【解】 如解图，连结OC ，AC.(第8题解)由题意，得OC ＝OA ＝AC ＝2，∴△AOC 为等边三角形，∴∠BOC ＝30°， ∴扇形OCB 的面积为30×π×22360＝13π，△AOC 的面积为12×2×3＝3，扇形AOC 的面积为60×π×22360＝23π，∴阴影部分的面积为13π＋3－23π＝3－13π.9.如图，在Rt△ABC 中，∠C ＝90°，AC ＝2，BC ＝4，分别以AC ，BC 为直径作半圆，则图中阴影部分的面积为52π－4 .(第9题)【解】 过点C 作CD⊥AB 于点D ，则∠ADC＝∠BDC＝90°，故点D 既在以AC 为直径的半圆上，又在以BC 为直径的半圆上.∴S 阴影＝(S 小半圆－S △ADC )＋(S 大半圆－S △BDC )＝S 小半圆＋S 大半圆－S △ABC ＝180360π×12＋180360π×22－12×2×4＝52π－4. 10.如图，在边长为1的正方形网格中，△ABC 的顶点均在格点上，点A ，B 的坐标分别是A(4，3)，B(4，1)，把△ABC 绕点C 逆时针旋转90°后得到△A 1B 1C.(1)画出坐标系以及△A 1B 1C ，直接写出点A 1，B 1的坐标. (2)求在旋转过程中，△ABC 所扫过的面积.(第10题)【解】 (1)所求作的坐标系与△A 1B 1C 如解图所示.(第10题解)则点A 1的坐标为(－1，4)，点B 1的坐标为(1，4). (2)∵AC＝AB 2＋BC 2＝22＋32＝13，∠ACA 1＝90°， ∴在旋转过程中，△ABC 所扫过的面积为： S 扇形CAA 1＋S △ABC ＝90π×（13）2360＋12×3×2＝13π4＋3. 11.如图，在⊙O 中，半径OA⊥OB，过OA 的中点C 作FD∥OB 交⊙O 于D ，F 两点，且CD ＝3，以点O 为圆心，OC 长为半径作CE ︵，交OB 于点E.(1)求⊙O 的半径. (2)求阴影部分的面积.(第11题)【解】 (1)如解图，连结OD.(第11题解)∵OA ⊥OB ， ∴∠AOB ＝90°.∵FD ∥OB ，∴∠OCD ＝90°. 设OC ＝x ，则OD ＝OA ＝2x.在Rt△OCD 中，∵OC 2＋CD 2＝OD 2， ∴x 2＋(3)2＝(2x)2，解得x ＝1(负值舍去)， ∴OD ＝2，即⊙O 的半径为2.(2)∵在Rt △OCD 中，CO OD ＝12，∴∠CDO ＝30°. ∵FD ∥OB ，∴∠DOB ＝∠CDO＝30°. ∴S 阴影＝S △CDO ＋S 扇形OBD －S 扇形OCE ＝12×1×3＋30π×22360－90π×12360 ＝32＋π12.12.如图，在△ABC 中，CA ＝CB ，∠ACB ＝90°，以AB 的中点D 为圆心，作圆心角为90°的扇形DEF ，点C 恰在EF ︵上，设∠BDF＝α(0°＜α＜90°)，当α由小到大变化时，图中阴影部分的面积(C)(第12题)A. 由小到大B. 由大到小C. 不变D. 先由小到大，后由大到小【解】 如解图，过点D 作DM⊥AC 于点M ，DN ⊥BC 于点N ，连结DC.(第12题解)易得∠MDN＝∠EDF＝90°，DM ＝12BC ，DN ＝12AC ，∴∠MDG ＝∠NDH，DM ＝DN ＝24AB.又∵∠DMG＝∠DNH＝90°， ∴△DMG ≌△DNH(AAS).∴S 四边形DGCH ＝S 正方形DMCN ＝DM 2＝18AB 2.∵S 扇形DEF ＝90π·CD 2360＝πAB 216，∴S 阴影＝S 扇形DEF －S 四边形DGCH ＝（π－2）AB 216(定值).。

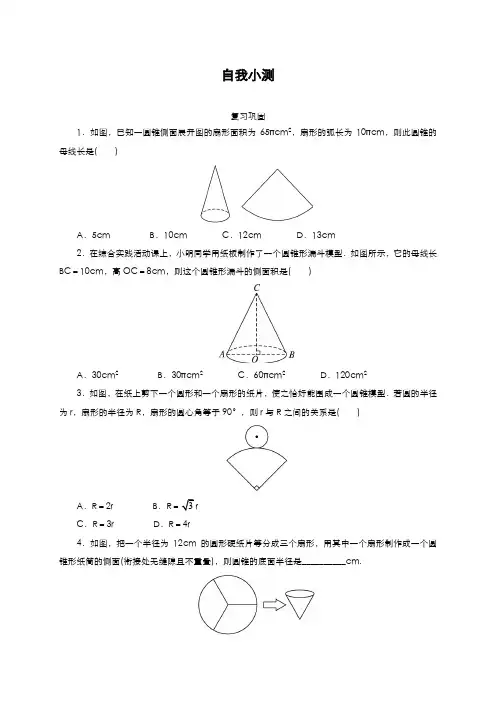
自我小测复习巩固1．如图，已知一圆锥侧面展开图的扇形面积为65πcm2，扇形的弧长为10πcm，则此圆锥的母线长是( )A．5cm B．10cm C．12cm D．13cm2．在综合实践活动课上，小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的母线长BC＝10cm，高OC＝8cm，则这个圆锥形漏斗的侧面积是( )A．30cm2B．30πcm2C．60πcm2D．120cm23．如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则r与R之间的关系是( )A．R＝2r B．R＝3rC．R＝3r D．R＝4r4．如图，把一个半径为12cm的圆形硬纸片等分成三个扇形，用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠)，则圆锥的底面半径是__________cm.5．下面是一圆锥的轴截面图，则此圆锥的侧面展开图的圆心角等于______．6．一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为__________．(结果保留π)7．如图所示，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB＝12cm，高BC＝8cm，求这个零件的表面积．(结果保留根号)能力提升8．已知点O为一圆锥的顶点，点M为该圆锥底面上一点，点P在母线OM上，一只蚂蚁从P 点出发，绕圆锥侧面爬行，回到P点时所爬过的最短路线的痕迹如图所示．若沿母线OM将圆锥侧面剪开展开，则所得侧面展开图是( )9．现有30%圆周的一个扇形彩纸片，该扇形的半径为40cm，小红同学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为10cm 的圆锥形纸帽(接缝处不重叠)，那么剪去的扇形纸片的圆心角为( )A．9° B．18° C．63° D．72°10．一个圆锥的高为3，侧面展开图是半圆，求：(1)该圆锥的母线与底面半径之比；(2)该圆锥的表面积．11．如图，一个纸杯的母线延长后形成的立体图形是圆锥，该圆锥的侧面展开图是扇形OAB，经测量，纸杯上开口圆的直径是6cm，下底圆直径为4cm，母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积．(面积计算结果用π表示)参考答案复习巩固1．D2．C 由勾股定理，得OB＝2222108CB CO-=-＝6(cm)．lO＝2π×6＝12π.故这个圆锥的侧面积是12lr＝12×12π×10＝60π(cm2)．3．D 因为圆形和扇形纸片能围成一个圆锥模型，所以圆的周长等于扇形的弧长，故2π4R＝2πr，即R＝4r.故选D.4．4 半径为12cm圆的三分之一弧长为13·2π·12＝8π，它等于圆锥的底面周长，故有8π2π＝4(cm)．5．90°∵2π×3＝π12180n⨯，∴n＝90.6．68π圆锥的母线长是2234+＝5.圆锥的侧面积是12×8π×5＝20π，圆柱的侧面积是8π×4＝32π.几何体的下底面面积是π×42＝16π.故所求几何体的全面积(即表面积)为20π＋32π＋16π＝68π.7．解：这个零件的底面积＝π×2122⎛⎫⎪⎝⎭＝36π(cm2)，这个零件的外侧面积＝12π×8＝96π(cm2)，圆锥母线长OC＝221282⎛⎫+ ⎪⎝⎭＝10(cm)，这个零件的内侧面积＝12×12π×10＝60π(cm2)，因此这个零件的表面积为36π＋96π＋60π＝192π(cm2)．能力提升8．D9．B 30%圆周的扇形彩纸片的圆心角为360°×30%＝108°. 设剪去的扇形纸片的圆心角为n°，则2π×10＝108π40180n (-)⨯，解得n ＝18.故选B.10．解：如图，设圆锥的轴截面为△ABC ，过点A 作AO ⊥BC 于点O ，设母线长AB ＝l ，底面O 的半径为r ，高AO ＝h.(1)∵圆锥的侧面展开图是半圆， ∴2πr＝12×2πl＝πl，l r ＝2.(2)在Rt △ABO 中， ∵l 2＝r 2＋h 2，l ＝2r ，h ＝3， ∴(2r)2＝32＋r 2.由r 为正数，解得r ＝3，l ＝2r ＝23.故S 表＝S 侧＋S 底＝πrl＋πr 2＝π×3×23＋π×(3)2＝9π.11．解：(1)由题意，知AB ＝6πcm，CD ＝4πcm. 设∠AOB ＝n°，AO ＝Rcm ， 则CO ＝(R －8)cm ， 根据弧长公式，得π180n R ＝6π，π8180n R (-)＝4π. 解得n ＝45，R ＝24.所以扇形圆心角的度数为45°. (2)由R ＝24，得R －8＝16. 所以S 扇形OCD ＝12×4π×16＝32π(cm 2)， S 扇形OAB ＝12×6π×24＝72π(cm 2)． 所以S 纸杯侧＝S 扇形OAB －S 扇形OCD ＝72π－32π＝40π(cm 2)．又因为S纸杯底＝24π2⎛⎫⎪⎝⎭＝4π(cm2)，所以S纸杯表＝40π＋4π＝44π(cm2)．。

中考数学复习 圆的弧长和图形面积的计算一、选择题1．扇形的半径为30 cm ，圆心角为120°，此扇形的弧长是( A ) A ．20π cm B ．10π c m C ．10 cm D ．20 cm【解析】弧长＝120π×30180＝20π(cm)，故选A.2．如图，⊙O 是△ABC 的外接圆，BC ＝2，∠BAC ＝30°，则劣弧BC 的长等于( A ) A.2π3 B.π3 C.23π3 D.3π3【解析】如图，连结OB ，OC ，∵∠BAC ＝30°，∴∠BOC ＝2∠BAC ＝60°，又OB ＝OC ，∴△OBC 是等边三角形，∴BC ＝OB ＝OC ＝2，∴劣弧BC 的长为60π×2180＝2π3.,第2题图) ,第3题图)3．如图，在Rt △ABC 中，AC ＝5 cm ，BC ＝12 cm ，∠ACB ＝90°，把Rt △ABC 所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为( B )A ．60π cm 2B ．65π cm 2C ．120π cm 2D ．130π cm 2【解析】∵在Rt △ABC 中，AC ＝5 cm ，BC ＝12 cm ，∠ACB ＝90°，∴由勾股定理得AB＝13 cm ，∴圆锥的底面周长＝10π cm ，∴几何体的侧面积＝12×10π ×13＝65π (cm 2) .故选B.4．如图，⊙O 的半径为3，四边形ABCD 内接于⊙O ，连结OB ，OD ，若∠BOD ＝∠BCD ，则BD ︵的长为( C )A ．π B.32π C ．2π D ．3π【解析】根据圆内接四边形对角互补可得∠BCD ＋∠A ＝180°，由圆周角定理可得∠BOD ＝2∠A ，再由∠BOD ＝∠BCD 可得2∠A ＋∠A ＝180°，所以∠A ＝60°，即可得∠BOD ＝120°，所以BD ︵的长＝120π×3180＝2π；故选C.,第4题图) ,第5题图)5．用等分圆周的方法，在半径为1的图中画出如图所示图形，则图中阴影部分面积为( A )A ．π－332B ．π－3 3 C.332 D ．π－334【解析】如图，设AB 的中点P ，连结OA ，OP ，AP ，△OAP 的面积是：34×12＝34，扇形OAP 的面积是：S 扇形＝π6，AP 直线和AP 弧面积：S 弓形＝π6－34，阴影面积：3×2S 弓形＝π－332. 二、填空题6．如图，扇形纸扇完全打开后，外侧两竹条AB ，AC 的夹角为120°，AB 长为30 cm ，求则BC ︵的长为__20π_cm __.(结果保留π)【解析】根据弧长公式l ＝n πr 180可得：弧BC 的长＝n πr 180＝120×π×30180＝20π (cm)．7．120°的圆心角所对的弧长是6π，则此弧所在圆的半径是__9__．【解析】根据弧长的公式l ＝n πr 180，得到6π＝120πr180，解得r ＝9.8．如图，某数学兴趣小组将边长为5的正方形铁丝框ABCD 变形为以A 为圆心，AB 为半径的扇形(忽略铁丝的粗细)，则所得的扇形ABD 的面积为__25__．【解析】扇形ABD 的弧长DB ︵＝BC ＋DC ＝10，扇形ABD 的半径为正方形的边长5，∴S扇形ABD ＝12×10×5＝25.9．如图，在▱ABCD 中，AB 为⊙O 的直径，⊙O 与DC 相切于点E ，与AD 相交于点F ，已知AB ＝12，∠C ＝60°，则FE ︵的长为__π__．【解析】如图连结OE ，OF ，∵CD 是⊙O 的切线，∴OE ⊥CD ，∴∠OED ＝90°，∵四边形ABCD 是平行四边形，∠C ＝60°，∴∠A ＝∠C ＝60°，∠D ＝120°，∵OA ＝OF ，∴∠A ＝∠OF A ＝60°，∴∠DFO ＝120°，∴∠EOF ＝360°－∠D －∠DFO －∠DEO ＝30°，FE ︵的长＝30π×6180＝π.故答案为π.三、解答题10．如图，AB 切⊙O 于点B ，OA ＝2，∠OAB ＝30°，弦BC ∥OA .求劣弧BC 的长．(结果保留π)解：连结OC ，OB ，∵AB 为圆O 的切线，∴∠ABO ＝90°，在Rt △ABO 中，OA ＝2，∠OAB ＝30°，∴OB ＝1，∠AOB ＝60°，∵BC ∥OA ，∴∠OBC ＝∠AOB ＝60°，又OB＝OC ，∴△BOC 为等边三角形，∴∠BOC ＝60°，∴劣弧BC 长为60π×1180＝π311．如图，在平面直角坐标系中，点A ，B ，C 的坐标分别为(－1，3)，(－4，1)，(－2，1)，先将△ABC 沿一确定方向平移得到△A 1B 1C 1，点B 的对应点B 1的坐标是(1，2)，再将△A 1B 1C 1绕原点O 顺时针旋转90°得到△A 2B 2C 2，点A 1的对应点为点A 2.(1)画出△A 1B 1C 1，△A 2B 2C 2；(2)求出在这两次变换过程中，点A 经过点A 1到达A 2的路径总长．解：(1)如图，△A 1B 1C 1，△A 2B 2C 2即为所作(2)OA 1＝42＋42＝42，点A 经过点A 1到达A 2的路径总长＝52＋12＋90π×42180＝26＋22π12．如图，AB 与⊙O 相切于点C ，OA ，OB 分别交⊙O 于点D ，E ，CD ︵＝CE ︵. (1)求证：OA ＝OB ；(2)已知AB ＝43，OA ＝4，求阴影部分的面积．解：(1)连结OC ，则OC ⊥AB.∵CD ︵＝CE ︵，∴∠AOC ＝∠BOC.在△AOC 和△BOC 中， ⎩⎨⎧∠AOC ＝∠BOC ，OC ＝OC ，∠OCA ＝∠OCB ＝90°，∴△AOC ≌△BOC (ASA )，∴OA ＝OB(2)由(1)可得AC ＝BC ＝12AB ＝23，∴在Rt △AOC 中，OC ＝2，∴∠AOC ＝∠BOC ＝60°，∴S △BOC ＝12BC· OC ＝12×23×2＝23，S 扇形EOC ＝60°×π×22360°＝23π，∴S 阴影＝S △BOC －S 扇形EOC ＝23－23π13．如图，在正方形ABCD 中，AD ＝2，E 是AB 的中点，将△BEC 绕点B 逆时针旋转90°后，点E 落在CB 的延长线上点F 处，点C 落在点A 处．再将线段AF 绕点F 顺时针旋转90°得线段FG ，连结EF ，CG .(1)求证：EF ∥CG ；(2)求点C ，A 在旋转过程中形成的，与线段CG 所围成的阴影部分的面积．解：(1)在正方形ABCD 中，AB ＝BC ＝AD ＝2，∠ABC ＝90°，∵△BEC 绕点B 逆时针旋转90°得到△ABF ，∴△ABF ≌△CBE ，∴∠FAB ＝∠ECB ，∠ABF ＝∠CBE ＝90°，AF ＝EC ，∴∠AFB ＋∠FAB ＝90°，∵线段AF 绕点F 顺时针旋转90°得线段FG ，∴∠AFB ＋∠CFG ＝∠AFG ＝90°，∴∠CFG ＝∠FAB ＝∠ECB ，∴EC ∥FG ，∵AF ＝EC ，AF ＝FG ，∴EC ＝FG ，∴四边形EFGC 是平行四边形，∴EF ∥CG(2)∵AD ＝2，E 是AB 的中点，∴FB ＝BE ＝12AB ＝12×2＝1，∴AF ＝AB 2＋BF 2＝22＋12＝5，由平行四边形的性质，△FEC ≌△CGF ，∴S △FEC ＝S △CGF ，∴S 阴影＝S 扇形BAC＋S △ABF ＋S △FGC －S 扇形FAG ＝90·π·22360＋12×2×1＋12×(1＋2)×1－90π×（5）2360＝52－π4。

九上数学每日一练：圆心角、弧、弦的关系练习题及答案_2020年单选题版答案答案答案答案答案2020年九上数学：图形的性质_圆_圆心角、弧、弦的关系练习题~~第1题~~(2020北仑.九上期末) 下列四个结论，不正确的是（ ）①过三点可以作一个圆； ②圆内接四边形对角相等③平分弦的直径垂直于弦；④相等的圆周角所对的弧也相等A . ②③B . ①③④C . ①②④D . ①②③④考点： 垂径定理;圆心角、弧、弦的关系;圆内接四边形的性质;确定圆的条件;~~第2题~~(2020慈溪.九上期中) 如图，已知A ，B ，C 在⊙O 上， 的度数为300°，∠C 的度数是（ ）A . 30°B . 40°C . 50°D . 60°考点： 圆心角、弧、弦的关系;圆周角定理;~~第3题~~(2020高平.九上期末) 如图，A ， B ， C 是⊙O 上的三个点，若∠C ＝35°，则∠OAB 的度数是（ ）A . 35°B . 55°C . 65°D . 70°考点： 等腰三角形的性质;圆心角、弧、弦的关系;圆周角定理;~~第4题~~(2020莘.九上期末) 如图，A 、D 是⊙O 上的两个点，若∠ADC=33°，则∠ACO 的大小为A . 57°B . 66°C . 67°D . 44°考点： 圆心角、弧、弦的关系;圆周角定理;~~第5题~~(2020定州.九上期中) 下图是几种汽车轮毂的图案，图案绕中心旋转90°后能与原来的图案重合的是（ ）A .B .C .D .考点： 圆心角、弧、弦的关系;旋转的性质;答案答案答案答案答案~~第6题~~(2019柯桥.九上期末) 如图，若AB 是⊙O 的直径，CD 是⊙O 的弦，∠ABD=58°，则∠C 的度数为（ ）A . 116°B . 58°C . 42°D . 32°考点： 圆心角、弧、弦的关系;~~第7题~~(2019西湖.九上期末) 如图，半径为5的⊙A 中，弦BC ，ED 所对的圆心角分是∠BAC ，∠EAD ，若DE=6，∠BAC+∠EAD=180°，则圆心A 到弦BC 的距离等于（ ）A .B .C . 4D . 3考点： 三角形中位线定理;垂径定理;圆心角、弧、弦的关系;~~第8题~~(2019海曙.九上期末) 下列说法：①三点确定一个圆，②平分弦（不是直径）的直径垂直于弦，③相等的圆心角所对的弦相等，④三角形的内心到三边的距离相等，其中正确的有（ ）A . 1个B . 2个C . 3个D . 4个考点： 垂径定理;圆心角、弧、弦的关系;确定圆的条件;三角形的内切圆与内心;~~第9题~~(2019鄞州.九上期末) 如图，△ABC 内接于半径为5的⊙O ，点B 在⊙O 上，cosB= ，则下列量中，值会发生变化的量是( )A . ∠B 的度数 B . BC 的长 C . AC 的长D . 的长考点： 圆心角、弧、弦的关系;锐角三角函数的定义;~~第10题~~(2019杭州.九上期中) 如图，AB 是半圆的直径，点D 是AC 的中点，∠ABC=50°，则∠DAB 等( )A . 55°B . 60°C . 65°D . 70°考点： 圆心角、弧、弦的关系;圆周角定理;2020年九上数学：图形的性质_圆_圆心角、弧、弦的关系练习题答案1.答案：D2.答案：A3.答案：C4.答案：A5.答案：B6.答案：D7.答案：D8.答案：B9.答案：B10.答案：C。

第3章 圆的基本性质3.8 弧长及扇形的面积 第2课时 扇形面积的相关计算知识点1 扇形的面积1．半径为6，圆心角为60°的扇形的面积是( ) A ．3π B ．6π C ．9π D ．12π2．2017·温州已知扇形的面积为3π，圆心角为120°，则它的半径为________． 3．如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”，那么半径为2的“等边扇形”的面积为( )A ．πB ．1C ．2 D.23π4．若扇形的面积为15π cm 2，半径为5 3 cm ，则这个扇形的圆心角的度数为________． 5．杭州市某中学的铅球场如图3－8－11所示，已知扇形AOB 的面积是36 m 2，弧AB 的长度为9 m ，那么半径OA 为________m.图3－8－11图3－8－126．如图3－8－12，在3×3的方格中(共有9个小方格)，每个小方格都是边长为1的正方形，O ，B ，C 是格点，则扇形OBC 的面积等于________(结果保留π)．7．已知扇形的圆心角为120°，面积为253π cm 2，求扇形的弧长．知识点2 弓形的面积8．如图3－8－13，一个圆心角为90°的扇形，半径OA ＝2，那么图中阴影部分的面积为________(结果保留π)．3－8－133－8－149．如图3－8－14，AB 是⊙O 的直径，弦AC ＝2，∠ABC ＝30°，则图中阴影部分的面积是________．知识点3 不规则图形的面积10．如图3－8－15，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，BC ＝2，以点B 为圆心，BC 的长为半径作弧，交AB 于点D ，则阴影部分的面积是( )A ．2 3－23πB ．4 3－23πC ．2 3－43π D.23π3－8－153－8－1611．课本例3变式如图3－8－16，一扇形纸扇完全打开后，外侧两竹条AB 和AC 的夹角为120°，竹条AB 的长为25 cm ，贴纸部分的宽BD 为15 cm ，若纸扇两面贴纸，则一面贴纸的面积为________cm 2(结果保留π)．12．如图3－8－17，在⊙O 中，直径AB ＝2，CA ⊥AB ，BC 交⊙O 于点D .若∠C ＝45°，则：(1)BD 的长是________； (2)求阴影部分的面积．图3－8－1713．如图3－8－18，AB 是⊙O 的直径，弦CD⊥AB，∠CDB ＝30°，CD ＝2 3，则阴影部分的面积为( )A ．2πB ．πC .π3D .2π33－8－183－8－1914．用等分圆周的方法，在半径为1的圆中画出如图3－8－19所示的图形，则图中阴影部分的面积为________．15．如图3－8－20①，将一圆形纸片向右、向上两次对折后得到如图②所示的扇形AOB.已知OA ＝6，取OA 的中点C ，过点C 作CD⊥OA 交AB ︵于点D ，F 是AB ︵上一点，若将扇形BOD 沿OD 翻折，点B 恰好与点F 重合．用剪刀沿着线段BD ，DF ，FA 依次剪下，则剪下的纸片(阴影图形)面积之和为__________．图3－8－2016．如图3－8－21所示，已知菱形ABCD 的边长为1.5 cm ，B ，C 两点在扇形AEF 的EF ︵上，求BC ︵的长度及扇形ABC 的面积．图3－8－2117．如图3－8－22①是某公园一块草坪上的自动旋转喷水装置，这种旋转喷水装置的旋转角度为240°，它的喷灌区是一个扇形．小涛同学想了解这种装置能够喷灌的草坪面积，他测量出了相关数据，并画出了示意图(如图②)，A ，B 两点的距离为18 m ，求这种装置能够喷灌的草坪面积．图3－8－2218．如图3－8－23所示，已知AB为⊙O的直径，CD是弦，AB⊥CD于点E，OF⊥AC于点F，BE＝OF.(1)求证：OF∥BC；(2)求证：△AFO≌△CEB；(3)若EB＝5 cm，CD＝10 3 cm，设OE＝x cm，求x的值及阴影部分的面积．图3－8－2319．如图3－8－24，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD 沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴图3－8－24围成图形的面积为( )A.π2＋12B.π2＋1C．π＋1 D．π＋1 2详解详析1．B2．3 [解析] 设半径为r ，由题意，得120πr2360＝3π，解得r ＝3.3．C [解析] 根据扇形面积公式得S ＝12lr ＝12r 2＝2.4．72°5．8 [解析] S 扇形＝12lR ，∴12×9×R ＝36，∴R ＝8. 6.54π 7．解：∵扇形的圆心角为120°，面积为253π cm 2，∴120π×R 2360＝253π，∴πR ＝5，∴l ＝120πR 180＝103 cm.即扇形的弧长为103 cm.8．π－2 [解析] ∵S 扇＝n πr 2360＝90×π×22360＝π，S △AOB ＝12OA ·OB ＝12×2×2＝2，∴阴影部分的面积＝S 扇－S △AOB ＝π－2. 9.4π－3 33[解析] 连结OC ，过点C 作CH ⊥AB 于点H . ∵AB 为⊙O 的直径，∴∠ACB ＝90°.∵∠B ＝30°，∴AB ＝2AC ＝4，∠AOC ＝2∠B ＝60°，∴∠BOC ＝120°，CH ＝3， ∴S 弓形＝S 扇形OBC －S △BOC ＝120π·OB 2360－12OB ·CH ＝4π3－12×2×3＝4π－3 33.10．A [解析] ∵在Rt △ABC 中，∠A ＝30°，BC ＝2， ∴AB ＝4，∠B ＝60°，∴AC ＝2 3，∴S 阴影＝S △ABC －S 扇形CBD ＝12×2 3×2－60π×22360＝2 3－23π.11．175π [解析] 设AB ＝R ，AD ＝r ，则S 贴纸＝13πR 2－13πr 2＝13π(R 2－r 2)＝13π(R ＋r )(R －r )＝13×(25＋10)×(25－10)π＝175π(cm 2)．即一面贴纸的面积为175π cm 2. 12．解：(1) 2 (2)连结AD .∵AB 是⊙O 的直径，∴AD ⊥BC .又∵∠C ＝45°，AC ⊥AB ，∴∠B ＝45°， ∴△ACD ，△ABD 均是等腰直角三角形， ∴AD ＝BD ＝2，∴弓形BD 的面积＝弓形AD 的面积，∴阴影部分的面积＝△ADC 的面积＝12×(2)2＝1.13．D [解析] 如图，连结OD . ∵CD ⊥AB ，∴CE ＝DE ＝12CD ＝3(垂径定理)，故S △OCE ＝S △ODE ，即可得阴影部分的面积等于扇形OBD 的面积．又∵∠CDB ＝30°，∴∠COB ＝60°(圆周角定理)， ∴OC ＝2.∵OC ＝OD ，CD ⊥OB ， ∴∠BOD ＝∠COB ＝60°，∴S 扇形OBD ＝60π×22360＝2π3，即阴影部分的面积为2π3.故选D.14．π－3 32 [解析] 如图，连结OA ，OP ，AP ，则△OAP 的面积是34，扇形POA 的面积是60π×12360＝π6，∴弓形OA 的面积和弓形AP 的面积都是π6－34，∴阴影部分的面积是3×2×⎝ ⎛⎭⎪⎫π6－34＝π－3 32.15．9π－27 [解析] 由题意，得∠DOB ＝30°， ∴△DOB 的面积为12×6×3＝9.∴剪下的纸片(阴影图形)面积之和为π×624－3×9＝9π－27.16∵四边形ABCD 是菱形且边长为1.5 cm ， ∴AB ＝BC ＝1.5 cm.又∵B ，C 两点在扇形AEF 的EF ︵上， ∴AB ＝BC ＝AC ＝1.5 cm ，∴△ABC 是等边三角形，∴∠BAC ＝60°，∴BC ︵的长＝60π×1.5180＝π2(cm)，S 扇形ABC ＝12lR ＝12×π2×1.5＝38π(cm 2)．17．解：如图，过点O 作OC ⊥AB 于点C .∵OC ⊥AB ，AB ＝18 m ， ∴AC ＝12AB ＝9 m.∵OA ＝OB ，∠AOB ＝360°－240°＝120°， ∴∠AOC ＝12∠AOB ＝60°.在Rt △OAC 中，OA 2＝OC 2＋AC 2， 又∵OC ＝12OA ，∴r ＝OA ＝6 3 m ， ∴S ＝240360πr 2＝72π(m 2)．18．(1)证明：∵AB 为⊙O 的直径，∴∠ACB ＝90°. 又∵OF ⊥AC 于点F ，∴∠AFO ＝90°， ∴∠ACB ＝∠AFO ， ∴OF ∥BC .(2)证明：由(1)知，∠CAB ＋∠ABC ＝90°. ∵AB ⊥CD ， ∴∠BEC ＝90°， ∴∠CBE ＋∠BCE ＝90°，11 ∴∠CAB ＝∠BCE .又∵∠AFO ＝∠CEB ，OF ＝BE ，∴△AFO ≌△CEB .(3)∵AB 为⊙O 的直径，CD 是弦，AB ⊥CD 于点E ，∴∠OEC ＝90°，EC ＝12CD ＝12×103＝53(cm)． 在Rt △OCE 中，OE ＝x cm ，OB ＝OC ＝(5＋x )cm.由勾股定理，得OC 2＝EC 2＋OE 2，即(5＋x )2＝(53)2＋x 2，解得x ＝5， 即OE ＝5 cm ，OC ＝10 cm.在Rt △OCE 中， OC ＝2OE ，故∠OCE ＝30°，∴∠COE ＝60°.由圆的轴对称性可知阴影部分的面积为S 阴影＝2(S 扇形OBC －S △OEC )＝2×(60π×102360－12×53×5) ＝(100π3－253)cm 2. 19．C[解析] 如图所示，点A 运动的路径线与x 轴围成图形的面积＝S 扇形BAA 1＋S 扇形CA 1A 2＋S 扇形DA 2A 3＋2S △A 1BC ＝90π×12360＋90π×（2）2360＋90π×12360＋⎝ ⎛⎭⎪⎫2×12×1×1＝π＋1.。