北京大学数学科学学院直博生摸底考试试题.pdf

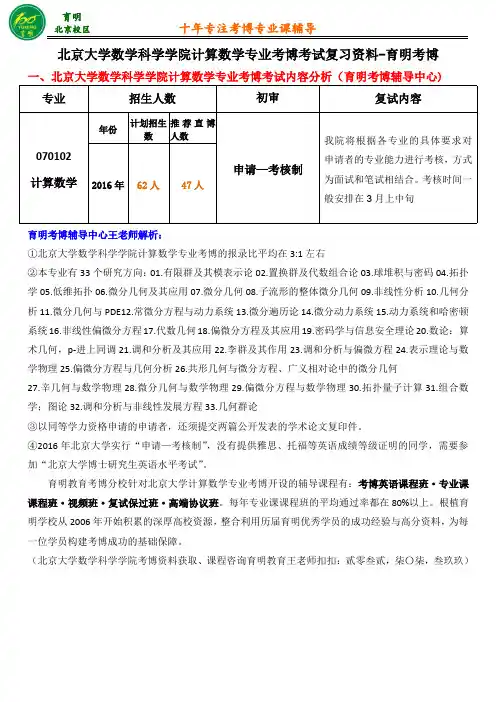
北京大学数学科学学院计算数学专业考博考试复习资料-育明考博一、北京大学数学科学学院计算数学专业考博考试内容分析（育明考博辅导中心)专业招生人数初审复试内容070102计算数学年份计划招生数推荐直博人数申请—考核制我院将根据各专业的具体要求对申请者的专业能力进行考核，方式为面试和笔试相结合。

考核时间一般安排在3月上中旬2016年62人47人育明考博辅导中心王老师解析：①北京大学数学科学学院计算数学专业考博的报录比平均在3:1左右②本专业有33个研究方向：01.有限群及其模表示论02.置换群及代数组合论03.球堆积与密码04.拓扑学05.低维拓扑06.微分几何及其应用07.微分几何08.子流形的整体微分几何09.非线性分析10.几何分析11.微分几何与PDE12.常微分方程与动力系统13.微分遍历论14.微分动力系统15.动力系统和哈密顿系统16.非线性偏微分方程17.代数几何18.偏微分方程及其应用19.密码学与信息安全理论20.数论：算术几何，p-进上同调21.调和分析及其应用22.李群及其作用23.调和分析与偏微方程24.表示理论与数学物理25.偏微分方程与几何分析26.共形几何与微分方程、广义相对论中的微分几何27.辛几何与数学物理28.微分几何与数学物理29.偏微分方程与数学物理30.拓扑量子计算31.组合数学；图论32.调和分析与非线性发展方程33.几何群论③以同等学力资格申请的申请者，还须提交两篇公开发表的学术论文复印件。

④2016年北京大学实行“申请—考核制”，没有提供雅思、托福等英语成绩等级证明的同学，需要参加“北京大学博士研究生英语水平考试”。

育明教育考博分校针对北京大学计算数学专业考博开设的辅导课程有：考博英语课程班·专业课课程班·视频班·复试保过班·高端协议班。

每年专业课课程班的平均通过率都在80%以上。

根植育明学校从2006年开始积累的深厚高校资源，整合利用历届育明优秀学员的成功经验与高分资料，为每一位学员构建考博成功的基础保障。

2016级博士生数学复习题1. 设()||||f x x =是实Hilbert 空间H 上的泛函，证明，当0x ≠，()f x 在点x 处沿着h 方向的Gateaux 微分。

P81 证明：xhx x th x t thth th x x th x t x x th x th x x th x t x th x x th x t x th x x th x t x th x t x f th x f t t t t t t ,)(,,2lim )(,,lim )(lim )())((lim lim )()(lim00220000=++-=++-++=++-+++++-+=-+=-+→→→→→→于是，当0≠x 时，f 在x 处沿着h 方向的teaux a G )微分为：xhx h x Df ,),(=2. 设泛函342, (,)(0,0)(,)0, (,)(0,0)x yx y x y f x y x yx y ⎧++≠⎪=+⎨⎪=⎩，证明(,)f x y 在点(0,0)处不是Frechet 微分。

P84证明：由于R y x x y x y x ∈∀≤+,,21243所以f 在点（0,0）处连续，令),(ηξ=h ，则有ηξηξηξηξ+=+++=-+→→tt t t t t t t f th f t t 24300)()()(lim )0()0(lim 因此，f 在点（0,0）处沿方向h 的teaux a G )微分为ηξηξ+=)),(),0,0((Df ，但是，如果令2ηξ=，则有2/1422/122)()(ξξηξ+=+=h于是021)()(lim )()(lim ),0()0()(lim 2/1422242302/14224300≠=++=++-+++=--→→→ξξξξξξξξηξηξηξηξh h h h h Df f h f所以，f 在点（0,0）处不是chet e Fr )可微的。

2021北大强基数学试题2021年北京大学强基数学试题涵盖了高中数学知识的各个方面，包括代数、几何、函数、微积分等内容。

下面是对其中一些试题的解析和参考内容：1. 一个有趣的排列问题：将1到n这n个整数排成一个圆环，要求相邻两个数的和是一个完全平方数。

试问n能否为奇数？如果能，求出一种排列方式。

解析：此问题属于组合数学中的排列问题。

可以通过逐个计算n的值，找到满足条件的排列方式。

当n为奇数时，可以找到一种排列方式，满足相邻两个数的和为完全平方数。

2. 函数极限问题：已知函数f(x) = {x^2 (x≤1)，x^3+ln(x) (x>1)}，求lim(x→1)f(x)。

解析：利用数列极限的性质，可以证明对于任意一个实数a，lim(x→a) x^n = a^n。

则对于本题中函数f(x)，当x≤1时，lim(x→1) x^2 = 1^2 = 1；当x>1时，lim(x→1) (x^3+ln(x)) =1^3+ln(1) = 1。

因此，lim(x→1) f(x) = 1。

3. 组合数学问题：求证：对于任意正整数n，有C(n-1, 0)-C(n, 1)+C(n+1, 2)-...+(-1)^(n-1)C(2n-1, n) = 1。

解析：利用组合数学中的性质，可以证明C(n, k) = C(n-1, k-1) + C(n-1, k)，即组合数的性质。

在本题中，利用组合数的性质可以展开等式的左边，然后利用组合数的递推关系进行化简。

这样就可以证明等式的成立。

以上只是对部分试题的解析和参考内容，真正的试题可能更加复杂，需要根据具体情况进行分析和求解。

在准备数学考试时，掌握基础知识、理解概念的意义和运用、灵活运用各种数学方法和技巧，以及进行充分的练习是非常重要的。

北京大学 2021 年博雅方案数学试卷选择题共 20 小题，在每题的四个项中，只有一项切合题目要求，请把正确选项的代号填在表格中，选对得 5 分，选错扣 1 分，不选得 0 分。

1. 设 n 为正整数，C n k n!为组合数，那么 C202103C202115C20212...4037C20212021等于〔〕k!(n k)!A. 2021 22021B. 2021！C.C40362021D.前三个答案都不对【答案】 Dn n n n n n n分析：(2k1)C n k2kC n k C n k 2 nC n k11C n k2n C n k11C n k，k 0k 0k 0k 1k 0k 1k 0202120212021C202103C 202115C20212...4037C20212021(2 k 1)C2021k 2 2021C2021k1C2021kk0k 1k0 40362202122021202122021，应选D。

2.设 a， b，c 为非负实数，知足 a b c，那么a ab abc 的最大值为〔〕++=3++A. 3B. 4C. 3 2D.前三个答案都不对【答案】 B分析： a ab abc a(1b(1 c)) a 1(1 b c)2 a 1 (4a)2，对其求导获得 a 2 时取44最大值为 4。

3.一个正整数 n 称为拥有3-因数积性质假定n的所有正因数的乘积等于 n3，那么不超出400的正整数中拥有3- 因数积性质的数的个数为〔〕A. 55B. 50C. 51D.前三个答案都不对【答案】C分析：设 n 的所有正因数的乘积为T，即T n3。

n 1 明显切合题意；下边证明当 n 2 时，正整数n的质因数的个数最多为 2：假定n的质因数的个数大于或等于3，即n的所有质因数为p1, p2 ,..., p k (k3) ，并设 n p11 p22 ... p k k，那么 n 的所有正因数的乘积中， p i i (i1,2,...k) 起码在 p i i , p i i p1 , p i i p2 ,..., p i i p i1, p i i p i1..., p i i p k , p i i p2 ... p k这些因子中出现，即i 出现的次数大于或等于，这样 T12k)44，这与题意T n3p i4( p1p2... p k n 矛盾，因此假定不建立，即n 的质因数的个数最多为2。

2020年北京海淀区北京大学自主招生数学试卷（强基计划）-学生用卷一、选择题（本大题共20个小题，每小题5分，共100分）1、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第1题5分正实数x ，y ，z ，ω满足x ⩾y ⩾ω和x +y ⩽2(z +ω)，则ωx +z y 的最小值为（ ）．A. 34B. 78C. 1D. 前三个答案都不对2、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第2题5分2020~2021学年北京高三单元测试2020~2021学年北京高二单元测试竞赛在(2019×2020)2021的全体正因数中选出若干个，使得其中任意两个的乘积都不是平方数，则最多可选因数个数为（ ）．A. 16B. 31C. 32D. 前三个答案都不对3、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第3题5分2020~2021学年北京高三单元测试2020~2021学年北京高二单元测试整数列{a n }n⩾1满足a 1=1，a 2=4，且对任意n ⩾2有a n 2−a n+1a n−1=2n−1，则a 2020的个位数字是( )A. 8B. 4C. 2D. 前三个答案都不对4、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第4题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试设a，b，c，d是方程x4+2x3+3x2+4x+5=0的4个复根，则a−1a+2+b−1b+2+c−1c+2+d−1d+2的值为()A. −43B. −23C. 23D. 前三个答案都不对5、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第5题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试设等边三角形ABC的边长为1，过点C作以AB为直径的圆的切线交AB的延长线于点D，AD>BD，则△BCD的面积为()A. 6√2−3√316B. 4√2−3√316C. 3√2−2√316D. 前三个答案都不对6、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第6题5分2020~2021学年北京高三单元测试2020~2021学年北京高二单元测试竞赛)π，其中k为整数，已知sin⁡(y+z−x)，sin⁡(x+z−y)，sin⁡(x+y−z)设x，y，z均不为(k+12成等差数列，则依然成等差数列的是（）．A. sin⁡x，sin⁡y，sin⁡zB. cos⁡x，cos⁡y，cos⁡zC. tan⁡x，tan⁡y，tan⁡zD. 前三个答案都不对7、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第7题5分2020~2021学年北京高二单元测试竞赛2020~2021学年北京高三单元测试方程19x+93y=4xy的整数解个数为（）．A. 4B. 8C. 16D. 前三个答案都不对8、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第8题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试+y2=1引切线，两个切点间的线段称为切点弦，则椭圆C内从圆x2+y2=4上的点向椭圆C：x22不与任何切点弦相交的区域面积为()A. π2B. π3C. π4D. 前三个答案都不对9、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第9题5分2020~2021学年10月上海浦东新区华东师范大学第二附属中学高一上学期月考第16题 竞赛2020~2021学年11月浙江杭州滨江区浙江省杭州第二中学高一上学期周测A 卷第9题 2020~2021学年北京高二单元测试使得5x +12√xy ⩽a (x +y )对所有正实数x ，y 都成立的实数a 的最小值为（ ）．A. 8B. 9C. 10D. 前三个答案都不对10、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第10题5分 设点P 为单位正方体ABCD −A 1B 1C 1D 1上的一点，则PA 1+PC 1的最小值为（ ）．A. √2+√2B. √2+2√2C. 2−√22D. 前三个答案都不对11、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第11题5分 数列{a n }(n ⩾1)满足a 1=1，a 2=9，且对任意n ⩾1，有a n+2=4a n+1−3a n −20，记S n 为数列的前n 项和，则S n 的最大值等于（ ）．A. 28B. 35C. 47D. 前三个答案都不对12、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第12题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试设直线y=3x+m与椭圆x 225+y216=1交于A，B两点，O为坐标原点，则△OAB面积的最大值为()A. 8B. 10C. 12D. 前三个答案都不对13、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第13题5分2020~2021学年北京高三单元测试2020~2021学年北京高二单元测试正整数n⩾3称为理想的，若存在正整数1⩽k⩽n−1使得C n k−1，C n k，C n k+1构成等差数列，其中C n k=n!k!(n−k)!为组合数，则不超过2020的理想数个数为()A. 40B. 41C. 42D. 前三个答案都不对14、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第14题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试在△ABC中，∠A=150°，已知D1，D2，⋯，D2020依次为边BC上的点，且有BD1=D1D2= D2D3=⋯=D2019D2020=D2020C．设角度∠BAD1=α1，∠D1AD=α2，⋯，∠D2019AD2020=α2020，∠D2020AC=α2021，则sin⁡α1sin⁡α3⋯sin⁡α2021的值为()sin⁡α2sin⁡α4⋯sin⁡α2020A. 11010B. 12020C. 12021D. 前三个答案都不对15、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第15题5分函数√3+2√3cos⁡θ+cos2θ√5−2√3cos⁡θ+cos2θ+4sin2θ的最大值为（）．A. √2+√3B. 2√2+√3C. √2+2√3D. 前三个答案都不对16、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第16题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试竞赛方程√x+5−4√x+1+√x+2−2√x+1=1的实根个数为（）．A. 1B. 2C. 3D. 前三个答案都不对17、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第17题5分竞赛2020~2021学年北京高三单元测试2020~2021学年北京高二单元测试凸五边形ABCDE的对角线CE分别与对角线BD和AD交于点F和G，已知BF:FD=5:4，AG:GD= 1:1，CF:FG:GE=2:2:3，S△CFD和S△ABE分别为△CFD和△ABE的面积，则S△CFD:S△ABE的值等于（）．A. 8:15B. 2:3C. 11:23D. 前三个答案都不对18、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第18题5分2020~2021学年北京高二单元测试2020~2021学年北京高三单元测试设p，q均为不超过100的正整数，则有有理根的多项式f(x)=x5+px+q的个数为()A. 99B. 133C. 150D. 前三个答案都不对19、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第19题5分2020~2021学年北京高三单元测试2020~2021学年北京高二单元测试满足对任意n⩾1，都有a n+1=2n−3a n且严格递增的数列{a n}(n⩾1)的个数为（）．A. 0B. 1C. 无穷多个D. 前三个答案都不对20、【来源】 2020年北京海淀区北京大学自主招生（强基计划）第20题5分设函数f(x,y,z)=xx+y+yy+z+zz+x，其中x，y，z均为正实数，则（）．A. f(x,y,z)既有最大值也有最小值B. f(x,y,z)有最大值但无最小值C. f(x,y,z)有最小值但无最大值D. 前三个答案都不对1 、【答案】 D;2 、【答案】 C;3 、【答案】 A;4 、【答案】 A;5 、【答案】 C;6 、【答案】 C;7 、【答案】 B;8 、【答案】 A;9 、【答案】 B;10 、【答案】 D;11 、【答案】 A;12 、【答案】 B;13 、【答案】 C;14 、【答案】 D;15 、【答案】 D;16 、【答案】 D;17 、【答案】 A;18 、【答案】 B;19 、【答案】 B;20 、【答案】 D;。