沪科版数学七年级上册一次方程与方程组知识点

2
－1的值是( ) C
A．3 B．4
C．5
D．6
导引：要紧扣方程的解及整式的值的意义解题． 因为2是关于x的方程x322－2a＝0的一个解， 所以×322－2a＝0，a＝3，因此2a－1＝
2
2×3－1＝5.故选C.
知3－练
1 写出一个一元一次方程，同时满足下列两个条件： ①未知数的系数是2；②方程的解为3，则这个方程 为.
知2－讲
例3 已知方程(a＋3) ＋x a2-2＝a－3是关于x的一元一次 方程，求a的值．
导引：根据一元一次方程的定义，可知|a|－2＝1，且 a＋3≠0.
解：由题意可知：|a|－2＝1， 所以|a|＝3，则a＝±3. 又因为a＋3≠0， 所以a≠－3， 所以a＝3.
知2－讲
一元一次方程中未知数的系数不能为0，这一 点要特别注意．
解：(5)(6)是一元一次方程．
知2－讲
判断一个方程是否为一元一次方程，不仅要看 原方程，还要看化简后的方程．原方程必须具备： 等式两边都是整式；化简后的方程必须具备：①未 知数次数为1；②未知数的系数不为0；③只含一个 未知数；以上条件，缺一不可． 易错警示：本例易出现只看原方程，而没有看 化简后的方程的错误．
（来自《教材》）
知2－讲
像上面得到的两个方程都只含有一个未知数 （元），未知数的次数都是1，且等式两边都是整 式的方程叫做一元一次方程.
知2－讲
要点精析： (1)一元一次方程的标准形式：ax＋b＝0(a≠0)，其中： x是未知数，a、b是已知数； (2)一元一次方程的条件：①等式两边都是整式；②是 方程；③化简后只含一个未知数且未知数系数不为 0；④未知数的次数是1(化简后)．
知4－讲
解：(1)x的3倍减5，即3x－5；x的2倍加1，即2x＋1，

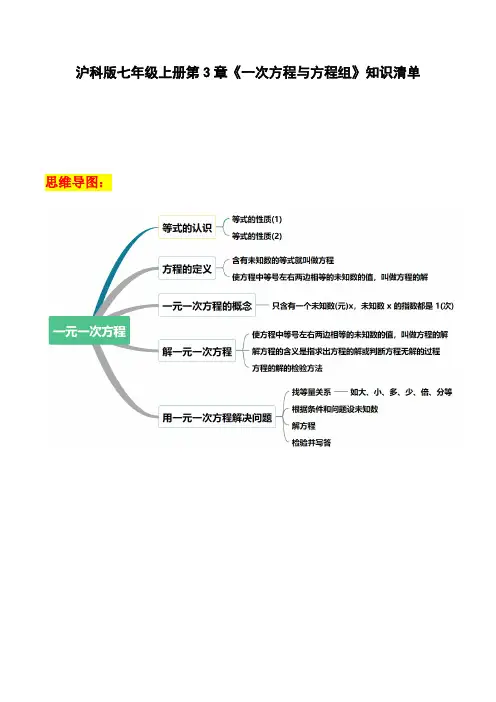
沪科版七年级上册第3章《一次方程与方程组》知识清单思维导图：知识点一、从问题到方程1. 等式的定义：用等号（“=”）来表示相等关系的式子叫做等式。

① 等式可以是数字算式，可以是公式、方程，也可以是运算律、运算法则等，所以等式可以表示不同的意义。

② 不能将等式与代数式混淆，等式含有等号，是表示两个式子的“相等关系”，而代数式不含等号，它只能作为等式的一边。

如x x 2735-=+才是等式。

2. 等式的性质性质1：等式两边同时加（或减）同一个数（或式子），结果仍相等。

即如果b a =，那么c b c a ±=±。

性质2：等式两边同时乘同一个数，或除以同一个不为0的数，结果仍相等。

即如果b a =，那么bc ac =；如果b a =()0≠c ，那么cbc a =。

3、方程（1）.定义：含有未知数的等式叫做方程。

方程有两层含义：① 方程必须是一个等式，即是用等号连接而成的式子。

② 方程中必有一个待确定的数，即未知的字母，这个字母就是未知数。

如12=+x 。

（2）. 方程与等式的区别与联系（3）方程的解与解方程① 检验一个数是否是方程的解，只要用这个数代替方程中的未知数，如果方程两边的值相等，那么这个数就是方程的解；如果不相等，这个数就不是方程的解。

② 方程可能无解，可能只有一个解，也可能有多个解。

③ 等式的基本性质是解方程的依据。

④ 方程的解是结果，而解方程是得到这个结果的一个过程。

知识点二、一元一次方程1.定义：只含有一个未知数（元），未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程。

2.标准形式：方程0=+b ax （其中x 是未知数，a 、b 是已知数，并且0≠a ）叫做一元一次方程的标准形式。

① 一元一次方程中未知数所在的式子是整式，即分母不含未知数。

② 一元一次方程只含有一个未知数，未知数的次数都为1。

如321=+x ，6=+y x ，+2x 06=-x 都不是一元一次方程。

的左边，常数项放在等号的右边 .若移项时为计 算简便不是这样放置的，在合并时可直接交换 过来，这不需要变号，因为等式有对称性 .
感悟新知
例3 解方程：8－3x=x+6.
知2－练
解题秘方：利用移项解一元一次方程的步骤(移项 →合并同类项→系数化为 1)解方程.
解： 移项，得 －3x－x=6 － 8. 合并同类项，得 －4x=－2.
常数， a≠ 0) 的形式，如 果 ax+b=0 是一元一次 方程，那么必有a≠ 0.
感悟新知
例1 下列各式中，哪些是一元一次方程？
知1－练
(1) 12x+y=1－2y； (2) 7x+5=7( x－2)；
(3)
5x2－
1 3
x－2=0；
(4)
2 x－1
=5；(5)
3 4
x=
1 2
；
(6) 2x2+5=2(x2－x) .
感悟新知
解：根据题意，可得 |m|－1=1，且 m+2 ≠ 0. 由 |m|－1=1，得 |m|=2，解得 m=± 2. 由 m+2 ≠ 0，得 m ≠ －2，所以 m=2.
切勿忽略未知数的 系数不为0 的条件.
知1－练
感悟新知
知1－练
2-1.已知关于x的方程(m2－1) x2+(m－1) x+7m2=0 是一 元一次方程，则m= ( C )
3. 解方程中去括号的顺序 先去小括号，再去中括号，最后去
大括号，一般是由内向外去括号，也可以由外向内去括号.
感悟新知
知3－讲
特别提醒 1. 去括号的目的是能利用移项解方程，其实质
是乘法分配律 . 2. 解方程中的去括号法则与整式运算中的去括

第3章 一次方程与方程组知识点一次方程与方程组知识点知识点1：一元一次方程的概念只含有一个未知数,并且未知数的次数都是1,像这样的整式方程叫做一元一次方程。

（如:21,314223x x x x --=+=-) 特点：①等号两边都是整式②只含有一个未知数③未知数的次数都为1。

判断方法：首先要将整式方程化简，然后再判断是否满足一元一次方程的三个特点。

知识点2：等式的基本性质1.等式的两边都加上（或减去)同一个数或同一个整式，所得结果仍是等式。

即如果a b =，那么a c b c ±=±；2。

等式的两边都乘以（或除以）同一个数（除数不能为0）,所得结果仍是等式.即如果a b =，那么ac bc =,(0)ab c c c=≠； 3。

对称性：如果a b =，那么b a =；4。

传递性：如果a b =，b c =,那么a c =。

知识点3:一元一次方程的解法1。

移项法则把方程的某一项改变符号后，从方程的一边移到方程的另一边，叫做移项法则.2。

解一元一次方程的步骤①去分母：在方程两边都乘以各分母的最小公倍数； ②去括号：先去小括号,再去中括号，最后去大括号； ③移项:把含有未知数的项都移到方程的一边，其它项都移到方程的另一边(移项要变号）④合并同类项：把方程变成(0)ax b a =≠的形式⑤系数华为1：在方程两边都除以未知数的系数a ,得到方程的解b x a=。

知识点4：（1)二元一次方程的概念含有两个未知数，且未知项的最高次数是1的整式方程叫做二元一次方程。

如：1,323,32m x y x y n +=-=+=都是二元一次方程。

（2）二元一次方程组的概念由两个二元一次方程组成的方程组叫做二元一次方程组。

（如：2324x y x y +=⎧⎨-=⎩) 知识点5：二元一次方程组的解使二元一次方程组中每个方程都成立的两个未知数的值,叫做二元一次方程组的解。

知识点6:二元一次方程组的解法（1）用代入法求解二元一次方程组步骤：①从方程组中选一个系数比较简单的方程,将这个方程的一个未知数用含另一个未知数的代数式表示出来；②将变形后的关系式代入另一个方程，消去一个未知数，得到一个一元一次方程;③解这个一元一次方程，求出x(或y）的值；④将求得的未知数的值代入变形后的关系式中,求出另一个未知数的值；⑤把求得的x、y的值用“｛”联立起来,就是方程组的解.（2)用加减法解方程组步骤:①方程组中的两个方程中,如果同一个未知数的系数即不互为相反数又不相等，那么就用适当的数乘方程的两边，使同一个未知数的系数变为相反数或相等;②把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；③解这个一元一次方程，求出x（或y）的值；④将求得的未知数的值代入原方程组中的任意一个方程中，求出另一个未知数的值，并把求得的两个未知数的值用符号“{"联立起来.知识点7：用一次方程（或方程组）解决实际问题①行程问题:行程问题中涉及的量有路程、平均速度、时间。

第5单元知识点七：二元一次方程组的应用【典型例题】 1、某市举办中学生足球赛，规定胜一场得3分，平一场得1分。

市第二中学足球队比赛11场，没输过一场，共得27分。

问该队胜几场，平几场？2、某市举办中学生足球比赛，规定胜一场得3分，平一场得1分，输一场得0分；市第二中学足球队比赛11场，胜的场次是输的场次的3倍，共得21分。

试问该队胜几场，平几场，输几场？3、甲、乙两人相距4km，以各自的速度同时出发，如果同向而行，甲2h追上乙；如果相向而行，两人0.5h后相遇，试问两人的速度各是多少？4、玻璃厂熔炼玻璃液，原料是石英砂和长石粉混合而成，要求原料中含二氧化硅70%，根据化验，石英砂中含二氧化硅99%，长石粉中含二氧化硅67%，试问3.2t原料中，石英砂和长石粉各多少吨？5、某医院利用甲乙两种原料为病人配制营养品。

已知每克甲原料含0.6单位蛋白质和0.08单位铁质，每克乙原料含0.5单位蛋白质和0.04单位铁质，如果病人每餐需34单位蛋白质和4单位铁质，那么每餐甲乙两种原料各多少克恰好满足病人的需要？6、某商场向银行申请了甲、乙两种贷款，共计68万元。

每年应付利息3.82万元，甲种贷款年利率是6%，乙种贷款年利率是5%，试问这两种贷款的金额各是多少？7、甲对乙说：“当我的岁数是你现在的岁数时，你才4岁．”乙对甲说：“当我的岁数是你现在的岁数时，你将61岁．”问甲、乙现在各多少岁？8、某村18位农民筹集5万元资金，承包了一些低产田地。

根据市场调查，他们计划对种植作物的品种进行调整，改种蔬菜和荞麦，种这两种作物每公顷所需的人数和需投入的资金如下表：在现有的条件下，这18位农民应承包多少公顷田地，怎样安排种植才能使所有的农民都有工作，且资金正好够用？知识点八：三元一次方程组及其解法【知识要点】解三元一次方程组的基本思路是通过“代入”或“加减”进行消元，把“三元”转化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而再转化为解一元一次方程。

所以(－2)★3
＝(－2)×32＋2×(－2)×3＋(－2)
＝(－2)×9＋2×(－2)×3＋(－2)
＝－18＋(－12)＋(－2)
＝－32.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(2)若
+
★

★(－2)＝16，求 a 的值.
【解】因为 a ★ b ＝ ab2＋2 ab ＋ a ，
7
8
9
10
11
12
13
14
15
16
17
10. [新考向 传承数学文化]我国古代数学著作《孙子算经》
中有这样一道题，原文如下：今有百鹿入城，家取一
鹿，不尽，又三家共一鹿，适尽，问：城中家几何？大
意为：今有100头鹿进城，每家取一头鹿，没有取完，剩
下的鹿每3家共取一头，恰好取完，问：城中有多少户人
家？在这个问题中，城中人家的户数为
所以
+
★3

+
+
+
2
＝
×3 ＋2×
×3＋



＝
+
+
×9＋3( a ＋1)＋


＝8 a ＋8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
因为
+
★

★(－2)＝16，
所以(8 a ＋8)★(－2)＝16，

（4）三元一次方程解题思想 三元一次方程组 消元 二元一次方程组 消元 一元一次方程
消元方法： ① 代入法（代入消元法） ② 加减法（加减消元法）
2020年10月2日
5
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
第3章 一次方程与方程组复习课
2020年10月2日
1
知识回顾
1、等式的基本性质
（1）性质1 如果a=b，那么a+c=b+c，a-c=b-c。
（2）性质2 如果a=b，那么ac=bc， a b （c≠0）
cc
（3）如果a=b，那么b=a。（对称性） ห้องสมุดไป่ตู้4）如果a=b，b=c，那么a=c。（传递性）
例
1、下列方程中是一元一次方程的是（ ） A、x-y=2005 B、3x-2004 C、x2+x=1
D、x 1
x2
=
2
3
2、x42.5 x3
0.2
0.05
2020年10月2日
3
3、二元一次方程组
（1）二元一次方程：象2x+y=60,含有两个未知数，并且未知数的项 的次数都是1的整式方程叫做二元一次方程
汇报人：XXX 汇报日期：20XX年10月10日
6
2020年10月2日
4
4、三元一次方程组
（1）三元一次方程：含有三个未知数，并且未知数的项的次数都 是1的整式方程叫做三元一次方程

17．一家商店进行装修，若请甲、乙两个装修队同时施工，8天可以完 成，需付两队费用3 520元，若先请甲队单独做6天，再请乙队单独做16 天可以完成，需付费用4 040元． (1)甲、乙两队工作一天，商店各应付多少钱？ (2)若装修完，商店每天可盈利200元，则如何安排施工更有利于商店？ 请说明理由．
•A．14
B．－26
•C．26
D．－14
的解是二元一次方程3x－2y＝2 ( B)
11．已知方程组 A．6 C．8 12．解方程(组)：
，那么代数式8x－y－z的值是 B．7 D．9
(B)
•(1)3(2x－1)－7＝2x＋10；
解：去括号，得6x－3－7＝2x＋10，移项，得6x－2x＝10＋3＋7，合 并同类项，得4x＝20，两边都除以4，得x＝5；
()
•A．1.5
B．2.5
C．3.5 C
D．4.5
•4．由3x＝2x－1得3x－2x＝－1，在此变形中，方程两边同 时 减去2x .
•5．若关于x的方程3x－5＝2x＋a的解与方程4x＋3＝7的解相同，
则a＝－4
.
•6．若方程x＋2y＝－4，kx－y－5＝0,2x－y＝7有公共解，则k的
值是 1
.
6x+16y=1,
y=1/40,
要40天完成，甲单独做需要费用3000元，少盈利200×10=2000元，相当于 损失5000元；乙单独做需费用5600元，少盈利200×40=8000元，相当于损 失13600元；甲乙合作需费用3520元，少盈利200×8=1600元，相当于损失 5120元；因为13600＞5120＞5000，所以甲单独做损失费用最少.
•②陈老师突然想起，所做的预算中还包括校长让他买的一支签字 笔．如果签字笔的单价为小于10元的整数，请通过计算，直接写 出签字笔的单价可能为2或6元．

第3章 |复习（二）
[解析] 方程组中 y 项的系数相等，可以采用减法消去 y. 方法技巧 用加减消元法解方程组的一般步骤： (1)方程组的两个方程中，如果同一个未知数的系数既不互为 相反数又不相等，那么就用适当的数乘方程的两边，使同一个未 知数的系数互为相反数或相等； (2)把两个方程的两边分别相加或相减，消去一个未知数，得 到一个一元一次方程； (3)解这个一元一次方程，求得一个未知数的值； (4)将这个求得的未知数的值代入原方程组中的任意一个方 程中，求出另一个未知数的值，并把求得的两个未知数的值用符 号“{”联立起来．
数学·沪科版（HK）
第3章 |复习（一） 针对第9题训练 1．如图 3－1，下列四个天平中，相同形状的物体的 质量是相等的，其中第①个天平是平衡的，根据第①个天 平，后三个天平仍然平衡的有( C ) A．0 个 B．1 个 C．2 个 D．3 个
数学·沪科版（HK）
第3章 |复习（一）
2．设“●，■，▲”分别表示三种不同的物体，如图 3－2 所示，前两个天平保持平衡，如果要使第三个天平也
平衡，那么“？”处应放“■”的个数为( A )
A．5 B．4 C．3 D．2
数学·沪科版（HK）
第3章 |复习（一）
针对第16题训练
关于 x 的方程13x＋2＝－16(4x＋m)的解是－161，则(m －1)2013＝____0____.
[解析] 解这个方程13x＋2＝－16(4x＋m)，得出 m＝ －6x－12.把 x＝－161代入，得 m＝－1，从而求出式子的 值．
(1)根据题意列出方程(组)； (2)所列方程(组)是二元一次方程组吗？
数学·沪科版（HK）
第3章 |复习（二）
解：(1)5xx＝＝26y－y，40. (2)是二元一次方程组．

等量关系： 本息和 = 本金 + 利息 = 本金 + 本金×利率×年数．
解：设现应购买这种国库券 x 元. 依题意得 x + 2.89%×3x = 20000. 解得 x≈18404 .
2.常见的几种方程类型及等量关系： (1)行程问题中基本量之间的关系： ① 路程＝速度×时间； ②相遇问题：全路程＝甲走的路程＋乙走的路程； ③追及问题：甲为快者，被追路程＝甲走路程－乙走路程； ④流水问题：v顺＝v静＋v水，v逆＝v静－v水．
（2）等积变形问题中基本量之间的关系： ① 原料面积 = 成品面积； ② 原料体积 = 成品体积.
提解示：：去先括号用，分得配律1、x去 1括号6 简3化x.方程，再求解较
容易． 移项，得
24 2 1 x 3 x 1 6.
22 4
合并同类项，得 x 6 1 .
4
系数化为 1，得 x 6 1 .
4
针对训练
4. 解方程：x 2 2 x 3 .
5
2
解：去分母，得 2(x－2) = 20－5(x＋3).
(除如数果不a能＝为b，0 那)，么所a得c＝结果_b_c仍_ ，是等ac 式＝．__bc_ (c ≠ 0).
3. 如果 a = b，那么 b = a.（对称性）
4. 如果 a = b，b = c，那么 a = c.（传递性）
四、一元一次方程的解法 解一元一次方程的一般步骤： (1)去分母：方程两边都乘各分母的最小公倍数，别漏乘． (2)去括号：注意括号前的系数与符号． (3)移项：把含有未知数的项移到方程的左边，
【解析】由题意，未知数 x 的系数为 a - 3， 所以 a - 3≠0.
由未知数 y 的次数为 | a | - 2，所以 | a | - 2 = 1， 即 a =±3. 但 a≠3. 所以 a = -3.

►考点三 一次方程与方程组的应用
例 4 [2012·铁岭] 为奖励在文艺汇演中表现突出的同学， 班主任派生活委员小亮到文具店为获奖同学购买奖品。小 亮发现，如果买 1 个笔记本和 3 支钢笔，则需要 18 元； 如果买 2 个笔记本和 5 支钢笔，则需要 31 元。求购买每 个笔记本和每支钢笔各多少元？
2．已知等式 3a＝2b＋5，则下列等式中不一 定成立的是（C ） A．3a－5＝2b B．3a＋1＝2b＋6
C．3ac＝2bc＋5 D．a＝23b＋53
3．下列结论错误的是（ D） A．若 a＝b，则 a－c＝b－c B．若 a＝b，则c2＋a 1＝c2＋b 1 C．若 x＝2，则 x2＝2x D．若 ax＝bx，则 a＝b
►考点二 二元一次方程组的解法
例 2 用代入法解方程组： 3x－y＝7， 5x＋2y＝8.
解：35xx－ ＋y2＝y＝7，8.②① 由①，得 y＝3x－7，③ 把③代入②，得 5x＋2（3x－7）＝8 解得 x＝2。把 x＝2 代入③， 得 y＝－1，即xy＝＝－2，1.
[解析] 观察两个方程系数的特点，可以发现方程 3x－y＝7 中的 y 的系数是－1，所以选择方程 3x－y ＝7 变形比较简便。
第3章 一次方程与方程组 复习课件
第3章复习（一）
知识归纳
1．方程的有关概念
（1）方程：含有未知数的 等式 就叫做方程。 （2）一元一次方程：只含有 一 个未知数（元）， 未知数的次数都是 1 ，这样的整式方程叫做一元
一次方程。
（3）二元一次方程：含有 两 个未知数，并且
未知数的次数都是 1 的整式方程叫二元一次
A．5 B．4 C．3 D．2
6.关于 x 的方程13x＋2＝－16(4x＋m)的解是－161，则（m－

第3章 一次方程与方程组一元一次方程一、基本概念（一）方程的变形法则法则1：方程两边都 或 同一个数或同一个 ，方程的解不变。

例如：在方程7-3x =4左右两边都减去7，得到新方程：-3x =4-7。

在方程6x =-2x -6左右两边都加上2x ，得到新方程：8x =-6。

移项：将方程中的某些项改变符号后，从方程的一边移动到另一边，这样的变形叫做移项，注意移项要变号。

例如：(1)将方程x －5＝7移项得：x ＝7+5即x ＝12(2)将方程4x ＝3x －4移项得：4x －3x ＝－4即x ＝－4法则2：方程两边都除以或 同一个 的数，方程的解不变。

例如： (1)将方程－5x ＝2两边都除以-5得：x = —52 (2)将方程32 x ＝13 两边都乘以32得：x =92 这里的变形通常称为“将未知数的系数化为1”。

注意：（1）如遇未知数的系数为整数，“系数化为1”时，就要除以这个整数；如遇到未知数的系数为分数，“系数化为1”时，就要乘以这个分数的倒数。

（2）不论上一乘以或除以数时，都要注意结果的符号。

方程的解的概念：能够使方程左右两边都相等的未知数的值，叫做方程的解。

求方程的解的过程，叫做解方程。

（二）一元一次方程的概念及其解法1．定义：只含有一个未知数，并且含有未知数的式子都是 ，未知数的次数是 ，这样的方程叫做一元一次方程。

例如：方程7-3x =4、6x =-2x -6都是一元一次方程。

而这些方程5x 2－3x +1＝0、2x +y ＝l －3y 、1x -1＝5就不是一元一次方程。

2．一元一次方程的一般式为：ax +b =0（其中a 、b 为常数，且a ≠0）一元一次方程的一般式为：ax =b （其中a 、b 为常数，且a ≠0）3．解一元一次方程的一般步骤步骤：去分母，去括号，移项，合并同类项，未知数的系数化为1。

注意：（1）方程中有多重括号时，一般应按先去小括号，再去中括号，最后去大括号的方法去括号，每去一层括号合并同类项一次，以简便运算。

3
性质3：如果 a＝b，那么 b＝a.（对称
性例） 如.，由 -4=x，得 x=-4.
4
性质3：如果 a＝b，b=c，那么 a＝c. （传递性）.
例如，x=3，又y=x，所以y=3.
在解题过程中，根据等式的传递性，一个 量用与它相等的量代替，简称等量代换.
2 一元一次方程
只含有一个未知数，未知数的次数是1，且 等式两边都是整式的方程叫做一元一次方程.
本章小结与复习
1 等式的基本性质
1
性质1：等式的两边都加上（或减去）同 一个数或同一个整式，所得结果仍是等式.即
如果 a＝b，那么 a＋c＝b＋c，a-c＝b-c.
2
性质2：等式的两边都乘以（或除以）同一
个数（除数不能为0），所得结果仍是等式. 即
如果
a＝b，那么
ac＝bc，
a c
=
bc（c≠0）.
②将变形后的方程代入另一个方程中，消去y(或x)，得 到一个关于x(或y)的一元一次方程；
③解这个一元一次方程，求出x(或y)的值； ④把x(或y)的值代入方程中，求y(或x)的值； ⑤用“{”联立两个未知数的值，得到方程组的解.
用加减法解二元一次方程组的一般步骤：
（1）如果某个未知数的系数的绝对值相等时，采用加减消 去一个未知数.
x＝4，x＝2， 解：x＝6－2y 的正整数解有y＝1，y＝2；
x＝4，x＝2， 把y＝1，y＝2 分别代入方程 x－y＝9－3k， 得 k＝2 或 k＝3.
例 2 若 2x＝43与 3(x＋a)＝a－5x 有相同的解，求 a 的值．
[解析] 因为两个方程的解相同，先求出方程 2x ＝43的解，再将其代入方程 3(x＋a)＝a－5x 中得到 关于 a 的一元一次方程，从而求出 a 的值．

《一次方程与方程组》全章复习与巩固（提高）知识讲解【学习目标】1．理解方程，等式及一元一次方程、二元一次方程组的概念，并掌握它们的区别和联系；2．会解一元一次方程及二元一次方程组，并理解每步变形的依据；3．会根据实际问题列方程或方程组解应用题．【知识网络】【要点梳理】要点一、方程及方程组的相关概念1．方程：含有未知数的等式叫做方程．2．一元一次方程：只含有一个未知数（元），未知数的次数都是1，且等式两边都是整式的方程叫做一元一次方程．3．二元一次方程：方程中含有两个未知数，并且未知数的次数都是1，像这样的方程叫做二元一次方程．要点诠释：（1）在方程中“元”是指未知数，“一元”就是指方程中只含有一个未知数；“二元”就是指方程中有且只有两个未知数．（2）无论是一元一次方程还是二元一次方程，未知数的次数都为1，是指含有未知数的项（单项式）的次数是1．（3）未知数所在的式子是整式，即分母中不含未知数，二元一次方程的左边和右边都必须是整式．4．二元一次方程的解：使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解． 要点诠释：二元一次方程的每一个解，都是一对数值，而不是一个数值，一般要用大括号联立起来，即二元一次方程的解通常表示为⎩⎨⎧ba＝＝y x 的形式．5．二元一次方程组：把具有相同未知数的两个二元一次方程合在一起，就组成了一个二元一次方程组． 此外，组成方程组的各个方程也不必同时含有两个未知数．例如，二元一次方程组3452x y x +=⎧⎨=⎩．6． 二元一次方程组的解：使二元一次方程组中每个方程都成立的两个未知数的值，叫做二元一次方程组的解． 要点诠释：（1）方程组中每个未知数的值应同时满足两个方程，所以检验是否是方程组的解，应把数值代入两个方程，若两个方程同时成立，才是方程组的解，而方程组中某一个方程的某一组解不一定是方程组的解．（2）方程组的解要用大括号联立；（3）一般地，二元一次方程组的解只有一个，但也有特殊情况，如方程组⎩⎨⎧=+=+6252y x y x 无解，而方程组⎩⎨⎧-=+-=+2221y x y x 的解有无数个．7．三元一次方程组：由三个一次方程组成的含有三个未知数的方程组，叫做三元一次方程组．要点诠释：（1）方程组中的每一个方程都是一次方程； （2）如果三个一元一次方程合起来共有三个未知数，它们就能组成一个三元一次方程组． 要点二、等式的性质1．等式的概念：用符号“=”来表示相等关系的式子叫做等式． 2．等式的性质：等式的性质1：等式两边加上（或减去）同一个数或同一个整式，所得结果仍是等式，即：如果，那么,a c b c a c b c +=+-=-等式的性质2：等式的两边都乘同或除以同一个数（除数不能为0），所得结果仍是等式，即：如果，那么；(0)c ≠．等式的性质3：如果，那么b a =．（对称性） 等式的性质4：如果，b c =，那么a c =．（传递性） 要点诠释：（1）根据等式的性质，对等式进行变形，等式两边必须同时进行完全相同的变形； （2）等式性质1中，强调的是整式，如果在等式两边同加的不是整式，那么变形后的等式不一定成立，如x ＝0中，两边加上得x ＋，这个等式不成立；（3）等式的性质4中一个量用与它相等的量代替，简称等量代换．3．移项：在解方程的过程中，等号的两边加上（或减去）方程中某一项的变形过程，相当于把方程中某一项改变符号后，从方程的一边移到另一边．这种变形过程叫做移项． 要点诠释：移项通常是指把含有未知数的项移到方程的一边，其他项移到方程的另一边，但无论是移含有未知数的项还是其他项都要改变符号，然后再进行移项． 要点三、方程及方程组的解法 1．解一元一次方程的一般步骤：(1)去分母：在方程两边同乘以各分母的最小公倍数．(2)去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最后去大括号． (3)移项：把含有未知数的项移到方程一边，常数项移到方程另一边．(4)合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax ＝b(a ≠0)的形式．(5)系数化为1：方程两边同除以未知数的系数得到方程的解bx a=(a ≠0)． (6)检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相等，则不是方程的解．2．解二元一次方程组的基本方法：代入消元法和加减消元法 （1）用代入消元法解二元一次方程组的一般过程：①从方程组中选定一个系数比较简单的方程进行变形，用含有x （或y ）的代数式表示y （或x ），即变成b ax y +=（或b ay x +=）的形式； ②将b ax y +=（或b ay x +=）代入另一个方程（不能代入原变形方程）中，消去y （或x ），得到一个关于x （或y ）的一元一次方程； ③解这个一元一次方程，求出x （或y ）的值；④把x （或y ）的值代入b ax y +=（或b ay x +=）中，求y （或x ）的值； ⑤用“{”联立两个未知数的值，就是方程组的解．要点诠释：(1)用代入法解二元一次方程组时，应先观察各项系数的特点，尽可能选择变形后比较简单或代入后化简比较容易的方程变形；(2)变形后的方程不能再代入原方程，只能代入原方程组中的另一个方程；(3)要善于分析方程的特点，寻找简便的解法．如将某个未知数连同它的系数作为一个整体用含另一个未知数的代数式来表示，代入另一个方程，或直接将某一方程代入另一个方程，这种方法叫做整体代入法．整体代入法是解二元一次方程组常用的方法之一，它的运用可使运算简便，提高运算速度及准确率．（2）用加减消元法解二元一次方程组的一般过程：①根据“等式的两边都乘以（或除以）同一个不等于0的数，等式仍然成立”的性质，将原方程组化成有一个未知数的系数绝对值相等的形式； ②根据“等式两边加上（或减去）同一个整式，所得的方程与原方程是同解方程”的性质，将变形后的两个方程相加（或相减），消去一个未知数，得到一个一元一次方程； ③解这个一元一次方程，求出一个未知数的值；④把求得的未知数的值代入原方程组中比较简单的一个方程中，求出另一个未知数的值； ⑤将两个未知数的值用“{”联立在一起即可．要点诠释：当方程组中有一个未知数的系数的绝对值相等或同一个未知数的系数成整数倍时，用加减消元法较简单．3．三元一次方程组的解法解三元一次方程组的基本思想仍是消元，一般的，应利用代入法或加减法消去一个未知数，从而化三元为二元，然后解这个二元一次方程组，求出两个未知数，最后再求出另一个未知数．解三元一次方程组的一般步骤是：（1）利用代入法或加减法，把方程组中一个方程与另两个方程分别组成两组，消去两组中的同一个未知数，得到关于另外两个未知数的二元一次方程组； （2）解这个二元一次方程组，求出两个未知数的值； （3）将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程，得到一个一元一次方程；（4）解这个一元一次方程，求出最后一个未知数的值； （5）将求得的三个未知数的值用“{”合写在一起． 要点四、方程及方程组的应用 1．常见类型：行程问题：路程＝速度×时间和差倍分问题：增长量＝原有量×增长率 利润问题：商品利润＝商品售价－商品进价工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量 银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数 数字问题：多位数的表示方法：例如：32101010abcd a b c d =⨯+⨯+⨯+ 2．实际问题与二元一次方程组要点诠释：（1）解实际应用问题必须写“答”，而且在写答案前要根据应用题的实际意义，检查求得的结果是否合理，不符合题意的解应该舍去； （2）“设”、“答”两步，都要写清单位名称；（3）一般来说，设几个未知数就应该列出几个方程并组成方程组． 【典型例题】类型一、方程及方程组的相关概念1．已知方程(3m-4)x 2-(5-3m)x-4m ＝-2m 是关于x 的一元一次方程，求m 和x 的值． 【思路点拨】若一个整式方程经过化简变形后，只含有一个未知数，并且未知数的次数都是1，系数不为0，则这个方程是一元一次方程． 【答案与解析】解：因为方程(3m-4)x 2-(5-3m)x-4m ＝-2m 是关于x 的一元一次方程， 所以3m-4＝0且5-3m ≠0． 由3m-4＝0解得43m =，又43m =能使5-3m ≠0，所以m 的值是43． 将43m =代入原方程，则原方程变为485333x ⎛⎫--⨯= ⎪⎝⎭，解得83x =-．所以43m =，83x =-．【总结升华】解答这类问题，一定要严格按照一元一次方程的定义．方程(3m-4)x 2-(5-3m)x-4m ＝-2m 2是关于x 的一元一次方程，就是说x 的二次项系数3m-4＝0，而x 的一次项系数5-3m ≠0，m 的值必须同时符合这两个条件． 举一反三：【变式】如果5(x+2)＝2a+3与(31)(53)35a x a x +-=的解相同，那么a 的值是________． 【答案】711提示 ：由5(x+2)＝2a+3，解得275a x -=． 由(31)(53)35a x a x +-=，解得95x a =-． 所以27955a a -=-，解得711a =．2．在下列方程中，只有一个解的是（ ）A ． 1330x y x y +=⎧⎨+=⎩B ． 1332x y x y +=⎧⎨+=-⎩C ． 1334x y x y +=⎧⎨-=⎩D ． 1333x y x y +=⎧⎨+=⎩【思路点拨】逐一求每个选项中方程组的解，便得出正确答案 【答案】C ．【解析】选项A 、B 、D 中，将方程1x y +=，两边同乘以3得333x y +=，从而可以判断A 、B 选项中的两个二元一次方程矛盾，所以无解；而D 中两个方程实际是一个二元一次方程，所以有无数组解，排除法得正确答案为C ． 【总结升华】在111222a xb yc a x b y c +=⎧⎨+=⎩（其中1a ，2a ，1b ，2b 均不为零），（1）当121222a a c a b c =≠时，方程组无解；（2）当121222a a c a b c ==，方程组有无数组解； （3）当1222a a ab ≠，方程组有唯一解． 举一反三： 【变式】已知方程组531x y ax y b -=⎧⎨+=-⎩有无数多个解，则a 、b 的值等于 ．【答案】a ＝﹣3，b ＝﹣14． 类型二、方程及方程组的解法3．解关于x 的方程：11()(2)34m x n x m -=+ 【思路点拨】这个方程化为标准形式后，未知数x 的系数和常数都是以字母形式出现的，所以方程的解的情况与x 的系数和常数的取值都有关系． 【答案与解析】解：原方程可化为：(43)462(23)m x mn m m n -=+=+当34m ≠时，原方程有唯一解：4643mn m x m +=-； 当33,42m n ==-时，原方程无数个解；当33,42m n =≠-时，原方程无解；【总结升华】解含字母系数的方程时，一般化为最简形式ax b =，再分类讨论进行求解，注意最后的解不能合并，只能分情况说明． 举一反三：【变式】若关于x 的方程230x m -+=无解，340x n -+=只有一个解，450x k -+=有两个解，则,,m n k 的大小关系为 ( )A ． m n k >>B ．n k m >>C ．k m n >>D ．m k n >>【答案】A提示：方程无解m ＞0，只有一个解n=0，有两个解k ＜0.4．解方程：|x-1|+|x-3|=3【思路点拨】分别讨论①x＜1，②1＜x ＜3，③x＞3，根据x 的范围去掉绝对值符号，解方程即可．【答案与解析】解：当x ＜1时，原方程就可化简为：1-x+3-x=3，解得：x=0．5； 第二种：当1＜x ＜3时，原方程就可化简为：x-1-x+3=3，不成立； 第三种：当x ＞3时，原方程就可化简为：x-1+x-3=3，解得：x=3．5； 故x 的解为0．5或3．5．【总结升华】解含绝对值的方程的关键，就是根据绝对值的定义或性质去掉绝对值符号，化它为一般的方程，从而解决问题，注意讨论x 的取值．5．解方程组2()5335()322x y y x y y ⎧-+=⎪⎪⎨⎪--=-⎪⎩①②【思路点拨】本题结构比较复杂，一般应先化简，再消元．仔细观察题目，不难发现，方程组中的每一个方程都含有(x-y)，因此可以把(x-y)看作一个整体，消去(x-y)可得到一个关于y 的一元一次方程．【答案与解析】解：由①×9得：6(x-y)+9y ＝45 ③ ②×4得：6(x-y)-10y ＝-12 ④ ③-④得：19y ＝57， 解得y ＝3．把y ＝3代入①，得x ＝6．所以原方程组的解是63x y =⎧⎨=⎩．【总结升华】本题巧妙运用整体法求解方程组，显然比加减法或代入法要简单，在平时求方程组的解时，要善于发现方程组的特点，运用整体法求解会收到事半功倍的效果． 举一反三：【变式】方程2311x y x y --+++=的整数解的个数是 ． 【答案】2组提示：把1表示成两个非负整数的和，这两个数只能是1与0，于是一个方程裂变为多个方程组，通过解方程组来求解的个数． 类型三、方程及方程组的应用6．李伟从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟；若每小时行18千米，则比火车开车时间迟到15分钟，现在李伟打算在火车开车前10分钟到达火车站，求李伟此时骑摩托车的速度应是多少?【思路点拨】本题中的两个不变量为：火车开出的时间和李伟从家到火车站的路程不变． 【答案与解析】解：设李伟从家到火车站的路程为y 千米，则有：151530601860y y +=-，解得：452y =由此得到李伟从家出发到火车站正点开车的时间为4515213060+=(小时)．李伟打算在火车开车前10分钟到达火车站时，设李伟骑摩托车的速度为x 千米/时, 则有：452271010116060y x ===--(千米/时)答：李伟此时骑摩托车的速度应是27千米/时．【总结升华】在解决问题时，当发现某种方法不能解决问题时，应该及时变换思维角度，如本题直接设未知数较难时，应迅速变换思维的角度，合理地设置间接未知数以寻求新的解决问题的途径和方法．7． 已知：用2辆A 型车和1辆B 型车载满货物一次可运货10吨；用1辆A 型车和2辆B 型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A 型车a 辆，B 型车b 辆，一次运完，且恰好每辆车都载满货物． 根据以上信息，解答下列问题：（1）1辆A 型车和1辆车B 型车都载满货物一次可分别运货多少吨？ （2）请你帮该物流公司设计租车方案；（3）若A 型车每辆需租金100元/次，B 型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．【答案与解析】 解：（1）设每辆A 型车、B 型车都装满货物一次可以分别运货x 吨、y 吨， 依题意列方程组得：210211x y x y +=⎧⎨+=⎩解方程组，得：34x y =⎧⎨=⎩答：1辆A 型车装满货物一次可运3吨，1辆B 型车装满货物一次可运4吨．（2）结合题意和（1）得：3a+4b=31， ∴3143ba -=∵a 、b 都是正整数 951147a a a b b b ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩或或答：有3种租车方案：方案一：A 型车9辆，B 型车1辆； 方案二：A 型车5辆，B 型车4辆； 方案三：A 型车1辆，B 型车7辆．（3）∵A 型车每辆需租金100元/次，B 型车每辆需租金120元/次，∴方案一需租金：9×100+1×120=1020（元） 方案二需租金：5×100+4×120=980（元） 方案三需租金：1×100+7×120=940（元） ∵1020＞980＞940∴最省钱的租车方案是方案三：A 型车1辆，B 型车7辆，最少租车费为940元． 【总结升华】本题实际上是求二元一次方程组的正整数． 举一反三：【变式】甲、乙两班学生到集市上购买苹果，价格如下：甲班分两次共购买苹果70千克(第二次多于第一次)，共付出189元，而乙班则一次购买苹果70千克.(1)乙班比甲班少付出多少元？(2)甲班第一次、第二次分别购买苹果多少千克？ 【答案】解：（1）18970249-⨯= （元） 答：乙班比甲班少付出49元．（2）设甲班第一次、第二次分别购买苹果x 、y 千克，则依据题意得：①当030x ≤≤，3050y ≤≤，则有：703 2.5189x y x y +=⎧⎨+=⎩，解得：2842x y =⎧⎨=⎩，经检验满足题意； ②当030x ≤≤，50y >，则有：7032189x y x y +=⎧⎨+=⎩，解得：4921x y =⎧⎨=⎩，经检验不满足题意；③当3050x ≤≤，3050y ≤≤，则有：2.570175189⨯=≠，不满足题意． 答：甲班第一次购买苹果28千克，第二次购买42千克．。

初一数学寒假专题——一次方程与方程组某某科技版【本讲教育信息】一. 教学内容：寒假专题——一次方程与方程组二. 主要内容： 1. 一元一次方程：①概念：只含有一个未知数（元）并且未知数的次数都是l ，像这样的方程叫做一元一次方程。

如：5x －4＝3（x ＋2）；21x －3＝31x －2。

都是一元一次方程。

但是像1x 1+＝5，3x ＋5＝2y －7就不是一元一次方程。

②解一元一次方程的依据： 等式的性质：1. 等式的两边都加上（或减去）同一个数或同一个整式，所得结果仍是等式. 即 如果a ＝b ，那么a±c ＝b±c.2. 等式的两边都乘以（或除以）同一个数（除数不能为零），所得结果仍是等式. 即 如果a ＝b ，那么ac ＝bc ；cbc a =（c ≠0） ③解一元一次方程的一般步骤：首先要知道使方程两边相等的未知数的值叫做方程的解；一元方程的解，也可叫做根。

列表：为 1 解出方程2. 二元一次方程组： ①概念：形如：ax ＋by ＝c （ab ≠0，a 、b 、c 为常数）的方程叫做二元一次方程。

如：3x ＋5y ＝8是二元一次方程。

由两个一次方程组成的，并含有两个未知数的方程组叫做二元一次方程组。

如：⎩⎨⎧=-=+2y x 34y 3x ⎪⎩⎪⎨⎧=+=+7y x 2y 41x 31都是二元一次方程组；但是方程组⎩⎨⎧=-=+2z x 34y 3x 就不是二元一次方程组。

能使二元一次方程组中每个方程都成立的两个未知的值，叫做二元一次方程组的解。

如：⎩⎨⎧=-=+2y x 34y 3x 的解为：⎩⎨⎧==1y 1x ⎪⎩⎪⎨⎧=+=+7y x 2y 41x 31的解为：⎩⎨⎧==4y 3x ②如何解二元一次方程组解二元一次方程组的解题思想是：消元解二元一次方程组的解题方法有：代入消元法，加减消元法。

3. 用一次方程（组）解决问题 表格： 题中涉及的数量及公式等量关系注意事项 和倍、差倍问题由题意知弄清倍数关系及“多”、“少”关系等等积变形问题 长方体体积＝长×宽×高圆柱体体积＝πr 2h （h 为高，r 为底面半径） 变形前、后体积相等注意分清直径、半径行 程 相遇问题路程＝速度×时间时间＝路程÷速度快行距＋慢行距＝原距相向而行注意出发时间、地点【典型例题】例1. 已知方程组⎩⎨⎧=+=+4y 5ax 3y x 5与⎩⎨⎧=+=-1by x 55y 2x 有相同的解，求a 、b 的值。

即如果a＝b，那么a±_c___＝b±c.
(2)等式两边都乘以同一个数，或除以 同一个不为0的数，所得结果仍是等
式．即如果a＝b，那么 ac＝b_c___或
a = b (c≠0)．
c
c
（3）、如果a=b，那么b=a.(对称性） (4)、如果a=b,b=c,那么a=c(传递性）
3．一元一次方程的解法：
解：设支援拔草的有x人，支援植树的 有(19－x)人． 由题意，得32＋x＝2×[18＋(19－x)]， 解得x＝14， ∴19－x＝5. 答：支援拔草的有14人，支援植树的有 5人．
第二部分：二元一次方程组及应用
大家好
1、什么是二元一次方程？
1．下列是二元一次方程的是 （ B ）
A、3x6x
B、3x = 2 y
① ②
大家好
2. 加减消元法
（1）方程组中同一未知数的系数相等或相反数.
3x -y= -8 x +y= 5
① ②
3x -2y= -8 3x +y= 5
① ②
（2）方程组中同一未知数的系数是变成相同或相
反数.
3x -2y= -8 2x +3y= 5
① ②
大家好
一、用代入法解二元一次方程组
例1 解方程组：
6、下列属于二元一次方程组的是 （ A ）
A、
x y 1
35
B 3 5 1
xy
x y0
x y 0
C、 x+y=5 x2+y2=1
D
y 1 x2 2
xy 1
大家好
7)用加减法解方程组{3x+4y=16①，
5x-6y=33② 若要消去Y，则应由 ①×？，②× ？ 再 相加，从而消去y。