贝叶斯决策的经典例题练习说课材料
- 格式:doc
- 大小:33.00 KB
- 文档页数:4

实验一贝叶斯决策一、 实验原理1. 最小错误率贝叶斯决策规则:对于两类问题,最小错误率贝叶斯决策有以下裁决规则:P( 1 | x) P( 2 | x),则 x 1 ; 反之,则 x 2。
因为先验概率 P( i )可以确立,与当前样本 x 没关,因此决策规则也可整理成下边的形式:若l (x) P( x | 1 ) P( 2 ) ,则 x1 ,不然 x 。
P(x |2 ) P( 1) 22. 均匀错误率决策界限把 x 轴切割成两个地域,分别称为第一类和第二类的决策地域 .样本在中但属于第二类的错误概率和样本在中但属于第一类的错误概率就是出现错误的概率, 再考虑到样本自己的分布后就是均匀错误率:t P( 2 | x) p( x)dx P( 1 | x) p( x)dxP(e)t tp( x | 2 ) P( 2 )dx p( x | 1 ) P( 1 )dx t3. 此实验中的裁决门限和均匀错误率(1)裁决门限假设随机脉冲信号 f 中 0 的概率为 ,高斯噪声信号 n 服从,信号叠加时的放大倍数为 a ,叠加后的信号为s f * a n 。
由最小错误率贝叶斯决策可得:P( 1 ) p( x | 1 )P( 2 ) p( x |2)a2 2a2 2 (ln(1 p0 ) ln p0 )化简计算得: t2a(2)均匀错误率由上述积分式可计算。
二、实验内容1、已知均值和方差,产生高斯噪声信号,计算其统计特征实验中利用 MATLAB产生均值为 0,方差为 1 的高斯噪声信号,信号统计分布的程序和结果以下:%产生高斯噪声并统计其特征x=0;%均值为 0y=1;%方差为 1n=normrnd(x,y,[1 1000000]);%产生均值为 0,方差为 1 的高斯噪声m1=mean(n);%高斯噪声的均值v1=var(n); %高斯噪声的方差figure(1)plot(n(1:400)); title( '均值为 0,方差为 1 的高斯噪声 ');figure(2)hist(n,10000); title('高斯噪声的统计特征 ');获得 m1=-4.6534e-005 ;v1= 0.9971 。

贝叶斯公式经典例题讲解
《贝叶斯公式经典例题讲解》
贝叶斯公式是一种概率公式,它可以在条件概率中派上用场。
贝叶斯公式可以用来计算在已知事实的情况下,某个事件发生的可能性。
一、贝叶斯公式
贝叶斯公式可以表示为:P(A|B)= P(B|A)* P(A)/ P(B)其中,P(A|B)是条件概率,即事件A在B已发生的情况下发生的概率;P(B|A)是反条件概率,表示事件B在A已发生的情况下发生的概率;P(A)表示事件A发生的概率;P(B)表示事件B发生的概率。
二、经典例题讲解
以下是贝叶斯公式的一个典型例题:
假设在一个学校中,有1000名学生,其中90%的学生爱看书,80%的学生爱看电视,另外有30%的学生同时喜欢看书和看电视。
现在随机抽取一名学生,问这位学生是否同时喜欢看书和看电视?
解:P(同时喜欢看书和看电视|随机抽取一名学生)= P(随机
抽取一名学生|同时喜欢看书和看电视)* P(同时喜欢看书和看电视)/ P(随机抽取一名学生)
= 0.3*0.3/1
=0.09
因此,这位学生同时喜欢看书和看电视的概率为0.09。
- 1 -。



贝叶斯公式典型例题
贝叶斯公式是一种计算条件概率的公式,常用于根据已知条件更新某个事件发生的概率。
下面是一个贝叶斯公式的典型例题:
例:假设有两种类型的围棋棋手,分别是专业棋手和业余棋手。
专业棋手在比赛中获胜的概率为0.9,而业余棋手获胜的概率为0.3。
已知在所有棋手中,专业棋手占70%,业余棋手占30%。
现在有一场比赛,我们只知道其中一位棋手获胜了,那么这位棋手是专业棋手的概率是多少?
解:首先,我们定义以下事件:
•A:棋手是专业的
•B:棋手获胜
根据题意,我们知道:
•P(A) = 0.7(专业棋手占比)
•P(¬A) = 0.3(业余棋手占比)
•P(B|A) = 0.9(专业棋手获胜的概率)
•P(B|¬A) = 0.3(业余棋手获胜的概率)
我们要找的是P(A|B),即在已知棋手获胜的条件下,棋手是专业的概率。
根据贝叶斯公式,我们有:
P(A|B) = \frac{P(A) \times P(B|A)}{P(A) \times P(B|A) + P(¬A) \times P(B|¬A)}将已知的概率值代入公式中,我们得到:
P(A|B) = \frac{0.7 \times 0.9}{0.7 \times 0.9 + 0.3 \times 0.3} = \frac{0.63}{0.63
+ 0.09} = \frac{0.63}{0.72} = 0.875
所以,在已知棋手获胜的条件下,这位棋手是专业棋手的概率为0.875。
这个例题展示了贝叶斯公式在更新条件概率方面的应用。
通过已知的概率值和贝叶斯公式,我们可以计算出在给定条件下的未知概率。


贝叶斯决策的例题练习公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品,有两种方案可供选择:—是进行批量生产,二是出售专利。
这种新产品投放市场,估计有3种可能:畅销、中等、滞销,这3种情况发生的可能性依次估计为:,和。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销,则调查结果为畅销、中等和滞销的概率分别为、和;若实际市场状况为中等,则调查结果为畅销、中等和滞销的概率分别为、和;若实际市场状况为滞销,则调查结果为畅销、中等和滞销的概率分别为、和。
问:企业是否委托专业市场调查机构进行调查解:1.验前分析:记方案d1为批量生产,方案d2为出售专利E(d1)=*80+*20+*(-5)=(万元)E(d2)=40*+7*+1*=(万元)记验前分析的最大期望收益为E1,则E1=max{E(d1),E(d2)}=(万元)因此验前分析后的决策为:批量生产E1不作市场调查的期望收益2.预验分析:(1)设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=*+*+*=P(H2)=*+*+*=P(H3)=*+*+*=(2)由贝叶斯公式有P(?1|H1)=*=P(?2|H1)=*=P(?3|H1)=*=P(?1|H2)=*=P(?2|H2)=*=P(?3|H2)=*=P(?1|H3)=*=P(?2|H3)=*=P(?3|H3)=*=(3)用后验分布代替先验分布,计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(?1|H1)+20* P(?2|H1)+(-5)* P(?3|H1)=80*+20*+(-5)*=(万元)E(d2|H1)=40* P(?1|H1)+7* P(?2|H1)+1* P(?3|H1)=40*+7*+1*=(万元)因此,当市场调查畅销时,最优方案是d1,即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(?1|H2)+20* P(?2|H2)+(-5)* P(?3|H2)=(万元)E(d2|H2)=40* P(?1|H2)+7* P(?2|H2)+1* P(?3|H2)=40*+7*+1*=(万元)所以市场调查为中等时,最优方案是:d1,即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(?1|H3)+20* P(?2|H3)+(-5)* P(?3|H3)=80*+20*+(-5)*=(万元)E(d2|H3)=40* P(?1|H3)+7* P(?2|H3)+1* P(?3|H3)=40*+7*+1*=(万元)因此市场调查为滞销时,最优方案是:d2,即出售专利(4)通过调查,该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=*+*+*=(万元)通过调查,该企业收益期望值能增加E2-E1=(万元)因此,在调查费用不超过万元的情况下,应进行市场调查3.验后分析(1)本题中调查费用1000<9600,所以应该进行市场调查(2)当市场调查结果为畅销时,选择方案1,即批量生产(3)当市场调查结果为中等时时,选择方案1,即批量生产(4)当市场调查结果为滞销时,选择方案2,即出售专利。

贝叶斯准则例题⼀、贝叶斯准则:例题1:设⼆元假设检验的观测信号模型为:H 0: x = -1+n H 1: x = 1+n其中n 是均值为0,⽅差为212nσ=的⾼斯观测噪声。
若两种假设是等先验概率的,⽽代价因⼦为000110111,8,4,2,c c c c ==== 试求贝叶斯(最佳)表达式和平均代价C:解:因为两种假设是等先验概率的所以 011()()2P H P H ==,这样,贝叶斯准备的似然⽐函数()x λ为:① 122110221(1)exp 1122(|)22()exp(4)(|)(1)1exp 112222x p x H x x p x H x πλπ--?==?=+ ?-??⽽似然⽐检测门限η为:010********(41)()()21()()(82)2P H c c P H c c η--=?=-- =1/2于是贝叶斯判决表达式为11exp(4)2H x H ><,两边取⾃然对数,并整理的最简判决表达式为10.1733H x H >-<②现在计算判决概率01(|)P H H 和00(|)P H H ,由于本例中检验统计量()l x x =,所以在两个假设下检验统计量的概率密度函数分别为:122012211(1)(|)exp 1122221(1)(|)exp 112222l p l H l p l H ππ+=-???-=-???这样,0.17330111220.1733(|)(|)1(1)exp 0.0486112222P H H p l H dll dl π--∞--∞=-=-=0.17330001220.1733(|)(|)1(1)exp 0.8790112222P H H p l H dll dl π--∞--∞=+=-=最后,利⽤贝叶斯平均代价表达式,01011110111010100000()()()()(|)()()(|)C P H c P H c P H c c P H H P H c c P H H =++---代⼊0000110(),(|),(|),P H P H H P H H c 等各数据,计算得: 1.8269C=总结:如果我们把判决表达式中的检测门限-0.1733稍作调整,例如调整为-0.1700极品-0.1800,则计算出的平均代价均⼤于检测门限为-0.1733的平均代价,这⼀结果从侧⾯验证了贝叶斯准则的确能使平均代价最⼩。

贝叶斯精炼纳什均衡解经典例题和解答贝叶斯精炼纳什均衡(Bayesian refinement of Nash equilibrium)是博弈论中的一个概念,它结合了贝叶斯理论和纳什均衡的概念,用于描述在不完全信息博弈中玩家对其他玩家类型的不确定性。
这里我将为你提供一个经典的例题,并给出相应的解答。
考虑一个简化的拍卖场景,有两个潜在的买家:买家A和买家B。
拍卖的物品是一幅画,卖家想以尽可能高的价格卖出这幅画。
买家A和买家B对这幅画的估值分别服从正态分布,其均值和标准差如下:买家A的估值:均值为100,标准差为20买家B的估值:均值为120,标准差为15拍卖的规则如下:卖家首先设定一个底价p(reserve price),然后买家A和买家B分别出价。
如果买家A的出价高于底价p,并且买家B的出价也高于底价p,那么拍卖的赢家是出价最高的买家,并且他们需要支付自己的出价。
如果只有一个买家的出价高于底价p,那么这个买家获胜,并以底价p购买这幅画。
如果两个买家都没有出价高于底价p,那么拍卖失败,画作不会被卖出。
现在我们来解答这个问题:1. 假设卖家设定底价p为90,请计算在这个底价下,买家A和买家B的最优出价以及对应的期望收益。
为了计算买家A和买家B的最优出价,我们可以使用贝叶斯精炼纳什均衡的概念。
在这个场景中,买家A和买家B都面临不完全信息,即对方的估值是未知的。
我们需要通过贝叶斯理论来计算每个买家对对方估值的后验概率分布,然后根据这些概率分布来确定最优出价。
买家A的后验概率分布可以通过贝叶斯定理计算得到:P(v_A|p) = P(p|v_A) * P(v_A) / P(p)其中,v_A表示买家A对画作的估值,P(v_A)表示买家A对估值的先验概率分布(正态分布),P(p|v_A)表示在买家A估值为v_A的情况下,底价p被设定的概率,P(p)表示底价被设定为p的概率。
根据题目中给出的信息,买家A的估值服从均值为100,标准差为20的正态分布,我们可以计算P(v_A)。

贝叶斯决策模型及实例分析一、贝叶斯决策的概念贝叶斯决策,是先利用科学试验修正自然状态发生的概率,在采用期望效用最大等准则来确定最优方案的决策方法。
风险型决策是根据历史资料或主观判断所确定的各种自然状态概率(称为先验概率),然后采用期望效用最大等准则来确定最优决策方案。
这种决策方法具有较大的风险,因为根据历史资料或主观判断所确定的各种自然状态概率没有经过试验验证。
为了降低决策风险,可通过科学试验(如市场调查、统计分析等)等方法获得更多关于自然状态发生概率的信息,以进一步确定或修正自然状态发生的概率;然后在利用期望效用最大等准则来确定最优决策方案,这种先利用科学试验修正自然状态发生的概率,在采用期望效用最大等准则来确定最优方案的决策方法称为贝叶斯决策方法。
二、贝叶斯决策模型的定义贝叶斯决策应具有如下内容贝叶斯决策模型中的组成部分:)(,θθPSAa及∈∈。
概率分布SP∈θθ)(表示决策者在观察试验结果前对自然θ发生可能的估计。
这一概率称为先验分布。
一个可能的试验集合E,Ee∈,无情报试验e0通常包括在集合E之内。
一个试验结果Z取决于试验e的选择以Z0表示的结果只能是无情报试验e0的结果。
概率分布P(Z/e,θ),Zz∈表示在自然状态θ的条件下,进行e试验后发生z结果的概率。
这一概率分布称为似然分布。
一个可能的后果集合C,Cc∈以及定义在后果集合C的效用函数u(e,Z,a,θ)。
每一后果c=c(e,z,a,θ)取决于e,z,a和θ。
.故用u(c)形成一个复合函数u{(e,z,a,θ)},并可写成u(e,z,a,θ)。
三、贝叶斯决策的常用方法3.1层次分析法(AHP)在社会、经济和科学管理领域中,人们所面临的常常是由相互关联,相互制约的众多因素组成的复杂问题时,需要把所研究的问题层次化。
所谓层次化就是根据所研究问题的性质和要达到的目标,将问题分解为不同的组成因素,并按照各因素之间的相互关联影响和隶属关系将所有因素按若干层次聚集组合,形成一个多层次的分析结构模型。
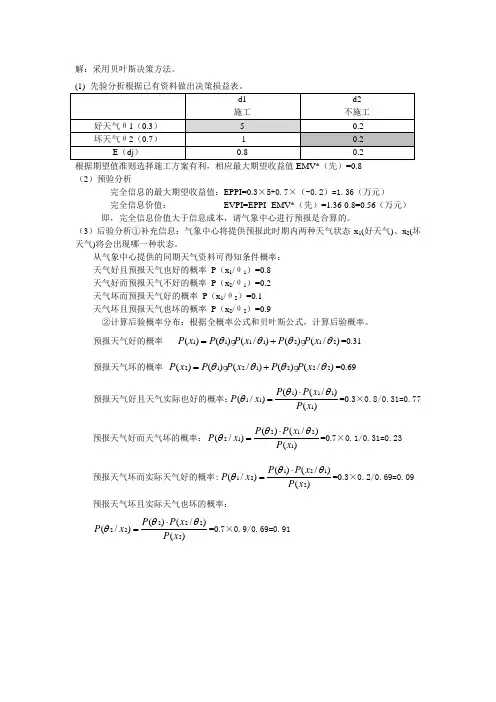
解:采用贝叶斯决策方法。
根据期望值准则选择施工方案有利,相应最大期望收益值EMV*(先)=0.8(2)预验分析完全信息的最大期望收益值:EPPI=0.3×5+0.7×(-0.2)=1.36(万元)完全信息价值: EVPI=EPPI- EMV*(先)=1.36-0.8=0.56(万元) 即,完全信息价值大于信息成本,请气象中心进行预报是合算的。
(3)后验分析①补充信息:气象中心将提供预报此时期内两种天气状态x 1(好天气)、x 2(坏天气)将会出现哪一种状态。
从气象中心提供的同期天气资料可得知条件概率:天气好且预报天气也好的概率 P (x 1/θ1)=0.8天气好而预报天气不好的概率 P (x 2/θ1)=0.2天气坏而预报天气好的概率 P (x 1/θ2)=0.1天气坏且预报天气也坏的概率 P (x 2/θ2)=0.9②计算后验概率分布:根据全概率公式和贝叶斯公式,计算后验概率。
预报天气好的概率 1111212()()(/)()(/)P x P P x P P x θθθθ=+ =0.31预报天气坏的概率 2121222()()(/)()(/)P x P P x P P x θθθθ=+ =0.69预报天气好且天气实际也好的概率:111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77 预报天气好而天气坏的概率:212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23 预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09 预报天气坏且实际天气也坏的概率:222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91。
Equation Chapter 1 Section 1例:某工程项目按合同应在三个月内完工,其施工费用与工程完工期有关。
假定天气是影响能否按期完工的决定因素,如果天气好,工程能按时完工,获利5万元;如果天气不好,不能按时完工,施工单位将被罚款1万元;若不施工就要付出窝工费2千元。
根据过去的经验,在计划实施工期天气好的可能性为30%。
为了更好地掌握天气情况,可以申请气象中心进行天气预报,并提供同一时期天气预报资料,但需要支付资料费800元。
从提供的资料中可知,气象中心对好天气预报准确性为80%,对坏天气预报准确性为90%。
问如何进行决策。
解:采用贝叶斯决策方法。
先验分析根据期望值准则选择施工方案有利,相应最大期望收益值EMV*(先)=0.8(2)预验分析完全信息的最大期望收益值:EPPI=0.3×5+0.7×(-0.2)=1.36(万元)完全信息价值: EVPI=EPPI- EMV*(先)=1.36-0.8=0.56(万元) 即,完全信息价值大于信息成本,请气象中心进行预报是合算的。
(3)后验分析①补充信息:气象中心将提供预报此时期内两种天气状态x1(好天气)、x2(坏天气)将会出现哪一种状态。
从气象中心提供的同期天气资料可得知条件概率: 天气好且预报天气也好的概率 P (x1/θ1)=0.8 天气好而预报天气不好的概率 P (x2/θ1)=0.2 天气坏而预报天气好的概率 P (x1/θ2)=0.1 天气坏且预报天气也坏的概率 P (x2/θ2)=0.9②计算后验概率分布:根据全概率公式和贝叶斯公式,计算后验概率。
预报天气好的概率1111212()()(/)()(/)P x P P x P P x θθθθ=+=0.31预报天气坏的概率2121222()()(/)()(/)P x P P x P P x θθθθ=+=0.69 预报天气好且天气实际也好的概率:111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77预报天气好而天气坏的概率:212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09预报天气坏且实际天气也坏的概率: 222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91上述计算可以用表格表示:③ 后验决策:若气象中心预报天气好(x1),则每个方案的最大期望收益值 E(d1/x1)=0.77×5+0.23×(-1)=3.62 E(d2/x1)=0.77×(-0.2)+0.23×(-0.2)=-0.2选择d1即施工的方案,相应在预报x1若气象中心预报天气不好(x2) E(d1/x2)=0.09×5+0.91×(-1)=-0.46 E(d2/x2)=0.09×(-0.2)+0.91×(-0.2)=-0.2选择d2即不施工的方案,相应在预报x2时的最大期望收益值E (X2)=-0.2④ 计算补充信息的价值:得到天气预报的情况下,后验决策的最大期望收益值:1122*()()()()()EMV P x E x P x E x =⋅+⋅后=0.31×3.62+0.69×(-0.2)=0.9842则补充的信息价值为:EMV*(后)- EMV*(先)=0.9842-0.8=0.1842补充信息价值大于信息费(800元),即这种费用是合算的。
一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品,有两种方案可供选择:—是进行批量生产,二是出售专利。
这种新产品投放市场,估计有3种可能:畅销、中等、滞销,这3种情况发生的可能性依次估计为:0.2,0.5和0.3。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销,则调查结果为畅销、中等和滞销的概率分别为0.9、0.06和0.04;若实际市场状况为中等,则调查结果为畅销、中等和滞销的概率分别为0.05、0.9和0.05;若实际市场状况为滞销,则调查结果为畅销、中等和滞销的概率分别为0.04、0.06和0.9。
问:企业是否委托专业市场调查机构进行调查?解:1.验前分析:记方案d1为批量生产,方案d2为出售专利E(d1)=0.2*80+0.5*20+0.3*(-5)=24.5(万元)E(d2)=40*0.2+7*0.5+1*0.3=11.8(万元)记验前分析的最大期望收益为E1,则E1=max{E(d1),E(d2)}=24.5(万元)因此验前分析后的决策为:批量生产E1不作市场调查的期望收益2.预验分析:(1)设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=0.9*0.2+0.06*0.5+0.04*0.3=0.232P(H2)=0.05*0.2+0.9*0.5+0.05*0.3=0.475P(H3)=0.04*0.2+0.06*0.5+0.9*0.3=0.308(2)由贝叶斯公式有P(Ɵ1|H1)=0.9*0.2/0.232=0.776P(Ɵ2|H1)=0.06*0.5/0.232=0.129P(Ɵ3|H1)=0.04*0.3/0.232=0.052P(Ɵ1|H2)=0.05*0.2/0.475=0.021P(Ɵ2|H2)=0.9*0.5/0.475=0.947P(Ɵ3|H2)=0.05*0.3/0.475=0.032P(Ɵ1|H3)=0.04*0.2/0.308=0.026P(Ɵ2|H3)=0.06*0.5/0.308=0.097P(Ɵ3|H3)=0.9*0.3/0.308=0.877(3)用后验分布代替先验分布,计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(Ɵ1|H1)+20* P(Ɵ2|H1)+(-5)* P(Ɵ3|H1)=80*0.776+20*0.129+(-5)*0.052=64.4(万元)E(d2|H1)=40* P(Ɵ1|H1)+7* P(Ɵ2|H1)+1* P(Ɵ3|H1)=40*0.776+7*0.129+1*0.052=31.995(万元)因此,当市场调查畅销时,最优方案是d1,即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(Ɵ1|H2)+20* P(Ɵ2|H2)+(-5)* P(Ɵ3|H2)=20.46(万元)E(d2|H2)=40* P(Ɵ1|H2)+7* P(Ɵ2|H2)+1* P(Ɵ3|H2)=40*0.021+7*0.947+1*0.032=7.501(万元)所以市场调查为中等时,最优方案是:d1,即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(Ɵ1|H3)+20* P(Ɵ2|H3)+(-5)* P(Ɵ3|H3)=80*0.026+20*0.097+(-5)*0.877=-0.365(万元)E(d2|H3)=40* P(Ɵ1|H3)+7* P(Ɵ2|H3)+1* P(Ɵ3|H3)=40*0.026+7*0.097+1*0.877=2.596(万元)因此市场调查为滞销时,最优方案是:d2,即出售专利(4)通过调查,该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=64.4*0.232+20.46*0.475+2.596*0.308=25.46(万元)通过调查,该企业收益期望值能增加E2-E1=25.46-24.5=0.96(万元)因此,在调查费用不超过0.96万元的情况下,应进行市场调查3.验后分析(1)本题中调查费用1000<9600,所以应该进行市场调查(2)当市场调查结果为畅销时,选择方案1,即批量生产(3)当市场调查结果为中等时时,选择方案1,即批量生产(4)当市场调查结果为滞销时,选择方案2,即出售专利Welcome 欢迎您的下载,资料仅供参考!。
1.什么叫贝叶斯决策?如何进行贝叶斯决策?风险型决策方法是根据预测各种事件可能发生的先验概率,然后再采用期望值标准或最大可能性标准来选择最佳决策方案。
这样的决策具有一定的风险性,因为先验概率是根据历史资料或主观判断所确定的概率,未经试验证实,为了减少这种风险,需要较准确的掌握和估计这些先验概率。
这就要通过科学实验,调查,统计分析等方法获得较为准确的情报信息,以修正先验概率,并据以确定各方案的期望损益值,拟订可供选择的决策方案,协助决策者做出正确的决策。
一般来说,利用贝叶斯定理要求得后验概率,据以进行决策的方法称为贝叶斯决策方法。
贝叶斯决策方法步骤:(1)进行预后验分析,决定是否值得搜集补充资料以及从补充资料中可能得到的结果和如何决定最优对策。
(2)收集补充资料,取得条件概率,包括历史概率和逻辑概率,对历史概率要加以检验,辨明其是否适合计算后验概率。
(3)用概率的乘法定理计算联合概率,用概率的加法定理计算边际概率,用贝叶斯定理计算后验概率。
(4)用后验概率进行决策分析。
2.如何进行预后验分析和后验分析?预后验分析是后验概率决策分析的一种特殊形式的演算,这里的特殊形式是指用一套概率对多种行动策略组合进行多次计算,从中择优。
预后验分析有两种形式,一是扩大型,预后验分析,这实际上是一种反推决策树分析,二是常规型预后验分析,这实际上是一种正向分析,用表格形式进行。
扩大型分析要解决的问题是搜集追加信息对决策者有多大的价值,如果试验应采取什么行动策略,常规型分析要解决的问题是,如果试验应采取什么行动策略,但是这两种分析方法所得出的结论是一致的。
根据预后验分析,如果认为采集信息和进行调查研究是值得的,那么就应该决定去做这项工作。
一旦取得了新的信息,决策者就结合这些新信息进行分析,计算各种方案的期望损益值,选择最佳的行动方案,结合运用这些信息并修正先验概率,称为后验分析,这正是发挥贝叶斯决策理论威力的地方。
3.什么是先验分析?先验分析就是决策者要详细列出各种自然状态及其概率,各种备选行动方案与自然状态的损益值,并根据这些信息对备选方案作出抉择的决策过程,当时间,人力和财力不允许搜集更完备的信息时,决策者往往用这类方法进行决策,在贝叶斯决策中,先验分析是进行更深入分析的必要条件。
例:某工程项目按合同应在三个月内完工,其施工费用与工程完工期有关。
假定天气是影响能否按期完工的决定因素,如果天气好,工程能按时完工,获利5万元;如果天气不好,不能按时完工,施工单位将被罚款1万元;若不施工就要付出窝工费2千元。
根据过去的经验,在计划实施工期天气好的可能性为30%。
为了更好地掌握天气情况,可以申请气象中心进行天气预报,并提供同一时期天气预报资料,但需要支付资料费800元。
从提供的资料中可知,气象中心对好天气预报准确性为80%,对坏天气预报准确性为90%。
问如何进行决策。
解:采用贝叶斯决策方法。
(1)先验分析根据已有资料做出决策损益表。
根据期望值准则选择施工方案有利,相应最大期望收益值EMV*(先)=0.8(2)预验分析完全信息的最大期望收益值:EPPI=0.3×5+0.7×(-0.2)=1.36(万元)完全信息价值: EVPI=EPPI- EMV*(先)=1.36-0.8=0.56(万元)即,完全信息价值大于信息成本,请气象中心进行预报是合算的。
(3)后验分析①补充信息:气象中心将提供预报此时期内两种天气状态x 1(好天气)、x 2(坏天气)将会出现哪一种状态。
从气象中心提供的同期天气资料可得知条件概率: 天气好且预报天气也好的概率 P (x 1/θ1)=0.8 天气好而预报天气不好的概率 P (x 2/θ1)=0.2 天气坏而预报天气好的概率 P (x 1/θ2)=0.1 天气坏且预报天气也坏的概率 P (x 2/θ2)=0.9②计算后验概率分布:根据全概率公式和贝叶斯公式,计算后验概率。
预报天气好的概率1111212()()(/)()(/)P x P P x P P x θθθθ=+=0.31预报天气坏的概率2121222()()(/)()(/)P x P P x P P x θθθθ=+=0.69 预报天气好且天气实际也好的概率:111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77预报天气好而天气坏的概率:212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09预报天气坏且实际天气也坏的概率: 222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91上述计算可以用表格表示:③ 后验决策:若气象中心预报天气好(x1),则每个方案的最大期望收益值 E(d1/x1)=0.77×5+0.23×(-1)=3.62 E(d2/x1)=0.77×(-0.2)+0.23×(-0.2)=-0.2选择d1即施工的方案,相应在预报x1时的最大期望收益值E (X1)=3.62若气象中心预报天气不好(x2),各方案的最大期望收益值 E(d1/x2)=0.09×5+0.91×(-1)=-0.46 E(d2/x2)=0.09×(-0.2)+0.91×(-0.2)=-0.2选择d2即不施工的方案,相应在预报x2时的最大期望收益值E (X2)=-0.2④ 计算补充信息的价值:得到天气预报的情况下,后验决策的最大期望收益值:1122*()()()()()EMV P x E x P x E x =⋅+⋅后=0.31×3.62+0.69×(-0.2)=0.9842则补充的信息价值为:EMV*(后)-EMV*(先)=0.9842-0.8=0.1842补充信息价值大于信息费(800元),即这种费用是合算的。
贝叶斯决策的经典例
题练习
一、贝叶斯决策(Bayes decision theory)
【例】某企业设计出一种新产品,有两种方案可供选择:—是进行批量生产,二是出售专利。
这种新产品投放市场,估计有3种可能:畅销、中等、滞销,这3种情况发生的可能性依次估计为:0.2,0.5和0.3。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销,则调查结果为畅销、中等和滞销的概率分别为0.9、0.06和0.04;若实际市场状况为中等,则调查结果为畅销、中等和滞销的概率分别为0.05、0.9和0.05;若实际市场状况为滞销,则调查结果为畅销、中等和滞销的概率分别为0.04、0.06和0.9。
问:企业是否委托专业市场调查机构进行调查?解:
1.验前分析:
记方案d1为批量生产,方案d2为出售专利
E(d1)=0.2*80+0.5*20+0.3*(-5)=24.5(万元)
E(d2)=40*0.2+7*0.5+1*0.3=11.8(万元)
记验前分析的最大期望收益为E1,则E1=max{E(d1),E(d2)}=24.5(万元)
因此验前分析后的决策为:批量生产
E1不作市场调查的期望收益
2.预验分析:
(1)设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示
由全概率公式
P(H1)=0.9*0.2+0.06*0.5+0.04*0.3=0.232
P(H2)=0.05*0.2+0.9*0.5+0.05*0.3=0.475
P(H3)=0.04*0.2+0.06*0.5+0.9*0.3=0.308
(2)由贝叶斯公式有
P(Ɵ1|H1)=0.9*0.2/0.232=0.776
P(Ɵ2|H1)=0.06*0.5/0.232=0.129
P(Ɵ3|H1)=0.04*0.3/0.232=0.052
P(Ɵ1|H2)=0.05*0.2/0.475=0.021
P(Ɵ2|H2)=0.9*0.5/0.475=0.947
P(Ɵ3|H2)=0.05*0.3/0.475=0.032
P(Ɵ1|H3)=0.04*0.2/0.308=0.026
P(Ɵ2|H3)=0.06*0.5/0.308=0.097
P(Ɵ3|H3)=0.9*0.3/0.308=0.877
(3)用后验分布代替先验分布,计算各方案的期望收益值
a)当市场调查结果为畅销时
E(d1|H1)=80* P(Ɵ1|H1)+20* P(Ɵ2|H1)+(-5)* P(Ɵ3|H1)
=80*0.776+20*0.129+(-5)*0.052=64.4(万元)
E(d2|H1)=40* P(Ɵ1|H1)+7* P(Ɵ2|H1)+1* P(Ɵ3|H1)
=40*0.776+7*0.129+1*0.052=31.995(万元)
因此,当市场调查畅销时,最优方案是d1,即批量生产
b)当市场调查结果为中等时
E(d1|H2)=80* P(Ɵ1|H2)+20* P(Ɵ2|H2)+(-5)* P(Ɵ3|H2)=20.46(万元)
E(d2|H2)=40* P(Ɵ1|H2)+7* P(Ɵ2|H2)+1* P(Ɵ3|H2)
=40*0.021+7*0.947+1*0.032=7.501(万元)
所以市场调查为中等时,最优方案是:d1,即批量生产
c)当市场调查结果为滞销时
E(d1|H3)=80* P(Ɵ1|H3)+20* P(Ɵ2|H3)+(-5)* P(Ɵ3|H3)
=80*0.026+20*0.097+(-5)*0.877=-0.365(万元)
E(d2|H3)=40* P(Ɵ1|H3)+7* P(Ɵ2|H3)+1* P(Ɵ3|H3)
=40*0.026+7*0.097+1*0.877=2.596(万元)
因此市场调查为滞销时,最优方案是:d2,即出售专利
(4)通过调查,该企业可获得的收益期望值为
E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)
=64.4*0.232+20.46*0.475+2.596*0.308=25.46(万元)
通过调查,该企业收益期望值能增加
E2-E1=25.46-24.5=0.96(万元)
因此,在调查费用不超过0.96万元的情况下,应进行市场调查
3.验后分析
(1)本题中调查费用1000<9600,所以应该进行市场调查(2)当市场调查结果为畅销时,选择方案1,即批量生产(3)当市场调查结果为中等时时,选择方案1,即批量生产(4)当市场调查结果为滞销时,选择方案2,即出售专利。