当前位置：文档之家 › 第九章 相关与回归

第九章 相关与回归

  • 格式：doc
  • 大小：61.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

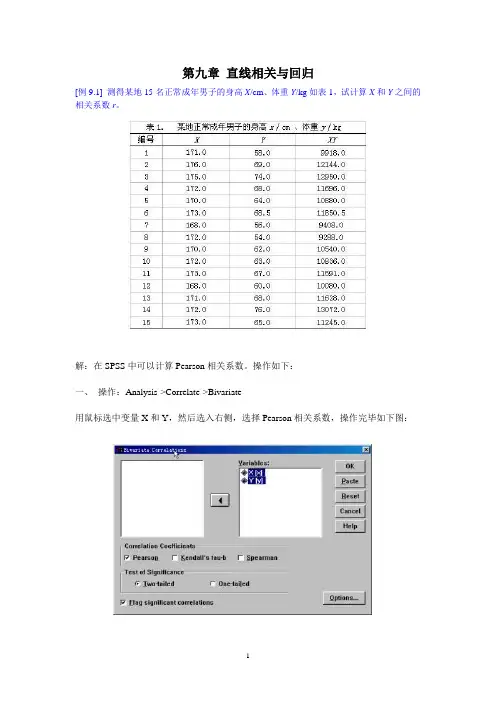
第九章 直线相关与回归

第九章 直线相关与回归

第九章直线相关与回归[例9.1] 测得某地15名正常成年男子的身高X/cm、体重Y/kg如表1，试计算X和Y之间的相关系数r。

解：在SPSS中可以计算Pearson相关系数。

操作如下：一、操作：Analysis->Correlate->Bivariate用鼠标选中变量X和Y，然后选入右侧，选择Pearson相关系数，操作完毕如下图：二、结果见下：SPSS给出相关系数交叉表，可以看出X和Y的相关系数为0.599，p=0.000。

可以认为X和Y线性相关，并且有统计意义。

[例9.2] 为了研究3岁至8岁男孩身高与年龄的规律，在某地区在3岁至8岁男孩中随机抽样，共分6个年龄层抽样：3岁，4岁，…，8岁，每个层抽3名男孩，共抽18名男孩。

资料列于表2。

解：本题需要计算回归方程式，在SPSS中可以直接菜单完成。

操作如下：一、操作：Analysis->Regression->Linear用鼠标选中变量X和Y，分别选入自变量和应变量对话框，操作完毕如下图：二、主要结果见下首先给出方差分析表，由p=0.000，可以认为回归模型有统计意义。

根据回归系数得到回归方程式为：Y=75.363+6.257X。

由p=0.000，可以认为回归系数有统计意义。

[例9.3] 调查了某地区10个乡的钉螺密度与血吸虫感染率/%数据如表3。

试分析该地区螺密度与感染率之间有无相关关系？解：本题选用Spearman秩相关，在SPSS中操作如下：一、操作：Analysis->Correlate->Bivariate用鼠标选中变量X和Y，分别选入右侧对话框，并且选择Spearman相关系数，操作完毕如下图：二、主要结果见下：可见Spearman相关系数为0.817，p=0.004。

可以认为Spearman相关系数有统计意义。

统计学原理第九章(相关与回归)习题答案

统计学原理第九章(相关与回归)习题答案

第九章相关与回归一．判断题部分题目1：负相关指的是因素标志与结果标志的数量变动方向是下降的。

（）答案：×题目2：相关系数为+1时，说明两变量完全相关；相关系数为-1时，说明两个变量不相关。

（）答案：√题目3：只有当相关系数接近+1时，才能说明两变量之间存在高度相关关系。

（）答案：×题目4：若变量x的值增加时，变量y的值也增加，说明x与y之间存在正相关关系；若变量x的值减少时，y变量的值也减少，说明x与y之间存在负相关关系。

（）答案：×题目5：回归系数和相关系数都可以用来判断现象之间相关的密切程度。

（）答案：×题目6：根据建立的直线回归方程，不能判断出两个变量之间相关的密切程度。

（）答案：√题目7：回归系数既可以用来判断两个变量相关的方向，也可以用来说明两个变量相关的密切程度。

（）答案：×题目8：在任何相关条件下，都可以用相关系数说明变量之间相关的密切程度。

（）答案：×题目9：产品产量随生产用固定资产价值的减少而减少，说明两个变量之间存在正相关关系。

（）答案：√题目10：计算相关系数的两个变量，要求一个是随机变量，另一个是可控制的量。

（）答案：×题目11：完全相关即是函数关系，其相关系数为±1。

（）答案：√题目12：估计标准误是说明回归方程代表性大小的统计分析指标，指标数值越大，说明回归方程的代表性越高。

（）答案×二．单项选择题部分题目1：当自变量的数值确定后，因变量的数值也随之完全确定，这种关系属于（）。

A.相关关系B.函数关系C.回归关系D.随机关系答案：B题目2：现象之间的相互关系可以归纳为两种类型，即（）。

A.相关关系和函数关系B.相关关系和因果关系C.相关关系和随机关系D.函数关系和因果关系答案：A题目3：在相关分析中，要求相关的两变量（）。

A.都是随机的B.都不是随机变量C.因变量是随机变量D.自变量是随机变量答案：A题目4：测定变量之间相关密切程度的指标是（）。

9 第九章 回归与相关

9 第九章 回归与相关

估计。
一）、加权最小二乘估计 假定各观测值的权重为Wi，求解回归方 程就要使得以下加权后的残差平方和最小
ss残W Wi Yi aw bw X
2
bw
aW
WX WY WXY W l l WX WX W WY b WX Y b W
二、直线回归方程的求法 直线方程为： a为Y轴上的截距；b为斜率，表示X 每改变一个单位，Y的变化的值，称为回 归系数； 表示在X值处Y的总体均数 估计值。为求a和b两系数，根据数学上 的最小二乘法原理，可导出a和b的算式 如下：
例9-1 某地方病研究所调查了8名正常 儿童的尿肌酐含量（mmol/24h）如表91。估计尿肌酐含量（Y）对其年龄（X） 的关系。
表14，rs界值表，P<0.01,故可认为当地居 民死因的构成和各种死因导致的潜在工作损 失年数WYPLL的构成呈正相关。 二、相同秩次较多时rs的校正 当X及Y中，相同秩次个数多时，宜用下式校 正
第四节
加权直线回归
在一些情况下，根据专业知识考虑 并结合实际数据，某些观察值对于估计 回归方程显得更“重要”，而有些不 “重要”，此时可以采用加权最小二乘
lYY的分析 如图9－4，p点的纵坐标被回归直线与均数 截成三个线段：
图9－4
平方和划分示意图
第一段 第二段
第三段
上述三段代数和为：
移项：
p点是散点图中任取一点，将所有的点子都
按上法处理，并将等式两端平方后再求和，
则有：
它们各自的自由度分别为： 可计算统计量F：
SS回 SS 残
2
F
回 残
表9-3某省1995年到1999年居民死因构成与WYPLL构成

统计学第9章 相关分析和回归分析

统计学第9章 相关分析和回归分析

回归模型的类型
回归模型
一元回归
线性回归
10 - 28
多元回归
线性回归 非线性回归
非线性回归
统计学
STATISTICS (第二版)
一元线性回归模型
10 - 29
统计学
STATISTICS (第二版)
一元线性回归
1. 涉及一个自变量的回归 2. 因变量y与自变量x之间为线性关系


被预测或被解释的变量称为因变量 (dependent variable)，用y表示 用来预测或用来解释因变量的一个或多个变 量称为自变量 (independent variable) ，用 x 表示
统计学
STATISTICS (第二版)
3.相关分析主要是描述两个变量之间线性关 系的密切程度；回归分析不仅可以揭示 变量 x 对变量 y 的影响大小，还可以由 回归方程进行预测和控制 4.回归系数与相关系数的符号是一样的，但 是回归系数是有单位的，相关系数是没 有单位的。
10 - 27
统计学
STATISTICS (第二版)
10 - 19
统计学
STATISTICS (第二版)
相关系数的经验解释
1. 2. 3. 4.
|r|0.8时，可视为两个变量之间高度相关 0.5|r|<0.8时，可视为中度相关 0.3|r|<0.5时，视为低度相关 |r|<0.3时，说明两个变量之间的相关程度 极弱，可视为不相关
10 - 20
10 - 6
统计学
STATISTICS (第二版)
函数关系
(几个例子)

某种商品的销售额 y 与销售量 x 之间的关系 可表示为 y = px (p 为单价)

第九章 第四节 相关性、最小二乘估计、回归分析与独立性检验

第九章 第四节 相关性、最小二乘估计、回归分析与独立性检验
第四节 相关性、最小二乘估计、回归
分析与独立性检验
9/30/2013
9/30/2013
1.相关性 （1）散点图：在考虑两个量的关系时，为了对_____之间的关 变量 系有一个大致的了解，人们通常将___________的点描出来， 变量所对应 这些点就组成了变量之间的一个图，通常称这种图为变量之间 的散点图.
1.利用统计量χ 2来判断“两个变量X,Y有关系”计算公式为：

2
（A）ad-bc越小，说明X与Y关系越弱
（B）ad-bc越大，说明X与Y关系越强 （C）(ad-bc)2越大，说明X与Y关系越强 （D）(ad-bc)2越接近于0，说明X与Y关系越强
a b c d a c b d
1 2
9/30/2013
【拓展提升】线性相关关系与函数关系的区别 （1）函数关系中的两个变量间是一种确定性关系．例如，正 方形面积S与边长x之间的关系S＝x2就是函数关系．
（2）相关关系是一种非确定性关系，即相关关系是非随机变
量与随机变量之间的关系．例如，商品的销售额与广告费是相
关关系．两个变量具有相关关系是回归分析的前提．
50 13 20－10 7） （ 4.844， 23 27 20 30
2
因为χ 2≥3.841，所以有
答案：95%
9/30/2013
考向 1
相关关系的判断
【典例1】（1）对变量x，y有观测数据(xi，yi)(i＝1,2，„，
10)，得散点图(1)；对变量u，v有观测数据(ui,vi)(i＝1,
9/30/2013
3.独立性检验
（1）2×2列联表
设A，B为两个变量，每一个变量都可以取两个值，变量A：

西南财经大学向蓉美、王青华《统计学》第三版——第9章：相关与回归分析

西南财经大学向蓉美、王青华《统计学》第三版——第9章：相关与回归分析

相关关系（例）
▪ 单位成本(y)与产量(x) 的关系…… ▪ 父亲身高(y)与子女身高(x)之间的关系 ▪ 社会商品零售额(y)与居民可支配收入(x)之
间的关系 ▪ 收入 (y)与文化程度(x)之间的关系 ▪ 商品销售量(y)与广告费支出(x1)、价格(x2)
之间的关系 ▪ 需要PPT配套视频，请加VX：1033604968
简单相关系数（简单线性相关系数） 对两个变量（定量变量）之间线性相关程 度的度量。 也称直线相关系数, 常简称相关系数。
等级相关（秩相关）
对两个定序变量之间线性相关程度的度量。
9--19
相关系数（Pearson’s
correlation coefficient）
有总体相关系数与样本相关系数之分：
• 总体相关系数ρ
变量间的相互依存关系有 两种类型：
——函数关系 ——相关关系
9--3
函数关系
1. 指变量之间确定性的数量依存关系；
2. 当变量 x 取某个数值时，
y 有确定的值与之对应， 则称 y 是 x 的函数 y = f
(x)
• 通常将作为变动原因的变 量 x 称为自变量，作为变
Y
动结果的变量y 称为因变量
将两个变量成对的观测数据在坐标图上标示出来， 变量 x 的值为横坐标，另一个变量 y 对应的数值 为纵坐标，一对观测值对应一个点，样本数据若 有n 对观测值，则相应的 n 个点形成的图形就称为 散点图。
如果一个是解释变量另一个是被解释变量，则通常 将解释变量放在横轴。
有助于分析者判断相关的有无、方向、形态、密 切程度。
9--5
相关关系
1. 指变量间数量上不确定的依存关系；
2. 一个变量的取值不能唯一地由 另一个变量来确定。当变量 x 取某个值时，与之相关的 变量 y 的取值可能有若干个 （按某种规律在一定范围内

第九章 相关与回归分析

第九章 相关与回归分析

第9章相关与回归分析【教学内容】相关分析与回归分析是两种既有区别又有联系的统计分析方法。

本章阐述了相关关系的概念与特点;相关关系与函数关系的区别与联系;相关关系的种类;相关关系的测定方法(直线相关系数的含义、计算方法与运用);回归分析的概念与特点;回归直线方程的求解及其精确度的评价;估计标准误差的计算。

【教学目标】1、了解相关与回归分析的概念、特点和相关分析与回归分析的区别与联系；2、掌握相关分析的定性和定量分析方法；3、掌握回归模型的拟合方法、对回归方程拟合精度的测定和评价的方法。

【教学重、难点】1、相关分析与回归分析的概念、特点、区别与联系；2、相关与回归分析的有关计算公式和应用条件。

第一节相关分析的一般问题一、相关关系的概念与特点（一）相关关系的概念在自然界与人类社会中,许多现象之间是相互联系、相互制约的,表现在数量上也存在着一定的联系。

这种数量上的联系和关系究其实质,可以概括为两种不同类型,即函数关系与相关关系。

相关关系:是指现象之间客观存在的,在数量变化上受随机因素的影响,非确定性的相互依存关系。

例如,商品销售额与流通费用率之间的关系就是一种相关关系。

（二）相关关系的特点1、相关关系表现为数量相互依存关系。

2、相关关系在数量上表现为非确定性的相互依存关系。

二、相关关系的种类1、相关关系按变量的多少,可分为单相关和复相关2、相关关系从表现形态上划分,可分为直线相关和曲线相关3、相关关系从变动方向上划分,可分为正相关和负相关4、按相关的密切程度分,可分为完全相关、不完全相关和不相关三、相关分析的内容相关分析是对客观社会经济现象间存在的相关关系进行分析研究的一种统计方法。

其目的在于对现象间所存在的依存关系及其所表现出的规律性进行数量上的推断和认识,以便为回归分析提供依据。

相关分析的内容和程序是:(1)判别现象间有无相关关系(2)判定相关关系的表现形态和密切程度第二节相关关系的判断与分析一、相关关系的一般判断（一）定性分析对现象进行定性分析,就是根据现象之间的本质联系和质的规定性,运用理论知识、专业知识、实际经验来进行判断和分析。

医学科研中的统计方法(第九章)直线相关与回归

医学科研中的统计方法(第九章)直线相关与回归

例9.1某地测量十二名健康儿童头发中的硒含量与 血中的硒含量，其结果如表9.1所示：
编号 发硒 血硒
ห้องสมุดไป่ตู้
X
1
2 3 4
X2
5505.64
4435.56 7885.44 4830.25
Y
13.5
10.5 13.8 11.0
Y2
182.25
110.25 190.44 121.00
XY
1001.70
699.30 1225.44 764.50
f X X f
2
x
X
2
f X f
x
2
(264.625) 2 [875.641 ] 11.12 81
f Y Y f Y
2 y y
2
f Y f
y
2
(627.25) 2 [4919 .08 ] 61.76 81
医学科研中的统计方法
第九章
直线相关与回归
第一节 线性相关
一、相关（correlation）的意义 在医学上，所研究的两个事物或现象之间， 既存在着密切的数量关系，但是，又不象函数关 系那样，能以一个变量的数值精确（特例除外） 地求出另一个变量的数值。 这种事物或现象之间的关系称为相关关系， 简称相关。
73.5 64.8 78.6
3457.44
5402.25 4199.04 6177.96
5.8
10.0 7.6 11.5
33.64
100.00 57.76 132.25
2
341.04
735.00 492.48 903.90
EG0901
X
901.9

第9章 相关与回归分析

第9章 相关与回归分析

第九章相关与回归分析习题一、单选题1．下面的函数关系是（）。

A、销售人员测验成绩与销售额大小的关系B、圆周的长度决定于它的半径C、家庭的收入和消费的关系D、数学成绩与统计学成绩的关系2．若要证明两变量之间线性相关程度是高的，则计算出的相关系数应接近于（）。

A、+1B、0C、0.5D、+1或-13．回归系数和相关系数的符号是一致的，其符号均可用来判断现象（）。

A、线性相关还是非线性相关B、正相关还是负相关C、完全相关还是不完全相关D、单相关还是复相关4．在线性相关的条件下，自变量的均方差为2，因变量均方差为5，而相关系数为0.8时，则其回归系数为( )。

A、8B、0.32C、2D、12.55．下面现象间的关系属于相关关系的是（）。

A、圆的周长和它的半径之间的关系B、价格不变条件下,商品销售额与销售量之间的关系C、家庭收入愈多,其消费支出也有增长的趋势D、正方形面积和它的边长之间的关系6．下列关系中，属于正相关关系的是（）。

A、合理限度内，施肥量和平均单产量之间的关系B、产品产量与单位产品成本之间的关系C、商品的流通费用与销售利润之间的关系D、流通费用率与商品销售量之间的关系7．相关分析是研究（）。

A、变量之间的数量关系B、变量之间的变动关系C、变量之间的相互关系的密切程度D、变量之间的因果关系8．在回归直线y=a+bx中，b<0，则x与y之间的相关系数( )。

A、r=0B、r=lC、0<r<1D、-1<r<09．在回归直线y=a+bx中，b表示（）。

A、当x增加一个单位时，y增加a的数量B、当y增加一个单位时，x增加b的数量C、当x增加一个单位时，y的平均增加量D、当y增加一个单位时，x的平均增加量10．当相关系数r=0时，表明（）。

A、现象之间完全无关B、相关程度较小C、现象之间完全相关D、无直线相关关系11．下列现象相关密切程度最高的是（）。

A、某商店的职工人数与商品销售额之间的相关系数0.87B、流通费用水平与利润率之间的相关关系为-0.94C、商品销售额与利润率之间的相关系数为0.51D、商品销售额与流通费用水平的相关系数为-0.8112．估计标准误差是反映（）。

第九章双变量线性回归与相关

第九章双变量线性回归与相关

1 ( X X )2 SYˆ SY .X n ( X X )2
当X
X时，SYˆ
SY X n
Syˆ 是 Yˆ 的标准误。
例 计算当X0=150时， yˆ 95%可信区间。 yˆ 的95%可信区间为：
（46.52, 51.75）Kg
其含义是：当身高为150cm时，15岁男童的体重
的总体均数为49.135kg（点值估计），95%可信区 间为：（46.52, 51.75）Kg （区间估计）。
男性：身高(cm)-105＝标准体重(kg) 女性：身高(cm)-100＝标准体重(kg)
北方人理想体重＝(身高cm-150)×0.6+50(kg) 南方人理想体重＝(身高cm-150)×0.6+48(kg)
回归与相关是研究变量之间相互关系的统计分 析方法，它是一类双变量或多变量统计分析方法 （本章主要介绍双变量分析方法），在实际之中有 着广泛的应用。
如年龄与体重、年龄与血压、身高与体重、体 重与肺活量、体重与体表面积、毒物剂量与动物死 亡率、污染物浓度与污染源距离等都要运用回归与 相关方法对资料进行统计分析。
变量之间的关系： （１）直线关系（线性 关系）； （２）曲线关系（非线 性关系）。 在回归与相关分析中， 直线回归与相关是最简单 的一种，是本章主要内容。
变量间的关系 函数关系： 确定的关系。 例如园周长与半径：y=2πr 。
回归关系：不确定的关系（随机的关系）。 例如血压和年龄的关系，称为直线 回归 (linear regression)。
北方人理想体重＝(身高cm-150)×0.6+50(kg)
变量间的回归关系 由于生物间存在变异，故两相关变量之间的关 系具有某种不确定性，如同性别、同年龄的人，其 肺活量与体重有关，肺活量随体重的增加而增加， 但体重相同的人其肺活量并不一定相等。因此，散 点呈直线趋势，但并不是所有的散点均在同一条直 线上，肺活量与体重的关系与严格对应的函数关系 不同，它们之间是一种回归关系，称直线回归。这 种关系是用直线回归方程来定量描述。

(整理)统计学原理第九章相关与回归习题答案

(整理)统计学原理第九章相关与回归习题答案

第九章相关与回归一．判断题部分题目1：负相关指的是因素标志与结果标志的数量变动方向是下降的。

（）答案：×题目2：相关系数为+1时，说明两变量完全相关；相关系数为-1时，说明两个变量不相关。

（）答案：√题目3：只有当相关系数接近+1时，才能说明两变量之间存在高度相关关系。

（）答案：×题目4：若变量x的值增加时，变量y的值也增加，说明x与y之间存在正相关关系；若变量x的值减少时，y变量的值也减少，说明x与y之间存在负相关关系。

（）答案：×题目5：回归系数和相关系数都可以用来判断现象之间相关的密切程度。

（）答案：×题目6：根据建立的直线回归方程，不能判断出两个变量之间相关的密切程度。

（）答案：√题目7：回归系数既可以用来判断两个变量相关的方向，也可以用来说明两个变量相关的密切程度。

（）答案：×题目8：在任何相关条件下，都可以用相关系数说明变量之间相关的密切程度。

（）答案：×题目9：产品产量随生产用固定资产价值的减少而减少，说明两个变量之间存在正相关关系。

（）答案：√题目10：计算相关系数的两个变量，要求一个是随机变量，另一个是可控制的量。

（）答案：×题目11：完全相关即是函数关系，其相关系数为±1。

（）答案：√题目12：估计标准误是说明回归方程代表性大小的统计分析指标，指标数值越大，说明回归方程的代表性越高。

（）答案×二．单项选择题部分题目1：当自变量的数值确定后，因变量的数值也随之完全确定，这种关系属于（）。

A.相关关系B.函数关系C.回归关系D.随机关系答案：B题目2：现象之间的相互关系可以归纳为两种类型，即（）。

A.相关关系和函数关系B.相关关系和因果关系C.相关关系和随机关系D.函数关系和因果关系答案：A题目3：在相关分析中，要求相关的两变量（）。

A.都是随机的B.都不是随机变量C.因变量是随机变量D.自变量是随机变量答案：A题目4：测定变量之间相关密切程度的指标是（）。

统计学第九章 相关与回归分析

统计学第九章 相关与回归分析

第九章相关与回归分析Ⅰ. 学习目的和要求本章所要学习的相关与回归分析是经济统计分析中最常重要的统计方法之一。

具体要求：1.掌握有关相关与回归分析的基本概念；2.掌握单相关系数的计算与检验的方法，理解标准的一元线性回归模型，能够对模型进行估计和检验并利用模型进行预测；3.理解标准的多元线性回归模型，掌握估计、检验的基本方法和预测的基本公式，理解复相关系数和偏相关系数及其与单相关系数的区别；4.了解常用的非线性函数的特点，掌握常用的非线性函数线性变换与估计方法，理解相关指数的意义；5.能够应用Excel软件进行相关与回归分析。

Ⅱ. 课程内容要点第一节相关与回归分析的基本概念一、函数关系与相关关系当一个或几个变量取一定的值时，另一个变量有确定值与之相对应，这种关系称为确定性的函数关系。

当一个或几个相互联系的变量取一定数值时，与之相对应的另一变量的值虽然不确定，但仍按某种规律在一定的范围内变化。

这种关系，称为具有不确定性的相关关系。

变量之间的函数关系和相关关系，在一定条件下是可以互相转化的。

116117二、相关关系的种类按相关的程度可分为完全相关、不完全相关和不相关。

按相关的方向可分为正相关和负相关。

按相关的形式可分为线性相关和非线性相关。

按所研究的变量多少可分为单相关、复相关和偏相关。

三、相关分析与回归分析相关分析是用一个指标来表明现象间相互依存关系的密切程度。

回归分析是根据相关关系的具体形态，选择一个合适的数学模型，来近似地表达变量间的平均变化关系。

通过相关与回归分析虽然可以从数量上反映现象之间的联系形式及其密切程度，但是无法准确地判断现象内在联系的有无，也无法单独以此来确定何种现象为因，何种现象为果。

只有以实质性科学理论为指导，并结合实际经验进行分析研究，才能正确判断事物的内在联系和因果关系。

四、相关图相关图又称散点图。

它是以直角坐标系的横轴代表变量X ，纵轴代表变量Y,将两个变量间相对应的变量值用坐标点的形式描绘出来，用来反映两变量之间相关关系的图形。

第九章 相关与回归分析 《统计学原理》PPT课件

第九章 相关与回归分析 《统计学原理》PPT课件

［公式9—4］
r xy n • xy
x y
［公式9—5］
返回到内容提要
第三节 回归分析的一般问题
一、回归分析的概念与特点
(一)回归分析的概念
现象之间的相关关系，虽然不是严格 的函数关系，但现象之间的一般关系值， 可以通过函数关系的近似表达式来反映， 这种表达式根据相关现象的实际对应资料， 运用数学的方法来建立，这类数学方法称 回归分析。
单相关是指两个变量间的相关关系，如 自变量x和因变量y的关系。
复相关是指多个自变量与因变量间的相关 关系。
(二)相关关系从表现形态上划分，可分为 直线相关和曲线相关
直线相关是指两个变量的对应取值在坐标 图中大致呈一条直线。
曲线相关是指两个变量的对应取值在坐 标图中大致呈一条曲线，如抛物线、指数曲线、 双曲线等。
0.578
a y b x 80 0.578 185 3.844
n
n7
7
yˆ 3.844 0.578x
二、估计标准误差 (一)估计标准误差的概念与计算 估计标准误差是用来说明回归直线方程 代表性大小的统计分析指标。其计算公式为：
Syx
y yˆ 2
n
［公式9—8］
实践中，在已知直线回归方程的情况下， 通常用下面的简便公式计算估计标准误差：
［例９—２］ 根据相关系数的简捷公式计算有：
r
n xy x y
n x2 x2 n y2 y2
7 218018580
0.978
7 5003 1852 7 954 802
再求回归直线方程：
yˆ a bx
b
n xy x y
n x2 x2
7 2180 18580 7 50031852

09第九章++++相关与回归

09第九章++++相关与回归

结果：
Pearson Correlation=0.978
皮尔逊相关系数= 0.978
在显著性水平为0.01的情况下，汽车销售量与时间 密切相关。
（2）回归分析

绘制散点图，确定回归方程的类型。 SPSS操作步骤： 1、点击Graphs Scatter 2、选择Simple，单击Define进入对话框； 3、将销售量y选入Y Axis，年次x选入X Axis； 4、单击OK。
（2）回归分析
汽车销售量散点图 （1985-2003）
300
200
100
y
0 0 10 20
年次
结论：可以配合直线模型。
（2）回归分析


拟合回归模型并进行预测分析。 SPSS操作步骤： 1、点击Analyze Regression Linear…； 2、将销售量y选入dependent，年次x选入independent； 3、单击Save进入保存对话框： 在Predicted Values中的Unstandardized前的 中打， 在Prediction Interval中的Individual前的 中打。
60 40 20 0 0 5 10 15
正相关图
负相关图

（二）相关系数 相关系数R：它是直线相关分析中用来衡量两个 变量之间相关程度的重要指标。
ˆ ˆ yiቤተ መጻሕፍቲ ባይዱ y yi yi R 1 2 2 yi y yi y
2
2
（1）相关系数的取值范围－1 ≤ R ≤ 1 （2）R=0，称零相关 （3）︱R︱=1，称完全相关 （4） 当0＜︱R︱＜1，称普通相关


简单直线回归模型

第九章 直线回归与相关分析

第九章 直线回归与相关分析

ˆ L1 = y − t0.05 s y = 19.0645 − 2.447 × 2.1603 = 13.7782 ˆ L2 = y + t0.05 s y = 19.0645 + 2.447 × 0.8559 = 24.3508
第三节 直线相关
一、相关系数和决定系数 如果两个变量间呈线性关系，又不需要由x来估计 如果两个变量间呈线性关系，又不需要由 来估计 y，只需了 和y相关以及相关的性质，可通过计算 相关以及相关的性质， ，只需了x和 相关以及相关的性质 x和y相关程度和性质的统计数－相关系数来进行 相关程度和性质的统计数－ 和 相关程度和性质的统计数 研究。 研究。 相关系数r为 相关系数 为： SP
ˆ L1 = y − t0.05 s y = 19.0645 − 2.447 × 0.8559 = 16.9701 ˆ ˆ L2 = y + t0.05 s y = 19.0645 + 2.447 × 0.8559 = 21.1589 ˆ
（四）单个y值的置信区间
单个y观测值的标准误为： 单个 观测值的标准误为： 观测值的标准误为
2
ˆ L1 = y − t a s y ˆ ˆ L2 = y + t a s y ˆ
根据例1，估计出黏虫孵化历期平均温度为 ℃ 根据例 ，估计出黏虫孵化历期平均温度为15℃时， 历期天数为多少（ 置信区间）。 历期天数为多少（取95%置信区间）。 置信区间
x = 15 df = n − 2 = 8 − 2 = 6 ˆ y = a + bx = 57.04 + (−2.5317) × 15 = 19.0645 sy = sy / x ˆ 1 ( x − x )2 1 (15 − 16.8375) 2 + = 1.9835 × + = 0.8559 n SS x 8 55.1788
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（3）0.361017
（4）10.059～12.4272
2.（1）y=-0.38591+2.2932x
（2）r=0.9874img ，所以回归方程是显著的。
（3）估计标准误为0.8627
（4）20.951～24.1414
第九章相关与回归
（一）判断题
1、正相关是指两个变量之间的变化方向都是止升的趋势，而负相关是指两个变量之间的变化方向都是下降的趋势。（）
2、负相关是指两个量之间的变化方向相反，即一个呈下降（上升）而另一个呈上升（下降）趋势。（）
3、函数关系是一种完全的相关关系。（）
4、已知两变量直线回归方程为:Y^=-45.25+1.61x，则可断定这两个变量之间一定存在正相关关系。（）
（二）单项选择题
1、确定现象之间是否存在相关关系，首先要对现象进行（）。
定性分析
定量分析
数值分析
定性与定量分析
2、相关关系与函数关系之间的联系体现在（）。
相关关系普遍存在，函数关系是相关关系的特例
函数关系普遍存在，相关关系是函数关系的特例
相关关系与函数关系是两种完全独立的现象
相关关系与函数关系没有区别
7、相关系数等于零，说明两变量之间_________;相关系数等于1，说明两变量之间_________;相关系数等于-1，说明两变量之间________。
8、最小平方法的中心思想，是通过数学方程，配合一条较为理想的趋势线，这条趋势线必须满足两个条件:一是_________;二是____________。
复相关
直线相关
曲线相关
负相关
6、直线相关分析的特点表现为（）。
两个变量之间的地位是对等关系
只能算出一个相关系数
相关系数有正负号
相关的两个变量必须都是随机变量
不反映任何自变量和因变量的关系
7、直线回归分析的特点表现为（）。
两个变量之间的地位不是对等关系
自变量是给定的非随机变量，因变量是随机变量
利用一个回归方程，两个变量之间可以互相推
单位产品成本与原材料消耗之间的关系
工业企业的劳动效率与生产单位产品的消耗时间之间的关系
在合理限度内，农业生产中施肥量与平均单位面积产量之间的关系
4、变量之间的不完全相关可以表现为（）。
零相关
正相关
负相关
曲线相关
相关系数为1
5、商品销售额与流通费用率，在一定条件下存在相关关系。这种相关关系属于（）。
单相关
3、相关系数的取值范围是（）。
-1<r<1
0≤r≤1
-1≤r≤1
|r|>1
4、当相关系数r=O时，说明（）。
现象之间完全无关
现象之间相关程度较小
现象之间完全相关
现象之间无直线相关
5、下列现象中，相关密切程度高的是（）。
商品销售量与商品销售额之间的相关系数为0.90
商品销售额与商业利润率之间的相关系数为0.60
ANSWER 9
（一）判断题
1.（×）
2.（√）
3.（√）
4.（√）
5.（×）
6.（×）
7.（×）
8.（×）
（二）单项选择题
1.①
2.①
3.③
4.④
5.④
6.②
7.②
8.④
（三）多项选择题
1.②③④⑤
2.①④⑤
3.③⑤
4.②③④
5.①④⑤
6.①②③④⑤
7.①②③④
8.①④
(四)填空题
1．相关关系
2．线性相关，非线性相关
相关系数相同
8、以下错误的概念是：在抽样调查中，抽样误差（）。
因变量的数列
因变量的总变差
因变量的回归变差
因变量的剩余变差
（三）多项选择题
1、相关关系与函数关系各有不同的特点，主要体现在（）。
函数关系是一种不严格的相互依存关系
函数关系可以用一个数学表达式精确表达
函数关系中各现象均为确定型现象
相关关系时现象之间具有随机因素影响的依存关系
5、回归分析和相关分析一样，所分析的两个变量郡一定是随机变量。（）
6、在其他条件不变的情况下，相关系数越大，估计标准误差就越大;反之，估计标准误差就越小。可见估计标准误差的大小与相关系数的大小是一致的。（）
7、相关系数的数值越大，说明相关程度越高;同理，相关系数的数值越小，说明相关程度越低。（）
8、不具有因果关系的两个变量之间，一定不存在相关关系。（）
直线回归方程中的回归系数有正负号
可以求出两个回归方程
8、估计标准误差是反映（）。
回归方程代表性的指标
自变量离散程度的指标
因变量数列离散程度的指标
因变量估计值可靠程度的指标
自变量可靠程度的大小
（四）填空题
1、_________是指现象之间存在着非严的、不确定的依存关系。
2、相关关系按相关形式的不同，分为_________和_________。
相关关系中现象之间仍然可以通过大量观察法来寻求其变化规律
2、下列现象属于相关关系的是（）。
家庭收入与支出的关系
圆的半径与圆的面积的关系
产品产量与单位成本的关系
施肥量与粮食单位面积产量的关系
机械化程度与农业人口的关系
3、下述关系中属于正相关的是（）。
工业产品产量与单位成木之间的关系
商业企业的劳动效率与流通费用之间的关系
商品销售额与流通费用率之间的相关系数为-0.85
商业利润率与流通费用率之间的相关系数为-0.95
6、回归方程^Y=a+bx中的回归系数b说明自变量变动一个单位时，因变量（）。
变动b个单位
平均变动Байду номын сангаас个单位
变动a+b个单位
变动1/b个单位
7、回归估计的估计标准误差的计量单位与（）。
自变量相同
因变量相同
自变量及因变量相同
3．正相关，负相关
4．完全相关，不完全相关，不相关
5．回归变差与总变差
6．精确
7．不存在线性相关，完全正线性相关，完全负线性相关
8．原数列的观测值与方程估计值的离差平方和最小，原数列的观测值与方程估计值的离差总和为零
(五)计算题
1.（1）Y=1.21333+0.59x
（2） ，所以回归方程是显著的。
2、某市10家百货公司人均销售额和利润率资料如下:
要求:
(1)判别该数列相关与回归的种类，配合适当的回归方程;
(2)计算相关系数，在显著性水平α=0.05时，对回归方程进行显著性检验;
(3)计算估计标准误差;
(4)当某百货公司人均销售额为10万元时，在95.45%的概率保证下，对其利润率作区间估计。
（五）计算题
1、某国营农场在试验田上研究耕种深度对水稻产量的关系，所得资料如下表。
要求:(1)试求水稻产量与耕种深度的直线回归方程;(2)计算相关系数，在显著性水平α=0.05时，对回归方程进行显著性检验;(劝计算估计标准误差;(4)若耕种深度为17厘米，在94.45%的概率保证下，试推算水稻产量的区间范围。
3、相关关系按相关方向的不同，分为_________和_________。
4、相关关系按相关程度的高低，分为_________和_________。
5、可决系数是_______之比，它是评价两个变量之间线性相关关系强弱的一个重要指标。
6、估计标准误差越小，则根据直线回归方程计算的估计值就越__________。