位错的能量

图⑴科肯道械应血钢斡?址贞的旷散聞⑹护散嗚中不同第子单相固 溶体中不仅 存在 热过冷，还 可能存在 成分过冷，当 G/R<mv 0（1-k 0）/Dk 0时，即存在成分过冷，平面生长被破坏。

当成分过冷 较小时，凸起部分不可能有较大的伸展，使界面形成胞状组织；若成分 过冷区较大，则界面可形成树枝状组织。

温度梯度较小不形成成分过冷 时，仍可保持平直状生长。

5.许多金属材料的塑性比陶瓷好，为什么？纯铁和纯铜的相比，谁的塑 性比较好，为什么？金属材料的塑性好，因为陶瓷烧结过程中具有很多先天性微裂 纹，在拉伸时，裂纹尖端会产生严重的应力集中，当裂纹达到临界尺寸 时就会失稳扩展而断裂；且构成陶瓷晶体相的主要为离子键和共价键， 共价键的饱和性和方向性使陶瓷的塑性较低。

（加上金属材料主要是金属键。

）纯铜的塑性好，因为纯铜是FCC 结构，纯铁是 BCC 结构，虽然BCC 的滑移系较多，但是滑移方向较 FCC 的少，且BCC 滑移面原子的密排程度较低，所以面心立方的塑性高于体心立方。

6.简述影响再结晶后晶粒长大的晶粒大小的因素7.1.温度，退火温度是影响晶粒长大的最主要因素；2.分散相微粒，分散相微粒阻碍晶界迁移，晶界受钉扎，长大速率减小；3.微量熔质或杂质，金属中固熔的微量熔质或杂质的存在能阻碍晶界的移动；4.晶粒间位向差，晶粒间位向差影响晶界活性从而影响晶粒长大速度；5.表面热蚀沟，热蚀沟的存在对晶界运动增加了一个约束力从而影响晶粒大小。

晶界特性1）晶粒的长大和晶界的平直化能减少晶界面积和晶界能，在适当的温度下是一个自发的过程；须原子扩散实现 2）晶界处原子排列不规则，常温下对位错的运动起阻碍作用，宏观上表现出提高强度和硬度；而高温下晶界由于起粘滞性，易使晶粒间滑动；3）晶界处有较多的缺陷，如空穴、位错等，具有较高的动能，原子扩散速度比晶内高； 4）固态相变时，由于晶界能量高且原子扩散容易，所以新相易在晶界处形核；5）由于成分偏析和内吸附现象，晶界容易富集杂质原子，晶界熔点低， 加热时易导致晶界先熔化；过热6）由于晶界能量较高、原子处于不稳定状态，以及晶界富集杂质原子的缘故，晶界腐蚀比晶内腐蚀速率快。

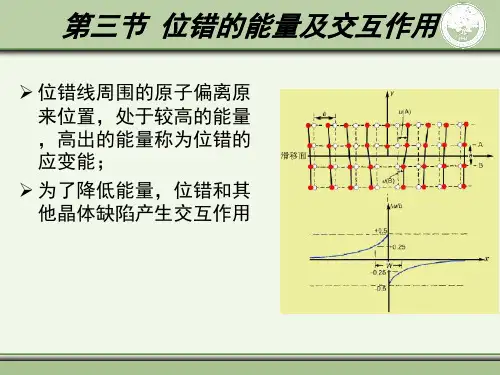
位错的应变能名词解释
位错是晶体中的一种缺陷，指的是晶体中原子排列的错位或错配。

位错可以通过晶体中的原子平面错位或原子排列的错配来描述。

位错的存在会导致晶体中的局部应变，而位错的应变能则是描述位错所引起的应变能量。

位错的应变能是指位错周围的晶体结构发生畸变时所需要的能量。

当位错发生时，晶体中的原子排列会发生变化，周围的晶格也会受到影响。

位错周围的晶体结构会发生弯曲、扭曲或拉伸等变形，这些变形所需要的能量就是位错的应变能。

位错的应变能可以通过位错的类型、位错的密度以及晶体的力学性质来计算或估算。

位错的类型包括边位错和螺位错，它们的应变能计算方法略有不同。

位错的密度是指单位体积内位错的数量，位错密度越高，位错的应变能也会相应增加。

晶体的力学性质包括弹性模量、剪切模量等，这些性质会影响位错的应变能。

位错的应变能在材料科学和固体力学中具有重要的意义。

它不仅可以用来解释晶体中的塑性变形和断裂行为，还可以用来研究材料的力学性能和变形机制。

位错的应变能也是材料强度和韧性的重要参数之一，它可以影响材料的力学性能和使用寿命。

总之，位错的应变能是描述位错所引起的应变能量的概念。

它是研究晶体中位错行为和材料力学性能的重要参数，对于理解材料的塑性变形和断裂行为具有重要意义。

位错反应的几何条件和能量条件位错反应的几何条件和能量条件在固体材料的位错运动和塑性变形中起着至关重要的作用。

位错是晶格中的一种缺陷，对于材料的力学性能和变形行为有着巨大影响。

了解位错反应的几何条件和能量条件，有助于深入理解材料的塑性变形机制。

一、位错反应的几何条件1. 位错的同型反应：同型反应是指位错线路的移动引发的位错线路的转化，即位错与位错间的关系保持不变。

同型反应可以使位错简化或者复杂化，也可以使位错线路变得更加密集或者稀疏。

同型反应的几何条件包括位错线路的接触、位错线路的夹角以及位错的移动方向等。

2. 位错的异型反应：异型反应是指位错线路的移动引发的位错线路的变化，即位错与位错间的关系发生变化。

异型反应通常会导致位错的相互吸引或排斥，从而影响位错的运动。

异型反应的几何条件包括位错线路的对齐程度、位错的类型以及位错的相对位置等。

3. 位错的滑移系统：滑移系统指的是能够支持位错运动的晶体平面和滑移方向的组合。

滑移系统的几何条件决定了位错在晶体中的运动方式和路径。

对于位错线路的移动，其平移方向必须与滑移方向相同，并且位错线路与滑移面要尽量垂直以减小阻力。

位错线路的移动沿滑移方向的绝对值必须大于或等于晶格常数的一半。

二、位错反应的能量条件1. 弹势能差异：位错的移动需要消耗或释放能量，其中包括位错线路的伸展和压缩产生的位错能以及晶格原子的重新排列所涉及的点阵能。

位错反应的能量条件要求位错运动的总能量变化为负值，即能量减小。

2. 切应力差异：位错移动时，晶体中的切应力会沿滑移系统产生梯度。

位错的移动速度正比于这一切应力梯度。

因此，能量条件要求滑移方向上的切应力梯度足够大，以推动位错的移动。

3. 点阵潜能差异：位错移动过程中，晶格中的原子需要重新排列以适应位错的新位置。

点阵潜能是指晶格中原子位置的稳定状态。

能量条件要求位错移动引起的点阵潜能变化足够小，以维持晶格结构的稳定。

综上所述，位错反应的几何条件和能量条件在位错运动和塑性变形中起着重要作用。

位错能量计算公式位错能量是指晶体中位错线所储存的能量，其大小决定了位错的稳定性和晶体的机械性能。

位错能量的计算公式可通过弹性理论推导得到。

在弹性理论中，晶体中的位错可看作一种线状缺陷，其引起的应变场可以用线弹性理论来描述。

对于螺旋位错和较长的位错线，它们的位错能量主要由弹性畸变能和位错线周围的弹性应力张力贡献。

位错线周围的弹性应力能表达式为：$$E_s = \frac{1}{2}b\sigma s$$其中，$E_s$是位错线的弹性应力能，$b$是位错的Burgers矢量大小，$\sigma$是外界应力，$s$是位错线的长度。

位错线引起的弹性畸变能表达式为：$$E_d = \frac{1}{2}\mu b^2\ln\left(\frac{r}{r_0}\right)$$其中，$E_d$是位错线的弹性畸变能，$\mu$是材料的剪切模量，$r$是位错线的半径，$r_0$是材料的截断半径。

位错能量$E_t$的总和即为弹性能量和畸变能量之和，即：$$E_t = E_s + E_d = \frac{1}{2}b\sigma s + \frac{1}{2}\mub^2\ln\left(\frac{r}{r_0}\right)$$当位错线的长度很长时，即$s$趋近于无穷大时，弹性应力能会远大于弹性畸变能，因此位错能量主要由位错线周围的弹性应力能决定。

在某些特殊情况下，位错线周围的弹性应力能也可忽略不计，如边界位错、近排斥位错等。

需要注意的是，上述位错能量的计算公式是在弹性理论假设下推导得到的，且仅适用于线性弹性材料。

在非线性和脆性材料中，由于位错特性的变化，计算位错能量可能需要采用其他方法。

位错能量的计算对于研究位错的稳定性、位错运动行为以及晶体的力学性能具有重要意义，可以为材料的设计和性能优化提供理论基础。

位错能量的算法位错能量的算法是一种用于计算材料中位错能量的方法。

位错是材料中晶体结构中的一种缺陷，它是晶体中原子排列顺序的偏离。

位错能量是位错的形成和移动所需的能量，它对材料的力学性质和变形行为起着重要作用。

了解和计算位错能量可以帮助人们更好地理解材料的力学行为和变形机制，对材料设计和性能改进具有重要意义。

位错能量的计算可以通过原子尺度模拟方法进行。

通常，人们使用分子动力学模拟或离子力学模拟来模拟材料中的位错和位错运动。

这些模拟方法可以根据原子间相互作用力场和位错的移动规律，计算出位错形成和移动所需的能量。

具体而言，分子动力学模拟通过求解牛顿运动方程，模拟材料中原子的运动和相互作用，从而得到位错的能量。

离子力学模拟则是通过构建原子间相互作用势能函数，通过优化位错的结构和能量，来计算位错能量。

在位错能量的计算中，需要考虑位错的类型和形态。

不同类型的位错具有不同的结构和能量，因此计算方法也有所不同。

常见的位错类型包括位错线、位错环和位错面。

位错线是晶体中原子排列顺序的偏移线，位错环是位错线的闭合形式，位错面则是晶体中原子排列顺序的偏移面。

这些位错类型的能量计算方法可以根据其结构特征进行选择和优化。

位错能量的计算结果可以用来预测材料的变形行为和力学性能。

位错能量越高，材料的抗变形性能越好；位错能量越低，材料的变形性能越差。

因此，通过计算位错能量，人们可以评估材料的变形能力和强度，为材料设计和应用提供指导和参考。

除了计算位错能量，人们还可以通过实验方法来测量位错能量。

常用的实验方法包括透射电子显微镜和原子力显微镜等。

透射电子显微镜可以通过电子束的透射和散射来观察和测量材料中的位错结构和能量。

原子力显微镜则是通过探针和样品之间的相互作用力，来测量位错的结构和能量。

实验方法可以与计算方法相互验证，提高位错能量的计算和测量的准确性和可靠性。

位错能量的算法是一种用于计算材料中位错能量的方法。

通过计算位错能量，可以帮助人们更好地理解材料的力学行为和变形机制，为材料设计和性能改进提供指导和参考。

位错能量计算公式
首先，我们需要了解位错是什么。

位错是晶体中的一个结构缺陷，它
是由于原子在晶体内部的错位或滑移而引起的。

位错会导致晶体局部应力
的集中，因此会对材料的性质产生重要影响。

位错线的长度可以通过以下公式计算：
L=N×l
其中，L表示位错线的长度，N是位错的数量，l是单个位错线的平
均长度。

位错的线密度可以通过以下公式计算：
λ=N/A
其中，N是位错的数量，A是晶体截面的面积。

E=μ×b^2×λ×L
其中，E 是位错能量，μ 是材料的剪模量，b 是位错的Burgers矢量。

需要注意的是，位错能量的计算是一个估算值，它假设了位错线为直线，并且忽略了其他形变的能量贡献。

位错能量的计算对于了解材料的塑性变形行为和材料性能具有重要意义。

通过计算位错能量，我们可以评估材料的强度、韧性和可塑性等特性。

这些信息对于材料的设计和加工过程中的材料选择非常关键。

另外，位错能量的计算还可以用于预测位错的移动和位错的消失。

位
错的移动或消失会导致材料的塑性变形或回复。

因此，通过计算位错能量，我们可以预测材料的塑性形变和回复过程。

综上所述，位错能量的计算公式是通过位错线的长度和位错的线密度
来确定的。

这个公式提供了估算材料位错能量的方法，对于了解材料的塑
性变形行为和材料性能具有重要意义。

位错能量计算公式位错能量是描述晶体中位错形成和运动所需的能量大小的物理量。

位错是晶体中由于晶格缺陷引起的一个原子位于虽然理论上它该处于的位置附近但不精确的位置上。

位错能量的计算涉及到很多细节和复杂的数学模型，下面将简要介绍一种常用的位错能量计算公式。

为了计算位错能量，首先需要根据晶格结构的类型和位错的类型选择适当的位错模型。

常见的位错包括线性位错、螺旋位错、点阵位错等。

在这里，我们以线性位错为例进行讨论。

对于线性位错，可以用一个面向位错线的面来表示位错的位置。

我们假设这个面与位错线之间的距离为γ，单位为m。

位错能量可以通过以下公式进行计算：E = μb ln (R / r)其中，E表示位错能量，μ为位错线的位错系数，b为布尔矢量，R 为边长为R的正方形窗口，r为边长为r的小正方形窗口。

位错能量是单位面积上位错的能量密度，单位为焦耳/平方米(J/m^2)。

位错线的位错系数μ是一个用于描述位错能量的材料特性常数，它与材料的弹性性质和位错的特征有关。

位错系数可以通过实验测量或者通过计算得到。

布尔矢量b表示位错线的布尔矢量，它是位错锁定时，位错线沿着刃位错面的方向。

布尔矢量是一个有向的矢量，用来表示位错线的方向和方向性。

边长为R的正方形窗口内部包含一个线性位错。

边长为r的小正方形窗口是一个用于计算位错能量的局部窗口，它的位置被布尔矢量b确定。

这个公式的物理意义是位错能量与位错线的长度有关，位错线的长度越长，位错能量越大。

窗口的选择可以影响到位错能量的计算结果，窗口的大小对位错能量的计算也有一定影响。

通常情况下，位错能量的计算是对无穷大晶体中的位错进行近似计算，因此选取一个较大的窗口能够更好地描述位错的能量分布。

需要注意的是，上述公式只适用于线性位错，并且对于特定的位错类型和晶体类型，可能需要使用更为复杂的位错能量计算模型。

此外，该公式还是一种近似计算方法，无法考虑到晶体的真实形变情况和体系的初始结构。

因此，位错能量的具体计算需要综合考虑实际情况和所需精度，辅以实验数据和模拟计算手段进行。