多元非线性回归的动力学分析

论文题目：多自由度非线性机械系统的全局分叉和混沌动力学研究作者简介：姚明辉，女，1971年11月出生，2002年09月师从于北京工业大学张伟教授，于2006年06月获博士学位。

中文摘要在机械系统中，有许多问题的数学模型和动力学方程都可用高维非线性系统来描述，对于高维非线性动力系统来说，其研究难度比低维非线性动力系统要大得多，不仅理论方法上有困难，几何描述和数值计算都有困难。

目前研究高维非线性系统的全局分叉和混沌动力学的理论方法还不是很多，国际上处于发展阶段，国内尚处于起步阶段，因此发展处理高维非线性动力学系统的理论研究方法是非常重要和迫切的。

在高维非线性动力学的全局分叉和混沌动力学问题中，除了单脉冲混沌运动外，还有多脉冲混沌运动，目前研究多脉冲混沌运动的解析方法主要有两种，即广义Melnikov方法和能量相位法。

本论文改进和推广了Kovacic、Haller和Wiggins等人提出的广义Melnikov方法和能量相位法，利用这两种全局摄动解析方法首次研究了非线性非平面运动悬臂梁、粘弹性传动带非平面运动和面内载荷和横向载荷联合作用下四边简支薄板的多脉冲轨道和Shilnikov型混沌运动。

理论研究发现这些系统存在多脉冲混沌运动；利用数值方法模拟、验证了理论分析的结果。

论文的研究内容及取得的创新性成果有以下几个方面。

(1) 综述了高维非线性系统的分叉和混沌动力学的国内外研究现状；简要介绍了Melnikov 方法的发展，高维Melnikov方法的应用，以及广义Melnikov方法的提出和建立；概括了能量相位法的国内外主要研究进展；介绍了研究高维非线性系统的全局分叉和混沌运动的其它方法。

总结了能量相位法和广义Melnikov方法的研究进展、成果及存在的不足和有待深入研究的问题。

(2) 介绍了由Haller和Wiggins提出的能量相位法；以及由Kovacic等人提出的广义Melnikov方法。

由于能量相位法和广义Melnikov方法提出和发展的时间较短，而且一直是独立的两种解析方法，在本论文中，首次详细地研究了两种全局摄动解析方法的区别和联系。

第一章非线性动力学分析方法(6学时）一、教学目标1、理解动力系统、相空间、稳定性得概念;2、掌握线性稳定性得分析方法;ﻩ3、掌握奇点得分类及判别条件;ﻩ4、理解结构稳定性及分支现象;5、能分析简单动力系统得奇点类型及分支现象.二、教学重点1、线性稳定性得分析方法；ﻩ２、奇点得判别。

三、教学难点ﻩ线性稳定性得分析方法四、教学方法讲授并适当运用课件辅助教学五、教学建议ﻩ学习本章内容之前，学生要复习常微分方程得内容。

六、教学过程本章只介绍一些非常初步得动力学分析方法，但这些方法在应用上就是十分有效得。

1、1相空间与稳定性ﻩ一、动力系统在物理学中,首先根据我们面对要解决得问题划定系统，即系统由哪些要素组成。

再根据研究对象与研究目得，按一定原则从众多得要素中选出最本质要素作为状态变量。

然后再根据一些原理或定律建立控制这些状态变量得微分方程,这些微分方程构成得方程组通常称为动力系统。

研究这些微分方程得解及其稳定性以及其她性质得学问称为动力学.假定一个系统由n个状态变量，,…来描述。

有时,每个状态变量不但就是时间t得函数而且也就是空间位置得函数。

如果状态变量与时空变量都有关,那么控制它们变化得方程组称为偏微分方程组.这里假定状态变量只与时间t有关，即X＝X i（t),则控制它们ｉ得方程组为常微分方程组。

ﻩﻩﻩﻩﻩ（１。

1．1)…其中代表某一控制参数.对于较复杂得问题来说，(i＝l，2，…n)一般就是得非线性函数，这时方程（1．1.1）就称为非线性动力系统。

由于不明显地依赖时间ｔ，故称方程组（1。

1．１)为自治动力系统。

若明显地依赖时间t，则称方程组（1、１、1）为非自治动力系统.非自治动力系统可化为自治动力系统.对于非自治动力系统，总可以化成自治动力系统。

例如：令,,上式化为上式则就是一个三维自治动力系统。

又如:令,则化为它就就是三微自治动力系统、对于常微分方程来说,只要给定初始条件方程就能求解。

对于偏微分方程,不但要给定初始条件而且还要给定边界条件方程才能求解。

第一章非线性动力学分析方法（6学时）一、教学目标1、理解动力系统、相空间、稳定性的概念；2、掌握线性稳定性的分析方法；3、掌握奇点的分类及判别条件；4、理解结构稳定性及分支现象；5、能分析简单动力系统的奇点类型及分支现象。

二、教学重点1、线性稳定性的分析方法；2、奇点的判别。

三、教学难点线性稳定性的分析方法四、教学方法讲授并适当运用课件辅助教学五、教学建议学习本章内容之前，学生要复习常微分方程的内容。

六、教学过程本章只介绍一些非常初步的动力学分析方法，但这些方法在应用上是十分有效的。

相空间和稳定性一、动力系统在物理学中，首先根据我们面对要解决的问题划定系统，即系统由哪些要素组成。

再根据研究对象和研究目的，按一定原则从众多的要素中选出最本质要素作为状态变量。

然后再根据一些原理或定律建立控制这些状态变量的微分方程，这些微分方程构成的方程组通常称为动力系统。

研究这些微分方程的解及其稳定性以及其他性质的学问称为动力学。

假定一个系统由n 个状态变量1x ，2x ，…n x 来描述。

有时，每个状态变量不但是时间t 的函数而且也是空间位置r的函数。

如果状态变量与时空变量都有关，那么控制它们变化的方程组称为偏微分方程组。

这里假定状态变量只与时间t 有关，即X i ＝X i (t)，则控制它们的方程组为常微分方程组。

),,,(2111n X X X f dtdX ),,,(2122n X X X f dtdX (1.1.1)…),,,(21n n nX X X f dtdX 其中 代表某一控制参数。

对于较复杂的问题来说，i f (i ＝l ，2，…n)一般是 i X 的非线性函数，这时方程(1.1.1)就称为非线性动力系统。

由于 i f 不明显地依赖时间t ，故称方程组(1.1.1)为自治动力系统。

若 i f 明显地依赖时间t ，则称方程组为非自治动力系统。

非自治动力系统可化为自治动力系统。

对于非自治动力系统，总可以化成自治动力系统。

多元非线性回归分析是一种多元非线性回归模型。

传统的求解多元非线性回归模型的方法仍然是将其转化为标准的线性多元回归模型。

一些非线性回归模型通过适当的数学变换可以得到线性化的表达式，而对于其他非线性回归模型，仅仅通过变量变换是没有帮助的。

属于前者的非线性回归模型通常称为内在线性回归，而后者称为内在非线性回归。

补充资料：线性回归线性回归是利用数理统计中的回归分析来确定两个或多个变量之间的定量关系的一种统计分析方法。

表达式形式为y=w'x+e，e为误差的正态分布，平均值为0。

在回归分析中，只包含一个自变量和一个因变量，二者之间的关系可用直线近似。

这种回归分析称为单变量线性回归分析。

如果回归分析包含两个或两个以上的自变量，且因变量与自变量之间是线性关系，则称为多元线性回归分析。

在统计学中，线性回归是一种回归分析，它使用称为线性回归方程的最小二乘函数来建模一个或多个自变量和因变量之间的关系。

这个函数是一个或多个模型参数的线性组合，称为回归系数。

只有一个自变量的情况称为简单回归，有多个自变量的情况称为多元回归。

（这应该再次通过由多个因变量而不是单个标量变量预测的多元线性回归来区分。

）在线性回归中，数据由线性预测函数建模，未知模型参数由数据估计。

这些模型称为线性模型。

最常用的线性回归模型是仿射函数，其中给定值x的条件平均值为x。

在不太常见的情况下，线性回归模型可以是Y或其他分位数条件分布的中值。

与所有形式的回归分析一样，线性回归侧重于给定x值的Y的条件概率分布，而不是x和Y的联合概率分布（在多元分析领域）。

线性回归是第一个经过严格研究并在实际应用中得到广泛应用的回归分析方法。

这是因为与未知参数线性相关的模型比与位置参数非线性相关的模型更容易拟合，并且更容易确定结果估计值的统计特性。

线性回归模型通常采用最小二乘法进行拟合，但也可以采用其他方法进行拟合，如最小化其他规范中的“拟合缺陷”（如最小绝对误差回归）或最小化桥梁回归的惩罚函数最小二乘法，最小二乘法可用于拟合这些非线性模型。

多元非线性回归
第一，我们事前并不知道该用什么样的非线性模型去拟合数据？
第二，即使我们知道了需要的非线性模型，但是里面的参数设置，要靠自己专业和经验来设置，没错——靠经验！问题是我们（除了一些大牛）是没经验的。

为了降低难度，结合今天设计学院一位学姐问的问题，赋文君利用别人的模型，去尝试的复现别人的结果，顺便介绍非线性回归分析的基本步骤！
问题背景：
为了研究建筑材料的抗压强度，某个硕士研究生设计了一个实验，实验材料：石灰，细砂，水玻璃；实验器材：若见先进设备，其实我也没用那些工程机械。

通过一些列物理等方面的参数分析检验，得出了一些实验结果，在利用回归模型分析和相关性分析深入了解石灰，水玻璃和细砂，抗压强度四者之间的数量关系和相关程度。

抗压强度是因变量，石灰，水玻璃和细砂是自变量。

3.非线性回归分析步骤
将数据导入或者录入spss中，接着就可以对其进行回归分析了。

按钮点击顺序，找到“分析”——“回归”——“非线性”：
为了便于录入模型和分析，把上面的模型分解开：变量x的前面系数（即参数）分别设定为a，b，c，其中a1表示石灰的系数，a2表示水玻璃的系数，a3表示细砂的系数，b1表示石灰*水玻璃的系数，b2表示石灰*细砂的系数，b3表示水玻璃*细砂的系数，c1 c2 c3分别表示，石灰，水玻璃和细砂平方的系数，d是常数量。

非线性动力学方法
非线性动力学方法是一种用于研究复杂系统的数学和计算方法。

它可以描述非线性系统中随时间演化的行为，并揭示系统的动力学性质。

非线性动力学方法包括以下几个方面:
1. 非线性微分方程: 非线性动力学方法主要研究非线性微分方程的解，这些方程描述了系统中各个变量之间的相互作用关系。

2. 相空间分析: 相空间是描述系统状态的空间，非线性动力学方法通过绘制相轨迹来分析系统在相空间中的运动轨迹，以揭示系统的稳定性、周期性和混沌行为等。

3. 分岔理论: 分岔理论研究系统在参数变化过程中出现的稳定性变化和态势的转变。

通过分析系统在不同参数值下的解的性质，可以确定系统的分岔点和分岔类型。

4. 混沌分析: 非线性动力学方法还研究系统中的混沌行为。

混沌是一种高度不确定和敏感依赖于初始条件的动力学行为，通过混沌分析方法，可以确定系统的Lyapunov指数和分岔图等。

非线性动力学方法在物理学、生物学、化学、经济学等众多领域具有重要应用，它可以揭示复杂系统的内在规律和行为特征，帮助人们更好地理解和预测自然和
人类活动中的各种现象。

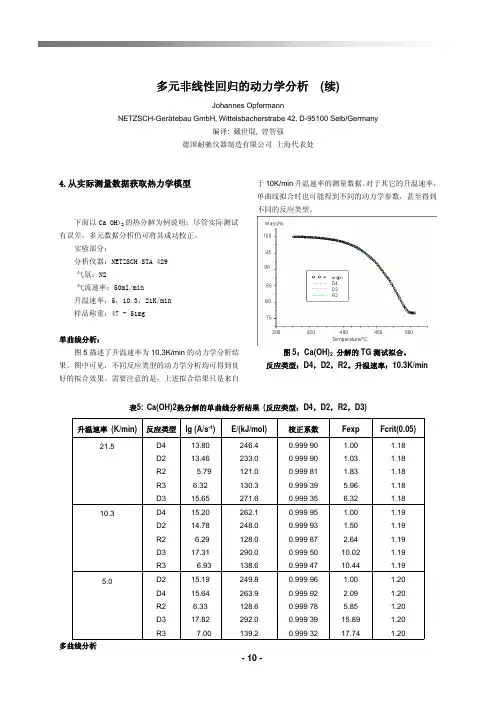
多元非线性回归的动力学分析(续)Johannes OpfermannNETZSCH-Gerätebau GmbH,Wittelsbacherstrabe42,D-95100Selb/Germany编译:戴世琨,曾智强德国耐驰仪器制造有限公司上海代表处4.从实际测量数据获取热力学模型下面以Ca(OH)2的热分解为例说明：尽管实际测试有误差，多元数据分析仍可将其成功校正。

实验部分：分析仪器：NETZSCH STA429气氛：N2气流速率：50ml/min升温速率：5，10.3，21K/min样品称重：47-51mg单曲线分析：图5描述了升温速率为10.3K/min的动力学分析结果。

图中可见，不同反应类型的动力学分析均可得到良好的拟合效果。

需要注意的是，上述拟合结果只是来自于10K/min升温速率的测量数据。

对于其它的升温速率，单曲线拟合时也可能得到不同的动力学参数，甚至得到不同的反应类型。

图5：Ca(OH)2分解的TG测试拟合。

反应类型：D4，D2，R2。

升温速率：10.3K/min表5:Ca(OH)2热分解的单曲线分析结果(反应类型：D4，D2，R2，D3)升温速率(K/min)反应类型lg(A/s-1)E/(kJ/mol)校正系数Fexp Fcrit(0.05)21.5D4D2R2R3D313.8013.465.796.3215.65246.4233.0121.0130.3271.60.999900.999900.999810.999390.999351.001.031.835.966.321.181.181.181.181.1810.3D4D2R2D3R315.2014.786.2917.316.93262.1248.0128.0290.0138.60.999950.999930.999870.999500.999471.001.502.6410.0210.441.191.191.191.191.195.0D2D4R2D3R315.1915.646.3317.827.00249.8263.9128.6292.0139.20.999960.999920.999780.999390.999321.002.095.8515.8917.741.201.201.201.201.20多曲线分析由此，我们有必要将多种不同升温速率的曲线综合分析。

A题思路之一——多元非线性回归分析本题求解关键为建立工资与其他7个因素之间的关系模型，可以考虑采用回归分析法，也可以考虑其他方法；以下仅以回归分析法过程为例给出分析思路，仅供参考：注意：根据下述结果发现本问题应该考虑为多元非线性回归，因此请大家优先挑出使用非线性回归模型的论文，其余酌情考虑。

1.数据预处理1）为数据分析方便，应该考虑名义变量或有序变量的量化处理（编码），如可以考虑如下编码方案（含符号约定）：y－日平均工资的对数，便于回归分析；作为因变量。

11~ 0~x⎧=⎨⎩男性女性；2x：工龄31~ 0~x⎧=⎨⎩男性或单身女性已婚女性；40x ⎧⎪⎪⎨⎪⎪⎩～本科1～硕士（受教育状况）＝2～博士3～博士后；51~ ()0~x⎧=⎨⎩管理岗位工作部门性质技术岗位；61~ 0~x⎧=⎨⎩受过培训（培训情况）未受过培训；71~ 0~x⎧=⎨⎩两年以上未从事一线工作（一线工作情况）其它情况2）分别作出y与各自变量之间的散点图，发现与x2非线性关系较为明显（下图所示），所以应该考虑为非线性模型，data=xlsread('Adata.xls',2);y=data(:,1);x=data(:,2:8);plot(x(:,2),y,'r*')title('lny vs x2')0501001502002503003504004505003.43.63.844.24.44.64.85lny vs x23）相关性分析data=xlsread('Adata.xls',2);y=data(:,1);x=data(:,2:8);s=corrcoef(data);xlswrite('coef.xls',s)lny X1 X2 X3 X4 X5 X6 X71 0.266995 0.775291 0.286135 0.505526 0.277929 0.199178 0.489786 0.266995 1 0.160389 0.679446 0.312348 0.417621 -0.10498 0.316025 0.775291 0.160389 1 0.226096 0.103146 0.098854 0.151146 0.156321 0.286135 0.679446 0.226096 1 0.266937 0.213363 -0.27966 0.229535 0.505526 0.312348 0.103146 0.266937 1 0.412745 0.219762 0.855236 0.277929 0.417621 0.098854 0.213363 0.412745 1 -0.05307 0.423355 0.199178 -0.10498 0.151146 -0.27966 0.219762 -0.05307 1 0.255665 0.489786 0.316025 0.156321 0.229535 0.855236 0.423355 0.255665 1相关系数表也提示y 仅与x2,x4关系密切.与婚姻状况x1,x3关系不明显.2、建模及简易求解（第1、3问）以下考虑分别用多元线性回归模型、线性逐步回归模型、非线性模型分析，从中选择相对最优的模型。

非线性回归分析简介非线性回归分析是一种用于建立非线性关系模型的统计方法。

与线性回归不同，非线性回归可以更好地拟合非线性数据，提供更准确的预测结果。

在许多实际问题中，数据往往呈现出非线性的趋势，因此非线性回归分析在实际应用中具有广泛的应用价值。

一、非线性回归模型的基本形式非线性回归模型的基本形式可以表示为：y = f(x, β) + ε其中，y是因变量，x是自变量，β是模型参数，f(x, β)是非线性函数，ε是误差项。

非线性函数可以是任意形式的函数，如指数函数、对数函数、幂函数等。

二、非线性回归模型的参数估计与线性回归不同，非线性回归模型的参数估计不能直接使用最小二乘法。

常见的非线性回归参数估计方法有以下几种：1. 非线性最小二乘法（NLS）非线性最小二乘法是一种常用的参数估计方法，它通过最小化残差平方和来估计模型参数。

具体而言，通过迭代的方式不断调整参数，使得残差平方和最小化。

2. 非线性广义最小二乘法（GNLS）非线性广义最小二乘法是对非线性最小二乘法的改进，它在最小化残差平方和的同时，还考虑了误差项的方差结构。

通过引入权重矩阵，可以更好地处理异方差性的数据。

3. 非线性加权最小二乘法（WNLS）非线性加权最小二乘法是对非线性广义最小二乘法的进一步改进，它通过引入加权矩阵，对不同数据点赋予不同的权重。

可以根据数据的特点，调整权重矩阵，提高模型的拟合效果。

三、非线性回归模型的评估指标在进行非线性回归分析时，需要对模型进行评估，以确定模型的拟合效果。

常见的评估指标有以下几种：1. 残差分析残差分析是一种常用的评估方法，通过分析残差的分布情况，判断模型是否符合数据的分布特征。

如果残差呈现随机分布，说明模型拟合效果较好；如果残差呈现一定的规律性，说明模型存在一定的问题。

2. 决定系数（R-squared）决定系数是衡量模型拟合优度的指标，其取值范围为0到1。

决定系数越接近1，说明模型对数据的解释能力越强；决定系数越接近0，说明模型对数据的解释能力越弱。

A题思路之一——多元非线性回归分析本题求解关键为建立工资与其他7个因素之间的关系模型，可以考虑采用回归分析法，也可以考虑其他方法；以下仅以回归分析法过程为例给出分析思路，仅供参考：注意：根据下述结果发现本问题应该考虑为多元非线性回归，因此请大家优先挑出使用非线性回归模型的论文，其余酌情考虑。

1.数据预处理1）为数据分析方便，应该考虑名义变量或有序变量的量化处理（编码），如可以考虑如下编码方案（含符号约定）：y－日平均工资的对数，便于回归分析；作为因变量。

11~ 0~x⎧=⎨⎩男性女性；2x：工龄31~ 0~x⎧=⎨⎩男性或单身女性已婚女性；40x ⎧⎪⎪⎨⎪⎪⎩～本科1～硕士（受教育状况）＝2～博士3～博士后；51~ ()0~x⎧=⎨⎩管理岗位工作部门性质技术岗位；61~ 0~x⎧=⎨⎩受过培训（培训情况）未受过培训；71~ 0~x⎧=⎨⎩两年以上未从事一线工作（一线工作情况）其它情况2）分别作出y与各自变量之间的散点图，发现与x2非线性关系较为明显（下图所示），所以应该考虑为非线性模型，data=xlsread('Adata.xls',2);y=data(:,1);x=data(:,2:8);plot(x(:,2),y,'r*')title('lny vs x2')0501001502002503003504004505003.43.63.844.24.44.64.85lny vs x23）相关性分析data=xlsread('Adata.xls',2); y=data(:,1); x=data(:,2:8); s=corrcoef(data); xlswrite('coef.xls',s)lny X1 X2 X3 X4X5 X6 X7 10.2669950.775291 0.286135 0.505526 0.277929 0.199178 0.489786 0.266995 10.1603890.679446 0.312348 0.417621 -0.10498 0.316025 0.775291 0.160389 10.2260960.103146 0.098854 0.151146 0.156321 0.286135 0.679446 0.226096 10.2669370.213363 -0.27966 0.229535 0.505526 0.312348 0.103146 0.266937 10.4127450.219762 0.855236 0.277929 0.417621 0.098854 0.213363 0.412745 1-0.053070.423355 0.199178 -0.10498 0.151146 -0.27966 0.219762 -0.05307 10.2556650.489786 0.316025 0.156321 0.229535 0.855236 0.423355 0.255665 1相关系数表也提示y 仅与x2,x4关系密切.与婚姻状况x1,x3关系不明显.2、建模及简易求解（第1、3问）以下考虑分别用多元线性回归模型、线性逐步回归模型、非线性模型分析，从中选择相对最优的模型。

实验三多元线性回归模型和非线性回归模型【实验目的】掌握建立多元线性回归模型和非线性回归模型，以及比较、筛选模型的方法。

【实验内容】建立我国国有独立核算工业企业生产函数。

根据生产函数理论，生产函数的基本形式为：(,,,)Y f t L Kε=。

其中，L、K 分别为生产过程中投入的劳动与资金，时间变量t反映技术进步的影响。

表3.1列出了我国1978-1994年期间国有独立核算工业企业的有关统计资料；其中产出Y为工业总产值（可比价），L、K分别为年末职工人数和固定资产净值（可比价）。

表3.1 我国国有独立核算工业企业统计资料年份时间t 工业总产值Y（亿元）职工人数L（万人）固定资产K（亿元）1978 1 3289.18 3139 2225.70 1979 2 3581.26 3208 2376.34 1980 3 3782.17 3334 2522.81 1981 4 3877.86 3488 2700.90 1982 5 4151.25 3582 2902.19 1983 6 4541.05 3632 3141.76 1984 7 4946.11 3669 3350.95 1985 8 5586.14 3815 3835.79 1986 9 5931.36 3955 4302.25 1987 10 6601.60 4086 4786.05 1988 11 7434.06 4229 5251.90 1989 12 7721.01 4273 5808.71 1990 13 7949.55 4364 6365.79 1991 14 8634.80 4472 7071.35 1992 15 9705.52 4521 7757.25 1993 16 10261.65 4498 8628.77 1994 17 10928.66 4545 9374.34【实验步骤】一、建立多元线性回归模型（一）建立包括时间变量的三元线性回归模型；在命令窗口依次键入以下命令即可：⒈建立工作文件：CREATE A 1978 1994⒉输入统计资料：DATA Y L K⒊生成时间变量t：GENR T=@TREND(77)⒋建立回归模型：LS Y C T L K则生产函数的估计结果及有关信息如图3-1所示。

非线性动力学的研究与应用动力学是描述物理系统运动状态的数学分支，是现代科学中重要的基础学科之一。

而线性动力学是指系统受到的外界激励与其响应之间呈现线性关系的情况。

然而，当系统受到的激励越来越复杂，不再满足线性关系时，就需要非线性动力学来描述。

非线性动力学是指系统的响应与激励之间呈现非线性关系，其中包含的非线性现象十分丰富，如混沌、分叉、周期等。

本文将介绍非线性动力学的基本概念、研究方法以及应用领域。

一、基本概念1. 混沌混沌是指一种看似无规律的运动状态，但实际上却具有自组织、自复制、自相似等特点。

混沌现象最早是在研究天体运动的过程中被发现的。

随着科技的发展，混沌现象在流体力学、生物学、金融学、电子电路等领域也得到了广泛应用。

2. 分岔分岔是指当控制参数发生微小变化时，系统从稳定状态跃迁到不同的稳定状态的现象。

这种现象在自然界中也很常见，如树枝的生长、音乐乐器的音高变化等都包含分岔现象。

3. 周期周期是指在某个时间段内，系统的状态会反复出现相同的模式。

周期现象在自然界的很多地方都可以观察到，如心脏的跳动、季节的交替、行星的运动等都包含周期性现象。

二、研究方法非线性动力学是一种理论研究工具，其研究方法也非常多样化。

现代非线性动力学的研究方法主要包括数学建模、数值计算、实验观测和理论分析等。

1. 数学建模数学建模是指将实际问题抽象为数学模型，以求解问题的方法。

非线性动力学的数学建模可以使用微分方程、差分方程和离散映射等方法，也可以用图论、复杂网络等方法来描述复杂的系统。

2. 数值计算非线性动力学的数值计算是指利用计算机进行模拟，以便更准确的预测系统的行为。

计算实验室中使用的方法包括常微分方程求解器、混沌系统的仿真和计算图像处理等技术。

3. 实验观测非线性动力学的实验观测是指通过实验观察来获取系统的信息。

实验容易造成不确定性，因此需要专业领域的实验室来进行数据分析、处理和解释。

4. 理论分析非线性动力学的理论分析是指使用数学工具来推导模型的数学性质，如稳定性、周期行为等。

多元非线性回归分析是具有两个以上变量的非线性回归模型。

解决多元非线性回归模型的传统方法仍然是找到一种将其转换为标准线性多元回归模型的方法。

一些非线性回归模型可以通过适当的数学变换来获得其线性化表达式，但是对于其他非线性回归模型，仅变量变换没有帮助。

属于前一种情况的非线性回归模型通常称为内在线性回归，而后者称为内在非线性回归。

补充数据：线性回归线性回归是一种统计分析方法，在数学统计中使用回归分析来确定两个或多个变量之间的定量关系。

表达式形式为y = w'x + e，E为误差的正态分布，平均值为0。

在回归分析中，仅包含一个自变量和一个因变量，并且两者之间的关系可以近似地由一条直线表示。

这种回归分析称为单变量线性回归分析。

如果回归分析包括两个或多个自变量，并且因变量和自变量之间的关系是线性的，则称为多元线性回归分析。

在统计中，线性回归是一种回归分析，它使用称为线性回归方程的最小二乘函数对一个或多个自变量与因变量之间的关系进行建模。

此函数是一个或多个称为回归系数的模型参数的线性组合。

仅一个自变量的情况称为简单回归，而一个以上自变量的情况称为多重回归。

（这又应通过多个因变量而不是单个标量变量预测的多个线性回归来区分。

）在线性回归中，数据是通过线性预测函数建模的，未知模型参数是通过数据估算的。

这些模型称为线性模型。

最常用的线性回归建模是给定x值的Y的条件平均值是X的仿射函数。

在不太常见的情况下，线性回归模型可以是Y的条件分布的中位数或其他分位数像所有形式的回归分析一样，线性回归关注于给定x值的Y的条件概率分布，而不是X和Y的联合概率分布（在多元变量领域）分析）。

线性回归是经过严格研究并在实际应用中广泛使用的第一类回归分析。

这是因为与未知参数线性相关的模型比对位置参数非线性相关的模型更容易拟合，并且更容易确定结果估计的统计特征。

线性回归模型通常通过最小二乘近似进行拟合，但也可以通过其他方法进行拟合，例如最小化某些其他规范中的“拟合缺陷”（例如最小绝对误差回归）或最小化最小二乘的惩罚桥回归中的损失函数，最小二乘近似可用于拟合那些非线性模型。

多元线性回归与非线性回归的比较与分析回归分析是一种广泛应用于数据挖掘、机器学习、统计学等领域的一种方法。

线性回归是回归分析中最常用的一种方法，但是有时候我们需要考虑更为复杂的模型，比如多元线性回归和非线性回归模型。

那么什么是多元线性回归和非线性回归？它们有什么不同？我们该如何选择合适的回归模型呢？本文将从理论和实践两方面对这些问题进行探讨。

1. 多元线性回归多元线性回归是一种线性回归模型，与简单线性回归不同的是，它考虑多个自变量对因变量的影响。

可以用下面的公式来表示：Y = β0 + β1X1 + β2X2 + … + βpXp + ɛ其中，Y是因变量，X1 ~ Xp是自变量，β0 ~ βp是模型的系数，ɛ是误差项。

在多元线性回归中，我们需要对变量之间的相关性进行检验。

如果变量之间存在多重共线性，会导致模型的不稳定性和准确性。

因此，在多元线性回归中，我们需要通过方差膨胀因子、特征选择等方法来解决多重共线性的问题。

2. 非线性回归当自变量和因变量之间的关系不是线性的时候，我们需要使用非线性回归模型。

比如，当因变量随着自变量的增加呈指数增长或递减的趋势，就可以使用指数回归模型；当因变量随着自变量的增加呈对数增长或递减的趋势，就可以使用对数回归模型。

非线性回归的建模过程和多元线性回归类似，但是对于不同的非线性模型，我们需要使用不同的方法进行参数估计。

例如，对于指数回归模型，我们可以使用最小二乘法或非线性最小二乘法进行参数估计。

3. 多元线性回归与非线性回归的比较在实际应用中，我们需要根据数据本身的性质来选择合适的回归模型。

如果数据呈现出线性关系，那么多元线性回归是一个理想的选择；如果数据呈现出非线性关系，那么非线性回归模型会更为合适。

在多元线性回归模型中，我们有比较丰富的理论基础和应用方法，可以广泛应用于各种场景。

多元线性回归模型的优点是简单、易解释、易拓展和广泛适用。

而在非线性回归模型中，我们需要根据数据本身的特点进行调整和优化，因此建模过程会稍显复杂。

第一章非线性动力学分析方法（6学时）一、教学目标1、理解动力系统、相空间、稳定性的概念；2、掌握线性稳定性的分析方法；3、掌握奇点的分类及判别条件；4、理解结构稳定性及分支现象；5、能分析简单动力系统的奇点类型及分支现象。

二、教学重点1、线性稳定性的分析方法；2、奇点的判别。

三、教学难点线性稳定性的分析方法四、教学方法讲授并适当运用课件辅助教学五、教学建议学习本章内容之前，学生要复习常微分方程的内容。

六、教学过程本章只介绍一些非常初步的动力学分析方法，但这些方法在应用上是十分有效的。

相空间和稳定性一、动力系统在物理学中，首先根据我们面对要解决的问题划定系统，即系统由哪些要素组成。

再根据研究对象和研究目的，按一定原则从众多的要素中选出最本质要素作为状态变量。

然后再根据一些原理或定律建立控制这些状态变量的微分方程，这些微分方程构成的方程组通常称为动力系统。

研究这些微分方程的解及其稳定性以及其他性质的学问称为动力学。

假定一个系统由n 个状态变量1x ，2x ，…n x 来描述。

有时，每个状态变量不但是时间t 的函数而且也是空间位置r的函数。

如果状态变量与时空变量都有关，那么控制它们变化的方程组称为偏微分方程组。

这里假定状态变量只与时间t 有关，即X i ＝X i (t)，则控制它们的方程组为常微分方程组。

),,,(2111n X X X f dtdX ),,,(2122n X X X f dtdX (1.1.1)…),,,(21n n nX X X f dtdX 其中 代表某一控制参数。

对于较复杂的问题来说，i f (i ＝l ，2，…n)一般是 i X 的非线性函数，这时方程(1.1.1)就称为非线性动力系统。

由于 i f 不明显地依赖时间t ，故称方程组(1.1.1)为自治动力系统。

若 i f 明显地依赖时间t ，则称方程组为非自治动力系统。

非自治动力系统可化为自治动力系统。

对于非自治动力系统，总可以化成自治动力系统。