多元函数全微分
- 格式:ppt
- 大小:873.00 KB
- 文档页数:2

多元函数的全微分与偏导数多元函数是数学分析中非常重要的一个概念,它描述了多个自变量对应的函数值的变化规律。
全微分和偏导数则是研究多元函数性质的重要工具。
在本文中,我们将探讨多元函数的全微分与偏导数的定义、性质和应用。
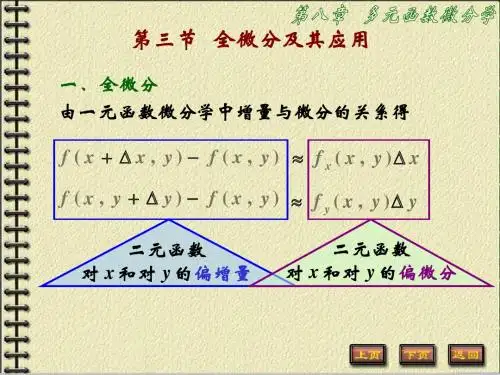
一、全微分的概念与性质1.1 全微分的定义设函数 $f(x_1,x_2,\cdots,x_n)$ 在点$(x_{1_0},x_{2_0},\cdots,x_{n_0})$ 具有一阶连续偏导数,则在该点的全微分为:$$\mathrm{d} f=f_{x_1}\mathrm{d} x_1+f_{x_2}\mathrm{d}x_2+\cdots+f_{x_n}\mathrm{d} x_n$$其中 $f_{x_i}$ 表示 $f$ 对 $x_i$ 的偏导数,$\mathrm{d}x_i$ 表示 $x_i$ 的微小增量。
1.2 全微分的性质全微分具有以下性质:(1)全微分的值与路径无关。
即,从点 $A$ 到点 $B$ 的全微分值相等。
(2)全微分对各变量的求导顺序不影响结果。
(3)全微分的二阶导数与求导顺序无关。
二、偏导数的定义与求解方法2.1 偏导数的定义函数 $f(x_1,x_2,\cdots,x_n)$ 对自变量 $x_i$ 的偏导数定义为:$$\frac{\partial f}{\partial x_i}=\lim_{\Delta x_i\rightarrow0}\frac{f(x_1,x_2,\cdots,x_{i-1},x_i+\Delta x_i,x_{i+1},\cdots,x_n)-f(x_1,x_2,\cdots,x_n)}{\Delta x_i}$$偏导数表示 $f$ 在某一自变量上的变化率。
2.2 偏导数的求解方法对于多元函数 $f(x_1,x_2,\cdots,x_n)$,求偏导数的方法如下:(1)保持其他自变量不变,对于某个自变量求导数。
(2)对于每个自变量都求一遍偏导数。

全微分的计算公式全微分是微积分中一个重要的概念,它用于描述函数变量之间的微小变化关系。
全微分的计算可以使用泰勒展开、导数定义和偏导数等方法。
本文将介绍全微分的计算公式和应用。
一、一元函数的全微分设函数y = f(x)在点(x0, y0)处可微分。
此时,函数f(x)在x0附近可以用其局部线性近似代替。
根据导数的定义,可得到函数f(x)在点x0处的导数f'(x0)。
函数f(x0)的全微分df表示函数f(x)在x0附近的微小变化量,可以通过以下公式计算:df = f'(x0)dx其中,f'(x0)表示函数f(x)在x0处的导数,dx表示自变量x的微小变化量。
二、二元函数的全微分对于二元函数z = f(x, y),如果在点(x0, y0)处可微分,那么z在(x0, y0)处的全微分dz可以表示为:dz = ∂f/∂x*dx + ∂f/∂y*dy其中,∂f/∂x表示函数f(x, y)对x的偏导数,∂f/∂y表示函数f(x, y)对y的偏导数,dx表示自变量x的微小变化量,dy表示自变量y的微小变化量。
需要注意的是,在计算二元函数的全微分时,要先对函数进行偏导数运算,然后与自变量的微小变化量相乘,再将结果相加。
三、多元函数的全微分对于多元函数z = f(x1, x2, ..., xn),如果在点(x1^0,x2^0, ..., xn^0)处可微分,那么z在(x1^0, x2^0, ..., xn^0)处的全微分dz可以表示为:dz = ∂f/∂x1*dx1 + ∂f/∂x2*dx2 + ... + ∂f/∂xn*dxn其中,∂f/∂x1表示函数对变量x1的偏导数,∂f/∂x2表示函数对变量x2的偏导数,dx1表示自变量x1的微小变化量,dx2表示自变量x2的微小变化量,以此类推。
四、全微分的应用例如,在概率论与统计学中,我们常常需要计算函数的期望和方差。
对于连续型随机变量,若已知其概率密度函数f(x)和函数g(x),可以通过全微分的公式计算函数g(x)的期望和方差。


多元函数的全微分公式
微分
多元函数的全微分公式
一、定义
全微分是对多元函数的求导,并且把多元函数的求导公式写成一个全微分的公式形式。
二、公式
多元函数的全微分为:
dF=Fx1dx1+Fx2dx2+…+Fxndxn
其中,F为多元函数,x1,x2,…,xn为多元函数的变量,
Fx1,Fx2,…,Fxn为多元函数求导的部分,dx1,dx2,…,dxn是多元函数变量的微小变化量。
三、应用
多元函数的全微分公式可以用来计算某些复杂的多元函数的求
导结果,简化多元函数的求导过程,和解决关于多元函数的求导问题。
它还可以用来帮助计算函数的极值问题。
- 1 -。

多元函数的微分知识点介绍整理人王浩多元函数的微分是求解多元函数的局部变化率的方法。
在微分学中,多元函数的微分包括偏导数和全微分两个概念。
偏导数是指某一变量在其他变量不变的情况下所产生的变化率,而全微分则是指所有变量同时改变时函数值的变化率。
1. 偏导数偏导数是导数概念在多元函数中的应用。
对于一个多元函数f(x,y),它的偏导数df/dx和df/dy表示当变量x或y分别增加一个微小的量时,函数f的局部变化率。
它们的定义如下:df/dx = lim(f(x+Δx,y)-f(x,y))/Δx (当Δy=0时)其中,Δx和Δy分别表示x和y的增量。
需要注意的是,偏导数只对某一变量求导,其他变量视作常数,可以将其视为单变量函数的导数。
2. 全微分全微分是将多元函数视为一个整体来求解其局部变化率的方法。
如果函数f(x,y)在某一点(x0,y0)处可微分,那么它的全微分df可以表示为:df = ∂f/∂x * dx + ∂f/∂y * dy其中,dx和dy分别表示x和y的增量,∂f/∂x和∂f/∂y分别表示函数f在(x0,y0)处的偏导数。
需要注意的是,全微分只适用于可微分的函数。
如果函数在某些点处不可微分,那么全微分也不存在。
3. 链式法则在多元函数求导中,链式法则是一种常用的方法。
它用于求解由多个函数复合而成的函数的导数。
如果h(x)是一个由f(u)和g(v)复合而成的函数,且u=u(x)和v=v(x)是关于x的函数,那么h(x)在x处的导数可以表示为:4. 梯度梯度是多元函数中的一种重要概念,它表示函数在某一点的最大变化方向。
对于一个多元函数f(x,y),它在某一点(x0,y0)的梯度grad(f)(x0,y0)可以表示为:可以看出,梯度是一个向量,它的方向是函数在某一点的最大变化方向,大小则表示变化率的大小。
总之,多元函数的微分是一个重要的数学工具,它可以帮助我们研究各种复杂的自然现象和社会现象,如气象学、地质学、金融学等。





考研多元函数微分公式
以下是考研多元函数微分的基本公式:
1. 偏导数的定义:设函数 z=f(x,y) 在点 (x0,y0) 的某邻域内有定义,如果当(x,y) 在 (x0,y0) 这一点处沿任何方向趋于 (x0,y0) 时,函数 z=f(x,y) 的改变量的极限存在,则称此极限为函数 z=f(x,y) 在点 (x0,y0) 处的偏导数。
记作
fₛₐ(x0,y0),ₛₐ表示从a平面偏到b平面。
2. 全微分的定义:如果函数 z=f(x,y) 在点 (x0,y0) 处的偏导数 fₛₐ(x0,y0) 都存在,则称函数 z=f(x,y) 在点 (x0,y0) 处可微,并称 fₛₐ(x0,y0) 的线性组合(即fₛₐ(x0,y0)dx+fy(x0,y0)dy)为函数z=f(x,y) 在点(x0,y0) 处的全微分。
记作 df(x0,y0)。
3. 可微与连续的关系:如果函数 z=f(x,y) 在点 (x0,y0) 处可微,则函数
z=f(x,y) 在点 (x0,y0) 处一定连续。
4. 方向导数的定义:设函数 z=f(x,y) 在点 P(x0,y0) 的某邻域内有定义,在
从点 P 沿某一方向 l 趋于 P 时,函数 z=f(x,y) 的改变量的极限称为函数
z=f(x,y) 在点 P 处沿方向 l 的方向导数,记作 fₛₐl(x0,y0)。
以上是考研多元函数微分的基本公式,建议查阅高等数学相关书籍了解更多细节。
多元函数在某点极限、连续、偏微商、全微分之间的关系多元函数是在数学中极为常见的,它们在物理学、化学、工程学、经济学等科学中得到了应用。
针对某点极限、连续、偏微分、全微分之间的关系,本文将对多元函数作出详细讨论。
首先,来看某点极限。
当某多元函数在某点处取到极限时,它在该点处取到的极限值就是函数的极限值。
这时,多元函数的极限值越小,函数的极限越大,反之亦然。
因此,极限值可以反映函数在某点处的连续性。
其次,论及连续性。
多元函数的连续性是指函数图象上的连续性,即若函数在某点处的极限存在,则该多元函数在该点上是连续的。
因此,某点的极限与连续性有一定的联系,可以通过极限值来反映函数的连续性。
再次,论及偏微分。
当求解多元函数某点处的最大或最小值时,必须求解偏微分,因此偏微分显得尤为重要。
它是指函数在某个方向上的增长率,即沿某一极限方向求解函数在某点处的切线斜率,可以反映函数在某点处的变化状况。
最后,论及全微分。
全微分指的是对多元函数在每一点处的变化性的研究,因此使用全微分可以完整地反映函数的变化状况。
而且,当求解多元函数某点处的最大或最小值时,也可以使用全微分,将多元函数在最大或最小点处的变化幅度求出来。
总而言之,某点极限、连续、偏微分、全微分之间的关系是十分密切的,可以通过对多元函数各个方面的研究来体现。
当求解某多元
函数某点处的最大或最小值时,可以根据这些不同的关系来确定哪种方法是最合适的。