矢量量化

图像编码是将图像信号转化成数字信号的过程，而矢量量化是一种常用的图像编码技术。

在图像编码中，矢量量化误差是一个重要的指标，它反映了图像编码的准确性和失真程度。

本文将重点讨论图像编码中的矢量量化误差分析。

首先，我们先来了解一下什么是矢量量化。

矢量量化是一种将一组相关的信号样本映射到一个有限的代码矢量集合中的过程。

图像编码中的矢量量化可以将图像信号划分为不同的区域，并用一组特定的矢量来代表每个区域。

这样做的好处是可以大大减少编码后的数据量，提高图像传输和存储的效率。

然而，在矢量量化过程中，由于采样和量化的误差以及矢量量化算法本身的限制，会产生一定的失真。

为了评估图像编码的质量和准确度，我们需要对矢量量化误差进行分析。

矢量量化误差是指原始信号与量化后信号之间的差异。

它的计算方式可以采用信号的欧氏距离或曼哈顿距离来度量。

通常情况下，我们会将所有像素点的误差求和，得到总的误差值。

在矢量量化误差分析中，最常用的指标是均方误差（Mean Square Error，MSE）。

它是评估图像编码质量的重要指标之一，计算方式为每个像素点的误差平方的平均值。

MSE越小，说明图像编码的失真越小，图像质量越好。

除了均方误差，我们还可以使用其他指标来评估图像编码的质量，如峰值信噪比（Peak Signal-to-Noise Ratio，PSNR），结构相似性指标（Structural Similarity Index，SSIM）等。

在实际的图像编码中，我们会遇到一些特殊的情况，例如低比特率编码和动态图像编码。

在低比特率编码中，由于编码的数据量较小，往往伴随着较大的失真。

因此，在设计低比特率编码算法时，需要权衡数据压缩和图像质量之间的平衡。

动态图像编码是指对连续变化的图像序列进行编码。

在动态图像编码中，除了要考虑单帧图像的编码质量，还需要关注连续帧之间的连贯性和平滑度。

因此，矢量量化误差的分析和评估需要结合时间维度来进行。

总结起来，图像编码中的矢量量化误差分析对于评估图像编码质量和选择适当的编码算法是非常重要的。

第四章矢量量化1、矢量量化？(VQ)是1956年由steinhaus首次提出的，1970年代后期发展起来的数据压缩和编码技术。

它主要应用于：语音编码、语音合成、语音识别和说话人识别。

矢量量化在语音信号处理中占有重要地位。

2、标量量化和矢量量化？✓标量量化：是对标量进行量化，即一维的矢量量化。

将动态范围分成若干个小区间，每小区间有一个代表值。

当输入信号落入某区间时，量化成该代表值。

✓矢量量化：是对矢量进行量化。

将矢量空间分成若干个小区域，每小区域有一个代表矢量。

当输入矢量落入某区域时，量化成该代表矢量。

矢量量化是标量量化的发展。

矢量量化总是优于标量量化，维数越高，性能越优越。

矢量量化有效利用各分量间的互相关性。

1970年代末，Linde，Buzo，Gray和Markel等人首次解决了矢量量化码书生成的方法，并首先将矢量量化用于语音编码获得巨大成功。

如，在语音通信方面，将在原来编码速率为2.4kbit/s的线性预测声码器基础上，将每帧的10个反射系数加以10维的矢量量化，就可使编码速率降低到800bit/s，而声音质量基本未下降。

又如分段声码器，由于采用矢量量化，可以使数码率降低到150bit/s。

3、矢量量化的基本原理？标量量化是对信号的单个样本或参数的幅度进行量化；标量是指被量化的变量，为一维变量。

矢量量化的过程是将语音信号波形的K个样点的每一帧，或有K个参数的每一参数帧构成K维空间的一个矢量，然后对这个矢量进行量化。

标量量化可以说是K=1的矢量量化。

矢量量化的过程和标量量化过程相似。

在标量量化时，在一维的零至无穷大值之间设置若干个量化阶梯，当某输入信号的幅度值落在某相邻的两个量化阶梯之间时，就被量化成两阶梯的中心值。

而在矢量量化时，则将K维无限空间划分为M 个区域边界，然后将输入矢量与这些边界进行比较，并被量化为“距离”最小的区域边界的中心矢量值。

矢量量化的定义将信号序列{}i y 的每K 个连续样点分成一组，形成K 维欧氏空间中的一个矢量，矢量量化就是把这个K 维输入矢量X 映射成另一个K 维量化矢量。

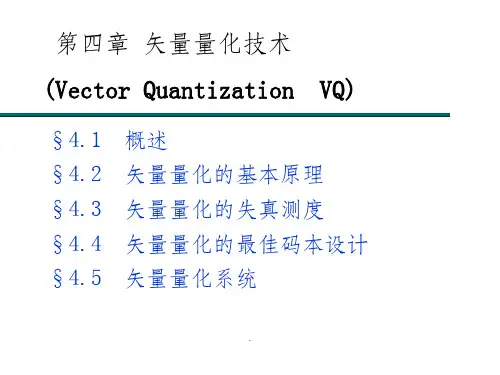
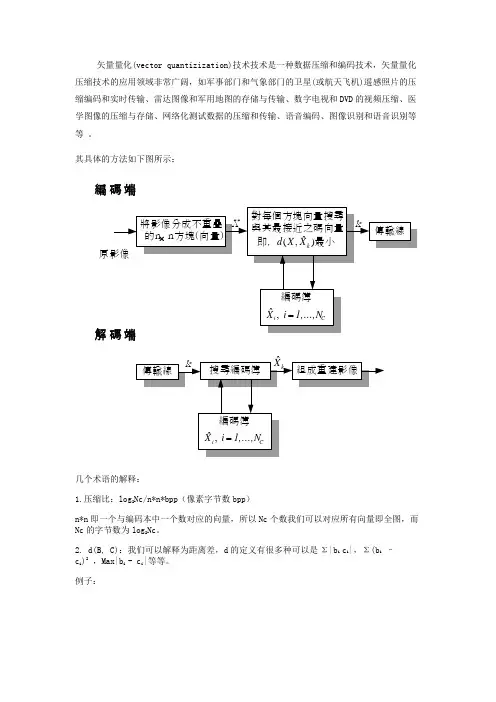
矢量量化(vector quantizization)技术技术是一种数据压缩和编码技术，矢量量化压缩技术的应用领域非常广阔，如军事部门和气象部门的卫星(或航天飞机)遥感照片的压缩编码和实时传输、雷达图像和军用地图的存储与传输、数字电视和DVD 的视频压缩、医学图像的压缩与存储、网络化测试数据的压缩和传输、语音编码、图像识别和语音识别等等 。

其具体的方法如下图所示：
几个术语的解释：
1.压缩比：log 2Nc/n*n*bpp （像素字节数bpp ）
n*n 即一个与编码本中一个数对应的向量，所以Nc 个数我们可以对应所有向量即全图，而Nc 的字节数为log 2Nc 。

2. d(B, C)：我们可以解释为距离差，d 的定义有很多种可以是Σ|b i c i |，Σ(b i – c i )2 ，Max|b i - c i |等等。

例子：
編碼端解
由上图我们可以看到左边为原图像，而右边为编码本。

例如我们可以讲原图像以如图所示的方式分为若干个有四个量的向量如（100,100,80,80）其余编码本中的
（100,100,90,90）计算的d （X ，Xk ）最小故我们可以用数字k 表示向量
（100,100,80,80）。

其实我们可以理解为矢量量化就是讲图像中分割成若干的小块，然后再将小块分类，一类用一个码表示。

下面是一个我论文中看到的也是最常用的VQ 算法：LBG 算法也叫K 平均分类算法。

以下是步骤：
当然我们可以设置一个收敛的条件，这个可以根据自己需求设置ε大小,当到达某一步 时 收敛即迭代结束。

ε≤---)1()1(l l l D D
D。

矢量量化(Vector Quantization)一．矢量量化初步1.基本原理2.设计码本(LBG)3.量化二．矢量量化进一步1.分裂矢量量化(Splitted VQ)2.多极矢量量化(Cascaded VQ)3.树形矢量量化器4.其它各种类型矢量量化器三. 几个矢量量化的工程实现问题1.分级矢量量化中的多路径搜索问题2.用模拟退火(Simulated Annealing) 算法训练最佳码本[2]四. 矢量量化的应用一．矢量量化初步1. 基本原理结论：在信息论中已证明，矢量量化优于标量量化。

❑矢量量化是先将K 个(2≥K )个采样值形成K 维空间K R 中的一个矢量，然后将这个矢量一次进行量化。

它可以大大降低数码率。

❑基础是信息论的分支: 率失真(畸变)理论对于一定的量化速率R(以每个采样信号平均所用的量化比特数来衡量，bit/采样)，量化失真D(以量化信号与原信号之间的误差均方值和原信号均方值之比来衡量)是一定的。

矢量量化总是优于标量量化的。

这是因为矢量量化有效地应用了矢量中各分量间的四种相互关联的性质：线性依赖性，非线性依赖性，概率密度函数的形状以及矢量维数。

定义：1) 源：若将K M ⋅个信号采样组成的信源序列{}j x 中每K 个为一组分为M 个随机矢量，构成信源空间{}MXX X X,,,21 =(X在K 维欧氏空间KR中)，其中第j 个矢量可记为{}12,,,j k X x x x = ，M j ,,2,1 =。

2) 子空间：把KR无遗漏地划分成nN 2=个互不相交的子空间N R R R ,,,21 ，满足：⎪⎩⎪⎨⎧≠===ji R RR R j i N i K i ,013) 码本：在每个子空间i R 中找一个代表矢量i Y ，令恢复矢量集为：{}N Y Y Y Y ,,,21 =。

Y 也叫输出空间、码本或码书(Code Book)，i Y 称为码矢(Code V ector)或码字(Code Word)，Y 内矢量的数目N，则叫做码本长度。

第四章矢量量化1、矢量量化？(VQ)是1956年由steinhaus首次提出的，1970年代后期发展起来的数据压缩和编码技术。

它主要应用于：语音编码、语音合成、语音识别和说话人识别。

矢量量化在语音信号处理中占有重要地位。

2、标量量化和矢量量化？✓标量量化：是对标量进行量化，即一维的矢量量化。

将动态范围分成若干个小区间，每小区间有一个代表值。

当输入信号落入某区间时，量化成该代表值。

✓矢量量化：是对矢量进行量化。

将矢量空间分成若干个小区域，每小区域有一个代表矢量。

当输入矢量落入某区域时，量化成该代表矢量。

矢量量化是标量量化的发展。

矢量量化总是优于标量量化，维数越高，性能越优越。

矢量量化有效利用各分量间的互相关性。

1970年代末，Linde，Buzo，Gray和Markel等人首次解决了矢量量化码书生成的方法，并首先将矢量量化用于语音编码获得巨大成功。

如，在语音通信方面，将在原来编码速率为2.4kbit/s的线性预测声码器基础上，将每帧的10个反射系数加以10维的矢量量化，就可使编码速率降低到800bit/s，而声音质量基本未下降。

又如分段声码器，由于采用矢量量化，可以使数码率降低到150bit/s。

3、矢量量化的基本原理？标量量化是对信号的单个样本或参数的幅度进行量化；标量是指被量化的变量，为一维变量。

矢量量化的过程是将语音信号波形的K个样点的每一帧，或有K个参数的每一参数帧构成K维空间的一个矢量，然后对这个矢量进行量化。

标量量化可以说是K=1的矢量量化。

矢量量化的过程和标量量化过程相似。

在标量量化时，在一维的零至无穷大值之间设置若干个量化阶梯，当某输入信号的幅度值落在某相邻的两个量化阶梯之间时，就被量化成两阶梯的中心值。

而在矢量量化时，则将K维无限空间划分为M 个区域边界，然后将输入矢量与这些边界进行比较，并被量化为“距离”最小的区域边界的中心矢量值。

矢量量化的定义将信号序列{}i y 的每K 个连续样点分成一组，形成K 维欧氏空间中的一个矢量，矢量量化就是把这个K 维输入矢量X 映射成另一个K 维量化矢量。

矢量量化矢量量化（VQ —Vector Quantization）是70年代后期发展起来的一种数据压缩技术基本思想：将若干个标量数据组构成一个矢量，然后在矢量空间给以整体量化，从而压缩了数据而不损失多少信息矢量量化编码也是在图像、语音信号编码技术中研究得较多的新型量化编码方法，它的出现并不仅仅是作为量化器设计而提出的，更多的是将它作为压缩编码方法来研究的。

在传统的预测和变换编码中，首先将信号经某种映射变换变成一个数的序列，然后对其一个一个地进行标量量化编码。

而在矢量量化编码中，则是把输入数据几个一组地分成许多组，成组地量化编码，即将这些数看成一个k维矢量，然后以矢量为单位逐个矢量进行量化。

矢量量化是一种限失真编码，其原理仍可用信息论中的率失真函数理论来分析。

而率失真理论指出，即使对无记忆信源，矢量量化编码也总是优于标量量化。

在矢量量化编码中，关键是码本的建立和码字搜索算法。

码本的生成算法有两种类型，一种是已知信源分布特性的设计算法；另一种是未知信源分布，但已知信源的一列具有代表性且足够长的样点集合（即训练序列）的设计算法。

可以证明，当信源是矢量平衡且遍历时，若训练序列充分长则两种算法是等价的。

码字搜索是矢量量化中的一个最基本问题，矢量量化过程本身实际上就是一个搜索过程，即搜索出与输入最为匹配的码矢。

矢量量化中最常用的搜索方法是全搜索算法和树搜索算法。

全搜索算法与码本生成算法是基本相同的，在给定速率下其复杂度随矢量维数K以指数形式增长，全搜索矢量量化器性能好但设备较复杂。

树搜索算法又有二叉树和多叉树之分，它们的原理是相同的，但后者的计算量和存储量都比前者大，性能比前者好。

树搜索的过程是逐步求近似的过程，中间的码字是起指引路线的作用，其复杂度比全搜索算法显著减少，搜索速度较快。

由于树搜索并不是从整个码本中寻找最小失真的码字，因此它的量化器并不是最佳的，其量化信噪比低于全搜索。

图像编码中的矢量量化误差分析引言：图像编码技术在现代通信系统、多媒体应用和图像处理中起着重要的作用。

其中，矢量量化是一种常用的图像编码方法。

矢量量化通过将相邻像素点划分成不同的矢量，并用矢量代表这些相邻像素点，从而实现图像的压缩。

然而，在矢量量化的过程中，会产生一定的误差。

本文将重点讨论图像编码中的矢量量化误差分析。

一、矢量量化的基本原理矢量量化是一种基于块的图像编码技术，其基本原理是将图像划分成许多块，并用矢量代表每个块，从而减少存储和传输的数据量。

具体而言，矢量量化的过程包括以下几个步骤：首先，将图像划分成不同的块。

然后，通过计算每个块的特征向量，将其转化为一个矢量。

最后，将这些矢量进行编码和解码，从而实现图像的压缩和恢复。

二、矢量量化误差的产生原因在矢量量化的过程中，误差主要是由两个方面引起的：矢量量化的离散化和矢量量化的精度损失。

1. 矢量量化的离散化矢量量化将连续的图像块划分为离散的矢量，这个离散化过程本身就会引入误差。

因为图像块是连续的，但矢量量化将其离散化后，会导致块内部的像素值与矢量表示之间存在差距，从而产生误差。

2. 矢量量化的精度损失在矢量量化的过程中，每个块被用一个矢量表示，但是这个矢量无法完全精确地表示原始图像块的所有特征。

因此，在编码和解码的过程中，矢量量化会引入一定的精度损失。

当图像块的特征难以用有限的几个矢量表示时，会导致较大的编码误差。

三、矢量量化误差的评估方法为了对图像编码中的矢量量化误差进行评估和分析，我们可以使用以下几种方法：1. 平均误差平均误差是矢量量化误差的一种常用评估方法。

它通过计算每个像素点的实际值与矢量量化值之间的差异，并取平均值来评估误差的大小。

平均误差越小，表示矢量量化的效果越好。

2. 均方误差均方误差是另一种常用的评估方法。

它通过计算每个像素点的实际值与矢量量化值之间的差的平方，并取平均值来评估误差的大小。

均方误差越小，表示矢量量化的效果越好。

图像编码是一门重要的技术，在数字图像的传输和存储过程中发挥着关键的作用。

矢量量化作为一种常用的图像编码技术，可以有效地减少数据量，并保持较高的图像质量。

在图像编码中，我们常常需要对矢量量化的误差进行分析。

本文将从图像编码的基本概念出发，探讨矢量量化误差的成因及其对图像质量的影响。

首先，我们需要了解什么是矢量量化。

矢量量化是一种基于向量量化的图像编码方法，其基本思想是将图像分割为若干个子向量，并将每个子向量用一个集合中的某个向量代替。

这样可以大大减少数据量，提高图像的压缩效率。

然而，在这个过程中，由于信息的丢失和误差的引入，图像质量也将受到一定的影响。

矢量量化的误差主要来源于两个方面：一是子向量的选择带来的误差，二是量化过程中的近似误差。

首先，子向量的选择是矢量量化中十分关键的一步。

选择合适的子向量用于表示图像的不同部分，可以有效地降低误差。

如果选择不当，误差将会增大，导致图像质量下降。

其次，在量化过程中，我们往往需要利用近似方法对子向量进行编码。

这种近似方法虽然可以减少数据量，但也会引入误差。

因此，我们需要对这两方面的误差进行详细的分析。

首先，对于子向量的选择误差，我们可以通过计算矢量量化的失真度来评估。

失真度是指原始图像与编码后解码得到图像之间的差异程度。

失真度越高，说明选择的子向量与原始图像的不匹配程度越大，误差也就越大。

在矢量量化中，我们通常采用均方差（Mean Squared Error，MSE）来度量失真度。

MSE可以用公式表示为：MSE = Σ（xi - yi）^2 / N，其中xi为原始信号，yi为解码得到的信号，N为信号维度。

通过计算MSE，我们可以比较不同子向量选择方法的优劣，并选择最优解码方法。

其次，量化过程中的近似误差也是影响图像质量的重要因素。

在矢量量化中，为了减少数据量，我们通常采用近似方法对子向量进行编码。

这种近似方法会引入一定的误差，对图像质量造成影响。

为了评估这种近似误差，我们可以使用信噪比（Signal-to-Noise Ratio，SNR）来度量。