浙江工业大学自动控制原理笔记

浙江工业大学2010/2011（1）期终考试《自动控制原理》试题课程自动控制原理姓名班级学号第一部分简答题（共5题，每题3分，共15分。

答题必须简明扼要。

）1滞后—超前串联校正改善系统性能的原因。

（1）降低截止频率，（2）中频段提高相位裕度，（3）避免了单独采用超前校正或单独采用滞后校正的不足。

2惯性环节在什么条件下可以近似为比例环节。

在惯性时间常数很小的情况下。

3列举3种非线性系统与线性系统特性的不同之处。

（1）是否满足叠加原理（2）是否有可能产生自激振荡，（3）系统的特性（如稳定性）与初始状态是否有关。

4现实中，真实的系统都具有一定程度的非线性特性和时变特性，但是理论分析和设计经常采用线性时不变模型的原因。

（1）通常系统工作在平衡点附近的小范围内，（2）近似的精度通常满足工程要求，（3）线性系统的分析与设计方法成熟、方便。

（4）对于本质非线性，或者非线性明显的情况，或者要求比较高的情况，必须采用非线性的方法5零阶保持器传递函数1()TsheG ss--=中是否包含积分环节？为什么？不包含积分环节，因为s趋向0时，G(s)并不趋向无穷。

第二部分 填空题（共25分。

）6图示调节器的传递函数()/()o i U s U s 为 。

（图中运放器为理想运算放大器）（4分） 12111120010()(1)(1),,,()o i U s T s T s R KK T R C T R C U s T sR ++==-==其中C o第6题图7零初始条件下，某系统在单位脉冲()t δ作用下的响应为))(()(1211212T t eT T T t T T K t k ---=δ，该系统的输入输出间的传递函数为11)(12++=s T s T Ks G ，该系统输入输出间的微分方程为12()()(()())T y t y t K T u t u t +=+ 。

（每空3分）8 已知单位负反馈系统的开环传递函数为2(1)()()K s G s H s s+=，0,K >在单位阶跃1()t 、单位斜坡t 、单位加速度2t 作用下系统的稳态误差分别为 0 ， 0 ， 2/K 。

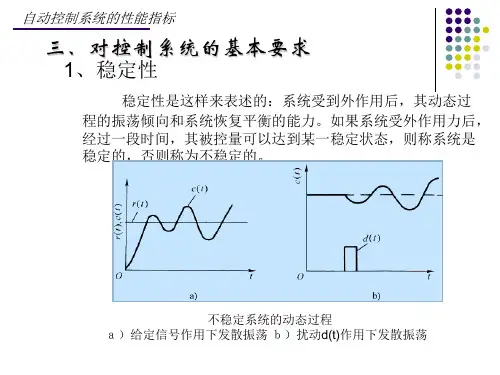
自动控制原理笔记齐**1稳定性取决于系统的固有特性给扰动后偏移越来越小则稳定偏移发散则不稳定数学表达稳定=脉冲函数t趋于无穷脉冲响应趋于0化简思路：输出相应=输入*传递函数拉变后输出拉变=1（脉冲函数拉变为1）*传递函数=传递函数将传递函数拆项后反拉氏变换脉冲响应归成指数和稳定情况1负实根稳定2有负实部共轭虚根可以化成指数和三角函数乘积稳定3共轭纯虚根变换后为三角函数不稳定4 原点常数不稳定5正实根不稳定6正实数共轭虚根不稳定口诀有负实部就稳定所以判断方法只需要判断是否有负实根就可以劳斯稳定性判据（确实系统是否稳定与稳定度）1稳定性的初步检查：特征方程所有系数同号且不缺项则稳定（必要条件）2正式判断步骤列Routh表前两行第一项和之后的不断进行（-行列式运算）/第二行第一个数字没有数字需要运算的地方0补齐判断若第一列均为正数则稳定否则不稳定且符号改变数为右半面s的根数特殊1若某行第一个数字为0但这行不全为0 可用小正数代替。

算完后取极限它本身算一个正数2一行全为0则用上一行构造辅助数列求导得出的系数最后解辅助数列根据是否稳定选出对的根想要有良好相应，常希望左半面系统特征根位置与虚轴有一定距离（稳定度）解具体问题思路：1写闭环传递函数2根据稳定度，对传递函数进行变换（闭环点全在a左则将s变成s1+a保证稳定度）过渡过程一个稳态到新稳态的变化过程单位阶跃信号tr上升时间0开始首次达到稳态时间（百分之10到百分之90）Tp 峰值时间超调量相应最大偏移量与终值之差的百分比太大会影响系统状态Ts调节时间保持在允许误差范围内，所需最短时间震荡次数延迟时间td 到终值一半的时间Tr tp （快慢）超调量（稳）Ts （综合性指标反应快慢）非阶跃无超调量ts只有稳态误差时域分析一阶系统。

自动控制原理笔记一、自动控制理论的分析方法：（1）时域分析法； （2）频率法； （3）根轨迹法； （4）状态空间方法； （5）离散系统分析方法； （6）非线性分析方法 二、系统的数学模型(1)解析表达：微分方程；差分方程；传递函数；脉冲传递函数；频率特性；脉冲响应函数；阶跃响应函数(2)图形表达：动态方框图（结构图）；信号流图；零极点分布；频率响应曲线；单位阶跃响应曲线时域响应分析一、对系统的三点要求：(1)必须稳定，且有相位裕量γ和增益裕量g K(2)动态品质指标好。

p t 、s t 、r t 、σ% (3)稳态误差小，精度高 二、结构图简化——梅逊公式 例1、解：方法一：利用结构图分析：()()()()[]()()[]()s X s Y s R s Y s X s R s E 11--=+-=方法二：利用梅逊公式 ∆∆=∑=nk KK P s G 1)(其中特征式 (11),,1,1+-+-=∆∑∑∑===Qf e d f e dMk j kjNi i L L LLL L式中： ∑i L 为所有单独回路增益之和∑jiLL 为所有两个互不接触的单独回路增益乘积之和∑f e dL L L为所有三个互不接触的单独回路增益乘积之和其中，k P 为第K 条前向通路之总增益；k ∆ 为从Δ中剔除与第K 条前向通路有接触的项；n 为从输入节点到输出节点的前向通路数目 对应此例，则有：通路：211G G P ⋅= ，11=∆特征式：312131211)(1G G G G G G G G ++=---=∆则：3121111)()(G G G G P s R s Y ++∆= 例2：[2002年备考题]解：方法一：结构图化简继续化简：于是有：结果为其中)(s G =…方法二：用梅逊公式[]012342321123+----=∆H G G H G G G H G G)(s G ()5342112361G G G G G H G G G ⎪⎪⎭⎫ ⎝⎛+++()()2342112334211H G G G G H G G G G G G ++++5G 2H 6G ()12342131H G G G G G G ++ ()34211231G G G G H G G ++5G 2H 6G 421G G G +12331H G G G +1G 2G 5G 2H 3G 4G 12H G通路：1,1321651=∆=G G G G G P1232521,H G G G P +=∆= 1,334653=∆=G G G G P于是：()()......332211=∆∆+∆+∆=P P P s R s Y三、稳态误差（1）参考输入引起的误差传递函数：()HG G s R s E 2111)(+=； 扰动引起的误差传递函数：()()HG G H G s N s E 2121+-=（2）求参考输入引起的稳态误差ssr e 时。

1、控制系统的工作原理：→检测输出量（被控制量）的实际值；→将输出量的实际值与给定值（输入量）进行比较得出偏差；→用偏差值产生控制调节作用去除偏差，使得输出量维持期望的输出。

2、反馈控制方式工作原理：根据被控量的反馈信息，即实际输出量，来修正控制装置对被控对象的控制作用，完成控制任务。

3、开环控制方式工作原理：在控制器和被控对象之间只有正向控制而没有反馈控制，即系统的输出量对控制量没有影响。

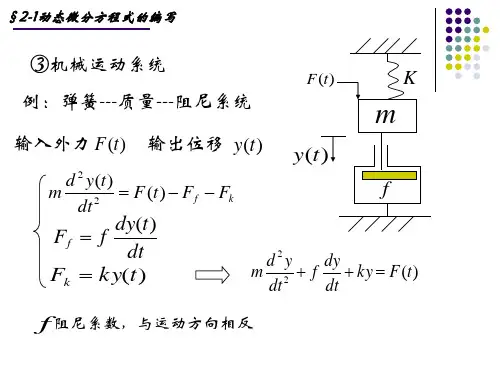
4、复合控制方式工作原理：开环+反馈5、自动控制系统的分类： →线性定常控制系统11010111()()...()()()...()n n m m n m n n m m d d d d a c t a c t a c t b r t b r t b r t dt dt dt dt----+++=+++ 其中：()c t ——系统输出，()r t ——系统输入。

→线性定常离散控制系统（m n ≤）011011()(1)...(1)()()(1)...(1)()n n m m a c k n a c k n a c k a c k b r k m b r k m b r k b r k --+++-++++=+++-++++其中：r ——输入采样序列，c ——输出采样序列。

→非线性控制系统（系数与变量有关）222()()()()()d y t dy t y t y t r t dt dt++=6、典型外作用：→单位阶跃信号（unit step function ）1,0()0,0t t t ε≥⎧=⎨<⎩→单位斜坡信号（unit ramp function ）,01()0,0t t t t ≥⎧=⎨<⎩→单位脉冲信号（unit pulse function ）,0()0,0t t t δ∞=⎧=⎨≠⎩单位脉冲信号的一个性质：()1t dt δ+∞-∞=⎰→单位加速度信号（unit acceleration function ）21,0()20,0t t a t t ⎧≥⎪=⎨⎪<⎩7、线性元部件及系统的微分方程：RLC 串联电路如下图所示，试写出系统的微分方程ru cu CRLi()()()()()r c c di t u t L Ri u t dt du t i t C dt ⎧=++⎪⎪⎨⎪=⎪⎩22()()11()()c c c r d u t du t R u t u t dt L dt LC LC++=8、拉氏变换： →拉氏变换()[()]()st F s L f t f t e dt ∞-==⎰s j σω=+→拉氏反变换11()[()]()2j st j f t L F s F s e ds j σσπ+∞--∞==⎰→拉氏变换性质齐次性和叠加性：1212[()()]()()L af t bf t aF s bF s +=+ 延时定理：[()]()sL f t e F s ττ--=衰减定理：[()]()atL e f t F s a -=+相似定理：1[()]()sL f at F a a =微分性质：222[()](),[()](),...[()]()n n n d d d L f t sF s L f t s F s L f t s F s dt dt dt===积分性质：22111[()](),[()](),...[...()]()n n L f t dt F s L f t dt F s L f t dt F s s s s===⎰⎰⎰⎰⎰ 终值定理：0lim ()lim ()t s f t sF s →∞→=初值定理：0lim ()lim ()t s f t sF s →→∞=卷积定理：121212[()*()][()][()]()()L f t f t L f t L f t F s F s == 像函数的微分性质：()[()]dF s L tf t ds=- 像函数的积分性质：1[()]()sL f t F s ds t∞=⎰9、部分分式展开法：已知12()()()()()()...()n B s B s F s A s s p s p s p ==--- →若()0A s =有n 个单根，则有112()()()()()()...()()ni i n i k B s B s F s A s s p s p s p s p ====----∑其中各部分分式的系数为lim()()ii i s p k s p F s →=-→若()0A s =有重极点，假设有m 重极点1s p =，则有111()()()()()mni i i i i m i k k B s F s A s s p s p ==+==+--∑∑ 其中111()1,2,...1()1, 2...lim()()1lim [()()]()!lim()()i m i m s p m i m i m m m i s p i m m i s p k s p F s d k s p F s m i ds k s p F s =→-=---→=++→⎧=-⎪⎪⎪=-⎨-⎪⎪=-⎪⎩10、传递函数：线性定常系统在零初始条件下，输出量的拉氏变换与输入量的拉氏变化之比，称为传递函数。

第8章 状态反馈控制与状态观测器设计8.1 状态反馈与输出反馈8.1.1 状态反馈图8.1所示是一单输入单输出连续系统状态反馈的例子。

图8.1 单输入系统的状态反馈记[]321k k k K =则r Kx u +=多输入多输出状态反馈系统的一般形式如图8.2所示。

被控对象的状态空间表达式为(8.1) Du Cx y Bu Ax x+=+=&控制输入u 为(8.2) Kx r u +=因此，状态反馈闭环系统的状态空间表达式为(设0=D )，则(8.3) ⎩⎨⎧=++=Cx y Br x BK A x )(&状态反馈闭环系统的传递函数阵为(8.4)B BK A sIC s G K 1)()(−−−=图8.2 多输入系统的状态反馈8.1.2 输出反馈图8.3 多输入系统的输出反馈设被控对象的状态空间表达式为式(8.1)，被控系统的控制信号为(8.5) Hy r u +=于是)()()()(1HCx r HD I u HCxr u HD I HDuHCx r Du Cx H r u +−=+=−++=++=−代入被控对象的状态空间表达式(8.1)，得(8.6a)[][]rHD I D x HC HD I D C HCx r HD I D Cx y r HD I B x HC HD I B A HCx r HD I B Ax x111111)()()()()()()()(−−−−−−−+−+=+−+=−+−+=+−+=&式(8.6a)就是输出反馈系统状态空间表达式。

当0=D 时，有(8.6b)Cxy Br x BHC A x =++=)(&输出反馈的闭环传递函数阵为(8.7)B BHC A sI C s G H 1)()(−−−=8.1.3 状态反馈系统的能控性与能观性1.状态反馈系统的能控性定理：多变量线性系统（定常的或时变的）{}C B A ,,0=∑，在任何形如的状态反馈下，状态反馈闭环系统)()()()(t x t K t r t u +={}C B BK A K ,,+=∑完全能控的充要条件是被控对象{}C B A ,,0=∑完全能控。