有限元分析 均布荷载作用下深梁的变形和应力

有限元受力分析–结构梁-力-计算1. 前言受力分析是工程设计中至关重要的一环，能够帮助工程师完善设计并避免安全事故的发生。

在此，我们将介绍有限元受力分析在结构梁设计中的应用。

本文将重点讲解有限元受力分析的相关理论和计算方法。

2. 有限元受力分析有限元分析是数值计算的一种方法，可用于解决工程中的受力分析问题。

它把结构离散为有限个单元，然后对每个单元进行分析。

有限元分析可分为线性有限元分析和非线性有限元分析两种类型。

本文我们只讨论线性有限元分析。

在有限元分析中，结构被分解为离散的单元，每个单元都是基于解析解的一部分。

有限元的形状、尺寸和材料属性可以通过计算机程序进行定义。

使用数学模型和有限元方法，可以计算单元的应力、变形和应变，从而进行结构的受力分析。

3. 结构梁结构梁相信大家应该都知道，它是工程中最为常用的结构之一。

它具有一定的强度和刚度，可以支撑和传递载荷。

一般来说，结构梁通常由简单的杆件单元组成。

在进行结构梁受力分析时，我们需要考虑弯曲、剪切和挤压等不同形式的载荷，以及结构在工作条件下的应变和应力分布情况。

有限元受力分析对于这些问题的研究提供了很好的解决方案。

4.力的分析在受力分析中，载荷是非常关键的参数。

载荷可以是点载荷、均布载荷、集中荷载等。

在本文中，我们将分别介绍这些载荷类型的有限元分析方法。

4.1 点载荷分析点载荷通常是一个单点受到的载荷。

对于点载荷的有限元分析，我们可以通过构建一个网格模型，然后将点载荷作用在网格的节点上。

此外，还需要设定材料的弹性模量和截面的截面面积，以计算结构的应力和变形。

需要注意的是，点载荷分析过程中的网格划分应当尽量精细，以达到更为优秀的数值精度。

4.2 均布载荷分析均布载荷是沿着梁的长度方向均匀分布的载荷，例如一根梁的自重、荷载等。

在进行均布载荷的有限元分析时，我们可以在网格的中央位置放置均布载荷，然后将梁的边缘节点设置为固定的约束条件。

同样，需要设定材料的弹性模量和截面的截面面积以计算结构的应力和变形。

梁的有限元分析原理梁的有限元分析原理是一种工程结构分析方法，广泛应用于建筑、桥梁、航空航天、汽车等领域。

它通过将连续的结构离散化为有限数量的小单元，通过数学模型进行计算，得出结构的力学性能和响应情况。

梁的有限元分析原理是有限元分析的基础，下面将对其进行详细介绍。

首先，梁的有限元分析原理基于梁理论，即在横向较小、纵向较长的情况下，结构可以近似为一维梁。

梁的有限元分析原理通过将梁划分为多个单元，每个单元内部可以看作两个节点之间的一段杆件，通过建立节点之间的力学关系方程，得到整个结构的力学性能。

其次，梁的有限元分析原理利用了变分原理，即将结构的势能取极小值，建立了结构的力学方程。

通过对于梁的弯曲、剪切和轴向力等方面的力学模型进行合理的假设与简化，可以得到结构的位移与力的关系，从而解决结构的力学问题。

在梁的有限元分析中，需要进行以下几个步骤：1.几何离散化：将梁结构划分为多个单元，每个单元具有相同的形状与尺寸，通常为矩形或三角形。

2.模型建立：根据梁理论以及力学方程的简化假设，建立节点的力学关系方程，包括位移、应力、应变等参数。

3.材料性能定义：确定梁材料的力学性能参数，如弹性模量、截面惯性矩等。

这些参数对梁结构的力学性能具有重要影响。

4.边界条件施加：根据实际问题设定边界条件，包括固定支座、约束条件等。

这些条件对于解决梁结构的位移、应力等问题至关重要。

5.方程求解：通过数学方法求解得到节点之间的力学关系方程，利用数值计算技术进行迭代求解，得到梁结构的位移、应力等参数。

6.结果分析：根据求解得到的结果，进行力学性能分析，如最大应力、挠度、模态分析等。

根据分析结果评估结构的强度与稳定性。

总结起来，梁的有限元分析原理是一种基于梁理论的工程结构分析方法，通过将结构离散化为多个小单元，利用力学关系方程和数值计算技术求解得到结构的力学性能。

通过梁的有限元分析原理，工程师可以更加准确地评估结构的强度与稳定性，对结构进行优化设计。

梁变形与梁应力部分小结一、梁的应力与变形公式1、平面弯曲的正应力σ公式 y Ey I M Zρσσ==研究方法：平面弯曲、纯弯曲平面假设、单向受力假设①变形几何关系（条件、方程）ρεy=（应变沿截面高度的分布规律）y ——截面上某点到中性轴的距离 ②物理关系（条件、方程）ρσyE εE ⋅=⋅= （应力沿截面高度的分布规律）③静力学关系（条件、方程）dAy Ey σdA M0ydA EσdA F A2AZAAN ⎰⎰⎰⎰=⋅====⊗ρρ⎪⎩⎪⎨⎧=⎰中性轴—Z dA y I A 2Z ()4m()⎰=⋅=→AZ Z 0dA y S S 3m 静矩 （中性轴Z 轴通过形心）2、弯曲变形基本公式（方程）⎪⎪⎭⎫ ⎝⎛±==22Zdx y d EIM ρρ1（ρ1曲率）3、任一点处弯曲正应力的表达式（对同一截面而言）y I M Z=σ ZI ——截面对中性轴的惯性M ——该截面上的弯矩值 y ——该截面上某点至中性轴之矩 4、平面弯曲剪应力公式 ①基本公式：bI S Fs Z Z *=τ 式中：b ——横截面上要计算剪应力之点处的宽度Z I ——整个截面对中性（形心）轴的惯性矩*ZS ——横截面上距中性轴为y 的横线以外部分截面对中性轴Z 的静矩②横截面上最大剪应力（危险点在中性轴上各点）记忆⎪⎪⎭⎪⎪⎬⎫====2maxmax 3ππ16Fs A Fs 34τbh Fs 1.5A Fs23τ查表Z I ：m ax Z S 值（应用）二、平面弯曲强度条件与刚度条件1、弯曲正应力强度条件 []σσ≤=ZW M m ax （对称）[][][][])() ( 2m ax m ax σy y I M y I M Zl 1Z 压拉压拉σσσσσ≤=≤=（不对称）2、弯曲剪应力强度条件 []ττ≤=bI S Fs Z Zmaxmax m ax 危险点均在危险截面的中性轴各点处应力沿截面高度的成抛物线分布规律3、刚度条件（用叠加法求出梁中最大转角与挠度）转角[]θθ≤m ax 、()角度弧度⇒⋅πθ180m ax rad挠度[] max max ωω≤(m) 满足刚度条件三、提高弯曲强度与弯曲刚度的措施1、选择合理的截面（考虑材料力学性质） ①AW Z一般情况该比值越大越合理 工＞＞②铸铁[]压σ＞[]拉 σ，中性轴偏于受拉边 Z (中性轴) 2、合理布置梁的支座和载荷①合理布置梁的支座 ②合理布置梁的载荷 ③等强度梁（变截面梁）m ax m ax τ矩形梁 圆截面梁 工字梁危险点均在危险截面的上、下边缘点处应力沿截面高度成线性分布四、用变形比较法求解超静定（静不定）梁1、确定静定基。

本次土木工程仿真实验实习旨在通过实际操作，加深对土木工程基本原理和工程实践的理解，提高学生的实际操作能力和工程意识。

通过实验，使学生掌握土木工程仿真软件的基本操作，了解不同工程结构在荷载作用下的受力特性，培养学生在实际工程中分析问题和解决问题的能力。

二、实习时间及地点实习时间：2021年X月X日至2021年X月X日实习地点：XX大学土木工程实验室三、实习内容1. 土木工程仿真软件介绍本次实习主要使用ANSYS软件进行土木工程仿真实验。

ANSYS是一款功能强大的有限元分析软件，广泛应用于土木工程、机械工程、航空航天等领域。

通过ANSYS软件，可以模拟不同工程结构在荷载作用下的受力状态，为工程设计提供理论依据。

2. 实验项目（1）钢筋混凝土梁受力分析本次实验主要研究钢筋混凝土梁在均布荷载作用下的受力特性。

实验内容如下：1）建立钢筋混凝土梁的有限元模型；2）施加均布荷载，分析梁的变形和应力分布；3）通过改变梁的截面尺寸、配筋率等参数，研究其对梁受力性能的影响。

（2）桩基承载性能分析本次实验主要研究桩基在竖向荷载作用下的承载性能。

实验内容如下：1）建立桩基的有限元模型；2）施加竖向荷载，分析桩基的变形和应力分布；3）通过改变桩长、桩径、桩间距等参数，研究其对桩基承载性能的影响。

（3）地基沉降分析本次实验主要研究地基在荷载作用下的沉降特性。

实验内容如下：1）建立地基的有限元模型；2）施加荷载，分析地基的沉降和应力分布；3）通过改变地基土的性质、荷载大小等参数，研究其对地基沉降的影响。

四、实习过程1. 实验准备在实习开始前，学生需熟悉ANSYS软件的基本操作，包括建模、网格划分、材料属性设置、荷载施加、求解等。

同时，查阅相关资料，了解实验目的、实验原理和实验步骤。

2. 实验操作（1）钢筋混凝土梁受力分析1）建立钢筋混凝土梁的有限元模型，包括梁的几何尺寸、材料属性、边界条件等；2）施加均布荷载，设置求解参数，进行计算；3）分析梁的变形和应力分布，观察不同参数对梁受力性能的影响。

兴关于深弯构件的抗剪研究 ， 黄乔等关于简支深梁的受剪研究 和邹建文的混凝土构件受剪计算理论的有限 元分析。试验研究表明， 影响钢筋混凝土构件抗剪强度的因素有很多 ， 包括混凝土的强度、 箍筋配筋率 、 纵筋 配筋 率 、 剪跨 比和弯起 钢筋 、 截 面尺寸 和形状 、 荷载 类型 和作 用形 式等 因素 ， 所 以构件 受剪是 一个 很复 杂 的问
Ｖｏ １ ． ３ ６ Ｎｏ ．１
２ ０ １ ４年 １ 月
Ｊ ａ ｎ ． ２ ０ ቤተ መጻሕፍቲ ባይዱ ４
文章编号 ： ２ ０ ９ ５ － ２ ７ １ ６ （ ２ ０ １ ４ ） Ｏ １ － ０ ０ ９ ７ － ０ ４
均 匀 受 力 的 混 凝 土 深 梁 抗 剪 性 能
刘君 阳， 杨 梅
（ 河北联合 大学 河北省地震 工程研究 中心 ， 河北 唐 山 ０ ６ ３ ０ ０ ９ ）
中图分 类号 ： Ｔ Ｕ ３ ７ ５ ． １ 文献 标志 码 ： Ａ
钢筋混 凝 土结构 具 有取材 容易 、 造价 相对较 低 、 耐久性 、 耐火性 好及 良好 的可模 性 等优点 ， 因此 在土 木工 程 中得 到 了广 泛 的应 用 。在钢 筋混 凝土结 构设计 中要求尽 可 能避免 构 件发 生脆 性破 坏 ， 其 中典 型 的脆性 破 坏 是 构件 的剪 切破 坏 。为 了避 免构 件发 生剪切 破坏 ， 就需要 研究构 件发 生剪切破 坏 的机理 ， 再 采取 针对 性 的 措 施 。近 年来 关于 混凝 土构件 受剪 的试验 做 了很多 的研究 Ｊ ， 潘 柏荣关 于高 强混凝 土梁 的抗剪 研究 ， 张 复
图 ２ 梁 的 网格 划 分 图
对实体的深梁模型施加 ５ ０ Ｋ Ｎ ／ ｍ的均布荷载 ， 分别对混凝土强度 ； 箍筋 ； 纵筋等方面进行了分析。深梁 在均 布 受力情 况 下 ， 梁 的裂缝 开裂 图。

有限元分析中的应力在有限元分析中，应力是对物体内部的力学状态的描述。

它描述了物体在受力作用下产生的应变情况。

应力可以分为正应力和剪应力两个方向。

正应力是物体内部的力在其中一截面上的投影，即单位面积上的力。

根据胡克定律，正应力与应变成正比。

正应力可以分为拉应力和压应力两种情况。

当物体受到拉力作用后，该截面上的应力为正值，被称为拉应力。

当物体受到压力作用后，该截面上的应力为负值，被称为压应力。

正应力的单位为帕斯卡(Pascal)，常用符号是σ。

剪应力是物体内部的力在其中一截面上的切向分力，即单位面积上的切力。

剪应力有时也被称为切应力。

剪应力在工程中非常重要，因为它反映了物体在受力作用下的剪切变形情况。

剪应力的单位也是帕斯卡(Pascal)，常用符号是τ。

在有限元分析中，通过计算每个单元上的位移，然后通过应力-应变关系求解每个单元上的应力。

应力的计算可以通过以下公式得到：σ=E*ε其中，σ是应力，E是材料的弹性模量，ε是应变。

有限元分析还可以计算相应的应力激活互换载荷。

这意味着，在一些特殊的情况下，我们可以通过改变结构的加载条件来获得相同的应力分布情况。

这对于优化设计非常重要，因为我们可以根据需要来改变材料和几何形状，并通过有限元分析来确定最佳的结构配置。

总之，有限元分析是一种强大的工具，用于求解结构的应力分布情况。

通过计算每个单元上的位移，并应用应力-应变关系，我们可以得到结构的应力分布情况。

应力分析在结构设计和优化中起着至关重要的作用，帮助工程师确定合适的材料和几何形状，并最大程度地减少结构的应力集中。

哈工程有限元大作业均布荷载作用下简支梁结构分析院（系）名称：船舶工程学院专业名称：港口航道与海岸工程学生姓名：白天华学号：03摘要本文利用ANSYS软件中的BEAM系列单元建立简支梁有限元模型，对其进行静力分析与模态分析，得出梁的结构变形，分析梁的受力情况。

并用有限元刚度矩阵知识求解简支梁端点处得位移和旋度。

在此基础上，利用经典力学对以上所得的结果进行梁的有关计算，并将结果与有限元刚度矩阵和ANSYS软件所得结果进行比较。

通过比较得出不同方法在简支梁求解过程中自己的优势和缺点。

1.问题求解问题描述钢制实心梁的截面尺寸为10mm×10mm(如图1所示)，弹性模量为200GPa，均布荷载的大小及方向如图1所示。

图1利用力学方法求解运用力学方法将上述结构求解，易得A、B支座反力相等为500N，该简支梁的计算简图、弯矩图以及剪力图如下图所示1000N/m1000mm图2简支梁计算简图图3简支梁弯矩图支座反力500N图4简支梁剪力图利用ANSYS软件建立模型与求解通过关键点创建实体模型，然后定义材料及单元属性，然后划分网格，建立有限元模型。

具体步骤包括：添加标题、定义关键点、定义直线、选择单元，定义实常数、定义材料属性、设定网格尺寸、划分网格、施加荷载求解（选择分析类型、定义约束、施加荷载）查看分析结果。

图5简支梁变形前后的情况图6简支梁应力图图7简支梁剪力图2计算结果对比简支梁内力分析结果比较节点应力有下面公式计算求得：ᵟ=有限元计算所得结果与力学的计算结果对比如下表所示：单位(N/㎡)节点应力1 02 2703 4804 6305 7206 7507 7208 6309 48010 270ANSYS模态结果结构力学计算结果简支梁竖向位移分析结果比较（1）结构力学计算求得的简支梁最大位移由下面图乘法求得：aFpx实际荷载作用下梁弯矩表达式：M(x)=500x-500x2单位荷载作用下梁弯矩表达式：Mp= (1-a)x (0<x<a)a(1-x) (a<x<1)则在梁上任意点的竖向位移f：f=500+500dx= ……)分别代入分段点的a的数值得各点的位移如下表：a 位移（2）有限元计算所得简支梁y方向位移如下图8所示：图8端点旋度分析结果比较（1）利用结构力学图乘法求得端点处得旋度旋度：Ф=（）=（2）利用有限元刚度矩阵求得端点位移与旋度为：假设梁的两端固定，并计算等价的节点荷载用以表示均匀变化的荷载力M1 -M2R1 R2-1/2qL 12 6L -12 6L v1-1/12qL2 6L 4L2-6L 2L2Ө1-1/2qL =EI/L3-12L -6L 12 -6L v2 (a)1/12qL2 6L 2L2-6L 4L2 Ө2方程（a）是固定的精确模型，因为如果从中解出的所有位移和旋度，它们的计算值都将为零。

第6章梁的应力分析与强度计算梁是一种常见的结构构件，在建筑、桥梁、机械等领域都有广泛的运用。

在使用梁时，需要对其进行应力分析与强度计算，以确保其安全运行。

本章将介绍梁的应力分析与强度计算的基本原理和方法。

1.梁的应力分析梁的应力分析是指对梁内部各点的应力状态进行分析。

应力是指单位截面上受力的大小，常用的应力有轴力、弯矩和剪力。

对于梁的应力分析，主要有两个基本的方程：平衡方程和应变-位移关系。

1.1平衡方程平衡方程是指在梁内力平衡的条件下，梁内部各点的受力平衡。

对于梁来说，平衡方程可以表示为：∑Fx=0∑Fy=0∑M=0其中，∑Fx和∑Fy分别表示横截面上各点受力在X和Y方向的合力，∑M表示横截面上各点受力对横截面上其中一点产生的力矩。

通过求解平衡方程可以得到梁内力的分布情况。

1.2应变-位移关系应变-位移关系是指梁内部各点的应变与位移之间的关系。

梁的应变可以分为轴向应变、横向应变和剪应变三种，位移则可以分为平移位移和旋转位移。

应变-位移关系可以表示为：εx = du/dxεy = dv/dyγxy = (dudv + dvdx)/2其中，εx和εy分别表示横截面上各点的轴向应变，γxy表示横截面上各点的剪应变，du和dv分别表示横截面上各点的位移在X和Y方向上的微分。

2.梁的强度计算梁的强度计算是指根据应力分析的结果，对梁的强度进行评估。

梁的强度主要包括弯曲强度、剪切强度和扭转强度。

2.1弯曲强度弯曲强度是指梁在受到弯矩作用时的抗弯承载能力。

根据弯曲的理论，可以得到梁的最大正应力和最大剪应力。

对于矩形截面的梁来说，最大正应力和最大剪应力可以分别表示为：σmax = M * y / Iτmax = T * Q / It其中，M表示弯矩，y表示梁离中性轴的距离，I表示梁的惯性矩，T表示剪力，Q表示横截面的剪力传递量，It表示横截面的扭转惯性矩。

2.2剪切强度剪切强度是指梁在受到剪力作用时的抗剪承载能力。

ANSYS分析实例与工程应用命令流学习笔记1大纲静力分析：2杆、3梁、5薄膜和板壳、4实体单元梁单元：简化计算，结构总体受力情况实体单元：较复杂的结构，局部细节的受力情况稳定性分析：6振动、模态分析：7简单振动和梁的振动、8膜板和实体振动2杆系结构的静力分析2.1铰接杆在外力作用下的变形二维杆单元LINK1*AFUN,DEG：三角函数默认为弧度，改为角度后处理：结构变形图、显示节点位移和杆件应力2.2人字形屋架的静力分析后处理：杆单元的轴力、轴向应力、轴向应变2.3超静定拉压杆的反力计算后处理：节点反力2.4平行杆件与刚性梁连接的热应力问题定义3点的UY为耦合自由度，即三者的UY位移相等温度（增量）后处理：寻找特定位置的节点和单元，并从单元表中提取它们的内力2.5端部有间隙的杆的热膨胀二维带厚度的平面应力单元PLANE42、二维接触单元CONTACT26温度（始、末）后处理：定义水平应力和铅直应力单元表，并提取3号单元的应力结果*Status,ParmFINISH定义数组变量，将计算结果通过数组变量输出到文件3梁的弯曲静力分析3.1单跨等截面超静定梁的平面弯曲二维弹性梁单元BEAM3后处理：定义以两端弯矩和剪力的单元表，并列出单元表数据并用单元表数据绘制剪力图和弯矩图更细的节点划分方案，更精细3.2四跨连续梁的内力计算体素建模：keypoint, line, area, volume便于细分单元3.3七层框架结构计算3.4工字形截面外伸梁的平面弯曲3.5矩形截面梁的纵横弯曲分析考虑应力强化效应后处理：迭代过程3.6空间刚架静力分析三维梁单元BEAM43.7悬臂梁的双向弯曲三维8节点耦合场实体单元SOLID5三维20节点固体单元SOLID92三维10节点耦合场实体单元SOLID98三维结构实体自适应单元SOLID147定义宏程序，对应四种工况，各种结果差别不大3.8圆形截面悬臂杆的弯扭组合变形三维直管单元PIPE16（只定义外直径，不定义内直径）3.9悬臂等强度梁的弯曲四边形壳单元SHELL63（这里用退化的三角形单元，并使用节点耦合自由度保证模型的对称变形）三维非对称锥形梁单元BEAM44（定义横截面主轴，单元宽度线性变化）计算结果都很好，但壳体单元更能模拟出等强度梁的实际几何形状，更直观，截面定义更简单。

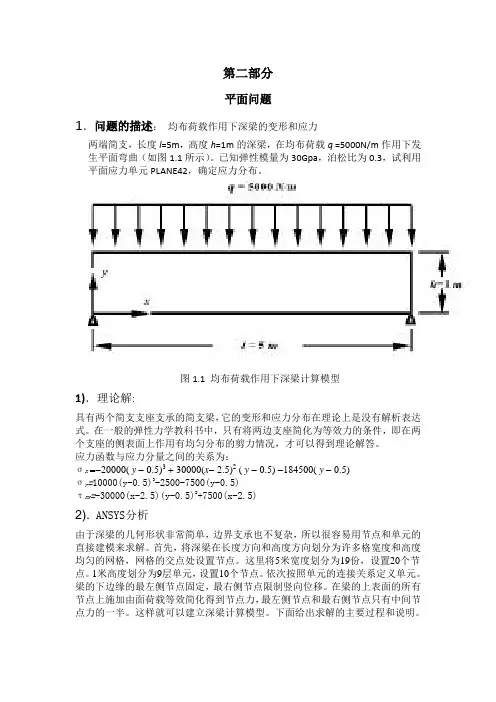
第二部分平面问题1．问题的描述：均布荷载作用下深梁的变形和应力两端简支，长度l=5m，高度h=1m的深梁，在均布荷载q =5000N/m作用下发生平面弯曲（如图1.1所示）。

已知弹性模量为30Gpa，泊松比为0.3，试利用平面应力单元PLANE42，确定应力分布。

图1.1 均布荷载作用下深梁计算模型1)．理论解:具有两个简支支座支承的简支梁，它的变形和应力分布在理论上是没有解析表达式。

在一般的弹性力学教科书中，只有将两边支座简化为等效力的条件，即在两个支座的侧表面上作用有均匀分布的剪力情况，才可以得到理论解答。

应力函数与应力分量之间的关系为：σX=-20000( y - 0.5)3+ 30000(x- 2.5)2 ( y - 0.5) -184500( y - 0.5)σy=10000(y-0.5)3-2500-7500(y-0.5)τXY=-30000(x-2.5)(y-0.5)2+7500(x-2.5)2)．ANSYS分析由于深梁的几何形状非常简单，边界支承也不复杂，所以很容易用节点和单元的直接建模来求解。

首先，将深梁在长度方向和高度方向划分为许多格宽度和高度均匀的网格，网格的交点处设置节点。

这里将5米宽度划分为19份，设置20个节点。

1米高度划分为9层单元，设置10个节点。

依次按照单元的连接关系定义单元。

梁的下边缘的最左侧节点固定，最右侧节点限制竖向位移。

在梁的上表面的所有节点上施加由面荷载等效简化得到节点力，最左侧节点和最右侧节点只有中间节点力的一半。

这样就可以建立深梁计算模型。

下面给出求解的主要过程和说明。

(1) 定义文件名、标题、在前处理模块中通过循环定义节点。

(2) 定义单元类型、实常数、材料参数、循环定义所有单元。

(3) 施加支座位置的约束和上表面的压力荷载(4) 在求解模块开始求解。

(5) 在后处理模块绘制变形图和节点应力云图。

2.Anasys程序：FINISH/CLEAR,NOSTART ! 清除内存中的所有数据,不读入初始化文件/Filename,EX1.1/Title,EX1.1,Deep Beam Under Uniform LoadYS=3E10U=0.3t=1q=5000/PREP7*DO,i,1,20,1 ! 水平方向节点的循环*DO,j,1,10,1 ! 高度方向节点循环N,i+(j-1)*20,(i-1)*5/19,(j-1)*1/9*ENDDO*ENDDOET,1,PLANE42,,,3 ! 定义第1类单元为带厚度的平面单元PLANE82 R,1,t ! 定义单元的第1类实常数:厚度为1MP,EX,1,YSMP,NUXY,1,U*DO,i,1,19,1 ! 水平方向单元循环*DO,j,1,9,1 ! 高度方向单元循环E,i+(j-1)*20,i+(j-1)*20+1,i+(j-0)*20+1,i+(j-0)*20*ENDDO*ENDDOD,1,ALLD,20,UY*DO,k,9,171,9SFE,k,3,PRES,,q*ENDDOFINISH/SOLUSOLVEFINISH! 在后处理模块绘制变形图和节点应力云图/POST1SET,1 ! 读入第1个荷载步的计算结果PLDISP,2 ! 显示变形图(保留原结构轮廓)PLNSOL,S,X ! 在图形窗口显示节点上的X方向正应力PLNSOL,S,Y ! 在图形窗口显示节点上的Y方向正应力PLNSOL,S,XY ! 在图形窗口显示节点上的XY方向的剪应力PLNSOL,S,1 ! 在图形窗口显示节点上的第一主应力PLNSOL,S,3 ! 在图形窗口显示节点上的第三主应力PLNSOL,S,EQV ! 在图形窗口显示节点Mises应力FINISH3．结果分析通过上面程序的计算，可以得到更符合实际模型情况的变形和应力分析结果。

前言在科学研究和工程设计中，基于建模与仿真的数字化已经成为当今科技发展的必然趋势，有限元分析已成为该领域的最重要方法之一。

随着有限元理论和计算机硬件的发展，有限元软件越来越成熟，已逐渐成为工程师实现工程创新和产品创新的得力助手和有效工具。

ANSYS软件是融结构、流体、电磁场、声场和热场分析与一体的大型通用有限元分析软件。

可广泛应用与土木、地质、矿业、材料、机械、仪器仪表、热工电子、水利、生物医学和原子能等工程的分析和科学研究。

经过近40年的发展及完善，ANSYS软件已经成为国际上最知名、应用领域最广泛、使用人员最多的软件之一，是实施有限元分析的最重要平台之一。

对于特定的物理学领域，ANSYS 的软件可让用户能更深入地钻研，从而解决更多种类的问题，处理更为复杂的情况。

除了ANSYS外，没有哪家工程仿真软件供应商能提供如此深入的技术能力。

以真正耦合的方式使用ANSYS 技术，开发工程师即可获得符合现实条件的解决方案。

综合多物理场场产品组合能使用户利用集成环境中的多个耦合物理场进行仿真与分析。

ANSYS的成套产品极具灵活性。

不论是为企业中新手还是能手使用；是单套部署还是企业级部署；是首次通过还是复杂分析；是桌面计算、并行计算还是多核计算，这一工程设计的高扩展性均能满足当前与未来的需求。

ANSYS 是唯一一家能提供客户所需能力水平的仿真软件供应商，而且能随此类需求的发展无限扩展。

工程设计与开发可使用多种CAD产品、内部开发代码、物料库、第三方求解器、产品数据管理流程等其他工具。

与那些刻板、僵化的系统不同，ANSY的软件具有开放性和适应性特性，能实现高效的工作流程。

此外，其产品数据管理可使知识和经验在工作组间与企业内的实现共享。

简单桁架的问题分析问题阐述：设有如图14-1所示的桁架，具体尺寸及受力标注如图。

假设所有杆件为木质材料，弹性模量E=1.90*10^6lb/in^2,且横截面积为8 in^2.试确定每个节点的变形以每个杆件的平均应力。

均布荷载作用下静定多跨连续梁变形分析摘要：从几何构造分析可知，静定多跨连续梁可分解为一个基本部分和多个附属部分。

本文通过逐步计算附属部分受力，将附属部分的计算结果施加到基础部分上，得到整个静定多跨连续梁变形分析，推出梁中的挠度及悬挑端挠度最值的公式。

经过算例表明，最大受力与变形均发生在第一跨附属部分上，将这一变化规律与软件计算结果作比较，提出对于多跨连续梁只需取五跨进行计算的结论，对今后幕墙结构计算中多跨连续梁的分析有一定的借鉴意义。

关键词：多跨连续梁；悬挑梁；均布荷载作用；叠加法；变形0. 引言幕墙结构计算中，整个幕墙的立柱应该是一个整体，简化计算时，为更符合实际情况，取多跨连续梁【1】对立柱进行计算，但是往往幕墙结构都是几十层甚至几百层，对于这类幕墙立柱的计算，目前还没有一个规定，但是实际工程中又比较常见，故本文通过对多跨连续梁在均布荷载作用下的变形分析，得出几点结论，对幕墙龙骨的简化计算具有一定的借鉴意义。

均布荷载作用下的多跨等截面铰接梁的计算简图如图1所示。

1. 静定多跨连续梁的内力求解根据建筑结构静力计算手册【2】和材料力学【3】中的计算公式，将静定多跨连续梁分解为一个基本部分和多个附属部分来逐步计算，将每一个部分外伸梁看作由简支梁AB与固定在截面B的悬挑梁两部分组成。

外伸梁受力分析如图2所示。

1.1 计算计算简支梁跨中截面C的挠度yC和B面的转角θB，由叠加法得出悬挑端的挠度值为：由于，当i=1时，FA为零，Mi值最小，则跨中截面挠度值yc最大，2. 有限元实例分析使用有限元软件3D3S【4】和sap2000【5】分别进行1跨到7跨的连续梁有限元分析，寻求模型变形的规律，梁体的分析模型为每跨梁长4.2米，悬挑端长度为0.4米，梁体采用50*50*5的方钢管【6】，施加1N/mm单位线荷载【7】。

2.1 3D3S模拟分析3D3S建模计算得到各种连续梁的最大挠度（见图3-1—图3-7）。

梁的受力分析与计算梁是一种常见的结构，在建筑工程和机械设计中被广泛应用。

对于梁的受力分析与计算，可以通过数学方法和力学原理进行有效求解。

本文将从基本原理、受力分析、应力求解和变形计算等方面，对梁的受力分析与计算进行详细介绍。

一、基本原理在进行梁的受力分析与计算前，我们首先需要了解一些基本原理。

梁的力学性质由两个主要方面组成：受力分析和变形计算。

受力分析是指对梁的内力分布进行分析，包括弯矩、剪力和轴力等。

变形计算是指对梁的纵向与横向变形进行计算，包括挠度和切变变形等。

二、受力分析1. 弯矩分析梁在受到外力作用时，会产生弯曲变形，形成弯矩。

根据梁的几何形状和外力情况，可以通过弯矩图和弯矩计算公式来进行弯矩分析。

弯矩的大小和分布对梁的受力性能和承载能力有重要影响。

2. 剪力分析剪力是指梁受到垂直于轴线方向的内力作用所引起的剪切应力。

剪力分析可以通过剪力图和剪力计算公式进行求解。

剪力的大小和分布对梁的稳定性和强度具有重要影响。

3. 轴力分析轴力是指梁受到沿轴线方向的内力作用所引起的轴向应力。

轴力分析可以通过轴力图和轴力计算公式进行求解。

轴力的大小和分布对梁的承载能力和变形性能具有重要影响。

三、应力求解在进行梁的受力分析时，除了要对弯矩、剪力和轴力进行计算外，还需要对梁的应力进行求解。

应力是指梁内外部形成的力与横截面积的比值，反映了梁内部的受力状态。

当梁受到外力作用时，会在横截面产生不同的应力分布，包括正应力、剪应力和轴向应力等。

四、变形计算在进行梁的受力分析与计算时，除了要考虑梁的内力分布和应力情况外，还需要对梁的变形进行计算。

梁在受到外力作用时，会产生不同形式的变形，包括弯曲变形、挠度和切变变形等。

这些变形对梁的受力性能和使用寿命有一定影响，需要进行相应的计算和分析。

五、实例分析以下是一个简单的梁实例，通过对这个实例进行受力分析和计算，可以更好地理解梁的受力性能。

假设梁的长度为L，宽度为b，高度为h，材料的弹性模量为E，弯矩M作用在梁的中心位置。

集中力作用下深梁四点弯曲应力计算方法2010年第1期结构强度研究集中力作用下深梁四点弯曲应力计算方法刘志民(中航工业飞机强度研究所四室,西安)摘要:深梁受力机理及影响因素之多决定了深梁计算的复杂性.由于存在纵向纤维挤压和截面的翘曲,深梁不能简单的应用材料力学细长梁纯弯曲应力的计算公式.虽然,深梁计算理论中已有了各种各样的方法,包括级数解法及差分法,有限元法,但应用上,这些理论过于复杂,本文从弹性力学半平面体受集中载荷作用的计算理论出发,推倒出一种简单且易于实现的四点弯曲深梁计算公式,可为工程设计人员在设计深梁时借鉴.关键词:深梁;弯剪耦合;弹性理论;应力计算;翘曲应力1引言工程结构中,梁是最常用构件之一,在试验中考虑梁的成本因素,缩小梁跨高比,一般小于8[1],这种短梁在工程结构中称为深梁.当梁上作用集中载荷时,出现弯剪耦合现象,此时梁横截面上不仅有正应力还有剪应力.由于剪应力的存在,梁的横截面上会发生翘曲现象,并与中性层平行的截面出现挤压现象.一般来说,跨高比小于5的梁,用材料力学中细长梁的纯弯曲理论及假设计算时,误差会随跨高比减小而迅速增大,这样,细长梁理论就不适应了.文献[2]的研究表明:深梁应力计算主要影响因素有截面,支座约束,跨高比,究其原因是在集中力作用下发生弯曲变形时,平截面假设和纵向纤维相互不挤压的假设与实际相差太大,这就决定了深梁应力分析的复杂性.虽然,复杂截面的深梁应力分析有很多方法,如文献[3]和文献[4]研究了有限元方法在深梁理论的应用;文献E53研究了有限积分法的应用;文献E6J研究了级数解法的应用.文献[7]给出对于均布载荷作用下深梁横力弯曲应力的解, 在集中力作用下,梁内应力分布的研究较少,文献[8]研究了大变形下集中力作用的梁的受力特性; 文献[9]研究了集中力在三点弯曲下对深梁弯剪耦合变形应力计算方法,但未见有关论文研究四点弯【Hj深梁在集中力影响下的应力分布问题.因收稿日期:2009—10—15此,研究四点弯曲作用下的深梁的受力特性及简化计算方法对于工程设计具有重要意义,对于掌握复杂截面深梁应力分布也有理论价值.:1.1集中力产生的应力场本文研究两端简支时四点弯曲的横力问题,以矩形截面为例,结果推广到工字型截面.本文基于以下考虑:梁跨中有单位厚度上的集中力F1,F2的作用;当梁为简支时,梁两端受剪力和弯距的共同作用.由深梁的特点可知:当梁承受集中力时,跨度小,梁高大,其跨中截面的挠度较小.故对深梁而言,在以力的作用点为圆心的区域内按半平面体考虑集中力P引起的应力分布,如图1所示.这样即可根据弹性力学半平面体在边界上受集中力时的应力计算方法得出梁内的应力分布.P\』/'./,一///1y图1计算简图结构强度研究2010年第1期由文献[10]知,集中力F在其作用点为圆心的区域内引起的正应力的直角坐标表达式为: ,一一兰!r丌(z.+Y.).同理,梁两端在集中反力作用下,梁内也会产生应力场,按照叠加原理,梁内应力由4个集中力产生的应力场叠加而得.本文为统一起见,建立如图2所示整体坐标系,为此,需要对各个集中力作用点的局部坐标系进行坐标变换.F1F2图2坐标系的定义对于F1的应力场,有如下坐标变换式:』F一z+(Ls—(2)1YF1一Y+h/2对于F2的应力场,有如下坐标变换式:』z咒一一(Ls一(3)1yFz—Y+h/2对于R1的应力场,有如下坐标变换式:』确一一z—Ls(4)1YRI一一Y+h/2对于R2的应力场,有如下坐标变换式:,戤一一z十Ls(5)1YR2一一Y+h/2以上各式中,(z,1,,1),(zF2,Y),(zRl,Ym),(,Y)分别为集中力F1,F2,支座反力R1,R2的作用点在图2所示的整体坐标.由于在试验机进行四点弯曲试验时,F1,F2是由加载夹具实现的,并保证F1一F2一g/2,由力的平衡原理知F1 =::F2=R1一R2一l:/Z,F1,F2,R1,R2的正负以梁的总体方向为标准.将式(2)～式(5)代入式(1),可以得FF(z+Ls—Z).(+h/2)一,F(z—Ls+Z).(+h/2)'丌[(z—Ls+z)+(+h/Z).]F(z+Ls).(～Y+h/2)7r[(z+Ls)+(一Y+h/2).]一￡三二!=±垒丌[(—Ls)+(一Y+h/2).]式中:Ls为单侧跨距,为力臂.(6)1.2弯矩和剪力共同作用时的弯曲正应力梁在集中力的作用下,不仅有剪力也有弯矩,所以不仅有剪力产生的应力,还有弯矩产生的应力.按照细长梁理论弯矩产生的应力一,另根据1.1节分析,剪力产生的应力如(6)式所示,按照叠加原理在弯剪共同作用下,正应力应为:一～F+MMy.F(z+Ls—Z)(+h/2)一丁十FYh—/2孵)I',r[(z+Ls—z)+(+].F(z—Ls+Z)(+h/2)丌[(z—Ls+z)+(+h/2)]F(+Ls)(一Y-+-h/2)7r[(z+Ls)+(一Y+h/2)].F(z—Ls)(一Y+h/Z)7f[(z—Ls)+(一Y+h/2)].(7)当式中l=L,式(7)可转化成三点弯曲时应力分布形式见图3.图3三点弯曲受力状态.2Fz0(v+h/2)一亍十F(+Ls)(一Y+hi2)丌[(z+Ls).+(一Y+h/2)].F(—Ls)(一Y+h/2)丌[(z—Ls)+(一Y+h/2).].(8)将图3中坐标系统变为图4中坐标系统,此时坐标变换式为:l011【),,11一三1一},图4文献[9]坐标系统十.-2010年第1期刘志民:集中力作用下深梁四点弯曲应力计算方法fz1一z+Ls《l1一Y将式(9)代入(8)得甘2㈣一:二一My+2F丌Fz;(一Y+h/2)7r[(z;-4-(一Y+h/2)].F(z1一Z112).(一1+h/2)7r[(1一z1/2)+(一Y1+h/2)]式(1O)与文献[9]保持一致.2公式的无量纲化分析(10)为了方便计算和分析,引入下列无量纲量一,剪跨比17一麦(o&lt;1),跨高比a一兰,h一,五是用来描述四点弯曲与三点弯的近似程度,当志一1时候,即四点弯曲转化成三点弯曲. 将无量纲量带入式(7),可得My.Ff4(-4-1——忌)0a.(-4-1)一丁十{干研,4(刁一1+是)口.(+1).[(刁一1+忌)口+(+1)]一垒±2::!二至±[(刁+1)口+(一+1).]一洋},[(叩一1).a+(一+1).]}u令】一4(互+1一忌)口(+1)"[(刀+1一是)a+(+1)].二±生生±2'[(一1+).口.+(+1)]4(+1)口.(～+1)[(叩+1).口+(～+1)]一!望二:!(二皇±[(一1).a.+(～+1)].则一+,一十(1z)易知,式(t2)无量纲量反映了深梁应力计算方法与材料力学细长梁理论应力之差别.由于它是从深梁微元受力分析得出的,考虑了弯剪对梁共同作用的结果,所以具有通性.为了更直观的表示F1,F2引起的翘曲应力的影响,将(12)式无量纲化,则无量纲正应力为:式中:一?志为无量纲翘曲应力.以下分不同支座约束,不同截面形状给出无量纲翘曲应力.1)当支座形式为简支时,当剪跨比17&lt;1一k时,M=等?z;171一k,M一?(Ls—z).a)对于矩形截面,J一b3代入无量纲应力表达式,得:一卜忌J一——一171一k3~m$(1--J一——y)172一b)对于双轴对称工字梁截面(如图5),设上缘条,下缘条面积为A,宽度为b,距中性轴距离为hz,h,腹板高度为ho,厚度为,面积为A,,梁高为h.I\l\●,Ah2ho^Ahl,l/J为便于计算,在设一口,一n,A一卢则口一日一1,A=(1+2f1)A,,一等?一&lt;一是酶一忌3分析验证由式(13)可以看出,本文定义的无量纲翘曲结构强度研究2010年第1期应力实际上是深梁应力计算结果与细长梁理论解之间的差值.为方便起见,如图6,图7所示给出了不同跨高a比下,矩形截面梁和工字型截面梁一的关系图,由图6可以看出,当梁为矩形截面时候,随着跨高比的增大,梁的上表面(一一l时)无量纲翘曲应力影响范围逐渐减小并且误差较小,当跨高比为5时,梁的上表面的应力和材料力学计算结果相比误差不超过15,在结构设计中是可以接受的范围.而对于工字型截面梁来说,由于截面形状对于梁内应力分布有影响,当跨高比为5时候,剪跨比为0.6处时,计算结果比材料力学理论解大2O以上.对同一跨高比下的深梁而言,从图6和图7可以看到,当深梁跨高比一定时,在力F处均出现拐点这是由于支座集中力在梁内产生的应力场和集中力F1,F2产生的应力场叠加的结果,随着剪跨比的增加,支座产生的应力场的影响大于集中力的影响,从而出现拐点.跨高比越大,拐点越明显,这说明本文解是符合真实情况的.图6和图7可以看出,无论矩形截面深梁还是工字型截面深梁无量纲翘曲应力的值都在支点附近明显增大,在纯弯曲段(图中剪跨比77&lt;O.533时)无明显变化,且数值较弯剪耦合段(图中剪跨比l&gt;叩&gt;0.533)时小,这说明,剪力引起的翘曲在深梁计算中有重要的影响. 由图6,图7中拐点和可以看出,工字型截面受到弯剪耦合的影响比矩形截面的大.lo0%一90%80%70%60%枢50%霸40%鞣0%l00%90%80%70%.50%钽40%嗣30%萋:0%--I从上到下跨高比a:1,2,3,4,5卜_————_【\/I\/』\/7\//f\//』/\,—X,l剪跨比()图6矩形梁的一关系图]从上跨高I//7[{～\//————～二/|\—～—\///——,——:===—√——\0.3040.5060.70809l剪跨比()工字梁的一k关系图为了验证公式的正确性,本文以一例来说明.设有一矩形截面深梁,两端简支,h一30mm,l一50mm,L一100mm,E一210GPa,v一0.3.当Fl =F2—1000N时,分别用本文解,材料力学细长梁理论,有限元法计算出集中力F2截面应力沿梁高度变化如图8所示.l_///一细长梁理论解r//lIl,////'/,剡本文解【越枢J/一/J',,-{有限元法I/一一,/一一x向应】图8集中力F2作用截面相对应力分布规律图1)从上图可以看出,本文计算结果介于有限元计算结果和材料力学解之间,由圣维南原理可知,这是符合事实的.2)深梁中性轴下移,而不是与梁中心线重合,此结论与文献[6]和文献[9]相同,是因为考虑了纵向纤维受挤压.3)矩形截面四点弯曲深梁在纯弯曲段应用本文公式计算结果比材料力学细长梁理论计算结果大10以内,弯剪耦合段的结果比材料力学细长梁理论计算结果大20以上,所以试验件设计不得不考虑在集中力作用点处的应力水平.若集中力作用点处的应力水平大于纯弯曲段的应力水平则梁可能在集中力作用点处先断裂.4)在梁内力推导过程中,认为力是垂直于梁上下表面的,事实上梁受到力的作用时候,发生弯曲,力不再垂直梁上下面的,所以本文公式是有误差的,因为深梁挠度很小,所以误差是可以忽略的.4结论综上所述,深梁在集中力作用下,按照细长梁理论计算会产生一定误差,这是由于深梁承受的剪力也产生较大的应力.用无量纲应力.来描述这种影响,则k随剪跨比增大而增大,随跨高比减小而增大,截面形式也对的变化产生影响.当然,本文推导也不是没有误差,主要表现为梁受到集中力F1,F2作用时候产生挠度,这导致2010年第1期刘志民:集中力作用下深梁四点弯曲应力计算方法39 梁轴线不再是直线,使支座处集中力不再垂直于梁下表面.但由于深梁挠度小,本文提出的计算方法引起误差较小.本文用弹性力学理论推导出了集中力作用下弯曲正应力的计算公式,一改以往在深梁理论中求解的复杂性,使深梁问题的解更接近工程实际.公式优点表现在:(1)在概念上较清晰,计算简单;(2)在精度上,较材料力学细长梁理论精确,可以作为工程设计用.参考文献[1]王正中,沙际德.深孔钢闸门主梁横力弯曲正应力与挠度计算[J].水利,1995(9):4o一46.[2]王正中,李良晨.薄壁刚梁的临界跨高比[J].力学与实践,1997,19(4):23—24.[3]杨伯源,巫绪涛,李和平.剪切弯曲下短梁位移数值计算精度的研究[J].应力学,2003,20(2):145—146.[4]甫良,曾德顺.深梁的精确解[J].力学与实践,2002,24 (3);58—6O.[5]王贵芳.简支深梁的应力分析口].成都科技大学, 1993,70(3);70—76.[6]丁大钧,刘伟庆.深梁杆件力学解[J].工程力学,1993, 10(1):10—18.[7]陈林之,李章政.均布载荷作用下连续深梁问题的级数解答[J].设计与研究,2005,32(9):3O一32.[8]蒋玉川,胡兴福,陈辉.简支梁用和函数法的级数解答[J].四川大学(工程科学版),2006,38(6).[9]王正中,朱军柞,郭佳陇.集中力作用下深梁弯剪耦合变形应力计算方法[J].工程力学,2008,25(4),115—12O.[10]徐芝纶.弹性力学简明教程[M](第三版).北京:高等教育出版社,2002.作者简介:刘志民(1983一)男,天津市人,中航工业飞机强度研究所四室助理工程师,毕业于南京航空航天大学,学士,主要从事热强度与综合环境强度研究.通信地址:西安市86号信箱邮政编码:710065联系电话:029—88268609(上接第43页)果的精度与网格数,网格疏密程度,松弛因子等因素密切相关.只有在合适的网格数和网格疏密程度以及一定的松弛因子条件下才能达到比较满意的结果.参考文献[1]Gray,D.D.,andGiorgin,A.,TheV alidityofthe BoussinesqApproximationforLiquidsandGases,Int.J.HeatMassTransfer,vo1.19,1976,PP.545—551.[2]PaillereH,ViozatC,KumbaroA,eta1.Conparisonof lowroachnumbermodelsfornaturalconvectionprob—lems[J].HeatandMassTransfer,2000,36:567—534.[3]陶文铨.数值传热学(第二版)rM-].西安交通大学出版社,2001.1-4]杨世铭.传热学[M].西安交通大学出版社,1982.作者简介:秦强(1983一)男,河南安阳人,中航工业飞机强度研究所在读硕士研究生,主要从事结构传热,强度分析与优化设计研究.通信地址:西安市86号信箱邮政编码:710065联系电话:029—88268609。

体同山阿。 57、春秋多佳日，登高赋新诗。 58、种豆南山下，草盛豆苗稀。晨兴 理荒秽 ，带月 荷锄归 。道狭 草木长 ，夕露 沾我衣 。衣沾 不足惜 ，但使 愿无违 。 59、相见无杂言，但道桑麻长。 60、迢迢新秋夕，亭亭月将圆。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非

不同荷载条件下的梁的应力研究梁是一种常见的结构元素，广泛应用于建筑、桥梁和机械等领域。

在设计和使用梁时，了解不同荷载条件下的应力状况对于确保结构的安全性至关重要。

本文将探讨不同荷载条件下梁的应力研究。

一、自重荷载下的梁应力研究自重荷载是指梁自身的重量所产生的荷载。

在没有外部荷载作用下，梁承受着自重荷载。

自重荷载会导致梁产生弯曲应力和剪切应力。

弯曲应力主要集中在梁的上、下表面，而剪切应力则主要集中在梁的截面中部。

根据梁的几何形状和材料特性，可以通过弯曲理论和剪切理论计算出梁在自重荷载下的应力分布情况。

二、集中荷载下的梁应力研究集中荷载是指作用于梁上的单个荷载点，例如悬挂物体或集中力。

集中荷载会导致梁产生局部应力集中现象。

在集中荷载作用下，梁的应力分布与自重荷载下的情况有所不同。

集中荷载会引起梁的弯曲和剪切应力的集中，特别是在荷载作用点附近。

为了确保梁的安全性，需要根据荷载大小和梁的几何形状，进行应力计算和结构设计。

三、均布荷载下的梁应力研究均布荷载是指作用于梁上的均匀分布的荷载，例如自重荷载、人员荷载或储物荷载。

均布荷载会导致梁产生均匀的弯曲应力和剪切应力。

在均布荷载作用下，梁的应力分布相对均匀，但仍然需要进行准确的应力计算和结构设计，以确保梁的稳定性和安全性。

四、动荷载下的梁应力研究动荷载是指梁上的变化荷载，例如行人或车辆的移动荷载。

动荷载会导致梁产生动态响应和振动，从而引起应力的变化。

在设计梁结构时，需要考虑动荷载对梁的应力影响，并进行相应的振动分析和结构设计，以确保梁的安全性和舒适性。

五、总结不同荷载条件下的梁应力研究对于结构设计和安全评估至关重要。

自重荷载、集中荷载、均布荷载和动荷载都会对梁的应力分布产生影响。

通过准确的应力计算和结构设计，可以确保梁在各种荷载条件下的稳定性和安全性。

同时，应力研究的结果也为梁的优化设计和结构改进提供了重要的参考依据。

在实际工程中，还需要考虑梁的材料特性、梁的几何形状和支座条件等因素对应力的影响。

有限元分析上级报告学院：专业：姓名：班级：学号：均布荷载作用下深梁的变形和应力两端简支，长度l=5m，高度h=1m的深梁，在均布荷载q =5000N/m作用下发生平面弯曲（如图4.1所示）。

已知弹性模量为30Gpa，泊松比为0.3，试利用平面应力单元PLANE82，确定跨中的最大挠度，和上下边缘的最大拉压应力。

4.1 均布荷载作用下深梁计算模型1．理论解具有两个简支支座支承的简支梁，它的变形和应力分布在理论上是没有解析表达式。

在一般的弹性力学教科书中，只有将两边支座简化为等效力的条件，即在两个支座的侧表面上作用有均匀分布的剪力情况，才可以得到理论解答。

(1) 设定应力函数。

获得这种情况下的解答的主要思路是：按照应力解法，考虑到应力分量关于该梁中心位置（x=2.5，y=0.5）有对称和反对称关系。

可以首先假定一个应力函数为：Φ = A(y - 0.5)5+ B(x - 2.5)2 (y -0.5)3 +C(y -0.5)3+ D(x- 2.5)2+ E(x -2.5)2 (y - 0.5) (4.1)依据这个应力函数，可以获得各个应力分量，按照上表面受均布压力作用简支梁的上下表面和左右侧表面的应力边界条件，确定出应力函数（4.1）中的各个待定系数A，B，C，D和E。

按照应力求解平面应力问题方法，应力函数应该满足双调和函数：∇2∇2Φ = 0 (4.2)将（4.1）应力函数代入上式后，得到：24 B( y - 0.5) +120A(y - 0.5) = 0 (4.3)即：B = -5A (4.4)(2)确定应力分量。

应力函数与应力分量之间的关系为：(3) 利用梁的上下表面边界条件确定积分常数。

上表面受均布压力作用简支梁的上表面（y=h=1m）的应力边界条件:下表面(y=0)的应力边界条件:(5) 将梁的左右端面边界条件降低为积分满足。

考察边界条件（4.13）到（4.16），可以看出，无法找到能满足两端侧表面的所有应力边界条件的待定系数。