自动控制理论(邹伯敏)第3版_第6章答案 khdaw

《自动控制原理（第3版）》部分习题答案第2章C2-1(a) 21211()(1)()()(1)R sL R Cs G s R sL R Cs R ++=+++C2-221114232233342526()()(1)(1)()()()()()()()()()()()()()m a a a a a e ma a L a a a a e m f fR G s K R R G s R Cs K T s R G s K c s G s U s JL s L f JR s fR c c L s R s G s M s JL s L f JR s fR c c U s G s K s =-=-=-+=-+=-Ω==++++-+Ω==++++==Ω 123412346512346()()()()()()1()()()()()()()()1()()()()()r L G s G s G s G s s U s G s G s G s G s G s G s s M s G s G s G s G s G s Ω=+Ω=+C2-4(a) 3123123()()()R LsG s R R R Ls R R R =++++C2-4(b) 323123()()()R LsG s R R Ls R R R =+++C2-5321122211212311(1)(1)(),(),(),()()1a b c d R Cs R Cs R C s R C s RG s RCs G s G s G s R Cs R C s R R R Cs ++++=-=-=-=-++ C2-612314512123214342123312341232233344()()()()()()()1()()()()()()()()()()()()()()()()()()()()1()()()()()()()()()()a b G s G s G s G s G s G s G s G s G s H s G s G s H s G s G s H s G s H s G s G s G s H s G s G s G s G s G s G s G s G s H s G s G s H s G s G s H s +=++++++=+++-12341()()()()()G s G s G s G s H sC2-713241761113241762851324()()[1()()]()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ 283261213241762851324()()()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +=+++++ 24132852213241762851324()()[1()()]()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ 17413152113241762851324()()()[1()()]()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ C2-812341123243123312312()()()()()1()()()()()()()()()()()()()()()()G s G s G s G s G s G s H s G s G s H s G s H s G s G s G s H s G s G s G s H s H s +=+++++C2-9 12345214561111452145145124561112322()()()[1()()()]()()()()()()()1()()()()()()()()()()()()()()()()[1()()]()()(()()()G s G s G s G s G s H s G s G s G s G s C s s R s G s H s G s G s H s G s G s G s G s G s G s H s H s G s G s G s G s H s G s G s G C s s R s --Φ==+-+-++Φ==4511452145145121122)()()1()()()()()()()()()()()()()()()()()()s G s G s G s H s G s G s H s G s G s G s G s G s G s H s H s C s s R s s R s +-+-=Φ+Φ C2-1013453564256313421356253431342535643535123561434523345624()()[1()()]()[1()()]()()1()()()()()()()()()a G s G G G s G H s G G H s G G G s G H s G G H s G G G G s G G G G s G H s G G H s G H s G G H s G G s G G H H s G G G H H s G G G H H s G G G G H H s =++++++-+++++++++12353241212131223123()()()()()[1()]()[1()()2()()]()1()()2()()()()2()()()b G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++++++=+++++第3章C3-1 21()Ts TsK e Tse G s T s ----=C3-2 220.910()1110s s s s s ++Φ=++C3-3105050()10.283sin(545)()1 1.4sin(545)t t tc t e e t c t et ---=--+=-+精近C3-422*0.23()(0.5)2*0.23()0.50.23G s s s s s s =+Φ=++C3-51212T T bK T T ε+<<C3-6 阶跃信号作用下稳态误差为零，要求n m a b =加速度信号作用下稳态误差为零，要求1122,,n m n m n m a b a b a b ----=== C3-7 21()(1)c sG s K T s =+C3-8 24()(46)G s s s s =++C3-9 250()(1225)G s s s s =++ C3-100.243τ=C3-11 (1)06,(2)303,(4)010/3K K K <<<<<<结构不稳（）C3-12 (1)015,(2)0.72 6.24K K <<<< C3-13(1)(2)34系统稳定系统不稳定，有两个右根，（）系统稳定（）系统不稳定，有三个右根C3-14 3,K ω==C3-1533231()()1()()()()()n r G s G s G s H s G s G s G s =-+=第4章C4-1 图略C4-2 (1)图略 (2) 2233()24x y ++=C4-3 (1)图略 (2) 0.40.5K <<C4-4 分会点和渐近线123=0,,2,22a a d d d a πδϕ-+==±12320,2a d d d ====-(1)当时，图略 123180,6a d d d ====-(2)当时，图略 120,0a a d σ<=>(3)当0<时，图略 1180,0a a d δ<=<(4)当2<时，图略12318,,0a a d d d δ><(5)当时，三个不同实数分会点，图略C4-5(1) 图略,原系统不稳定;(2)增加零点且选择合适位置,可是系统稳定,零点05z << C4-6图略,系统稳定34K > C4-7 (1) 图略(2)当0.8629.14K <<,系统为欠阻尼状态,且 1.87K =阻尼比最小,系统地闭环极点为3 2.8j -±(3)试探求得 2,4 2.8K j =-±闭环极点, 1.06,0.75~1P s M t == C4-8 (1)等效开环传递函数为: (1)()(2)K s G s s s --=+正反馈系统根轨迹, 图略(2)系统稳定02K <<(3) 2,K ω==C4-9等效开环传递函数为: 22()===10)(44)(4410)Ka K G s K a s s s K s s s ''++++等（,图略 C4-10(1) 图略(2) 64,K ω==(3)1,20.5,1s ζ==-±C4-11(1) 图略 (2) 不在根轨迹上; (3) ()1cos 4c t t =-C4-12等效开环传递函数为: 322()=(4416)(4)(4)K KG s s s s s s s s =+++++等,K=8时试探求第5章C5-1(1)C5-1(2)C5-1(3)C5-2000(1)()0.83sin(30 4.76)(2)()0.83sin( 4.76) 1.64cos(2459.46)c t t c t t t =+-=----C5-3当12T T <,系统稳定当12T T >,系统不稳定. C5-4 2100()10100G s s s =++ C5-5(a) 0110(1)300(),4111(1)(1)510s G s s s γ+==++ (b) 00.1(),2581(1)50sG s s γ==+(c) 032(),141(1)2G s s s γ==+(d) 025(), 1.66(1001)(0.11)G s s s s γ==-++(e) 020.5(21)(),36.8(0.51)s G s s s γ+==+ (f) 0231.62(),9.860.010.0981G s s s γ==++ C5-6 (1) K=1(2)K=25(3)K=2.56(或精确求K=3.1) C5-7()()()a g i 稳定，(b)不稳定，(c)稳定，(d)稳定，(e)不稳定，(f)稳定，不稳定，(h)不稳定，不稳定，(j)不稳定，C5-8 102510000K K <<<和 C5-9（1）（2）闭环系统稳定； （3）078.5,g K γ==∞（4）K 增大10倍，对数幅值上升，但相频特性不变，系统的快速性提高，平稳性降低，系统地抗干扰性降低。

2012年6月23日星期六课程名称: 自动控制理论 （A/B 卷 闭卷）一、填空题（每空 1 分，共15分）1、反馈控制又称偏差控制，其控制作用是通过 与反馈量的差值进行的。

2、复合控制有两种基本形式：即按 的前馈复合控制和按 的前馈复合控制。

3、两个传递函数分别为G 1(s)与G 2(s)的环节，以并联方式连接，其等效传递函数为()G s ，则G(s)为 （用G 1(s)与G 2(s) 表示）。

4、典型二阶系统极点分布如图1所示，则无阻尼自然频率=n ω ，阻尼比=ξ ，该系统的特征方程为 ，该系统的单位阶跃响应曲线为 。

5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+，则该系统的传递函数G(s)为 。

6、根轨迹起始于 ，终止于 。

7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--，则该系统的开环传递函数为 。

8、PI 控制器的输入－输出关系的时域表达式是 ， 其相应的传递函数为 ，由于积分环节的引入，可以改善系统的 性能。

二、选择题（每题 2 分，共20分）1、采用负反馈形式连接后，则 ( )A 、一定能使闭环系统稳定；B 、系统动态性能一定会提高；C 、一定能使干扰引起的误差逐渐减小，最后完全消除；D 、需要调整系统的结构参数，才能改善系统性能。

2、下列哪种措施对提高系统的稳定性没有效果 ( )。

A 、增加开环极点；B 、在积分环节外加单位负反馈；C 、增加开环零点；D 、引入串联超前校正装置。

3、系统特征方程为 0632)(23=+++=s s s s D ，则系统 ( )A 、稳定；B 、单位阶跃响应曲线为单调指数上升；C 、临界稳定；D 、右半平面闭环极点数2=Z 。

4、系统在2)(t t r =作用下的稳态误差∞=ss e ，说明 ( )A 、 型别2<v ；B 、系统不稳定；C 、 输入幅值过大；D 、闭环传递函数中有一个积分环节。

第一章习题参考答案1-1多速电风扇的转速控制为开环控制。

家用空调器的温度控制为闭环控制。

1-2 设定温度为参考输入，室内温度为输出。

1-3 室温闭环控制系统由温度控制器、电加热装置、温度传感器等组成，其中温度控制器可设定希望达到的室温，作为闭环控制系统的参考输入，温度传感器测得的室温为反馈信号。

温度控制器比较参考输入和反馈信号，根据两者的偏差产生控制信号，作用于电加热装置。

1-4 当实际液面高度下降而低于给定液面高度h r ，产生一个正的偏差信号，控制器的控制作用使调节阀增加开度，使液面高度逼近给定液面高度。

第二章 习题参考答案2-1 （1）()()1453223++++=s s s s s R s C ； （2）()()1223+++=s s s ss R s C ； （3）()()1223+++=-s s s e s R s C s2-2 （1）单位脉冲响应t t e e t g 32121)(--+=；单位阶跃响应t t e e t h 3612132)(----=； (2)单位脉冲响应t e t g t 27sin72)(-=；单位阶跃响应)21.127sin(7221)(2+-=-t e t h t 。

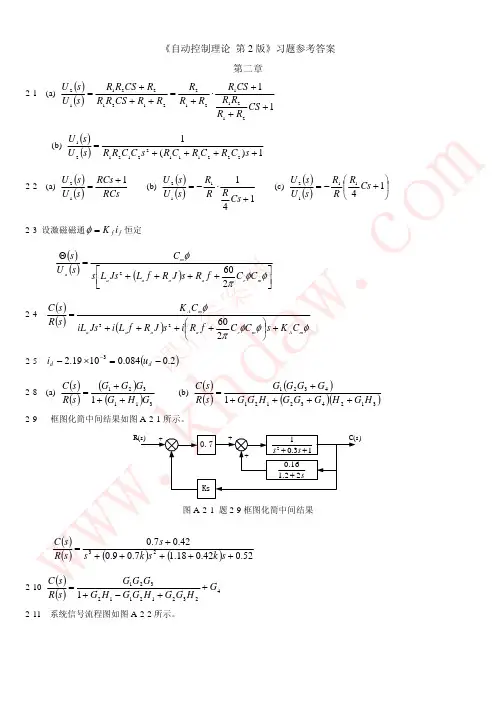
2-3 （1）极点3,1--，零点2-；(2) 极点11j ±-.2-4)2)(1()32(3)()(+++=s s s s R s C . 2-5 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U ;(b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-6 (a)()()RCsRCs s U s U 112+=;(b)()()141112+⋅-=Cs RR R s U s U ; (c)()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U . 2-7 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602.2-8()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=26023.2-9 ()2.0084.01019.23-=⨯--d d u i . 2-10 (2-6) 2-11(2-7)2-12 前向传递函数)(s G 改变、反馈通道传递函数)(s H 改变可引起闭环传递函数)()(s R s C 改变。

119第六章习题及解答6-1 试求下列函数的z 变换T ta t e =)()1(()()223e t t e t=- 21)()3(ss s E +=)2)(1(3)()4(+++=s s s s s E解 （1）∑∞=---=-==0111)(n nnaz z azza z E（2）[]322)1()1(-+=z z z T t Z由移位定理：[]333323333232)()()1()1(TTTTTTte z ez zeT ze ze zeT et Z -----+=-+=（3）22111)(ssss s E +=+=2)1(1)(-+-=z Tz z z z E （4）21)(210++++=s c s c sc s E21)1(3lim212)2(3lim23)2)(1(3lim221100=++=-=-=++==+++=-→-→→s s s c s s s c s s s c s s s2211223+++-=s s s)(22)1(23)(2TT e z ze z z z z z E ---+---=6－2 试分别用部分分式法、幂级数法和反演积分法求下列函数的z 反变换。

120()()()()11012E z z z z =-- 211213)()2(---+-+-=z zz z E 解 （1）)2)(1(10)(--=z z zz E① 部分分式法)12(10210110)()2(10)1(10)(210110)2)(1(10)(-=⨯+⨯-=-+--=-+--=---=nnnT e z zz z z E z z z z zz E② 幂级数法：用长除法可得+-+-+-=+++=+-=--=---)3(70)2(30)(10)(7030102310)2)(1(10)(*3212T t T t T t t e z z z z z z z z z z E δδδ③ 反演积分法[][])()12(10)()12(10210110)(210110lim)(Re 10210lim)(Re 0*221111nT t t e nT e z zzz E s z z z z E s n nnnnnz z n nz z n --=-=⨯+⨯-=⨯=-=⋅-=-=⋅∑∞=→→-→→-δ（2） 2221)1()13(12)13(213)(-+-=+-+-=+-+-=--z z z z z z z zz zz E① 部分分式法∑∑∞=∞=---=-⎥⎦⎤⎢⎣⎡--=⨯--=----=----=--=0*222)()32()(32)()(132)(13)1(2)(13)1(2)1(31)(n n nT t n nT t nT Tt e t t Tt e z z z z z E z z z z zz E δδ121② 幂级数法：用长除法可得--------=-----=+-+-=---)3(9)2(7)(5)(3)(9753123)(*32122T t T t T t t t e zzzz z z z z E δδδδ③ 反演积分法[][]12111)3(lim!11)(Re )(-→→-⋅+-=⋅=n s z n zz zdzd z z E s nT e[]32)1(3lim 11--=++-=-→n nzz n n ns∑∞=---=*)()32()(n nT t n t e δ6-3 试确定下列函数的终值()()()11112E z Tzz =--- )208.0416.0)(1(792.0)()2(22+--=z z z zz E解 （1）∞=--=---→21111)1()1(lim zTz z e z ss（2）1208.0416.01792.0208.0416.0792.0lim)()1(lim 2211=+-=+-=-=→→z z zz E z e z z ss6-4 已知差分方程为c k c k c k ()()()-+++=4120初始条件：c(0)=0,c(1)=1。

第一章绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答：1开环系统(IX 点：结构简单，成本低，工作稳定。

用于系统输入信号及扰动作 用能预先知道时，可得到满意的效果。

(2)缺点：不能自动调节被控量的偏差。

因此系统元器件参数变化， 外来未知扰动存在时，控制精度差。

2闭环系统(1) 优点：不管由于干扰或由于系统本身结构参数变化所引起的被控量 偏离给定值，都会产生控制作用去清除此偏差，所以控制精度较高。

它是一种按偏差调节的控制系统。

在实际中应用广泛。

(2) 缺点：主要缺点是被控量可能出现波动，严重时系统无法工作。

1- 2 什么叫反馈？为什么闭环控制系统常采用负反馈？试举例 说明之。

解答：将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。

闭环控制系统常釆用负反馈。

由IT 中的描述的闭环系统的优点所证 明。

例如，一个温度控制系统通过热电阻(或热电偶)检测出当前炉 子的温度，再与温度值相比较，去控制加热系统，以达到设定值。

试判断下列微分方程所描述的系统属于何种类型(线性，非 线性，定常，时变)？2心芈+ 3如+ 4、⑺=5如+ 6叩) (1) dr dt ・Clt⑵ y(r) = 2 + w(r)(2)非线性定常 (3)线性时变 (5)非线性定常 (6)非线性定常(4)(5)(6)(7)牛2曲)=4響+叩)dtdt ——+ 2 y(∕) = “(f) Sin ωt dt学+ W)攀+ 2W)j ⑴ dr dt 学+ F ⑴=2“⑴ dtdty(t) = 2u(t) + 3du ⑴ +dt 5∫M(r)Jr 解答：(1)线性定常(4)线性时变 (7)线性定常1-4如图1-4是水位自动控制系统的示意图，图中Q1, Q2分别为进水流量和出水流量。

控制的目的是保持水位为一定的高度。

试说明该系统的工作原理并画出其方框图。

QlQ2O―题1-4图水位自动控制系统解答：(1)方框图如下:⑵工作原理：系统的控制是保持水箱水位高度不变。

第一章 习题答案1-11-21-3 闭环控制系统主要由被控对象，给定装置，比较、放大装置，执行装置，测量和变送装置，校正装置等组成。

被控对象：指要进行控制的设备和过程。

给定装置：设定与被控量相对应给定量的装置。

比较、放大装置：对给定量与测量值进行运算，并将偏差量进行放大的装置。

执行装置：直接作用于控制对象的传动装置和调节机构。

测量和变送装置：检测被控量并进行转换用以和给定量比较的装置。

校正装置：用以改善原系统控制性能的装置。

题1-4 答：（图略）题1-5 答：该系统是随动系统。

（图略） 题1-6 答：（图略）第二章习题答案题2-1 解：（1）F(s)=12s 1+-Ts T（2）F(s)=0.5)421(2+-s s（3）F(s)=428+⋅s es sπ （4）F(s)=25)1(12+++s s（5）F(s)=32412ss s ++ 题2-2 解：(1) f(t)=1+cost+5sint(2) f(t)=e -4t(cost-4sint) (3) f(t)=t t t te e e 101091811811----- (4) f(t)= -t t tte e e ----+-3118195214 (5) f(t)= -t te e t 4181312123--+++ 题2-3 解：a)dtduu C R dt du R R c c r 22111=++）（ b)r c c u CR dt du R R u C R dt du R R 1r 12112111+=++）（ c) r r r c c c u dtdu C R C R dtu d C C R R u dtdu C R C R C R dtu d C C R R +++=++++）（）（1211222121122111222121 题2-4 解：a) G(s)=1)(212++s T T sT (T 1=R 1C, T 2=R 2C )b) G(s)=1)(1212+++s T T s T (T 1=R 1C, T 2=R 2C )c) G(s)= 1)(1)(32122131221+++++++s T T T s T T s T T s T T (T 1=R 1C 1, T 2=R 1C 2, T 3=R 2C 1, T 4=R 2C 2 ) 题2-5 解：(图略) 题2-6 解：33)(+=Φs s 题2-7 解：a) ksf ms s +-=Φ21)(b) )()()(1))(1)(()(21221s G s G s G s G s G s +++=Φc) )()(1)())()(()(31321s G s G s G s G s G s ++=Φd) )()()()(1))()()(323121s G s G s G s G s G s G s -+-=Φe) G(s)=[G 1(s)- G 2(s)]G 3(s)f) )()()()()()()()()()(1)()()()()(43213243214321s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +-++=Φg) )()()()()()()()(1)()()()(43213212321s G s G s G s G s G s G s G s G s G s G s G s -+-=Φ题2-8 解：102310)1()()(k k s s T Ts k k s R s C ⋅++++⋅=1023101)1()()(k k s s T Ts k k s N s C ⋅++++⋅=1023102)1()()(k k s s T Ts s T k k s N s C ⋅++++⋅⋅⋅= 题2-9 解：)()()()(1)()()(4321111s G s G s G s G s G s R s C +=)()()()(1)()()(4321222s G s G s G s G s G s R s C +=)()()()(1)()()()()(432142121s G s G s G s G s G s G s G s R s C +=)()()()(1)()()(4321412s G s G s G s G s G s R s C +=题2-10 解：(1)3212321)()(k k k s k k k s R s C +=3212032143)()()(k k k s s G k k k s k k s N s C +⋅+=(2) 2140)(k k sk s G ⋅-= 题2-11 解：122212211111)()1()()(z z s T s T T C s T T s T k k s s m m d e L ⋅++⋅+++⋅=ΘΘ (T 1=R 1C, T 2=R 2C, T d =L a /R a , T m =GD 2R a /375C e C m )第三章 习题答案3-1． s T 15=（取5%误差带） 3-2． 1.0=H K K=2 3-3．当系统参数为：2.0=ξ，15-=s n ω时，指标计算为：%7.52%222.0114.32.01===-⨯---e eξξπσs t ns 352.033=⨯==ξωs t n p 641.02.01514.3122=-⨯=-=ξωπ当系统参数为：0.1=ξ，15-=s n ω时，系统为临界阻尼状态，系统无超调，此时有：st ns 95.057.10.145.67.145.6=-⨯=-=ωξ3-4．当110-=s K 时，代入上式得：110-=s n ω，5.0=ξ，此时的性能指标为：%3.16%225.0114.35.01===-⨯---e eξξπσs t ns 6.0105.033=⨯==ξωs t n p 36.05.011014.3122=-⨯=-=ξωπ当120-=s K 时，代入上式得：11.14-=s n ω，35.0=ξ，此时的性能指标为：%5.30%2235.0114.335.01===-⨯---e eξξπσs t ns 6.01.1435.033=⨯==ξω由本题计算的结果可知：当系统的开环放大倍数增大时，其阻尼比减小，系统相对稳定性变差，系统峰值时间变短，超调量增大，响应变快，但由于振荡加剧，调节时间不一定短，本题中的调节时间一样大。

第六章习题E6.1 A system has a characteristic equation :s3+3Ks2+(2+K)s+5=0.Determine the range of K for a stable system.E6.7 A negative feedback system has a loop transfer function(a)Find the value of the gain when the ζ of the closed-loop roots is equal to 0.707.(b)Find the value of the gain when the closed system has two roots on the imaginary axis.E6.11 A system with a transfer function Y(s)/R(s) isDetermine the steady-state error to a unit step input.is the system stable?E6.14 A system has a characteristic equationq(s)=s4+9s3+45s2+87s+50=0.(a) Determine whether the system is stable,using the Routh-Hurwitz criterion.(b)Determine the roots of the characteristic equation.E6.23 A closed-loop feedback system is shown in Figure E6.23.For what range of values of the parameters K and p is the system stable?P6.3 Arc welding is one of the most important areas of application for instustrial robots.In most manufacturing welding situation,uncertainties in dimensions of part,geometry of the joint,and the weiding process itself require the use of sensors for maintaining weld quality.Several systems use a vision system to measure the qeometry of the puddle of melted metal,as shown in Figure P6.3. This system uses a constant rate of feeding the wire to be melted.(a)Calculate the maximum value for K for the system that will result in a stable sytem(b)For half of the maximum value of K found in part(a). Determine the roots of the characteristic equation.(c)Estimate the overshoot of the system of part(b) when it is subjected to step input.P6.4 A feedback control system is shown in Figure P6.4. The process transfer function isAnd the feedback transfer function is H(s)=1/(s+20).(a)Determine the limiting value of gain K for a stable system(b)For the gain that results in marginal stability,determine themagnitude of the imaginary roots(c)Reduce the gain to half the magnitude of the marginal value and determine the relative stability of the system (1)by shifting the axis and using Routh-Hurwitz criterion and (2)by determining the root locations.Show the roots are between -1 and -2.P6.7 The linear model of a phase detector(phase-lock loop) can be represented by Figure P6.7.The phase-lock systems are designed to maintain zero difference in phase between the input carrier signal and a local voltage-controlled oscillator.Phase-lock loops find application in color television,missile tracking,and space telemetry.The filter for a particular application is chosen asWe want to minimize the steady-state error of the system for a ramp change in the phase information signal(a)Determine the limiting value of the gain K a k=k v in order to maintain a stable system(b)A steady-state error equal to 1o,Is acceptable for a ramp signal of 100% rad/s.For that value of K v,determine the location of the roots of the system.P6.8 A very interesting and useful velocity control system has been designed for a wheelchair control system.We want to enable people paralyzed from the neck down to drive themselves about in motorized wheelchairs.A proposed system utilizing velocity sensors mounted in a headgear is shown in Figure P6.8.The headgear sensor provides an output proportional to magnitude of the head movement.There is a sensor mounted at 90o intervals so that forward,left right,or reverse can be commaded.Typical values for the time constant are τ1=0.5s τ3=1s,and τ4=1/4s.(a)Determine the limiting gain K=K1K2K3 for a stable system(b)When the gain K is set equal to one-third of the limiting value,determine whether the setting time(to within 2% of thefinal value of the system) is less than 4s.(c)Determine the value of gain that results in s system with a settling time of 4s.Also,obtain the value of the roots of the characteristic equation when the settling time is equal to 4s.P6.9 A cassette tape storage device has been designed for mass-storage.It is necessary to control the velocity of the tape accurately.The speed control of the tape is represented by the system shown in FigureP6.9.(a)Determine the limiting gain for a stable system(b)Determine a suitable gain so that the overshoot to a step command is approximately 5%.P6.10 Robots can be used in manufacturing and assembly operation that require accurate,fast,and versatile manipulation.The open-loop transfer function of a direct-drive arm may be approximateed by(a)Determine the value of the gain K when the system oscillates.(b)Calculate the roots of the closed-loop system for the K determined in part(a).P6.15 On July 16,1993,the elevator in Yokohama's 70-story Landmark Tower,operating at a peak speed of 45km/hr(28 mph),was inaugurated as the fastest super-fast elevator.To reach such a speed without leaving passengers'stomachs on the ground floor,the lift accelerates for longer periods,rather than more than more precipitously.Going up,it reaches full speed only at 27th floor;it begins decelerating 15 floor later.The result is a peak acceleration similar to that of other skyscraper elevator-a bit less than a thenth of force of gravity.Admirable ingenuity has gone into making this safe and comfortable.Special ceramic brakess had to be developed;iron ones would puter-controlled system damp out vibrations.The lift has been streamlined to reduce the wind noise as it hurtles up and down.One proposed control system for the elevator'vertical position is shown in Figure P6.15.Determine the range of K for a stable system.AP6.4 A bottle-fillinf lines uses a feeder screw mechannism,as shown in Figure AP6.4.The tachometer feedback is used to maitain accurate speed control.Determine and plot the range of K and p that permits stable operation.FIGURE AP6.4 Speed control of a bottle-filling line(a)System layout(b)Bloack diagramCDP6.1 The capstan drive system uses the amplifier Gc(s)=Ka as the controller.Dertermine the maximum value of the gain Ka before the system becomees unstable.DP6.2 An automatically guided vehicle on mars is represented by the system in Figure DP6.2.The system has a steerable wheel in both the front and back of the vehicle,and the design requires that H(s)=ks+1.(a)Determine the value of K required for stablity.(b)The value of K when one root of the characteristic equation is equal to s=-5.(c)The value of the two remaining roots for the gain selected in part(b).(d)Find the response of the system to a step command for the gain selected in part(b).DP6.6 Consider the potential for a robot steering a motorcycle,as shown in Figure DP6.6(a).The blockdiagram ofthe system model is shown in Figure DP6.6(b).Determine the range of K for stable operation of the cycle when α1=g/h=9.α2=V2/hc=2.7,and α3=VL/hc=1.35.We assume the motorcycle is moving with a constant velocity V=2m/s.The time constant of the controller is τ=0.2,and K>0.DP6.7 Consider the feedback control system in Figure Dp6.7. The system has an inner loop and an outer loop must be stable and have a quick speed of response.(a)Consider the inner loop first.determine the range of K1 resulting in a stable inner loop.That is,the transfer function Y(s)/U(s) must be stable.(b)Select the value of K1in the sstable range leading to the fastest step response.(c)For the value of K1 selected in (b),determine the range of K2 such that the closed-loop system,T(s)=Y(s)/R(s),is stable.。