当前位置：文档之家 › 自动控制理论(邹伯敏)第四章答案

自动控制理论(邹伯敏)第四章答案

  • 格式：docx
  • 大小：406.74 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

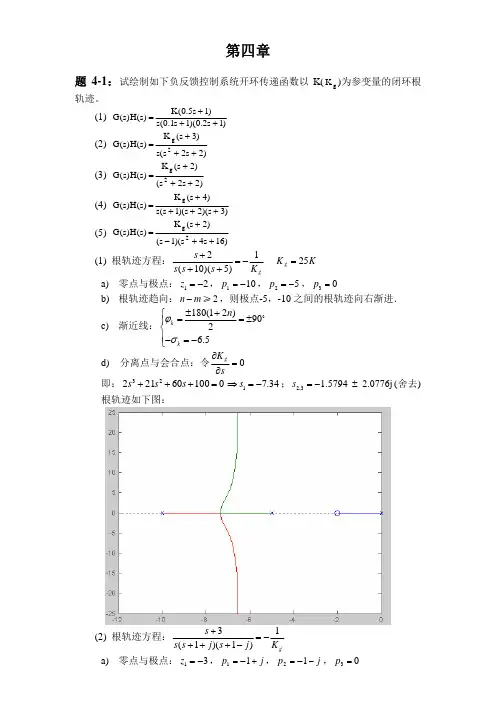
自动控制原理参考答案-第4章

自动控制原理参考答案-第4章

d) 与虚轴交点：
特征方程： s3 + 2s2 + (2 + Kg )s + 3Kg = 0
s3
1
2+ Kg
s2
2
3Kg
s1 2 − 0.5Kg
s0
3Kg
当 Kg = 4 时， 2s2 +12 = 0 ⇒ s = ±2.45 j
e) 出射角： βsc = ±180(1+ 2n) − ∑ β + ∑α
s3
1
7
s2
2
Kg −10
s1 12 − 0.5Kg
s0 Kg −10
当 Kg = 24 时， 2s2 +14 = 0 ⇒ s1,2 = ±2.65 j
劳斯表的 s0 行为正 ⇒ Kg > 10 ，即10 < Kg < 24 根轨迹如下图：
题 4-6：已知负反馈控制系统的开环传递函数为
G(s)H(s)
b) 根轨迹趋向： n − m≥ 2 ，则极点-5，-10 之间的根轨迹向右渐进．
c)
渐近线： ⎧⎪⎨ϕk
=
±180(1 + 2
2n)
=
±90o
⎪⎩−σ k = −6.5
d) 分离点与会合点：令 ∂Kg = 0 ∂s
即： 2s3 + 21s2 + 60s +100 = 0 ⇒ s1 = −7.34 ； s2,3 = −1.5794 ± 2.0776j (舍去) 根轨迹如下图：
(4) 稳态速度误差系数是多少？
(5) 系统指标比该点的二阶指标大还是小？如果要求系统有该点二阶指标
的超调量，能否通过改变阻尼线而获得？是增大阻尼比还是减小它？

自动控制理论 第三版(邹伯敏)第04章

自动控制理论 第三版(邹伯敏)第04章

求解根轨迹的分离点和会合点
令
G s H s
KB s As
图4-10 根轨迹的分离点和会合点
方程出现重根的条件是 S必须同时满足下列方程 Ds As KB s 0 D s As KB s 0
由上述两式导出确定分 离点和会合点的方程 As B s As B s 0 或 dK 0 ds
根轨迹终点就是当
K0
m l i 1
时根的位臵；
i
1 K0
s p s z 0
l 1
n
当K 0 时,则有
s z 0
i i 1
m
由 此 式 可 知 , 开 环 传 递 函 数 的 零 点 支 的 终 点
zi i 1,2, ,m 是 m条 根 轨 迹 分
i 1 m
p
l 1
n
,n m
4 - 14
l
绘制根轨迹的基本规则
规则1：根轨迹的对称性 由于系统特征方程式的系数均为实数,因而特征根或为实数,或为共轭复 数.根轨迹必然对称于S平面的实轴 规则2：根轨迹的分支数及其起点和终点 闭环特征方程：
n m
s p K s z 0
2
自动控制理论 稳定性：根轨迹若越过虚轴进入S右半平面，与虚轴交点处的K即为临界增益； 稳态要求：根据坐标原点的根数，确定系统的型别，同时可以确定对应的静态误差。 动态性能：对于不同的K值,系统有下列三种不同的工作状态 1) 0≤K＜¼ ， s1、 s1为两相异的实数根（过阻尼状态） 2) K=¼ ， s1、 s1为两相等实根，s1 = s2 =-0.5，（临界阻尼） 3) ¼ ＜K＜≦， s1 、s2为一对共轭复根（欠阻尼） 如要求系统在阶跃信号的作用下，超调量为49%。

自动控制理论邹伯敏第3版课后答案总.doc

自动控制理论邹伯敏第3版课后答案总.doc

《自动控制理论 第2版》习题参考答案第二章2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i2-8 (a)()()()()3113211G H G G G G s R s C +++= (b) ()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()⎪⎭⎫⎝⎛++-=-=-t e t t c s n t n nn n 21222,1ωωωωω()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。

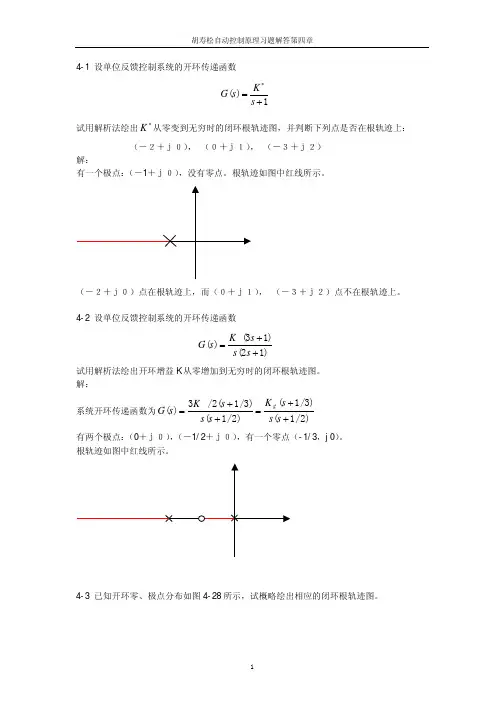
自动控制原理第四章习题解答

自动控制原理第四章习题解答

4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上： （－２＋ｊ０）， （０＋ｊ１）， （－３＋ｊ２） 解：有一个极点：（－1＋ｊ０），没有零点。

根轨迹如图中红线所示。

（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１）， （－３＋ｊ２）点不在根轨迹上。

4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。

解：系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点：（0＋ｊ０），（－1/2＋ｊ０），有一个零点（-1/3，j0）。

根轨迹如图中红线所示。

4-3 已知开环零、极点分布如图4-28所示，试概略绘出相应的闭环根轨迹图。

图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d)：　 (1) )15.0)(12.0()(++=s s s Ks G解：系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点：（0＋ｊ０），（－2＋ｊ０），（－5＋ｊ０）没有零点。

分离点坐标计算如下：051211=++++d d d 3解方程的010142=++d d 7863.31−=d ，d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。

（2） )12()1()(++=s s s K s G解：系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。

分离点坐标计算如下：115.011+=++d d d 解方程的05.022=++d d 7.11−=d ，d 29.02−=取分离点为7.11−=d ，29.02−=d 根轨迹如图中红线所示。

自动控制理论邹伯敏第3版课后答案总.doc

自动控制理论邹伯敏第3版课后答案总.doc

《自动控制理论 第2版》习题参考答案第二章2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i2-8 (a)()()()()3113211G H G G G G s R s C +++= (b) ()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()⎪⎭⎫⎝⎛++-=-=-t e t t c s n t n nn n 21222,1ωωωωω()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。

自动控制理论基础答案

自动控制理论基础答案
G3
C
G1G3 G1G2 G3 H 1 G1G2 C R ( s) R( s ) 1 G2 H 1 G1G3 G1G2 G3 H 1 G1G2
2）令R(s)=0, 求出CN(s)
R+ +
G1 (s)
G4 (s)
N
G 2(s) H 1(s) G3(s)
+
+
+ +
C
U r (s)
R2
u c u o -
-
图E2.3 题2-3 RLC电路
+
R1 ur
u u co
C
L
+
IR1
IC
IL
R2 uo c u -
-
Ur -
1 R1
IR1
-
IC
1 C1 s
UC
-
1 R Ls IL 2
Uo
U o ( s) R2 G( s) U r ( s) ( R1Cs 1)(Ls R2 ) R1
C(s)
G4 (G1G3 G1G2 G3 H 1 G1G2 ) 1 G2 H 1
N(s)
+ + G1G3 G1G2 G3 H 1 G1G2 1 G2 H 1
C(s)
G4 (G1G3 G1G2 G3 H 1 G1G2 ) 1 G2 H 1
C (s) 1 G2 H1 G4 (G1G3 G1G2 G3 H1 G1G2 ) 则 N ( s) 1 G2 H1 G1G3 G1G2 G3 H1 G1G2 1 G2 H 1 G4 (G1G3 G1G2 G3 H 1 G1G2 ) C N ( s) N ( s) 1 G2 H 1 G1G3 G1G2 G3 H 1 G1G2

《自动控制理论(第版)》邹伯敏课件第4章


i1
n
n
s n pl s n1
pl
l 1
l 1
3、用分子除以分母得
GsH s
K0
s nm
n l 1
pl
m i 1
zi s nm1
2020/5/4
第四章 根轨迹法
14
自动控制理论
当s 时,
令某系统的开环传递函数为W s
s
K0
A
nm
K0
snm
n
m
s nm1
A
1 W s 0,有n m条根轨迹分支,它们是由实轴上s σA点出发的射线,
图4-4 一阶系统
2020/5/4
图4-5 图4-4系统的等增益轨迹和根轨迹
第四章 根轨迹法
6
自动控制理论
结论：
根轨迹就是s 平面上满足相角条件点的集合。由于相角条件是绘制根轨迹 的基础，因而绘制根轨迹的一般步骤是：
➢找出s 平面上满足相角条件的点，并把它们连成曲线 ➢根据实际需要，用幅值条件确定相关点对应的K值
例4-4
已知GsH s
ss
K0
4s 2
4s
20
求根的分离点
图4-12 例4-4的根轨迹
解：1）有4条根轨迹分支,它们的始点分别为0，-4，-2±j4
2） 渐近线与正实轴的夹角
2k 1 , 3 , 5 , 7 , k 0,1,2,3
4
44 4 4
渐近线与实轴的交点为
2020/5/4
-A
422 4 第四章
规则2：根轨迹的分支数及其起点和终点
闭环特征方程：
n
m
s pl K 0 s zi 0
l 1

自动控制原理 4-5章习题与解答习题课后校对稿


可知： K 增大时， % ， t p 。
4
4-9 设电子心率起搏器系统如图 4-41 所示，其中模仿心脏的传递函数相当于一个纯积 分器。要求：
（1）若 0.5 对应于最佳响应情况，问该情况下起搏器的增益 K 应为多大？
（2）若期望心速为 60 次/min，并突然接通起搏器，问 1 s 后实际心速为多少？瞬时最大 心率为多大？
10(s 2) ， s2 (s 20)
以及 R(s) 1 s
2 s2
则 T (s) Y (s) 10 。 R(s) s 20
4-5 某控制系统结构图如图 4-38 所示，其中 K1 5 ， T1 0.5 。 （1）求系统的单位阶跃响应； （2）计算系统的性能指标 tr ， t p ， ts ( 5% )， % ；
T1 5T1
（1）该系统的单位阶跃响应为
y(t) 2.51

e nt 1 2
sin(d t


)

2.51


23 3
e nt
sin(
3t


)
3

2.51

1.1547e t
sin(1.7321t

3
)
（2）系统的性能指标为：
解之得： K 25 ， n 25
（2）闭环传递函数写为： T (s)

s2
625 25s 625
，闭环极点 s1,2

12.5
j12.5
3。
方法一：系统的阶跃响应为
y(t) 1
1 1
2
e nt
sin( n

自动控制原理课后答案第4章


i
sz
j 1
j
1
相角条件
m j j 1 n i i 1
(s z ) (s p ) (2k 1) ,
4、根轨迹绘制的基本规则 绘制根轨迹的 9 条基本规则归纳如下：
表 4-1 绘制根轨迹的基本规则
序号 1 2 3 名 称
k 0, 1, 2,
规 根轨迹具有连续性，且关于实轴对称 根轨迹的分支数与开环极点数 n 相等
i 1 j 1 j g
根轨迹与虚轴交点的坐标和临界开环根轨迹增益 K*，可由下列方法之一确定： 8 根轨迹与虚轴的交点 ① 利用劳斯判据计算 ② 用 s＝jω 代入闭环特征方程式求解 根之和： sl pi （n-m≥2）
l 1 i 1 n n
9
根之和与根之积
根之积： ( 1)
n n m
( 1) n sl ( 1)n pi (1) m K z j
l 1 i 1 j 1
若系统无开环零点，则上式可简化为如下形式：
n n
( 1) n sl ( 1)n pi K
l 1 i 1
利用这一关系，可用来求解已知闭环特征根所对应的 K*值。 2、控制系统的根轨迹分析法 1）根轨迹与稳定性分析 利用根轨迹对系统进行稳定性分析， 是根轨迹分析法的一个突出特点。 对于稳定的系统 来说，其闭环特征根必然全部位于[s] 左半平面，而且其离虚轴距离越远，相对稳定性就越 好。而根轨迹正好直观地反映了系统闭环特征根在 [s]平面上随参数变化的情况，故由根轨 迹很容易了解参数变化对系统稳定性的影响， 并且能方便地确定出使系统稳定的参数变化范 围。 2）根轨迹与动态性能分析 高阶系统的动态性能基本是由接近虚轴的闭环极点确定的。因此，把那些既靠近虚轴， 又不十分接近闭环零点的闭环极点称为主导极点。 主导极点对系统性能的影响最大， 而那些 比主导极点的实部大 5 倍以上的其它闭环零、极点，其对系统的影响均可忽略。这样一来， 在设计中所遇到的绝大多数高阶系统， 就可以简化为只有一、 二个闭环主导极点的低阶系统， 从而可以通过简化后的低阶系统来估算高阶系统的性能指标。 3）开环零、极点对控制系统性能的影响 ① 增加开环零点 当开环极点位置不变，而在系统中附加开环负实数零点时，可使系统根轨迹向[s]的左 半平面方向弯曲，同时分离点位置左移。或者说，附加开环负实数零点后，可使系统根轨迹 发生趋向于附加零点方向的变形，而且这种影响将随开环零点接近坐标原点的程度而加强。 如果附加零点不是负实数零点， 而是具有负实部的共轭复数零点， 那么它们的作用与负实数 零点的作用完全相同。因此，在[s]的左半平面内的适当位置上附加开环零点，可以显著提 高系统的稳定性。除此之外，还可对系统的动态性能有明显改善。然而，附加开环零点位置

自动控制原理第四章


σ
-0.5 0
k' WK ( s ) = s ( s + 2)( s + 4)
jω
σ
-4 -2 0
0−2−4 = −2 σ= 3 2k + 1 π 5π θ= π = ,π , 3 3 3
k' WK ( s ) = s ( s + 1)( s + 2)( s + 5)
jω
-5 -2 -1 0
σ = −2 π θ =±
kN ( s ) Wk ( s ) = D(s)
F ( s ) = D( s ) + kN ( s )
k =0 k →∞
F ( s) = D( s) F (s) = N (s)
n > m时，有（n－m) 条分支趋于无穷。 条分支趋于无穷。 时
根轨迹的渐近线：共有（ 3、根轨迹的渐近线：共有（n－m）条渐近线 与实轴交点 与实轴夹角
Wk ( s ) = 1 ∠Wk ( s ) = (2k + 1)π
幅值条件 相角条件
Wk (s) =
k ∏ (Ti s + 1) s N ∏ (τ j s + 1)
j =1 i =1 r
m
时间常数表达式
N＋ r = n > m
零极点表达式 K’为根轨迹增益 为根轨迹增益
=
k ' ∏ ( s + zi ) s N ∏ (s + p j )
dk' = −3s 2 − 12 s − 8 = 0 ds
k' = − s 3 − 6 s 2 − 8 sσ来自-4-20
s1,2
2 3 2 3 = −2 ± 舍去 − 2 − 3 3 k' = 3.08
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

题4-1 (a) (b) (c)
(d) (e) (f)
题4-2 解：
由开环传递函数容易得到3,0n m ==，三个极点分别为1230,42,42p p j p j ==-+=--，因此，有3条根轨迹趋于无穷远，其渐近线倾角为(21)5,,
333
k πππ
θπ+=
=，渐近线与实轴交点为1
1
()()
8
3
n m
l
i
l i A p z n m
σ==----=
=--∑∑。

下面确定根轨迹的分离点和汇合点
2020
12()(0.050.41)00.150.81010
2,3D s s s s K dK s s ds
s s =+++=⇒
=---=⇒=-=-
计算根轨迹的出射角与入射角
2322(arctan())63.4
4
2
63.4
p p p π
θππθθ=---=-=-=
确定根轨迹与虚轴的交点
σ
j ω
O
σ
σ
σ
202
03
00,()(0.050.41)0
0.400080.050s j D s j j K K K K ωωωωωωωωω==-+++=⎧⎧-+==⎧=±⎪⎪⇒⇒⎨⎨⎨==-+=⎪⎪⎩⎩⎩
令特征方程或
σ
题4-5 解：
由开环传递函数容易得到3,0n m ==，三个极点分别为1230,2,4p p p -=-=--=-，因此，有3条根轨迹趋于无穷远，其渐近线倾角为(21)5,,
333
k ππ
π
θπ+=
=，渐近线与实轴交点为1
1
()()
2n m
l
i
l i A p z n m
σ==----=
=--∑∑。

下面确定根轨迹的分离点和汇合点
确定根轨迹与虚轴的交点
02
0300,()(2)(4)0
60004880
s j D s j j j K K
K K ωωωωωωωωω==+++=⎧⎧-+==⎧=±⎪⎪⇒⇒⎨⎨⎨
==-+=⎪⎪⎩⎩⎩令特征方程或
020
12()(2)(4)0312802,233
D s s s s K dK s s ds
s s =+++=⇒
=---=⇒=-+
=--（舍去）
(2)
要产生阻尼振荡，需要00σω<≠且。

当102=3.08s K =-+
，所以，当03.148K <<时，系统呈阻尼振荡。

(3) 当048K =时，系统产生持续等幅振荡，振荡频率为(4)
=0.5arccos 0.5
60
ζββ⇒=⇒=±过s 平面原点，与实轴负方向夹角为60±作射线，与根轨迹的
交点即为主导极点。

由图知，主导极点为0.7 1.2j -±。

又
123123364.6
c c c c p p p p p p p ++=++=-⇒=-
所以
004.6*( 4.62)*( 4.64)07.176
K K --+-++=⇒=
题4-6 解：
(1)由开环传递函数容易得到3,1n m ==，三个极点和一个零点分别为
12310,1,3,2p p p z ==-=-=-，因此，有2条根轨迹趋于无穷远，其渐近线倾角为
(21)3,222
k πππ
θ+==，渐近线与实轴交点为1
1
()()
1n
m
l i l i A p z n m
σ==----==--∑∑。

下面确定根轨迹的分离点和汇合点
02()(1)(3)(2)0(1)(2)10.55
D s s s s K s s s s =++++=⇒++=⇒≈-
σ
(2)
=0.5arccos 0.5
60
ζββ⇒=⇒=±过s 平面原点，与实轴负方向夹角为60±作射线，与根轨迹的
交点即为主导极点。

由图知，主导极点为0.7 1.1j -±。

又
123123342.6
c c c c p p p p p p p ++=++=-⇒=-,
所以
002.6*( 2.61)*( 2.63)( 2.62)02.77
K K --+-++-+=⇒=
题4-9 解：
系统的闭环传递函数32222.50
(1)
10
2.5
s s s Ts Ts T s s s ++++=+⇒+=++，等效开环传递函数为12
(1)
() 2.5
T s G s s s +=
++。

由等效开环传递函数容易得到2,1n m ==，两个极点和一个零点分别为
1211313
,,122j j p p z -+--=
==-，因此，有1条根轨迹趋于无穷远，其渐近线倾角为(21)1k πθπ+==。

下面确定根轨迹的分离点和汇合点
22012() 2.5(1)002 1.50
11D s s s T s dK s s ds s s =++++=⇒=⇒+-=⇒=-=-+
计算根轨迹的出射角与入射角
232
arctan 3161.6
2161.6
p p p π
θπθθ=+-==-=-
σ
题4-12 解：
由开环传递函数容易得到3,0n m ==，三个极点分别为1232p p p ===-，因此，有3条根轨迹趋于无穷远，其渐近线倾角为(21)5,,
333
k πππ
θπ+=
=，渐近线与实轴交点为1
1
()()
2n m
l
i
l i A p z n m
σ==----=
=--∑∑。

下面确定根轨迹的分离点和汇合点
3020
12()(2)03(2)02D s s K dK s ds
s s =++=⇒
=-+=⇒==-
确定根轨迹与虚轴的交点
302
0300,()(2)0
6800864120
s j D s j K K K K ωωωωωωω==++=⎧⎧-++==⎧=±⎪⎪⇒⇒⎨⎨⎨
=-=-=⎪⎪⎩⎩⎩令特征方程（舍去）或
(1) 令064
s
j K ωω⎧=⎪=⇒⎨=⎪⎩(2)
=0.5arccos 0.5
60
ζββ⇒=⇒=±过s 平面原点，与实轴负方向夹角为60±作射线，与根轨迹的交
点即为主导极点。

由图知，主导极点为1-±。

又
123123364
c c c c p p p p p p p ++=++=-⇒=-
所以
300(42)08
K K -++=⇒=
3
08
lim ()()lim
1(2)p s s K G s H s s →→===+
(3) 系统的闭环传递函数可以近似为
212()88
()()()24
c c C s R s s p s p s s ==--++
2222
0.54n n n ζωωζω=⎧=⎧⎪⇒⇒⎨⎨
==⎪⎩⎩
100%16.3%p M e
⇒=⨯=
1.8138p d t s πω⇒=
== 3
5% 34
2% 4s n s n t s
t s
ωζ
ωζ
⇒∆=≈=∆=≈
=。