函数极限的定义的多种表达
- 格式:doc
- 大小:241.50 KB
- 文档页数:7


描述极限的概念描述极限概念简介描述极限是数学分析中的一个重要概念,用于刻画函数在某一点处的局部行为。
在现实生活和实际问题求解中,描述极限也被广泛应用于物理、工程等领域。
极限的定义极限的定义可以分为数列极限和函数极限两种情况。
数列极限对于数列 {an},当其趋于无穷大时,如果存在实数A,对任意给定的正数ε(epsilon),总存在正整数N,使得当n>N时,有|an-A|<ε成立,则称数列 {an} 的极限为A,记作lim (n→∞) an = A。
函数极限对于实函数 f(x),当自变量 x 趋于某一实数a时,如果存在实数A,对任意给定的正数ε(epsilon),总存在正数δ(delta),使得当0<|x-a|<δ时,有|f(x)-A|<ε成立,则称函数 f(x) 在 x=a 处的极限为A,记作lim (x→a) f(x) = A。
极限的性质和计算方法极限具有一些重要的性质,可以通过这些性质来计算极限。
极限唯一性一个数列或者函数的极限只能有一个唯一确定的值。
四则运算法则对于数列或函数的四则运算,如果可以将其拆分为多个已知极限的数列或函数,则可以利用极限的四则运算法则计算最终的极限。
夹逼准则当函数 f(x) 处于两个其他已知函数 g(x) 和 h(x) 之间,并且g(x) 和 h(x) 的极限在某一点 a 处相等时,可以利用夹逼准则求得f(x) 在点 a 处的极限。
常见极限值有一些常见的极限值可以直接根据定义或通过运算法则进行计算,如lim (x→0) sin(x)/x = 1。
应用领域极限在数学、物理、工程等领域都有广泛的应用。
数学分析极限是数学分析中的核心概念,它在微积分、级数收敛性、函数连续性等方面起着重要作用。
物理学在物理学中,极限被用来描述粒子在物理过程中的变化趋势,例如速度的极限可以表示加速度。
工程学在工程学中,极限可以用来描述材料的耐力和荷载的极限承载能力,有助于工程结构的设计和安全性分析。



极限定义的总结
极限主要包括两个方面,即自变量的变化趋势和函数的变化趋势。
我们就这两个变化趋势来总结极限的定义:
函数的变化趋势自变量变化趋势=)(lim x f
自变量的变化趋势主要有六种:
-+→→→-∞→+∞→∞→0
00,,,,,x x x x x x x x x 函数的变化趋势主要有四种:
-∞→+∞→∞→→)(,)(,)(,)(x f x f x f A x f 自变量的描述格式如下:
,0>∃X 当X |x |>时;(∞→x )
,0>∃X 当X x >时;(+∞→x )
,0>∃X 当-X x <时;(-∞→x )
,0>∃δ当δ<<|x -x |00时;(0x x →)
,0>∃δ
当δ<<0x -x 0时;(+→0x x ) ,0>∃δ 当δ<<|x -x |00时;(-→0x x )
函数的描述格式如下:
,0>∀ε ,
恒时:ε<-|)(|A x f (A x f →)() ,0>∀ε ,
恒时:M x f >|)(|(∞→)(x f ) ,0>∀ε , 恒时:M x f >)((+∞→)(x f )
,0>∀ε ,
恒时:M x f ->)((-∞→)(x f ) 那么函数极限的定义可以是这241416=⋅C C 种中的任意一种。
当然还有一种最特殊的函数极限,即数列的极限。
它是一种自
变量的变化不连续的特殊情形。

极限的二十四种定义“极限”是数学中的分支——微积分的基础概念,广义的“极限”是指“无限靠近而永远不能到达”的意思。
此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近a点的趋势”。
极限是一种“变化状态”的描述。
此变量永远趋近的值a叫做“极限值”(当然也可以用其他符号表示)。
数学中的“极限”指:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值a不断地逼近而“永远不能够重合到a”(“永远不能够等于a,但是取等于a‘已经足够取得高精度计算结果)的过程中。
数列音速定义可定义某一个数列{xn}的发散:设{xn}为一个无穷实数数列的集合。
如果存在实数a,对于任意正数ε (不论其多么小),总存在正整数n,使得当n\uen时,均有不等式成立,那么就称常数a是数列{xn} 的极限,或称数列{xn} 收敛于a。
记作或。
如果上述条件不设立,即为存有某个正数ε,无论正整数n为多少,都存有某个n\uen,使,就说道数列{xn}不发散于a。
如果{xn}不发散于任何常数,就表示{xn}收敛。
对定义的理解:1、ε的任意性定义中ε的促进作用是来衡量数列通项与常数a的吻合程度。
ε越大,则表示吻合得越将近;而正数ε可以任一地变大,表明xn与常数a可以吻合至任何不断地紧邻的程度。
但是,尽管ε存有其任意性,但一经得出,就被暂时地确认下来,以便依靠它用函数规律xi出来n;又因为ε是任意小的正数,所以ε/2 、3ε 、ε2 等也都在任意小的正数范围,因此可用它们的数值近似代替ε。
同时,正由于ε是任意小的正数,我们可以限定ε小于一个某一个确定的正数。
2、n的适当性一般来说,n随ε的变大而变小,因此常把n文学创作n(ε),以特别强调n对ε的变化而变化的依赖性。
但这并不意味著n就是由ε唯一确认的:(比如说若n\uen并使设立,那么似乎n\uen+1、n\ue2n等也并使设立)。
关键的就是n的存有性,而不是其值的大小。

连续函数极限极限是一种经典问题,是数学中非常重要的概念,它把不同的概念联系起来,使得我们可以建立更为普遍的概念和数学模型,例如对函数求极限和对应的定义。
极限描述的是一个函数当其变量趋近某一数值时,函数值的取值情况。
极限函数的一般定义为:在某一点的极限值,只要在一定的接近区域内,函数值都非常接近该极限值,那么就称该极限值为该点的极限。
二、极限的分类极限有很多分类,我们重点讨论连续函数的极限。
极限可以分为有限极限和无限极限,有限极限是指在某一点的极限值是有限的,而无限极限则是指该点的极限值是无限大或无限小。
例如:函数f(x)=2x+2,其中在点x=2的极限为有限的6,而对于函数g(x)=1/x,其中在点x=0的极限值为无限小。
三、连续函数极限在前文中,我们简单介绍了极限的分类,在数学中,极限可以分为连续函数极限和间断函数极限。
连续函数是指在某一区间内,任何区间内的两个不同的点,其函数值之间的连续性性质,即函数值的变化是比较连续的,而间断函数则是指在某一区间内,任何区间内的两个不同的点,其函数值之间的连续性是不能保证的。
关于连续函数极限,需要注意以下几点:1.于连续函数,某一点的极限可以称为函数定义域中该点的值。
2.于连续函数,极限只能通过对其定义域中某一点的值来确定,而不能通过其函数值。
3.于连续函数,极限可以用其偏导数来表示,偏导数的计算可以用公式的形式表示,并且可以用来求极限的值。
4.于不满足连续性性质的函数,连续函数极限的计算仍然可以采用偏导数的方法,但是该函数的连续性性质会给求取极限的过程带来困难。
四、总结连续函数极限是数学中一个重要的概念,它把函数的分段性和连续性联系起来,让我们可以计算函数极限的值,而这些值具有重要的意义,对于分析函数特性有着重要意义。



函数极限的定义24种函数极限是指计算函数值时,这个函数接近某个值的情况。
它的定义有24种,如下:1. 左极限:当x趋近于a时,f(x)趋近于L。
2. 右极限:当x趋近于a时,f(x)趋近于M。
3. 对称的极限:当x趋近于a时,f(x)趋近于N。
4. 在点a上的极限:如果存在L使得对于任意δ>0,当0 < |x- a | < δ时,f(x)都 > L,那么,f在点a处的极限就是L。
5. 在点a上的右极限:如果存在M使得对于任意δ>0,当0 < |x- a | < δ 当x→a右时,f(x)都 < M,那么,f在点a处的右极限就是M。
6. 在点a上的对称极限:如果存在N使得对于任意δ>0,当0< |x-a | <δ时,当x→a时,f(x) → N,那么,f在点a处的对称极限就是N。
7. 内极限:当x在a处时,f(x)趋近于L,此时,f(x)的极限就是L。
8. 内右极限:当x在a处时,f(x)趋近于M,此时,f(x)的极限就是M。
9. 内对称极限:当x在a处时,f(x)趋近于N,此时,f(x)的极限就是N。
10. 外极限:当x在a处时,f(x)趋近于L,此时,f(x)的极限就是L。
11. 外右极限:当x在a处时,f(x)趋近于M,此时,f(x)的极限就是M。
12. 外对称极限:当x在a处时,f(x)趋近于N,此时,f(x)的极限就是N。
13. 下无穷极限:当x→-∞ 时,f(x)趋近于L。
14. 上无穷极限:当x→+∞ 时,f(x)趋近于M。
15. 无穷极限:当x→ ± ∞时,f(x)趋近于N。
16. 上渐近极限:当x趋近于a时,f(x)逐渐趋近于L。
17. 下渐近极限:当x取越大值时,f(x) 逐渐趋近于M。
18. 上唯一极限:当x趋近于a时,f(x)只能趋近于唯一的L。
19. 下唯一极限:当x趋近于a时,f(x)只能趋近于唯一的M。
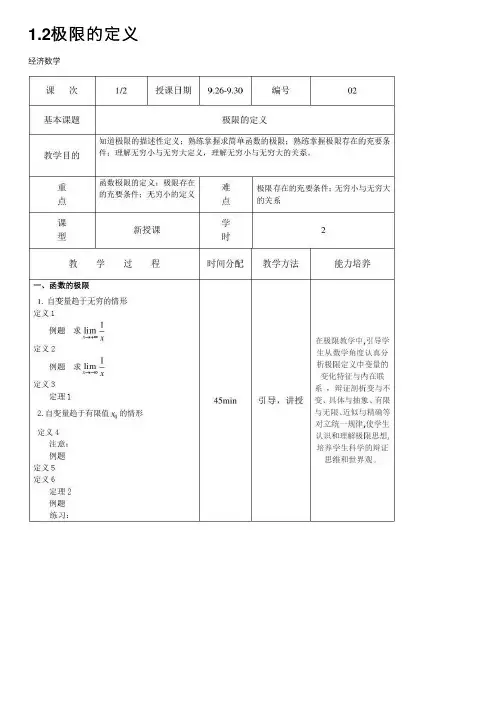
1.2极限的定义经济数学⼀、函数的极限1. ⾃变量趋于⽆穷的情形⾃变量趋于⽆穷可分为趋于正⽆穷和负⽆穷,先讨论当x →+∞时,函数的极限。
定义1 设函数a a x f y (),()(+∞=在为某个实数)内有定义,如果当⾃变量x ⽆限增⼤时,相应的函数值)(x f ⽆限接近于某⼀个固定的常数A ,则称A 为+∞→x (读作“x 趋于正⽆穷”)时函数)(x f 的极限,记作A x f x =+∞→)(lim 或 )()(+∞→→x A x f例题求1limx x→+∞ 由图像可知,当x 趋于正⽆穷时,1x趋于零,故1lim x x →+∞=0定义 2 设函数()y f x =∞在(-,a)(a 为某个实数)内有定义,如果当⾃变量x ⽆限增⼤且0x <时,相应的函数值()f x ⽆限接近于某⼀个固定的常数A ,则称A 为x →-∞(读作“x 趋⽯家庄财经职业学院于负⽆穷”)时函数()f x 的极限,记作lim ()x f x A →-∞=或)()(-∞→→x A x f例题求1limx x→-∞ 由图像可知,当x 趋于负⽆穷时,1x趋于零,故1lim x x →-∞=0定义3 设函数)(x f y =在b x >b (为某个正实数)时有定义,如果当⾃变量x 的绝对值⽆限增⼤时,相应的函数值⽆限接近于某⼀个固定的常数A ,则称A 为∞→x (读作“x 趋于⽆穷”)时函数)(x f 的极限记作A x f x =∞→)(lim 或)()(∞→→x A x f由上述两个例题可知,1lim0x x →∞=,同理可证,21lim 0x x→∞= 定理1当x →∞时,函数()f x 的极限存在的充分必要条件是当x →+∞时和x →-∞时函数()f x 的极限都存在⽽且相等。
即lim ()x f x A →∞=的充分必要条件是lim ()lim ()x x f x f x A →-∞→+∞==.2.⾃变量趋于有限值0x 的情形引例对于函数21()1x f x x -=-当1x →时, 21()1x f x x -=-于常数2,此时我们称当x 趋近于1时,函数21()1x f x x -=-的极限为2定义4设函数)(x f y =在点0x 的去⼼邻域内有定义,如果当⾃变量x 在),?(0δxN 内⽆限接近于0x 时,相应的函数值)(x f ⽆限接近于某⼀个固定的常数A ,则称A 为当0x x →(读作“x 趋近于0x ”)时函数)(x f 的极限,记作A x f x x =→)(lim 0或)()(0x x A x f →→注意:1.()f x 在0x x →时的极限是否存在,与()f x 在0x 点处有⽆定义以及在点0x 处的函数值⽆关.2.在定义5中, x 是以任意⽅式趋近于0x 的,但在有些问题中,往往只需要考虑点x 从0x 的⼀侧趋近于0x 时,函数()f x 的变化趋向.例题求23lim x x →由函数图像可知,⽆论x 从哪⼀侧趋近于3时,函数值总是⽆限接近于9,故23lim 9x x →=定义5 设函数)(x f y =在点0x 的左半邻域),(00x x δ-内有定义,如果当⾃变量x 在此半邻域内从0x 左侧⽆限接近于0x 时,相应的函数值)(x f ⽆限接近于某个固定的常数A ,则称A 为当x 趋近于0x 时函数)(x f 的左极限,记作A x f x x =-→)(lim 0或0()()f x A x x -→→定义6 设函数)(x f y =的右半邻域)(0,0δ+x x 内有定义,如果当⾃变量x 在此半邻域内从0x 右侧⽆限接近于0x 时,相应的函数值)(x f ⽆限接近于某个固定的常数A ,则称A 为当x 趋近于0x 时函数)(x f 的右极限,记作0lim ()x x f x A +→=或0()()f x A x x +→→函数的左右极限有如下关系:定理2 0lim ()x x f x A →=的充分必要条件是00lim ()lim ()x x x x f x f x A -+→→==.例题设函数()xf x x=,求()f x 在0x =处的左、右极限,并讨论()f x 在0x =处是否有极限存在.解: 因为当0x <时, ()1f x =-,因此0lim ()1x f x -→=-,⼜当0x >时, ()1f x =,因此0lim ()1x f x +→= 由定理2可知, 0lim ()x f x →不存在。
极限重要知识点总结一、极限的定义1.1 函数的极限在数学中,函数的极限描述了当自变量趋于某一特定值时,函数的取值趋于的某一确切值。
数学上用符号“lim”表示函数的极限,具体定义如下:对于函数f(x),当x趋于a时,如果存在一个确定的常数L,使得对于任意小的正数ε,总存在着另一个正数δ,使得当0<|x-a|<δ时,就有|f(x)-L|<ε成立,那么就称函数f(x)在x趋于a时的极限为L,记作lim(x→a)f(x)=L。
1.2 数列的极限除了函数的极限,数列的极限也是极限的一种特殊情况。
对于数列{an},当n趋于无穷大时,如果存在一个确定的常数a,使得对于任意小的正数ε,总存在着自然数N,使得当n>N时,就有|an-a|<ε成立,那么就称数列{an}在n趋于无穷大时的极限为a,记作lim(n→∞)an=a。
1.3 极限的重要性极限对于微积分的发展具有非常重要的意义,它为导数和积分的定义提供了理论基础。
在实际问题中,极限也具有很高的应用价值,它可以帮助我们研究和描述诸如速度、加速度、概率等问题,因此对于学习微积分和实际问题的解决都具有非常重要的意义。
二、极限的性质2.1 极限的唯一性如果函数f(x)在x=a的极限存在,那么这个极限是唯一的。
这意味着在某一点的极限值是确定的,不会有多个不同的极限值。
2.2 极限的有界性如果函数f(x)在x=a的极限存在且有限,那么函数f(x)在x=a的某个邻域内是有界的。
在实际应用中,有界性可以帮助我们判断函数在某个点附近的变化规律。
2.3 极限的保号性如果函数f(x)在x=a的某个邻域内恒大于(或小于)一个有限数L,则函数f(x)在x=a的极限也恒大于(或小于)L。
这个性质在实际问题中也具有很高的应用价值,可以帮助我们快速判断函数在某一点附近的变化规律。
2.4 极限的四则运算法则如果函数f(x)和g(x)在x=a的极限分别存在,那么它们的和、差、积、商的极限也分别存在,并且有如下关系:lim(x→a)(f(x)±g(x))=lim(x→a)f(x)±lim(x→a)g(x),lim(x→a)(f(x)×g(x))=lim(x→a)f(x)×lim(x→a)g(x),lim(x→a)(f(x)÷g(x))=lim(x→a)f(x)÷lim(x→a)g(x)(其中lim(x→a)g(x)≠0)。
数学中的极限概念及其应用极限是数学中一种重要的概念,它在各个数学领域都有广泛的应用。
极限用于描述函数的趋势和变化,解决许多实际问题,并且是微积分的基础概念之一。
本文将首先介绍极限的定义和基本性质,然后探讨它在微积分、数列和级数以及物理学中的应用。
极限可以简单地理解为函数在某个特定点的趋近情况。
具体而言,给定一个函数和一个点,当自变量趋近于该点时,函数的值是否趋近于某个特定值。
数学上,我们用极限符号"lim"来表示,比如lim(x→a)f(x)。
在定义极限时,我们需要考虑函数在该点的左右两侧。
如果当自变量从左侧趋近于该点时,函数的值趋近于某个特定值,我们称之为左极限。
同样地,当自变量从右侧趋近于该点时,函数的值趋近于某个特定值,我们称之为右极限。
只有当左极限和右极限相等时,函数才有极限,否则就是无极限。
极限有许多有用的性质。
其中一个是极限的唯一性,即一个函数在某个点只能有一个极限值。
另一个是极限的保号性,即当函数的极限为正时,函数在该点的右侧值也必须为正。
此外,还有极限的四则运算法则和复合函数的极限法则等。
这些性质使得我们可以通过对已知函数的极限进行简单的计算来获得新的函数的极限。
极限在微积分中扮演着重要的角色。
微积分研究函数的变化和趋势,而极限正是描述函数在某一点的趋近情况。
通过计算函数在特定点的极限,我们可以了解函数在该点的行为,比如函数是否连续或者是否存在切线。
例如,求解函数在某点的导数时,我们可以通过极限的定义来计算函数的变化率。
极限在数列和级数中也有广泛的应用。
数列是由一系列实数按照一定规律排列而成的序列。
当数列中的元素趋近于某个数时,我们称之为数列的极限。
通过求解数列的极限,我们可以了解数列的增长方式、收敛性以及散度性。
类似地,级数是由一系列项按照一定规律相加而得到的无穷序列。
通过计算级数的部分和的极限,我们可以判断级数的收敛性和散度性。
此外,极限在物理学中也具有重要的应用。
函数极限的定义
林芳 20101101903
数学科学学院 2010级(1)班
指导教师 韩刚
摘要 极限是数分中的重要内容,用定义证明极限类型题都要用到它。
本文就给出二十四个函数极限的定义。
关键词 极限
1函数在一点的极限的定义
1.1函数在0x 点的极限的定义
设函数f(x)在0x 点的附近(但可能除掉点本身)有定义,又设A 是一个定数。
如果对任意给定的ε>0,一定存在δ>0,使得当0<0x x -<δ时,总有A x f -)(<ε,我们就称A 是函数在点0x 的极限,记为
A x f x x =→0
)(lim ,
或者记为 f(x)→A(x 0x →).
这时也称函数f(x)在0x 点极限存在,其极限值是A.
1.2函数在点0x 右侧的极限的定义
设函数f(x)在(0x ,η+0x )内有定义,η是一个确定的正数,又设A 是一个定数。
如果对任意给定的ε>0,总存在δ>0,当0<x-x 0<δ时,有A x f -)(<ε,
我们就称A 是函数f(x)在点x 0的右极限,记为
0)(lim +→x x x f =A 或f(x 0+0)=A
或 f(x)→A (x 0x →+0)
这时也称函数f(x)在点0x 右极限存在。
1.3函数在0x 点左侧的极限的定义
设函数f(x)在(00,x x η-)内有定义,η是一个确定的正数,又设A 是一个定数。
如果对任意给定的ε>0,总存在δ>0,当0<δ<-x x 0时,有A x f -)(<ε,我们就称A 是函数f(x)在点的左极限,记为
0)(lim -→x x x f =A 或 f(00-x )=A
或 f(x))0(0-→→x x A
这时也称函数f(x)在0x 点左极限存在.
2函数在无限远处的极限
2.1函数在无限远处极限的定义
若对任意给定的ε>0,存在X>0,当X x >时,总有ε<-A x f )(,我们说A 是f(x)在无限远处的极限,或者说A 是当x 的极限时)(x f ∞→,记为
)
()()()(lim ∞→→=∞=∞→x A x f A
f A x f x 或
这时也称函数f(x)在无限远处极限存在
2.2函数在正无限远处的极限的定义
若对任意给定的0>ε,存在X>0,当x>X 时,总有ε<-A x f )(,就称A 为f(x)在无限远处的极限,或者称A 是当+∞→x 时f(x)的极限,记为
A f A x f x =+∞=+∞
→)()(lim 或
或 f(x))(+∞→→x A
这时也称函数f(x)在正无限远处的极限存在。
2.3函数在负无限远处的极限的定义
若对任意给定的0>ε,存在X>0,当x<-X 时,总有ε<-A x f )(,就称A 为f(x)在负无限远处的极限,或者称A 是当+∞→x 时f(x)的极限,记为
A f A x f x =-∞=-∞
→)()(lim 或
或 f(x))(-∞→→x A
这时也称函数f(x)在负无限远处极限存在。
3函数在一点处函数值趋于无穷大
3.1函数在0x 点处函数值趋于无穷大的定义
如果对于任何G>0,存在δ>0,当0<G x f x x ><-)(0时,有δ,就说函数f(x)在0x 点趋于无穷大(或发散到无穷大),记为
)(lim x x x f →=∞或f(x))(0x x →∞→
3.2函数在0x 点右侧函数值趋于无穷大的定义
如果对于任何G>0,存在0>δ,当0<x-x δ<0时,有G x f >)(,就说函数f(x)在0x 点右侧趋于无穷大(或发散到无穷大),记为
0+→x x 3.3函数在0x 点左侧函数值趋于无穷大的定义
如果对于任何G>0,存在G x f x x ><-<>)(0,00时,有当δδ,就说函数f(x)在0x 点左侧趋于无穷大(或发散到无穷大),记为
)0()()(lim 00
0-→∞→∞=-→x x x f x f x x 或
4函数在一点处函数值趋于正无穷大
4.1函数在0x 点处函数值趋于正无穷大的定义
如果对于任何G>0,存在G x f x x ><-<>)(0,00时,有当δδ,就说函数f(x)在0x 点处趋于正无穷大(或发散到正无穷大),记为
)()()(lim 00
x x x f x f x x →+∞→+∞=→或
4.2函数在0x 点右侧函数值趋于正无穷大的定义
如果对于任何G>0,存在0>δ,当0<x-x δ<0时,有f(x)>G,就说函数f(x)在0x 右侧趋于正无穷大(或发散到正无穷大),记为
)0()()(lim 00
0+→+∞→+∞=+→x x x f x f x x 或
4.3函数在0x 点左侧函数值趋于正无大穷的定义
如果对于任何G>0,存在,)(0,00G x f x x ><-<>时,有当δδ就说函数f(x)在0x 右侧趋于正无穷大(或发散到正无穷大),记为
0-→x x 5函数在一点处函数值趋于负无穷大
5.1函数在0x 点处函数值趋于负无穷大的定义
如果对于任何G>0,存在G x f x x -<<-<>)(0,00时,有当δδ,就说函数f(x)在0x 点处趋于负无穷大(或发散到负无穷大),记为
)()()(lim 00
x x x f x f x x →-∞→-∞=→或
5.2函数在0x 点右侧函数值趋于负无穷大的定义
如果对于任何G>0,存在,)(0,00G x f x x -<<-<>时,有当δδ就说函数f(x)在0x 右侧趋于正负穷大(或发散到负无穷大),记为
)0()()(lim 00
0+→-∞→-∞=+→x x x f x f x x 或
5.3函数在0x 点左侧函数值趋于负无穷大的定义
如果对于任何G>0,存在,)(0,00G x f x x -<<-<>时,有当δδ就说函数f(x)在0x 右侧趋于负无穷大(或发散到负无穷大),记为
)0()()(lim 00
0-→-∞→-∞=-→x x x f x f x x 或
6函数在无限远处函数值趋于无穷大
6.1函数在无限远处函数值趋于无穷大的定义
如果对于任何G>0,存在X>0,当G x f X x >>)(时,有,就说函数在无限远处趋于无穷大(或发散到无穷大),记为
)()()(lim ∞→∞→∞=∞
→x x f x f x 或
6.2函数在正无限远处函数值趋于无穷大的定义
如果对于任何G>0,存在X>0,当G x f X x >>)(时,有,就说函数在正无限远处趋于无穷大(或发散到无穷大),记为
)()()(lim +∞→∞→∞=+∞
→x x f x f x 或
6.3函数在负无限远处函数值趋于无穷大的定义
如果对于任何G>0,存在X>0,当G x f X x >-<)(时,有,就说函数在负无限远处趋于无穷大(或发散到无穷大),记为
)()()(lim -∞→∞→∞=-∞
→x x f x f x 或
7函数在无限远处函数值趋于正无穷大
7.1函数在无限远处函数值趋于正无穷大的定义
如果对于任何G>0,存在X>0,当G x f X x >>)(时,有,就说函数在无限远处趋于正无穷大(或发散到正无穷大),记为
)()()(lim ∞→+∞→+∞=∞
→x x f x f x 或
7.2函数在正无限远处函数值趋于正无穷大的定义
如果对于任何G>0,存在X>0,当G x f X x >>)(时,有,就说函数在正无限远处趋于正无穷大(或发散到正无穷大),记为
)()()(lim +∞→+∞→+∞=+∞
→x x f x f x 或
7.3函数在负无限远处函数值趋于正无穷大的定义
如果对于任何G>0,存在X>0,当G x f X x >-<)(时,有,就说函数在负无限远处趋于正无穷大(或发散到正无穷大),记为
)()()(lim -∞→+∞→+∞=-∞
→x x f x f x 或
8函数在无限远处函数值趋于负无穷大。