幂函数的图像和性质

幂函数•冥函数的定义：一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数。

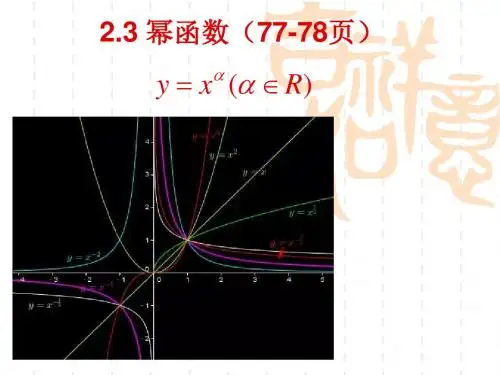
幂函数的解析式：y=xα幂函数的图像：•幂函数图像的性质：所有幂函数在(0，+∞)上都有定义．①α＞0，图像都过定点（0，0）和（1，1）；在区间（0，+∞）上单调递增；②α＜0，图像都过定点（1，1）；在区间（0，+∞）上单调递减;③当O<a<l时，曲线上凸，当a>l时，曲线下凸．④当a=l时，图象为过点(0，0)和(1，1)的直线．⑤当a=0时，表示过点(1，1)且平行于x轴的直线(除去点(0，1)) 。

幂函数图象的其他性质：(1)图象的对称性：把幂函数的幂指数a（只讨论a是有理数的情况）表示成既约分数的形式（整数看作是分母1的分数），则不论a>0还是a<0，幂函数的图象的对称性用口诀记为：“子奇母偶孤单单；母奇子偶分两边；分子分母均为奇，原点对称莫忘记”，(2)图象的形状：①若a>0，则幂函数的图象为抛物线形，当a>l时，图象在[0，+∞）上是向下凸的（称为凸函数）；当O<a<l时，图象在[o，+∞）上是向上凸的（称为凹函数）．②若a<0，则幂函数y=x“的图象是双曲线形，图象与x轴、y轴无限接近，在(0，+∞)上图象都是向下凸的。

幂函数的单调性和奇偶性：对于幂函数（a∈R)．(1)单调性当a>0时，函数在第一象限内是增函数；当a<0时，函数在第一象限内是减函数．(2)奇偶性①当a为整数时，若a为偶数，则是偶函数；若a为奇数，则是奇函数。

②当n为分数，即（p，q互素，p，q∈Z）时，若分母q为奇数，则分子p为奇数时，为奇函数；分子p为偶数时，为偶函数，若分母q为偶数，则为非奇非偶函数．。

幂函数图像及性质总结幂函数是高中数学中的一个重要概念，它是指形式为f(x)=ax^k的函数，其中a 为非零实数，k为实数。

幂函数在数学中具有广泛的应用，在图像的研究中，掌握幂函数的图像及其性质是非常重要的。

首先，我们来看幂函数的图像特点。

当k为正数时，幂函数的图像呈现出“增长”或“递减”的趋势。

当k>1时，曲线会明显上升，形成类似于指数函数的图像特征。

而当0<k<1时，曲线则会下降，但下降的速率逐渐减慢。

特别地，当k=1时，幂函数成为一次函数，即f(x)=ax，其图像为一条直线。

此外，当k为负数时，幂函数的图像则出现在第二、第四象限，并且具有对称轴。

接下来，我们来讨论幂函数的性质。

首先，我们来看函数的定义域和值域。

由于幂函数的底数a不能为零，函数的定义域为除以0的集合，即R-{0}。

而幂函数的值域则依赖于指数k的正负情况。

当k为正数时，函数的值域为正实数集(0,+∞)。

当k为负数时，函数的值域为(0, +∞)的实数集。

由于底数a的正负情况也会影响函数的关系，故在具体分析时需要考虑a的取值范围。

其次，我们来讨论幂函数的奇偶性。

当指数k为偶数时，幂函数f(x)=ax^k是一个偶函数，即满足f(x)=f(-x)。

这是因为对于任意x∈R，有(-x)^k=x^k，从而f(x)=ax^k=f(-x)。

相应地，当指数k为奇数时，幂函数f(x)=ax^k是一个奇函数，即满足f(x)=-f(-x)。

这是因为对于任意x∈R，有(-x)^k=-x^k，从而f(x)=ax^k=-ax^k=-f(-x)。

进一步地，我们来讨论幂函数的增减性和极值点。

当指数k为正数时，幂函数在定义域上是递增的。

当a>1时，函数的增长速度更快；当0<a<1时，函数的增长速度更慢。

而当指数k为负数时，幂函数在定义域上是递减的。

在图像上，幂函数具有一个最小值或最大值，该点称为极值点。

当k为偶数时，函数的极值点出现在定义域的最小值点，当k为奇数时，函数的极值点出现在定义域的最大值点。

幂函数的图像与性质幂函数是一类常见的数学函数，它的表达形式为y = x^n，其中x是自变量，n是常数指数。

在本文中，我们将探讨幂函数的图像以及它的一些基本性质。

一、幂函数图像的特点幂函数的图像是由指数n的不同取值而呈现出多种形态。

下面我们将分别讨论指数为正偶数、正奇数、负偶数和负奇数时的情况。

1. 指数为正偶数时（n > 0且n为偶数）当指数为正偶数时，幂函数的图像呈现出关于y轴对称的特点。

以y = x^2为例，当x取正负值时，y值都为正，且当x取0时，y值为0。

图像在原点处有一个最小值点，随着x的逐渐增大或减小，y也逐渐增大，但增长速度逐渐减慢。

2. 指数为正奇数时（n > 0且n为奇数）当指数为正奇数时，幂函数的图像呈现出关于原点对称的特点。

以y = x^3为例，当x取正值时，y值为正；当x取负值时，y值为负。

图像在原点处有一个零点，当x逐渐增大或减小时，y也随之增大或减小，但增长速度较快。

3. 指数为负偶数时（n < 0且n为偶数）当指数为负偶数时，幂函数的图像呈现出关于x轴对称的特点。

以y = x^-2为例，当x取正值时，y值小于1；当x取0时，y值无定义；当x取负值时，y值同样小于1。

图像在x轴上有一个渐近线y=0，当x逐渐增大或减小时，y的绝对值逐渐减小。

4. 指数为负奇数时（n < 0且n为奇数）当指数为负奇数时，幂函数的图像呈现出关于原点对称的特点。

以y = x^-3为例，当x取正值时，y值大于1；当x取负值时，y值小于-1。

图像在原点处有一个零点，当x逐渐增大或减小时，y的绝对值逐渐增大。

二、幂函数的基本性质除了图像的特点，幂函数还有一些其他的基本性质。

下面我们将介绍其中的两个重要性质。

1. 幂函数的增减性根据幂函数的指数正负，我们可以判断幂函数的增减性。

当指数为正时，幂函数是递增函数，随着自变量的增大，函数值也随之增大；当指数为负时，幂函数是递减函数，随着自变量的增大，函数值却减小。

幂函数的图像与性质幂函数的图像与性质是指，如果将一个函数定义为f(x)=ax，其中a是一个正常数，那么这个函数就叫做幂函数。

注意，这里的x不必要是整数，可以是任意实数值。

一般来说，如果a>0，则函数的图形表示为一条递增的直线；如果a<0，则函数的图形表示为一条递减的直线；如果a=1，则函数的图形表示为一条水平直线。

在函数的图形中，如果a>1，则函数的图形表示为一条右上斜线，即函数的导数增加得越来越快；如果a<1，则函数的图形表示为一条左下斜线，即函数的导数减少得越来越快；如果a=1，则函数的图形表示为一条水平直线，即函数的导数保持不变。

在函数的性质方面，幂函数的表达式可以写成y=ax，其中a是一个实数，x是一个实数变量，y是一个实数函数。

事实上，它是一个特殊的多项式函数，可以用指数形式表示，即y=ax=e^(lna)x=exlnax。

如果a>0，则此函数在定义域中是递增函数；如果a<0，则此函数在定义域中是递减函数；如果a=1，则此函数在定义域中是一条水平线。

另外，幂函数的导函数为y'=axlnax，其中a、x均为实数，而y'为函数y的导函数。

此外，幂函数的图形也会因其中的参数a的值的大小而有所不同。

如果a>1，则函数的图形表示为一条右上斜线，即函数的导数增加得越来越快；如果a<1，则函数的图形表示为一条左下斜线，即函数的导数减少得越来越快；如果a=1，则函数的图形表示为一条水平直线，即函数的导数保持不变。

综上所述，幂函数的图形与性质取决于参数a的值，它是一个特殊的多项式函数，其导函数为y'=axlnax，其中a、x均为实数，而y'为函数y的导函数。

幂函数的图像和性质（学习版）编制人：__________________审核人：__________________审批人：__________________编制学校：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如英语单词、英语语法、英语听力、英语知识点、语文知识点、文言文、数学公式、数学知识点、作文大全、其他资料等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of classic sample essays, such as English words, English grammar, English listening, English knowledge points, Chinese knowledge points, classical Chinese, mathematical formulas, mathematics knowledge points, composition books, other materials, etc. Learn about the different formats and writing styles of sample essays, so stay tuned!幂函数的图像和性质概念一般地，y=xα（α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。

幂函数的性质与图像1、幂函数的定义一般地，形如y x α=（x ∈R ）的函数称为幂函数，其中x 是自变量，α是常数.如11234,,y x y x y x -===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数. 2、函数的图像（1）y x = （2）12y x = （3）2y x = （4）1y x -= （5）3y x =用描点法在同一坐标系内画出以上五个函数图像，通过观察图像，可以看出幂函数的性质。

3．幂函数性质（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）；（2）x ＞0时，幂函数的图象都通过原点，并且在[0， +∞]上，是增函数（3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数. （4）在第一象限内，图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数 . y 轴和直线1x =之间，图象由上至下，指数α .：4. 规律总结1．在研究幂函数的性质时，通常将分式指数幂化为根式形式，负整指数幂化为分式形式再去进行讨论；2．对于幂函数y ＝αx ，我们首先应该分析函数的定义域、值域和奇偶性，由此确定图象的位置，即所在象限，其次确定曲线的类型，即α＜0，0＜α＜1和α＞1三种情况下曲线的基本形状，还要注意α＝0，±1三个曲线的形状；对于幂函数在第一象限的图象的大致情况可以用口诀来记忆：“正抛负双，大竖小横”，即α＞0（α≠1）时图象是抛物线型；α＜0时图象是双曲线型；α＞1时图象是竖直抛物线型；0＜α＜1时图象是横卧抛物线型． 在[0，+∞]上，y x =、2y x =、3y x =、12y x =是增函数， 在（0，+∞）上， 1y x -=是减函数。

例1．已知函数()()2531m f x m m x --=--，当 m 为何值时，()f x ：（1）是幂函数；（2）是幂函数，且是()0,+∞上的增函数；（3）是正比例函数；（4）是反比例函数；（5）是二次函数； 简解：（1）2m =或1m =-（2）1m =-（3）45m =-（4）25m =-（5）1m =- 变式训练：已知函数()()2223m m f x m m x --=+，当 m 为何值时，()f x 在第一象限内它的图像是上升曲线。