牛顿的后向差分公式

使用泰勒定理推导牛顿方法的误差公式我们来了解一下泰勒定理。

泰勒定理是由英国数学家泰勒在17世纪提出的，它是一种用多项式来逼近函数的方法。

具体而言，泰勒定理可以将一个函数在某一点附近展开成一个无穷级数，从而可以用级数的有限项来近似表示函数的值。

泰勒定理的表达式如下：f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...其中，a是展开点，f(x)是函数在点x处的值，f'(x)、f''(x)、f'''(x)分别是函数的一阶、二阶和三阶导数。

接下来，我们来介绍一下牛顿方法。

牛顿方法是一种求解方程近似解的方法，它的基本思想是通过不断逼近函数的零点来求解方程。

具体而言，牛顿方法从一个初始的近似解开始，然后通过迭代的方式不断改进近似解，直到满足所需的精度要求为止。

牛顿方法的迭代公式如下：x_(n+1) = x_n - f(x_n)/f'(x_n)其中，x_n是第n次迭代的近似解，f(x_n)是函数在x_n处的值，f'(x_n)是函数在x_n处的导数。

现在，我们开始推导牛顿方法的误差公式。

假设我们要求解方程f(x) = 0，在方程的一个近似解x_n处，我们可以利用泰勒定理将函数f(x)展开成级数形式：f(x) = f(x_n) + f'(x_n)(x-x_n) + f''(x_n)(x-x_n)^2/2! + f'''(x_n)(x-x_n)^3/3! + ...我们希望找到一个近似解x_{n+1}，使得f(x_{n+1}) = 0。

因此，我们可以将上式中的x替换为x_{n+1}，并忽略高阶项，得到近似的零点表达式：0 ≈ f(x_n) + f'(x_n)(x_{n+1}-x_n)由于我们希望找到方程的零点，即f(x_{n+1}) = 0，因此上式可以简化为：0 ≈ f(x_n) + f'(x_n)(x_{n+1}-x_n)进一步整理得到：x_{n+1} - x_n ≈ - f(x_n)/f'(x_n)将牛顿方法的迭代公式x_{n+1} = x_n - f(x_n)/f'(x_n)代入上式，得到：x_{n+1} - x_n ≈ - (f(x_n)/(f'(x_n)))我们可以将上式右边的分数形式进行展开，得到误差公式：x_{n+1} - x_n ≈ - (f(x_n)/f'(x_n)) ≈ - (f(x_n)/f'(x_n)) + (f(x_n)f''(x_n))/(2(f'(x_n))^2) - (f(x_n)f''(x_n))/(2(f'(x_n))^2)继续展开得到更多项，最后得到牛顿方法的误差公式：x_{n+1} - x_n ≈ - (f(x_n)/f'(x_n)) + (f(x_n)f''(x_n))/(2(f'(x_n))^2) - (f(x_n)f''(x_n)f'''(x_n))/(6(f'(x_n))^3) + ...根据以上推导，我们可以得出牛顿方法的误差公式。

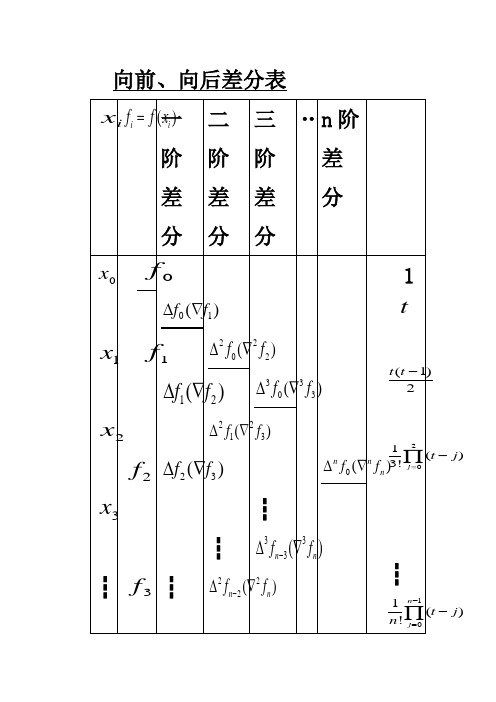
向前、向后差分表
-
)j
-
)j
例：在微电机设计计算中需要查磁化曲线表，通常给出的表是磁密B每间隔100高斯磁路每厘米长所需安匝数at的值，下面要解决B 从4000至11000区间的查表问题。

为节省计算机存储单元，采用每
500高斯存入一个at值，在利用差分公式计算。

从差分表中看到三阶差分近似于0，计算时只需二阶差分。

当4000≤B≤10500时用牛顿前插公
式；当10500≤B ≤11000时用牛顿后插公式；
例如，求f （5200）时取
2
00005000, 1.58,0.11,B f f f ==∆=∆=
，h=500,B=5200,t=0.4,取n=2，由公式
000(1)
()2!
n t t N x th f t f -+=+∆+
计算得：
(0.4)(0.
(5200) 1.58(0.4)(0.11)2
f -≈++
这个结果与直接查表得到的值相同，说明用此算法在计算机上求值是可行的。

newton-cotes 公式牛顿-科特斯（Newton-Cotes）公式是用来在有限的数据点上进行数值积分的公式，它有助于解决一些数学里复杂的积分问题。

牛顿-科特斯（Newton-Cotes）公式是建立在具有固定的插值点的基础上的，它的基本思想是将积分区间上的函数值用一个多项式曲线表示，根据多项式的函数值，通过运用权重系数求出函数对应积分区间上的积分值。

牛顿-科特斯（Newton-Cotes）公式具有理论可靠性和可计算性，可以用来计算任何一类好的函数在有限积分区间上的数值积分值。

牛顿-科特斯（Newton-Cotes）公式有如下几种：前向 - 望厄（Forward-Newton-Cotes）公式，中间 - 望厄（Midpoint-Newton-Cotes）公式，后向 - 望厄（Backwards-Newton-Cotes）公式和梯形 - 望厄（Trapezoid-Newton-Cotes）公式，每种公式都是以一定的格式形式来进行积分计算的，它们在实用水平上是相通的，可以用来求取给定函数在有限划分区间上的近似数值积分值。

不同的是，每种公式都有不同的特点，比如，前向 - 望厄（Forward-Newton-Cotes）公式算法效率高但精度低，后向 - 望厄（Backwards-Newton-Cotes）公式算法精度高但效率低，梯形 - 望厄（Trapezoid-Newton-Cotes）公式精度取决于区间的分段数，而中间 - 望厄（Midpoint-Newton-Cotes）公式适合单次积分的计算。

牛顿-科特斯（Newton-Cotes）公式可以用来解决一些数学里比较复杂的积分问题，它对于提高程序自动执行效率也必不可少，所以它在很多地方都有实际应用。

§2 差商、牛顿插值多项式在计算过程中，若需要再增加插值节点并求出新的插值函数，则Lagrange 插值公式所有的基函数都要重新计算，造成计算量的很大浪费。

而以下介绍的牛顿插值公式可以克服这一缺陷，可在原有插值多项式的基础上灵活的增加插值节点。

一、 差商及其性质： 1、相关定义设给出函数)(x f 在点0x ，1x ，… ，n x ，…上的函数值 ，则有：称],[10x x f 1010()()f x f x x x -=-为函数)(x f 在0x 、1x 点的一阶差商。

一阶差商的差商],,[210x x x f 121020],[],[x x x x f x x f --= 称为函数)(x f 在0x ,1x 和2x 点的二阶差商。

1-n 阶差商的差商],,,[10n x x x f 112020],,,[],,,[------=n n n n n n x x x x x f x x x f称为函数)(x f 在n x x x ,,,10 点的n 阶差商。

见插商表4-12、性质：性质1 ：差商],,,[10n x x x f 可表示为函数值的线性组合，即 ∑==ni i i n x f a x x x f 010)(],,,[ ，其中：∏≠=-=nij j j ii x xa ,0)(/1。

该性质表明：差商与节点的排列次序无关，即：],,,[10n x x x f ＝],,,[01n x x x f ＝…＝],,,[01x x x f n这就是差商的对称性。

性质 2101010[,,][,,][,,,]n n n n f x x f x x f x x x x x --=-01110[,,,][,,,]n n n f x x x f x x x x -=11100[,,][,,,]n n n f x x f x x x x x --=-10110[,,][,,,]n n n f x x f x x x x x --=-性质 3 设)(x f 在所含节点n x x x ,,,10 的区间],[b a 上有n 阶导数，则在该区间内至少有一点],[b a ∈ξ，使得：!/)(],,,[)(10n f x x x f n n ξ= 由该性质可知，若)(x f 为n 次多项式，则其n 阶差商为一常数。

牛顿定律全部公式
牛顿定律是经典力学中最为基础且重要的定律之一，描述了
物体受力和运动之间的关系。

下面是牛顿定律的全部公式：
第一定律（惯性定律）：
物体在没有外力作用下，或合力为零时保持静止或匀速直线
运动。

其表达式为：
∑F=0或F=0
第二定律（运动定律）：
物体的加速度与作用在它上面的合外力成正比，与物体的质
量成反比。

其表达式为：
F=m*a
其中，F为合外力，m为物体的质量，a为物体的加速度。

第三定律（作用反作用定律）：
任何两个物体之间的相互作用力都成对出现，并且大小相等、方向相反。

其表达式为：
F₁₂=F₂₁
其中，F₁₂为物体1对物体2的作用力，F₂₁为物体2对物体
1的作用力。

这些公式是牛顿定律的核心内容，通过这些公式我们可以计算出物体受力和运动的相关参数。

牛顿定律适用于大多数日常生活中的力学问题，是理解和研究物体的运动行为的基础。

它在工程学、物理学等领域得到了广泛的应用。

2012-2013（1）专业课程实践论文牛顿后插公式王瑜，0818180218，R数学08-2班一、算法理论由牛顿前插公式)()!1())...(1()()1(1ξ+++--=n a n n f h n n t t t x R ，),(0n x x ∈ξ如果要求表示函数在n x 附近的值)(x f ，此时应用Newton 插值公式，插值点应按的次序排列，有)()](,,,[))(](,,[)](,[)()(1011211x x x x x x x f x x x x x x x f x x x x f x f x N n n n n n n n n n n n n n --++--+-+=----- 作变换)01(≤≤-+=t th x x n 错误！未找到引用源。

，并利用公式代入上式带入得n n n n n n n f n n t t t f t t f t f th x N ∇-++++∇++∇+=+!)1()1(!2)1()(2称为Newton 后插公式，其余项。

。

),(,)!1()()()1()()()(0)1(1n n n n n n x x n f h n t t t th x N x f x R ∈+++=+-=++ξξ 若用Newton 后插公式求)(x f 的值，因x 在n x 附近，则其系数)(x f 在点n x 的各阶向后差分。

二、算法框图结束判断是否继续输入提示是否继续输入输出结果判断输入区间合法性Input x 提示正确的X 区间信息开始是否是否三、算法程序class Interpolation{public:Interpolation(int num, double x1, double x2, double func[]);double ComputeBackwardValue(double x); // compute backward interpolation value ~Interpolation();private:// Check(); // checking the inputsvoid GetBackwardTable(); // get the backward differential tableprivate:int m_num; // the number of interpolation pointsdouble m_x1, m_x2; // the first point m_x1 and last point m_x2double m_step; // the interpolation stepdouble* m_func; // the function value of interpolation pointsdouble* m_btable; // the backward differential table};#include <iostream>#include <limits>using namespace std;#define NUM 15//样本个数#define MIN 4000//上面输入区间下限#define MAX 11000//上面输入区间上限int main(){double func[NUM]={1.38, 1.48, 1.58, 1.69, 1.81,1.94,2.10, 2.28, 2.50, 2.76,3.06, 3.41, 3.83,4.33, 4.93};//输入对应的函数值double x1=MIN, x2=MAX, x;int num=NUM;char flag='Y';Interpolation test(num, x1, x2, func);while(flag=='Y'){cout<<"Input x: ";cin>>x;if (!cin){cin.clear();cin.ignore(numeric_limits<int>::max(), '\n'); // clear input buffercontinue;}if(x<x1 || x>x2){cout<<"---Invalid input: "<<x<<"---"<<endl;cout<<"Only the number between "<<x1<<" and "<<x2<<" is valid..."<<endl; }else{cout<<"Backward interpolation value:"<<puteBackwardValue(x)<<endl;}cout<<endl<<"Do you want to process? please input(Y/N):"<<endl;cin>>flag;}return 0;}Interpolation::Interpolation(int num, double x1, double x2, double func[]) {m_num = num;m_x1 = x1;m_x2 = x2;m_step = (m_x2-m_x1)/(num-1);m_func = new double[m_num];m_btable = new double[m_num];for (int i=0; i<m_num; ++i){m_func[i] = func[i];m_btable[i] = func[i];}GetBackwardTable();}Interpolation::~Interpolation(){delete m_func;delete m_btable;}void Interpolation::GetBackwardTable(){// get the backward differential tableint i, j;double tmp;for (i=1; i<m_num; ++i) {tmp = m_btable[m_num-1];for (j=m_num-1; j>=i; --j) {m_btable[j] = m_btable[j]-m_btable[j-1];}m_btable[i-1] = tmp;}}double Interpolation::ComputeBackwardValue(double x){// compute backward interpolation valuedouble* coef; //coefficient talbedouble result, t;int i;coef = new double[m_num];t = (x-m_x2)/m_step;for (i=1, coef[0]=1; i<m_num; ++i) //compute the coefficient table {coef[i] = coef[i-1]*(t+i-1)/i;}for (i=0, result=0; i<m_num; ++i){result += m_btable[i]*coef[i];}delete coef;return result;}四、算法实现例1．在微电机设计计算中需要查磁化曲线表，通常给出的表如图是磁密B每间隔100高斯磁路每厘米长所需安匝数at的值，下面要解决B从4000到11000区间的查表问题书上给出的可以用后插公式的区间为10500＜B≤11000解：在此谨以10500以上的数为例，首先输入样本个数和所在区间然后逐一输入对应的函数值。

计算方法引论课后答案第一章误差1.什么是模型误差，什么是方法误差？例如，将地球近似看为一个标准球体，利用公式 $A=4\pi r$ 计算其表面积，这个近似看为球体的过程产生的误差即为模型误差。

在计算过程中，要用到 $\pi$，我们利用无穷乘积公式计算 $\pi$ 的值：pi=2\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot\f rac{4}{5}\cdot\frac{6}{5}\cdot\frac{6}{7}\cdot\frac{8}{7}\cdot\ frac{8}{9}\cdot\cdots我们取前9项的乘积作为 $\pi$ 的近似值，得$\pi\approx3.xxxxxxxx5$。

这个去掉 $\pi$ 的无穷乘积公式中第9项后的部分产生的误差就是方法误差，也称为截断误差。

2.按照四舍五入的原则，将下列各数舍成五位有效数字：816.956，76.000，.322，501.235，.182，130.015，236.23.解：816.96，76.000，.501.24，.130.02，236.23.3.下列各数是按照四舍五入原则得到的近似数，它们各有几位有效数字？81.897，0.008，136.320，050.180.解：五位，三位，六位，四位。

4.若 $1/4$ 用 0.25 表示，问有多少位有效数字？解：两位。

5.若 $a=1.1062$，$b=0.947$，是经过舍入后得到的近似值，问：$a+b$，$a\times b$ 各有几位有效数字？已知 $da<\frac{1}{2}\cdot10^{-4}$，$db<\frac{1}{2}\cdot10^{-3}$，又 $a+b=0.\times10$。

begin{aligned}d(a+b)&=da+db\leq da+db=\frac{1}{2}\cdot10^{-4}+\frac{1}{2}\cdot10^{-3}=0.55\times10^{-3}<\frac{1}{2}\cdot10^{-2}end{aligned}所以 $a+b$ 有三位有效数字；因为 $a\timesb=0.xxxxxxxx\times10$。

数值分析学习公式总结数值分析是以计算机为工具，对数学问题进行数值计算和近似方法的研究。

在数值分析中，有许多重要的数学公式和算法被广泛应用。

下面是一些数值分析中常用的公式和算法的总结。

1.插值公式：-拉格朗日插值公式：假设有给定的n个点(x_0,y_0),(x_1,y_1),...,(x_n,y_n)，则对于任意一个x，可以通过拉格朗日插值公式计算出相应的y值。

-牛顿插值公式：利用差商构造的插值公式，对给定n个点进行插值，得到一个多项式函数。

2.数值积分公式：-矩形法：将区间分割成若干小矩形，计算每个矩形的面积然后求和。

-梯形法：将区间分割成若干个梯形，计算每个梯形的面积然后求和。

-辛普森法则：将区间分割成若干个小区间，通过对每个小区间应用辛普森公式计算出近似的定积分值。

3.数值微分公式：-前向差分公式：利用函数在特定点的导数与函数在该点附近的值之间的关系，通过近似计算导数的值。

-后向差分公式：类似于前向差分公式，但是利用函数在特定点的导数与函数在该点附近的值之间的关系，通过近似计算导数的值。

-中心差分公式：利用函数在特定点的导数与函数在该点两侧的值之间的差异，通过近似计算导数的值。

4.数值解线性方程组方法：-直接法：高斯消元法，LU分解法等。

-迭代法：雅可比迭代法，高斯-赛德尔迭代法等。

5.最小二乘拟合法：-线性最小二乘拟合：通过线性回归的方法，寻找最佳的拟合直线。

-非线性最小二乘拟合：通过非线性回归的方法，寻找最佳的非线性拟合曲线。

6.数值求解常微分方程方法：-欧拉法：将微分方程离散化，通过迭代计算得到近似解。

-改进欧拉法：利用欧拉法的计算结果进行修正，提高近似解的精度。

- 二阶龙格-库塔法：利用四阶Runge-Kutta法的计算结果进行修正，提高近似解的精度。

7.插值法的误差估计：-真实误差：插值函数与原函数之间的差异。

-误差界：对于给定的插值公式，通过计算条件和边界限制，得到误差的上限。

8.特殊函数的数值计算：-常用特殊函数的近似计算方法，如阶乘函数，指数函数，对数函数等。