东南大学通信复试数字信号处理(吴镇杨)课后答案

1、时域和频域的区别2、信号在各个频率的幅度分布图称为3、采样率就是4、抗混叠滤波器的目的是5、如果复信号频率是120Hz，采样频率是150Hz，信号的混叠频率是6、对频率在1kHz到1.1kHz的实带限信号进行抽样，若抽样频率为750Hz，则基带信号位于什么频带？7、以800Hz抽样的300Hz实信号的最先4个镜像频率是8、x[n] = cos(n3 /4)可以描述为a每个数字周期 个采样点，覆盖 个模拟信号周期9、低通滤波器的截至频率是1kHz，则将削弱哪个频率a 0 Hzb 500 Hzc 1k Hzd 2k Hz10、在x1[n] = sin(n /9)上作如下（ ）变化，得到x2[n] = sin(n /9 + /3)a 不变b 右移3位c左移3位d 关于y轴对称11、滤波器y[n] + 0.8y[n-1] = x[n] - 0.5x[n-1] 的单位脉冲响应的头4个样点值为12、h[n] * x[n]数字上等于a 对所有k，将h[k]x[n-k]求和的值b 对所有k，将x[k]h[n-k]求和的值c x[n] * h[n]d以上均是13、描述某系统的差分方程y[n] = 0.7y[n-2] + x[n] - 0.3x[n-1]，该系统的转移函数为14、某系统单位脉冲响应h[n] = 0.5d[n] - 0.4d[n-1] + 0.25d[n-2],对应转移函数为a H(z) = 1 - 0.4z^-1 + 0.25z^-2b H(z) = z^2 - 0.4z + 0.25c H(z) = z^-2 - 0.4z^-1 + 0.25d 非以上答案15、极点为0.5 + j0.8和0.5 - j0.8，零点为-1.2的滤波器是a 稳定的b 边缘稳定c 不稳定d 不能决定16、滤波器的单位脉冲响应的DTFT给出了滤波器的a 频谱b 频率响应c 幅度d 相位17、频谱图平坦的信号对应如下哪个信号a 正弦信号b 方波c 白噪声d 直流信号18、离散实正弦信号的频谱的一个周期中包括a 无峰点b 1个峰点c 2个峰点d 多于2个峰点19、讨论连续非周期与离散非周期信号(即连续非周期信号采样前后)以及连续周期与离散周期信号(即连续周期信号采样前后)这四种信号频谱的周期性和连续性,并总结其规律性。

1. 解丗由题意可知 N=5
则周期为丗其中为整数丆且满足使N为最小整数。

2. •i1•j解丗由题意可知 N=14
则周期为丗
•i2•j解丗由题意可知 N= 8
则
则所求周期 N=14
最小公倍数丆即为丗56
3.19 (1)周期卷积的主值序列为丗f(n)R(n) ={6,3, 6,10,14,12,9};
(2)循环卷积f (n) ={6,3, 6,10,14,12,9};
•i3•j线性卷积为f(n) ={1,3, 6,10,14,12,9,5, 0, 0, 0, 0}
2.21 •i 第二种方法乯按频率抽取算法丗输入顺
序丆
输出倒序(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7, 15);
4
共有4(16=2*2*2*2 )节
第一节丗数据点间距、蝶形类型均是8•C
0 1 2 3 4 5 6 7
所乘因子丗W ,W ,W ,W ,W ,W ,
W ,W ;
N N N N N N N N N
第二节丗数据点间距、蝶形类型均是4 •C
0 2 4 6
所乘因子丗W ,W ,W ,W ;
N N N N
0 4
第三节丗数据点间距、蝶形类型均是2 •C所乘因
子丗W ,W ;
N N
第四节丗数据点间距、蝶形类型均是1 •C所乘因
子丗W ;
N。

习题一 (离散信号与系统)1.1周期序列，最小周期长度为5。

1.2 (1) 周期序列，最小周期长度为14。

(2) 周期序列，最小周期长度为56。

1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑F 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1)0n z -(2)5.0||,5.0111>--z z(3)5.0||,5.0111<--z z(4)0||,5.01)5.0(11101>----z zz1.8 (1) 0,)11()(211>--=---z z z z z X N (2) a z az az z X >-=--,)1()(211(3)a z az z a az z X >-+=---,)1()(311211.9 1.10(1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ1.11 (1) )(1z c X - (2) )(2z X (3) )()1(21z X z -+ (4) -+<<x x R z R z X /1/1),/1(1.12 (1)1,11<-ab ab(2) 1 (3) 00n a n1.13 (1) 该系统不是线性系统；该系统是时不变系统。

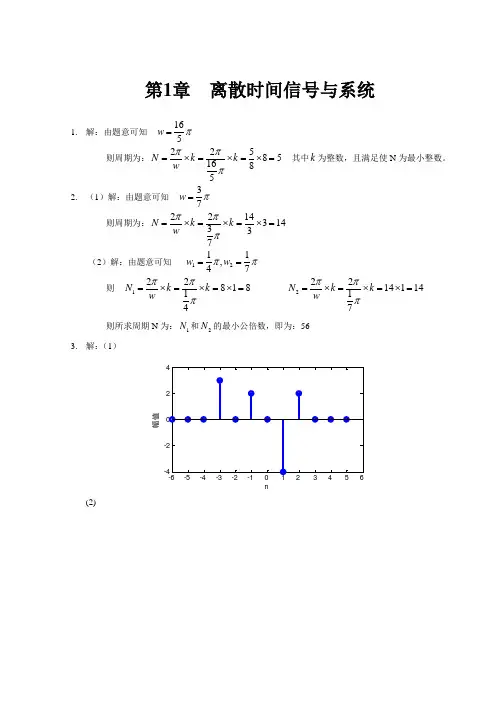
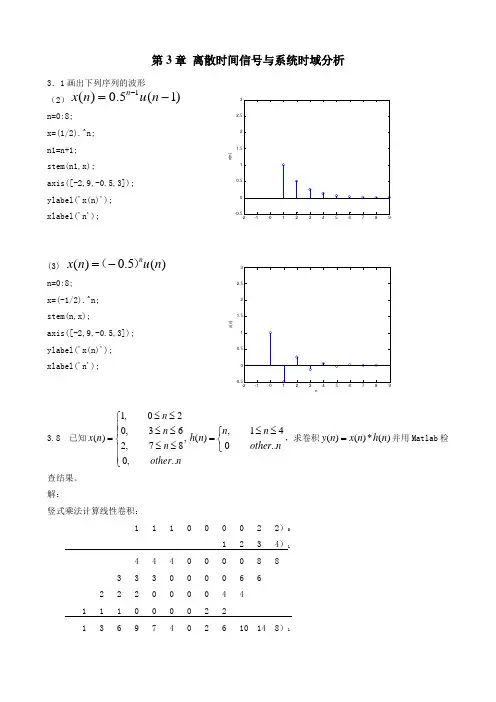
第3章 离散时间信号与系统时域分析3．1画出下列序列的波形（2）1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-（）n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩，求卷积()()*()y n x n h n =并用Matlab 检查结果。

解：竖式乘法计算线性卷积： 1 1 1 0 0 0 0 2 2）01 2 3 4）14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8）1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果：x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx （n ）=5sin(n) 解：2214337w πππ==，所以N=14 (2) 326n ππ-x （n ）=sin()-sin(n)解：22211213322212,2122612T N w T N w N ππππππ=========，所以(6) 3228n π-x （n ）=5sin()-cos(n) 解：22161116313822222()T N w T w x n ππππππ=======，为无理数，所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=，()4()nx n u n -=，(1)4y -=，(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应，并画出图形。

数字信号处理（吴镇扬）课后习题答案（比较详细的解答过程）第二章测试训练题解1.DFT和DTFT之间的关系是2.DFT和DFS之间的关系是3.对于一个128点的DFT，最先4个DFT相应于数字频率4.某滤波器的频响为H(ω) = 0.3cos2ω- 0.2cosω+ 0.05，相应于6点的DFT的H[k]为5.采样频率为22.05kHz的1024点DFT所对应的频率分辨率为6.采样率为8kHz的信号的256点DFT的第一个周期覆盖的频率范围是从0Hz至7.信号[ 1 0 2 ]的DFT每隔3个样点值重复，为8.以1600Hz对一220Hz的信号采样，进行64点DFT，最接近的DFT频率为9.以12kHz的信号对一4.25kHz的信号抽样，其256点DFT幅谱图的基带最大峰值点所对应的下标为10.采样频率为6kHz，1kHz信号的频率分辨率要达到50Hz，需11.采样频率为16kHz，1024点DFT的窗口长度为12.关于谱泄漏与窗口长度的关系是13.频谱图是展现信号的什么14.周期性方波的频谱图15.在FFT中的乘数因子是16.与512点的DFT相比，512点的FFT只需约几分之一的计算量17、一个长度为N的有限长序列可否用N个频域的采样值唯一地确定？18、计算两个Ｎ点序列的线性卷积，至少要做多少点的ＤＦＴ？19、x(2n)与x(n)的关系20、对于高斯序列x(n)=exp[-(n-p)2/q]，取16点作FFT，其幅度谱中低频分量最多的是21、一般地说按时间抽取基二FFT的_______序列是按位反转重新排列的。

22、信号x（n）＝sin(nπ/4) - cos(nπ/7)的数字周期为23、Ｎ＝２Ｌ点基二ＦＦＴ，共有______列蝶形，每列有____个蝶形。

24、信号s(t)=sin(4000πt)+sin(600πt)，则采样频率至少应为25、用按时间抽取法计算256点的FFT时，n=233的二进制位反转值是26、FFT之所以能减少DFT的运算量，是因为：，FFT减少DFT 运算量的基本处理思想是。

【最新整理，下载后即可编辑】习题一 (离散信号与系统)1.1周期序列，最小周期长度为5。

1.2 (1) 周期序列，最小周期长度为14。

(2) 周期序列，最小周期长度为56。

1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑ 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1) 0n z -(2) 5.0||,5.0111>--z z (3) 5.0||,5.0111<--z z (4)0||,5.01)5.0(11101>----z z z1.8 (1) 0,)11()(211>--=---z zz z z X N(2) a z az az z X >-=--,)1()(211 (3) a z az z a az z X >-+=---,)1()(311211.91.10 (1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ 1.11(1))(1z c X - (2) )(2z X (3))()1(21z X z -+ (4)-+<<x x R z R z X /1/1),/1(1.12 (1) 1,11<-ab ab(2) 1 (3)00n a n1.13 (1) 该系统不是线性系统；该系统是时不变系统。

实验四 有限长单位脉冲响应滤波器设计朱方方 03 通信四班(1) 设计一个线性相位FIR 高通滤波器，通带边界频率为π，阻带边界频率为π，阻带衰减不小于40dB 。

要求给出h(n)的解析式，并用MATLAB 绘出时域波形和幅频特性。

解：(1)求数字边界频率:0.6 , 0.4c r ωπωπ== (2)求理想滤波器的边界频率:0.5n ωπ=(3)求理想单位脉冲响应:[]d sin ()sin[()]()()1n n n n n n h n n παωααπαωαπ⎧---≠⎪⎪-=⎨⎪-=⎪⎩(4) 选择窗函数。

阻带最小衰减为-40dB ，因此选择海明窗(其阻带最小衰减为-44dB)；滤波器的过渡带宽为ππ=π，因此6.210.231 , 152N N N ππα-=⇒=== (5) 求FIR 滤波器的单位脉冲响应h(n):[]31d sin (15)sin[0.5(15)]1cos ()15()()()15(15)115n n n R n n h n w n h n n n ππππ⎧---⎡⎤⎛⎫-⋅⋅≠⎪ ⎪⎢⎥==-⎝⎭⎨⎣⎦⎪=⎩程序：clear;N=31; n=0:N-1;hd=(sin(pi*(n-15))-sin*pi*(n-15)))./(pi*(n-15)); hd(16)=; win=hanning(N); h=win'.*hd;figure; stem(n,h);xlabel('n'); ylabel('h(n)'); grid;title('FIR 高通滤波单位脉冲响应h(n)'); [H,w]=freqz(h,1); H=20*log10(abs(H)); figure;3plot(w/pi,H);axis([0 1 -100 10]);xlabel('\omega/\pi'); ylabel('幅度/dB');grid;title('FIR 高通滤波器，hanning 窗，N=31');51015202530nh (n )FIR 高通滤波器的单位脉冲响应h(n)0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-10010ω/π幅度/d BFIR 高通滤波器，hanning 窗，N=31分析：由图知阻带衰减最小值大于40，满足要求。

（1） 观察高斯序列的时域和幅频特性，固定信号)(n x a 中参数p=8,改变q 的值，使q 分别等于2、4、8，观察他们的时域和幅频特性，了解当q 取不同值时，对信号序列的时域和幅频特性的影响；固定q=8，改变p,使p 分别等于8、13、14，观察参数p 变化对信号序列的时域和幅频特性的影响，注意p 等于多少时会发生明显的泄漏现象，混叠是否也随之出现？记录实验中观察到的现象，绘出相应的时域序列和幅频特性曲线。

()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解：程序见附录程序一：P=8,q 变化时：t/T x a (n )p=8 q=2k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )p=13 q=851015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析：由高斯序列表达式知n=p 为期对称轴； 当p 取固定值时，时域图都关于n=8对称截取长度为周期的整数倍，没有发生明显的泄漏现象；但存在混叠，当q 由2增加至8过程中，时域图形变化越来越平缓，中间包络越来越大，可能函数周期开始增加，频率降低，渐渐小于fs/2,混叠减弱；当q 值固定不变，p 变化时，时域对称中轴右移，截取的时域长度渐渐地不再是周期的整数倍，开始无法代表一个周期，泄漏现象也来越明显，因而图形越来越偏离真实值，p=14时的泄漏现象最为明显，混叠可能也随之出现；（2） 观察衰减正弦序列 的时域和幅频特性，a=0.1,f=0.0625,检查谱峰出现的位置是否正确，注意频谱的形状，绘出幅频特性曲线，改变f ，使f 分别等于0.4375和0.5625，观察这两种情况下，频谱的形状和谱峰出现的位置，有无混叠和泄漏现象？说明产生现象的原因。

数字信号处理课后答案 1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值； （2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。