全国“希望杯”八年级数学竞赛试题(第一届至第二十二届)【含答案】

2005年首届“希望杯”全国中小学数学大赛决赛试题（初二）一 选择题1．下列从左到右的变形中是因式分解的是（ ）。

（A ） (a+b)(a-b) = a 2-b 2 （B ） (x-1)(y-1)=(1-x)(1-y)（C ） ab+a+b+1 =(a+1)(b+1) （D ） m+2m+3=m(m+3+m3) 2．下列各式与分式ba a +--的值相等的是（ ）。

（A ）b a a -- （B ）b a a + （C ）a b a - （D ）ba a - 3．小明要从长度分为5cm,6cm,11cm,16cm 的四根木棒中选出三根摆成一个三角形，那么这个三角形的周长是（ ）。

（A ） 33cm （B ） 22cm （C ） 27cm （D ）32cm4．为了保护环境，某企业决定购买10台污水处理设备，现有A ，B 两种型号的有（ ）种。

（A ）1 （B ）2 （C ）3 （D ） 45．已知正整数a,m,n 满足542-a ，则这样的a,m,n 的取值（ ）。

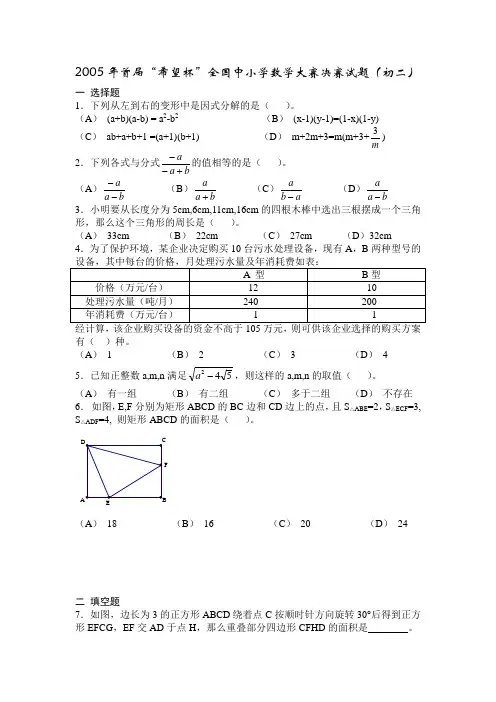
（A ） 有一组 （B ） 有二组 （C ） 多于二组 （D ） 不存在6． 如图，E,F 分别为矩形ABCD 的BC 边和CD 边上的点，且S △ABE =2，S △ECF =3, S △ADF =4, 则矩形ABCD 的面积是（ ）。

F（A ） 18 （B ） 16 （C ） 20 （D ） 24二 填空题7．如图，边长为3的正方形ABCD 绕着点C 按顺时针方向旋转30°后得到正方形EFCG ，EF 交AD 于点H ，那么重叠部分四边形CFHD 的面积是 。

CG8=== …… , =则a+b 值为 。

9．司机小王驾车在公路上行驶，他看到里程碑上的数是两位数；一小时后，看到里程碑上的数恰是第一次看到的数颠倒了顺序的两位数；再过一小时后，第三次看到里程碑上的数又恰好是第一次见到的两位数字之间添上一个0的三位数，这三块里程碑上的数分别是 。

历届希望杯初二试题及答案一、选择题（每题5分，共20分）1. 下列哪个数不是质数？- A. 2- B. 3- C. 4- D. 5答案：C2. 如果一个直角三角形的两条直角边分别为3和4，那么斜边的长度是多少？- A. 5- B. 6- C. 7- D. 8答案：A3. 一个数的平方根是4，这个数是多少？- A. 16- B. 8- C. 4- D. 2答案：A4. 一个圆的半径是5厘米，那么它的面积是多少平方厘米？- A. 25π- B. 50π- C. 100π- D. 200π答案：B二、填空题（每题3分，共15分）1. 一个数的立方根是2，这个数是______。

答案：82. 如果一个数的绝对值是5，那么这个数可能是______或______。

答案：5，-53. 一个数的倒数是1/4，这个数是______。

答案：44. 一个圆的直径是10厘米，那么它的半径是______厘米。

答案：55. 一个直角三角形的两个锐角的度数之和是______度。

答案：90三、解答题（每题10分，共30分）1. 一个长方形的长是宽的两倍，如果长是10厘米，求这个长方形的面积。

答案：首先，我们知道长方形的宽是长的一半，即5厘米。

长方形的面积是长乘以宽，所以面积是10厘米乘以5厘米，等于50平方厘米。

2. 一个数列的前三项是2，4，8。

如果这个数列是一个等比数列，求第四项。

答案：等比数列的每一项都是前一项的固定倍数。

这里，每一项都是前一项的2倍。

所以，第四项是8乘以2，等于16。

3. 一个水池的容积是100立方米，如果每小时流入水池的水是5立方米，求需要多少小时才能填满水池。

答案：要填满100立方米的水池，每小时流入5立方米，需要的时间是100除以5，等于20小时。

结束语希望杯数学竞赛不仅考查学生的数学知识，更注重考查学生的逻辑思维和解决问题的能力。

通过这样的竞赛，学生能够更好地理解数学知识，提高自己的数学素养。

第二十二届（2011年）“希望杯”全国数学邀请赛培训题初中二年级一、选择题（以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母填在每题后面的圆括号内）1.如图1，数轴上的四个点A B C D 、、、分别代表整数a b c d 、、、.若1,1a b c b --=--=-，则d 的值是（ ）（A ）3- (B) 0 (C)1 （D ）4 1. 已知201020111,,20092011201020122011a b c ===⨯⨯，则（ ）（A ）a b c <<(B)c b a << （C ）b a c << （D ）c a b <<2. 下列各数中，最大的是（ ）（A ）37+ (B) 26+ （C ）20 （D ）114522+3. 已知a 是实数，并且2201040a a -+=则代数式228040200954a a a -+++的值是（ ）（A ）2009 (B) 2010 （C ）2011 （D ）2012 4. Giventwonon－zerorealnumbersaandb,satisfy()2242342a b a b a -+++-+=,then the value of a b + is ( )（A ）－1 (B) 0 （C ）1 （D ）25. If the linear function y ax b =+ passes through the point (－2, 0),but not the first Quadrant,then the solution set for ax b > is ( )（A ）2x >- (B) 2x <- （C ） 2x > （D ）2x < 6. 已知反比例函数k y x =的图像经过点1,b a -⎛⎫⎪⎝⎭，那么它可能不经过点（ ） （A ）1,b a ⎛⎫- ⎪⎝⎭ (B) 1,a b -⎛⎫ ⎪⎝⎭ （C ）,1b a ⎛⎫- ⎪⎝⎭ （D ）,1b a -⎛⎫ ⎪⎝⎭7. 已知a 是实数，关于x y 、的二元一次方程组235212x y ax y a-=⎧⎨+=-⎩的解不可能出现的情况是（ ）（A ）x y 、都是正数 (B) x y 、都是负数 （C ）x y 是正数、是负数 （D ）x y 是负数、是正数8. If a and b are non －zero real numbers and ()()1991991a b -+=,then the value for111ab-+ is ( )（A ）1 (B)100 （C ）－1 （D ）－1 9. 如图2是反比例函数ky x=在第二象限的图像，则k 的可能取值是（ ）（A ）2 (B)－2 （C ）12 （D ）12-11． 在直角坐标系上，点(),11x y 关于电()22,x y 的对称点坐标是（ ）（A ）()2121,22x y x y -- (B) ()1212,22x y y x -- （C ）()12122,2x x y y -- （D ）()21212,2x x y y --12． 一个长方体盒子的最短边长50cm ，最长边长90cm.则盒子的体积可能是（ ）（A ）45003cm (B) 1800003cm （C ）900003cm （D ）3600003cm 13． 若两个角可以构成内错角，则称为“一对内错角”.四条直线两两相交，且任意三条直线不交于同一点.那么，在这个几何图形中，可以构成的内错角的两个角的对数是（ ）（A ）12 (B) 24 （C ）36 （D ）48 14． 如图3，已知ABC 中，,AB AC BAC ACB =∠∠和的角平分线相交于D 点，130ADC ∠=︒,那么CAB ∠的大小是（ ） （A ）80︒ (B) 50︒ （C ）40︒ （D ）20︒ 15． GivenABC with 90ACB ∠=︒,15ABC ∠=︒,1AC =,then the length of BC is ( )（A ）23+ (B) 32+（C ）32- （D ）23+16． 已知三角形三边的长分别为,,a b c ，且,,a b c 均为整数，若7,b a b =<，则满足条件的三角形的个数是（ ）（A ）30 (B)36 （C ）40 （D ）45 17． 三角形三边的长分别为,,a b c ，且a ab cb c b c a++=+-，则三角形是（ ） （A ）等边三角形 (B) 直角三角形（C ）以a 为腰的等腰三角形 （D ）以a 为底的等腰三角形 18． 有4个命题：一组对边相等，一组对角相等的四边形是平行四边形； 一组对边平行，一组对角相等的四边形是平行四边形；O 是四边形ABCD 内一点，若AO=BO=CO=DO ，则四边形ABCD 是矩形；若四边形的两条对角线互相垂直，则这个四边形是菱形。

希望杯第一届（1990年）初中二年级第一试试题一、选择题:（每题1分，共10分）1．一个角等于它的余角的5倍，那么这个角是 ( )A ．45°.B ．75°.C ．55°.D ．65°2．2的平方的平方根是 ( )A ．2.B ．2. C ．±2. D ．43．当x=1时，a 0x 10-a 1x 9+a 0x 8-a 1x 7-a 1x 6+a 1x 5-a 0x 4+a 1x 3-a 0x 2+a 1x 的值是( ) A ．0B ．a 0.C ．a 1D ．a 0-a 14. ΔABC,若AB=π27则下列式子成立的是( )A ．∠A ＞∠C ＞∠B;B ．∠C ＞∠B ＞∠A;C ．∠B ＞∠A ＞∠C;D ．∠C ＞∠A ＞∠B 5．平面上有4条直线，它们的交点最多有( ) A ．4个B ．5个.C ．6个.D ．76．725-的立方根是[ ]（A ）12-. （B ）21-.（C ）)12(-±. （D ）12+. 7．把二次根式a a 1-⋅化为最简二次根式是[ ](A) a . (B)a -. (C) a --. (D) a -8．如图1在△ABC 中，AB=BC=CA ，且AD=BE=CF ，但D ，E ，F 不是AB ，BC ，CA 的中点．又AE ，BF ，CD 分别交于M ，N ，P ，如果把找出的三个全等三角形叫做一组全等三角形，那么从图中能找出全等三角形( ) A ．2组B ．3组.C ．4组D ．5组。

9.已知 1112111222222--÷-+++-⨯--++x y x y xy y y x y xy x 等于一个固定的值， 则这个值是( ) A ．0.B ．1.C ．2.D ．4.把f 1990化简后，等于 ( ) A ．1-x x . B.1-x. C.x1. D.x.二、填空题（每题1分，共10分） 1..________6613022=-2.().__________125162590196.012133=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+÷- 3.89850-+=________.4．如图2，∠A=60°，∠1=∠2，则∠ABC 的度数是______．5．如图3,O 是直线AB 上一点,∠AOD=117°,∠BOC=123°,则∠COD 的度数是____度． 6．△ABC 中，∠C=90°，∠A 的平分线与∠B 的平分线交于O 点，则∠AOB 的度数是______度．7．计算下面的图形的面积（长度单位都是厘米）（见图4）.答：______． 8．方程x 2+px+q=0，当p ＞0，q ＜0时，它的正根的个数是______个． 9．x ，y ，z 适合方程组826532113533451x y z x z x yx y z x y x y z -+++⎧=-⎪⎪++-+⎪+=⎨⎪+=-⎪⎪⎩则1989x-y+25z=______．10．已知3x 2+4x-7=0，则6x 4+11x 3-7x 2-3x-7=______．答案与提示一、选择题提示：1．因为所求角α=5(90°-α),解得α=75°．故选(B)．2．因为2的平方是4，4的平方根有2个，就是±2．故选(C)．3．以x=1代入，得a0-a1+a0-a1-a1+a1-a0+a1-a0+a1=2a0-3a1+3a1-2a0=0．故选(A)．＜3，根据大边对大角，有∠C＞∠B＞∠A．5．如图5，数一数即得．又因原式中有一个负号．所以也不可能是(D)，只能选(A)．7．∵a＜0，故选(C)．8．有△ABE，△ABM，△ADP，△ABF，△AMF等五种类型．选(D)．9．题目说是一个固定的值，就是说：不论x，y取何值，原式的值不变．于是以x=y=0代入，得：故选(B)．故选(A)．二、填空题提示：4．∠ADC=∠2+∠ADB=∠1+∠ADB=180°--∠A=120° 所以∠ADC 的度数是120度． 5．∠COD 度数的一半是30度．8．∵Δ=p 2-4q ＞p 2．9．方程组可化简为：解得： x=1，y=-1，z=0． ∴1989x-y+25z=1990．10．∵6x 4+11x 3-7x 2-3x-7=(3x 2+4x-7)(2x 2+x+1)而3x 2+4x-7=0．希望杯第一届（1990）第二试试题一、选择题:（每题1分，共5分）1.等腰三角形周长是24cm ，一腰中线将周长分成5∶3的两部分，那么这个三角形的底边长是[ ] A ．7.5B ．12.C ．4.D ．12或42.已知P=2)1989(11991199019891988-++⨯⨯⨯，那么P 的值是[ ] A ．1987B ．1988.C ．1989D ．19903．a ＞b ＞c ，x ＞y ＞z ，M=ax+by+cz ，N=az+by+cx ，P=ay+bz+cx ，Q=az+bx+cy ，则[ ] A ．M ＞P ＞N 且M ＞Q ＞N. B ．N ＞P ＞M 且N ＞Q ＞MC ．P ＞M ＞Q 且P ＞N ＞Q.D ．Q ＞M ＞P 且Q ＞N ＞P4．凸四边形ABCD 中，∠DAB=∠BCD=900, ∠CDA ∶∠ABC=2∶1,AD ∶CB=1∶3,则∠BDA=[ ] A ．30°B ．45°.C ．60°.D ．不能确定5．把一个边长为1的正方形分割成面积相等的四部分，使得在其中的一部分内存在三个点，以这三个点为顶点可以组成一个边长大于1的正三角形，满足上述性质的分割[ ]A ．是不存在的.B ．恰有一种.C ．有有限多种，但不只是一种.D ．有无穷多种 二、填空题:（每题1分，共5分）1． △ABC 中，∠CAB ∠B=90°，∠C 的平分线与AB 交于L ，∠C 的外角平分线与BA的延长线交于N ．已知CL=3，则CN=______． 2． 21(2)0a ab -+-=,那么111(1)(1)(1990)(1990)ab a b a b ++++++的值是_____.3． 已知a ，b ，c 满足a+b+c=0，abc=8，则c 的取值范围是______．4． ΔABC 中, ∠B=30053三个两两互相外切的圆全在△ABC 中，这三个圆面积之和的最大值的整数部分是______．5． 设a,b,c 是非零整数,那么a b c ab ac bc abc a b c ab ac bc abc++++++的值等于_________.三、解答题:（每题5分，共15分）1．从自然数1，2，3…，354中任取178个数，试证：其中必有两个数，它们的差是177．2．平面上有两个边长相等的正方形ABCD 和A ＇B ＇C ＇D ＇，且正方形A ＇B ＇C ＇D ＇的顶点A ＇在正方形ABCD 的中心．当正方形A ＇B ＇C ＇D ＇绕A ＇转动时，两个正方形的重合部分的面积必然是一个定值．这个结论对吗？证明你的判断．3．用1，9，9，0四个数码组成的所有可能的四位数中，每一个这样的四位数与自然数n之和被7除余数都不为1，将所有满足上述条件的自然数n由小到大排成一列n1＜n2＜n3＜n4……，试求：n1·n2之值．答案与提示一、选择题提示：1．若底边长为12．则其他二边之和也是12，矛盾．故不可能是(B)或(D)．又：底为4时，腰长是10．符合题意．故选(C)．=19882+3×1988+1-19892=(1988+1)2+1988-19892=19883．只需选a=1，b=0，c=-1，x=1，y=0，z=-1代入，由于这时M=2，N=-2，P=-1，Q=-1．从而选(A)．4．由图6可知：当∠BDA=60°时，∠CDB5．如图7按同心圆分成面积相等的四部分．在最外面一部分中显然可以找到三个点，组成边长大于1的正三角形．如果三个圆换成任意的封闭曲线，只要符合分成的四部分面积相等，那么最外面部分中，仍然可以找到三个点，使得组成边长大于1的正三角形．故选(D)．二、填空题提示：1．如图8：∠NLC=∠B+∠1=∠CAB-90°+∠1=∠CAB-∠3 =∠N．∴NC=LC=3．5．当a，b，c均为正时，值为7．当a，b，c不均为正时，值为-1．三、解答题1．证法一把1到354的自然数分成177个组：(1，178)，(2，179)，(3，180)，…，(177，354)．这样的组中，任一组内的两个数之差为177．从1~354中任取178个数，即是从这177个组中取出178个数，因而至少有两个数出自同一个组．也即至少有两个数之差是177．从而证明了任取的178个数中，必有两个数，它们的差是177．证法二从1到354的自然数中，任取178个数．由于任何数被177除，余数只能是0，1，2，…，176这177种之一．因而178个数中，至少有两个数a，b的余数相同，也即至少有两个数a，b之差是177的倍数，即a b=k×177．又因1~354中，任两数之差小于2×177=354．所以两个不相等的数a，b之差必为177．即a b=177．∴从自然数1，2，3，…，354中任取178个数，其中必有两个数，它们的差是177．2．如图9，重合部分面积S A＇EBF是一个定值．证明：连A＇B，A＇C，由A＇为正方形ABCD的中心，知∠A＇BE=∠A＇CF=45°．又，当A＇B＇与A＇B重合时，必有A＇D＇与A＇C重合，故知∠EA＇B=∠FA＇C．在△A＇FC和△A＇EB中，∴S A＇EBF=S△A＇BC．∴两个正方形的重合部分面积必然是一个定值．3．可能的四位数有9种：1990，1909，1099，9091，9109，9910，9901，9019，9190．其中 1990=7×284+2，1909=7×272+5．1099=7×157,9091=7×1298+5,9109=7×1301+2,9910=7×1415+5，9901=7×1414+3，9019=7×1288+3，9190=7×1312+6．即它们被7除的余数分别为2，5，0，5，2，5，3，3，6．即余数只有0，2，3，5，6五种．它们加1，2，3都可能有余1的情形出现．如0+1≡1，6+2≡1，5+3≡(mod7)．而加4之后成为：4，6，7，9，10，没有一个被7除余1，所以4是最小的n．又：加5，6有：5+3≡1，6+2≡1．(mod7)而加7之后成为7，9，10，12，13．没有一个被7除余1．所以7是次小的n．即 n1=4，n2=7∴ n1×n2=4×7=28．第二届（1991年）初中二年级第一试试题一、选择题:（每题1分，共15分）1．如图1，已知AB=8，AP=5，OB=6，则OP的长是[ ]A．2; B．3; C．4; D．52．方程x2-5x+6=0的两个根是[ ]A．1，6 ; B．2，3; C．2，3; D．1，63．已知△ABC是等腰三角形，则[ ]A．AB=AC;B．AB=BC;C．AB=AC或AB=BC;D．AB=AC或AB=BC或AC=BC344134b c-==+,则a,b,c的大小关系是[ ]A．a＞b＞c B．a=b=c C．a=c＞b D．a=b＞c5.若a≠b,则[ ]6．已知x，y都是正整数，那么三边是x，y和10的三角形有[ ]A．3个B．4个; C．5个D．无数多个7．两条直线相交所成的各角中，[ ]A．必有一个钝角;B．必有一个锐角;C．必有一个不是钝角;D．必有两个锐角8．已知两个角的和组成的角与这两个角的差组成的角互补，则这两个角 [ ]A．一个是锐角另一个是钝角;B．都是钝角;C．都是直角;D．必有一个角是直角9．方程x2+|x|+1=0有[ ]个实数根．A．4; B．2; C．1; D．010．一个两位数，用它的个位、十位上的两个数之和的3倍减去-2，仍得原数，这个两位数是[ ]A．26; B．28; C．36; D．3811．若11个连续奇数的和是1991，把这些数按大小顺序排列起来，第六个数是[ ] A．179; B．181; C．183; D．18512.1,>+等于[ ]A．2x+5 B．2x-5; C．1 D．113．方程2x5+x4-20x3-10x2+2x+1=0有一个实数根是[ ]14．当a＜-1时，方程(a3+1)x2+(a2+1)x-(a+1)=0的根的情况是 [ ]A．两负根;B．一正根、一负根且负根的绝对值大(1)BOC ．一正根、一负根且负根的绝对值小;D ．没有实数根15．甲乙二人，从M 地同时出发去N 地．甲用一半时间以每小时a 公里的速度行走，另一半时间以每小时b 公里的速度行走；乙以每小时a 公里的速度行走一半路程，另一半路程以每小时b 公里的速度行走．若a ≠b 时，则[ ]到达N 地． A ． 二人同时; B ．甲先;C ．乙先;D ．若a ＞b 时，甲先到达，若a ＜b 时，乙先 二、填空题:（每题1分，共15分）1．一个角的补角减去这个角的余角，所得的角等于______度． 2.有理化分母=______________.3.0x =的解是x=________. 4．分解因式：x 3+2x 2y+2xy 2+y 3=______．5．若方程x 2+(k 2-9)x+k+2=0的两个实数根互为相反数，则k 的值是______．6．如果2x 2-3x-1与a(x-1)2+b(x-1)+c 是同一个多项式的不同形式,那么a bc+=__.7．方程x 2-y 2=1991有______个整数解．8．当m______时，方程(m-1)x 2+2mx+m-3=0有两个实数根．9．如图2，在直角△ABC 中，AD 平分∠A ，且BD ∶DC=2∶1，则∠B 等于______度．CBAFFEDCBA(2) (3) (4)10．如图3，在圆上有7个点，A ，B ，C ，D ，E ，F ，和G ，连结每两个点的线段共可作出__条． 11．D ，E 分别是等边△ABC 两边AB ，AC 上的点，且AD=CE ，BE 与CD 交于F ，则∠BFC 等于__度． 12．如图4，△ABC 中，AB=AC=9，∠BAC=120°，AD 是△ABC 的中线，AE 是△ABD 的角平分线，DF ∥AB 交AE 延长线于F ，则DF 的长为______．13．在△ABC 中，AB=5，AC=9，则BC 边上的中线AD 的长的取值范围是______．14．等腰三角形的一腰上的高为10cm ，这条高与底边的夹角为45°，则这个三角形的面积是______．15．已知方程x 2+px+q=0有两个不相等的整数根，p ，q 是自然数，且是质数，这个方程的根是______．答案与提示一、选择题提示：1．∵OP=OB-PB=OB-(AB-AP)=6-(8-5)=3．∴选(B)．2．∵以2，3代入方程，适合．故选(B)．3．∵有两条边相等的三角形是等腰三角形．∴选(D)．4．∵a=1，b=-1，c=1．∴选(C)．6．∵x=y＞5的任何正整数，都可以和10作为三角形的三条边．∴选(D)．7．两直线相交所成角可以是直角，故而(A)，(D)均不能成立．∴选(C)．8．设两个角为α,β.则(α+β)+(α-β)=180°,即α=90°．故选(D)．9．∵不论x为何实数，x2+|x|+1总是大于零的．∴选(D)．即7a=2b+2，可见a只能为偶数，b+1是7的倍数．故取(A)．11．设这11个连续奇数为：2n+1，2n+3，2n+5，…，2n+21．则(2n+1)+(2n+3)+(2n+5)+…+(2n+21)=1991．即 11(2n+11)=1991．解得n=85．∴第六个数是2×85+11=181．故选(B)．∴选(A)．13．原方程可化为(2x5-20x3+2x)+(x4-10x2+1)=0．即 (2x+1)(x4-10x2+1)=0．即 x4-10x2+1=0．故取(C)．14．a＜-1时，a3+1＜0，a2+1＞0，a+1＜0．而若方程的两根为x1，x2，则有15．设M，N两地距离为S，甲需时间t1，乙需时间t2，则有∴t1＜t2，即甲先．另外：设a=1，b=2，则甲走6小时，共走了9公里，这时乙走的时间为从这个计算中，可以看到，a，b的值互换，不影响结果．故取(B)．二、填空题提示：1．设所求角为α，则有(180°-α)-(90°-α)=90°．4．x3+2x2y+2xy3+y3=(x3+y3)+(2x2y+2xy2)=(x+y)(x2-xy+y2)+2xy(x+y)=(x+y)(x2+xy+y2)5．设二根为x1，-x1，则x1+(-x1)=-(k2-9)．即k2-9=0．即k=±3．又，要有实数根，必须有△≥0．即 (k2-9)2-4(k+2)＞0．显然 k=3不适合上面的不等式，∴k=-3．6．由2x2-3x-1=a(x+1)2+b(x-1)+c是恒等式，故由x=1代入，得c=-2；x2项的系数相等，有a=2，这时再以x=0代入，得-1=a-b+c．即b=1．7．x2-y2=1991，(x-y)(y+x)=11×181可以是9．BD∶DC=2∶1，故有AB∶AC=2∶1，直角三角形斜边与直角边之比为2∶1，则有∠B=30°．10．从A出发可连6条，从B出发可连5条，（因为BA就是AB），从C出发可连4条，…，从F出发可连一条．共计1+2+3+4+5+6=21（条）．另法：每个点出发均可连6条，共有42条．但每条都重复过一次，11．如图28．∠F=∠1+∠A+∠2．又：△ADC≌△CEB．∴∠1=∠3．∴∠F=∠3+∠A+∠2=∠B+∠A=120°．12．△ABC是等腰三角形，D为底边的中点，故AD又是垂线，又是分角线，故∠BAD=60°，∠ADB=90°．又：AE是分角线，故∠DAE=∠EAB=30°．又：DF∥AB，∴∠F=∠BAE=30°．在△ADF中，∠DAF=∠F=30°．∴AD=DF．而在△ADB中，AB=9，∠B=30°．13．∵4＜BC＜14．∴当BC为4时，BD=CD=2，AD＜7．当BC=14时，BC=CD=7，有AD＞2．∴2＜AD＜7．14．等腰三角形一腰上的高与底边的夹角是45°，则顶角是90°，高就是腰，其长为10cm．15．设两根为x1，x2．则x1+x2=-p① x1x2=q②由题设及①，②可知，x1，x2均为负整数．q为质数，若q为奇数，则x1，x2均为奇数．从而p为偶数，而偶质数只有2，两个负整数之和为-2，且不相等，这是不可能的．若q为偶数（只能是2），两个负整数之积为2，且不相等，只能是-1和-2．∴方程的根是-1和-2．希望杯第二届（1991年）初中二年级第二试试题一、选择题:（每题1分，共10分）1．如图29，已知B是线段AC上的一点，M是线段AB的中点，N为线段AC的中点，P为NA的中点，Q为MA的中点，则MN∶PQ等于( )A．1 ; B．2; C．3; D．42．两个正数m，n的比是t(t＞1)．若m+n=s，则m，n中较小的数可以表示为( )A.ts; Bs-ts; C.1tss+; D.1st+.3.y>0时,3x y-等于( )4．(x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)是完全平方式，则a ，b ，c 的关系可以写成( ) A ．a ＜b ＜c. B ．(a-b)2+(b-c)2=0. C ．c ＜a ＜b. D ．a=b ≠c 5．如图30，AC=CD=DA=BC=DE ．则∠BAE 是∠BAC 的 ( ) A ．4倍.B ．3倍.C ．2倍.D ．1倍6．D 是等腰锐角三角形ABC 的底边BC 上一点，则AD ，BD ，CD 满足关系式( ) A.AD 2=BD 2+CD 2. B ．AD 2＞BD 2+CD 2. C ．2AD 2=BD 2+CD 2. D ．2AD 2＞BD 2+CD 2 7.方程2191()1010x x -=+的实根个数为( ) A ．4 B ．3. C ．2 D ．18.能使分式33x y y x-的值为x 2、y 2的值是( )A.x 2，y 22y 2;C. x 2，y 2; D. x 2y 2.9．在整数0，1，2，3，4，5，6，7，8，9中，设质数的个数为x ，偶数的个数为y ，完全平方数的个数为z ，合数的个数为u ．则x+y+z+u 的值为 ( ) A ．17B ．15.C ．13D ．1110．两个质数a ，b ，恰好是x 的整系数方程x 2-21x+t=0的两个根,则b aa b+等于( ) A.2213; B.5821; C.240249; D.36538.二、填空题（每题1分，共10分）1.1989×19911991-1991×19891988=______．2.分解因式:a 2+2b 2+3c 2+3ab+4ac+5bc=______．3.(a 2+ba+bc+ac):[(b 2+bc+ca+ab):(c 2+ca+ab+bc)]的平方根是______．4．边数为a ，b ，c 的三个正多边形，若在每个正多边形中取一个内角,其和为1800,那么111a b c++=_________. 5.方程组51x ay y x +=⎧⎨-=⎩有正整数解,则正整数a=_______.6.从一升酒精中倒出13升,再加上等量的水,液体中还有酒精__________升;搅匀后,再倒 出13升混合液,并加入等量的水, 搅匀后,再倒出13升混合液, 并加入等量的水,这时,所得混合液中还有______升酒精.7．如图31，在四边形ABCD 中．AB=6厘米，BC=8厘米，CD=24厘米，DA=26厘米．且∠ABC=90°，则四边形ABCD 的面积是______． 8．如图32，∠1+∠2+∠3∠4+∠5+∠6=______． 9.2243x x +++的最小值的整数部分是______.10．已知两数积ab ≠1．且2a 2+1234567890a+3=0,3b 2+1234567890b+2=0,则ab=______. 三、解答题:（每题5分，共10分，要求：写出完整的推理、计算过程，语言力求简明，字迹与绘图力求清晰、工整）1. 已知两个正数的立方和是最小的质数．求证：这两个数之和不大于2．2．一块四边形的地（如图33）(EO ∥FK ，OH ∥KG)内有一段曲折的水渠，现在要把这段水渠EOHGKF 改成直的．（即两边都是直线）但进水口EF 的宽度不能改变，新渠占地面积与原水渠面积相等，且要尽可能利用原水渠，以节省工时．那么新渠的两条边应当怎么作？写出作法，并加以证明．答案与提示一、选择题提示：3．由y＞0，可知x＜0．故选(C)．4．容易看到a=b=c时，原式成为3(x+a)2，是完全平方式．故选(B)．5．△ACD是等边三角形,△BCA和△ADE均为等腰三角形.故知∠BAC=30°,而∠BAE=120°,所以选(A)．6．以等边三角形为例，当D为BC边上的中点时，有AD2＞BD2+CD2，当D为BC边的端点时，有AD2=BD2+CD2，故有2AD2＞BD2+CD2．故选(D)．故选(C)．∴选(C)．9．∵x=4，y=5，z=4，u=4．∴选(A)．10．由a+b=21，a，b质数可知a，b必为2与19两数．二、填空题提示：1．1989×19911991-1991×19891988=1989(1991×104+1991)-1991(1989×104+1988)=1989×1991-1991×1988=1991．2．原式=a2+b2+c2+2ab+2bc+2ca+b2+2c2+ab+2ac+3bc=(a+b+c)2+(b+c)(b+2c)+a(b+2c)=(a+b+c)2+(b+2c)(a+b+c)=(a+b+c)(a+2b+3c)．3．原式=(a+c)(a+b)∶[(b+a)(b+c)∶(c+a)(c+b)]∴平方根为±(a+c)．4．正多边形中，最小内角为60°，只有a，b，c均为3时，所取的内角和才可能为180°．5．两式相加有(1+a)y=6，因为a，y均为正整数，故a的可能值为5，这时y=1，这与y-x=1矛盾，舍去；可能值还有a=2，a=1，这时y=2，y=3与y-x=1无矛盾．∴a=1或2．7．在直角三角形ABC中，由勾股定理可知AC=10cm，在△ADC中，三边长分别是10，24，26，由勾股定理的逆定理可△ADC为直角三角形．从而有面积为8．∠1+∠2+∠3+∠4+∠5+∠6，正好是以∠2，∠3，∠5为3个内角的四边形的4个内角之和．∴和为360°．10．由已知条件可知a是方程2x2+1234567890x+3=0的一个根，b是方程3y2+1234567890y+2=0的一个根，后者还可以看成：三、解答题1．设这两个正数为a，b．则原题成为已知a3+b3=2，求证a+b≤2．证明（反证法）：若a+b＞2由于a3+b3=2，必有一数小于或等于1，设为b≤1，→a＞2b，这个不等式两边均为正数，→a3＞(2-b)3．→a3＞8-12b+6b2-b3．→a3+b3＞8-12b+6b2．→6b2-12b+6＜0．→b2-2b+1＜0．→(b-1)2＜0．矛盾．∴a+b≤2．即本题的结论是正确的．2．本题以图33为准．由图34知OK∥AB，延长EO和FK，即得所求新渠．这时，HG=GM（都等于OK），且OK ∥AB，故△OHG的面积和△KGM的面积相同．即新渠占地面积与原渠面积相等．而且只挖了△KGM这么大的一块地．我们再看另一种方法，如图35．作法：①连结EH，FG．②过O作EH平行线交AB于N，过K作FG平行线交于AB于M．③连结EN和FM，则EN，FM就是新渠的两条边界线．又：EH∥ON∴△EOH面积=△FNH面积．从而可知左半部分挖去和填出的地一样多，同理，右半部分挖去和填出的地也一样多．即新渠面积与原渠的面积相等．由图35可知，第二种作法用工较多（∵要挖的面积较大）．故应选第一种方法。

第二十二届“希望杯”全国数学邀请赛初二 第1试一、选择题(每小题4分，共40分)以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英语字母写在1、将a 千克含盐10%的盐水配制成含盐15%的盐水，需加盐水x 千克，则由此可列出方程为( ) A 、%)151)(x a (%)101(a -+=- B 、%15)x a (%10a ⨯+=⨯ C 、%15a x %10a ⨯=+⨯ D 、%)151(x %)101(a -=-2、一辆汽车从A 地匀速驶往B 地，如果汽车行驶的速度增加a%，则所用的时间减少b%，则a ，b 的关系是( ) A 、%a 1a 100b +=B 、%a 1100b +=C 、a 1a b +=D 、a100a100b +=3、当1x ≥时，不等式|2x |m 1x |1x |--≥-++恒成立，那么实数m 的最大值是( ) A 、1 B 、2 C 、3 D 、44、在平面直角坐标系中，横、纵坐标都是整数的点称为整点，已知k 为整数，若函数1x 2y -=与k kx y +=的图象的交点是整点，则k 的值有( )A 、2个B 、3个C 、4个D 、5个5、The sum of all such integers x that satisfy inequality 6|1x 2|2≤-≤ is ( ) A 、8 B 、5 C 、2 D 、0(英汉词典：sum 和；integer 整数；satisfy 满足；inequality 不等式)6、若三角形的三条边的长分别为a ，b ，c ，且0b c b c a b a 3222=-+-，则这个三角形一定是( ) A 、等腰三角形 B 、直角三角形 C 、等三角形 D 、等腰直角三角形7、As shown in figure 1，point C is on the segment BG and quadrilateral ABCD is a square. AG intersects BD and CD at points E and F, respectively. If AE=5 and EF=3, then FG=( ) A 、316 B 、38C 、4D 、5 (英汉词典：square 正方形；intersect …at … 与…相交于…) 8、1215-能分解成n 个质因数的乘积，n 的值是( ) A 、6 B 、5 C 、4 D 、3 9、若关于x ，y 的方程组⎩⎨⎧=+-=++0a y 2bx 01ay x 没有实数解，则( )A 、2ab -=B 、2ab -=且1a ≠C 、2ab -≠D 、2ab -=且2a ≠10、如图2，∠AOB=45°，OP 平分∠AOB ，PC ⊥OB 于点C ， 若PC=2，则OC 的长是( )A 、7B 、6C 、222+D 、32+二、A 组填空题(每小题4分，共40分) 11、化简：5252549+=++；12、若关于x ，y 的方程组⎩⎨⎧=--=+2y 3x 21k y 2x 3的解使2y 7x 4>+，则k 的取值范围是3k >；figure 1A O BP C 2 图213、如图3，平行于BC 的线段MN 把等边△ABC 分成一个 三角形和一个四边形，已知△AMN 和四边形MBCN 的周长相 等，则BC 与MN 的长度之比是 4:3 ；14、小华测得自家冰箱的压缩机运转很有规律，每运转5分钟， 停机15分钟，再运转5分钟，再停机15分钟，……，又知8月份 这台冰箱的耗电量是24.18度 (1度=1千瓦时)，则这台冰箱的压缩 机运转时的功率是 130 瓦；15、已知自然数a ，b ，c ，满足c 12b 4a 442c b a 222++<+++和02a a 2>--，则代数式c1b 1a 1++的值是 1； 16、已知A 、B 是反比例函数x2y =的图象上的两点，A 、B 的横坐标分别是3，5.设O 为原点，则△AOB 的面积是1516；17、设完全平方数A 是11个连续整数的平方和，则A 的最小值是 121 ；18、将100个连续的偶数从小到大排成一行，其中第38个数与第63个数的和为218，则首尾两个数的和是 218 ； 19、A 、B 两地相距15km ，甲、乙两人同时从A 出发去B 。

初二希望杯数学竞赛培训题班级__________学号__________姓名______________得分______________一、选择题（以下每题的四个结论中，仅有一个是正确的） 1．一个多项式经分解后为(2－a 3)(a 3＋2)，那么该多项式是 （ ）（A ）a 6－4（B ）a 9－4（C ）4－a 9（D ）4－a 62．下列多项式：①a 2＋4ab ＋4b 2；②9m 2＋4n 2－12mn ；③4p 2＋q 2－4p ＋2q ；④25a 4＋16b 4＋40a 2b 2；⑤9s 2－12s ＋6．其中是完全平方式的是（ ） （A ）①，④，⑤ （B ）①，②，⑤ （C ）①，②，④ （D ）①，③，④ 3．当分式1111－＋x 无意义时，x 的取值情况是（ ）（A ）x ＝1 （B ）x ＝±1 （C ）x ＝±1或x ＝0 （D ）x ＝±1且x ＝04．下列根式中与32a -相同的是 （ ）（A ）a a 2-（B ）a a 2--（C ）32a -（D ）aa 22-- 5．a 是实数，且满足05362＝－－aa ，则a 的值是（ ）（A ）6（B ）±6 （C ）≠5的数 （D ）－66．如果a -是整数，则（ ）（A ）a 是正整数 （B ）a 是非负整数 （C ）a 是完全平方数 （D ）－a是完全平方数 7．11＋－n n 与1＋＋n n 的关系是 （ ）（A ）相等 （B ）互为相反数 （C ）互为倒数 （D ）互为负倒数8．方程x 2＋3y 2＝16的整数解的组数是（ ）（A ）5（B ）6（C ）7（D ）7组以上9．若a ＜b ＜0，则()()22b b a －－÷＝ （ ）（A ）bab －－（B ）bab － （C ）－b (b －a ) （D ）bb a －10．某同学从家到学校的路程为s ，速度为v 1，从学校回家的速度为v 2，那么他来回的平均速度是 （ ）（A ）221v v ＋ （B ）212v v s ＋ （C ）2121v v v v ＋ （D ）21212v v v v ＋11．各边长均为整数且各边长均不相等的三角形周长小于13，则这样的三角形共有（ ）（A ）1个（B ）2个（C ）3个（D ）4个12．三角形的三个外角平分线所在的直线围成的三角形是（ ）（A ）锐角三角形（B ）钝角三角形 （C ）直角三角形 （D ）直角或钝角三角形13．在△ABC 和△A ´B ´C ´中，∠A ＋∠B ＝∠C ，∠B ´＋∠C ´＝∠A ´，且b －a ＝b ´－c ´，b＋a ＝b ´＋c ´则这两个三角形 （ ）（A ）不一定全等（B ）不全等（C ）根据“SAS ”全等 （D ）根据“ASA ”全等14．下列说法中，正确的是（ ）（A ）每个命题都有逆命题 （B ）每个定理都有逆定理 （C ）真命题的逆命题是真命题 （D ）假命题的逆命题是假命题 15．等腰△ABC 的顶角A ＝100°，两腰AB 、AC 的垂直平分线相交于点P ，则 （ ）（A ）P 点在△ABC 内 （B ）P 点在BC 边上（C ）P 点在△ABC 外 （D ）P 点位置与BC 边的长度有关16．下列命题中，真命题是（ ）（A ）两个全等三角形是关于某条直线成轴对称的两个图形 （B ）两个全等的等腰三角形是关于某条直线成轴对称的两个图形 （C ）两个全等的等边三角形是关于某条直线成轴对称的两个图形 （D ）关于某条直线成轴对称的两个三角形一定是全等三角形 17．如图，在等腰直角△ABC 中，∠BAC ＝90°，又AD ∥BC ，在AD 上取一点E ，使∠EBC ＝30°，则BE 和BC 的大小关系是 （ ） （A ）BE ＞BC（B ）BE ＜BC（C ）BE ＝BC （D ）不确定的 18．四边形中，有两条边相等，另两条边也相等，则这个四边形（ ）（A ）一定是菱形（B ）一定是轴对称图形（C ）一定是平行四边形（D ）可能是平行四边形，也可能是轴对称图形19．如图，D 为等腰△ABC 的腰AB 上的一点，E 为另一腰AC延长线上的一点，且BD ＝CE ，则 （ ）（A ）DE ＝BC （B ）DE ＞BC（C ）DE ＜BC（D ）DE 与BC 大小关系决定于角A 的大小20．设△ABC 的三边为c b a ，，，且满足c b a cb a 5.1225.3222＋＝＋＋ ，则△ABC 是 （ ）（A ）直角三角形 （B ）等腰三角形 （C ）等边三角形 （D ）形状不确定的三角形21．分解因式：＝＋－－412422a b a ____________________．22．如果(x －a )(x ＋2)－1能够分解成两个二项式(x ＋3)和(x ＋b )的乘积，那么a ＝______，b ＝_______．AC BDEAC BD E23．分解因式：xy (m 2－n 2)－mm (x 2－y 2)＝_________________． 24．分解因式：＝＋－233x x ___________________． 25．a ，b 均为实数，且满足()0425322＝－－＋＋aa b a ，那么b ＝_________．26．x ，y 均为实数，且4111222＋＋－＋－＝x x x y ，则x ＋y 的值是__________．27．x 是实数，则25101222＋－－＋＋x x x x 的最大值是____________．28．已知m ，n 互为倒数，且m ＋n ＋1998＝0，那么(m 2＋1999m ＋1)(n 2＋1999n ＋1)的值为____．29．已知两数的和为12，此两数的立方和为108，那么这两个数的平方和是___________． 30．若61＝＋yx ，25122＝＋y x ，那么＝∶y x ____________ 31．若3939＝＋，＝＋zy yx ，则xz 9＋的值等于______________．32．已知实数a ，b ，c 满足a ＋b ＋c ＝0，a 2＋b 2＋c 2＝32，abc ＝8，那么cb a 111＋＋的值等于___________．33．若a 2＋3b 2－4a －12b ＋16＝0，则a ＋b 的值是________． 34．已知N＋＋＋＋＝4141412，则N 的值是___________．35．若实数x ，y ，z 适合方程组⎩⎨⎧0720634＝－＋＝－－z y x z y x ，那么1999y －1997x ＋1993z ＝_______．36．方程组⎩⎨⎧34231232＝－－＝－＋z y x z y x 中的x ，y 满足条件x ＋y ＝6，那么z 的值等于___________．37．a 为实数，那么aa a a 119991999－＋－＋－的值等于_________． 38．已知12－＝x ，那么xx x－－342的值为__________ 39．化简623232－＋＋，结果是_______________．40．方程x x x －＝＋－41682的正整数解是_____________． 41．化简：(6－2)(3＋2)32-＝_____________．42．已知：A ＝53＋，B ＝53－，若存在正整数N ，使N ＜A 3＋B 3＜N ＋1，则N ＝____． 43．116201－的整数部分是__________．44．求值：100999910014334132231221＋＋＋＋＋＋＋＋ ＝___________．45．若y ≠z ，且满足()()23322＝－＋＝－＋zy x z y x z y ，则x ＋y ＋z 的值等于__________． 46．已知(x ＋2y －1)是二元二次式3x 2＋axy ＋by 2＋x ＋9y －4的一个因式，则a ＝_______，b ＝______．47．大小不超过(3＋2)6的最大整数为_____________．48．若x ＜0，y ＞0，a －b ＞0，M ＝ax ＋by ，N ＝bx ＋ay ，则M 与N 的大小关系是M ______N ．（填“＞”或“＜”）49．5的整数部分是a ，小数部分为b ，则ba 1－的大小是____________．50．已知a ，b ，c 都是正实数，()()c b a c b a y c b a x ＋＋＋＋＋＝，＋＋＝22222，则x 与y 的大小关系是x ______y ．（填“＞”或“＜”）51．如图，a ，b ，c ，d 为数轴上对应点的数，则｜a ＋b －c ｜＋｜d －a ｜－｜c －d ｜＋｜a －d ｜＝_______． 52．如图，AB 、CD 、MN 三条直线相交，交点分别为E 、F 、G ，则∠EFB 的同位角是________． 53．两个对顶角的和是它的一个邻补角的4倍，则这个邻补角的度数是_________． 54．△ABC 的周长是15，若a ＋c ＝2b ，c －a ＝4则a 2＋b 2＋c 2＝____________． 55．如图，则∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＝_____________．56．△ABC 中，AD 是BC 边上的中线，若AB ＝9，AC ＝5，则AD 的取值范围是__________．（第52题图） （第55题图） （第57题图） （第58题图）57．如图，△ABC 中，∠C ＝90°，AC ＝BC ，AD 平分∠CAB ，交BC 于D ，DE ⊥AB 于E ，若AC ＝4厘米，则△BDE 的周长是___________．58．如图，△ABC 和△ADE 均为等边三角形，C 、D 、E 在一条直线上，∠ABE ＝20°，则∠CAD 的大小是____________．59．如图，△ABC 中，D 在AC 上，AD ＝AB ，∠ABC ＝∠C ＋30°，则∠CBD ＝_______． 60．如果一个三角形的两条中线又是它的两条高线，那么这个三角形的形状是___________．c 0 a bd C EFA B D G M N C EF A B D O A D E C B A D CB E第十一届希望杯数学竞赛初二第一试一．选择题1．与的关系是（）。

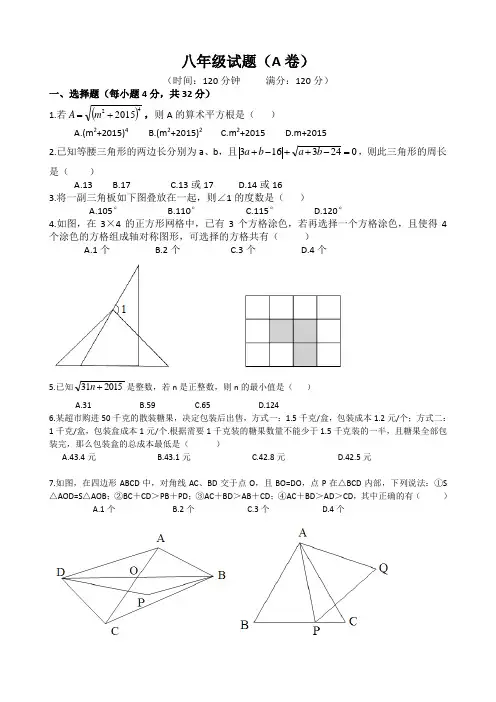
八年级试题（A 卷）（时间：120分钟 满分：120分）一、选择题（每小题4分，共32分） 1.若()422015+=mA ，则A 的算术平方根是（ ）A.(m 2+2015)4B.(m 2+2015)2C.m 2+2015D.m+20152.已知等腰三角形的两边长分别为a 、b ，且0243163=-++-+b a b a ，则此三角形的周长是（ ）A.13B.17C.13或17D.14或163.将一副三角板如下图叠放在一起，则∠1的度数是（ ）A.105°B.110°C.115°D.120°4.如图，在3×4的正方形网格中，已有3个方格涂色，若再选择一个方格涂色，且使得4个涂色的方格组成轴对称图形，可选择的方格共有（ ）A.1个B.2个C.3个D.4个5.已知201531+n 是整数，若n 是正整数，则n 的最小值是（ ）A.31B.59C.65D.1246.某超市购进50千克的散装糖果，决定包装后出售，方式一：1.5千克/盒，包装成本1.2元/个；方式二：1千克/盒，包装盒成本1元/个.根据需要1千克装的糖果数量不能少于1.5千克装的一半，且糖果全部包装完，那么包装盒的总成本最低是（ ）A.43.4元B.43.1元C.42.8元D.42.5元7.如图，在四边形ABCD 中，对角线AC 、BD 交于点O ，且BO=DO ，点P 在△BCD 内部，下列说法：①S △AOD=S △AOB ；②BC ＋CD ＞PB ＋PD ；③AC ＋BD ＞AB ＋CD ；④AC ＋BD ＞AD ＞CD ，其中正确的有（ ） A.1个 B.2个 C.3个 D.4个8.如图，等边三角形ABC 边长为6，点P 从B 点开始在BC 上向点C 运动，运动到点C 停止，以AP 为边在直线BC 的同侧作等边三角形APQ ，得到点Q ，则点Q 的运动路径长（ ） A.6 B.33 C.24 D.23π二、填空题：（每小题5分，共40分）9.化简：.________________)2015(201522=+--x x ）（10.已知正n 边形的一个内角是一个外角的5倍，则n=____________.11.如图，△ABC 是格点三角形，点D 是异于点A 的一个格点，则使△DBC 和△ABC 全等的D 点共有__________个.12.方程3100820151210071=+-+-xx x 的解是___________________.13.如图，等边三角形的边长为1，现将其各边n(n ＞2)等分，并以相邻分点为顶点向外作小等边三角形，再将相邻分点之间的线段去掉，得到一个锯齿图形，当n=k 时，锯齿图形的周长为___________.(用含k 的代数式表示).14.将1、2、3、4、5这五个数排成一列，要求第一个数和最后一个数都是偶数，且其中任意三个相邻的数之和都能被这三个数中的第一个数整除，这样的排列方法共有_____________种.15.对于实数m 、n ，定义运算m ※n=m(1-n)，下面是关于这种运算的几个结论：①2※3=-4；②若m ※n=0，则n=0；③m ※n=（1-n ）※(1-m)；④若m+n=1，则（m ※n ）-(n ※n)=0.其中正确的是___________. 16.如图，已知点A(1，1)，点B （7,3），点P 为x 轴上一个动点，当PA+PB 的值最小时，点P 的坐标为_______________.三、解答题（10+12+12+14=48分）17..)32(32,2,29的值）求（若+--==-y x xy y x18.如图，△ABC 为等边三角形，点D 是BC 延长线上一点，且CD ＜BC ，BD 的垂直平分线交AC 于E ，过点E 作EF ∥BC 交AB 于F.（1）求证：△AEF 为等边三角形； （2）若BC=3CD ，求ECAE的值.19.某数学俱乐部组织60名会员租车进行自驾游，共有两种车型可供选择，A 型车共有8个座位，B 型车有4个座位，要求租用的车不能空座，也不能超载. （1）共有多少种不同的租车方案？（2）若A 型车的租金是400元/天，B 型车的租金是260元/天，请设计最划算的租车方案，并说明理由.20.已知：直角三角形斜边上的中线等于斜边的一半，如图1，在△ABC 中，∠CAB=90°，D 是BC 的中点，连接AD ，则AD=CD=BD.（1）如图2，过点D作DE⊥AB于E，以E为边作等边三角形AEF，以DF为边作等边三角形DFG，连接AG，求证：AG平分∠FAB.（2）如图3，过点C作CH⊥AF于H，连接DH，求证：DH=FG.1 2 3 4 5 6 7 8C B AD B C D A9 10 11 12 13 14 15 1610 1/2-8060X12 3 1008KK 66-6 ①③④⎪⎭⎫ ⎝⎛0,25。

历届希望杯试题希望杯数学竞赛是中国举办的一项全国性中学生数学竞赛活动，每年都吸引了大批对数学有热情和天赋的学生参与。

本文将回顾并介绍历届希望杯试题，以展示这项竞赛的内容和特点。

1996年希望杯试题一. 解三个方程组：⎧⎪⎨⎪⎩xy+z=4,2y+3x-6z=-1,4x-2y+8z=12.二. 求下列各式中字母代表的数值：(1) √144，(2) a0^{2}−b0^{2}，(3) 时速每小时60公里的车，一小畜去年年龄是今年年龄的1/5,洋茉甲今年年龄是小莉的1/6,今年的年龄和小杰的和等于去年的年龄，今年的年龄和小围的和是188，因此去年的年龄是多少？(4) 入有人共34 人，男多______,女多______.(5) 入有人A,B,C,D,E共5名，她们的年龄各为12周岁，13周岁，14周岁，15周岁，16周岁.5人的平均位25周岁，加上D的年龄和A,E的平均年龄的和等于何值？三. 将分県运算式献一理山，请将#值和自然数间的两个运ẩu符适当放在的#号上，把运算式中的问号填实。

四. 两个相等的数相加的结果是1818，试求那个数。

五. 暗算71×172=?六. 甲乙两管，相互形态，并且能饱耐益补，一只服满甲饱一只需要b毫升的时间，一只服满乙饱时需要a毫升的时间，如果甲乙两支同时台满，此后甲与乙同时饮水，那么t分钟以后唐哉甲多少毫升的还剩下?1997年希望杯试题一. 求实数x满足|1-|x|| < 4二. 当x=-6时如果4x-1=________.三. 长方形的长和宽的比是4/3,如果长是6米，那么宽是_______.四. P,Q是实数,|P|=|Q|=1,则√2(P+Q)的平方等于.五. 甲地和'S地两处都有汝音台，两个池台之间的距穝是L米.两个适台向同海同事拉一块木板，拉木板需要M埃的力，如果把拉力翻倍就能拉动'一块全新强度相同质材质的木板，那么'木板作为二个池台之间的摩擦力的比值是什么?六. |2x-7|=3x-5的解的结果是_______.2001年希望杯试题一. 如果(x^2-12x+35)(x^2-5x+6)=0的话，那么x的值是什么?二. 如果|a|=|b|=|c|=1,且a+b+c=0,那么|a+b+2c|的取值范围是什么?三. 在α三角形AP是中线,求对角APAC两边之比.四. 将+ II M=¯¯¯¯¯¯连接起来,证明RABP、PBQ是等腰直角梯角形，AC=21,BC=56,求正弦RABP两角的值.五. 27a^3-59a^2b^2+27ab^3=0,(a/b)^3的值是什么?六. -11a^2=11at-4t^2,则a+t=多少?通过以上对历届希望杯试题的回顾和介绍，我们可以看到这项竞赛的题目涵盖了多个数学领域，包括代数、几何、概率等。

全国数学邀请赛初二第一试一、选择题（每小题4分，共40分）以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在下面的表格内。

1．下列运动属于平移的是（）（A）乒乓球比赛中乒乓球的运动．（B）推拉窗的活动窗扇在滑道上的滑行．（C）空中放飞的风筝的运动．（D）篮球运动员投出的篮球的运动．2．若x=1满足2m x2-m2x-m=0，则m的值是（）（A）0．（B）1．（C）0或1．（D）任意实数．3．如图1，将△APB绕点B按逆时针方向旋转90 后得到△A P B'''，若BP=2，那么PP'的长为( )（A）（B（C）2 ．（D）3．4．已知a是正整数，方程组48326ax yx y+=⎧⎨+=⎩的解满足x>0，y<0，则a的值是（）（A）4 ．（B）5 ．（C）6．（D）4，5，6以外的其它正整数．5．让k依次取1，2，3,…等自然数，当取到某一个数之后，以下四个代数式：①k+2；②k2；③2 k；④2 k 就排成一个不变的大小顺序，这个顺序是（）（A）①<②<③<④．（B）②<①<③<④．(C) ①<③<②<④．(D) ③<②<①<④．6．已知1个四边形的对角线互相垂直，且两条对角线的长度分别是8和10 , 那么顺次连接这个四边形的四边中点所得的四边形的面积是（）（A）40 ．（B）（C）20．（D）．7．Let a be the length of a diagonal of a square, b and c be the length of two diagonals of a rhombus respectively. If b:a=a:c,then the ratio of area of the square and rhombus is ( )（A）1：1．（B）2（C）1（D）1：2．(英汉词典：length长度；diagonal对角线；square正方形；rhombus菱形；respectively分别地；ratio比；area面积)8．直角三角形有一条边长为11，另外两边的长是自然数，那么它的周长等于（）．（A）132．（B）121．（C）120．（D）111．9．若三角形三边的长均能使代数式是x2-9x+18的值为零，则此三角形的周长是（）．（A）9或18．（B）12或15 ．（C）9或15或18．（D）9或12或15或18．10．如图2，A、B、C、D是四面互相垂直摆放的镜子，镜面向内，在镜面D上放了写有字母“G”的纸片，某人站在M处可以看到镜面D上的字母G在镜面A、B、C中的影像，则下列判断中正确的是（）（A）镜面A与B中的影像一致．（B）镜面B与C中的影像一致．（C）镜面A与C中的影像一致．（D）在镜面B中的影像是“G”．二、A组填空题（每小题4分，共40分）11．如图3，在△BMN中，BM=6，点A、C、D分别在MB、BN、MN上，且四边形ABCD是平行四边形，∠NDC=∠MDA，则 ABCD的周长是．12．如果实数a ≠b，且101101a b ab a b++=++，那么a b+的值等于．13．已知x=a M的立方根，y =x 的相反数，且M =3a -7，那么x 的平方根是 ． 14．如图4，圆柱体饮料瓶的高是12厘米，上、下底面的直径是6厘米．上底面开有一个小孔供插吸管用，小孔距离上底面圆心2厘米，那么吸管在饮料瓶中的长度最多是= 厘米．15．小杨在商店购买了a 件甲种商品，b 件乙种商品，共用213元，已知甲种商品每件7元，乙种商品每件19元，那么a b +的最大值是 ．16．ABC是边长为D 在三角形内，到边AB 的距离是1，到A 点的距离是2，点E 和点D 关于边AB 对称，点F 和点E 关于边AC 对称，则点F 到BC 的距离是 ．17．如图5，小华从M 点出发，沿直线前进10米后，向左转20，再沿直线前进10米后，又向左转20，……，这样下去，他第一次回到出发地M 时，行走了 米．18．关于x 的不等式123x x -+-≤的所有整数解的和是 ． 19．已知点（1，2）在反比例函数ay x=所确定的曲线上，并且该反比例函数和一次函数1y x =+ 在x b =时的值相等，则b 等于 ．20．如图6，大五边形由若干个白色和灰色的多边形拼接而成，这些多边形（不包括大五边形）的所有内角和等于 ．三、B 组填空题（每小题8分，共40分，每一题两个空，每空4分） 21．解分式方程225111mx x x +=+--会产生增根，则m = 或 ． 22．Let A abcd = be a four-digit number. If 400abcd is a square of an integer, then A= 或 ．（英汉词典：four-digit number 四位数；square 平方、平方数；integer 整数）23．国家规定的个人稿酬纳税办法是：①不超过800元的不纳税；②超过800元而不超过4000元的，超过800元的部分按14%纳税；③超过4000元的按全部稿酬的11%纳税．某人编写了两本书，其中一本书的稿酬不超过4000元，第二本书的稿酬比第一本书多700元，两本书共纳税915元，则两本书的稿酬分别是= 元和 元．24．直线l交反比例函数y =的图象于点A ，交x 轴于点B ，点A 、B 与坐标原点o 构成等边三角形，则直线l 的函数解析式为 或 ． 25．若n 是质数，且分数417n n -+不约分或经过约分后是一个最简分数的平方，则n 或 ．第十八届“希望杯”全国数学邀请赛答案（初二）提示：1、略2、原式可化为：m(1-m)=0,m=0或m=13、由题意得△BPP ´是等腰直角三角形，由勾股定理得PP ´4、解方程组得：461236x aa y a ⎧=⎪⎪-⎨-⎪=⎪-⎩∵x>0,y<0 ∴601230a a ->⎧⎨-<⎩解得4<a<6, ∴a=5.5、当k>4时，2k>k 2>2k>k+2,所以选C6、顺次连接该四边形的四边中点所得的四边形是矩形，面积是：（12×10）×（12×8）=20 7、S 正=12a 2 ， S 菱形=12bc ，∵b:a=a:c ，即a 2=bc ，∴S 正 ：S 菱形 =1：18、设另两边为a ，b ，则a 2+b 2=112（不合题意舍去）或112= a 2- b 2=(a+b)(a-b)=121 =121×1; ∵a,b 是自然数 ∴a+b=121, ∴周长是121+11=1329、∵x2-9x+18=0，即（x-6）（x-3）=0 ，∴x=6或x=3，∴三角形三边分别是：3，3，3或6，6，6或6，6，3。

希望杯第八届（1997年）初中二年级第一试试题一、选择题:1．下列四个从左到右的变形中，是因式分解的是［］A．（x＋1）（x－1）＝x2－1. B．（a－b）（m－n）＝（b－a）（n－m）C．ab－a－b＋1＝（a－1）（b－1）.2．关于x的方程（5－2a）x＝－2的根是负数，那么a所能取的最大整数是［］A．3 B．2. C．1 D．03．直角三角形的两个锐角的外角平分线所夹的锐角的大小是［］A．30°B．45°. C．60°. D．15°或75°4．P是线段AB上的一点，AB＝1，以AP和BP为边分别作两个正方形,当这两个正方形的面积的差的绝对值为时,AP的长是[ ]A.;B.;C.;D..5.若a使分式没有意义,那么a的值应是[ ]A.0;B.;C.;D..6．已知四个代数式：①m＋n；②m－n；③2m＋n；④2m－n．当用2m2n乘以上述四个式中的两个时，便得到多项式4m4n－2m3n2－2m2n3，那么这两个式子的编号是［］A．①与② B．①与③. C．②与③D．③与④7．△ABC中，AB＝5，AC＝3，则BC边上的中线AD的长l的取值范围是［］A．1＜l＜4 B．3＜l＜5. C．2＜l＜3 D．0＜l＜58．A、B、C为平面上的三点，AB＝2，BC＝3，AC＝5，则［］A．可以画一个圆，使A、B、C都在圆周上B．可以画一个圆，使A、B在圆周上，C在圆内C．可以画一个圆，使A、C在圆周上，B在圆外D．可以画一个圆，使A、C在圆周上，B在圆内9．已知：m、n是整数，3m＋2＝5n＋3，且3m＋2＞30，5n＋3＜40，则mn的值是［］A．70 B．72. C．77 D．8410．甲、乙两种茶叶，以x∶y（重量比）相混合制成一种混合茶，甲种茶叶的价格每公斤50元，乙种茶叶的价格每公斤40元，现在甲种茶叶的价格上调了10％，乙种茶叶的价格下调了10％，但混合茶的价格不变，则x∶y等于［］A．1∶1 B．5∶4. C．4∶5 D．5∶6二、A组填空题:11.已知x0,化简所得的结果是____________.12．五个连续奇数的平均数是1997，那么其中最大数的平方减去最小数的平方等于___．13．现有8根木棍，它们的长分别是1，2，3，4，5，6，7，8，若从8根木棍中抽取3根拼三角形，要求三角形的最长边为8，另两边之差大于2（以上单位：厘米）．那么可以拼成的不同的三角形的种数为______．14．如图1，△ABC中，∠C＝90°，∠BAC的平分线交BC于D，且CD＝15，AC＝30，则AB 的长为______．15.已知,那么的值是________.16．已知：a＝－2000，b＝1997，c＝－1995，那么a2＋b2＋c2＋ab＋bc－ac的值是______．17．如图2，△ABC中，∠1＝∠2，∠EDC＝∠BAC，AE＝AF，∠B＝60°，则图中的线段AF、BF、AE、EC、AD、BD、DC、DF中与DE的长相等的线段有______条．18．如图3，∠A＝60°，线段BP、BE把∠ABC三等分，线段CP、CE把∠ACB三等分，则∠BPE的大小是______．19. 已知,那么的值是______．20．某仓库贮存水果a吨，为保证每天供应市场20吨，则需每天从外地调入b吨水果，现实际调入量每天多了2吨，而市场每天供应量不变，那么比原来多供应的天数是______（用a、b表示）．三、B组填空题21．若｜a｜－｜b｜＝1，且3｜a｜＝4｜b｜，则在数轴上表示a、b两数对应的点的距离是______或______．22．△ABC的周长为19，且满足a＝b－1，c＝b＋2，则a、b、c的长分别为a＝______，b ＝______，c＝______．23.x,y为实数,且,则x=________,y=_____.24．如图4，△ABC中，AD平分∠BAC，EG⊥AD，分别交AB、AD、AC、BC的延长线于E、H、F、G，已知下列四个式子：其中有两个式子是正确的，它们是______和______．25.已知abc0,且,则的值是_______或_________.答案·提示一、选择题提示：1．根据因式分解的概念，选（C）．2．由题意，方程的根为负，即∴ a所能取的最大整数是2，选（B）．3．两个外角分别等于其不相邻的锐角与直角之和，因此两个外角之和等于270°．所以选（B）．4．两正方形的面积差＝AP2－（1－AP）2＝2AP－16．对多项式做因式分解：原式＝2m2n（2m2－mn－n2）＝2m2n（2m＋n）（m－n），故选（C）．7．如图5，延长AD到E，使DE＝AD，连接EC，△DEC与△ABD全等，∴ EC＝AB＝5．在△AEC中，AC＋EC＞AE，也就是3＋5＞2l，即l＜4．AC＋AE＞EC，即3＋2l＞5，∴ l＞1．因此有1＜l＜4．故选（A）．8．由题意，A、B、C三点依次在同一直线上．排除（A），且（B）、（C）均不可能成立，选（D）．如果选（A），只能n＝7，m＝10，与题中等式相驳．如果选（B），72＝8×9或6×12，与题中不等式相驳．如果选（C），77＝11×7，也与题中等式相驳，只有选（D）正确．10．由题意有50x＋40y＝50(1＋10％)x＋40(1－10％)y二、A组填空题提示：12：由题意可知这五个奇数是：1993，1995，1997，1999和2001．20012－19932＝（2001＋1993）（2001－1993）＝3994×8＝31952．13：三角形其他两边可以是：7和4、7和3、7和2、6和3，可拼成四种不同的三角形．因为，7＋4＝11＞8且满足7－4＝3＞2；7＋3＝10＞8且满足7－3＝4＞2；7＋2＝9＞8且满足7－2＝5＞2；6＋3＝9＞8且满足6－3＝3＞2．14．如图6,作DE⊥AB,则△ABC≌△DBE，在直角△DBE中，BD2＝DE2＋BE2即（2y－15）2＝y2＋152化简得到 y（y－20）＝0，∴ y＝20．AB＝AE＋BE＝30＋20＝50．16．(a＋b)2＋(b＋c)2＋(a－c)2＝a2＋2ab＋b2＋b2＋2bc＋c2＋a2－2ac＋c2＝2(a2＋b2＋c2＋ab＋bc－ac)将a、b、c的值代入(a＋b)2＋(b＋c)2＋(a－c)2＝(－3)2＋(2)2＋(－5)2＝38．∴原式＝19．17．连接FE交AD于O，△AFE为等腰三角形．∵∠1＝∠2，∴AO⊥EF，且FO＝OE，得到DF＝DE．∵∠EDC＝∠BAC，∴△ABC≌△EDC，∵∠ABC＝60°，∴∠DEC＝60°，∠AED＝120°，则∠AFD＝120°，∴△FBD为等边三角形．∴BF＝BD＝DF＝DE．因此，与DE的长相等的线段有3条．（请注意：当∠BAC＝60°时，除了AD外的其他7条线段均与DE的长度相等．）17解：连接FE交AD于O，△AFE为等腰三角形．∵∠1=∠2，∴AO⊥EF，且FO=OE，得到DF=DE．∵∠EDC=∠BAC，∴△ABC∽△EDC，∵∠ABC=60°，∴∠DEC=60°，∠AED=120°，则∠AFD=120°，∴△FBD为等边三角形．∴BF=BD=DF=DE．因此，与DE的长相等的线段有3条．（请注意：当∠BAC=60°时，除了AD外的其他7条线段均与DE的长度相等）故答案为：3．18．在△BPC中，∵BE平分∠CBP，CE平分∠BCP，∴PE是∠BPC的平分线．∵∠A＝60°，∴∠ABC＋∠ACB＝120°．b(a2＋b2)＋a(a2＋b2)＋2(a＋b)ab＝0，a2b＋b3＋a3＋ab2＋2a2b＋2ab2＝0．20．设原来供应x天，现在供应y天．三、B组填空题提示：21．如图7，由题意｜a｜＝1＋｜b｜，∴3｜a｜＝3＋3｜b｜＝4｜b｜，∴｜b｜＝3，b＝±3．｜a｜＝1＋｜b｜＝4，∴a＝±4．22．将a＝b－1，c＝b＋2代入a＋b＋c＝19，得b＝6，则a＝5，c＝8．当b＋c＝-a,＋b＝-c,a＋c＝-b时,当b＝c,a＝b,a＝c即a＝b＝c时，。

“希望杯”全国数学竞赛（第1-23届）第一/二试题目录1.希望杯第一届（1990年）初中一年级第一试试题............................................. 003-0052.希望杯第一届（1990年）初中一年级第二试试题............................................. 010-0123.希望杯第二届（1991年）初中一年级第一试试题............................................. 018-0204.希望杯第二届（1991年）初中一年级第二试试题............................................. 024-0265.希望杯第三届（1992年）初中一年级第一试试题............................................. 032-0326.希望杯第三届（1992年）初中一年级第二试试题............................................. 038-0407.希望杯第四届（1993年）初中一年级第一试试题............................................. 048-0508.希望杯第四届（1993年）初中一年级第二试试题............................................. 056-0589.希望杯第五届（1994年）初中一年级第一试试题............................................. 064-06610.希望杯第五届（1994年）初中一年级第二试试题 .......................................... 071-07311.希望杯第六届（1995年）初中一年级第一试试题........................................... 078-080 12希望杯第六届（1995年）初中一年级第二试试题........................................... 085-08713.希望杯第七届（1996年）初中一年级第一试试题........................................... 096-09814.希望杯第七届（1996年）初中一年级第二试试题........................................... 103-10515.希望杯第八届（1997年）初中一年级第一试试题............................................ 111-11316.希望杯第八届（1997年）初中一年级第二试试题........................................... 118-12017.希望杯第九届（1998年）初中一年级第一试试题........................................... 127-12918.希望杯第九届（1998年）初中一年级第二试试题........................................... 136-13819.希望杯第十届（1999年）初中一年级第二试试题........................................... 145-14720.希望杯第十届（1999年）初中一年级第一试试题........................................... 148-15121.希望杯第十一届（2000年）初中一年级第一试试题....................................... 159-16122.希望杯第十一届（2000年）初中一年级第二试试题....................................... 167-16923.希望杯第十二届（2001年）初中一年级第一试试题....................................... 171-17424.希望杯第十二届（2001年）初中一年级第二试试题....................................... 176-17825.希望杯第十三届（2002年）初中一年级第一试试题....................................... 182-18426.希望杯第十三届（2001年）初中一年级第二试试题....................................... 186-18927.希望杯第十四届（2003年）初中一年级第一试试题....................................... 193-19628.希望杯第十四届（2003年）初中一年级第二试试题....................................... 198-20029.希望杯第十五届（2004年）初中一年级第一试试题 (203)30.希望杯第十五届（2004年）初中一年级第二试试题 (204)31.希望杯第十六届（2005年）初中一年级第一试试题....................................... 213-21832.希望杯第十六届（2005年）初中一年级第二试试题 (204)33.希望杯第十七届（2006年）初中一年级第一试试题....................................... 228-23334.希望杯第十七届（2006年）初中一年级第二试试题....................................... 234-23835.希望杯第十八届（2007年）初中一年级第一试试题....................................... 242-246 26.希望杯第十八届（2007年）初中一年级第二试试题....................................... 248-25137.希望杯第十九届（2008年）初中一年级第一试试题....................................... 252-25638.希望杯第十九届（2008年）初中一年级第二试试题....................................... 257-26239.希望杯第二十届（2009年）初中一年级第一试试题....................................... 263-26620.希望杯第二十届（2009年）初中一年级第二试试题....................................... 267-27121.希望杯第二十一届（2010年）初中一年级第一试试题................................... 274-27622.希望杯第二十二届（2011年）初中一年级第二试试题................................... 285-28823.希望杯第二十三届（2012年）初中一年级第二试试题................................... 288-301希望杯第一届（1990年）初中一年级第1试试题一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么( )A．a，b都是0．B．a，b之一是0．C．a，b互为相反数．D．a，b互为倒数．2．下面的说法中正确的是( )A．单项式与单项式的和是单项式．B．单项式与单项式的和是多项式．C．多项式与多项式的和是多项式．D．整式与整式的和是整式．3．下面说法中不正确的是( )A. 有最小的自然数．B．没有最小的正有理数．C．没有最大的负整数．D．没有最大的非负数．4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么( )A．a，b同号．B．a，b异号．C．a＞0．D．b＞0．5．大于－π并且不是自然数的整数有( )A．2个．B．3个．C．4个．D．无数个．6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身．这四种说法中，不正确的说法的个数是( )A．0个．B．1个．C．2个．D．3个．7．a代表有理数，那么，a和－a的大小关系是 ( )A．a大于－a．B．a小于－a．C．a大于－a或a小于－a．D．a不一定大于－a．8．在解方程的过程中，为了使得到的方程和原方程同解，可以在原方程的两边( ) A．乘以同一个数．B．乘以同一个整式．C．加上同一个代数式．D．都加上1．9．杯子中有大半杯水，第二天较第一天减少了10%，第三天又较第二天增加了10%，那么，第三天杯中的水量与第一天杯中的水量相比的结果是( )A．一样多． B．多了．C．少了．D．多少都可能．10．轮船往返于一条河的两码头之间，如果船本身在静水中的速度是固定的，那么，当这条河的水流速度增大时，船往返一次所用的时间将( )A．增多．B．减少．C．不变．D．增多、减少都有可能．二、填空题（每题1分，共10分）1. 21115160.01253(87.5)(2)4571615⨯-⨯-÷⨯+--= ______． 2．198919902－198919892=______． 3.2481632(21)(21)(21)(21)(21)21+++++-=________. 4. 关于x 的方程12148x x +--=的解是_________. 5．1－2＋3－4+5－6+7－8+…+4999－5000=______．6.当x=-24125时,代数式(3x 3－5x 2+6x －1)－(x 3－2x 2+x －2)+(－2x 3+3x 2+1)的值是____． 7．当a=－0.2，b=0.04时，代数式272711()(0.16)()73724a b b a a b --++-+的值是______. 8．含盐30%的盐水有60千克，放在秤上蒸发，当盐水变为含盐40%时，秤得盐水的重是______克．9.制造一批零件,按计划18天可以完成它的13.如果工作4天后,工作效率提高了15,那么完成这批零件的一半，一共需要______天．10．现在4点5分，再过______分钟，分针和时针第一次重合．答案与提示一、选择题1．C 2．D 3．C 4．D 5．C 6．B 7．D 8．D 9．C 10．A提示：1．令a=2，b=－2，满足2+(－2)=0，由此2．x2，2x2，x3都是单项式．两个单项式x3，x2之和为x3+x2是多项式，排除A．两个单项式x2，2x2之和为3x2是单项式，排除B．两个多项式x3+x2与x3－x2之和为2x3是个单项式，排除C，因此选D．3．1是最小的自然数，A正确．可以找到正所以C“没有最大的负整数”的说法不正确．写出扩大自然数列，0，1，2，3，…，n，…，易知无最大非负数，D正确．所以不正确的说法应选C．5．在数轴上容易看出：在－π右边0的左边（包括0在内）的整数只有－3，－2，－1，0共4个．选C．6．由12=1，13=1可知甲、乙两种说法是正确的．由(－1)3=－1，可知丁也是正确的说法．而负数的平方均为正数，即负数的平方一定大于它本身，所以“负数平方不一定大于它本身”的说法不正确．即丙不正确．在甲、乙、丙、丁四个说法中，只有丙1个说法不正确．所以选B．7．令a=0，马上可以排除A、B、C，应选D．8．对方程同解变形，要求方程两边同乘不等于0的数．所以排除A．我们考察方程x－2=0，易知其根为x=2．若该方程两边同乘以一个整式x－1，得(x－1)(x－2)=0，其根为x=1及x=2，不与原方程同解，排除B．若在方程x－2=0两边加上同一个代数式去了原方程x=2的根．所以应排除C．事实上方程两边同时加上一个常数，新方程与原方程同解，对D，这里所加常数为1，因此选D．9．设杯中原有水量为a，依题意可得，第二天杯中水量为a×(1－10%)=0.9a；第三天杯中水量为(0.9a)×(1+10%)=0.9×1.1×a；第三天杯中水量与第一天杯中水量之比为所以第三天杯中水量比第一天杯中水量少了，选C．10．设两码头之间距离为s，船在静水中速度为a，水速为v0，则往返一次所用时间为设河水速度增大后为v，(v＞v0)则往返一次所用时间为由于v－v0＞0，a+v0＞a－v0，a+v＞a－v所以(a+v0)(a+v)＞(a－v0)(a－v)∴t0－t＜0，即t0＜t．因此河水速增大所用时间将增多，选A．二、填空题提示：2．198919902－198919892=(19891990+19891989)×(19891990－19891989) =(19891990+19891989)×1=39783979．3．由于(2+1)(22+1)(24+1)(28+1)(216+1)=(2－1)(2+1)(22+1)(24+1)(28+1)(216+1)=(22－1)(22+1)(24+1)(28+1)(216+1)=(24－1)(24+1)(28+1)(216+1)=(28－1)(28+1)(216+1)=(216－1)(216+1)=232－1．2(1+x)－(x－2)=8,2+2x－x+2=8解得；x=45．1－2+3－4+5－6+7－8+…+4999－5000=(1－2)+(3－4)+(5－6)+(7－8)+…+(4999－5000)=－2500．6．(3x3－5x2+6x－1)－(x3－2x2+x－2)+(－2x3+3x2+1)=5x+27．注意到：当a=－0.2，b=0.04时，a2－b=(－0.2)2－0.04=0，b+a+0.16=0.04－0.2+0.16=0．8．食盐30%的盐水60千克中含盐60×30%（千克）设蒸发变成含盐为40%的水重x克，即0.001x千克，此时，60×30%=(0.001x)×40%解得：x=45000（克）．10．在4时整，时针与分针针夹角为120°即希望杯第一届（1990年）初中一年级第2试试题一、选择题（每题1分，共5分）以下每个题目里给出的A，B，C，D四个结论中有且仅有一个是正确的．请你在括号填上你认为是正确的那个结论的英文字母代号．1．某工厂去年的生产总值比前年增长a%，则前年比去年少的百分数是( )A．a%．B．(1+a)%． C.1100aa+D.100aa+2．甲杯中盛有2m毫升红墨水，乙杯中盛有m毫升蓝墨水，从甲杯倒出a毫升到乙杯里, 0＜a＜m，搅匀后，又从乙杯倒出a毫升到甲杯里，则这时( )A．甲杯中混入的蓝墨水比乙杯中混入的红墨水少．B．甲杯中混入的蓝墨水比乙杯中混入的红墨水多．C．甲杯中混入的蓝墨水和乙杯中混入的红墨水相同．D．甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定．3.已知数x=100,则( )A．x是完全平方数．B．(x－50)是完全平方数．C．(x－25)是完全平方数．D．(x+50)是完全平方数．4．观察图1中的数轴：用字母a，b，c依次表示点A，B，C对应的数,则111,,ab b a c-的大小关系是( )A.111ab b a c<<-; B.1b a-<1ab<1c; C.1c<1b a-<1ab; D.1c<1ab<1b a-.5．x=9，y=－4是二元二次方程2x2+5xy+3y2=30的一组整数解，这个方程的不同的整数解共有( )A．2组．B．6组．C．12组．D．16组．二、填空题（每题1分，共5分）1．方程|1990x－1990|=1990的根是______．2．对于任意有理数x，y，定义一种运算*，规定x*y=ax+by－cxy，其中的a，b，c表示已知数，等式右边是通常的加、减、乘运算．又知道1*2=3，2*3=4，x*m=x（m≠0），则m的数值是______．3．新上任的宿舍管理员拿到20把钥匙去开20个房间的门，他知道每把钥匙只能开其中的一个门，但不知道每把钥匙是开哪一个门的钥匙，现在要打开所有关闭着的20个房间，他最多要试开______次．4．当m=______时，二元二次六项式6x2+mxy－4y2－x+17y－15可以分解为两个关于x，y的二元一次三项式的乘积．5．三个连续自然数的平方和（填“是”或“不是”或“可能是”）______某个自然数的平方．三、解答题（写出推理、运算的过程及最后结果．每题5分，共15分）1．两辆汽车从同一地点同时出发，沿同一方向同速直线行驶，每车最多只能带24桶汽油，途中不能用别的油，每桶油可使一辆车前进60公里，两车都必须返回出发地点，但是可以不同时返回，两车相互可借用对方的油．为了使其中一辆车尽可能地远离出发地点，另一辆车应当在离出发地点多少公里的地方返回？离出发地点最远的那辆车一共行驶了多少公里？2．如图2，纸上画了四个大小一样的圆，圆心分别是A，B，C，D，直线m通过A，B，直线n通过C，D，用S表示一个圆的面积，如果四个圆在纸上盖住的总面积是5(S－1)，直线m，n之间被圆盖住的面积是8，阴影部分的面积S1，S2，S3满足关系式S3=13S1=13S2,求S．3.求方程11156x y z++=的正整数解.答案与提示一、选择题1．D 2．C 3．C 4．C 5．D提示：1．设前年的生产总值是m，则去年的生产总值是前年比去年少这个产值差占去年的应选D．2．从甲杯倒出a毫升红墨水到乙杯中以后：再从乙杯倒出a毫升混合墨水到甲杯中以后：乙杯中含有的红墨水的数量是①乙杯中减少的蓝墨水的数量是②∵①=②∴选C．∴x－25=(10n+2+5)2可知应当选C．4．由所给出的数轴表示（如图3）：可以看出∴①＜②＜③，∴选C．5．方程2x2+5xy+3y2=30可以变形为(2x+3y)(x+y)=1·2·3·5∵x，y是整数，∴2x+3y，x+y也是整数．由下面的表可以知道共有16个二元一次方程组，每组的解都是整数，所以有16组整数组，应选D．二、填空题提示：1．原方程可以变形为|x－1|=1，即x-1=1或-1，∴x=2或0．2．由题设的等式x*y=ax+by-cxy及x*m=x(m≠0)得a·0+bm-c·0·m=0，∴bm=0．∵m≠0，∴b=0．∴等式改为x*y=ax-cxy．∵1*2=3，2*3=4，解得a=5，c=1．∴题设的等式即x*y=5x-xy．在这个等式中，令x=1，y=m，得5-m=1，∴m=4．3．∵打开所有关闭着的20个房间，∴最多要试开4．利用“十字相乘法”分解二次三项式的知识，可以判定给出的二元二次六项式6x2+mxy-4y2-x+17y-15中划波浪线的三项应当这样分解：3x -52x +3现在要考虑y，只须先改写作然后根据-4y2，17y这两项式，即可断定是：由于(3x+4y-5)(2x-y+3)=6x2+5xy-4y2-x+17y-15就是原六项式，所以m=5．5．设三个连续自然数是a-1，a，a+1，则它们的平方和是(a-1)2+a2+(a+1)2=3a2+2，显然，这个和被3除时必得余数2．另一方面，自然数被3除时，余数只能是0或1或2，于是它们可以表示成3b，3b+1，3b+2（b是自然数）中的一个，但是它们的平方(3b)2=9b2(3b+1)2=9b2+6b+1，(3b+2)2=9b2+12b+4=(9b2+12b+3)+1被3除时，余数要么是0，要么是1，不能是2，所以三个连续自然数平方和不是某个自然数的平方．三、解答题1．设两辆汽车一为甲一为乙，并且甲用了x升汽油时即回返，留下返程需的x桶汽油，将多余的(24-2x)桶汽油给乙．让乙继续前行，这时，乙有(24-2x)+(24-x)=48-3x桶汽油，依题意，应当有48-3x≤24，∴x≥8．甲、乙分手后，乙继续前行的路程是这个结果中的代数式30(48-4x)表明，当x的值愈小时，代数式的值愈大，因为x≥8，所以当x=8时，得最大值30(48-4·8)=480（公里），因此，乙车行驶的路程一共是2(60·8+480)=1920（公里）．2．由题设可得即2S-5S3=8……②∴x，y，z都＞1，因此，当1＜x≤y≤z时，解(x，y，z)共(2，4，12)，(2，6，6)，(3，3，6)，(3，4，4)四组．由于x，y，z在方程中地位平等．所以可得如下表所列的15组解．希望杯第二届（1991年）初中一年级第1试试题一、选择题（每题1分，共15分）以下每个题目的A，B，C，D四个结论中，仅有一个是正确的，请在括号内填上正确的那个结论的英文字母代号．1．数1是( )A．最小整数．B．最小正数．C．最小自然数．D．最小有理数．2．若a＞b，则( )A.11a b; B．-a＜-b．C．|a|＞|b|．D．a2＞b2．3．a为有理数，则一定成立的关系式是( )A．7a＞a．B．7+a＞a．C．7+a＞7．D．|a|≥7．4．图中表示阴影部分面积的代数式是( )A．ad+bc．B．c(b-d)+d(a-c)．C．ad+c(b-d)．D．ab-cd．5．以下的运算的结果中，最大的一个数是( )A．(-13579)+0.2468; B.(-13579)+1 2468;C.(-13579)×12468; D.(-13579)÷124686．3.1416×7.5944+3.1416×(-5.5944)的值是( ) A．6.1632． B．6.2832．C．6.5132．D．5.3692．7.如果四个数的和的14是8,其中三个数分别是-6,11,12,则笫四个数是( )A．16． B．15． C．14． D．13．8.下列分数中,大于-13且小于-14的是( )A.-1120; B.-413; C.-316; D.-617.9.方程甲:34(x-4)=3x与方程乙:x-4=4x同解,其根据是( )A.甲方程的两边都加上了同一个整式x ．B.甲方程的两边都乘以43x; C. 甲方程的两边都乘以43; D. 甲方程的两边都乘以34. 10．如图: ，数轴上标出了有理数a ，b ，c 的位置,其中O 是原点,则111,,a b c的大小关系是( ) A.111a b c>>; B.1b >1c >1a ; C. 1b >1a >1c ; D. 1c >1a >1b .11.方程522.2 3.7x =的根是( ) A ．27． B ．28． C ．29． D ．30． 12.当x=12,y=-2时,代数式42x y xy -的值是( )A ．-6．B ．-2．C ．2．D ．6．13．在-4，-1，-2.5，-0.01与-15这五个数中，最大的数与绝对值最大的那个数的乘积是( )A ．225．B ．0.15．C ．0.0001．D ．1．14.不等式124816x x x xx ++++>的解集是( ) A ．x ＜16． B ．x ＞16．C ．x ＜1． D.x>-116. 15．浓度为p%的盐水m 公斤与浓度为q%的盐水n 公斤混合后的溶液浓度是 ( ) A.%2p q +; B.()%mp nq +; C.()%mp nq p q ++;D.()%mp nq m n++.二、填空题（每题1分，共15分）1． 计算：(-1)+(-1)-(-1)×(-1)÷(-1)=______． 2． 计算：-32÷6×16=_______.3．计算：(63)36162-⨯=__________.4．求值：(-1991)-|3-|-31||=______．5．计算:111111 2612203042-----=_________.6．n为正整数，1990n-1991的末四位数字由千位、百位、十位、个位、依次排列组成的四位数是8009．则n的最小值等于______．7. 计算：19191919199191919191⎛⎫⎛⎫---⎪ ⎪⎝⎭⎝⎭=_______.8. 计算：15[(-1989)+(-1990)+(-1991)+(-1992)+(-1993)]=________.9.在(-2)5,(-3)5,512⎛⎫-⎪⎝⎭,513⎛⎫-⎪⎝⎭中,最大的那个数是________.10．不超过(-1.7)2的最大整数是______．11.解方程21101211,_____. 3124x x xx-++-=-=12.求值:355355113113355113⎛⎫---⎪⎝⎭⎛⎫- ⎪⎝⎭=_________.13．一个质数是两位数，它的个位数字与十位数字的差是7，则这个质数是______．14.一个数的相反数的负倒数是119,则这个数是_______.15．如图11，a，b，c，d，e，f均为有理数．图中各行，各列、两条对角线上三个数之和都相等,则ab cd efa b c d e f+++++++=____.答案与提示一、选择题1．C 2．B 3．B 4．C 5．C 6．B 7．B 8．B 9．C 10．B 11．D 12．A 13．B 1 4．A 15．D提示：1．整数无最小数，排除A；正数无最小数，排除B；有理数无最小数，排除D．1是最小自然数．选C．有|2|＜|-3|，排除C；若2＞-3有22＜(-3)2，排除D；事实上，a＞b必有-a＜-b．选B．3．若a=0，7×0=0排除A；7+0=7排除C|0|＜7排除D，事实上因为7＞0，必有7+a＞0+a=a．选B．4．把图形补成一个大矩形，则阴影部分面积等于ab-(a-c)(b-d)=ab-[ab-ad-c(b-d)]=ab-ab+ad+c(b-d)=ad+c(b-d)．选C．5．运算结果对负数来说绝对值越小其值越大。

初二“希望杯”数学竞赛练习卷解答(2016.3，18)一、填空1．若a，b，c是3个不同的正整数，并且abc=16，则a b-b c+c a可能的最大值是（C）A．B．C．D．∴OB=3A ．210B ．217C ．317D ．310210.如如图1所示，在直角梯形ABCD 中，AB ∥CD ，∠B=90°，动点P 从点B 出发，沿梯形的边由B→C→D→A 运动，设点P 运动的路程为x ，△ABP的面积为y ，把y 看作x 的函数，函数图象如图2所示，则△ABC 的面积为（ ）25．如图所示，△ABC是正三角形，△A1B1 C1的三条边A1B1、B l C1、C1A1交△ABC各边分别于C2、C3，A2、A3，B2、B3．已知A2C3=C2B3=B2A3，且C2C32+B2B32=A2A32．请你证明：A l B1⊥C1A1．解答：证明：如图，过A2作C3C2的平行线交过C2所作C3A2的平行线于点O，连接OA3、0B3，∴A2OC2C3是平行四边形，∴A2O∥C3C2，且A2O=C3C2，OC2∥A2C3且OC2=A2C3=B3C2，∴△OB3C2是正三角形，∴∠OB3C2=60°=∠B，∴OB3∥A3B2，又∵0B3=B3C2=A3B2，∴OB3B2A3是平行四边形，∴OA3∥B3B2且OA3=B3B2，∵C2C32+B2B32=A2A32，∴OA22+OA32=A2A32，在△A2OA3中，∵OA22+OA32=A2A32，∴由勾股定理的逆定理得∠A2OA3=90°，∵已证OA3∥B3B2，即OA3∥A1C1，A2O∥C3C2，即A2O∥B1A1，∴∠C1A1B1=90°，∴A1B1⊥C1A1．26.图：四边形ABCD中，AD=DC，∠ABC=30°，∠ADC=60°．试探索以AB、BC、BD为边，能否组成直角三角形，并说明理由．解答：解：以AB、BC、BD为边，能够组成直角三角形．理由如下：以BC为边作等边△BCE，连接AE、AC．如右图所示．∵∠ABC=30°，∠CBE=60°，∴∠ABE=90°，∴AB2+BE2=AE2①，∵AD=DC，∠ADC=60°，∴△ADC是等边三角形，在△DCB和△ACE中，DC=AC，∴∠DCB=∠DCA+∠ACB=∠ECB+∠ACB=∠ACE，又∵BC=CE，∴△DCB≌△ACE，∴BD=AE，∵BC=BE，由①式，可得BD2=AB2+BC2．∴以AB、BC、BD为边，能够组成直角三角形．附加17．如图（十二），直线l 的解析式为4y x =-+，它与x 轴、y 轴分别相交于A B 、两点．平行于直线l 的直线m 从原点O 出发，沿x 轴的正方形以每秒1个单位长度的速度运动，它与x 轴、y 轴分别相交于M N 、两点，设运动时间为t 秒（04t <≤）．（1）求A B 、两点的坐标；（2）用含t 的代数式表示MON △的面积1S ；1（3）以MN 为对角线作矩形OMPN ，记MPN △和OAB △重合部分的面积为2S ，①当2t <≤4时，试探究2S 与t 之间的函数关系式；②在直线m 的运动过程中，当t 为何值时，2S 为OAB △面积的516？或t=3．。

历年初中希望杯数学竞赛试题大全][ 真诚为您服务试试题希望杯”全国数学邀请赛初二第 2 ·2009 年第20 届“次·161 ·[4-30]★ 详细简介请参考下载页]·[ 竞赛 2 试试题届“希望杯”全国数学邀请赛初一第年第·200920 次·153 ·[4-28]详细简介请参考下载页★]·[ 竞赛数学大赛初赛试卷（扫描版）届5“希望杯”年湖北省黄冈市第·2009 ·76 次·[4-17]★ 详细简介请参考下载页]·[ 竞赛试试题”全国数学邀请赛初二第1·2009 年第20 届“希望杯次·133 ·[4-7]对不起，尚无简介☆]竞赛·[ 试试题全国数学邀请赛初一第 1 届“希望杯”20 ·2009年第·122 次·[4-7]详细简介请参考下载页★]·[ 竞赛全国数学邀请赛初二训练题”第十四届“希望杯·次·44 ·[9-9]详细简介请参考下载页★]竞赛·[ 2 试试题“希望杯”全国数学邀请赛初一第19 ·2008年第届次·203 ·[9-4]详细简介请参考下载页★]·[ 竞赛 1 ”“19 ·2008 年第届希望杯全国数学邀请赛初一第试试题次·169 ·[9-4]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第219 年第届“希望杯”·2008 次·156 ·[9-2]详细简介请参考下载页★]·[ 竞赛 1 试试题希望杯”全国数学邀请赛初二第“·2008 年第19 届·146 次·[9-2]详细简介请参考下载页★]竞赛·[ 2 试试题”届“希望杯全国数学邀请赛初二第18 ·2007年第·101 次·[9-2]详细简介请参考下载页★]竞赛·[ 1 全国数学邀请赛初二第试试题” “18 ·2007 年第届希望杯次·95 ·[9-2]详细简介请参考下载页★]竞赛·[ 试试题”全国数学邀请赛初二第2·2006 年第17 届“希望杯次·76 ·[9-2]详细简介请参考下载页★]竞赛·[ 1 试试题“希望杯”全国数学邀请赛初二第届·2006年第17 ·76 次·[9-2]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第 2 希望杯·2005 年第16 届“”次·65 ·[9-1]详细简介请参考下载页★]·[ 竞赛 1 试试题全国数学邀请赛初二第届·2005 年第16“希望杯”次·52 ·[9-1]详细简介请参考下载页★]·[ 竞赛试试题全国数学邀请赛初二第希望杯”2·2004 年第15 届“次·47 ·[9-1]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第115 届“希望杯”年第·2004 次·38 ·[9-1]详细简介请参考下载页★]·[ 竞赛 2 试试题希望杯”全国数学邀请赛初二第届·2003 年第14 “次·30 ·[9-1]详细简介请参考下载页★]竞赛·[ 1 试试题希望杯届“”全国数学邀请赛初二第年第·200314 ·26 次·[9-1]详细简介请参考下载页★]竞赛·[ 2 试试题全国数学邀请赛初二第希望杯届年第·200213 “”·31 次·[9-1]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第 1 ”年第13 届“希望杯·2002 次·23 ·[9-1]详细简介请参考下载页★]竞赛·[ 2 试试题“希望杯”全国数学邀请赛初二第·2001 年第12 届·17 次·[9-1]详细简介请参考下载页★]]·[ 竞赛试试题”全国数学邀请赛初二第1“·2000 年第11 届希望杯次·15 ·[9-1]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第210 届“希望杯”·1999年第次·13 ·[9-1]详细简介请参考下载页★]·[ 竞赛试试题 1 希望杯”全国数学邀请赛初二第·1999 年第10 届“次·15 ·[9-1]详细简介请参考下载页★]竞赛·[ 2 试试题“希望杯”全国数学邀请赛初二第9 ·1998年第届次·11 ·[8-29]详细简介请参考下载页★]·试题[ 竞赛 1 ”“9·1998 年第届希望杯全国数学邀请赛初二第试竞赛·[ 试试题全国数学邀请赛初二第112 年第届“希望杯”·2001 ·17 次·[9-1]详细简介请参考下载页★]竞赛·[ 试试题2“届希望杯”全国数学邀请赛初二第11 ·2000 年第次·15 ·[9-1]★详细简介请参考下载页次·10 ·[8-29]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第28 年第届“希望杯”·1997 次·13 ·[8-29]详细简介请参考下载页★]·[ 竞赛 1 试试题希望杯”全国数学邀请赛初二第“·1997 年第8 届·10 次·[8-29]详细简介请参考下载页★]竞赛·[ 2 试试题”届“希望杯全国数学邀请赛初二第7·1996年第·11 次·[8-29]详细简介请参考下载页★]竞赛·[ 1 全国数学邀请赛初二第试试题” “7·1996 年第届希望杯次·10 ·[8-29]详细简介请参考下载页★]·[ 竞赛试试题”希望杯全国数学邀请赛初二第2·1995 年第6 届“次·14 ·[8-29]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第16 届“希望杯”·1995年第次·14 ·[8-29]★详细简介请参考下载页]·[ 竞赛 2 试试题希望杯”全国数学邀请赛初二第5·1994 年第届“次·12 ·[8-29]详细简介请参考下载页★]竞赛·[ 1 试试题“届希望杯”全国数学邀请赛初二第·1994年第5 ·12 次·[8-29]（每一、选择题: 年第五届希望杯全国数学邀请赛1994 初中二年级第一试试题[] Ax 1.303 小题分，共分）使等式成立的的值是．是]·[ 竞赛试试题初二第 2 ”年第4 届“希望杯全国数学邀请赛·1993 次·9 ·[8-29]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第14 届“希望杯”·1993年第次·10 ·[8-29]详细简介请参考下载页★]·[ 竞赛试试题2 希望杯”全国数学邀请赛初二第·1992 年第3 届“次·11 ·[8-29]详细简介请参考下载页★]竞赛·[ 1 试试题“希望杯”全国数学邀请赛初二第 3 ·1992年第届次·9 ·[8-29]详细简介请参考下载页★]·[ 竞赛 2 ”“2·1991 年第届希望杯全国数学邀请赛初二第试试题·14 次·[8-28]详细简介请参考下载页★]·[ 竞赛试试题”全国数学邀请赛初二第 1 年第·19912 届“希望杯次·12 ·[8-28]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初二第21 届“希望杯”·1990年第·13 次·[8-28]详细简介请参考下载页★]·[ 竞赛试试题”全国数学邀请赛初二第 1 希望杯·1990 年第1 届“次·11 ·[8-28]分，（每题1 ”全国数学邀请赛初二第一试一、选择题: “1990 年第一届希望杯() 倍，那么这个角是 1 ．一个角等于它的余角的 5 分）共10]竞赛·[ 2 试试题全国数学邀请赛初一第希望杯届年第·200718 “”·94 次·[8-28]详细简介请参考下载页★]竞赛·[ 试试题全国数学邀请赛初一第118 届“希望杯”·2007年第次·42 ·[8-28]详细简介请参考下载页★]·[ 竞赛试试题”希望杯全国数学邀请赛初一第2·2006 年第17 届“次·41 ·[8-28]详细简介请参考下载页★]竞赛·[ 试试题 1 希望杯”全国数学邀请赛初一第“·2006 年第17 届次·43 ·[8-28]试第1 全国数学邀请赛初一希望杯年第十七届2006 “”中考资源网，竞赛试题任你选！更多数学竞赛试题请点击。

1. 下列数中，是质数的是（）A. 14B. 15C. 16D. 172. 一个长方形的长是6cm，宽是4cm，它的周长是（）A. 20cmB. 24cmC. 30cmD. 40cm3. 如果a + b = 7，a - b = 3，那么a的值是（）A. 5B. 6C. 7D. 84. 下列各式中，能被3整除的是（）A. 21 ÷ 6B. 24 ÷ 7C. 27 ÷ 9D. 30 ÷ 85. 小明从家到学校的路程是1200米，他骑自行车用了20分钟，那么他骑自行车的速度是（）A. 30米/分钟B. 40米/分钟C. 60米/分钟D. 80米/分钟二、填空题（每题5分，共25分）6. 乘法口诀“六七四十二”中，7乘以6等于（）。

7. 一个等腰三角形的底边长是8cm，腰长是6cm，那么这个三角形的周长是（）cm。

8. 如果一个数的平方是25，那么这个数是（）。

9. 一个数加上它的倒数等于2，这个数是（）。

10. 下列各数中，有（）个正整数。

三、解答题（每题10分，共30分）11. （10分）已知一个数的4倍与9的和是23，求这个数。

12. （10分）一个长方形的长是x厘米，宽是y厘米，它的周长是30厘米，求x和y的值。

13. （10分）一个梯形的上底是5cm，下底是10cm，高是8cm，求这个梯形的面积。

14. （15分）一个正方形的边长增加10%，那么它的面积增加了多少？15. （15分）小明从家到学校的路程是3km，他骑自行车用了30分钟，骑电动车用了20分钟，求骑自行车和骑电动车的速度。

注意：本试卷共五部分，满分100分。

考试时间为60分钟。

请仔细阅读题目，认真作答。

2019-2020 学年八年级数学第 1届“希望杯”第 2试试题一、选择题 : （每题 1分，共 5分）1.等腰三角形周长是 24cm，一腰中线将周长分成 5∶3的两部分，那么这个三角形的底边长是 [ ]A．7.5B． 12. C ． 4.D． 12或42. 已知 P= 19881989199019911( 1989) 2，那么P的值是[ ]A． 1987B． 1988. C． 1989D． 19903．a＞b＞ c，x＞y＞ z，M=ax+by+cz，N=az+by+cx，P=ay+bz+cx ，Q=az+bx+cy，则 []A． M＞ P＞ N且 M＞ Q＞N. B ．N＞ P＞ M且 N＞ Q＞ MC． P＞ M＞ Q且 P＞ N＞Q. D ．Q＞ M＞ P且 Q＞ N＞ P∠ CDA∶∠ ABC=2∶ 1,AD∶CB=1∶3 , 则∠ BDA=[] 4．凸四边形 ABCD中，∠ DAB=∠ BCD=90,A． 30°B． 45°. C ． 60° .D．不能确定5．把一个边长为1的正方形分割成面积相等的四部分，使得在其中的一部分内存在三个点，以这三个点为顶点可以组成一个边长大于1的正三角形，满足上述性质的分割 []A．是不存在的 . B ．恰有一种 . C．有有限多种，但不只是一种.D ．有无穷多种二、填空题 : （每题 1分，共 5分）1．△ ABC中，∠∠ B=90°，∠ C的平分线与 AB交于 L，∠ C的外角平分线与BA的延长线交于 N．已知 CL=3，则 CN=______．2．若 a 1(ab2)20 ,那么111的值是 _____.ab(a1)(b1)(a1990)( b1990)3．已知 a， b， c满足 a+b+c=0， abc=8 ，则 c的取值范围是 ______．4． ABC中 ,∠ B=300,AB=5 ,BC=3 , 三个两两互相外切的圆全在△ABC中，这三个圆面积之和的最大值的整数部分是______．a b c ab ac bc abc 5．设 a,b,c 是非零整数 , 那么b c ab ac bc abc 的值等于a _________.三、解答 : （每 5分，共 15分）1．从自然数 1， 2，3⋯， 354中任取 178个数，：其中必有两个数，它的差是177．2．平面上有两个相等的正方形ABCD和A＇ B＇ C＇ D＇，且正方形 A＇ B＇ C＇ D＇的点 A＇在正方形 ABCD的中心．当正方形 A＇ B＇C＇D＇ A＇，两个正方形的重合部分的面必然是一个定．个？明你的判断．3．用 1， 9， 9，0四个数成的所有可能的四位数中，每一个的四位数与自然数 n之和被 7除余数都不 1，将所有足上述条件的自然数n由小到大排成一列n1＜ n2＜ n3＜n4⋯⋯，求： n1· n2之．答案与提示一、选择题提示：1．若底边长为12．则其他二边之和也是12，矛盾．故不可能是(B) 或 (D) ．又：底为 4时，腰长是 10．符合题意．故选(C) ．=19882+3× 1988+1-1989 2=(1988+1) 2+1988-1989 2=19883．只需选 a=1，b=0，c=-1 ，x=1，y=0，z=-1 代入，由于这时 M=2，N=-2，P=-1 ，Q=-1．从而选 (A) ．4．由图 6可知：当∠ BDA=60°时，∠ CDB5．如图 7按同心圆分成面积相等的四部分．在最外面一部分中显然可以找到三个点，组成边长大于1的正三角形．如果三个圆换成任意的封闭曲线，只要符合分成的四部分面积相等，那么最外面部分中，仍然可以找到三个点，使得组成边长大于1的正三角形．故选 (D) ．二、填空题提示：1．如图8：∠ NLC=∠ B+∠1=∠ CAB-90° +∠ 1=∠ CAB-∠3 =∠ N．∴ NC=LC=3．5．当 a， b， c均正，7．当 a， b， c不均正，-1 ．三、解答177个：(1 ，178) ， (2 ，179) ，(3 ，180) ，⋯，1．法一把 1到 354的自然数分成(177 ， 354) ．的中，任一内的两个数之差177．从 1~354中任取 178个数，即是从 177个中取出 178个数，因而至少有两个数出自同一个．也即至少有两个数之差是 177．从而明了任取的 178个数中，必有两个数，它的差是177．法二从 1到 354的自然数中，任取178个数．由于任何数被177除，余数只能是0，1， 2，⋯， 176 177种之一．因而 178个数中，至少有两个数a， b的余数相同，也即至少有两个数a， b之差是177的倍数，即×177．又因 1~ 354中，任两数之差小于2× 177=354．所以两个不相等的数a，b之差必177．即．∴从自然数 1，2，3，⋯， 354中任取 178个数，其中必有两个数，它的差是177．2．如图 9，重合部分面积S A＇EBF是一个定值．证明：连 A＇B， A＇ C，由 A＇为正方形 ABCD的中心，知∠A＇ BE=∠ A＇ CF=45°．又，当 A＇ B＇与 A＇ B重合时，必有 A＇ D＇与 A＇ C重合，故知∠ EA＇ B=∠FA＇ C．在△ A＇ FC和△ A＇ EB中，∴S A＇EBF=S△A＇BC．∴两个正方形的重合部分面积必然是一个定值．3．可能的四位数有9种：1990 ，1909， 1099， 9091， 9109，9910 ， 9901， 9 019， 9190．其中1990=7 ×284+2，1909=7 ×272+5．1099=7× 157,9091=7 × 1298+5,9109=7 × 1301+2,9910=7× 1415+5， 9901=7× 1414+3，9019=7× 1288+3， 9190=7× 1312+6．即它们被 7除的余数分别为 2， 5，0， 5， 2，5， 3， 3，6．即余数只有 0，2， 3， 5，6五种．它们加 1， 2， 3都可能有余 1的情形出现．如0+1≡ 1， 6+2≡ 1， 5+3≡ (mod7) ．而加 4之后成为： 4， 6 ，7， 9， 10，没有一个被 7除余 1，所以 4是最小的 n．又：加 5， 6有： 5+3≡ 1，6+2≡ 1．(mod7) 而加 7之后成为 7，9，10，12， 13．没有一个被 7除余 1．所以 7是次小的 n．即n 1=4， n2=7∴n 1× n2=4× 7=28．。

历届“希望杯”全国数学邀请赛问题精选详析(高二)题1 已知y x a b b y b b a x b a ,,,,0则--=-+=<<的大小关系是 .（第十一届高二第一试第11题）解法1 b b a a b b a x ++=-+=，ab b aa b b y -+=--=.y x a b b b b a b a <∴-+>++∴<<,,0 .解法2bb a ab b a b b b b a y x ++-+=---+=，y x y x a b b a <∴<∴->+,1, . 解法3a ab b a b b a ab b b b a y x -+-++=----+=-1111 =y x yx a a b b a <∴>-∴>--+,011,0.解法4 原问题等价于比较a b b a -++与b 2的大小.由,2)(222y x y x +≥+得b a b b a a b b a 4)(2)2=-++≤-++（，b a b b a 2≤-++∴. y x b a b b a a b b a <∴<-++∴-≠+,2, .解法5 如图1，在函数x y =的图象上取三个不同的点A （a b -，a b -）、B （b ，b ）、C （b a +，b a +）由图象，显然有AB BC k k <，即)()(a b b a b b b b a b b a ----<-+-+， 即a b b b b a --<-+，亦即y x <.解法6 令()f t =，tt a at f ++=)( 单调递减，而a b b ->，)()(a b f b f -<∴，即a b b b b a --<-+，y x <∴.解法7 考虑等轴双曲线)0(22>=-x a y x . 如图2，其渐近线为x y =.在双曲线上取两点图1A （b ，a b -）、B （a b +，b ）. 由图形，显然有1>ABk ，即1>-+--bb a ab b ，从而y x <.解法8 如图3.在Rt △ABC 中，∠C 为直角，BC=a ，AC=b ，BD=b ，则AB=b a +，DC=a b -. 在△ABD 中，AB-AD<BD ，即-+b a AD b <，从而-+b a AD-DC<-b DC ，即a b b b b a --<-+，故y x <.评析 比较大小是中学代数中的常见内容.其最基本的方法是作差比较法、作商比较法、利用函数的单调性.解法1通过分子有理化（处理无理式常用此法）将问题转化成比较两个分母的大小.解法2直接作商与1比较大小，顺理成章，也很简洁.要注意的是：0,>b a 时，1a a b b >⇔>；0,<b a 时，1aa b b>⇔<.此题直接作差难以确定差与0的大小，解法3对y x ,的倒数作差再与0比较大小，使得问题顺利获解，反映了思维的灵活性.解法6运用函数的单调性解题，构造一个什么样的函数是关键.我们认为构造的函数应使得y x ,恰为其两个函数值，且该函数还应是单调的（最起码在包含y x ,对应的自变量值的某区间上是单调的）.解法5与解法7分别构造函数与解几模型，将y x ,的大小关系问题转化成斜率问题加以解决，充分沟通了代数与几何之间的内在联系，可谓创新解法.解法8充分挖掘代数式的几何背景，构造平面图形，直观地使问题得到解决，这也是解决大小关系问题和证明不等式的常用方法.有人对此题作出如下解答：取,2,1==b a 则12112,23123+=-=+=-=y x，>10+>，.,121231y x <∴+<+可再取两组特殊值验证，都有y x <.故答案为y x <.从逻辑上讲，取2,1==b a ，得y x <.即使再取无论多少组值（也只能是有限组值）验证，都得y x <，也只能说明y x >或y x ≥作为答案是错误的，而不能说明y x <一定是正确的,因为这不能排除x y =的可能性.因此答案虽然正确，但解法是没有根据的.当然，如果将题目改为选择题：图2图3已知y x a b b y b b a x b a ,,,,0则--=-+=<<的大小关系是 （ ） A 、y x > B 、y x ≥ C 、y x = D 、y x <此时用上述解法，且不用再取特殊值验证就可选D ，并且方法简单，答案一定正确.总而言之，特殊值法在解许多选择题时显得特别简捷，那是因为选择支中的正确答案是唯一的，从而通过特殊值排除干扰支，进而选出正确答案.但特殊值法只能排除错误结论，而不能直接肯定正确答案，因此，用此法解填空题（少数特例除外）与解答题是没有根据的.当然，利用特殊值指明解题方向还是十分可取的.题2 设c b a >>N n ∈,，且11na b b c a c+≥---恒成立，则n 的最大值为 （ ） A 、2 B 、3 C 、4 D 、5（第十一届高二第一试第7题） 解法1 原式n c b c a b a c a ≥--+--⇔．mina c a c n ab bc --⎡⎤∴≤+⎢⎥--⎣⎦．而b a c a --+c b c a -- =b ac b b a --+-+b c a b b c -+--=2+b a c b --+c b b a --≥4，且当b ac b --=cb ba --，即bc a 2=+时取等号．mina c a c ab bc --⎡⎤∴+⎢⎥--⎣⎦4=．4n ∴≤．故选C ． 解法2 c b a >>，0,0,0>->->-∴c a c b b a ，已知不等式化为()()()2a c n a b b c -≤--．由()()()()22242a c a c ab bc a b b c --≥=---+-⎛⎫⎪⎝⎭，即()()()4min2=⎥⎦⎤⎢⎣⎡---c b b a c a ，故由已知得4≤n ，选C ．解法3 由c b a >>，知0,0,0>->->-c a c b b a ，有()⎪⎭⎫⎝⎛-+--≤c b b a c a n 11．又()()()[]()41111112=+≥⎪⎭⎫ ⎝⎛-+--+-=⎪⎭⎫⎝⎛-+--c b b a c b b a c b b a c a ，即()411min=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+--c b b a c a ，由题意，4≤n ．故选C ．解法4 c b a >>，0,0,0>->->-∴c a c b b a ．∴已知不等式可变形为()()()2a c n a b b c -≤--．记()()()2a c k ab bc -=--，则()()[]()()()()[]()()4222=----≥---+-=c b b a c b b a c b b a c b b a k ．由题意，4≤n ．故选C ．解法5 c b a >>110,0.a b b c∴>>--于是 ()()ca cb b ac b b a -=-+-≥-+-4411．比较得4≤n ．故选C ． 评析 由已知，可得()⎪⎭⎫⎝⎛-+--≤c b b a c a n 11恒成立．根据常识“若()a f x ≤恒成立，则()min x f a ≤；若()x f a ≥恒成立，则()max a f x ≥,”()⎪⎭⎫⎝⎛-+--c b b a c a 11的最小值就是所求n 的最大值，故问题转化为求()⎪⎭⎫⎝⎛-+--c b b a c a 11的最小值，上述各种解法都是围绕这一中心的，不过采用了不同的变形技巧，使用了不同的基本不等式而已．解法1运用了2,,b a a b R a b ++≥∈“”；解法2运用了”“22⎪⎭⎫⎝⎛+≤b a ab ；解法3运用了()”“411≥⎪⎭⎫ ⎝⎛++b a b a ；解法4运用了()”“+∈≥+R b a ab b a ,2；解法5运用了()”“+∈+≥+R b a ba b a ,411．虽解法异彩纷呈，但却殊途同归．此题使我们联想到最新高中数学第二册（上）P 30第8题： 已知c b a >>，求证：0111>-+-+-ac c b b a ． 证：令()0,0,>>=-=-y x y c b x b a ，则y x c a +=-．()22111111x y xya b b c c a x y x y xy x y ++∴++=+-=---++．0,0x y >> ， 0111>-+-+-∴ac c b b a ． 此证法通过换元将分母中的多项式改写成单项式，使得推证更简单了．运用这一思路，又可得本赛题如下解法：设()0,0,>>=-=-y x y c b x b a ，则y x c a +=-．ca nc b b a -≥-+-11恒成立，就是y x ny x +≥+11恒成立．也就是()⎪⎪⎭⎫ ⎝⎛++≤y x y x n 11恒成立．()411≥⎪⎪⎭⎫ ⎝⎛++y x y x 恒成立， ∴由题意得4≤n ．故选C ．再看一个运用这一思想解题的例子．例 设+∈R c b a ,,，求证：2222cb a b ac a c b c b a ++≥+++++． （第二届“友谊杯”国际数学竞赛题）证明 设,,,z b a y a c x c b =+=+=+则()()0,,21>++=++z y x z y x c b a ． ()()()02222≥+-=++-+y x xy bx ay y x b a y b x a ，()222a b a b x y x y+∴+≥+ ①， ()()()()222222222a b a b c a b c a b c c a b c x y z x y z x y z a b c +++++++∴++≥+≥==+++++,即 2222cb a zc y b x a ++≥++，2222c b a b a c a c b c b a ++≥+++++∴． 本赛题还可直接由下面的命题得解．命题 若021>>>>n a a a ，则()nn n a a n a a a a a a --≥-++-+--12132211111 ． 证明 021>>>>n a a a ，n n a a a a a a ---∴-13221,,, 都大于0．反复运用①式，可得: “若,(1,2,,)i i x y R i n +∈= ,则22111n i ni i ni iii x x y y ===⎛⎫⎪⎝⎭≥∑∑∑,当且仅当1212n n x x x y y y === 时取等号”.故有()()22122311223111111111n n n n nn a a a a a a a a a a a a a a --+++-+++≥=----+-++-- ．也可以这样证明：021>>>>n a a a ，12231,,,0n n a a a a a a -∴---> ．故由柯西不等式，得 ()()()1223112231111()n n n na a a a a a a a a a a a --+++-+-++-⎡⎤⎣⎦--- ()()211111n -≥+++ 个()21n =-，即()()21132211)111(-≥--++-+--n a a a a a a a a n nn ．01>-n a a ，()nn n a a n a a a a a a --≥-++-+-∴-12132211111 ． 由此可得本赛题的如下解法：c b a >>，0,0,0>->->-∴c a c b b a ，()ca cb b ac b b a -=-+-+≥-+-∴411112．由 题意，4≤n ．故选C ．由此命题还可直接解决第七届高二培训题第8题：设12320002001a a a a a >>>>> ，并且122320002001111m a a a a a a =+++--- ，200116104a a n -⨯=，则m 与n 的大小关系是 ( ) A 、n m < B 、n m > C 、n m ≥ D 、n m ≤ 解 12320002001a a a a a >>>>> ，2001162001121042000a a a a m -⨯=-≥∴．故选C ． 题3 设实数y x n m ,,,满足a n m =+22，b y x =+22，则ny mx +的最大值为 ( )A 、21()b a +B 、2122b a + C 、222b a + D 、ab（第十一届高二培训题第5题）解法1 设,sin ,cos ααa n a m ==,sin ,cos ββb y b x ==则,)cos(sin sin cos cos ab ab ab ab ny mx ≤-=+=+βαβαβα即)(ny mx +max =ab .故选D ．解法2 b n a b m a b a n m =+⇒=+2222,又b y x =+22,+=+∴mx abny mx a b )( ≤ny ab 2222()()2b m n x y a +++==.2b b a a b =+⋅mx +∴,ab ab b =≤x =,y =即my nx =时取等号，max )ny mx +∴（.ab = 解法3 2222222222222()2mx ny m x mxny n y m x m y n x n y +=++≤+++()()2222,m n x y ab =++=mx ny ∴+当且仅当m yn x =时取等号，故()max mx ny +=解法4 设()(),,,,p m n q x y →→==则cos ,p q p q p q θ→→→→→→⋅=⋅⋅≤⋅222,p q p q →→→→∴⋅≤⋅()()222mx ny m n+≤+即()22,xyab +=当且仅当,p q →→共线，即my nx =时取等号，故()max mx ny +=解法5 若设mx ny k +=，则直线mx ny k +=与圆22x y b +=有公共点，于是≤()max k mx ny mx ny =+≤+=解法6 设12,z m ni z x yi =+=-,则()()()()12,z z m ni x yi mx ny nx my i =+⋅-=++-∴1212,z z mx ny mx ny mx ny z z ⋅=≥=+≥+∴+≤12z z =⋅==当且仅当my nx=时取等号，故()max mx ny += 解法7 构造函数()()()222222f X m n X mx ny X x y =+++++，则()()()220.f X mX x nX y =+++≥故()()()2222244mx ny m nxy ∆=+-++()2440,mx ny ab =+-≤即()max mx ny mx ny +≤∴+.ab =解法8 由2222,m n a x y b +=+=还可构造图形（如图），其中90,ACB ADB ︒∠=∠=,AC=,BC n =,,BD x AD y AB ===为圆的直径，由托勒密定理,ADBC BD AC ⋅+⋅2,AB CD AB =⋅≤得,x n y b ⋅+⋅≤，从而得mx ny +，当且仅当my nx =且0mx >时取等号．()max mx ny ∴+=评析 解法1抓住已知条件式的结构特征，运用三角代换法，合情合理，自然流畅，也是解决此类型问题的通法之一．解法2运用基本不等式222b a ab +≤将ny mx +放大为关于22n m +与22y x +的式子，再利用条件求出最大值．值得注意的是，稍不注意，就会得出下面的错误解法：()()()22222222max ,22222m n x y m x n y a b a bmx ny mx ny ++++++++≤+==∴+=．故选A ．错误的原因就在于用基本不等式求最值时未考虑等号能否取到．上述不等式取等号的条件是x a =①且y b =②，而若①，②式同时取得，则2222m n x y +=+，即,a b =这与题设矛盾！即当a b ≠时，mx ny +取不到2a b+．解法2是避免这种错误的有效方法． 由于向量与复数的模的平方是平方和形式，与已知形式一致，故解法4与解法6分别运用了构造向量与构造复数的方法，新颖而简洁．解法5设k ny mx =+后，将其看作动直线，利用该直线与定圆b y x =+22有公共点，则圆心到直线的距离小于等于半径，得ab ny mx k ≤+=，充分体现了等价转化的解题功能．解法7运用的是构造函数法．为什么构造函数()()()2222f X m n X mx ny X =+++2x +2y +呢？主要基于两点：①()f X 为非负式（值大于等于0），②由于()0≥X f ，故有0≤∆，而∆沟通了已知与未知的关系，故使问题得到解决．解法8抓住已知两条件式的特征，构造了两个有公共边的直角三角形，利用托勒密定理及圆的弦小于等于半径使问题获解，充分揭示了这一代数问题的几何背景．拓展 此题可作如下推广 若2222221212,,n n a a a p b b b q +++=+++= 则()1122max n n a b a b a b +++=()1,2,,i i b i n == 时取得最大值）.证明 2222221212n n a a a p ⎫⎫⎫+++=⇒+++⎪⎪⎪⎪⎪⎪⎭⎭⎭.q =1122a b a b ∴+++1122n n n n a b b b b ⎫=⋅+⋅++⋅⎪⎪⎭≤+⎢⎥⎢⎥⎣⎦=(),22222222122221pq q p p q q p b b b a a a pq q p n n=⎪⎪⎪⎪⎭⎫⎝⎛+⋅=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++++++ 当且仅当()().,,2,1max 2211pq b a b a b a n i b a pqn n i i =+++∴== 时取等号，本推广实际就是由著名的Cauchy （柯西）不等式()()()222212222122211n n n n b b b a a a b a b a b a +++⋅+++≤+++ （当且仅当nn b a b a b a === 2211时取等号）直接得到的一个结论． 推广有十分广泛的应用，现举一例： 例 已知123,,,,,,234,8.a b c x y z R a b c x y z +∈++=++=且最大值． 解2221232344,8a b c b cx y z ++==++=22⇒+2+＝8=≤====即12ax by cz ===时取等号．max∴=.24题4 对于1≤m 的一切实数m ，使不等式221(1)x m x ->-都成立的实数x 的取值范围是＿＿＿＿（第十三届高二培训题第63题）解法1 题设等价于⎪⎩⎪⎨⎧--<>-1120122x x m x 或⎪⎩⎪⎨⎧--><-1120122x x m x 或⎩⎨⎧>-=-012012x x ，即⎪⎩⎪⎨⎧--<>-11210122x x x 或⎪⎩⎪⎨⎧-->-<-11210122x x x 或⎩⎨⎧>-=-012012x x ,所以21<<x 或113<<-x 或1=x ，即)2,13(-∈x . 解法2 已知不等式即()()01212<---x m x ，令()()121)(2---=x m x m f ，则当012≠-x ，即1±≠x 时，)(m f 是m 的一次函数，因为1≤m ，即11≤≤-m 时不等式恒成立，所以)(m f 在[]1,1-上的图象恒在m 轴的下方，故有⎩⎨⎧<+--=<+-+-=-0121)1(0121)1(22x x f x x f ，即⎩⎨⎧<->-+0202222x x x x ，解得213<<-x )1(≠x . 又当1=x 时，1)(-=m f ，适合题意，当1-=x 时，()3f m =不合题意. 故x 的取值范围是213<<-x .评析 解决本题的关键是如何根据条件构建关于x 的不等式或不等式组.解法1运用分离参数法，为了达到分离参数的目的，又对12-x 分大于0、小于0、等于0三类情形分别构建关于x 的不等式组，从而通过解不等式组解决了问题.解法2则转换思维角度，把已知不等式看成关于m 的不等式，从而将原问题转化为函数()()121)(2---=x m x m f 在[]1,1-上的图象恒在m 轴下方的问题.这种方法称为变更主元法.用此方法，使得此题的解决显得既简捷，又直观易懂.题5 当0x a <<时,不等式2)(1122≥-+x a x 恒成立,则a 的最大值是________. (第十一届高二培训题第45题)解法 1 当0x a <<时, 2≥-+-x a x x x a ①,又有2)()(2222≥-+-x a x x x a ②, ②+①×2,得6)(222222≥--+-x a x ax x x a ,6)()(122222≥---+-x a x a a x a ,8)(2222≥-+x a a x a ,即2228)(11a x a x ≥-+.由282≥a ,得02a <≤,2max =∴a . 解法2 2222)11()11()(112x a x x a x x a x--+-+=⎥⎦⎤⎢⎣⎡-+ , 又 =-+x a x 11 +a 4 (1a 2)x a x x x a ---, 222)4()(112a x a x ≥⎥⎦⎤⎢⎣⎡-+∴, 即2228)(11a x a x ≥-+, 当且仅当x a x xxa -=- 且 x a x -=11, 即 2a x = 时取等号. 2)(1122≥-+x a x 恒成立, ∴282,02a a ≥<≤. 于是2max =a . 解法 3 原不等式等价于12)(1122≥-+x a x ,由 0x a <<,可知10,x >10a x >-. 由 “两个正数的平方平均值不小于它们的调和平均值”, 可知只需1)(2≥-+x a x , 即2≤a 即可, 故02a <≤, 于是2max =a .解法 422)(11x a x -+2≥ 即 2)(112222≥⎥⎦⎤⎢⎣⎡--++x x a x x ①成立，又2122≥+x x 恒成立， ∴a 只要满足22)(1x x a --0≥②就能使①恒成立.由②式，得2x 2)(x a -1≤，1)(≤-x a x ，012≤-+-ax x ③.由于对称轴),0(2a ax ∈=，由二次函数的性质，当),0(a x ∈时，要③式恒成立，则24002a a ∆=-≤∴<≤ 2max =∴a .解法5 设αα22sin ,cos =-=a x a a x （0x a <<），则22)(11x a x -+=α42cos 1a +α42sin 1a ==+⋅αααα44442cos sin cos sin 1a =-⋅αα2sin 1612sin 2111422aαα2sin 2sin 28422-⋅a . )22(sin 2+αα2(sin 2－1）0≤，即2－αα2sin 2sin 42≥，则αα2sin 2sin 242-1≥)12sin (2时取等号当=α，于是2228)(11ax a x ≥-+，由已知，得282,02,a a ≥∴<≤2max =∴a . 解法6 设11,(0,0),X Y X Y x a x==>>-则 222X Y +≥表示在XOY 坐标系第一象限内以原点为圆心，2为半径的圆及其外部.由11,,X Y x a x==-得,aXY X Y =+又aXY X Y =+,4,22aXY XY ≥∴≥它表示双曲线24a XY =位于第一象限内的一支及其上方部分.依题意，双曲线2224(0)200XY X X Y X Y a=>+=>>与圆弧（，）相切或相离，从而282≥a，即02a <≤ 2max =∴a .解法7 运用结论“如果),,2,1(,n i R y x i i =∈+，则≥+++nn y x y x y x 2222121),()(21221*++++++nn y y y x x x 当且仅当k y x y xy x n n ==== 2211（常数）时取等号.” 0x a <<，∴0.a x ->由柯西不等式，有22222)11())(11)(11(x a x x a x -+≥-++①，由)(*得x a x -+11a 4≥②.故,)4())(11(2222a x a x ≥-+得2228)(11ax a x ≥-+，当且仅当2a x =时取等号，由282≥a，得02a <≤ 2max =∴a . 解法8 运用结论“212122311111(1),,n n n nn a a a a a a a a a a a -->>>+++≥---- 若则当O2 xO且仅当n a a a ,,,21 成等差数列时取等号.”2222111122()(0)()x a x x a x ⎡⎤⎡⎤+=+≥⎢⎥⎢⎥---⎣⎦⎣⎦2110x a x ⎛⎫+ ⎪--⎝⎭222160)13(a a =⎥⎦⎤⎢⎣⎡--≥.∴2228)(11a x a x ≥-+，当且仅当x a x -=，即2a x =时取等号.令282≥a ，得02a <≤ 2max =∴a . 评析2)(1122≥-+x a x 恒成立，∴2)(11m i n 22≥⎥⎦⎤⎢⎣⎡-+x a x.故问题的实质就是求22)(11x a x -+的最小值（关于a 的式子）大于等于2的解.因而在0x a <<的条件下，如何求22)(11x a x -+的最小值成了问题的关键.解法1运用“两个互为倒数的正数的和大于等于2”, 解法2运用配方再放缩, 解法3运用均值不等式及“两个正数的平方平均值不小于它们的调和平均值”,解法5运用三角代换，解决了这一关键问题.解法4巧妙地将原问题转化为一个含参（a ）一元二次不等式恒成立，求参数的范围问题，从而运用二次函数的性质解决问题.解法6将原问题转化为解析几何问题处理.解法7、8则是运用一些现成的结论（读者可自己证明），各种解法异彩纷呈，都值得细细品味.拓展 此题可作如下推广：推广1 若1210n x x x a -<<<<< ，则≥-++-+-2121221)(1)(11n x a x x x 23a n ，当且仅当a x x x n ,,,,121- 成等差数列时取等号.证明 由已知，1210n x x x a -<<<<< ，则12x x -0>，23x x -0>，, 1--n x a 0>.根据柯西不等式及解法7运用的不等式（*）,有⎥⎦⎤⎢⎣⎡-++-+-2121221)(1)(11n x a x x x n ≥21211111n x x x a x -⎛⎫+++≥ ⎪--⎝⎭ 2242,n n a a ⎛⎫= ⎪⎝⎭故≥-++-+-2121221)(1)(11n x a x x x 23a n . 当且仅当a x x x n ,,,,121- 成等差数列时取等号.推广2 若1210n x x x a -<<<<< ，,),,,2,1(++∈=∈N k n i R b i 则++kk x b 111kk n k n k n k k ab b b x a b x x b 121111212)()()(+-+++++≥-++- ，当且仅当∑==n i ii i b ab a 1时取等号. 证明 不妨设112211,,,--=-==n n x a a x x a x a ，=M ,)(11+=∑k ni i b 由已知得i a 0>且),,2,1(n i =,1a a ni i =∑=令a a c i i =，则∑=ni i c 1=111=∑=ni i a a .由均值不等式，++k i k i c b 1≥+++个k i i i Mc Mc Mc ,)1(11+++k k ik b M k 即k ik i c b1+k n i b b b k kMc ))(1(21++++≥+ i b ⋅，则11111(1)()k nn n k i i i k i i i i b kM c k b c ++===+≥+∴∑∑∑1111()k n n k i i k i i i b b c ++==≥∑∑，即11k nki k i ib a a +=≥∑11()n k i i b +=∑，11111()nk k i ni i k k n i ii i b b a a ++===≥⎛⎫ ⎪⎝⎭∑∑∑，当且仅当=i a ∑∑∑====⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n i i i i n i i n i i b ab b b a 111时取等号. ∴++kk x b 111++kk x b 212kn kn x a b )(1--+ k k n a b b b 121)(++++≥ . 题6 已知()⎪⎭⎫ ⎝⎛∈=2,0,log sin πθθx x f ，设⎪⎭⎫ ⎝⎛+=2cos sin θθf a ，()θθcos sin ⋅=fb ，⎪⎭⎫⎝⎛+=θθθcos sin 2sin f c ，那么c b a 、、的大小关系是 （ ）A 、b c a ≤≤B 、a c b ≤≤C 、a b c ≤≤D 、c b a ≤≤（第八届高二第一试第10题） 解法1 设p =θsin ，q =θcos .pq qp ≥+2，而()x f 是减函数，()pq fq p f ≤⎪⎭⎫ ⎝⎛+∴2，即b a ≤.2qp pq +≤，()2pq q p pq +≤∴， pq qp pq≤+2.()pq fq p pq f ≥⎪⎪⎭⎫⎝⎛+∴2，即b c ≥.故c b a ≤≤.选D.解法2 由题意，令6πθ=，则21sin =θ，cos 2θ=，4312cos sin +=+θθ ，23cos sin 4=θθ，233cos sin cos sin 2cos sin 2sin -=+=+θθθθθθθ，()1,021sin ∈=θ ，()x f ∴是减函数，又233234314->>+，()⎪⎭⎫⎝⎛+<<⎪⎭⎫⎝⎛+∴θθθθθθθcos sin 2sin cos sin 2cos sin f ff ，即c b a <<.故选D.评析 这是一个比较函数值大小的问题，通常利用函数的单调性.若函数()x f 单调递增（减），则当21x x <时，()()()()()2121x f x f x f x f ><，当21x x >时，()()21x f x f >()()()21x f x f <.因此解决问题的关键有两个：一是确定函数的单调性，二是确定自变量的大小关系.解法1就是这样解决问题的.因为正确答案应对一切⎪⎭⎫ ⎝⎛∈2,0πθ都正确，故又可以运用特殊值法.对⎪⎭⎫⎝⎛2,0π内的某个角不正确的选择支都是错误的，由正确选择支的唯一性，也可选出正确答案.解法2便是取特殊值6πθ=，排除了A 、B 、C 、而选D 的.当然，此题也可用作差比较法来解：⎪⎭⎫⎝⎛∈2,0πθ ，()1,0sin ∈∴θ，()x f ∴是单调减函数，0sin >θ，0cos >θ.=⋅-+=-∴θθθθθθcos sin log 2cos sin log sin sin b a01log cos sin 2cos sin log sin sin =≤⋅+θθθθθθ，b a ≤∴.又-⋅=-θθθcos sin log sin c b 01log cos sin 2cos sin log cos sin cos sin 2cos sin log cos sin 2sin log sin sin sin sin =≤+=+⋅=+θθθθθθθθθθθθθθθθθ，即c b ≤，c b a ≤≤∴.选D.题7 已知21=a ，不等式49321log <⎪⎭⎫ ⎝⎛-x a的解是 . （第三届高二第二试第13题）解 原不等式即2log 32321-⎪⎭⎫ ⎝⎛<⎪⎭⎫⎝⎛-x a. 指数函数x⎪⎭⎫⎝⎛32是减函数，21=a ，∴原不等式化为2log121->-x ，即22121121l o gl o g -⎪⎪⎭⎫⎝⎛->x .又 对数函数l o g x 是减函数，2211-⎪⎭⎫⎝⎛<-∴x ，即21<-x ，解得31<<-x . 对数函数121log-x 的定义域是1≠x 的实数，∴原不等式的解是11<<-x 或31<<x .评析 此题涉及到指数不等式、对数不等式、绝对值不等式的解法.解指数不等式与对数不等式的基本方法是同底法，即先将不等式两边的指数式或对数式化成底数相同的指数式或对数式，然后根据底数所属区间是()1,0或()+∞,1，确定以该底数为底的指数函数或对数函数的单调性，再去掉底数或对数符号，转化成别的不等式.主要依据如下：⑴若01a <<,则()()()()f x g x aa f x g x <⇔>；⑵若1a >,则()()()()f x g x a a f x g x <⇔<；⑶若01a <<,则()()()()log log 0f x g x aa f x g x <⇔>>；⑷若1a >,则()()()()log log 0f x g x a a f x g x <⇔<<.有时需要将常数化为指数式或对数式，其化法如下： ⑴ac ca log =（,0,0>>c a 且1≠c ）；（化为指数式）⑵log a c a c =（,0>c 且1≠c ）.（化为对数式） 例如，23log 32=将常数2化为3为底的指数式，233log 2=将常数2化为3为底的对数式.解指数不等式不需检验，但解对数不等式必须保证解使得对数式有意义，这点常被忽略. 若一个指数不等式的指数部分是对数式，常常采用取对数法求解. 例 不等式()x x x>lg的解集是 .（第十一届高二培训题第40题）解 两边取常用对数，得()x x lg lg 2>，即0lg ,0lg 4lg ,0lg lg 4122<>->-x x x x x 或10,4lg <<∴>x x 或410>x .故所求解集是()()+∞,101,04 .应当指出，两边取对数后，不等号的方向变不变，关键看取的是什么底数.如果底数大于1，则不等号方向不变，如果底数大于0且小于1，则不等号方向改变.关于绝对值不等式，主要是根据绝对值的几何意义求解.下列结论应当理解并熟记（a 为常数）.⑴()0≤<a a x 的解集是φ； ⑵()0><a a x 的解集是()a a ,-； ⑶()0<>a a x 的解集是R ；⑷()0x a a >>的解集是()()+∞-∞-,,a a . 下列题目供练习：⑴已知常数⎪⎭⎫⎝⎛∈4,0πθ，则不等式()()8103cot tan 2--->x x x θθ的解集是 .（第八届高二第一试第16题）⑵若函数()⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛=4222log log x xx f 的定义域是不等式211222log 7log 30x x ⎛⎫++≤ ⎪⎝⎭的解集，则()x f 的最小值= ；最大值= .（第十届高二第一试第23题）⑶不等式22222log 2log x x x x x x ++>的解集是 .（第九届高二培训题第23题）⑷不等式1323>--x 的解是 （ ）（A ）6>x 或232<≤x （B ）6>x 或2<x （C ）6>x （D ）2<x答案 ⑴(]⎪⎭⎫⎢⎣⎡-∞-1374,52, ⑵43 ；2 ⑶⎪⎭⎫⎝⎛2,21 ⑷A题8 不等式t x x +≥-21 的解集是∅ ,实数t 的取值范围(用区间形式)是 .(第一届高二第一试第18题)解法1 由t x x +=-21两边平方并整理得012222=-++t tx x ,此方程无实根,故()084184222<+-=--=∆t t t ,22>t .又0>t ,2>∴t .故填()+∞,2.解法2 作出函数21x y -=的图象(即图中的半圆)及函数t x y +=的图象(即图中斜率为1的直线系).由题意,直线应在半圆的上方,由图象可知直线t x y +=在y 轴上的截距2>t .故填()+∞,2.解法3 由012≥-x ,得11≤≤-x .故设θc o s =x ,[]πθ,0∈,则已知不等式就是t +≥θθcos sin ,即θθcos sin -≤t .⎪⎭⎫ ⎝⎛-=-4sin 2cos sin πθθθ ,又⎥⎦⎤⎢⎣⎡-∈⎪⎭⎫ ⎝⎛-43,44πππθ,()sin cos [θθ∴-∈-.由题意得2>t . 故填()+∞,2.评析 这是一道蕴含着丰富数学思想方法的好题.解法1﹑2﹑3分别运用方程思想﹑数形结合思想﹑化归转换思想,从不同的角度解决了问题,体现了这道题的丰富内涵.解法2揭示了本题的几何背景.解法3的依据是:不等式t x x +≥-21 的解集是∅等价于不等式x x t -->21恒成立.有人认为不等式t x x +≥-21 的解集是∅等价于不等式x x t -->21有解,这种观点是错误的.事实上,21=t 时,不等式x x t -->21就有解(比如53=x 就是其一个解),而21=t 时,不等式t x x +≥-21即2112+≥-x x 的解集却不是∅ (比如0就是它的一个解).拓展 通过上面的分析,并作进一步的研究,我们便有下面的 结论 已知t 为参数, ()f x 的值域是[],a b . (1) 若()t f x ≤恒成立,则t a ≤. (2) 若()t f x ≥恒成立,则t b ≥. (3) 若()t f x ≤的解集是∅,则t b >. (4) 若()t f x ≥的解集是∅,则t a <. (5) 若()t f x ≤有解,则t b ≤. (6) 若()t f x ≥有解,则t a ≥.若将()f x 的值域改为[),a b 、(],a b 、(),a b 等，也会有相应的结论，限于篇幅，不再一一列出．根据这一结论，请回答下列问题：1.t +的解集是∅，则实数t 的取值范围是 ． 2.t +的解集是∅，则实数t 的取值范围是 ． 3.t +有解，则实数t 的取值范围是 ． 4.t +有解，则实数t 的取值范围是 ． 5.t >+恒成立，则实数t 的取值范围是 ． 6.t +恒成立，则实数t 的取值范围是 ．答案 1. ()2,+∞2.(,-∞3.)⎡+∞⎣4.(],2-∞5.(,-∞6.()2,+∞题9 不等式03422≥+---x x x 的解集是 （ ）A 、⎥⎦⎤⎢⎣⎡++255,253B 、⎥⎦⎤⎢⎣⎡+-255,253 C 、⎪⎪⎭⎫⎢⎣⎡+∞+⎥⎦⎤ ⎝⎛+∞-,255253,D 、⎥⎦⎤⎢⎣⎡+-253,255 （第十三届高二第二试第8题）解法 1 当0342≥+-x x ，即1≤x 或3≥x 时，原不等式就是,03422≥-+--x x x 即0552≤+-x x ，解得2553.255255+≤≤∴+≤≤-x x . 当2430,13x x x -+<即<<时，原不等式就是，03422≥+-+-x x x 即，0132≥+-x x 解得253-≤x或3x x ≥≤<.综上，所求解集为,⎫⎡⎪⎢⎪⎣⎭⎣⎦ 即⎥⎦⎤⎢⎣⎡++255,253.故选A.解法2 如图，作函数2-=x y 和342+-=x x y 的图象.要求的解集就是21y y ≥，即1y 在2y 上方时x 的区间，即图中线段AB 上的点所对应的横坐标所组成的区间[]B A x x ,. 又(),1234222--=+-=x x x y 当32<<x 时，().2122--=x y 由()2212-=--x x 可解得253+=A x .当3>x 时，(),1222--=x y 由()2122-=--x x 可解得255+=Bx ，∴所求不等式的解集为⎥⎦⎤⎢⎣⎡++255,253，故选A. 解法 3 同解法2画出图形后，可知解集为一个闭区间[]b a ,，且()3,2∈a ，对照 选择支.可知选A.解法4 当5.1=x 时，03422<+---x x x 时，故1.5不是原不等式的解，从而排除含1.5的B 、C 、D ，故选A.评析 解含绝对值的不等式，一般是先去掉绝对值符号，然后再求解.解法1正是运用分类讨论思想这样解决问题的，也是一种通法.我们知道，方程()()x g x f =的解就是函数()x f y =与()x g y =的图象交点的横坐标；若图象无交点，则方程无解.而不等式()()x g x f >的解集则是函数()x f y =的图象在()x g y =的图象上方部分的点的横坐标的集合；若()x f y =的图象都不在()x g y =的图象的上方，则不等式无解.解法2正是运用这种数形结合思想解决问题的.许多超越不等式的近似解或解的所属范围也都运用此法解决.选择题的正确答案就在选择支中，只是要求我们把它选出来而已.因此,不是非要求出答案再对照选择支选择答案不可的.基于此，解法3运用估算的方法选出了正确答案(注意：估算能力是高考明确要求要考查的能力之一).而解法4则运用特殊值排除了干扰支，进而选出了正确答案.类似这种不等式（方程）的解集是什么的选择题几乎都可用这种方法解，而且十分方便.值得注意的是，特殊值只能否定错误结论，根据正确选择支的唯一性才能肯定正确答案.另外，如何选取特殊值也是很有讲究的，读者可在解题实践中体会并加以总结.题10 不等式199920003224>-+-x x 的解集是 . 1 3 A B（第十一届高二培训题第41题）解 设y=x x -+-3224 ，由⎩⎨⎧≥-≥-03024x x ，得定义域为[21，3]. 1999200010,106144410)3)(24(4)3(42422>≥∴≥-+-+=--+-+-=y x x x x x x y 即原不等式在定义域内恒成立，故所求解集为[21，3]. 评析 解无理不等式，通常是通过乘方去掉根号，化为有理不等式后再解.但从此题中不等式右边的数可以想象该有多么复杂，若将题目改为“276.571623.93224+>-+-πx x 的解集是 ”，还会有谁想通过平方化为有理不等式去解呢？显然，常规方法已难以解决问题，怎么办呢？考虑到不等式中的x ∈[21，3]，从而左边1999200010>≥，故解集就是定义域，这就启示我们，当常规思维受阻或难以奏效时，就应积极开展非常规思维，另辟蹊径，寻求解决问题的新方法.拓展 根据上面的分析，并加以拓广，我们可得结论 设a,b,c 是常数，若[,],()[,],()[,]x a b f x m n g x p q ∈∈∈,则当m c >时,不等式()f x c >的解集是[,],()a b f x c ≤的解集是φ；当n c <时, 不等式()f x c ≥的解集是φ,()f x c <的解集是[,]a b ;当n p >时, 不等式()()f x g x ≥的解集是φ, ()()f x g x <的解集是[,]a b ;当m q >时，不等式()()f x g x >的解集是[,]a b ，()()f x g x ≤的解集是φ.根据这一结论，不难求得下列不等式的解集：1、 2sinx+3cosx>4;2、 322163-->-x x ;3、 x x x -<-+-433)1(log 4;4、 sinx-cosx<32+x .答案：1、φ 2、[2，+∞) 3、φ 4、R。

数学希望杯初二试题及答案一、选择题（每题2分，共20分）1. 下列哪个数是正整数？A. -5B. 0C. 2D. -22. 如果\( a \)和\( b \)是互质数，那么\( a \times b \)的最小公倍数是：A. \( a \)B. \( b \)C. \( a + b \)D. \( a \times b \)3. 一个长方形的长是宽的两倍，如果宽是\( x \)米，那么长方形的面积是：A. \( x^2 \)B. \( 2x \)C. \( 2x^2 \)D. \( 4x^2 \)4. 一个数的平方根是它自己，这个数是：A. 0B. 1C. -1D. 25. 下列哪个是二次根式？A. \( \sqrt{16} \)B. \( \sqrt{2} \)C. \( 3\sqrt{2} \)D. \( \sqrt{-9} \)6. 一个数的相反数是它自己，这个数是：A. 0B. 1C. -1D. 27. 一个圆的半径是\( r \)，那么它的面积是：A. \( \pi r \)B. \( \pi r^2 \)C. \( 2\pi r \)D. \( \pi r^3 \)8. 一个数的绝对值是它自己，这个数是：A. 0B. 正数C. 负数D. 任意实数9. 一个等腰三角形，两边相等，如果底边是\( a \)，那么它的周长是：A. \( 2a \)B. \( 3a \)C. \( 4a \)D. \( 无法确定 \)10. 如果\( x \)和\( y \)是实数，\( x = y \)，那么下列哪个等式是正确的？A. \( x + 1 = y + 1 \)B. \( x^2 = y^2 \)C. \( x - y = 0 \)D. 所有选项都是正确的二、填空题（每题2分，共20分）11. 一个数的平方根是\( \sqrt{4} \)，那么这个数是______。

12. 如果\( a \)和\( b \)是相反数，那么\( a + b = ______。

2019-2020 学年八年级数学第 21 届“希望杯”第 1 试一试题一、选择题 ( 每题 4 分，共 40 分) 以下每题的四个选项中，仅有一个是正确的，请将正确答案前的英文字母写在下面的表格内。

1. 以下列图案都是由字母 m 组合而成的，其中不是中心对称图形的是(A) (B) (C) (D)2 32. 若 a a 0，则(A)a3a(B)a3 a(C)a 1(D) 0<a <1 。

3. 若代数式2010 x有意义，则 x 的取值范围是| x | 2009(A) x 2010 (B) x 2010，且 x 2009 (C) x 2010，且 x 2009(D) x 2010，且 x 20092 。

4. 正整数 a ， b ， c 是等腰三角形三边的长，并且a bcb ca =24，则这样的三角形有 (A) 1 个 (B) 2 个 (C) 3 个 (D) 4个 。

5. 按次连接一个凸四边形各边的中点，获取一个菱形，则这个四边形必然是(A) 任意的四边形 (B)两条对角线等长的四边形(C) 矩形(D)平行四边形 。

6. 设 = 37a 1 3 7b 137c 1 37d 1a b c da b c d =1p，其中 ， 是正实数，并且， ， ，则(A)p >5(B)p <5(C)p <4 (D)p =5 。

7. Given a ， b ， c satisfyc <b <a and ac <0， then which one is notsure to be correct in the followinginequalities？( A ) b >c(B )b a>0(C ) b 2 > a2(D )a c<0 。

a acccac( 英汉词典： be sure to 确定； correct正确的； inequality不等式 )8. 某公司的员工分别住在 A 、 B 、 C 三个小区， A 区住员工 30 人， B 区住员工 15 人， C 区住员工 10 人，三个小区在一条直线上，地址以下列图。