下载文档原格式
从范畴层次解析唯物史观的逻辑理路:什么是唯物史观的逻辑起点《德意志意识形态》(以下简称《形态》)是马克思恩格斯于1845～1846年合著的在马克思主义发展史上具有划时代意义里程碑性的著作。
哲学界以往的研究角度各异，阐述了许多精辟的见解：最常见最普通的是将它视为唯物史观的充分完整的展述，有学者认为它实现了人的本质观的革命变革，有学者强调人的主体地位在《形态》中是对《提纲》的并非丧失而是真正的回归，有学者则以其价值取向对未来共产主义的现实性作了分析与探讨，还有学者则从社会形态的角度提出了自己的看法，本文拟从《形态》中的范畴层次对马克思哲学的各个有机组成部分进行统一的认识。
列宁曾说：＂范畴是区分(人与自然界)过程中的一些小阶段，即认识世界的过程中的一些小阶段，是帮助我们认识和掌握自然现象之网的网上纽结。
＂任何科学都有自己特定领域里的范畴，范畴的合理性、有效性、规范性，并运用一定方法对范畴及范畴之间的关系进行合理描述及展开便形成科学。
在《形态》第一卷第一章中具有重要性的范畴达三四十个之多。
当然，由于马克思恩格斯世界观刚转变不久，一些范畴用语不太科学、合理，界线模糊，但不妨碍我们解读其中的天才思想。
认识这些范畴的确切内涵，明白它们之间的相互关系，理清它们的层次，对于我们把握马恩形成唯物史观的逻辑理路，了解唯物主义的科学观点和哲学观念，具有重要的理论意义和指导认识作用。
在《序言》中马克思恩格斯指出，德意志意识形态是种种＂关于自己本身，关于自己是何物或自己应当成为何物的虚假观念＂，＂这些哲学英雄们的咩咩叫声只不过是以哲学的形式来重复德国市民的观念＂，＂他们按照自己关于神关于模范人等等观念来建立自己的关系。
＂认为＂思想统治世界，把思想和概念看作是决定性的原则，把一定的思想看作是只有哲学家们才能揭示的物质世界的秘密。
＂这是一种纯粹主观抽象的思辨哲学。
马克思恩格斯觉得有必要揭穿＂这种如此投合于沉溺于幻想的精神萎靡的德国人民口味的哲学斗争＂，以＂使之得不到信任＂。
总结调研的方式方法1. 文献综述：通过查阅相关文献资料，对现有研究进行梳理和总结，了解已有的研究成果与研究方法。
2. 实地调研：到研究对象所在地进行实地考察和观察，收集第一手资料，并对调研对象进行深入了解和交流。
3. 问卷调查：设计并发放问卷，收集受访者的意见、看法和需求，通过统计分析获得调研结果。
4. 深度访谈：选择重要的调研对象进行个别深入交流，了解其专业见解和实际情况，获取更多细节性信息。
5. 专家咨询：邀请相关领域专家进行咨询，获取专业意见和建议，对研究方向和方法进行指导和优化。
6. 网络调研：通过互联网渠道搜集相关数据和资料，分析研究对象在网络上的行为和观点。
7. 归纳总结法：将不同调研方法得到的数据进行集中分析处理，并进行归纳总结，得出结论。
8. 对比分析法：对不同调研来源的数据进行对比分析，找出差异和规律，发现研究对象的特点和问题。
9. 专题研究法：根据调研需求，选定特定的主题进行研究，通过多种方式对该主题进行系统调查。
10. 参与观察法：调研人员融入到调研对象的工作和生活中，进行参与式观察，获取更真实的信息和数据。
11. 抽样调查法：设计合理的样本调查方案，通过对样本数据的收集和分析，推断总体的特征和规律。
12. 反馈验证法：将初步调研结果反馈给调研对象，验证和修正调研数据和结论，确保调研结果的准确性和可信度。
13. 数据挖掘法：运用数据挖掘技术对大量数据进行深入分析，发现隐藏的信息和规律，辅助调研结论的形成。
14. 实验研究法：设置实验条件，观察和测量研究对象在变量变化下的表现，获取特定情境下的实验数据。
15. 代码分析法：对大规模的数字化文本进行编码和分析，分析其中的关键主题、情感倾向等信息。
16. 可视化展示法：通过图表、地图等形式对调研结果进行可视化展示，帮助研究者和受众更直观地理解研究成果。
17. 质性研究法：采用质性研究方法，关注研究对象的内在特点、关系和现象，深入挖掘其背后的含义和机制。
分析报告中的模型应该如何构建在当今数据驱动的时代，分析报告在各个领域都扮演着至关重要的角色。
而一个准确、可靠且有效的分析报告往往依赖于合理构建的模型。
那么，如何构建这样的模型呢？首先，我们需要明确模型的目标和用途。
这是构建模型的基石。
例如，如果我们的目标是预测销售趋势，那么模型就需要重点关注与销售相关的因素，如市场需求、产品特点、竞争对手动态等。
只有清晰地定义了模型的目的，我们才能确定需要收集哪些数据以及如何处理这些数据。
数据的收集和整理是构建模型的关键步骤。
数据就如同建筑材料，质量和数量都会直接影响模型的性能。
我们要确保收集的数据具有代表性、准确性和完整性。
同时，对数据进行清洗和预处理也是必不可少的。
这包括处理缺失值、异常值以及对数据进行标准化或归一化等操作，以确保数据的质量和一致性。
在选择模型类型时，需要综合考虑多种因素。
不同的模型适用于不同的场景和数据特点。
常见的模型类型有线性回归、逻辑回归、决策树、随机森林、神经网络等。
如果数据呈现线性关系，线性回归可能是一个合适的选择；如果数据复杂且非线性，神经网络可能更能发挥作用。
此外，还要考虑模型的可解释性、计算复杂度以及对数据规模的适应性等因素。
确定了模型类型后，接下来就是模型的训练和优化。
在训练过程中，我们需要将数据分为训练集、验证集和测试集。
训练集用于模型的学习，验证集用于调整模型的参数，而测试集则用于评估模型的最终性能。
通过不断调整参数，如学习率、正则化参数等，来优化模型的性能，以达到最佳的预测效果或分类准确率。
特征工程也是模型构建中不可忽视的环节。
特征工程是指从原始数据中提取有意义的特征，以便模型更好地学习和理解。
这可能包括对数据进行转换、组合、降维等操作。
例如，将日期数据转换为季节、月份等特征，或者通过主成分分析等方法降低数据的维度，减少计算量和过拟合的风险。
在模型评估阶段，我们需要使用合适的指标来衡量模型的性能。
常见的评估指标包括准确率、召回率、F1 值、均方误差等。
中央经济工作会上指出，2024年要“突出重点，把握关键”“更加突出就业优先导向，确保重点群体就业稳定”。
在高质量发展背景下，就业形式的多样性成了研究的重要话题。
正规就业通常指在法律和政府监管范围内的就业，包括有正式工作合同、纳税和享受社会保险的工作。
与之相对，非正规就业包括自雇、临时工作、无合同工作或家庭内劳动等形式，这些通常未受到同等程度的法律保护和社会认可。
这些差异不仅影响着劳动者的经济福祉和工作满意度，也对社会经济结构和政策制定产生深远影响。
因此，探究正规与非正规就业的区别，以及影响个人选择这两种就业类型的因素，对于理解和改善劳动市场具有重要意义。
一、正规就业与非正规就业（一）正规就业的特征和发展趋势正规就业通常定义为在法定劳动市场中进行的就业，其特征包括有明确劳动合同、固定工作时间和地点、规定工资结构及社会保险和福利。
正规就业提供了工作安全性、职业发展机会以及保障的劳动权利。
随着全球化和经济发展，许多国家正经历从传统的非正规就业向正规就业的转变，特别是技术进步和数字化转型正在改变传统的正规就业形态，远程工作和灵活的工作安排变得越来越普及。
（二）非正规就业的特征和发展趋势非正规就业指在非正式经济部门中的就业，通常没有正式的劳动合同、缺乏社会保障和法律保护。
这类就业形式包括临时工、日工和家庭工业工人，特点是工作不稳定、收入波动和较低的工作安全性。
（三）正规与非正规就业的比较研究正规就业和非正规就业之间的比较研究表明，正规就业通常与更高的就业质量相关，包括更好的工作条件、更高的收入和更多的职业发展机会。
相反，非正规就业往往与较低的工作稳定性和较差的劳动条件相关联。
二、数据来源与研究设计本文通过分析大同市2023年度劳动力调查访问到的雇员身份城镇就业人口8033人的就业情况，以期揭示正规和非正规就业之间的具体差异，并探讨影响这些差异的关键因素。
研究将基于以下数据：是否签订合同、是否有社保、是否享有带薪休假、性别、年龄、婚姻状况、教育水平、月收入和每周工作时间。
数据分析的六种基本分析方法数据分析是如今商业决策中不可或缺的一个环节。
通过对大量数据的收集、整理和分析，可以揭示出隐藏在背后的有价值的信息和模式。
在数据分析的过程中，有许多基本的分析方法可供选择。
本文将介绍六种常用的数据分析方法。
1. 描述性分析描述性分析是数据分析的起点。
它通过对数据进行总结和描述，帮助我们了解数据的基本特征。
常用的描述性分析方法包括： - 平均值：计算数据集的所有值的平均数，反映数据的集中趋势。
- 中位数：将数据集按大小排序，找到中间的数值，反映数据的中心位置。
- 极值：识别出数据集的最大值和最小值，帮助我们了解数据的范围。
- 频数分布：将数据分成不同的组，统计每个组的频数，呈现数据的分布情况。
2. 相关性分析相关性分析用于探索变量之间的关系。
通过计算相关系数，我们可以确定两个变量之间的线性关系强度和方向。
常用的相关性分析方法包括：- 皮尔逊相关系数：衡量两个变量之间的线性关系强度，取值范围为-1到1。
- 斯皮尔曼相关系数：衡量两个变量之间的非线性关系强度，取值范围为-1到1。
- 散点图：将两个变量的值绘制在笛卡尔坐标系上，直观展示它们之间的关系。
3. 预测分析预测分析是根据过去的数据和模式，预测未来的结果。
它基于历史数据的趋势和模式，通过建立数学模型来进行预测。
常用的预测分析方法包括：- 线性回归：通过拟合一条直线来预测一个或多个自变量与因变量之间的关系。
- 时间序列分析：通过分析时间上的趋势和周期性模式来预测未来的结果。
- 预测模型评估：使用合适的评估指标来评估预测模型的准确性，如均方根误差（RMSE）和平均绝对误差（MAE）等。
4. 分类分析分类分析用于将数据集中的个体划分为不同的类别。
通过对已有的数据进行分类，我们可以预测新的数据属于哪个类别。
常用的分类分析方法包括：- 决策树：通过一系列的判定条件将数据划分为不同的类别，形成树状结构。
- 朴素贝叶斯分类：基于贝叶斯公式，计算数据属于每个类别的概率，选择概率最高的类别作为预测结果。
估算和评估报告中的定量和定性分析方法估算和评估报告在许多领域都起着至关重要的作用。
无论是在商业、经济、环境还是社会领域，定量和定性分析方法都被广泛运用来提供数据和评估结果的可信度。
在本文中，我们将探讨估算和评估报告中常用的定量和定性分析方法，以及它们的优缺点和适用范围。
定量分析方法是通过数值和统计数据来进行分析和估算的方法。
其中最常用的方法之一是回归分析。
回归分析通过建立数学模型来预测因变量与自变量之间的关系。
它可以通过线性回归、多元回归和逻辑回归等方法来进行。
回归分析在市场调研、经济预测和金融风险评估等领域得到广泛应用。
其优点是可以提供定量的预测和推断结果，但在实际应用中需要注意模型的合理性和数据的可靠性。
另一种常用的定量分析方法是成本效益分析。
成本效益分析通过比较项目投资所获得的效益与投资成本之间的关系，来确定项目的经济可行性。
它对于评估公共政策、基础设施建设和医疗决策等领域非常有用。
成本效益分析的优点是能够将不同项目的效益进行比较，并根据经济性和效益来做出决策。
然而，它也存在着一些局限性，比如很难量化某些效益，如环境效益和社会效益，以及对未来效益的不确定性。
相对于定量分析方法，定性分析方法更加关注主观性和描述性的评估。
定性分析方法通过文字描述、专家意见和案例研究等方式来进行，旨在提供对潜在影响和观点的理解。
其中最常用的方法之一是SWOT分析。
SWOT分析通过评估一个项目或组织的优势、劣势、机会和威胁来帮助制定战略和决策。
它可以提供全面的分析和评估，但受到个人主观性和信息收集的限制。
另一种常见的定性分析方法是焦点小组讨论。
焦点小组讨论是一种集体讨论的方式，通过邀请一组相关的个体或专家来分享意见和经验。
它可以在研究社会问题、开展市场调研和制定政策等方面提供宝贵的见解。
然而，焦点小组讨论也存在一些限制，如受到小组动力和成员意见偏见的影响。
综上所述，估算和评估报告中的定量和定性分析方法各有优缺点，适用于不同的场景和需求。
1.逻辑回归模型1.1逻辑回归模型考虑具有p个独立变量的向量,设条件概率为根据观测量相对于某事件发生的概率。
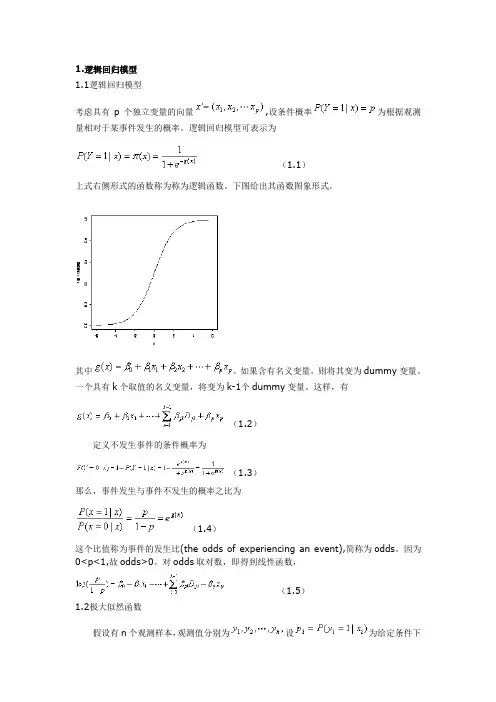
逻辑回归模型可表示为（1.1）上式右侧形式的函数称为称为逻辑函数。
下图给出其函数图象形式。
其中。
如果含有名义变量，则将其变为dummy变量。
一个具有k个取值的名义变量，将变为k-1个dummy变量。
这样，有（1.2）定义不发生事件的条件概率为（1.3）那么，事件发生与事件不发生的概率之比为（1.4）这个比值称为事件的发生比(the odds of experiencing an event),简称为odds。
因为0<p<1,故odds>0。
对odds取对数，即得到线性函数，（1.5）1.2极大似然函数假设有n个观测样本，观测值分别为设为给定条件下得到的概率。
在同样条件下得到的条件概率为。
于是，得到一个观测值的概率为（1.6）因为各项观测独立，所以它们的联合分布可以表示为各边际分布的乘积。
（1.7）上式称为n个观测的似然函数。
我们的目标是能够求出使这一似然函数的值最大的参数估计。
于是，最大似然估计的关键就是求出参数，使上式取得最大值。
对上述函数求对数（1.8）上式称为对数似然函数。
为了估计能使取得最大的参数的值。
对此函数求导，得到p+1个似然方程。
（1.9），j=1,2,..,p.上式称为似然方程。
为了解上述非线性方程，应用牛顿－拉斐森(Newton-Raphson)方法进行迭代求解。
1.3牛顿－拉斐森迭代法对求二阶偏导数，即Hessian矩阵为（1.10）如果写成矩阵形式，以Ｈ表示Hessian矩阵，Ｘ表示（1.11）令（1.12）则。
再令(注：前一个矩阵需转置)，即似然方程的矩阵形式。
得牛顿迭代法的形式为（1.13）注意到上式中矩阵Ｈ为对称正定的，求解即为求解线性方程ＨＸ＝Ｕ中的矩阵Ｘ。
对Ｈ进行cholesky分解。
最大似然估计的渐近方差（asymptotic variance）和协方差(covariance)可以由信息矩阵（information matrix）的逆矩阵估计出来。
常见逻辑谬误举例及解决之道2016-04-13译言现代社会信息量暴增，如何在形形色色的观点里分辨出正确的思想？如何防止被新闻媒体中的错误逻辑所欺骗？培养独立思考的能力至关重要。
本文主要介绍自己或者他人写作中可能发生的常见逻辑谬误，每一谬误均给出了相应定义、示例，以及如何防止这些谬误的建议。
为便于了解人们如何出现此类常见错误，本文选取了许多政治论题作为示例，目的并非要论证任何这些问题的任何一种观点立场，而是要籍此阐明什么叫推理有欠缜密，而这一问题可能发生在几乎任何论证之中。
逻辑谬误的判别以下介绍的每一逻辑谬误，都分别给出了它的定义或解说、示例，以及论证中可以如何避免的建议。
以偏概全定义：依据不充分的例证（通常不具代表性或者过于琐碎）得出普遍的结论。
诸如“大学男生联谊会的人都是醉鬼”以及“大学生都很书呆子气”等等成见，就是“以偏概全”的很好例子。
示例：“我的舍友说她的哲学课很难，我的哲学课也很难，因此，所有的哲学课必定都很难！”本例的依据仅为两个人的感受，是不足以得出这样的结论的。
建议：检查所选用的例证：是否只有不多几个人的观点或者经历？如是，则应考虑是否需要增加证据，抑或缩小结论涵盖范围。
（注意：本例结论若改为不那么绝对的“某些哲学课对某些学生来说是很难的”，则不属于“以偏概全”。
）推不出定义：给出的论据的确能够支撑某种结论，然而却非欲论证的结论。
示例：“惩罚的严厉程度应当与违法的严重程度相吻合。
现如今，对酒后驾车的惩罚也许不过只是罚款。
然而酒后驾车乃是非常严重的违法，可以导致无辜行人的丧命。
因此，酒后驾车应当适用死刑。
”这里的论据实际上可以支撑若干结论，例如“对酒后驾车应当严惩”等等，但是就本例而言，却不能支持适用死刑的正当性。
建议：分清论据与结论。
检查论据，看它们可以客观地给出什么结论。
检查结论，看它需要什么论据作为支撑，然后检查实际是否给出了这样的论据。
“推不出”的逻辑谬误往往发生在结论过于宽泛或者过于绝对之时，因此，如果所提主张较大，则应特别小心仔细。
基于结构方程模型的有调节的中介效应分析一、概述有调节的中介模型是一种中介过程受到调节变量影响的模型。
在社会科学研究中，如心理学、教育学等领域，这种模型被广泛应用于分析变量之间的复杂关系。
目前在有调节的中介效应分析中存在一些普遍问题。
大多数研究使用多元线性回归分析，这可能导致忽略测量误差的问题。
基于结构方程模型（SEM）的有调节的中介效应分析需要生成乘积指标，但这一过程可能会面临乘积指标生成和乘积项非正态分布的挑战。
为了解决这些问题，潜调节结构方程（LMS）方法被提出并建议使用。
LMS方法可以通过得到偏差校正的bootstrap置信区间来更准确地进行基于SEM的有调节的中介效应分析。
本文将介绍LMS方法，并提供一个有调节的中介SEM分析流程，包括示例和相应的Mplus程序。
文章将展望LMS和有调节的中介模型的发展方向，为相关研究提供指导。
1. 研究背景：简要介绍中介效应和结构方程模型在社会科学研究中的应用和重要性。
在社会科学研究领域，中介效应和结构方程模型的应用日益广泛，它们在理解和解释复杂的社会现象中发挥着重要作用。
中介效应分析能够帮助研究者揭示变量之间的间接影响路径，即一个变量如何通过一个或多个中介变量影响另一个变量。
这种分析方法在心理学、经济学、社会学等多个领域都有广泛的应用，有助于深入理解变量间的复杂关系，并为制定有效的干预策略提供科学依据。
结构方程模型（SEM）则是一种强大的统计分析工具，它允许研究者同时估计多个因果关系，并处理测量误差。
SEM不仅可以检验直接和间接效应，还能评估模型的拟合程度，从而判断理论模型与实际数据的一致性。
SEM还能够处理潜在变量，如智力、态度等不可直接观测的概念，进一步增强了其在社会科学研究中的应用价值。
基于结构方程模型的有调节的中介效应分析成为了社会科学研究的重要方法。
通过这种方法，研究者可以更准确地评估变量间的因果关系，揭示中介变量在复杂社会现象中的作用机制，并为政策制定和实践提供有力的科学依据。
多元逻辑斯蒂回归哑变量一、引言多元逻辑斯蒂回归（Multinomial Logistic Regression，MLR）是一种广泛用于分类问题的统计学习方法。
当自变量与因变量之间存在非线性关系或自变量之间的交互效应较强时，传统的线性回归模型可能无法准确地预测因变量，而多元逻辑斯蒂回归在这种情况下表现优异。
在多元逻辑斯蒂回归中，哑变量（Dummy Variables）是一种常见的处理分类变量的方法，它可以解决分类变量不能直接进入线性回归模型的问题。
二、多元逻辑斯蒂回归中的哑变量哑变量在多元逻辑斯蒂回归中起着至关重要的作用。
由于逻辑斯蒂回归是一个基于概率的二项式回归模型，因此无法直接使用分类自变量。
为了将分类自变量引入模型，需要将其转换为哑变量。
哑变量是一种虚拟变量，用于表示分类变量的不同类别。
通过将每个类别表示为一个虚拟变量，可以模拟分类变量与因变量之间的非线性关系。
三、哑变量的构造构造哑变量的基本步骤如下：1.确定分类变量的类别数量。
2.为每个类别创建一个虚拟变量。
3.将虚拟变量引入模型，并指定一个参考类别作为参照点。
4.为每个虚拟变量指定一个截距，以反映该类别的平均效应。
5.估计模型参数，以确定每个类别的相对风险或概率。
四、哑变量的解释在多元逻辑斯蒂回归中，哑变量的解释对于理解模型的输出至关重要。
以下是一些解释哑变量的要点：1.参照组选择：在逻辑斯蒂回归中，通常选择一个参照组作为基准类别。
该参照组在模型中通过截距项表示，所有其他类别的效应则通过与之比较的虚拟变量来解释。
因此，参照组的效应是所有其他类别的平均效应。
2.效应估计：通过估计每个虚拟变量的系数，可以了解各个类别相对于参照组的效应。
具体来说，系数的大小和符号可以揭示各个类别的风险或概率与参照组相比有何不同。
如果某个类别的系数为正数，则表示该类别的风险或概率高于参照组；如果系数为负数，则表示低于参照组。
3.交互效应：通过引入多个哑变量，可以模拟分类自变量之间的交互效应。
1.逻辑回归模型1.1逻辑回归模型考虑具有p个独立变量的向量,设条件概率为根据观测量相对于某事件发生的概率。
逻辑回归模型可表示为（1.1）上式右侧形式的函数称为称为逻辑函数。
下图给出其函数图象形式。
其中。
如果含有名义变量，则将其变为dummy变量。
一个具有k个取值的名义变量，将变为k-1个dummy变量。
这样，有（1.2）定义不发生事件的条件概率为（1.3）那么，事件发生与事件不发生的概率之比为（1.4）这个比值称为事件的发生比(the odds of experiencing an event),简称为odds。
因为0<p<1,故odds>0。
对odds取对数，即得到线性函数，（1.5）1.2极大似然函数假设有n个观测样本，观测值分别为设为给定条件下得到的概率。
在同样条件下得到的条件概率为。
于是，得到一个观测值的概率为（1.6）因为各项观测独立，所以它们的联合分布可以表示为各边际分布的乘积。
（1.7）上式称为n个观测的似然函数。
我们的目标是能够求出使这一似然函数的值最大的参数估计。
于是，最大似然估计的关键就是求出参数，使上式取得最大值。
对上述函数求对数（1.8）上式称为对数似然函数。
为了估计能使取得最大的参数的值。
对此函数求导，得到p+1个似然方程。
（1.9），j=1,2,..,p.上式称为似然方程。
为了解上述非线性方程，应用牛顿－拉斐森(Newton-Raphson)方法进行迭代求解。
1.3牛顿－拉斐森迭代法对求二阶偏导数，即Hessian矩阵为（1.10）如果写成矩阵形式，以Ｈ表示Hessian矩阵，Ｘ表示（1.11）令（1.12）则。
再令(注：前一个矩阵需转置)，即似然方程的矩阵形式。
得牛顿迭代法的形式为（1.13）注意到上式中矩阵Ｈ为对称正定的，求解即为求解线性方程ＨＸ＝Ｕ中的矩阵Ｘ。
对Ｈ进行cholesky分解。
最大似然估计的渐近方差（asymptotic variance）和协方差(covariance)可以由信息矩阵（information matrix）的逆矩阵估计出来。
而信息矩阵实际上是二阶导数的负值，表示为。
估计值的方差和协方差表示为，也就是说，估计值的方差为矩阵Ｉ的逆矩阵的对角线上的值，而估计值和的协方差为除了对角线以外的值。
然而在多数情况，我们将使用估计值的标准方差，表示为，for j=0,1,2,…,p （1.14）２.显著性检验下面讨论在逻辑回归模型中自变量是否与反应变量显著相关的显著性检验。
零假设：＝0（表示自变量对事件发生可能性无影响作用）。
如果零假设被拒绝，说明事件发生可能性依赖于的变化。
2.1 Wald test对回归系数进行显著性检验时，通常使用Wald检验，其公式为（2.1）其中, 为的标准误差。
这个单变量Wald统计量服从自由度等于１的分布。
如果需要检验假设：＝0,计算统计量（2.2）其中，为去掉所在的行和列的估计值，相应地，为去掉所在的行和列的标准误差。
这里，Wald统计量服从自由度等于p的分布。
如果将上式写成矩阵形式，有（2.3）矩阵Ｑ是第一列为零的一常数矩阵。
例如，如果检验，则。
然而当回归系数的绝对值很大时，这一系数的估计标准误就会膨胀，于是会导致Wald 统计值变得很小，以致第二类错误的概率增加。
也就是说，在实际上会导致应该拒绝零假设时却未能拒绝。
所以当发现回归系数的绝对值很大时，就不再用Wald统计值来检验零假设，而应该使用似然比检验来代替。
2.2似然比（Likelihood ratio test）检验在一个模型里面，含有变量与不含变量的对数似然值乘以-2的结果之差，服从分布。
这一检验统计量称为似然比(likelihood ratio)，用式子表示为（2.4）计算似然值采用公式（1.8）。
倘若需要检验假设：＝0,计算统计量（2.5）上式中，表示＝0的观测值的个数，而表示＝１的观测值的个数，那么n就表示所有观测值的个数了。
实际上，上式的右端的右半部分表示只含有的似然值。
统计量G服从自由度为p的分布2.3 Score检验在零假设：＝0下，设参数的估计值为，即对应的＝0。
计算Score统计量的公式为（2.6）上式中，表示在＝0下的对数似然函数（1.9）的一价偏导数值，而表示在＝0下的对数似然函数（1.9）的二价偏导数值。
Score统计量服从自由度等于１的分布。
2.4模型拟合信息模型建立后，考虑和比较模型的拟合程度。
有三个度量值可作为拟合的判断根据。
(1)-2LogLikelihood(2.7)(2) Akaike信息准则（Akaike Information Criterion,简写为AIC）(2.8)其中Ｋ为模型中自变量的数目，Ｓ为反应变量类别总数减１，对于逻辑回归有S=2-1=1。
-2LogL的值域为0至，其值越小说明拟合越好。
当模型中的参数数量越大时，似然值也就越大，-2LogL就变小。
因此，将２(K+S)加到AIC公式中以抵销参数数量产生的影响。
在其它条件不变的情况下，较小的AIC值表示拟合模型较好。
(3)Schwarz准则这一指标根据自变量数目和观测数量对-2LogL值进行另外一种调整。
SC指标的定义为(2.9)其中ln(n)是观测数量的自然对数。
这一指标只能用于比较对同一数据所设的不同模型。
在其它条件相同时，一个模型的AIC或SC值越小说明模型拟合越好。
3.回归系数解释3.1发生比odds=[p/(1-p)]，即事件发生的概率与不发生的概率之比。
而发生比率(odds ration),即(1)连续自变量。
对于自变量，每增加一个单位，odds ration为(3.1)(2)二分类自变量的发生比率。
变量的取值只能为0或1，称为dummy variable。
当取值为1，对于取值为0的发生比率为(3.2)亦即对应系数的幂。
(3)分类自变量的发生比率。
如果一个分类变量包括m个类别，需要建立的dummy variable的个数为m-1,所省略的那个类别称作参照类(reference category)。
设dummy variable为，其系数为，对于参照类，其发生比率为。
3.2 逻辑回归系数的置信区间对于置信度１-，参数的100%（１-）的置信区间为（3.3）上式中，为与正态曲线下的临界Ｚ值（critical value）, 为系数估计的标准误差，和两值便分别是置信区间的下限和上限。
当样本较大时，＝0.05水平的系数的95%置信区间为（3.4）4.变量选择4.1前向选择（forward selection）：在截距模型的基础上，将符合所定显著水平的自变量一次一个地加入模型。
具体选择程序如下（1）常数（即截距）进入模型。
（2）根据公式（2.6）计算待进入模型变量的Score检验值，并得到相应的P值。
（3）找出最小的p值，如果此p值小于显著性水平,则此变量进入模型。
如果此变量是某个名义变量的单面化(dummy)变量，则此名义变量的其它单面化变理同时也进入模型。
不然，表明没有变量可被选入模型。
选择过程终止。
（4）回到(2)继续下一次选择。
4.2 后向选择（backward selection）：在模型包括所有候选变量的基础上，将不符合保留要求显著水平的自变量一次一个地删除。
具体选择程序如下(1) 所有变量进入模型。
(2) 根据公式（2.1）计算所有变量的Wald检验值，并得到相应的p值。
(3) 找出其中最大的p值，如果此P值大于显著性水平，则此变量被剔除。
对于某个名义变量的单面化变量，其最小p值大于显著性水平，则此名义变量的其它单面化变量也被删除。
不然，表明没有变量可被剔除，选择过程终止。
(4) 回到(2)进行下一轮剔除。
4.3逐步回归(stepwise selection)(1)基本思想：逐个引入自变量。
每次引入对Ｙ影响最显著的自变量，并对方程中的老变量逐个进行检验，把变为不显著的变量逐个从方程中剔除掉，最终得到的方程中既不漏掉对Ｙ影响显著的变量，又不包含对Ｙ影响不显著的变量。
(2)筛选的步骤：首先给出引入变量的显著性水平和剔除变量的显著性水平，然后按下图筛选变量。
(3)逐步筛选法的基本步骤逐步筛选变量的过程主要包括两个基本步骤：一是从不在方程中的变量考虑引入新变量的步骤；二是从回归方程中考虑剔除不显著变量的步骤。
假设有p个需要考虑引入回归方程的自变量.①设仅有截距项的最大似然估计值为。
对p个自变量每个分别计算Score检验值，设有最小p值的变量为，且有，对于单面化(dummy)变量，也如此。
若，则此变量进入模型，不然停止。
如果此变量是名义变量单面化(dummy)的变量，则此名义变量的其它单面化变量也进入模型。
其中为引入变量的显著性水平。
②为了确定当变量在模型中时其它p-1个变量也是否重要，将分别与进行拟合。
对p-1个变量分别计算Score检验值，其p值设为。
设有最小p值的变量为，且有.若，则进入下一步，不然停止。
对于单面化变量，其方式如同上步。
③此步开始于模型中已含有变量与。
注意到有可能在变量被引入后，变量不再重要。
本步包括向后删除。
根据(2.1)计算变量与的Wald检验值，和相应的p值。
设为具有最大p值的变量，即=max(),.如果此p值大于，则此变量从模型中被删除，不然停止。
对于名义变量，如果某个单面化变量的最小p值大于，则此名义变量从模型中被删除。
④如此进行下去，每当向前选择一个变量进入后，都进行向后删除的检查。
循环终止的条件是：所有的p个变量都进入模型中或者模型中的变量的p值小于，不包含在模型中的变量的p值大于。
或者某个变量进入模型后，在下一步又被删除，形成循环。
