下载文档原格式
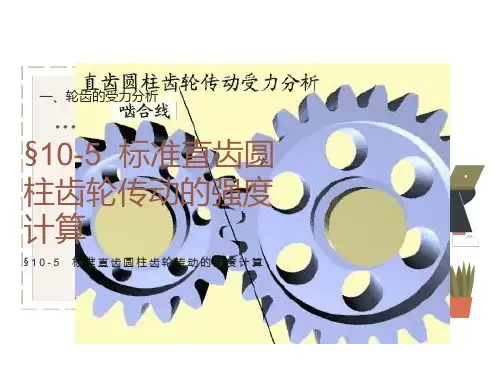
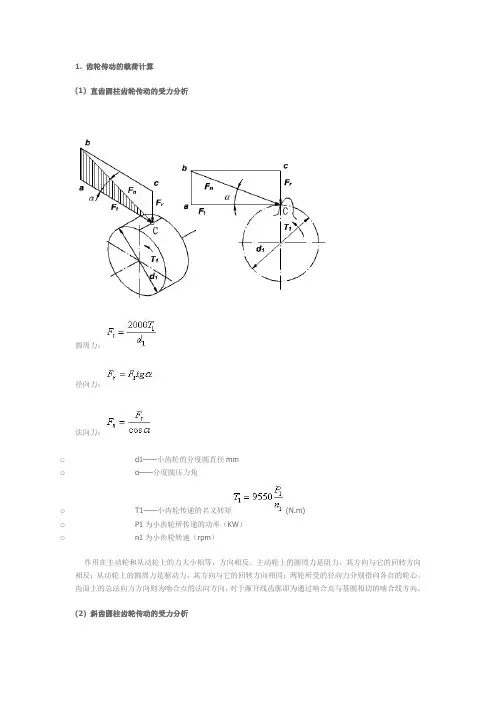
1. 齿轮传动的载荷计算(1) 直齿圆柱齿轮传动的受力分析圆周力：径向力：法向力：o d1——小齿轮的分度圆直径mmoα——分度圆压力角o T1——小齿轮传递的名义转矩(N.m)o P1为小齿轮所传递的功率（KW）o n1为小齿轮转速（rpm）作用在主动轮和从动轮上的力大小相等，方向相反。
主动轮上的圆周力是阻力，其方向与它的回转方向相反；从动轮上的圆周力是驱动力，其方向与它的回转方向相同；两轮所受的径向力分别指向各自的轮心。
齿面上的总法向力方向则为啮合点的法向方向，对于渐开线齿廓即为通过啮合点与基圆相切的啮合线方向。
(2) 斜齿圆柱齿轮传动的受力分析圆周力：径向力：轴向力：法向力：∙αt——端面分度圆压力角；∙αn——法向分度圆压力角；∙β——分度圆螺旋角；∙βt——基圆螺旋角。
(3) 直齿锥齿轮传动的受力分析法向力Fn集中作用在齿宽节线中点处，则Fn可分解为互相垂直的三个分力。
圆周力：径向力：轴向力：dm1——小齿轮齿宽中点分度圆直径mm；δ1——小锥齿轮分度圆锥角圆周力和径向力的方向判别与直齿圆柱齿轮判别方法相同，轴向力方向分别指向各自的大端。
由于锥齿轮传动两轴的空间交角为90°，因此存在以下关系：；。
负号表示方向相反。
(4) 齿轮传动的计算载荷齿轮承受载荷常表现为其传递的力矩或圆周力。
由上述力的分析计算所得出的圆周力为齿轮传动的名义圆周力。
实际工作中，由于各种因素的影响，齿轮实际承受的圆周力要大于名义圆周力。
考虑各种因素的影响，实际圆周力Ftc为：Ftc也称为计算载荷。
1）KA——使用系数。
2）KV——动载系数。
3) KHα和KFα——齿间载荷分配系数。
4) KHβ和KFβ——齿向载荷分布系数。
2. 齿轮传动应力分析齿轮传动工作过程中，相啮合的轮齿受到法向力Fn的作用，主要产生两种应力：齿面接触应力和齿根弯曲应力。
(1) 齿面接触应力σH齿轮传动工作中，渐开线齿面理论上为线接触，考虑齿轮的弹性变形，实际上为很小的面接触。
11-4直齿圆柱齿轮传动的作用力及计算载荷：一、齿轮上的作用力：为了计算齿轮的强度，设计轴和选用轴承，有必要分析轮齿上的作用力。
当不计齿面的摩擦力时，作用在主动轮齿上的总压力将垂直于齿面，（因为齿轮传动一般都加以润滑，齿轮在齿啮合时，摩擦系数很小，齿面所受的摩擦力相对载荷很小，所以不必考虑），即为P175图11-5b所示的F n（沿其啮合线方向），Fn可分解为两个分力：圆周力：Ft=2T1/d1 N径向力：Fr=Fttgα N而法向力：Fn=Ft/cosα NT1：小齿轮上的扭矩 T1=9550000p/n1 n·mmP：传递的功率（KW） d1：小齿轮分度圆直径 mmα：压力角 n1：小齿轮的转速(r·p·m)Ft1：与主动轮运动方向相反；Ft2与从动轮运动方向一致。
各力的方向 Fr：分别由作用点指向各轮轮心。
Fn：通过节点与基圆相切（由法切互为性质）。
根据作用力与反作用力的关系，主从动轮上各对的应力应大小相等，方向相反。
二、计算载荷：Fn是根据名义功率求得的法向力，称为名义载荷，理论上Fn沿齿宽均匀分布，但由于轴和轴承的变形，传动装置的制造安装误差等原因，载荷沿齿宽的分布并不均匀，即出现载荷集中现象（如P176图11-6所示，齿轮相对轴承不对称布置，由于轴的弯曲变形，齿轮将相互倾斜，这时，轮齿左端载荷增大，轴和轴承刚度越小，b越宽，载荷集中越严重。
此外，由于各种原动机和工作机的特性不同，齿轮制造误差以及轮齿变形等原因，还会引起附加动载荷。
精度越低，圆周速度V越大，附加载荷越大。
因此在计算强度时，通常以计算载荷K·Fn代替名义载荷Fn，以考虑上两因素的影响。
K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算：一、设计准则：齿轮强度计算是根据齿轮失效形式来决定的，在闭式传动中，轮齿的失效形式主要是齿面点蚀，开式传动中，是齿轮折断，在高速变截的齿轮传动中，还会出现胶合破坏，因胶合破坏的计算方法有待进一步验证和完善。
直齿圆柱齿轮的强度计算受力分析：圆周力F t =112d T 径向力αtan ∙=t r F F 法向载荷αcos t n F F = 1T ：小齿轮传递的转矩，mm N ∙ 1d ：小齿轮的节圆直径，mm α：啮合角，对标准齿轮， 20=α齿根弯曲疲劳强度的计算： 校核公式：[]F d Sa Fa Sa Fa F z m Y Y KT bmd Y Y KT σφσ≤==21311122 计算公式：[]32112F d Sa Fa z Y Y KT m σφ≥d φ：齿宽系数，1d b d =φ Fa Y ：齿形系数 Sa Y ：应力校正系数齿面接触疲劳强度的计算： 校核公式：[]H E H uu bd KT Z σσ≤±∙=125.2211 设计公式：[]3211132.2⎪⎪⎭⎫ ⎝⎛∙±∙=H E d Z u u KT d σφ标准斜齿圆柱齿轮的强度计算 受力分析： 圆周力：112d T F T = 径向力：βαcos tan n t r F F ∙= 轴向力：βtan ∙=t a F F齿根弯曲疲劳强度计算： 校核公式：[]F n Sa Fa t F bm Y Y Y KF σεσαβ≤=设计计算：[]32121cos 2F Sa Fa d n Y Y z Y KT m σεφβαβ∙=齿面接触疲劳强度计算： 校核计算：H E H Z Z uu bd KT ∙±∙=111αεσ 设计计算：[]321112⎪⎪⎭⎫ ⎝⎛∙±∙≥H Sa Fa d Y Y u u KT d σεφαu ：齿数比标准锥齿轮的强度计算 受力分析：11212m t t d T F F == 121cos tan δαt a r F F F == 121cos tan δαt r a F F F == αcos 1t n F F =齿根弯曲疲劳强度计算： 校核公式：()[]F R Sa Fa t F bm Y Y KF σφσ≤-=5.01 设计公式：()[]32212115.014F Sa Fa R R Y Y u z KT m σφφ∙+-≥齿面接触疲劳强度计算： 校核公式：()[]H R R E H u d KT Z σφφσ≤-=31215.015设计公式：[]()321215.0192.2u KT Z d R R H E φφσ-∙⎪⎪⎭⎫ ⎝⎛≥。
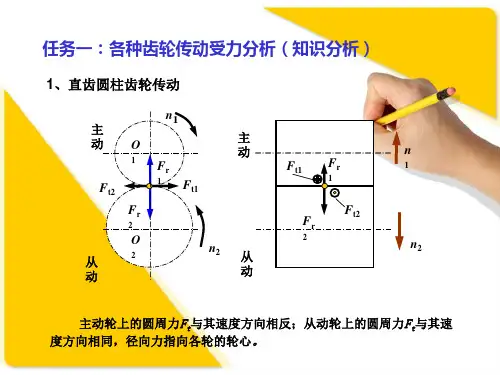
轮齿的受力分析
1. 直齿圆柱齿轮受力分析
图为直齿圆柱齿轮受力情况，转矩T1由主动齿轮传给从动齿轮。
若忽略齿面间的摩擦力，轮齿间法向力Fn的方向始终沿啮合线。
法向力Fn在节点处可分解为两个相互垂直的分力：切于分度圆的圆周力Ft 和沿半径方向的径向力Fr 。
式中：T1-主动齿轮传递的名义转矩（N·mm），，Pl为主动齿轮传递的功率（Kw），n1为主动齿轮的转速（r/min）；
d1-主动齿轮分度圆直径（mm）；
α-分度圆压力角（o）。
对于角度变位齿轮传动应以节圆直径d`和啮合角α`分别代替式（9.44）中的d1 和α。
作用于主、从动轮上的各对力大小相等、方向相反。
从动轮所受的圆周力是驱动力，其方向与从动轮转向相同；主动轮所受的圆周力是阻力，其方向与从动轮转向相反。
径向力分别指向各轮中心（外啮合）。
2. 斜齿轮受力分析
图示为斜齿圆柱齿轮受力情况。
一般计算，可忽略摩擦力，并将作用于齿面上的分布力用作用于齿宽中点的法向力Fn 代替。
法向力Fn 可分解为三个相互垂直的分力，即圆周力Ft 、径向力Fr 及轴向力Fa 。
它们之间的关系为
式中：αn-法向压力角（°）；
αt-端面压力角；（°）
β-分度圆螺旋角（°）；
作用于主、从动轮上的各对力大小相等、方向相反。
圆周力Ft 和径向力Fr 方向的判断与直齿轮相同。
轴向力Fa 的方向应沿轴线，指向该齿轮的受力齿面。
通常用左右手法则判断：对于主动轮，左旋时用左手（右旋时用右手），四指顺着齿轮转动方向握住主动轮轴线，则拇指伸直的方向即为轴向力Fa1 的方向。
2 计算载荷和载荷系数
名义载荷上述所求得的各力是用齿轮传递的名义转矩求得的载荷。
计算载荷由于原动机及工作机的性能、齿轮制造及安装误差、齿轮及其支撑件变形等因素的影响，实际作用于齿轮上的载荷要比名义载荷大。
因此，在计算齿轮传动的强度时，用载荷系数K对名义载荷进行修正，名义载荷与载荷系数的乘积称为计算载荷。
法向计算载荷Fnc 为：
式中：K -载荷系数
KA-使用系数
Kv-动载荷系数
Kα-齿间载荷分配系数
Kβ-齿向载荷分配系数
载荷系数K
1. 使用系数KA
使用系数KA 是考虑齿轮啮合时外部因素引起的附加动载荷的影响系数。
它取决于工作机和原动机的工作特性、轴与联轴器系统的质量和刚度以及运行状态。
对于一般设计，KA 值可按表9.10选取。
表9.10 使用系数KA
注：表中所列KA 值仅适用于减速传动；对于增速传动，建议取表中数值的1.1倍。
当外部机械与齿轮装置之间为挠性连接时，KA 可适当减小。
2. 动载荷系数Kv
动载荷系数Kv 是考虑齿轮副自身啮合误差引起的内部附加动载荷的影响系数。
产生附加动载荷的主要因素有：
1）齿轮制造产生的基节误差和齿形误差；
2）在啮合传动中，同时参加啮合轮齿的对数及位置在循环变化，轮齿啮合刚度也随之变化；3）轮齿受载变形；
4）齿轮支承件的弹性变形等。
上述因素导致啮合节点位置变化，故从动轮转速变化，产生附加动载荷。
动载荷系数Kv 值应通过实测或计算得到。
一般设计可参考下图选取。
适当提高制造精度，降低齿轮圆周速度，增加轮齿及支承件的刚度，对齿轮进行修形（即对齿顶的一小部分齿廓曲线进行适量修削）等，都能减小内部附加动载荷。
3. 齿间载荷分配系数Kα
齿间载荷分配系数Kα 是考虑同时啮合的各对轮齿间载荷分配不均匀影响的系数。
影响齿间载荷分配不均匀的主要因素有：受载后轮齿变形；齿轮的制造误差，特别是基节误差；齿轮的跑合效果及齿廓修形等。
对于一般工业传动用的直齿轮和β≤30°的斜齿轮Kα值可按表9.11选取。
表中：KHα为齿面接触疲劳强度计算用的齿间载荷分配系数；KFα为齿根弯曲疲劳强度计算用的齿间载荷分配系数。
表9.11 齿间载荷分配系数KHα，KFα
注：①适用于钢制及铸铁齿轮；
②对修形6级精度硬齿面斜齿轮，取KHα=KFα =1.0；
③齿轮副精度等级不同时，按精度等级较低者取值。
4. 齿向载荷分布系数Kβ
齿向载荷分布系数Kβ是考虑沿齿宽方向载荷分布不均匀对齿轮强度影响的系数。
影响沿齿宽方向载荷分布不均匀的因素很多，主要有：齿轮的制造和安装误差；轮齿、轴系部件和箱体的变形；齿宽及齿面硬度等。
齿面接触疲劳强度计算用的齿向载荷分布系数KHβ 值可根据齿轮在轴上布置形式、齿轮的精度等级、齿宽b及齿宽系数φd （=b/d）从表查取；
齿根弯曲疲劳强度计算用的齿向载荷分布系数KFβ 值可根据KHβ 值、齿宽与齿高比（b/h）按下图查取。
提高轮齿、轴系部件和箱体的刚度，合理布置齿轮位置（尽可能不用悬臂布置），合理选择齿宽，提高制造和安装精度，对轮齿作鼓形修形等，都有利于改善载荷分布不均匀现象。
(end)。
