第一章 直角三角形的边 角关系
4 解直角三角形
第一章 直角三角形的边角关系
4 解直角三角形
考场对接
考场对接
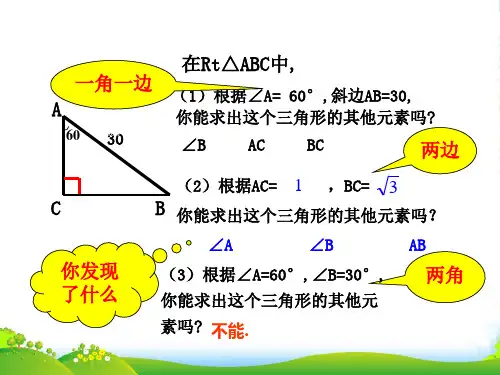
题型一 已知直角三角形中的两边, 解直角三角形
例题1 在Rt△ABC中, ∠C=90° , AC=1, AB=2, 求这个直角三角 形的其他元素.
锦囊妙计
已知两边解直角三角形的步骤 (1)利用勾股定理求出第三边的长; (2)利用已知两边所对应的三角函数求出一 锐角; (3)利用“直角三角形中两锐角互余”求出另一锐角.
(2)∵在Rt△ABD中, AB=10, AD=6, ∴由勾股定理, 得BD=8. 由(1)得CD=4, ∴BC=BD+CD=12.Fra bibliotek锦囊妙计
一般三角形的“化斜为直法” 通过作辅助线把非直角三角形的问题转化成 直角三角形 的问题的方法叫作“化斜为直法”. 通常构造含特殊角的直角 三角形. 若条件中有线段的 比或锐角三角函数, 可以设一个辅 助未知数, 利用勾股定理列方程求解.
AB于点D, 则 △BCD为等腰直角三角形, 所以BD=CD=
再计
算出∠A=30° , 所以
然后计算AD+BD即可.
解: 如图1-4-8, 由题意得∠ABE=45° , ∠ACE=75°, BC=10 m, 作CD⊥AB于点D, ∵∠DBC=45°, ∴△BCD为等腰直角三角形,
锦囊妙计
构造直角三角形进行数学建模 对于非直角三角形的实际问题, 往往通过作三角形的高, 构造直角三角形来解决, 而作高时, 一般从非特殊角的顶点作 高. 对于复杂的图形, 则可以利用“补形”或“分割”的方法, 构造直角三角形, 然后运用解直角三角形的方法求解即可.
题型五 解直角三角形的简单应用