下载文档原格式
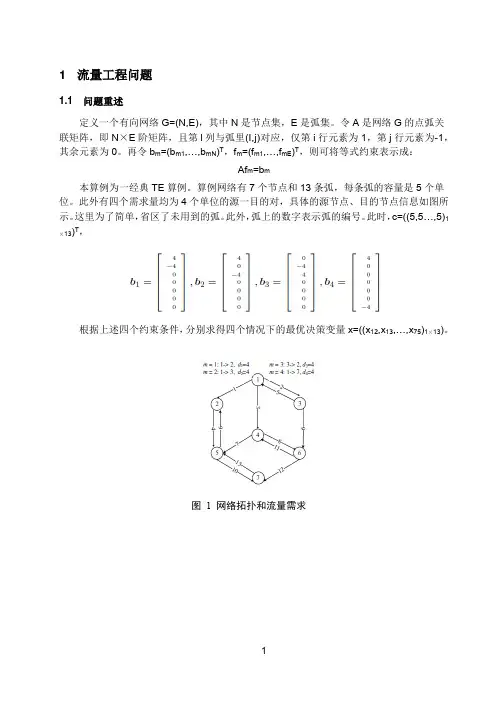
1 流量工程问题1.1 问题重述定义一个有向网络G=(N,E)，其中N是节点集，E是弧集。
令A是网络G的点弧关联矩阵，即N×E阶矩阵，且第l列与弧里(I,j)对应，仅第i行元素为1，第j行元素为-1，其余元素为0。
再令b m=(b m1,…,b mN)T，f m=(f m1,…,f mE)T，则可将等式约束表示成：Af m=b m本算例为一经典TE算例。
算例网络有7个节点和13条弧，每条弧的容量是5个单位。
此外有四个需求量均为4个单位的源一目的对，具体的源节点、目的节点信息如图所示。
这里为了简单，省区了未用到的弧。
此外，弧上的数字表示弧的编号。
此时，c=((5,5…,5)1 )T，×13)。
根据上述四个约束条件，分别求得四个情况下的最优决策变量x=((x12,x13,…,x75)1×13图 1 网络拓扑和流量需求1.2 7节点算例求解1.2.1 算例1（b1=[4;-4;0;0;0;0;0]T）转化为线性规划问题：Minimize c T x1Subject to Ax1=b1x1>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x1*=[4 0 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x1=201.2.2 算例2（b2=[4;0;-4;0;0;0;0]T）Minimize c T x2Subject to Ax2=b2X2>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x2*=[0 4 0 0 0 0 0 0 0 0 0 0 0]T对应的最优值c T x2=201.2.3 算例3（b3=[0;-4;4;0;0;0;0]T）Minimize c T x3Subject to Ax3=b3X3>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x3*=[4 0 0 0 4 0 0 0 0 0 0 0 0]T对应的最优值c T x3=401.2.4 算例4（b4=[4;0;0;0;0;0;-4]T）Minimize c T x4Subject to Ax4=b4X4>=0利用Matlab编写对偶单纯形法程序，可求得:最优解为x4*=[4 0 0 4 0 0 0 0 0 4 0 0 0]T对应的最优值c T x4=601.3 计算结果及结果说明1.3.1 算例1（b1=[4;-4;0;0;0;0;0]T）算例1中，由b1可知，节点2为需求节点，节点1为供给节点，由节点1将信息传输至节点2的最短路径为弧1。
结构优化设计课程总结通过对本课程的学习，我了解到工程设计的过程中，一般都是先粗略估计一些数值，然后进行校核分析，如果不合适，则需进一步修正数值后校核，使数值进一步去拟合理想值，如此多次进行以达到最优的效果。
但是这样做周期会比较长，计算量也比较大。
这门课就是讲解这些算法如何优化的。
由此总结出本课程前后主要由三部分构成。
第一，优化设计的基本理论，包括结构优化设计的数学模型、线性规划基本理论和计算方法、无约束非线性规划和约束非线性规划的基本理论、多种计算方法的公式、性质和流程、多目标优化的基本理论和计算方法；第二，工程结构优化设计，包括适用于工程设计的优化准则法、对飞行器结构设计具有重要意义的结构可靠性优化设计；第三，飞行器优化设计技术的新发展，包括多学科设计优化（MDO）、遗传算法及改进、智能优化设计技术。
这些分析方法都是以计算机为工具，将非线性数学规划的理论和力学分析方法结合，使用于受各种条件限制的承载结构设计情况。
优化问题的数学意义是在不等式约束条件下，求出使目标函数为最小或最大值的一组设计变量值。
在实际工程应用中，优化问题所包含的函数通常是非线性的和隐式的。
因此建立在数学规划基础上的优化算法，是依据当前设计方案所对应的函数值与导数值等信息，按照某种规则在多维设计变量空间中进行搜索，一步一步逼近优化解，也就是一个迭代的过程。
故在计算机上进行该类运算会更加具有实际意义。
一、有限元素法这是基于在结构力学、材料力学和弹性力学基础上的一种分析方法。
研究杆、梁，经简化薄板组成的结构的应力、变形等问题。
其方法是首先通过力学分析将结构离散化成单一元素，然后对单一元素进行分析，算出各单元刚度矩阵后，进行整体分析，根据方程组K·u=P求解。
这种方法求解的问题受限于结构的规模、形式和效率。
在有限元素法中,用网格将结构划分为若干小块,这些小块称为有限元素，简称有限元。
它们可以是三角形、四边形、四面体、六面体或其他形状，易于为计算机记录和鉴别。
《最优化方法》课程教学大纲Methods of Optimization课程代码： 课程性质：专业基础理论课/选修适用专业：信息计算、统计学开课学期：6总学时数：56总学分数：3.5编写年月：2002年3月修订年月：2007年7月执笔：刘伟一、课程的性质和目的最优化计算方法是在生产实践和科学实验中选取最佳决策，研究在一定限制条件下，选取某种方案，以达到最优目标的一门学科，广泛应用与空间科学、军事科学、系统识别、通讯、工程设计、自动控制、经济管理等各个领域，是工科院校高年纪学生、研究生、应用数学专业学生和搞优化设计的工程技术人员的一门重要课程。
通过本课程教学，使学生掌握最优化计算方法的基本概念和基本理论，初步学会处理应用最优化方法解决实际中的碰到的各个问题，培养解决实际问题的能力。
二、课程教学内容及学时分配（一）教学内容1. 最优化方法和最优化模型最优化方法定义、最优化问题的数学模型与分类；根据问题特点（无约束最优化与约束最优化），根据函数类型（线性规划，非线性规划）；最优化方法（解析法，直接法），最优解与极值点。
2.基础知识多元函数泰勒公式的矩阵形式，古典极值理论问题，二次函数求梯度公式，凸集，凸函数，凸规划，几个重要的不等式。
3. 常用的一维搜索方法一维搜索法是最优化的基础，“成功－失败”法的思想与算法，黄金分割法（０.618法）的思想与算法，二次插值法，三次插值法，Ｄ。
Ｓ。
Ｃ法，Ｐowell 法等方法的思想与算法。
4. 无约束最优化方法无约束最优化方法是最优化方法中的基本方法。
最速下降法的思想与算法步骤，牛顿法的思想与算法步骤，共轭方向法的思想与算法步骤，共轭梯度法的思想与算法步骤，变尺度法（ＤＦＰ法和ＢＦＧＳ法）的思想与算法步骤5. 约束最优化方法约束最优化方法通常约束问题转化为无约束问题求解。
序列无约束极小化方法（ＳＵＭＴ－外点法与ＳＵＭＴ－内点法）的思想与算法步骤，内点的求法，其他罚函数法,Frank-Wolfe法的思想与算法步骤6. 直接搜索法Ｐowell方向加速法的思想与算法步骤学时分配三、课程教学的基本要求1. 最优化模型了解最优化的数学模型与分类, 理解最优化模型的分类标准及最优化模型解法分类。
《最优化方法》课程教学大纲课程编号：英文名称：Optimization Methods一、课程说明1. 课程类别理工科学位基础课程2. 适应专业及课程性质理、工、经、管类各专业，必修文、法类各专业，选修3.课程目的（1）使学生掌握最优化问题的建模、无约束最优化及约束最优化问题的理论和各种算法；（2）使学生了解二次规划与线性分式规划的一些特殊算法；（3）提高学生应用数学理论与方法分析、解决实际问题的能力以及计算机应用能力。
4. 学分与学时学分2，学时405. 建议先修课程微积分、线性代数、Matlab语言6. 推荐教材或参考书目推荐教材：（1）《非线性最优化》（第一版）. 谢政、李建平、汤泽滢主编.国防科技大学出版社. 2003年（2）《最优化方法》（第一版）. 孙文瑜、徐成贤、朱德通主编. 高等教育出版社. 2004年参考书目：（1）《最优化原理》（第一版）. 胡适耕、施保昌主编. 华中理工大学出版社. 2000年（2）《运筹学》》（修订版）. 《运筹学》教材编写组主编. 清华大学出版社. 1990年7. 教学方法与手段（1）教学方法：启发式（2）教学手段：多媒体演示、演讲与板书相结合8. 考核及成绩评定考核方式：考试成绩评定：考试课（1）平时成绩占20%，形式有：考勤、课堂测验、作业完成情况。
（2）考试成绩占80%，形式有：笔试（开卷）。
9. 课外自学要求（1）课前预习；（2）课后复习；（3）多上机实现各种常用优化算法。
二、课程教学基本内容及要求第一章最优化问题与数学预备知识基本内容：（1）最优化的概念；（2）经典最优化中两种类型的问题--无约束极值问题、具有等式约束的极值问题的求解方法；（3）最优化问题的模型及分类；（4）向量函数微分学的有关知识；（5）最优化的基本术语。
基本要求：（1）理解最优化的概念；（2）掌握经典最优化中两种类型的问题--无约束极值问题、具有等式约束的极值问题的求解方法；（3）了解最优化问题的模型及分类；（4）掌握向量函数微分学的有关知识；（5）了解最优化的基本术语。
