下载文档原格式
质心教育原创物理竞赛模拟题第六套满分160分 命题人 蔡子星第一题（20分）Andy Riley 画了《找死的兔子》，该书中的兔子精通各种物理原理，从而成功自杀。
其中一个自杀的方式如下图，采用一个轻质的跷跷板，长度为 1.000l m =，支点在中间，高0.200m ，兔子从一定高度 2.000h m =做自由落体运动，与跷跷板发生完全非弹性碰撞，之后落地时与地面发生完全非弹性碰撞，问兔子是否可能自杀成功？如果可能兔子与石头的质量比/m M 应当为多少？29.80/g m s =第二题（20分）Andy Riley 画了《找死的兔子》，该书中的人们精通各种物理原理，从而帮助兔子成功自杀。
巨石的质量为5110kg ⨯，巨石下有10根圆木，人们拉着巨石缓缓移动。
圆木的质量可以忽略，所有地方均不滑动。
由于压力巨大，圆木的直径被压扁了0.2%（假设地面没有形变），圆木滚动之后被压扁的地方又恢复了原状。
假设圆木如图顺时针滚动的时候作用力集中在A 、B 两点。
重力加速度取9.8/g N kg =（1）原始人至少需要多大的拉力才能将巨石拉动？（2）各处摩擦系数至少达到多少才能保证不滑动？第三题（20分）空间中有沿着z 轴的静磁场，磁场强度和到z 轴的距离成正比0()rB r B r =。
一个带电为q ，质量为m 的粒子，在x y -平面内绕着z 轴在洛仑兹里作用下做圆周运动，半径为0r 。
（1）写出粒子速度大小0v 应当满足的式子（2）粒子在做圆周运动的时候收到一个径向扰动，略微偏离了原来的轨道，求解粒子之后的运动。
第四题（20分）找一个理想的电容C ，直接接到一个内阻可以忽略的电压为U 的电池上，会迅速充电，很显然充电完成的时候，电容器储存能量为212CU ，而电源做功为CU ，多出的能量，在没有电阻的情况下会ABfNN fθ以其它的方式耗散掉（例如电磁辐射等）。
如图所示电路中，电源电动势为ε，电阻为R ，电容为C 。
质心物理复赛模拟题
1. 什么是质心？
质心是一个物体或系统的平均位置，可以看作是物体的整体重心。
它是由物体的质量分布确定的一个点，物体在该点处的质量集中。
2. 如何计算质心？
质心的计算可以通过物体的质量分布来进行。
对于离散质点系统，质心的坐标可以通过质点的质量和坐标的加权平均来计算。
对于连续分布的物体，可以使用积分来计算质心的坐标。
3. 质心的性质有哪些？
质心具有以下性质：
质心的位置与物体的形状和质量分布有关，但与物体的姿态无关。
在均匀物体中，质心位于物体的几何中心。
质心是物体的一个稳定点，它在物体受力作用下保持静止或作
匀速直线运动。
对于一个系统，质心的运动受到外力和内力的共同影响。
4. 质心与平衡有什么关系？
质心在物体平衡时起着重要作用。
当物体受到平衡力的作用时，质心保持静止或作匀速直线运动。
物体平衡的一个条件是合外力矩
为零，而质心是合外力矩为零的位置。
因此，平衡物体的质心位置
对于平衡状态的确定至关重要。
5. 质心与其他物理概念的关系有哪些？
质心与其他物理概念有多种关系，例如：
动量，质心是一个系统的动量守恒的参考点，当外力合为零时，质心的动量保持不变。
转动惯量，质心是刚体转动惯量计算中的一个重要参考点，可
以简化计算。
重力，质心是重力作用点的位置，重力矩可以通过质心位置和
重力大小计算。
能量，质心动能和势能在物体运动和相互作用中发挥重要作用。
以上是对质心物理复赛模拟题的回答，希望能对你有所帮助。
如果你还有其他问题，请随时提问。
质心教育物理复赛模拟试题物理学是一门研究物质的运动和相互作用的科学，也是理工类学生必修的一门学科。
为了提高学生的物理学水平，培养学生的实验能力和科学思维，学校举办了质心教育物理复赛模拟试题。
以下是试题的详细描述及解答。
1. 问题描述：一辆汽车从静止开始匀加速行驶，经过10秒钟后，速度达到20米/秒。
求这辆汽车的加速度。
解答：根据物理学中的基本公式，速度的变化量可以用加速度乘以时间来表示。
即 v = at。
已知时间 t = 10秒，速度 v = 20米/秒。
将这些数值代入公式，可得到 a= v/t = 20/10 = 2米/秒²。
所以这辆汽车的加速度是2米/秒²。
2. 问题描述：一物体从100米的高空自由下落，求它下落的时间和下落的速度。
解答：根据物理学中的自由落体运动公式，下落的时间和速度可以通过物体的下落高度来计算。
下落时间可以通过公式t = √(2h/g) 来求解，其中 h 表示下落的高度， g 表示重力加速度。
已知下落的高度 h = 100米，重力加速度 g = 9.8米/秒²，将这些数值代入公式，可得到t = √(2×100/9.8) = √(200/9.8) ≈ √20.41 ≈ 4.52秒。
所以物体下落的时间约为4.52秒。
下落的速度可以通过公式 v = gt 来求解，将已知的重力加速度 g = 9.8米/秒²和下落的时间 t = 4.52秒代入公式，可得到v = 9.8 × 4.52 ≈ 44.6米/秒。
所以物体下落的速度约为44.6米/秒。
3. 问题描述：一个质点质量为2千克，向下施加一个力F = 10牛，则这个质点的加速度是多少？解答：根据牛顿第二定律，物体的加速度与所受的力和物体的质量成正比。
加速度可以用公式 a = F/m 来求解，其中 F 表示施加的力， m 表示物体的质量。
已知施加的力 F = 10牛，物体的质量 m = 2千克，将这些数值代入公式，可得到 a =10/2 = 5米/秒²。
第35届全国中学生物理竞赛决赛训练试题 第05套解答【第一题】40分疯狂的科学家想制造一条太空锁链.在地球赤道上两处，立起等长的足够坚固、长度可调的两根柱子，忽略地球自转，地球半径为R ，地表重力加速度为g .在两根柱子的顶端之间连接一根质量线密度为λ的链条，链条处于平衡状态. 锁链所能承受的最大张力为max T .若要求锁链最低点距离地心为0r 、有张力2002gR T r λ=，已知2max 00gR T T r λ<+，求在锁链恰好不断裂时：（1） 端点处链条切线与柱子的夹角C α； （2） 锁链的形状()r θ； （3） 两根柱子之间的夹角C φ；解答：易知引力势能为：2P R E mg r=-[1]由虚功原理，可以得到r 处张力T 的大小：()20011T T ds dsgR r r λ⎛⎫-=- ⎪⎝⎭()20011T T ds dsgR r r λ⎛⎫-=-⎪⎝⎭20011T T gR r r λ⎛⎫=+- ⎪⎝⎭[2]由于对称性，取一半锁链对地心有力矩平衡：00sin Tr T r α=[3]极坐标下有几何关系：sin α==[4]联立以上方程可得：22000011T gR T r r r λ⎡⎤⎛⎫+-=⎢ ⎪⎝⎭⎣ [5]作换元1u r=：()200011gR u u T u λ⎡⎤+-=⎢⎣进一步整理：()20000gR u u u u T λ⎡⎤+-=⎢⎥⎣⎦[6]由于θ↑r ↑u ↓，于是：d θ= [7]代入2002T gR u λ=及00r r θ==可以得到:()1arcsin1022rrπθθ⎡⎤⎛⎫=-+>⎪⎢⎥⎝⎭⎣⎦[8]()0rθ=>[9]()()()0r rθθθ=-<[10] 由[2]可知：11max0max220013CT T Trr gR r gRλλ--⎛⎫⎛⎫-=-=-⎪ ⎪⎝⎭⎝⎭[11]代入[3]有Cα：()2max00max02max max02arcsin1arcsin3CT TT T rgRT g T r gRλαλλ-⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦[12]代入[8]有：max0212arcsin422C CT rgRπφθλ⎡⎤⎛⎫==--⎢⎥⎪⎝⎭⎦[13][1-5]共10分[8][9]共10分[12]10分[13]10分【第二题】40分记太阳质量为sM、地球质量为eM、火星质量为MM、地球半径为er、火星半径为mr.认为地球和火星在同一平面内绕太阳圆周运动，轨道半径分别为eR和mR. 现通过某种机制使火星突然获得一指向太阳的速度v.（1）（15分）若火星此后的轨道可以与地球轨道相交，求v的最小值.（2）（25分）在（1）的条件下，设火星在到达地球轨道附近时地球恰在轨道上该位置，在地球与火星的间距d满足,,e m e mr r d R R<<<<时，火星相对地球的速度的矢量线与地球球心的距离为b（如图）. 若火星和地球可以发生碰撞，求b的最大值.解答：（1） 202m s mm m mv GM M M R R = [1]0m m m m t e M v R M v R =[2]()()22221122s m s m m m m m t m eGM M GM M M v v M v v R R +-=+-[3]由t v =22212m ms e m e R v GM v R R R ⎛⎫=--++ ⎪⎝⎭[4]则可知v ≥[5][1]-[4]共10分[5]5分（2） ()2220rel t e m v v v v =-+[6]由0e v =2231rels em v GM v R R ⎛=--+ ⎝[7]质心系角动量守恒()rel rel m e v b v r r μμ'=+[8]能量守恒221122e m rel relm eGM M v v r r μμ'=-+ [9]其中约化质量e me mM M M M μ=+可解得)max m e b r r =+[10][6]-[9]共15分[10]10分【第三题】（40分）如图所示, 一个粗糙的, 半径为b 的半球固定在水平面上, 其顶部有一个半径a 的匀质薄球壳. 重力加速度为g .1两球球心的连线与地面夹角为0θ。
1
质心教育原创物理竞赛模拟题第五套
满分160分 命题人 蔡子星
第一题（20分）
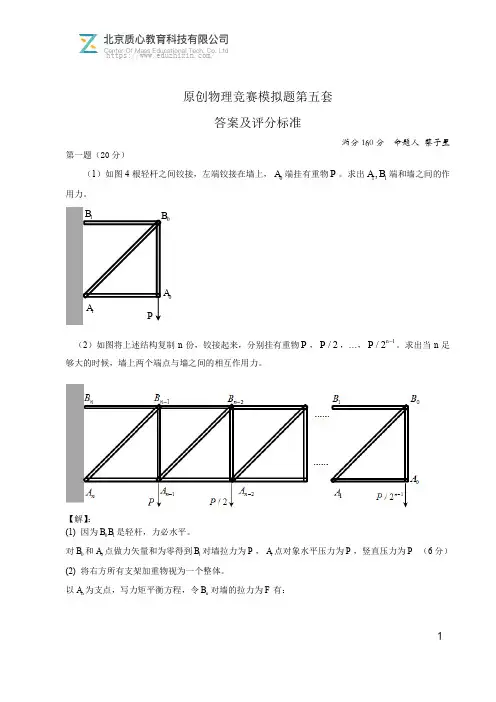
（1）如图4根轻杆之间铰接，左端铰接在墙上，0A 端挂有重物P 。
求出11,A B 端和墙之间的作用力。
（2）如图将上述结构复制n 份，铰接起来，分别挂有重物P ，/2P ，…，1
/2n P -。
求出当n 足
够大的时候，墙上两个端点与墙之间的相互作用力。
第二题（20分）
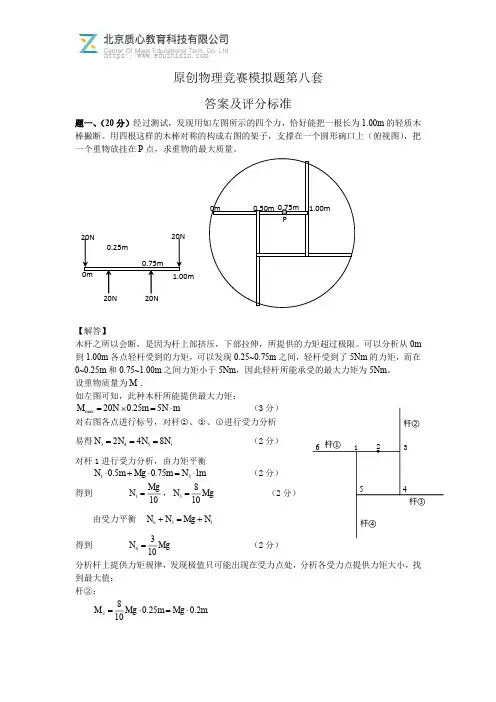
空间中有两层很薄的电荷，电荷密度为σ±，间距为h ，h 很小，叫做电偶极层。
一个电量为0q >，
质量为m 的点电荷，只能和电偶极层间发生静电相互作用（而不会碰撞）。
（1）粒子以速度0v ，角度θ，入射电偶极层，出射方向i 。
求出sin i 和sin θ之间的关系。
P
A 0
B 1
B 1
A
2
（2）将电偶极层弯成离心率为e 的双曲面形状，左边为正电荷，两个焦点沿着x 轴方向，要求所有平行于与x 轴方向入射的粒子都能汇交与焦点，则粒子速度，电偶极层厚度，电荷密度之间应当满足什么关系？ 第三题（20分）
空间中有沿着z 方向的磁场，磁场大小随着时间和空间变化，满足0cos()B B t kx ω=-。
一个桌面在0z =平面上，平面上有一个沿着x-y 方向正放的线框，线框边长为l ，总电阻为R 。
（1）假设线框相对于桌面静止，线圈的左端位于0x =的位置，求出线框中电动势随着时间的变化关系。
（2）若线框质量为m ，摩擦系数为μ，线框是否可能相对于桌面沿着x 方向做匀速直线运动？如果可能求出参数之间应当满足的条件，如果不可以，写明理由。
（以下不是考题：找到三个这样的线框，沿着x 轴发成一排，相邻两个之间用长度为'l 的绝缘木棒连接，问这三个线框是否可能一起做匀速直线运动，如果可以求出各参数应当满足条件，如果不可以写明理由。
）
第四题（20分）
一个金属球壳，半径为R ，质量为M ，带电量为Q ，初始时刻自由的静止在空间中。
球壳的一端有一个小洞。
球心与小洞的连线方向视为轴线方向。
在轴线上很远的地方有一个半径为r 的金属球，质量为m ，带电量为q ，以初速度0v 向着球心飞去。
（假设飞行速度很慢，电荷产生电场可以拿静电
σ
+σ
-h
v θ
x
y
x
y
3
力公式计算，金属球壳外表面导电性能良好，不考虑电磁辐射）
（1）求出当金属球进入球壳后达到球心时，金属球的速度为多少？
（2）金属球与球壳发生完全非弹性碰撞后连为一体，求整个过程中的发热Θ。
（以下不是试题：求出能够让金属球打入球壳所需的最小速度0v 。
仔细想哦。
答案得到
02()
kqQ m M v RmM
+≥
的同学回去面壁）
第五题（20分）
如图所示，一个信号源S 以恒定的速度u 向x 正方向运动。
信号在空中传播的速度为u 。
信号源本身的频率为0f 。
在地面上的静止的观察者P 所接受到的信号频率为f 。
在信号源的飞行轨迹上，O 点位最靠近P 的点。
以O 原点建立坐标系。
（改编自台湾物理竞赛试题）
（1）证明在信号源距离观察者足够远的时候，有0
cos 1f f v u
=
θ
-
人类的第一颗人造卫星绕地飞行的时候，地面上的观察者测量卫星发出的光信号频率。
纵轴为信号频率，单位为赫兹；横轴为测量时间，单位为分钟。
光速为82.99810/c m s =⨯。
（2）请由此图估算卫星相对于观察者的速度。
（3）请由此图估算卫星距离观察者的最近距离。
4
第六题（18分）
一个质量为2m 的星体A 和质量为m 的星体B ，绕着它们的质心分别做圆周运动。
在质心系中观察发现体系总角动量为L （1）求体系的总能量0
E （2）A 发生爆炸成为两个质量为m 的星体1A ，2A ，爆炸瞬间体系总机械能增加了E ，之后经历复杂的三体运动（以下省略刘慈欣写的《三体》）最后1A 和B 相互环绕着飞行，2A 与二者远离。
已知这时候以1A 为参照系B 的角动量为0
L 以1A 和B 的质心为参照系，1A 和B 构成的系统的能量最小值min E 为多少？这会对E 有什么限制？
第七题（20分）
如图是两冲程柴油机的工作原理图。
为了计算方便我们把工作流程化简如下： 假设气缸绝热光滑，活塞自身质量可以忽略。
第一阶段，气缸体积达到最大为1 1.5V L =，将空气鼓入气缸，把部分废气赶出气缸，同时将雾化的燃料（视为1430C H ）喷入气缸中，此时缸内气压为1 2.00P atm =，温度为1350T K =，新注入的空气占体积比为80%。
第二阶段，气缸进行绝热压缩至最小体积20.25V L =，此时混合气体发生爆炸，恰好完全反应，已知这个温度和压强下，燃烧的焓变为6
4010/J kg λ=⨯，即在这个温度和压强下，如果保持温度和压强不变，则单位质量燃料燃烧放热为λ。
假设燃烧速度很快，燃烧结束的时候气缸体积几乎没有改
θ
S
v
P
5
变。
第三阶段，气缸绝热膨胀对外做功到最大体积1 1.5V L =，回到第一阶段。
为了简化计算，空气的成分视为79%的2N ，21%的2O （体积分数）
，各种气体的参数如下: 2
N 2
O 2H O
2
CO 摩尔质量
(g/mol)
28 32 18
44 定容摩尔热容量 (R)
2.5
2.5
3.0
2.5
假设满足理想气体状态方程，气体做绝热变化的时候满足pV C γ
=，其中V V
C R
C γ+=，V C 是定容摩耳热容量。
（1）为了使得恰好完全反应，每次应当喷入多少质量的燃料？
（2）求出压缩到最小体积，点燃前的温度2T ，以及排出废气的温度1'T 。
第八题（22分）
在SLAC 中，一种产生高能γ射线（高能光子）的方式是拿高能电子与可见光（低能光子）对撞。
高能电子的总能量为1.00GeV ，可见光的波长为550nm ， 可见光与电子动量方向相反。
电子的静质量为0.51MeV 。
电子与光子发生弹性碰撞，出射粒子仍然是一个电子一个光子。
普朗克常数 6.628h Js =，电子电量191.60210q C -=⨯，光速 2.998/c m s
=（1）若光子在沿着原电子方向出射，则出射光子波长为多少？碰撞后电子能量变为多少？
（2）若出射的光子方向与原电子方向有小角度偏差1θ=︒，则出射光子的频率和第一问中频率的
比值为多少？
6
1.00
E GeV
=550nm
λ=。
