五年级上册数学多边形画图

人教版五年级上册数学第六单元多边形的面积求阴影部分面积训练1．如图所示，已知平行四边形的面积是28平方厘米，求阴影部分的面积。

2．如图所示，求阴影部分的面积。

（单位：dm）3．计算下图阴影部分的面积。

（单位：cm）4．求下面图形中阴影部分的面积。

（单位：厘米）5．计算下面阴影部分的面积。

6．梯形的面积是25平方厘米，求出阴影部分的面积。

7．下图中空白四边形是正方形，求图中阴影部分的面积。

（提示：你能把两个阴影三角形合成一个三角形吗？）8．求下面图形阴影部分的面积。

（单位：厘米）9．求如图阴影部分的面积。

（单位：厘米）10．求下面图形中阴影部分的面积。

（单位：cm）11．如下图，已知阴影部分的面积是80cm2，求大梯形的面积。

12．图中三个正方形的边长分别为1厘米、2厘米和4厘米，求图中阴影部分的面积。

13．求阴影部分面积。

14．求出下面图形阴影部分的面积。

（单位：厘米）15．计算图中阴影部分的面积。

（单位：cm）16．求阴影部分的面积。

（单位：毫米）17．求下列阴影部分的面积。

（单位：cm）18．求阴影部分面积。

（单位：厘米）19．如图，两个正方形边长分别为9dm、7dm，求阴影部分的面积。

20．求下面图形中阴影部分的面积。

（单位：厘米）参考答案：1．4平方厘米2．12dm23．4.2cm24．24平方厘米5．72平方厘米6．20平方厘米7．14cm28．8400平方厘米；22平方厘米9．53平方厘米10．1368平方厘米11．112平方厘米12．7平方厘米13．24平方米14．24平方厘米15．13.5平方厘米16．1208平方毫米17．350cm2；144 cm218．26平方厘米19．56平方分米20．325平方厘米。

第六单元多边形的面积单元解读一、链接课标《义务教育数学课程标准（2022年版）》指出在小学阶段“图形与几何”领域所对应的核心素养侧重于空间观念，几何直观，量感和推理意识。

学生要结合生活情境认识平面图形及特征，会计算图形的周长和面积，并解决一定的实际问题。

多边形的面积是图形与几何领域测量中的重要内容。

通过本单元的教学，要引导学生探索并掌握平行四边形、三角形和梯形的面积公式，会计算组合图形的面积，在观察、实验、猜想、验证等活动中，渗透平移、旋转、转化等数学思想方法，发展合情推理能力，促进学生空间观念的进一步发展、感受几何直观和符号意识的作用，渗透估测意识、策略，了解解决问题方法的多样性，培养学生的应用意识和创新意识。

二、单元目标学生已经在生活中积累了有关图形认识和图形测量的经验，同时已经研究了长方形、正方形、三角形的特征以及长方形、正方形的面积计算。

在研究本单元中，教师应引导学生紧密联系生活实际，从已有的认知基础和生活经验出发，让学生在数、剪、拼、摆等操作活动中，完成对新知的构建。

引导学生利用转化的数学思想，在操作中研究新知是本单元教学的重要环节。

通过实际操作活动，发展学生的空间观念，培养动手操作能力，为接下来研究圆的面积作好铺垫。

根据学情及教材内容制定了教学目标：1.理解并掌握各种图形的面积计算公式。

2.引导学生运用转化的方式来探索规律，认识新旧知识之间的联系。

3.会拼、摆、拆分各种组合图形，并正确计算组合图形的面积。

4.通过实验、操作、拼摆、割补等方法，使学生经历计算公式的推导过程，进一步发展学生的思维。

5.应用面积的计算公式，使学生运用转化的方法解决实际问题，发展学生的空间观念。

沟通知识与生活的联系，激发学生的学习兴趣，培养学生探究意识和创新能力，发展学生的空间观念。

三、单元教学重点、难点：教学重点：掌握平行四边形、三角形和梯形的面积计算公式，并能正确运用。

教学难点：通过探索活动，能够掌握平行四边形、三角形和梯形的面积计算公式推导的过程。

2022-2023学年五年级数学上册典型例题系列之第二单元多边形的面积组合图形面积部分（解析版）编者的话：《2022-2023学年五年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题、专项练习、分层试卷三大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

分层试卷部分是根据试题难度和掌握水平，主要分为基础卷、提高卷、拓展卷三大部分，其优点在于考点广泛，分层明显，适应性广。

本专题是第二单元多边形的面积组合图形面积部分。

本部分内容是组合图形的面积，题目综合性强，难度大，建议根据学生掌握情况选择性进行讲解，一共划分为六个考点，欢迎使用。

【考点一】加法分割思路求图形的面积：S=S1+S2。

【方法点拨】加法分割思路是把所求图形面积分割成几块能用公式计算的规则图形（三角形、正方形、长方形、平行四边形、梯形），然后分别计算出面积，最后相加得出所求图形的面积。

【典型例题】计算组合图形的面积。

（单位：分米）解析：16×6＝96（平方分米）（16－8）×（14－6）÷2＝8×8÷2＝64÷2＝32（平方分米）96＋32＝128（平方分米）【对应练习1】看图求面积（单位：厘米）解析：12×10÷2＋（8＋12）×10÷2＝12×10÷2＋20×10÷2＝120÷2＋200÷10＝60＋100＝160（平方厘米）则面积是160平方厘米。

【对应练习2】计算下面组合图形的面积。

（单位：厘米）解析：（4＋2＋2＋4）×（10－8）÷2＋8×（4＋2＋2）＝12×2÷2＋8×8＝12＋64＝76（平方厘米）【对应练习3】计算下面图形的面积。

五年级数学上册《多边形的面积》应用题及答案1．(变式题)一块平行四边形麦田(如下图)，中间有一条平行四边形小路。

(1)这块麦田的面积是多少平方米？(40－1.5)×25＝962.5(m²)答：这块麦田的面积是962.5 m²。

(2)如果每平方米收小麦约0.75 kg，这块麦田大约能收小麦多少千克？0.75×962.5＝721.875(kg)答：这块麦田大约能收小麦721.875 kg。

2．靠墙边围成一个花坛(如右图)，围花坛的篱笆长51 m，求这个花坛的面积。

51－20＝31(m) 31×20÷2＝310(m²)答：这个花坛的面积为310 m²。

3．(变式题)求阴影部分的面积。

(1)8×8÷2＝32(cm²)(2)下图中平行四边形的面积是36 cm²，A为底边中点。

36÷2÷2＝9(cm²)4．已知梯形的面积是96 dm²。

求阴影部分面积。

96×2÷8－15＝9(dm)9×8÷2＝36(dm²)5．求阴影部分面积。

(37－12)×18÷2＝225(cm²)6．一个直角梯形的下底是20 cm，如果上底再增加4 cm就成了正方形，这个梯形的面积是多少平方厘米？20－4＝16(cm)(16＋20)×20÷2＝360(cm²)答：这个梯形的面积是360 cm²。

7．(变式题)学校有一面平行四边形的“书香校园”文化墙，底是2.6 m，高是2 m，粉刷这面墙一共用去1.6 kg的外墙漆，平均每平方米大约用漆多少千克？(结果保留一位小数) 1.6÷(2.6×2)＝1.6÷5.2≈0.3(kg)答：平均每平方米大约用漆0.3 kg。

五年级上册数学人教版6 《多边形的面积》操作题专项练习（含答案）五上《多边形的面积》作图题专项练习学校:___________姓名：___________班级：___________考号：___________1．如图，在方格纸上找一个点C，连接AB、AC和BC后得到一个三角形，且使三角形的面积为2平方厘米。

2．（1）画出将三角形先向下平移3格，再向右平移4格后的图形B。

（2）以虚线a为对称轴，画出平移后图形B的轴对称图形C。

（3）画一个与三角形面积相等的梯形。

3．按要求画图。

（每小格都是边长为1厘米的正方形）。

（1）在下面的方格图中画出一个面积为12平方厘米的平行四边形。

（2）画出一个与平行四边形面积相等的钝角三角形。

（3）画出一个与平行四边形面积相等的梯形。

4．（1）请你在方格纸中用直尺画一个与图中平行四边形面积相等的三角形；（2）请你在方格纸中用直尺画一个与图中平行四边形面积相等的梯形。

5．在方格中按要求画出图形。

（小正方形的边长为1cm）（1）请你画出△向下平移四格，再向左平移两格的图形。

（2）以△的边为底，再画出一个和△面积相等的三角形。

（3）小明把两个完全一样的梯形DEFG拼成了两种不同的图形。

请你画出这两个图形，要求一个是轴对称图形，另一个不是轴对称图形。

（4）请你画出到线段a的距离等于1cm的所有的点。

6．在图中的平行线间，画出与三角形面积相等的平行四边形、梯形各一个，并标出底的长度（每小格表示1厘米）。

7．画一个面积为12cm2的平行四边形。

（图中每个小方格的面积是1cm2）8．如图，是把一个平行四边形等分成面积相等的三份的一种方法（提示：图1和图2是同一种分法，因为它们分的思路相同）。

请你再用三种不同的思路设计3种分法（不同于第一种分法），分别把下面3个平行四边形等分成面积相等的三份。

9.按要求画图形。

（每个小方格的边长都表示1厘米）（1）画一个面积是12平方厘米，高是3厘米的平行四边形。

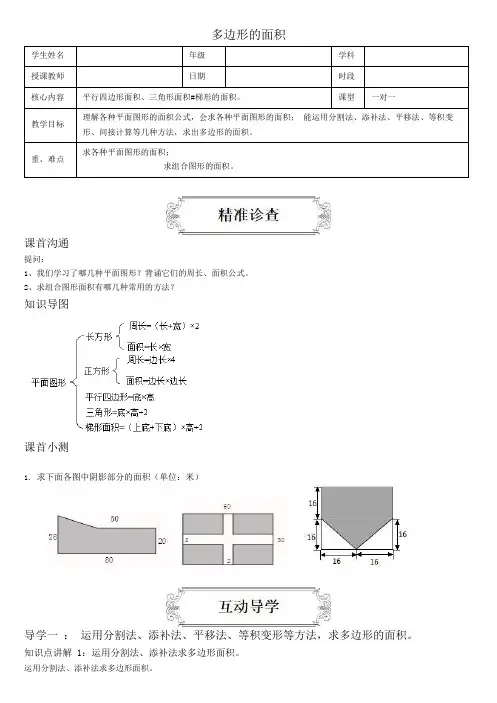
多边形的面积学生姓名年级学科授课教师日期时段核心内容平行四边形面积、三角形面积#梯形的面积。

课型一对一教学目标理解各种平面图形的面积公式，会求各种平面图形的面积；能运用分割法、添补法、平移法、等积变形、间接计算等几种方法，求出多边形的面积。

重、难点求各种平面图形的面积；求组合图形的面积。

课首沟通提问：1、我们学习了哪几种平面图形？背诵它们的周长、面积公式。

2、求组合图形面积有哪几种常用的方法？知识导图课首小测1. 求下面各图中阴影部分的面积（单位：米）导学一：运用分割法、添补法、平移法、等积变形等方法，求多边形的面积。

知识点讲解 1：运用分割法、添补法求多边形面积。

运用分割法、添补法求多边形面积。

分割法：将一个多边形分割成两个或多个基本图形，再求这几个基本图形的面积和。

添补法：将一个多边形缺少的部分补上，变成一个基本图形，再求两个图形的面积差。

知识点讲解 2：运用平移法求多边形面积。

运用平移法求多边形面积。

平移法：当多边形中间出现大小均匀的间隔时，可将旁边零碎的图形平移后，拼成一个基本图形，再求面积。

知识点讲解 3：运用间接计算法或等积变形求多边形面积。

运用间接计算法或等积变形求多边形面积。

间接计算法：当一个图形不规则时，它的面积难以直接求出，就用整个图形的面积减去空白部分面积来求它的面积。

等积变形法：将一个面积不容易计算的多边形变为一个面积容易计算的多边形。

例 1. 老师新买了一套房子，客厅大概是下图这种形状。

准备铺上地板砖，大家能帮老师计算一下客厅的总面积吗？例 1. 如图，平行四边形BCEF中，BC=8cm，直角三角形中，AC=10cm，阴影部分面积比三角形ADH的面积大8平方厘米，求AH长多少厘米？我爱展示1.学校少先大队准备给每个班做一面“中队旗”，不知道该用多少布？请你帮忙。

2.求下图阴影部分的面积。

3.一块梯形草坪中间有一条长8m，宽1m的小路。

这个草坪的面积是多少平方米？4.下图中每个长方形小格的面积都是1平方厘米，求阴影部分的面积。

画正多边形【教学目标】1．知识与技能（1）掌握REPEAT语句语法结构；（2）能够运用REPEAT语句绘制正多边形和圆形等图案。

2．过程与方法（1）通过对命令语句的归纳，概括出REPEAT命令边数与转角度数之间的关系；（2）通过对REPEAT命令的理解，演绎出画圆形和不同弧度的方法。

3．情感态度与价值观（1）经历由浅入深的思维过程，培养学生深度探究的思维习惯和学习态度；（2）初步感受程序编写带来的思维乐趣。

4．行为与创新（1）体验海龟行走路线，感知语句实现方式；（2）允许学生使用不同方法绘制图案，体验思维创新的力量。

【课时安排】1课时。

【教学重点与难点】1．教学重点正确运用REPEAT命令画出正多边形、圆形。

2．教学难点通过归纳总结出REPEAT命令的正确格式并合理使用REPEAT命令。

【教学方法与手段】自主探究、小组合作，引导学生自主归纳、演绎运用。

【课前准备】网络机房、课件和学生学案。

【教学过程】内容教师活动设计意图游戏导入我们一起玩一个正反话的小游戏。

游戏规则：女生听口令做动作，男生听口令做相反动作。

其他同学在LOGO语言中按照口令画出图形。

教师念口令：前进一步，右转90度；前进一步，右转90度；前进一步，右转90度；前进一步，右转90度。

念一句板书一句命令。

在刚刚的游戏中，你前进了几次？转动了几次？每次多少度？一共转了多少度？最后又回到了哪里？激发兴趣、迁移铺垫。

让学生在游戏中，通过转角、前进完成一个正方形行进过程。

激发学生兴趣的同时，让学生初步感受海龟运动的轨迹。

复习铺垫上课前，先来复习一下学习过的命令。

完成任务一：用FD和RT命令画出一个正三边形，并保证画完后海龟回到母位且头朝上。

请最快完成任务的学生到黑板上写出命令。

对比命令，发现了什么？正三边形重复相同语句三次；正四边形重复相同语句四次。

大胆地猜测一下，如果要画正五边形重复几次？正六边形？正十边形？正五十边形？有没有简单的方法可以画出正多边形呢？今天我们就一起来学习一个新的命令REPEAT重复命令。

2021秋人教版小学数学五年级上册第六章多边形的面积梯形的面积计算和应用题1. 计算下面每个梯形的面积。

(单位：分米)2. 计算下列图形的面积．（单位：cm）3. 下图梯形中，阴影部分面积是24平方分米，求梯形面积．4. 求下面梯形的面积．(单位：厘米)5.图形计算：求梯形的面积。

6. 选择适当条件，计算下图面积．(单位：厘米)7. 计算如图各图形的面积．8. 计算下面图形的面积。

9. 计算下列各图形的面积。

（单位：cm）10. 计算下面图形的面积11. 计算下面图形的面积。

12. 已知图中阴影部分的面积是8.2平方厘米，求梯形的面积．13. 计算下面图形中阴影部分的面积．(单位：厘米)14. 如下图，用7个同样的三角形拼成了一个梯形．根据图中的数据，你能算出这个梯形的面积吗？15. 用84米的长的篱笆，在靠墙的地方围一块菜地（如图），这块菜地如果每平方米地一年能收入25元计算，这块菜地一年能收入多少元？16. 一个梯形的上底长18㎝，下底长22㎝，高16㎝，它和一个平行四边形的面积相等，平行四边形的底是25㎝，高是多少厘米？17. 一块梯形苗圃，上底是26米，下底是34米，高是18米。

如果全部用来种枫树苗，那么种枫树苗的面积是多少平方米？18. 已知梯形的上底是10厘米，下底是17厘米，其中阴影部分的面积是221平方厘米，求这个梯形的面积。

19. 一条水渠横截面是梯形，渠深0.8米，渠底宽1.2米，渠口宽2米，横截面积是多少平方米？20. 一个平行四边形分成如下图的两个部分(左边为梯形，右边为三角形)．它们的面积之差为18.6平方厘米(梯形面积大于三角形的面积)，平行四边形一条边长15cm，这条边上的高为6.2cm，求此梯形上底的长．21. 求下图平行四边形中左、右两部分的面积．(图中单位：分米)22. 青山动物园把一块梯形土地分成了一个平行四边形和一个三角形(如下图)，平行四边形部分用来建孔雀园，三角形部分用来建鹦鹉园．已知梯形上底25米，下底50米，高24米．（1）孔雀园的面积是多少平方厘米？（2）鹦鹉园的面积是多少平方厘米？（3）自己提出一个问题并解答．23. 一块梯形铁板，上底是10分米，下底是6分米，高是5分米，如果每平方分米的铁板重0.78千克，这块铁板重多少千克？24. 幸福乡挖一条水渠的横截面是梯形，渠口宽2.8米，渠底宽1.4米，渠深1.2米，如下图所示，它的横截面的面积是多少平方米？25. 有一块面积是2080平方米的梯形田地，上底是30米，下底是50米.现在要在这块梯形田地上(如下图所示)划出一块平行四边形的地种棉花，剩下一块三角形的地种大豆，求种大豆的地是多少平方米.26. 一个鱼塘的形状是梯形，它的上底是21米，高是23米，面积是759平方米，则它的下底是多少米？27. 如下图所示，已知三角形ABE的面积比梯形DEBC的面积小200平方米，长方形ABCD 的长是30米，宽是20米，求ED的长.28. 一块梯形钢板，上底1.2米，下底2米，高1.1米，如果每平方米钢板重25千克，这块钢板重多少千克？29. 一个果园的形状是梯形．它的上底是180米，下底是160米，高是50米．如果每棵果树占地10平方米，这个果园共有果树多少棵？30. 一个果园近似梯形，它的上底120m，下底180m，高60m．如果每棵果树占地10m2，这个果园共有果树多少棵？31. 用阴影部分表示等腰梯形面积的，并测量出数据，求出阴影部分的面积．（测量时精确到整厘米数）32. 图中，把一个长方形分成A、B两个部分，A 是等腰直角三角形，B是梯形，根据图中的数据，求出梯形的面积．33. 求下面各图的周长和面积．（单位：厘米）34. 小明家的菜地是梯形的，上底是6米，下底是10米，高是12米，如果每平方米收西红柿7千克，这块菜地可以收西红柿多少千克？35. 万大伯家用100米长的竹篱笆在一块靠墙的空地上围了一个花圃（如图），这个花圃的面积是多少平方米？36. 一座堤坝的横截面是一个梯形，上底是3.6米，下底是8米，高是6米，这座堤坝的横截面的面积是多少平方米？37. 一块木板的面积是2.25平方米，锯成上底是0.6米，下底是0.4米，高是0.5米的梯形，最多可以锯多少块?38. 一条水渠横截面是梯形，渠深0.8米，渠底宽1.2米，渠口宽2米，横截面积是多少平方米？39.如图，直线a和直线b互相平行，且AB=CD。

多边形面积的知识点旧知回顾：（一）长方形1、长方形面积=长×宽字母公式：s=ab延伸：长=面积÷宽；宽=面积÷长；2、长方形周长=(长＋宽)×2 字母公式：c=(a＋b)×2延伸：长=周长÷2-宽；宽=周长÷2-长理解：长方形中面积、周长与长和宽之间的变化关系：（1）长方形的长加宽等于长方形周长的一半。

即 a + b = c ÷ 2（2）当长方形的周长不变时，长与宽的差越大，这个长方形的面积就越小；反之，长与宽的差越小，这个长方形的面积就越大。

（3）当长方形的面积不变时，长与宽的差越大，这个长方形的周长就越长；长与宽的差越小，这个长方形的周长就越短。

掌握：长方形框架拉成平行四边形，周长不变，面积变小。

（二）正方形1、正方形面积=边长×边长字母公式：s= a²或者s=a×a2、正方形周长=边长×4 字母公式：c=4a 或者c= a×4延伸：边长=周长÷4（三）单位及单位的换算：【掌握】单位：重量单位：1吨（t）=1000千克（kg）1千克（kg）=1000克（g）长度单位：1千米（km）=1000米（m）1米（m）=10分米（dm）=100厘米（cm）=1000毫米（mm）面积单位【掌握】：1平方米（m2）=100平方分米（dm2）=10000平方厘米（cm2）1平方千米（km2）=100公顷（hm2）=1000000平方米（m2）1公顷（hm2）=10000平方米（m2）货币单位:1元＝10角1角＝10分时间单位：1年=365天(闰年366天) 1天=24小时（h）1小时（h）=60分（min）1分（min）=60秒（s）单位换算方法：大单位化小单位用数乘以进率，小数点向右移动相应次数。

小单位化大单位用数除以进率，小数点向左移动相应次数。

新知讲解：一、平行四边形1、平行四边形面积=底×高字母公式：s=ah延伸：底=面积÷高；高=面积÷底；理解：平行四边形面积公式的推导过程：剪拼、平移沿着平行四边形的任意一条高剪开，将其一部分平移与另一部分正好拼成一个长方形，这个长方形的长就是平行四边形的底，这个长方形的宽就是平行四边形的高。