电容电感元件的串并联模型

注意电容和电感的串并联关系电容和电感是电路中常见的元器件，它们在电路中起着非常重要的作用。

在电路设计和应用中，了解电容和电感的串并联关系是非常重要的。

首先，让我们来了解一下电容和电感的基本概念。

电容是一种可以存储电荷的元器件。

当两个带有电荷的导体之间存在电势差时，它们之间就会形成一个电场。

电容器就是利用电场将电荷存储起来的器件。

通常，电容的单位是法拉（F）。

电感是一种可以存储磁能的元器件。

当通电的导线形成一个线圈时，会在周围产生一个磁场。

电感器就是利用磁场将能量存储起来的器件。

通常，电感的单位是亨利（H）。

在电路中，电容和电感可以串联或并联连接。

首先，我们来看一下电容的串并联关系。

当电容器串联连接时，它们的电容值会减小。

如果有n个相同的电容器C串联连接，总的电容值CT可以用以下公式来计算：CT = 1 /（1/C1 + 1/C2 + ... + 1/Cn）这意味着当电容器串联连接时，总的电容值会小于任何一个单独电容器的电容值。

这是因为串联连接会增加电容器之间的等效距离，从而降低了电容值。

当电容器并联连接时，它们的电容值会增加。

如果有n个相同的电容器C并联连接，总的电容值CT可以用以下公式来计算：CT = C1 + C2 + ... + Cn这意味着当电容器并联连接时，总的电容值会等于所有电容器的电容值之和。

这是因为并联连接会使电容器之间的等效电场增加，从而提高了电容值。

接下来，我们来看一下电感的串并联关系。

当电感器串联连接时，它们的电感值会增加。

如果有n个相同的电感器L串联连接，总的电感值LT可以用以下公式来计算：LT = L1 + L2 + ... + Ln这意味着当电感器串联连接时，总的电感值会等于所有电感器的电感值之和。

串联连接会使电感器之间的等效磁场增加，从而提高了电感值。

当电感器并联连接时，它们的电感值会减小。

如果有n个相同的电感器L并联连接，总的电感值LT可以用以下公式来计算：1 / LT = 1 / L1 + 1 / L2 + ... + 1 / Ln这意味着当电感器并联连接时，总的电感值会小于任何一个单独电感器的电感值。

信号完整性在高速电路中有着至关重要的作用，而很多信号完整性问题需要用「阻抗」的概念来解释和描述。

在高频信号下，很多器件失去了原有的特性，如我们经常听到的“高频时电阻不再是电阻，电容不再是电容”，这是咋回事呢？容抗的概念电容有两个重要特性，一个是隔直通交，另一个是电容电压不能突变。

简单说，虽然交流电能通过电容，但是不同频率的交流电和不同容值的电容，通过时的阻碍是不一样的，把这种阻碍称之为容抗。

容抗与电容和频率的大小成反比，也就是说，在相同频率下，电容越大，容抗越小；在相同电容下，频率越高，容抗越小。

如何理解容抗与电容大小和频率成反比呢？以R C一阶低通滤波器举例。

V i n通过R1电阻对电容C1进行充电，V i n的电势加在电容C的两个金属极板上，正负电荷在电势差作用下分别向电容的两个极板聚集而形成电场，这称「充电」过程。

若将Vi n拿掉，在Vo u t上加一个负载R2（青色部分），电容两端的电荷会在电势差下向负载流走，这称为「放电」过程。

（流过电容的电流并不是真正穿过了极板的绝缘介质，指的是外部的电流）衡量电容充电的电荷数为Q，Q=CV，其中C是常量，所以电荷数和电压呈正比。

C=Q/V，电容量代表了电容储存电荷的能力，微分表达式为：电流是单位时间内电荷数的变化量:结合(1)和(2)两个公式可得到：从公式可以看出：电容上的电流和电压的变化量成正比，或者说电容上电压的变化量和电流是成正比的。

即在电压一定时，电容越大，单位时间内电路中充、放电移动的电荷量越大，电流越大，所以电容对交变电流的阻碍作用越小，即容抗越小。

在交变电流的电压一定时，交变电流的频率越高，电路中充、放电越频繁，单位时间内电荷移动速率越大，电流越大，电容对交变电流的阻碍作用越小，即容抗越小。

表示，公式如下，其中f是频率，C是容值容抗用Xc因为（），所以容抗也可以用如下的公式表示：我们接着往下看一看感抗的概念。

感抗的概念电感的特性是隔交通直，与电容是相反的；所以说容抗和感抗的性质和效果几乎正好相反，而电阻则处在这两个极端中间。

电容与电感的等效电路模型研究电容与电感是电路中常用的两种元件，它们在电子设备的设计中起着重要作用。

为了更好地理解电容和电感的性质，我们需要研究它们的等效电路模型。

本文将从电容和电感的基本原理入手，探讨它们的等效电路模型的研究。

1. 电容的等效电路模型研究电容是一种能够存储电荷的元件。

在直流电路中，电容的等效电路模型可以简化为一个电压源和一个电容器。

这个等效电路模型称为冲击电路模型。

在交流电路中，电容的等效电路模型更加复杂。

由于电容器对不同频率的信号具有不同的阻抗，我们需要使用复数来表示其等效电路模型。

根据电容器的阻抗公式Zc = 1/jωC，我们可以得到电容的等效电路模型为一个串联的电容和电导的组合。

2. 电感的等效电路模型研究电感是一种通过产生磁场来存储能量的元件。

在直流电路中，电感的等效电路模型可以简化为一个电压源和一个电感器。

这个等效电路模型也称为瞬态电路模型。

在交流电路中，电感的等效电路模型也需要使用复数来表示。

根据电感器的阻抗公式ZL = jωL，我们可以得到电感的等效电路模型为一个串联的电感和电阻的组合。

3. 电容与电感的串联和并联等效电路模型研究在实际电路设计中，电容和电感经常需要进行串联和并联。

为了研究它们的等效电路模型，在串联时，我们可以将电容和电感的阻抗相加；在并联时，则可以将电容和电感的阻抗取倒数相加再取倒数。

这样，我们就得到了电容与电感的串联和并联的等效电路模型。

4. 电容与电感的等效电路模型应用研究电容和电感的等效电路模型在电子设备设计中具有广泛的应用。

例如，在通信系统中，我们经常需要进行信号的滤波，这时可以利用电容和电感的等效电路模型设计滤波器。

此外，在直流稳压电源中，我们可以通过电容的等效电路模型来设计稳压电路，以保证电路输出的稳定性。

总之，电容和电感的等效电路模型研究对于电子设备的设计与应用至关重要。

通过深入研究电容和电感的基本原理以及它们的等效电路模型，我们能够更好地理解电容和电感的性质，并将其应用于电子设备的设计与优化中。

交流电路电感电容串联和并联的计算交流电路中的电感和电容元件在串联和并联时具有不同的计算方法。

首先我们来看一下电感和电容的特点以及串联和并联的基本概念。

1.电感和电容的特点电感（L）和电容（C）是被动元件，用于储存和处理电能。

电感储存电能的方式是通过产生磁场，而电容则通过储存电荷的方式储存电能。

电感的单位是亨利（H），表示当通过一个电流变化速率为1安培/秒时，其产生的磁通量变化速率为1韦伯/亨利。

电感对交流电的元件具有阻抗特性，即在交流电路中电感对电流具有阻碍作用，其阻抗（ZL）与频率（f）成正比。

电容的单位是法拉（F），表示当电容器两极板间的电压变化速率为1伏特/秒时，其充放电时存储或释放的电荷量为1库仑。

电容对交流电的元件具有容抗特性，即在交流电路中电容对电流具有阻碍作用，其容抗（ZC）与频率（f）成反比。

2.串联电感和电容的计算串联是指将电感和电容元件按顺序连接在一起，形成一个串联电路。

串联电感和电容的总阻抗是各元件阻抗之和。

对于串联电感元件，其总阻抗（ZL_total）可通过下式计算：ZL_total = ZL1 + ZL2 + … + ZLn对于串联电容元件，其总阻抗（ZC_total）可通过下式计算：ZC_total = (1/ZC1 + 1/ZC2 + … + 1/ZCn)^-13.并联电感和电容的计算并联是指将电感和电容元件同时连接到一个节点上，形成一个并联电路。

并联电感和电容的总阻抗是各元件阻抗的倒数之和的倒数。

对于并联电感元件，其总阻抗（ZL_total）可通过下式计算：ZL_total = (1/ZL1 + 1/ZL2 + … + 1/ZLn)^-1对于并联电容元件，其总阻抗（ZC_total）可通过下式计算：ZC_total = ZC1 + ZC2 + … + ZCn4.并联电感和电容的共振在一些特定频率下，电感和电容的串联和并联可能会产生共振现象。

共振频率是指电路中电感和电容元件共同产生最大电压或最大电流时的频率。

电容与电感的串并联电路电容与电感是电路中常见的两种元件，它们在电路中具有重要的作用。

在电路中，电容和电感可以进行串联和并联的组合，形成串并联电路。

本文将探讨电容与电感的串并联电路的特点、计算方法和应用。

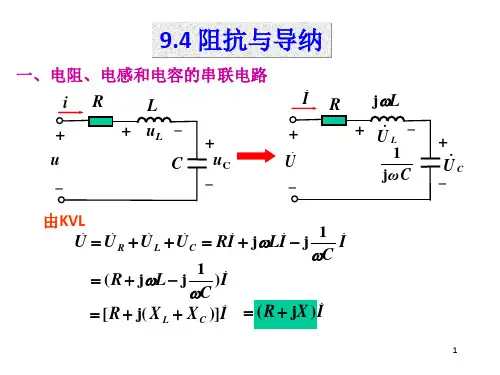
一、串联电路特点及计算方法串联电路是指电容和电感依次相连，电流在两个元件之间流动的电路。

串联电路中，电容和电感的总阻抗等于它们的阻抗之和。

电容和电感的串联电路示意图如下：（插入示意图）在串联电路中，电容的阻抗由以下公式计算：Zc = 1 / (jωC)其中，Zc为电容的阻抗，j为虚数单位，ω为频率，C为电容值。

电感的阻抗由以下公式计算：Zl = jωL其中，Zl为电感的阻抗，L为电感值。

串联电路的总阻抗Zs等于电容阻抗Zc和电感阻抗Zl之和：Zs = Zc + Zl串联电路中的电压分布按照电阻比例进行，即电压在电容和电感之间按阻抗比例分配。

二、并联电路特点及计算方法并联电路是指电容和电感同时连接在电路中，电流分别通过电容和电感的电路。

并联电路中，电容和电感的总阻抗等于它们的阻抗之和的倒数。

电容和电感的并联电路示意图如下：（插入示意图）在并联电路中，电容的阻抗由以下公式计算：Zc = 1 / (jωC)电感的阻抗由以下公式计算：Zl = jωL并联电路的总阻抗Zp等于电容阻抗Zc和电感阻抗Zl的倒数之和：Zp = 1 / (1/Zc + 1/Zl)并联电路中的电流分布通过电压比例进行，即电流在电容和电感之间按电压比例分配。

三、串并联电路的应用串并联电路在电子电路中有广泛的应用。

以下是几个典型的应用场景：1. 高通滤波器和低通滤波器：串并联电路可以用于构建不同频率特性的滤波器。

通过调节电容和电感的参数，可以实现对特定频率的信号进行滤波，达到去除高频或低频成分的目的。

2. 变压器：串并联电路在电力系统中常被用于构建变压器。

变压器通过串联和并联的电感，实现对电压的升降转换，并且能够有效进行能量传输。

3. 谐振电路：串并联电路可以用于构建谐振电路。

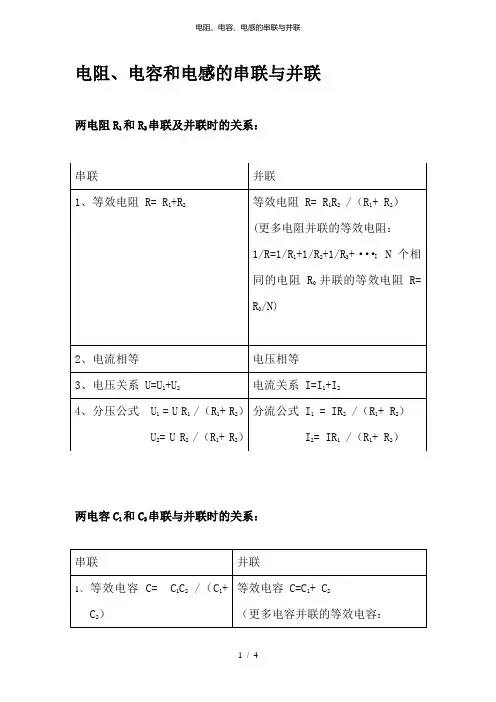
电阻、电容和电感的串联与并联两电阻R1和R2串联及并联时的关系：两电容C1和C2串联与并联时的关系：无互感的线圈的串联与并联：两线圈串联：L= L 1+ L 2两线圈并联：L= L 1L 2/（L 1+ L 2）有互感的线圈的串联与并联：有互感两线圈顺串（异名端相接）：L （顺） = L 1+ L 2+2M 有互感两线圈反串（同名端相接）：L （反）= L 1+ L 2 -2M L （顺）-L （反） =4M ， M= [L （顺） -L （反）]/4有互感两线圈并联：L （并）=（L 1 L 2-M 2）/（L 1+ L 22M ）（更多电容串联的等效电容： 1/C=1/C 1+1/C 2+1/C 3+···； N 个相同的电容C 0串联的等效电容C= C 0/N) C=C 1+C 2+C 3+···；N 个相同的电容C 0串联的等效电容C= NC 0）2、电流相等 电压相等3、电压关系 U=U 1+U 2电流关系 I=I 1+I 2 （对交流电而言） 4、分压公式 U 1 = U C 2/（C 1+ C 2）U 2= U C 1 /（C 1+ C 2）分流公式 I 1 = IC 1 /（C 1+ C 2）（对交流电而言）I 2= IC 2 /（C 1+ C 2）（对交流电而言）（2M项前的符号：同名端接在同一侧时取-，异名端接在同一侧时取+。

）（L1 L2-M2）≧0，M≤LL21M（最大）=LL21互感的耦合系数：K= M/LL21电桥直流电桥由4个电阻首尾相接构成菱形，共4端，A、C端接电源，B、D端之间为零位检测（检流计）。

上下两臂平衡时，B、D端电压差为零，检流计电流读数为0。

电桥平衡的条件：R1/R3= R2/R N（或R1R N= R2R3）R1、R2、和R3为阻值已知标准电阻，被测电阻R N = R2R3 / R1将4个电阻换为阻抗，即得到交流电桥。

压电元件的等效电路及其特点、电荷放大器
的特点
压电元件的等效电路及其特点：
压电元件常用的等效电路模型包括串联电容模型、并联电感模型和等效电阻模型。

串联电容模型：将压电元件视为一个与电容相连的可变电压源。

该模型适用于较低频率的应用。

特点是频率响应较平坦，但电压输出较低。

并联电感模型：将压电元件视为一个与电感相连的可变电流源。

该模型适用于较高频率的应用。

特点是频率响应较尖锐，但电流输出较低。

等效电阻模型：将压电元件视为一个与电阻相连的电压源和电流源的组合。

该模型适用于宽频带的应用。

特点是有较大的电流和电压输出，但频率响应较复杂。

压电元件的特点包括高灵敏度、快速响应、宽频带、线性度好以及耐压性能较好等。

电荷放大器的特点：
1. 高放大倍数：电荷放大器可以将微弱的电荷信号放大到较大的电荷输出。

2. 高输入阻抗：电荷放大器具有高输入阻抗，可以减少对被测量对象的影响，避免信号损失。

3. 低噪声：电荷放大器具有较低的噪声水平，可以提高信号的清晰度和准确性。

4. 高稳定性：电荷放大器通常具有良好的温度稳定性和时间稳定性，能够在各种环境下提供稳定的信号放大。

5. 宽频带：电荷放大器通常具有宽带特性，可以放大各种频率范围的信号。

6. 低输出阻抗：电荷放大器具有低输出阻抗，可以直接驱动负载，提高信号的传输效率。

综上所述，压电元件的等效电路模型有串联电容模型、并联电感模型和等效电阻模型，压电元件具有高灵敏度、快速响应、宽频带、线性度好以及耐压性能较好等特点；电荷放大器具有高放大倍数、高输入阻抗、低噪声、高稳定性、宽频带以及低输出阻抗等特点。