二年级奥数-搭配问题培训资料
- 格式:docx
- 大小:40.90 KB
- 文档页数:5
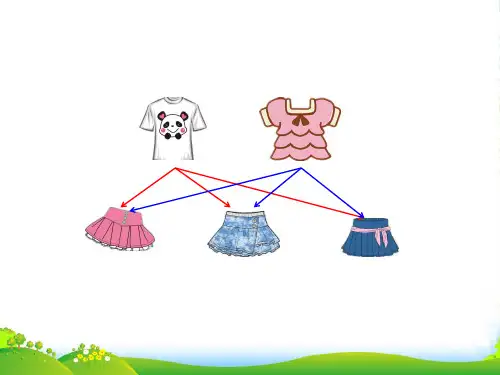


本讲我们将探索简单事物组合、排列的规律,培养有顺序地、全面地思考问题的意识.来看看最简单的搭衣服吧.上下装搭配的每种穿法需要两步来确定,一步是上装的选择,一步是下装的选择,一件上装搭配一件下装就是一种穿法.知识分类一:生活中的搭配小熊要穿衣服,它共有3件不同的上衣和4条不同的裤子.那么,小熊共有多少种不同的穿法?【提示】红色上衣可以和哪几条裤子搭配成一身衣服呢?用笔连一连.【解答】:3×4=12(种)答:小熊一共有12种穿法。
淘淘去餐厅点餐,看到菜单上写着,饮料有:可乐、橙汁;点心有:玉米、汉堡、薯条.如果饮料和点心只能各选一种,搭配成一份套餐,一共有多少种不同的搭配方法?【解答】:2×3=6(种)答:一共有6种不同的搭配方案。
知识分类二:路线问题小狗要去小猪家,必须经过小兔家,它一共有多少种不同的走法?【解答】:3×4=12(种)答:它一共有12种不同的走法。
丫丫从家到学校有3条路,从学校到少年宫有2条路,丫丫从家要到少年宫,中途必须经过学校,一共有多少种不同的走法?家少年宫学校【解答】:2×2=4(种)答:一共有4种不同的走法。
知识分类三:比赛和握手问题小明、小平、小丽、小花四个小朋友进行乒乓球单打比赛,要求每两个同学比赛一场,这次比赛一共要进行多少场?【解答】:3+2+1=6(种)答:这场比赛一共要进行6场。
白雪公主和7个小矮人在一起玩,每两个人都要握一次手,一共握了多少次手?【解答】:7+6+5+4+3+2+1=28(次)答:一共握了28次手。
体育课上,老师让小华去体育室拿3个球.体育室中有一个足球、一个篮球、一个排球和一个橄榄球.请问,小华共有多少种不同的拿法?【提示】当选好3个球之后,体育室中还剩余几个球?【解答】:4种。
跳跳的家里共有A、B、C、D、E这5盏吊灯.妈妈让跳跳关掉其中的4盏,请问,跳跳共有多少种不同的关灯方法?【解答】:5种。
知识分类四:搭配问题中的倒推法有一些游客去海边游玩,海边共停靠着7艘不同的快艇.如果这些游客要从中选出5艘快艇去游玩,那么共有多少种不同的选法?【提示】先把这7艘快艇编上序号吧!从7艘中选出5艘,那么会剩下几艘呢?【解答】:6+5+4+3+2+1=21(种)答:共有21种不同的选法熊老师有8个不同的礼物要奖励给6个优秀的学生(每人一个礼物),请问熊老师一共有多少种选法?【解答】:7+6+5+4+3+2+1=28(种)答:熊老师一共有28种选法。


第八单元数学广角——搭配(一)同步奥数1.排列问题例题1.用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?练习1.用1、4和8组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?例题2.用1、2和3组成三位数,每个数字只能用一次,能组成几个三位数?练习2.用2、3和5组成三位数,每个数字只能用一次,能组成几个三位数?例题3.把下面三种调味品装入调料盒中,一共有多少种不同的装法?练习3.把下面4本书放入4个抽屉里,每个抽屉放一本,一共有多少种不同的放法?例题4.3个人排成一排照相,一共有多少种不同的排法?练习4.小红和她的3个好朋友去照相,如果站成一排,有多少种不同的站法?例题5.老师要从班上4名同学中选出3名班干部,分别担任班长、学习委员和生活委员,问一共有多少种不同的安排方式?练习5.科技兴趣小组一共有5名同学,如果从中选出3名同学在第二天的早上、中午、晚上分别做值日,一共有多少种选法?2.组合问题例题1.有3个数5、7、9,任意选取其中2个求和,得数有几种可能?练习1.有3个数4、5、9,任意选取其中2个求积,得数有几种可能?例题2.小明在新华书店选中四本书,但他带的钱只够买其中的任意两本,小明有几种选法?练习2.任意先两项球类运动,一共有多少种不同的选法?排球 篮球 足球 羽毛球例题3.二(1)班举行羽毛球比赛,有3个人参加,每两个人之间都要比赛一场,一共要比赛多少场?练习3.巴西世界杯足球赛小组赛A 组有四支球队,每两支球队要比赛一场,一共要比赛多少场?例题4.5个人握手,每两个人握一次手,一共要握多少次手?练习4.7个人握手,每两个人握一次手,一共要握多少次手?例题5.一共有多少种不同的穿法?练习5.一顶帽子搭配一条围巾,有多少种不同的搭配方法?例题6.有多少种配餐方法?(只能 选择一种主食和一种菜)练习6.下面的早餐有( )种不同的搭配。
(饮料和点心只能各选1种)A. 8B. 6C. 4 豆浆 牛奶蛋糕 饼干 面包3.乘法原理例题1.儿童乐园经过小桥到动物园,一共有多少条路可以走?儿童乐园动物园练习1.某人要从北京到大连拿一份资料,之后再到天津开会。


第二讲搭配问题(必做与选做)1. 2套不同的运动服和3双不同的运动鞋一共有()搭配。
A. 4种B. 5种C. 6种D. 7种解析:这道题目不考虑顺序。
给2套运动服编号为①、②,给3双运动鞋编号为a、b、c。
就有①a、①b、①c、②a、②b、②c一共6种不同的搭配,可以写成2×3=6(种),故选C。
2.书店里有3种作文书,4种漫画书。
米德要买一本作文书和一本漫画书,一共有()种不同的选择。
A. 9B. 10C. 11D. 12解析:这道题目不考虑顺序。
第1种作文书可以搭配4种漫画书,第2种作文书可以搭配4种漫画书,第3种作文书也可以搭配4种漫画书,一共就有3×4=12(种)不同的选择,故选D。
3.莫拉斯餐厅里有3种套餐参加促销活动,从这三种套餐中任选一种就可以赠送牛奶、橙汁、可乐或者雪碧中的一杯饮料,一共()种不同的搭配。
A. 15B. 12C. 10D. 7这道题目跟顺序无关。
1种套餐有4种饮料可以选择,所以3种套餐就有3×4=12(种)搭配,故选B。
4. 6个好朋友见面,每2个人拥抱一次,一共拥抱了()次。
A. 12B. 15C. 21D. 30解析:这道题目不考虑顺序。
将6个小朋友分别编号为①,②,③,④,⑤,⑥。
①跟②拥抱后②就不用再跟①拥抱了。
先让①跟②-⑥拥抱,就有5次;再让②跟③-⑥拥抱就有4次……以此类推,一共拥抱了5+4+3+2+1=15(次),故选B。
5. 7个小组进行口算比赛,每2组比赛一场,一共有()场比赛。
A. 7B. 14C. 21D. 28解析:这道题目不考虑顺序,将7个组分别编号为①,②,③,④,⑤,⑥,⑦。
①跟②比赛后,②就不用再跟①比赛了。
第①组跟②-⑦组比赛,就是6场,第②组跟③-⑦组比赛,就是5场……以此类推,一共有6+5+4+3+2+1=21(场)比赛,故选C。
6.二年级5个班级进行踢毽子比赛,每2个班比赛一场,一共有()场比赛。

二年级数学上册8 数学广角--搭配(一)必备知识点二年级数学上册第八单元“数学广角——搭配(一)”的必备知识点主要包括以下内容:一、排列与组合的基本概念1. 排列:按照一定的顺序排列事物,需要考虑事物的先后顺序。
2. 组合:从多个事物中选取一部分事物,不考虑选取事物的先后顺序。
二、简单的排列1. 确定顺序:在进行排列时,需要明确事物的排列顺序。
2. 逐步排列:可以固定一个元素,再与其余元素进行排列,依次类推,直到完成所有排列。
3. 不重不漏:在排列过程中,要确保每个元素都被考虑到,并且不重复排列。
三、简单的组合1. 选择元素:从多个元素中选择一部分元素进行组合。
2. 不考虑顺序:组合时不需要考虑元素的先后顺序。
3. 列举法:对于较小的组合问题,可以通过列举所有可能的组合来求解。
四、排列与组合的应用1. 日常生活中的问题:如握手问题、搭配衣服问题等,可以通过排列或组合的方法来解决。
2. 实际问题:如密码锁的设置、电话号码的组合等,也需要运用排列或组合的知识。
五、排列与组合的区别与联系1. 区别:排列需要考虑元素的先后顺序,而组合不需要。
2. 联系:在某些情况下,排列和组合可以相互转化。
例如,在求解某些组合问题时,可以先通过排列得到所有可能的顺序,然后再去掉顺序的影响,从而得到组合的结果。
六、数学方法的应用1. 有序思考:在进行排列或组合时,需要有序地进行思考,避免重复或遗漏。
2. 图形辅助:可以通过画图或列表等方式来辅助思考,使问题更加直观易懂。
3. 逻辑推理:在解决排列或组合问题时,需要运用逻辑推理的方法,确保每一步的推理都是正确的。
七、练习题与拓展1. 基础练习题:通过完成一些基础的排列与组合练习题,巩固所学知识。
2. 拓展题目:尝试解决一些稍微复杂一些的排列与组合问题,提高解题能力。
综上所述,二年级数学上册第八单元“数学广角——搭配(一)”的必备知识点涵盖了排列与组合的基本概念、简单的排列与组合、排列与组合的应用、排列与组合的区别与联系以及数学方法的应用等方面。
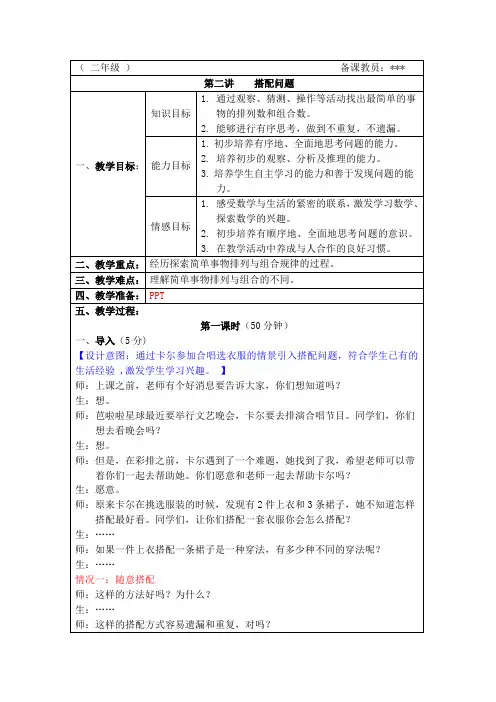
板书:遗漏、重复师:那怎么样才能够不遗漏、不重复地找出所有的穿法呢?生:……师:其实只要有序搭配就能不遗漏、不重复的找出所有的穿法了。
所以,今天这节课我们就来研究生活中的数学问题——搭配问题。
情况二:固定搭配师:这样的方法好吗?为什么?生:……师:这样的搭配方式,不遗漏、不重复,对吗?板书:不遗漏、不重复师:像这种和顺序无关的,我们把这一类数学问题叫做“组合”。
所以,今天这节课我们就来研究生活中的数学问题——搭配问题。
【探究新知,引入新课:在学生已经掌握一些乘法计算基础上,还需要初步理解不同物体进行组合会造成种类的差别。
】【板书课题:搭配问题】二、探索发现授课(40分)(一)例题1:(10分)阿派准备放学后回家换上运动鞋再去爬山,已知从学校有2条路可以回家,从家有4条路可以去爬山。
阿派有多少种不同的走法?(学校、家、山的位置如下图)讲解重点:路线不同,目的地相同,注意不遗漏路线。
师:同学们,我们来看下题目中的问题是什么?生:阿派有多少种不同的走法。
师:阿派是从哪里出发?生:从学校出发。
师:不错,阿派最后要去做什么?生:去爬山。
师:学校到山之间还要经过哪里?生:阿派自己家。
师:所以阿派要先从学校出发经过家,最后到爬山的地方。
我们已经知道从学校有2条路可以回家,从家有4条路可以去爬山。
这里路线的选择,我们要注意什么?生:注意不遗漏路线。
师:很好,奖励2个大拇指,那么为了帮助理解,我们给每条路编号。
我们先来看1号路线,从学校出发走1号路线回到家后,有几种情况可以去山的位置?生:①③、①④、①⑤、①⑥,一共是4种路线。
师:谁能再来说说如果阿派走2号路线,会有几种情况?生:②③、②④、②⑤、②⑥,也是4条情况。
师:所以阿派有多少种不同的走法?生:4+4=8(种)。
师:这里可以用加法列式,还有不同的方法吗?生:可以用乘法,4×2=8(种)。
师:你是怎么想的用乘法列式?生:乘法是几个相同加数的简便运算。

第1讲常见搭配问题-2022-2023学年二年级数学思维拓展讲义(通用版)一、教学目标1.了解搭配的概念。
2.掌握常见的搭配问题,包括“一共有多少种”,“每组的可能性有多少种”等问题的解决方法。
3.能够灵活运用所学内容解决相关问题。
二、教学内容1.搭配的概念让学生看一下下列图片:问:这张图中,你最喜欢哪个卡通人物?Bob和Sue是好朋友,他们想一起去游乐园玩,每个游乐项目只能坐两个人。
他们想先去划船,再去玩碰碰车。
现在有四个船和三辆碰碰车可供选择。
那么,他们一共有多少种玩法呢?2.“一共有多少种”问题的解决方法让学生想一想,在这道题中,我们可以用什么方法来计算他们一共有多少种玩法呢?教师给出提示:可以用乘法原理来解决。
乘法原理指的是:如果一个问题有m个步骤,而第一步有n1种选择,第二步有n2种选择,以此类推,最后一步有nk种选择,那么这整个问题共有n1×n2×n3×…×nk种选择。
让学生操作一下,看看能不能用乘法原理解决这个问题。
教师要注意,这一部分的学习要尽量贴近生活,使学生能够通过具体的例子加深理解。
3.每组的可能性有多少种问题的解决方法让学生看一下下列图片:问:这张图中,所有方格中的数字都不重复,每行每列的数字之和相等,而且都是26。
请问,多少种可能的排列方式呢?让学生想一想,这道问题与前面的问题有何不同?我们能否用乘法原理来解决它呢?教师要引导学生,通过观察题目的特点,理解它与前面问题的区别,并引出“组合”的概念。
让学生自己研究,发现组合的特点:无序性,不重复。
组合的公式:C(n,m)=n!/[m!(n-m)!]随后,教师可以让学生说出组合公式的含义:从n个物品中选择m个物品的所有方式。
4.解决实际问题接下来,让学生试着解决下面这个实际问题:班级里有10个男生和8个女生,老师要从班级里选出5名学生组成一个文艺团队。
问:老师一共有多少种选择的可能性呢?教师可以让学生,通过理解组合的公式,完成这个问题的解决方法。
二年级奥数-搭配问题(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--授课对象授课教师授课时间授课题目搭配问题课型二年级奥数使用教具教学目标1、使学生了解生活中的一些简单搭配现象,通过观察、猜测、实验等数学活动,提出不同的搭配方案。
2、经历探索简单事物搭配规律的过程,培养学生初步的观察、分析及推理能力以及有顺序地、全面地思考问题的意识。
教学重点和难点有序地找出简单事物的搭配数。
参考教材教学流程及授课详案【课题引入】有6个小朋友一起玩握手游戏,每2人握手1次,一共要握几次手?【例1】佳佳最喜欢玩给娃娃搭配服装的游戏。
一顶帽子搭配一条裙子,一共有几种不同的搭配?练习:于老师有5件不同颜色的上衣,3条颜色不同的裤子,他想穿衣服去上课,可有多少种不同的搭配方法?【例2】强强给妈妈买生日礼物。
用一枝鲜花搭配一块蛋糕,一共有几种不同的搭配呢?想一想,生活中,也有这样的搭配问题吗练习:学校食堂今天午餐的菜谱上有2个肉菜和2个素菜,小明想买1个肉菜和1个素菜,问共有几种的搭配方法?【例3】4位学生和2位老师进行乒乓球单打比赛,如果每位学生和每位老师、都打一局,一共打几局?练习:4个男同学和3个女同学进行乒乓球单打比赛,如果每个男同学和每个女同学都打1盘,一共要打几盘?【例4】食品店有奶糖3种,水果糖5种,现在从奶糖、水果糖中各拿1种混合成什锦糖出售。
有多少种配糖的方法?【例5】从小明家到电影院有5条路可走,从电影院到文化宫有4条路可走。
小明从家先去电影院,再到文化宫,一共有几种不同的走法?。
授课对象
授课教师
授课时间授课题目搭配问题课型二年级奥数使用教具
教学目标
1、使学生了解生活中的一些简单搭配现象,通过观察、猜测、实验等数学活动,提出不同的搭配方案。
2、经历探索简单事物搭配规律的过程,培养学生初步的观察、分析及推理能力以及有顺序地、全面地思考问题的意识。
教学重点和难点有序地找出简单事物的搭配数。
参考教材
教学流程及授课详案
【课题引入】
有6个小朋友一起玩握手游戏,每2人握手1次,一共要握几次手?
一共有几种不同的搭配?
【例1】佳佳最喜欢玩给娃娃搭配服装的游戏一顶帽子搭配一条裙子,
练习:
于老师有5件不同颜色的上衣,3条颜色不同的裤子,他想穿衣服去上课,
可有多少种不同的搭配方法?
种不同的搭配呢?
想一想,生活中,也有这样的搭配问题吗?
练习:学校食堂今天午餐的菜谱上有 2个肉菜和2个素 菜,小明想买1个
肉菜和1个素菜,问共有几种的搭配方法?
【例2】强强给妈妈买生日礼物。
用一枝鲜花搭配一块蛋糕,一共有几
【例3】4位学生和2位老师进行乒乓球单打比赛,如果每位学生和每位老师、都打一局,一共打几局?
练习:4个男同学和3个女同学进行乒乓球单打比赛,如果每个男同学和每个女同学都打1盘,一共要打几盘?
【例4】食品店有奶糖3种,水果糖5种,现在从奶糖、水果糖中各拿1种混合成什锦糖出售。
有多少种配糖的方法?
【例5】从小明家到电影院有5条路可走,从电影院到文化宫有4条路可走小明从家先去电影院,再到文化宫,一共有几种不同的走法?
练习:从甲地到乙地有2条路可走,从乙地到丙地有3条路可走,从甲地到丙地共有4条不同的路可走,问从甲地到丙地共有多少种不同的走法?
【让我们做一做】。