热点专题8 动态几何问题(解析版)

专题08 动态几何类压轴题一、单选题1．如图，在ABC 中，90ACB ∠=︒，4AC =，3BC =．线段PE 的两个端点都在AB 上，且1PE =，P 从点A 出发，沿AB 方向运动，当E 到达点B 时，P 停止运动，在整个运动过程中，空白部分面积DPEC S 四边形的大小变化的情况是（ ）A ．一直减小B ．一直增大C ．先增大后减小D ．先减小后增大【答案】C【分析】 设PD=x ，AB 边上的高为h ，求出h ，并运用相似三角形的性质求出AD ，构建二次函数，利用二次函数的性质解决问题即可．【详解】在Rt ABC ∆中，90ACB ∠=︒，4AC =，3BC =，5AB ∴===，设PD x =，则1205x ≤≤，AB 边上的高为h ，125AC BC h AB ==， //PD BC ， ADP ACB ∆∆∽∴， ∴PD AD BC AC=， 43AD x ∴=，53PA x = 221415122242333(4)2()23235353210△△APD CBE S S x x x x x x ∴+=+-=-+=-+， ()22233323()()32103210276△△△四边形ABC APD CBE DPEC S x S x S S ∴+-----+=-==， ∵203-<，∴32x≤<时，DPECS四边形随x的增大而增大，31225x<≤时，DPECS四边形随x的增大而减小，故选：C．【点睛】本题考查相似三角形的判定和性质，动点问题的函数图象，三角形面积，勾股定理等知识，解题的关键是构建二次函数，学会利用二次函数的增减性解决问题．2．如图，已知△ABC中，∠ACB=90°，∠BAC=30°，AB=6，点D为直线AB上一动点，将线段CD绕点C 逆时针旋转60°得到线段CE，连接ED、BE，当BE最小时，线段AD的值为（）A．5.5B．6C．7.5D．8【答案】C【分析】以BC为边作等边△BCF，连接DF，可证△BCE≌△FCD，可得BE=DF，则DF⊥AB时，DF的长最小，即BE的长最小，即可求解．【详解】如图，以BC为边作等边△BCF，连接DF，∵∠ACB=90°，∠BAC=30°，AB=6，∴∠ABC=60°，BC=3，∵将线段CD绕点C逆时针旋转60°得到线段CE，∴CD=CE，∠DCE=60°，∵△BCF是等边三角形，∴CF=BC=BF=3，∠BCF=∠DCE =60°，∴∠BCE=∠DCF，且BC=CF，DC=CE，∴△BCE≌△FCD(SAS)，∴ BE= DF，∴DF ⊥AB 时，DF 的长最小，即BE 的长最小，如图，此时作FD AB '⊥，∵FBD '∠=180°-60°-60°=60°，D F AB '⊥，∴ 1 1.52BD BF '==， ∴7.5AD AB BD '=+='，故选：C ．【点睛】本题考查了旋转的性质，全等三角形的判定与性质，直角三角形的性质，添加恰当的辅助线构造全等三角形是解题关键．二、解答题3．如图，在等腰直角三角形△ABC ，∠ABC=90°，AB=6，P 是射线AB 上一个动点，连接CP ，以CP 为斜边构造等腰直角△CDP （C 、D 、P 按逆时针方向），M 为CP 的中点，连接AD ，MB ．（1）当点P 在线段AB 上运动时，求证：△CDA ∽CMB ；（2）设AP x =，△ADP 的面积为y ．①当012x <<时，求y 关于x 的函数表达式；②记D 关于直线AC 的对称点为D ，若D 在△APC 的内部，求y 的取值范围．【答案】（1）见解析；（2）①2134y x x =-+；②189y << 【分析】 （1）根据等腰直角三角形的性质得BCM ACD ∠=∠，CB CM CA CD =，即可证明结论； （2）①分类讨论，当06x <≤时，或当612x <<时，过点D 作DE AB ⊥于点E ，根据（1）的相似三角形，得到AD=AP ，并且用x 表示出长度，即可求出函数表达式；②当点D 在APC △内部时，06x <<，过点P 作PN AC ⊥于点N ，利用面积法表示出PN 的长，得到x 的范围，即可求出y 的范围．【详解】解：（1）∵ABC 和CDP 是等腰直角三角形，∴45ACB DCP ∠=∠=︒，∴ACB ACP DCP ACP ∠-∠=∠-∠，即BCM ACD ∠=∠，∵ABC 和CDP 是等腰直角三角形，∴CB CA ==，CP CD = ∵M 是CP 的中点， ∴12CM CP =，∴21CM CD ==， ∴CB CM CA CD =， ∴CDA CMB ；（2）①∵M 是CP 中点， ∴12BM MC PC ==，若06x <≤，如图，过点D 作DE AB ⊥于点E ，∵AP x =，∴6PB x =-，∴PC = ∵DC DA MC MB=，∴2DC DA DP PC ==== ∵DE AB ⊥，∴12AE EP x ==，∴162DE x ===-， ∴21111632224ADP S AP DE x x x x ⎛⎫=⋅=⋅-=-+ ⎪⎝⎭； 若612x <<，如图，过点D 作DE AB ⊥于点E ，6BP x =-，PC =DC DA DP ====12AE EP x ==，162DE x ===-， ∴21111632224ADP S AP DE x x x x ⎛⎫=⋅=⋅-=-+ ⎪⎝⎭， 综上：2134y x x =-+； ②当点D 在APC △内部时，06x <<，点P 越往右，点D 离AC 越近，当点D 在PC 上时，过点P 作PN AC ⊥于点N ，∴DCA ACP PCB ∠=∠=∠，∴CP 为ACB ∠的角平分线，∴PN PB =，∵1131822ABC APC BPC S S S AC PN BC PB PN =+=⋅+⋅=+=，∴6PN PB ==，∴12AP AB PB =-=-，当126x -<<时，点D 在APC △内部，则根据2134y x x =-+，求出189y <<． 【点睛】本题考查相似三角形的综合题，解题的关键是掌握相似三角形的性质和判定，二次函数的几何运用，利用分类讨论的思想进行求解．4．如图，在平面直角坐标系中，直线3y x =-+与抛物线2y x bx c =-++交于A 、B 两点，点A 在x 轴上，点B 在y 轴上，点P 是抛物线上任意一点，过点P 作PQ ⊥y 轴，交直线AB 于点Q ，连接BP ，设点P 的横坐标为m ，△PQB 的边PQ 与PQ 边上的高之差为d ．（1）求此抛物线解析式.（2）求点Q 的横坐标（用含m 的代数式表示）；（3）∠BQP 为锐角.①求d 关于m 的函数关系式；②当△AOB 的顶点到PQ 的最短距离等于d 时，直接写出m 的值．【答案】（1）2y x 2x 3=-++；（2）22m m -；（3）①d m =-；②m =【分析】 （1）由直线解析式求解出A 、B 的坐标，再代入抛物线解析式求解即可；（2）由于PQ 垂直于y 轴，则P 、Q 的纵坐标相等，因此求出P 的纵坐标，再代入直线解析式求解Q 的横坐标即可；（3）①根据题中对d 的定义，分别求出PQ ，以及PQ 边上的高，再作差即可；②根据△AOB 的顶点到PQ 的最短距离等于d 时建立关于m 的一元二次方程求解，并注意运用条件判断合适的值即可．【详解】（1）由直线3y x =-+可知，A(3，0)，B(0，3)，将A(3，0)，B(0，3)代入2y x bx c =-++得： 9303b c c -++=⎧⎨=⎩，解得：23b c =⎧⎨=⎩， ∴抛物线的解析式为：2y x 2x 3=-++；（2）由题可知，P 、Q 的纵坐标相等，∵P 的横坐标为m ，且P 是抛物线上任意一点，∴P 的纵坐标为223y m m =-++，∴Q 的纵坐标为223y m m =-++，又∵Q 在直线上，∴将223y m m =-++代入3y x =-+得： 2233m m x -++=-+，解得：22x m m =-，∴Q 的横坐标为22m m -；（3）①由题意，()B P d PQ y y =--，由（2）可知： 2232Q P m P m m m m Q x x =-==---，()222332B P y m m m y m -+=+--=- ∴()B P d PQ y y m =--=-，∴d m =-；②由题可知：△AOB 为等腰直角三角形，其顶点为O ，则O 到PQ 的距离为223m m -++，当△AOB 的顶点到PQ 的最短距离等于d 时， 223m m m -++=-，解得：32m =， ∵∠BQP 为锐角，∴32m -=． 【点睛】本题考查二次函数与一次函数的综合运用，理解二次函数的性质，仔细分析题中表达的数量关系是解题关键．5．已知一次函数4y x =+的图象与二次函数()2y ax x =-的图象相交于()1,A b -和B ，点P 是线段AB 上的动点（不与A 、B 重合），过点P 作PC x ⊥轴，与二次函数()2y ax x =-的图象交于点C ．（1）求a 、b 的值；（2）如图1，M 为APC ∠内一点，且1PM =，E ，F 分别为边PA 和PC 上两个动点，求MEF 周长的最小值；（3）若PAC △是直角三角形，求点C 的坐标．【答案】（1）3b =，1a =；（2（3）()2,0C 或()3,3．【分析】∠1∠∠A∠∠∠∠∠∠b∠∠∠∠∠A∠∠∠∠∠∠∠a∠∠∠(2)∠∠∠M∠∠∠∠AB∠PC ∠∠∠∠,M M '''∠∠∠∠ ,,M M PM PM ''''''∠∠∠MEF∠∠∠∠∠∠∠∠ M M '''∠∠∠∠∠∠∠290M PM APC ∠=∠'=''︒∠∠∠ M M ==''='∠3∠∠∠PAC=90°∠∠ACP=90°∠∠∠∠∠∠∠【详解】解：∠1∠∠A 在直线y=x+4∠∠∠b=-1+4=3∠∠A∠∠∠∠∠-1∠3∠∠∠A∠∠∠∠∠y=ax(x -2)∠∠∠3=-a(-1-2)∠∠3=3a∠∠a=1∠∠3b =∠ 1a =∠∠2∠∠∠∠∠∠∠M ∠∠∠∠AB ∠PC ∠∠∠∠'M ∠''M ∠∠∠∠'''M M ∠'PM ∠''PM ∠∠MEF ∠∠∠∠∠∠∠'''M M ∠∠∠∠∠∠∠∠∠∠∠PM PM PM M PA APM MPC CPM ==∠=∠∠=∠''''''，，∠∠290M PM APC ∠=∠'=''︒,∠'''M M ===∠∠3∠∠(),4P m m +∠∠()2,2C m m m -∠ ∠∠∠PAC=90°∠∠222AP AC PC +=∠()()()()2222222112334m m m m m m ++++--=--∠ ∠∠1m =-∠∠∠∠∠2m =∠∠()2,0C ∠∠∠ACP=90°∠∠222AC PC AP +=∠()()()()2222221233421m m m m m m ++--+--=+∠ ∠∠1m =-∠∠∠∠∠3m =∠4m =∠∠∠∠∠∠()3,3C ∠∠∠()2,0C ∠()3,3∠【点睛】 本题考查二次函数与一次函数的综合运用，熟练掌握二次函数的图象与性质、一次函数的图象与性质、轴对称的性质、勾股定理的应用是解题关键．6．如图所示，直线AB 交x 轴于点(),0A a ，交y 轴于点()0,B b ，且a 、b ()240a -=． （1）如图1，若C 的坐标为()1,0-，且AH BC ⊥于点H ，AH 交OB 于点P ，试求点Р的坐标； （2）如图2，连接OH ，求证45OHP ∠=︒；（3）如图3，若点D 为AB 的中点，点M 为y 轴正半轴上一动点，连接MD ，过D 作DN DM ⊥交x 轴于N 点，当M 点在y 轴正半轴上运动的过程中，式子BDM ADN S S -△△的值是否发生改变？如发生改变，求出该式子的值的变化范围；若不改变，求该式子的值．【答案】（1）P 的坐标为()0,1-；（2）见解析；（3）S △BDM -S △ADN 的值不发生改变，等于4【分析】（1）先依据非负数的性质求得a 、b 的值，从而可得到OA=OB ，然后再∠COB=∠POA=90°，∠OAP=∠OBC ，最后，依据ASA 可证明∠OAP ≌△OBC ，得出OP=OC ，从而得出点P 的坐标；（2）过O 分别作OM ⊥CB 于M 点，作ON ⊥HA 于N 点，利用AAS 证明∠COM ≌△PON ，得出OM=ON ，再根据角平分线得到判定即可得出HO 平分∠CHA ，从而求出∠OHP ；（3）连接OD ，易证∠ODM ≌△ADN ，从而有S △ODM =S △ADN ，由此可得S △BDM -S △ADN =S △BDM -S △ODM =S △BOD =12S △AOB ． 【详解】解：（1()240a -=∴a+b=0，a -4=0，∴a=4，b=-4，则OA=OB=4．∵AH ⊥BC ，则∠AHC=90°，∠COB=90°，∴∠HAC+∠ACH=∠OBC+∠OCB=90°，∴∠HAC=∠OBC ．在∠OAP 和∠OBC 中， 90COB POA OA OB OAP OBC ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩∴△OAP ≌△OBC （AAS ）；∴OP=OC∵C 的坐标为()1,0-，∴OC=1∴OP=1∴P 的坐标为()0,1-（2）过O 分别作OM ⊥CB 于M 点，作ON ⊥HA 于N 点．在四边形OMHN 中，∠MON=360°-3×90°=90°，∴∠COM=∠PON=90°-∠MOP ．在∠COM 和∠PON 中，90COM PON OMC ONP OC OP ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩∴△COM ≌△PON （AAS ），∴OM=ON ．∵OM ⊥CB ，ON ⊥HA ，∴HO 平分∠CHA ，1452︒∴∠=∠=OHP CHA （2）S △BDM -S △ADN 的值不发生改变，等于4．理由如下：如图：连接OD ．∵∠AOB=90°，OA=OB ，D 为AB 的中点，∴OD ⊥AB ，∠BOD=∠AOD=45°，OD=DA=BD∴∠OAD=45°，∠MOD=90°+45°=135°，∴∠DAN=135°=∠MOD ．∵MD ⊥ND 即∠MDN=90°，∴∠MDO=∠NDA=90°-∠MDA ．在∠ODM 和∠ADN 中，,MDO NDA DOM DAN OD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ODM ≌△ADN （ASA ），∴S △ODM =S △ADN ， ∴12S ∆∆∆∆∆∆-=-==BDM ADN BDM ODM BOD AOB S S S S S ∴111144422S 22∆∆-=⨯⋅=⨯⨯⨯=BDM ADN S AO BO 【点睛】本题考查了全等三角形的判定与性质、角平分线的判定、二次根式及完全平方式的非负性等知识，在解决第（2）小题的过程中还用到了等积变换，而运用全等三角形的性质则是解决本题的关键．7．如图，已知等边ABC 的边长为16，点P 是AB 边上的一个动点（与点A 、B 不重合）．直线l 是经过点P 的一条直线，把ABC 沿直线l 折叠，点B 的对应点是点B '．（1）如图1，当8PB =时，若点B '恰好在AC 边上，则AB '的长度为_________；（2）如图2，当10PB =时，若直线//l AC ，则BB '的长度为_______；（3）如图3，点P 在AB 边上运动过程中，若直线l 始终垂直于AC ，ACB '△的面积是否变化？若变化，说明理由；若不变化，求出面积；（4）当12PB =时，在直线l 变化过程中，求ACB '△面积的最大值．【答案】（1）8或0；（2）（3）面积不变，（4）最大为96+【分析】（1）证明△APB′是等边三角形即可解决问题．（2）如图2中，设直线l 交BC 于点E ．连接BB′交PE 于O ．证明△PEB 是等边三角形，求出OB 即可解决问题．（3）如图3中，结论：面积不变．证明BB′∥AC 即可．（4）如图4中，当B′P ⊥AC 时，△ACB′的面积最大，设直线PB′交AC 于E ，求出B′E 即可解决问题．【详解】解：（1）如图1中，∵ABC 是等边三角形，∴60A ∠=︒，16AB BC CA ===，∵8PB =，∵8PB PB PA ==='，∵60A ∠=︒，∴APB '是等边三角形，∴8AB AP '==．当直线l 经过C 时，点B '与A 重合，此时0AB '=，故答案为8或0．（2）如图2中，设直线l 交BC 于点E ．连接BB '交PE 于O ．∵//PE AC ，∴60BPE A ∠=∠=︒，60BEP C ∠=∠=︒，∴PEB △是等边三角形，∵10PB =，且由于折叠，∴B ，B '关于PE 对称，∴BB PE '⊥，2BB OB '=，∴OP=12PB=5，∴OB =，∴BB '=故答案为（3）如图3中，结论：面积不变．连接BB ′，过点A 作AF ⊥BC ，垂足为F ，∵B ，B '关于直线l 对称，∴BB '⊥直线l ，∵直线l AC ⊥，∴//AC BB '，∴ACB ACB S S '=△△，∵BC=AB=AC=16，∴BF=8，∴=，∴1162ACB ACB S S '==⨯⨯= （4）如图4中，∵点B 和B′关于经过点P 的直线对称，∴B′到点P 的距离与点B 到点P 的距离相等，当B P AC '⊥时，ACB '△的面积最大，设直线PB '交AC 于E ，在Rt APE 中，∵4PA =，60PAE ∠=︒，∴AE=2，∴PE ==∵BP=B′P=12，∴12EB EP B P '=++'=∴(11612962ACB S '=⨯⨯+=+△ 【点睛】本题属于几何变换综合题，考查了等边三角形的性质和判定，轴对称变换，平行线的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考压轴题．8．已知抛物线2122y x x =-与x 轴交于点O 、A 两点，顶点为B ．（1）直接写出：A 点坐标________ ，B 点坐标_______ ，△ABO 的形状是_______；（2）如图，直线y x m =+(m<0)交抛物线于E 、F(E 在F 右边)，交对称轴于M ，交y 轴于N ．若EM -FN=MN ，求m 的值；（3）在(2)的条件下，y 轴上有一动点P ，当∠EPF 最大时，请直接写出此时P 点坐标___________【答案】（1）（4,0），（2，-2），等腰直角三角形；（2）52m =-；（3）（052-） 【分析】（1）令2122y x x =-中y=0，求出A 的坐标，由22112(2)242y x x x =--+=，求出顶点B 坐标，利用勾股定理的逆定理判定△ABO 是等腰直角三角形；（2）过点E 作EG ⊥y 轴于G ，过点F 作FH ⊥y 轴于H ，过点M 作MC ⊥y 轴于C ，设y x m =+（m ＜0）交x 轴于D ，先求出∠OND=45°，利用锐角三角函数可得FN=sin 45HF ︒，MN=sin 45CM ︒，EN=sin 45EG ︒，联立解析式求出点E 、F 的横坐标，最后根据已知等式即可列出方程，求出m ； （3）作以EF 为弦且与y 轴相切的圆D ，切点为P ，连接EP 、FP ，利用圆周角定理和三角形外角的性质先证此时∠EPF 最大，然后确定点P 的坐标，设点P 的坐标为（0，p ），用含p 的式子表示出DP 和DF ，列出方程即可求出结论．【详解】解：（1）令2122y x x =-中y=0，得21202x x -=， 解得x=0或x=4，∴A （4，0）； ∵22112(2)222y x x x =-=--， ∴顶点B 坐标为（2，-2）；连接AB 、OB ，∴22416OA ==，()()22224820AB =-+-=-，()()22220820OB =-+-=-，∴222OA AB OB =+，AB=OB ，∴△ABO 是等腰直角三角形，故答案为：（4,0），（2，-2），等腰直角三角形；（2）过点E 作EG ⊥y 轴于G ，过点F 作FH ⊥y 轴于H ，过点M 作MC ⊥y 轴于C ，设y x m =+（m ＜0）交x 轴于D将x=0代入y x m =+中，解得y=m ；将y=0代入y x m =+中，解得x=-m∴点N 的坐标为（0，m ），点D 的坐标为（-m ，0）∴ON=OD∴△OND 为等腰直角三角形∴∠OND=45°∴FN=sin 45HF ︒，MN=sin 45CM ︒，EN=sin 45EG ︒， ∴EM=EN －)EG CM - ∵抛物线2122y x x =-的对称轴为直线x=2 ∴CM=2 联立2122y x x y x m⎧=-⎪⎨⎪=+⎩消去y ，解得：x 1=3x 2=3+∴点F的横坐标为3-E的横坐标为3+∴HF=3-EG=3+∴3，MN=)321+=∵EM -FN=MN ，1+3-=解得：52m =-， 经检验，52m =-是原方程的解； （3）如下图所示，作以EF 为弦且与y 轴相切的圆D ，切点为P ，连接EP 、FP ，先证此时∠EPF 最大，在y 轴上任取一点P '，连接EP FP ''、，FP '与圆D 交于点C∴∠EPF=∠ECF∵∠ECF是△EP C'的外角∠∴∠ECF＞EP C'∴∠EPF＞EP F'∠即此时∠EPF最大，然后确定点P的坐标，设点P的坐标为（0，p），如下图所示，连接DP、DF，作EF的中垂线ST，交EF于S，交y轴于T，过点S作SK⊥y轴于K由（2）知52m =- ∴点E 的坐标为（5，52），点F 的坐标为（1，32-） ∴点S 的坐标为（3，12）， ∴OK=12，SK=3 由（2）知：∠SNO=45°，∵∠TSN=90°∴∠STK=45°∴△TSK 、△TDP 为等腰直角三角形∴TK=SK=3，TP=DP∴TP=TK ＋OK －OP=72p - ∴DP=72p -， ∴点D 的坐标为（72p -，p ）∴∵DP=DF∴72p -解得：52-或p=52∵∴ES=12EF=SK ∴以EF 为直径的圆与y 轴相离∴点P 必在以EF 为直径的圆的外边∴△EPF 为锐角三角形∴点D 在△EPF 内部，也必在S 的左上方∴点D 的纵坐标大于0，即p ＞0∴52∴点P 的坐标为（052）． 【点睛】此题考查的是二次函数、一次函数和圆的综合大题，掌握二次函数图象及性质、求一次函数解析式、等腰直角三角形的判定及性质、圆周角定理、锐角三角函数是解题关键．9．如图，已知在Rt ABC 中，90ACB ∠=︒，4AC BC ==，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，EDB ADC ∠=∠，过点E 作EF AD ⊥，垂足为点G ，交射线AC 于点F ．（1）如果点D 为边BC 的中点，求DAB ∠的正切值；（2）当点F 在边AC 上时，设CD x =，CF y =，求y 关于x 的函数解析式及定义域；（3）联结DF 如果CDF 与AGE 相似，求线段CD 的长．【答案】（1）1tan 3DAB ∠=；（2）()2402y x x =-+<≤；（3）-4、8-． 【分析】（1））过点D 作DH AB ⊥于H ，在Rt ACB 中，利用勾股定理解得AD 、AB 的长，再结合等积法，解得DH 、AH 的长即可解题；（2）根据相似三角形对应边成比例的性质，表示()444x EH x -=+， 再证明AFE BDE 由AF AE DB BE =即)4444x y x x --=-+得到与x 的关系； （3）根据相似三角形对应边成比例的性质，结合（2）中y 关于x 的函数解析式联立方程组，继而解得x 、y 的值即可解题．【详解】（1）过点D 作DH AB ⊥于H ，在Rt ACB 中，AD =AB ∴==142ADB SDB AC ∴=⋅= 12ADB S AB DH =⋅DH ∴=AH ==1tan 3DH DAB AH ∴∠==； （2）过E 作EH ⊥CB 于H∵EDB ADC ∠=∠，90C EHD ∠=∠=︒∴ACD EHD ． ∴AC EH CD DH = 即44EH x x EH=--． ∴()444x EH x -=+ ．∵EH ⊥CB ，90ACB ∠=︒，4AC BC ==∴)44x EB x -==+，AB =∴)44x AE x -=+ ∵EF AD ⊥，90C ∠=︒∴AFG ADC ∠=∠ ．∵EDB ADC ∠=∠∴AFG EDB ∠=∠．∵45FAE B ∠=∠=︒∴AFE BDE ． ∴AF AE DB BE =即)4444x y x x --=-+． 整理得，()2402y x x =-+<≤；（3）在Rt △MDB 中，DB=4-x,所以MD=MB=(4).2x - 在Rt △ADM 中，AM=AB 一MB=)(4).22x x -=+ 所以tan ∠DAB=44DM x AM x-=⋅+ 按照点F 的位置，分两种情况讨论△CDF 与△AGE 相似:①点F 在线段AC 上，此时y=4-2x.如图，如果∠FDC=∠DAB ，由tan ∠FDC=tan ∠DAB,得44y x x x-=⋅+ 结合y=4-2x ，整理，得x2+8x+16=0.解得-4 或--4 （舍去）, 如果∠CFD=∠DAB ，由tan ∠CFD=tan ∠DAB ，得4.4x x y x-=+ 结合y=4- -2x,整理，得x 2-16x+16=0.解得8x =-8+②点F 在线段AC 的延长线上，此时y=2x -4如图如果∠FDC=∠DAB,由44y x x x-=+结合y=2x -4，整理，得23160.x -=解得或3-（舍去） 如果∠CFD=∠DAB,44x x y x -=+与y=2x -4 整理，得238160.x x -+=此方程无解.综上，CD 的值为-4、8-． 【点睛】本题考查勾股定理、相似三角形的性质，涉及解二元一次方程组等知识，解题关键是根据题意利用相似三角形性质构造方程．10．如图，直线443y x =-+和x 轴、y 轴的交点分别为B 、C ，点A 的坐标是()2,0-．（1）试说明ABC 是等腰三角形；（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，MON △的面积为S ． ①求S 与t 的函数关系式；②设点M 在线段OB 上运动时，是否存在4S =的情形？若存在，求出对应的t 值；若不存在请说明理由； ③在运动过程中，当MON △为直角三角形时，求t 的值．【答案】（1）证明见解析；（2）①22455S t t =-+（02t <<），22455S t t =-（25t <≤）；②存在，(t s =；③5s 或25.8s 【分析】 （1）先求解,B C 的坐标，再求解,BC AB 的长度，从而可证明结论；（2）①过点N 作⊥ND x 轴于D ，则4sin 5ND BN OBC t =⋅∠=，分两种情况讨论，当02t <<时，当25t <≤时，分别画出符合题意的图形，再利用三角形的面积公式得到函数解析式即可；②分两种情况讨论，把4S =分别代入②中的两个函数解析式，再解方程即可得到答案；③分三种情况讨论；90∠=︒NMO 或90NOM ∠=︒或90MNO ∠=︒，再利用图形的性质与锐角三角函数可得答案．【详解】解：（1）将0y =代入443y x =-+，得3x =，∴点B 的坐标为3,0；将0x =代入443y x =-+，得4y =， ∴点C 的坐标为()0,4．在Rt OBC 中，∵4OC =，3OB =，∴5BC ==．又()2,0A -，∴5AB =，∴AB BC =，∴ABC 是等腰三角形．（2）∵5AB BC ==，故点M 、N 同时开始运动，同时停止运动．过点N 作⊥ND x 轴于D ， 则4sin 5ND BN OBC t =⋅∠=， ①当02t <<时（如图），2OM t =-，∴12S OM ND =⋅ ()14225t t =-⋅ 22455t t =-+． 当25t <≤时（如图），2OM t =-，∴12S OM ND =⋅ ()14225t t =-⋅ 22455t t =-． ②存在4S =的情形．当02t <<时∴ 224455t t -+=， 22100,t t ∴-+=()22411044036∴=--⨯⨯=-=-＜0，所以方程无解；当25t <≤时， ∴ 224455t t -=．解得11t =21t =（不合题意，舍去）．15t =+<，故当4S =时，(t =秒．③当MN x ⊥轴时，MON △为直角三角形．3cos 5MB BN MBN t =⋅∠=， 又5MB t =-． ∴355t t =-， ∴258t =． 当点M 、N 分别运动到点B 、C 时，MON △为直角三角形，5t =．当90MNO ∠=︒时，不合题意，舍去，故MON △为直角三角形时，258t =秒或5t =秒． 【点睛】本题考查了一次函数图象上点的坐标特征，勾股定理的应用，一元二次方程的解法，锐角三角函数的定义，等腰三角形的性质，直角三角形的性质，三角形的面积，分类讨论的思想，掌握分类讨论思想解决问题是解题的关键．11．如图，点O 在线段AB 上，OA =1，OB =3，以点O 为圆心、OA 为半径作∠O ，点M 在上运动．连接MB ，以MB 为腰作等腰Rt∠MBC ，使∠MBC =90°，M ，B ，C 三点按逆时针顺序排列．（1）当点M 在AB 上时，sin∠ACB =________________；（2）当BM 与∠O 相切时，求AM 的长；（3）连接AC ，求AC 长的取值范围．【答案】（1或2；（2）3；（3）46AC ≤≤． 【分析】（1）分当M 在AB 上和点M 和A 重合两种情况解答即可；（2）先证明△BMD ∽△BAM,然后根据相似三角形的性质列式解答即可；（3）如图：以B 为顶点、OB 为边向上方作等腰Rt △OBP ，连接CP ，OM ，有△BOM ≌△BPC （SAS ），PC=OM=1，则点C 在以点P 为圆心、1为半径的圆上，转化为“圆外一点到圆上的最值问题”，作射线AP ，交OP 于C 1、C 2两点，然后求得AC 1和AC 2的长即可解答．【详解】（1）①如图：当M 在AB 上时∵OA=OM=1∴AB=AO+OB=4,BM=OB -OM=2∵MB 为腰作等腰Rt∠MBC∴BC=BM=2=∠sin∠ACB =AB AC ==; ②如图：当M 和点A 重合时，AB=BC=4∴==∠sin∠ACB =AB AC ==综上，sin∠ACB 或2； （2）如图：∵BM 与∠O 相切∴∠BMO=90°==∠AB 是直径∠∠AMD=90°∠∠BMD+∠DMO=90°，∠AMO+∠DMO=90°，∴∠BMD=∠AMO∠OA=OM∠∠OAM=∠AMO∠∠OAM=∠BMD∠∠MBA=∠MBD∠△BMD ∽△BAM∴DM MB AM AB ===设AM=x ，则DM=2x2= ，解得x=3或x=-3（舍）；（3）以B 为顶点、OB 为边向上方作等腰Rt △OBP ，连接CP ，OM ，∴△BOM ≌△BPC （SAS ）∴PC=OM=1则点C 在以P 为圆心的M 上、1为半径的圆上，即求转化为“圆外一点到圆上的最值问题”，∴5=作射线AP ，交OP 于C 1、C 2两点，则A C 1=AP -P C 1=4, A C 2=AP+P C 2=6,∴46AC ≤≤．【点睛】本题属于几何综合题，考查了圆的性质、全等三角形的判定与性质、相似三角形的判定与性质以及锐角的三角函数，灵活应用所学知识成为解答本题的关键．12．如图，四边形ABCD 是矩形，点P 是对角线AC 上一动点（不与点C 和点A 重合），连接PB ，过点P作PF ⊥PB 交射线DA 于点F ，连接BF ．已知AD =CD=3，设CP 的长为x ．（1）线段BP 的最小值为________，当1x =时，AF =____________．（2）当动点P 运动到AC 的中点时，AP 与BF 的交点为G ，FP 的中点为H ，求线段GH 的长度． （3）若点P 在射线CA 上运动，点P 在运动的过程中，①试探究∠FBP 是否会发生变化？若不改变，请求出∠FBP 的大小；若改变，请说明理由．②若△AFP 是等腰三角形，直接写出x 的值．【答案】（1）2；（2；（3）①不发生变化，30； ②3或 【分析】（1）当BP 最小时，即BP AC ⊥，根据相似三角形的性质，可求得BP 的值，当x=1时，可得到BPN PMF ，由此可得出tan FBP ∠的值，继而得到AF 的值；（2）先证明BP 垂直平分AP ，得到PF =GH 是Rt FGP △的中线，即可得到GH 的长； （3）①过点P 作PN BC ⊥交AD 于点M ，可证明FMP PNB ，设,2x PC x PN ==，可求得NC 、MP 、BN 的长，tan =3FP MP FBP BP BN ∠==，即可求得∠FBP 的大小； ②分三种情况讨论即:当FA=FP ，AP=AF ，PA=PB 时，分别根据等腰三角形的性质解题．【详解】（1）当BP 最小时，A 与F 重合，即BP AC ⊥， 33AD CD ==6,30AC DAC ACB ∴=∠=∠=︒,在Rt ABC 与Rt APB △中，BAC PAB ∠=∠ABCAPB ∴ AB BP AC BC∴=36∴=2BP ∴= 作PM BC ⊥于N ，交AD 于M ，当x=1时，1522PN MP CN BN ====，， 90BNP PMF BPF ∠=∠=∠=︒,90,90FPM PFM FPM BPN ∴∠+∠=︒∠+∠=︒，PFM BPN ∴∠=∠，BPNPFM ∴，3MP FM BP BN NP FP ∴===，MF ∴=2663AF AM MF BN MF ∴=-=-=-==，故答案为：2，3； （2）P 为AC 的中点，3AP PC AB ∴===60ABP APB BAP ∴∠=∠=∠=︒在t R ABF 和t R PBF 中，AB=BP ，BF=BFt R ABF ∴≅t R PBF90AG PG AGB PGB ∴=∠=∠=︒，BF ∴垂直平分AP ，在t R BFP 中，303PBF BP ∠=︒=，PF ∴=取PF 的中点H ，连接GH ， H 为PF 中点，GH ∴为Rt PGF △的中线，12GH PF ∴==； （3）①不发生变化，30FBP ∠=︒，理由如下，作PM BC ⊥于点N ，交AD 于M ，,PBN FPM BPN PFM ∠=∠∠=∠，FMP PNB ∴，设,,,3,22x x CP x PN NC x MP BN x =∴===-=，3FP MP BP BN ∴== 30FBP ∴∠=︒；②当FA FP =时，BA BP =，ABP ∴为等边三角形,3AP AB ∴==，3x CP ∴==；当PA PF =时，12090APF ∠=︒>︒不符合题意；当AP=AD 时，75AFP APF ∠=∠=︒，75CBP CPB ∴∠=∠=︒，CP CB ∴==，即x =；综上所述，当3x =或AFP 是等腰三角形． 【点睛】本题考查矩形的性质、相似三角形的判定与性质、解直角三角形的应用、等腰三角形的判定与性质等知识，是重要考点，灵活运用分类讨论思想是解题关键．13．如图所示，在平面直角坐标系中，抛物线()230y ax bx a =++≠与x 轴交于点()1,0A -、()3,0B ，与y 轴交于点C ，点P 是第一象限内抛物线上的动点．（1）求抛物线的解析式；（2）连接BC 与OP ，交于点D ，求当PD OD的值最大时点P 的坐标； （3）点F 与点C 关于抛物线的对称轴成轴对称，当点P 的纵坐标为2时，过点P 作直线//PQ x 轴，点M 为直线PQ 上的一个动点，过点M 作MN x ⊥轴于点N ，在线段ON 上任取一点K ，当有且只有一个点K 满足135FKM ∠=︒时，请直接写出此时线段ON 的长．【答案】（1）2y x 2x 3=-++；（2）315,24⎛⎫⎪⎝⎭；（3）7+3+【分析】（1）直接利用待定系数法求解即可； （2）过P 作PG ∥y 轴，交BC 于点G ，则可构造出相似三角形，将PD OD 转换为PG OC求解即可； （3）分两种情况讨论，连接FM ，以FM 为斜边，作等腰直角△FHM ，当以H 为圆心FH 为半径作圆H ，与x 轴相切于K ，此时有且只有一个点K 满足∠FKM=135°，设点H （x ，y ），由“AAS”可证△FHE ≌△HMQ ，可得HE=QM=y -3，HQ=EF=x -2，由勾股定理可求y 的值，可求点M 坐标，即可求解．【详解】（1）将()1,0A -、()3,0B 代入抛物线解析式得：030933a b a b =-+⎧⎨=++⎩，解得：12a b =-⎧⎨=⎩， ∴抛物线的解析式为：2y x 2x 3=-++；（2）如图所示，作PG ∥y 轴，交BC 于点G ，则△DPG ∽△DOC ， ∴PD PG OD OC=， 由题可知：()0,3C ，设直线BC 的解析式为：y kx b =+，将()3,0B ，()0,3C 代入得：303k b b +=⎧⎨=⎩，解得：13k b =-⎧⎨=⎩，∴直线BC 的解析式为：3BC y x =-+，3OC =，设P 的坐标为()223m,m m -++，则G 的坐标为()3m,m -+， ∴23PG m m =-+， ∴223932433m PD PG m m OD OC ⎛⎫--+ ⎪-+⎝⎭===， ∴当32m =时，PD OD 有最大值，将32m =代入抛物线解析式得：154y =， ∴点P 的坐标为31524⎛⎫⎪⎝⎭，；（3）①当M 在F 右侧时，如图所示，连接FM ，以FM 为斜边构造等腰直角△FHM ，当以H 为圆心，FH 为半径作圆H ，与x 轴相切于K 时，此时有且只有一个K 点满足∠FKM=135°，此时，连接HK ，交PM 于点Q ，延长CF 交于HK 于E ，则HK ⊥x 轴，设H （x ，y ），由题可知，抛物线的对称轴为直线x=1，∵点F 与点C 关于抛物线的对称轴对称，∴点F 的坐标为（2，3），CF ∥x 轴，∴CF ∥PM ，∴HK ⊥CF ，HK ⊥PM ，∴∠FEH=∠HQM=90°，∵∠FHE+∠MHE=90°，∠FHE+∠HFE=90°，∴∠HFE=∠MHQ ，又∵HF=HM ，∴△HFE ≌△MHQ （AAS ），∴HE=QM=y -3，HQ=FE=x -2，而HQ=HK -QK=y -2，∴y -2=x -2，即：x=y ，∴FE=y -2，∵222FH FE HE =+，FH=HK=y ，∴()()22223y y y =-+-，解得：5y =，5y =-（舍去）∴532QM =-=，523FE =-=，∴点M 的坐标为()72,，∴7ON =+；②当M 在F 左侧时，如图所示，同①的过程，可证得△HFE ≌△MHQ ，此时设H 的坐标为（x ，y ），显然有，HE=QM=y -3，HQ=FE=2-x ，而HQ=HK -QK=y -2，∴y -2=2-x ，即：4-y=x ，∴FE=y -2，∵222FH FE HE =+，FH=HK=y ，∴()()22223y y y =-+-，同理解得：5y =，∴532QM =-=，523FE =-=，∴点M 的坐标为()32,-，∴3ON =+综上，线段ON 的长为7+3+【点睛】本题考查二次函数综合问题，考查了待定系数法求解析式，二次函数的性质，全等三角形的判定与性质，圆的相关性质，以及相似三角形的判定与性质等，添加恰当的辅助线构造全等三角形是解题关键． 14．如图，在矩形ABCD 中，AB =6，BC =8，点O 为对角线AC 的中点，动点P 从点A 出发沿AC 向终点C 运动，同时动点Q 从点B 出发沿BA 向点A 运动，点P 运动速度为每秒2个单位长度，点Q 运动速度为每秒1个单位长度，当点P 到达点C 时停止运动，点Q 也同时停止运动，连结PQ ，设点P 运动时间为t （t ＞0）秒．（1）cos∠BAC= ．（2）当PQ⊥AC时，求t的值．（3）求△QOP的面积S关于t的函数表达式，并写出t的取值范围．（4）当线段PQ的垂直平分线经过△ABC的某个顶点时，请直接写出t的值．【答案】（1）35；（2）1813t=秒；（3）22434512(0)552434512(5)552S t t tS t t t⎧=-+<<⎪⎪⎨⎪=-+-<≤⎪⎩；（4）当2t=或t=秒时，线段PQ的垂直平分线经过△ABC的某个顶点．【分析】（1）利用勾股定理先求得AC的长，即可求解；（2）在Rt△ABC中，利用余弦函数构建方程即可求解；（3）过P作PE⊥AQ于点E，过O作OF⊥AQ于点F，分52t<<，52t=和552t<≤三种情况讨论，利用三角形面积公式即可求解；（4）分线段PQ的垂直平分线经过点C时，经过点A时，经过点B时，三种情况讨论，求得结论即可．【详解】（1）在Rt△ABC中，AB=6，BC=8，10=，∴63 cos105ABBACAC∠===；故答案为：35；（2）当PQ⊥AC时，∵AP=2t，AQ=6t-，∴在Rt△ABC中，∴23cos 65AP t PAQ AQ t ∠===-， 解得：1813t =秒， 经检验，1813t =是方程的解， ∴1813t =(秒)； （3）过P 作PE ⊥AQ 于点E ，过O 作OF ⊥AQ 于点F ，在Rt △ABC 中，AB =6，BC =8，AC 10=， ∴4sin 5BC BAC AC ∠==，4sin 25PE PE PAE AP t ∠===，4sin 55OF OF OAF AO ∠===， ∴PE=85t ，OF=4， ①当502t <<时， ()()2POQ AOQ APQ 1184346461222555t S S S t t t t =-=-⨯--⨯=-+， 即24341255S t t =-+(502t <<)； ②当52t =时，POQ 不存在； ③当552t <≤时，()()2POQ APQ AOQ 1814346641225255t S S S t t t t =-=-⨯--⨯=-+-， 即24341255S t t =-+-(552t <≤)；综上，△QOP 的面积S 关于t 的函数表达式是22434512(0)552434512(5)552S t t t S t t t ⎧=-+<<⎪⎪⎨⎪=-+-<≤⎪⎩； （4）①当线段PQ 的垂直平分线经过点C 时，PC=QC=102t -，在Rt △QBC 中，222QB BC QC +=，∴()2228102t t +=-，解得：203t -=(负值已舍)； ②当线段PQ 的垂直平分线经过点A 时，AQ=AP ，即62t t -=，解得：2t =；③当线段PQ 的垂直平分线经过点B 时，过P 作PG ⊥BC 于点G ，3sin 5AB PG ACB AC PC ∠===，4cos 5BC PG ACB AC GC ∠===， ∴PG=()36102655t t -=-，CG=()48102855t t -=-， BG= BC -CG=888855t t ⎛⎫--= ⎪⎝⎭， 在Rt △BPG 中，222BG PG BP +=， 即22286655t t t ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭， 整理得：215721800t t -+=， ()2247241518056160b ac =-=--⨯⨯=-<，方程无解，∴线段PQ 的垂直平分线不会经过点B ，综上，当2t =或203t -=秒时，线段PQ 的垂直平分线经过△ABC 的某个顶点． 【点睛】本题考查了矩形性质，解直角三角形，线段垂直平分线性质等知识，主要考查学生分析问题和解决问题的能力，题目比较典型，但是有一定的难度．15．问题探究：如图，在Rt △ABC 和Rt △DEC 中，∠ACB =∠DCE =90°，∠CAB =∠CDE =60°，点D 为线段AB 上一动点，连接BE ．（1）求证：△ADC ∽△BEC ．（2）求证：∠DBE =90°．拓展延伸：把问题探究中的“点D 为线段AB 上一动点”改为“点D 为直线AB 上一动点”，其他条件不变，若点M 为DE 的中点，连接BM ，且有AD =1，AB =4，请直接写出BM 的长度．【答案】（1）见解析；（2）见解析；拓展延伸：BM ．【分析】（1）先证得∠ACD =∠BCE ，再利用tan 60BC CE AC CD ︒===AC BC CD CE=，即可证明结论； （2）由（1）的结论得∠CAD =∠CBE ，即可证明；拓展延伸：分D 在线段AB 上和D 在BA 延长线上两种情况讨论，利用△ADC ∽△BEC 的 性质求得BE 的长，再利用直角三角形的性质即可求解．【详解】（1）∵∠ACB =∠DCE =90°，∴∠ACD+∠BCD =∠BCE+∠BCD =90°，∴∠ACD =∠BCE ，∵∠CAB =∠CDE =60°，∴tan 60BC CE AC CD ︒===AC BC CD CE=， ∴△ADC ∽△BEC ；（2）由（1）得：∠CAD =∠CBE ，∴∠CBE +∠CBA =∠CAD +∠CBA =90°，∴∠DBE =90°；拓展延伸：在Rt △ABC 中，∠ACB =90°，∠CAB =60°，AB =4，∴AC=2，BC =由（1）得：△ADC ∽△BEC ， ∴AC AD BC BE=， ∵AD =1，∴由（2）得：∠DBE =90°，∵点M 为DE 的中点，∴BM=12DE ； ①当D 在线段AB 上时，如图：在Rt △BDE 中，BD=AB -AD=4-1=3，，∴DE ==∴BM=12 ②当D 在BA 延长线上时，如图：在Rt △BDE 中，BD=AB+AD=4+1=5，，∴DE ==∴BM=12综上，BM【点睛】本题考查了相似三角形的判定和性质，特殊角的三角函数值，勾股定理，等腰三角形的性质，直角三角形的性质，证明△ADC ∽△BEC 是本题的关键．16．如图，在△ABC 中，AB ＝BC ＝AC ＝12cm ，点D 为AB 上的点，且BD ＝34AB ，如果点P 在线段BC 上以3cm /s 的速度由B 点向终点C 运动，同时，点Q 在线段CA 上由C 点向终点A 运动．当一点到达终点时，另一点也随之停止运动．（1）如（图一）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，△BPD 与△CQP 是否全等，请说明理由．（2）如（图二）若点Q 的运动速度与点P 的运动速度相等（点P 不与点B 和点C 重合），连接点A 与点P ，连接点B 与点Q ，并且线段AP ，BQ 相交于点F ，求∠AFQ 的度数．（3）若点Q 的运动速度为6cm /s ，当点Q 运动几秒后，可得到等边△CQP ？【答案】（1）BPD CQP ≌，证明见解析；（2）60︒（3）43【分析】 （1）根据时间和速度求得BP 、CQ 的长，根据SAS 判定两个三角形全等．（2）利用第（1）小题的方法可证得ABP BCQ ≌，BAP CBQ ∠=∠，根据三角形外角性质可得APB PAC C ∠=∠+∠，根据等边三角形性质和三角形内角和定理可得18060BFP CBQ APB ∠=︒-∠-∠=︒，根据对顶角性质可得AFQ ∠的度数．（3）设点Q 运动时间是x 秒，根据CP CQ =列一元一次方程，根据任意一角为60︒的等腰三角形是等边三角形，即可求出答案．【详解】（1）BPD CQP ≌．证明：点P 在线段BC 上以3cm /s 的速度由B 点向终点C 运动，经过1s 后，∠133BP =⨯=，∠点Q 的运动速度与点P 的运动速度相等，∠3CQ BP ==，∠AB ＝BC ＝AC ＝12cm ，BD ＝34AB ， ∠ABC 是等边三角形，60B C ∠=∠=︒，31294BD =⨯=， ∠1239PC BC BP =-=-=，在BDP △和CPQ 中，BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∠BPD CQP ≌（SAS ）．（2）解：∠点Q 的运动速度与点P 的运动速度相等，∠BP CQ =，∠AB ＝BC ＝AC ，∠ABC 是等边三角形，60BAC ABC C ∠=∠=∠=︒，∠在ABP △和BCQ △中，AB BC ABC C BP CQ =⎧⎪∠=∠⎨⎪=⎩∠ABP BCQ ≌，∠BAP CBQ ∠=∠；在BPF △中，180()BFP CBQ APB ∠=︒-∠+∠，∵=CBQ APB CBQ CAP C ∠+∠∠+∠+∠，∵=60CBQ CAP BAP CAP ∠+∠∠+∠=︒，60C ∠=°，∴=6060=120CBQ APB ∠+∠︒+︒︒，∴180()=180120=60BFP CBQ APB ∠=︒-∠+∠︒-︒︒，∴=60AFQ BFP ∠∠=︒（对顶角相等）．（3）解：设点Q 运动时间是x 秒，若CP CQ =，可列方程：1236x x -=， 解得：43x =． ∵在CQP 中，CP CQ =，=60C ∠︒， ∴当43x =秒时，CQP 是等边三角形（任意角是60︒的等腰三角形是等边三角形）． ∴当点Q 运动43秒后，可得到等边CQP ． 【点睛】。

动点问题、动态几何问题专题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．【专题一：建立动点问题的函数解析式】函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式例1(2000上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P ,PH ⊥OA ,垂足为H ,△OPH 的重心为G .(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH =32NH =2132⋅OP =2. (2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴2362121x OH MH -==. 在Rt △MPH 中,.∴y =GP =32MP =233631x + (0<x <6). (3)△PGH 是等腰三角形有三种可能情况:①GP =PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意. ②GP =GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH =GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2. 二、应用比例式建立函数解析式例2（2006山东）如图2,在△ABC 中,AB =AC =1,点D ,E 在直线BC 上运动.设BD =,x CE =y . (1)如果∠BAC =30°,∠DAE =105°,试确定y 与x 之间的函数解析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB =AC ,∠BAC =30°, ∴∠ABC =∠ACB =75°, ∴∠ABD =∠ACE =105°. ∵∠BAC =30°,∠DAE =105°, ∴∠DAB +∠CAE =75°, 又∠DAB +∠ADB =∠ABC =75°, ∴∠CAE =∠ADB ,∴△ADB ∽△EAC , ∴ACBD CE AB =,2222233621419x x x MH PH MP +=-+=+=AEDCB 图2HM NG POAB图1xy∴11x y =, ∴xy 1=. (2)由于∠DAB +∠CAE =αβ-,又∠DAB +∠ADB =∠ABC =290α-︒,且函数关系式成立,∴290α-︒=αβ-, 整理得=-2αβ︒90. 当=-2αβ︒90时,函数解析式xy 1=成立. 例3(2005上海)如图3(1),在△ABC 中,∠ABC =90°,AB =4,BC =3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D ,交线段OC 于点E .作EP ⊥ED ,交射线AB 于点P ,交射线CB 于点F .(1)求证: △ADE ∽△AEP .(2)设OA =x ,AP =y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF =1时,求线段AP 的长. 解:(1)连结OD .根据题意,得OD ⊥AB ,∴∠ODA =90°,∠ODA =∠DEP .又由OD =OE ,得∠ODE =∠OED .∴∠ADE =∠AEP , ∴△ADE ∽△AEP .(2)∵∠ABC =90°,AB =4,BC =3, ∴AC =5. ∵∠ABC =∠ADO =90°, ∴OD ∥BC , ∴53x OD =,54xAD =, ∴OD =x 53,AD =x 54. ∴AE =x x 53+=x 58. ∵△ADE ∽△AEP , ∴AE AD AP AE =, ∴x x yx 585458=. ∴x y 516= (8250≤<x ). (3)当BF =1时，①若EP 交线段CB 的延长线于点F ,如图3(1)，则CF =4.∵∠ADE =∠AEP , ∴∠PDE =∠PEC . ∵∠FBP =∠DEP =90°, ∠FPB =∠DPE , ∴∠F =∠PDE , ∴∠F =∠FEC , ∴CF =CE . ∴5-x 58=4,得85=x .可求得2=y ,即AP =2.A3(2)3(1)②若EP 交线段CB 于点F ,如图3(2), 则CF =2. 类似①,可得CF =CE . ∴5-x 58=2,得815=x . 可求得6=y ,即AP =6.综上所述, 当BF =1时,线段AP 的长为2或6. 三、应用求图形面积的方法建立函数关系式例4（2004上海）如图,在△ABC 中,∠BAC =90°,AB =AC =22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO =x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O ,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC ,垂足为H . ∵∠BAC =90°,AB =AC =22, ∴BC =4,AH =21BC =2. ∴OC =4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA =1+x ,OH =x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA =1-x ,OH =2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21. 【专题二：动态几何型压轴题】动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

中考几何动态试题解法专题知识点概述一、动态问题概述1.就运动类型而言,有函数中的动点问题有图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。

2.就运动对象而言,几何图形中的动点问题有点动、线动、面动三大类。

3.就图形变化而言,有轴对称（翻折）、平移、旋转（中心对称、滚动）等。

4.动态问题一般分两类，一类是代数综合方面，在坐标系中有动点，动直线，一般是利用多种函数交叉求解。

另一类就是几何综合题，在梯形，矩形，三角形中设立动点、线以及整体平移翻转，对考生的综合分析能力进行考察。

所以说，动态问题是中考数学当中的重中之重，属于初中数学难点，综合性强，只有完全掌握才能拿高分。

二、动点与函数图象问题常见的四种类型1.三角形中的动点问题：动点沿三角形的边运动，根据问题中的常量与变量之间的关系，判断函数图象。

2.四边形中的动点问题：动点沿四边形的边运动，根据问题中的常量与变量之间的关系，判断函数图象。

3.圆中的动点问题：动点沿圆周运动，根据问题中的常量与变量之间的关系，判断函数图象。

4.直线、双曲线、抛物线中的动点问题：动点沿直线、双曲线、抛物线运动，根据问题中的常量与变量之间的关系，判断函数图象。

三、图形运动与函数图象问题常见的三种类型1.线段与多边形的运动图形问题：把一条线段沿一定方向运动经过三角形或四边形，根据问题中的常量与变量之间的关系，进行分段，判断函数图象。

2.多边形与多边形的运动图形问题：把一个三角形或四边形沿一定方向运动经过另一个多边形，根据问题中的常量与变量之间的关系，进行分段，判断函数图象。

3.多边形与圆的运动图形问题：把一个圆沿一定方向运动经过一个三角形或四边形，或把一个三角形或四边形沿一定方向运动经过一个圆，根据问题中的常量与变量之间的关系，进行分段，判断函数图象。

四、动点问题常见的四种类型解题思路1.三角形中的动点问题：动点沿三角形的边运动，通过全等或相似，探究构成的新图形与原图形的边或角的关系。

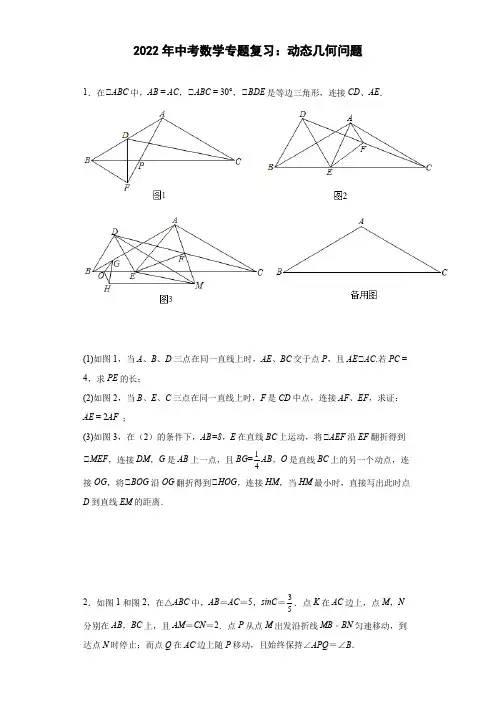
2022年中考数学专题复习：动态几何问题1．在△ABC中，AB = AC，△ABC = 30°，△BDE是等边三角形，连接CD、AE．(1)如图1，当A、B、D三点在同一直线上时，AE、BC交于点P，且AE△AC.若PC = 4，求PE的长；(2)如图2，当B、E、C三点在同一直线上时，F是CD中点，连接AF、EF，求证：AE = 2AF；(3)如图3，在（2）的条件下，AB=8，E在直线BC上运动，将△AEF沿EF翻折得到△MEF，连接DM，G是AB上一点，且BG=14AB，O是直线BC上的另一个动点，连接OG，将△BOG沿OG翻折得到△HOG，连接HM，当HM最小时，直接写出此时点D到直线EM的距离．2．如图1和图2，在△ABC中，AB＝AC＝5，sinC＝35．点K在AC边上，点M，N分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3≤x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝94，请直接写出点K被扫描到的总时长．3．如图，在等腰梯形ABCD中，AB△CD，AB=8cm，CD=2cm，AD=6cm．点P从A 点出发，以2cm/s的速度沿AB向B点运动（运动到B点即停止）；点Q从C点出发，以1cm/s的速度沿CD−DA向A点运动（当点P停止运动时，点Q也即停止），设P、Q同时出发并运动了t秒．(1)求梯形ABCD的高和△A的度数；(2)当PQ将梯形ABCD分成两个直角梯形时，求t的值；(3)试问是否存在这样的t的值，使四边形PBCQ的面积是梯形ABCD面积的一半，若存在，请求出t的值；若不存在，请说明理由．4．如图1，点O 是正方形ABCD 两对角线的交点，分别延长OD 到点G ，OC 到点E ，使OG ＝2OD ，OE ＝2OC ，然后以OG 、OE 为邻边作正方形OEFG ，连结AG 、DE ．（1）猜想AG 与DE 的数量关系，请直接写出结论；（2）正方形ABCD 固定，将正方形OEFG 绕点O 逆时针旋转，旋转角为α（0°＜α＜180°），得到图2，请判断：（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由； （3）在正方形OEFG 旋转过程中，请直接写出： △当α＝30°时，△OAG 的度数；△当△AEG 的面积最小时，旋转角α的度数．5．如图1，在ABC 中，90,ACB CD ∠=︒平分ACB ∠，且AD BD ⊥于点D ．（1）判断ABD △的形状；（2）如图2，在（1）的结论下，若3,75BQ DQ BQD ==∠=︒，求AQ 的长； （3）如图3，在（1）的结论下，若将DB 绕着点D 顺时针旋转()090αα︒<<︒得到DP ，连接BP ，作DE BP ⊥交AP 于点F ．试探究AF 与DE 的数量关系，并说明理由．6．如图，在Rt ABCAB=，4∠=︒，5AC=．动点P从点A出发，沿AB △中，90C⊥交AC或BC于点Q，以每秒4个单位长度的速度向终点B运动．过点P作PQ AB分别过点P、Q作AC、AB的平行线交于点M．设PQM与ABC重叠部分的面积为t t>秒．S，点P运动的时间为()0（1）当点Q在AC上时，CQ的长为______（用含t的代数式表示）．（2）当点M落在BC上时，求t的值．（3）当PQM与ABC的重合部分为三角形时，求S与t之间的函数关系式．（4）点N为PM中点，直接写出点N到ABC的两个顶点的距离相等时t的值．7．如图，△ABC是等边三角形，AB＝4cm，动点P从A出发，以2cm/s的速度沿AB 向点B匀速运动，过点P作PQ△AB，交折线AC﹣CB于点Q，以PQ为边作等边三角形PQD，使A，D在PQ异侧，设点P的运动时间是x（s）（0＜x＜2）．（1）AP的长为cm（用含x的代数式表示）；（2）当Q与C重合时，则x＝s；（3）△PQD的周长为y（cm），求y关于x的函数解析式，并写出自变量的取值范围．8．如图，已知△ABC中，AB＝AC＝10cm，BC＝8cm，点D为AB的中点．如果点P 在线段BC上以3cm/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．设P点的运动时间为t．（1）CP＝cm．（用含t的式子表示）；（2）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；（3）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？9．如图，在Rt△ABC中，△B=90°，BC=5 ，△C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF△BC于点F，连接DE、EF．（1）AC的长是________，AB的长是________．（2）在D、E的运动过程中，线段EF与AD的关系是否发生变化？若不变化，那么线段EF与AD是何关系，并给予证明；若变化，请说明理由．（3）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．（4）当t为何值，△BEF的面积是2 ？10．在Rt△ABC中，△BAC＝90°，AB＝AC，动点D在直线BC上（不与点B，C重合），连接AD，把AD绕点A逆时针旋转90°得到AE，连接DE，F，G分别是DE，CD的中点，连接FG．【特例感知】（1）如图1，当点D是BC的中点时，FG与BD的数量关系是，FG 与直线BC的位置关系是；【猜想论证】（2）当点D在线段BC上且不是BC的中点时，（1）中的结论是否仍然成立？△请在图2中补全图形；△若成立，请给出证明；若不成立，请说明理由．【拓展应用】（3）若AB＝AC，其他条件不变，连接BF、CF．当△ACF是等边三角形时，请直接写出△BDF的面积．11．如图，等腰三角形△ABC的腰长AB=AC=5cm，BC=8cm，动点P从B出发沿BC 向C运动，速度为2cm/s．动点Q从C出发沿CA向A运动，速度为1cm/s，当一个点到达终点时两个点同时停止运动．点P'是点P关于直线AC的对称点，连接PP′和P′Q，P′P和AC相交于点E．设运动时间为t秒．（1）若当t的值是多少时，P'P恰好经过点A？（2）设△P′PQ的面积为y，求y与t之间的函数关系式（0＜t≤4）；（3）是否存在某一时刻t，使PQ平分△P′PC？若存在，求出相应的t值，若不存在，请说明理由；（4）是否存在某一时刻t，使点Q在PC的垂直平分线上？若存在，求出相应的t值，若不存在，请说明理由．12．如图，△ABC为等腰三角形，AB＝AC，将CA绕点C顺时针旋转至CD，连接AD，E为直线CD上一点，连接AE；（1）如图1，若△BAC＝60°，△ACD＝90°，E为CD中点，AB=△BCE的面积；（2）如图2，若△ACD＝90°，点E在线段CD上且△DAE＋△ABC＝90°，AE的延长线与BC的延长线交于点F，连接DF，求证：BC=；（3）如图3，AB＝1，△BAC＝90°，△ACD＝105°，若BE恰好平分△AEC，点P为线段AE上的动点，点E′与点E关于直线DP对称，AE′与CD交于点Q，连接CE′，当'+-''的值最小时，直接写出CQ的值．AE CE13．已知，如图△，在平行四边形ABCD中，AB＝3cm，BC＝5cm，AC△AB，△ACD 沿AC的方向匀速平移得到△PNM，速度为1cm/s：同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图△，设移动时间为t（s）（0＜t＜4），连接PQ，MQ，MC，解答下列问题：（1）CQ＝，BQ＝，AP＝，CP＝．（2）当t为何值时，PQ∥MN；（3）设△OMC的面积为y（cm2），求y与t之间的函数关系式；（4）是否存在某一时刻t，使S△QMC：S四边形ABQP＝1：4．若存在，求出t的值；若不存在，请说明理由．14．如图，等腰ABC的底边BC＝8，高AD＝2，M是AB中点，连接MD．动点E从点B出发，以每秒1个单位的速度沿BC向点C运动，到点C停止，另一动点F从点B出发，以相同的速度沿BC运动，到点D停止．已知点E比点F早出发1秒，当点F出发后，以EF为边作正方形EFGH，使点G、H和点A在BC的同侧，设点E运动的时间为t秒．（1）当t≥1时，用含t的代数式表示EF的长；（2）设正方形EFGH面积为S 1，正方形EFGH与ABC重叠面积为S2，当S1：S2＝2时，求t的值；（3）在点F开始运动时，点P从点D出发，以每秒DM ﹣MB﹣BM﹣MD运动，到达点D停止，在点E的整个运动过程中，求点P在正方形EFGH内（含边界）的时长．15．如图1，正方形ABCD中，点P、Q是对角线BD上的两个动点，点P从点B出发沿着BD以1cm/s的速度向点D运动；点Q同时从点D出发沿着DB以2cm的速度向点B运动．设运动的时间为x s，△AQP的面积为y cm2，y与x的函数图象如图2所示，根据图象回答下列问题：（1）a＝．（2）当x为何值时，APQ的面积为6cm2；（3）当x为何值时，以PQ为直径的圆与APQ的边有且只有三个公共点．16．如图1，有一张矩形纸条ABCD ，边AB 、BC 的长分别是方程27100x x -+=的两个根()AB BC >，E 为CD 上一点，1CE =． （1）连接AE ，BE ，试说明90AEB =︒∠．（2）如图2，M 为边AB 上一个动点，将四边形BCEM 沿ME 折叠，使点B ，C 分别落在点B ′，C '上，边MB '与边CD 交于点N ． △如图3，当点M 与点A 重合时，求N 到ME 的距离．△在点M 从点A 运动到点B 的过程中，求点N 相应运动的路径长（路程）．17．如图，已知在Rt ABC 中，90ACB ∠=︒，8AC =，16BC =，D 是AC 上的一点，3CD =，点P 从B 点出发沿射线BC 方向以每秒2个单位的速度向右运动．设点P 的运动时间为t ，连接AP ．（1）当3t =秒时，求AP 的长度；（2）当ABP △为等腰三角形时，求t 的值；（3）过点D 作DE AP ⊥于点E ，连接PD ，在点P 的运动过程中，当PD 平分APC ∠时，直接写出t 的值．18．如图，已知在Rt△ABC 中，△ACB ＝90°，AB ＝10，AC ＝6，点D 是斜边AB 上的动点，联结CD ，作DE △CD 交射线CB 于点E ，设AD ＝x ． （1）当点D 是边AB 的中点时，求线段DE 的长； （2）当△BED 是等腰三角形时，求x 的值； （3）如果DEy DB=，求y 关于x 的函数解析式，并写出它的定义域．19．已知：如图，在长方形ABCD 中，4cm,6cm AB BC ==，点E 为AB 中点．点P 在线段BC 上以每秒2cm 的速度由点B 向点C 运动，同时，点Q 在线段CD 上由点C 向点D 运动．设点P 的运动时间为t 秒，解答下列问题：（1）线段,BP PC 的长可用含t 的式子分别表示为 cm ， cm ；（2）若某一时刻BPE 与CQP 全等，求此时t 的值和点Q 的运动速度．20．在平面直角坐标系中，点A（0，4），点B（4，0），连接AB，点P（0，t）是y 轴上的一动点，以BP为一直角边构造等腰直角△BPC（B，P，C的顺序为顺时针），且△BPC＝90°，过点A作AD△x轴并与直线BC交于点D，连接PD．（1）如图1，当t＝2时，求点C的坐标；（2）如图2，当t＞0时，求证：△ADC＝△PDB；（3）如图3，当t＜0时，求DP﹣DA的值（用含有t的式子表示）．。

动态几何之“双动点”问题（含解析）1. 已知，如图，在△ABC 中，已知AB =AC =5 cm ，BC =6 cm ．点P 从点B 出发，沿BA 方向匀速运动，速度为1 cm /s ；同时，直线QD 从点C 出发，沿CB 方向匀速运动，速度为1 cm /s ，且QD ⊥BC ，与AC ，BC 分别交于点D ，Q ；当直线QD 停止运动时，点P 也停止运动．连接PQ ，设运动时间为t （0＜t ＜3）s ．解答下列问题： （1）当t 为何值时，PQ//AC ？（2）设四边形APQD 的面积为y （cm 2），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使S 四边形APQD ：S △ABC =23：45？若存在，求出t 的值；若不存在，请说明理由．第1题图解：（1）当t s 时,PQ//AC ，∵点P 从点B 出发，沿BA 方向匀速运动，速度为1 cm /s ；同时，直线QD 从点C 出发，沿CB 方向匀速运动，速度为1 cm /s ， ∴BP ＝t ，BQ ＝6−t ． ∵PQ//AC ， ∴△BPQ ∽△BAC ，第1题解图∴C B Q B B A BP =，即665t t -=，解得t ＝1130s ． ∴当t 为1130s 时，PQ//AC ；（2）过点A 、P 作AN ⊥BC ，PM ⊥BC 于点N 、M ， ∵AB ＝AC ＝5cm ，BC ＝6cm ， ∴BN ＝CN ＝3cm ， ∴AN ＝222235-=-BN AB ＝4cm ．∵AN ⊥BC ，PM ⊥BC ， ∴△BPM ∽△BAN ， ∴AN PM AB BP =，即45PM t =，解得PM ＝t 54， ∴S △BPQ ＝21BQ ·PM ＝21（6−t ）·t 54＝t t 512522+-， ∵AB ＝AC ＝5cm ，AN=4cm ,CN=3cm ,DQ//AN , ∴△CDQ ∽△CAN ， ∴CN CQ AN DQ =，即34tDQ =，∴DQ=34t , ∴S △CDQ ＝21CQ ·DQ ＝32t 2． ∵S △ABC ＝21BC ·AN =21×6×4＝12， ∴y ＝S 四边形APQD ＝S △ABC −S △CDQ −S △BPQ ＝12−32t 2−（t t 512522+-）＝12−t t 5121542-（0＜t ＜3）； （3）存在．∵由（2）知，S 四边形APQD ＝S △ABC −S △CDQ −S △BPQ ＝12−21t 2−（t t 512522+-）＝12−t t 5121542-，S △ABC ＝12， ∴452312512154122=-t t -，解得t 1＝411412-+，t 2＝411412--（舍去）． ∴当t ＝4114123-+s 时，S 四边形APQD ：S △ABC ＝23：45．2. 如图①，在Rt △ABC 中，∠C ＝90°，AB ＝10，BC ＝6，点P 从点A 出发，沿折线AB −BC 向终点C 运动，在AB 上以每秒5个单位长度的速度运动，在BC 上以每秒3个单位长度的速度运动，点Q 从点C 出发，沿CA 方向以每秒34个单位长度的速度运动，P 、Q 两点同时出发，当点P 停止时，点Q 也随之停止．设点P 运动的时间为t 秒．（1）求线段AQ 的长；（用含t 的代数式表示）（2）连接PQ ，当PQ 与△ABC 的一边平行时，求t 的值；（3）如图②，过点P 作PE ⊥AC 于点E ，以PE ，EQ 为邻边作矩形PEQF ，点D 为AC 的中点，连接DF ．设矩形PEQF 与△ABC 重叠部分图形的面积为S ．①当点Q 在线段CD 上运动时，求S 与t 之间的函数关系式；②直接写出DF 将矩形PEQF 分成两部分的面积比为1：2时t 的值．第2题图解：（1）在Rt △ABC 中，∵∠C ＝90°，AB ＝10，BC ＝6，由勾股定理得：AC ＝2222610-=-BC AB ＝8，∵点Q 在CA 上，以每秒34个单位移动， ∴CQ ＝34t ， ∴AQ ＝AC -CQ =8−34t ．（2）∵P 点从AB -BC 总时间36510+=4s , ∵点P 在AB 或BC 上运动，点Q 在AC 上， ∴PQ 不可能与AC 平行， ①当点P 在AB 上，则PQ//BC ，此时AC AQ AB AP =，即834810t 5t-=，解得t =s 23; ②当点P 在BC 上,此时PQ//AB ，∴CA CQ BC CP =，即46-3t 2368t-=（），解得t ＝3s ， 综上所述，t ＝32s 或3s 时，PQ 与△ABC 的一边平行； （3）①∵点D 是AC 的中点， ∴CD=4，当点Q 运动到点D 时，t 34＝4，解得t ＝3， 点Q 与点E 重合时，t 316＝AC ＝8，得t ＝23，分三种情况讨论如下： （i ）点Q 与点E 重合时，316t ＝AC ＝8，得t ＝23，当0≤t ≤23，此时矩形PEQF 在△ABC 内，如解图①所示，∵AP ＝5t ，易得AE ＝4t ，PE ＝3t ，∴EQ ＝AQ －AE ＝8－34t －4t ＝8－316t ， ∴S ＝PE ×EQ ＝3t （8－316t ）＝－16t ２＋24t ；第２题解图（ii ）点P 与点B 重合时，5t ＝10，得t ＝2，当23≤t ≤2时，如解图②所示，设QF 交AB 与T ，则重叠部分是矩形PEQF 的面积减去△PFT 的面积． ∵AQ ＝8－34t ，∴QT ＝43AQ =43（8－34t ）=6-t ， ∴FT =PE -QT =3t -(6-t )=4t -6, EQ =AE -AQ =4t -(8-34t )=316t -8, ∴S =PE ·EQ -21EQ ·Ft =3t ·（316t -8)-21·（316t -8)（4t -6） =316t 2+8t -24； (iii )当2<t ≤3,点P 在BC 上，且点F 在△ABC 外，如解图③所示，此时点E 与点C 重合，PC ＝6－3（t －2）＝12－3t ，QC ＝34t ，QT ＝43(8-34t )＝6－t ，BP ＝3（t －2），PR ＝34·3（t －2）＝4t －8，FR ＝FP －PR ＝34t －（4t －8）＝8－38t ，FT ＝43FR ＝6－2t ． ∴S ＝PT ×QC －21FR ·FT ＝（12－3t ）·34t －21·（8－38t ）·（6－2t ） ＝－320t ２+32t －24；第２题解图②53，56. 3. 如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝3，BC ＝4．动点P 从点A 出发沿AC 向终点C 运动，同时动点Q 从点B 出发沿BA 向点A 运动，到达A 点后立刻以原来的速度沿AB 返回．点P ，Q 运动速度均为每秒1个单位长度，当点P 到达C 时停止运动，点Q 也同时停止．连接PQ ，设运动时间为t （0＜t ≤5）秒．（1）当点Q 从B 点向A 点运动时（未到达点A ）求S △APQ 与t 的函数关系式；写出t 的取值范围； （2）在（1）的条件下，四边形BQPC 的面积能否为△ABC 面积的1513？若能，求出相应的t 值；若不能，说明理由；（3）伴随点P 、Q 的运动，设线段PQ 的垂直平分线为l ，当l 经过点B 时，求t 的值．第3题图解：（1）在Rt △ABC 中，由勾股定理得：AC ＝222243+=+BC AB ＝5；如解图①，过点P 作PH ⊥AB 于点H ，AP ＝t ，AQ ＝3−t ，第3题解图①则∠AHP ＝∠ABC ＝90°，∵∠PAH ＝∠CAB ，∴△AHP ∽△ABC ， ∴BCPHAC AP =， ∵AP ＝t ，AC ＝5，BC ＝4， ∴PH ＝54t ，∴S △APQ ＝21（3−t ）·54t ， 即S ＝−2t 52＋t 56，t 的取值范围是：0＜t ＜3． （2）在（1）的条件下，四边形BQPC 的面积能为△ABC 面积的1513．理由如下： 依题意得：−2t 52＋t 56=21152 ×3×4，即−2t 52＋t 56=54． 整理，得（t −1）（t −2）＝0， 解得t 1＝1，t 2＝2， 又0＜t ＜3，∴当t ＝1或t ＝2时，四边形BQPC 的面积能为△ABC 面积的1513； （3）①如解图②，当点Q 从B 向A 运动时l 经过点B ，第3题解图②BQ ＝BP ＝AP ＝t ，∠QBP ＝∠QAP ， ∵∠QBP ＋∠PBC ＝90°，∠QAP ＋∠PCB ＝90° ∴∠PBC ＝∠PCB ，∴CP ＝BP ＝AP ＝t ∴CP ＝AP ＝21AC ＝21×5＝2.5， ∴t ＝2.5；②如解图③，当点Q 从A 向B 运动时l 经过点B ，第3题解图③BP ＝BQ ＝3−（t −3）＝6−t ，AP ＝t ，PC ＝5−t ，过点P 作PG ⊥CB 于点G ， 则PG//AB ， ∴△PGC ∽△ABC ， ∴BCGCAB PG AC PC ==， ∴PG ＝AC PC ·AB ＝53（5−t ）， CG ＝AC PC ·BC ＝54（5−t ）， ∴BG ＝4−54(5−t ）＝54t ， 由勾股定理得BP 2＝BG 2＋PG 2， 即（6−t ）2＝（54t ）2＋[53（5−t ）]2， 解得t ＝1445． 综上所述，伴随点P 、Q 的运动，线段PQ 的垂直平分线为l ，经过点B 时，t 的值是2.5或1445． 4. 如图，在Rt △ABC 中，∠C ＝90°，AC ＝6 cm ，BC ＝8 cm ，D 、E 分别是AC 、AB 的中点，连接DE ，点P 从点D 出发，沿DE 方向匀速运动，速度为1cm /s ；同时，点Q 从点B 出发，沿BA 方向匀速运动，速度为2cm /s ，当点P 运动到点E 停止运动，点Q 也停止运动．连接PQ ，设运动时间为t （s ）（0＜t ＜4）．解答下列问题： （1）当t 为何值时，PQ ⊥AB ？（2）当点Q 在BE 之间运动时，设五边形PQBCD 的面积为y （cm 2），求y 与t 之间的函数关系式； （3）在（2）的情况下，是否存在某一时刻t ，使PQ 分四边形BCDE 两部分的面积之比为S △PQE ：S 五边形PQBCD ＝1：29？若存在，求出此时t 的值以及点E 到PQ 的距离h ；若不存在，请说明理由．解：（1）如解图①，在Rt △ABC 中，第4题解图AC ＝6，BC ＝8， ∴AB ＝2286+＝10．∵D 、E 分别是AC 、AB 的中点．， AD ＝DC ＝3，AE ＝EB ＝5，DE//BC 且DE ＝21BC ＝4， ∵PQ ⊥AB ，∴∠PQB ＝∠C ＝90°， 又∵DE//BC ，∴∠AED ＝∠B ， ∴△PQE ∽△ACB ，∴BCQEAB PE =. 由题意得：PE ＝4−t ，QE ＝2t −5， 即852104-=-t t ，解得t ＝1441； （2）如解图②，过点P 作PM ⊥AB 于M ， 由△PME ∽△ACB ，得ABPEAC PM =， ∴10t -46=PM ，得PM ＝53（4−t ）．S △PQE ＝21EQ ·PM ＝21（5−2t ）·53（4−t ）＝53t 2−1039t ＋6， S 梯形DCBE ＝21×（4＋8）×3＝18， ∴y ＝S 梯形DCBE -S △PQE =18−（53t 2−1039t ＋6）＝−53t 2+1039t ＋12． （3）假设存在时刻t ，使S △PQE ：S 五边形PQBCD ＝1：29， 则此时S △PQE ＝301S 梯形DCBE ， ∴53t 2−1039t ＋6＝301×18，即2t 2−13t ＋18＝0， 解得t 1＝2，t 2＝29（舍去）． 当t ＝2时， PM ＝53×（4−2）=56，ME ＝54×（4−2）＝58， EQ ＝5−2×2＝1，MQ ＝ME ＋EQ ＝58＋1＝513， ∴PQ ＝22MQ PM +＝52055135622=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛．∵21PQ ·h ＝S △PQE =53， ∴h ＝56·)2056(20520562055或=. 5. 如图，在Rt △ABC 中，∠ACB =90°，AC =8，BC =6，CD ⊥AB 于点D ．点P 从点D 出发，沿线段DC向点C 运动，点Q 从点C 出发，沿线段CA 向点A 运动，两点同时出发，速度都为每秒1个单位长度，当点P 运动到C 时，两点都停止．设运动时间为t 秒． （1）求线段CD 的长；（2）设△CPQ 的面积为S ，求S 与t 之间的函数关系式，并确定在运动过程中是否存在某一时刻t ，使得S△CPQ ：S △ABC =9：100？若存在，求出t 的值；若不存在，则说明理由；（3）是否存在某一时刻t ，使得△CPQ 为等腰三角形？若存在，求出所有满足条件的t 的值；若不存在，则说明理由．解：（1）如解图①，∵∠ACB ＝90°，AC ＝8，BC ＝6，∴AB ＝10．∵CD ⊥AB ，∴S △ABC ＝21BC •AC ＝21AB •CD ． ∴CD ＝1086⨯=⨯AB AC BC ＝4.8， ∴线段CD 的长为4.8；（2）①过点P 作PH ⊥AC ，垂足为H ，如解图②所示．由题可知DP ＝t ，CQ ＝t ，则CP ＝4.8−t ．∵∠ACB ＝∠CDB ＝90°，∴∠HCP ＝90°−∠DCB ＝∠B ．∵PH ⊥AC ，∴∠CHP ＝90°,∴∠CHP ＝∠ACB ，∴△CHP ∽△BCA ， ∴AB PC AC PH =,∴10t 8.48-=PH ， ∴PH ＝t 54-2596，∴S △CPQ ＝21CQ ·PH ＝21t （t 54-2596）＝−52t 2+2548t ； ②存在某一时刻t ，使得S △CPQ ：S △ABC ＝9：100．∵S △ABC ＝21×6×8＝24，且S △CPQ ：S △ABC ＝9：100， ∴（−52t 2+2548t ）：24＝9：100． 整理得：5t 2−24t ＋27＝0．即（5t −9）（t −3）＝0．解得：t ＝59或t ＝3． ∵0≤t ≤4.8，∴当t ＝59秒或t ＝3秒时，S △CPQ ：S △ABC ＝9：100； （3）①若CQ ＝CP ，如解图①，则t ＝4.8−t ；解得：t ＝2.4；②若PQ ＝PC ，如解图②所示，∵PQ ＝PC ，PH ⊥QC ，∴QH ＝CH ＝21QC ＝21t ． ∵△CHP ∽△BCA ．∴ABCP BC CH =, ∴108.4621t t -=，解得：t ＝55144； ③若QC ＝QP ，过点Q 作QE ⊥CP ，垂足为E ，如解图③所示．同理可得：t ＝1124． 综上所述：当t 为2.4秒或55144秒或1124秒时，△CPQ 为等腰三角形．第5题解图6. 如图，在△ABC 中，AB =AC =10 cm ，BD ⊥AC 于点D ，且BD =8cm ．点M 从点A 出发，沿AC 的方向匀速运动，速度为2 cm /s ；同时直线PQ 由点B 出发，沿BA 的方向匀速运动，速度为1cm /s ，运动过程中始终保持PQ//AC ，直线PQ 交AB 于点P 、交BC 于点Q 、交BD 于点F ．连接PM ，设运动时间为t （0＜t ＜5）．（1）当t 为何值时，PM//BC ？（2）设四边形PQCM 的面积为y cm 2，求y 与t 之间的函数关系式； （3）已知某一时刻t ，有S 四边形PQCM =43S △ABC 成立，请你求出此时t 的值.第6题图解：（1）∵当PM//BC 时，△APM ∽△ABC ， ∴AP ＝AM ，∴10−t ＝2t ，∴t ＝310； （2）∵四边形PQCM 为梯形，y ＝21（PQ ＋MC ）DF ， ∵PQ ＝PB ＝t ，MC ＝10−2t ，BF ：BD ＝BP ：AB ,∴BF ＝54108 t t ， ∴DF ＝8−t 54, ∴y ＝21(t ＋10−2t )·(8−t 54）=252t −8t ＋40； （3）由（2）知，252t −8t ＋40=40×43， 解得t ＝10±53，又∵0<t<5,∴当t ＝10-53s 时，使S 四边形PQCM ＝43S △ABC 成立.7. 如图，在四边形ABCD 中，AD//BC ，AD ＝6 cm ，CD ＝4 cm ，BC ＝BD ＝10 cm ，点P 由B 出发沿BD方向匀速运动，速度为1cm /s ；同时，线段EF 由DC 出发沿DA 方向匀速运动，速度为1cm /s ，交BD 于Q ，连接PE ．若设运动时间为t （s ）（0＜t ＜5）．解答下列问题：（1）当t 为何值时，PE//AB ；（2）设△PEQ 的面积为y （cm 2），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使S △PEQ ＝252S △BCD ？若存在，求出此时t 的值；若不存在，说明理由； （4）连接PF ，在上述运动过程中，五边形PFCDE 的面积是否发生变化？说明理由．第7题图解：（1）当PE//AB 时，∴DBDP DA DE =． 而DE ＝t ，DP ＝10−t ，∴10106t t -=， ∴t ＝415， ∴当t ＝415s 时，PE//AB ； （2）∵AD//BC ,线段EF 由DC 出发沿DA 方向匀速运动，∴EF//CD ，∴四边形CDEF 是平行四边形,∴∠DEQ ＝∠C ，∠DQE ＝∠BDC ．∵BC ＝BD ＝10，∴△DEQ ∽△BCD ,∴CD EQ BC DE =,410EQ t =, ∴EQ ＝52t , 如解图，过B 作BM ⊥CD 交CD 于M ，过P 作PN ⊥EF 交EF 于N ，∵BC ＝BD ，BM ⊥CD ，CD ＝4cm ，∴CM ＝21CD ＝2cm ， ∴BM ＝6496410021022==-=-cm ，∵EF//CD ，∴∠BQF ＝∠BDC ，∠BFG ＝∠BCD ，又∵BD ＝BC ，∴∠BDC ＝∠BCD ，∴∠BQF ＝∠BFG ，∵ED//BC ，∴∠DEQ ＝∠QFB ，又∵∠EQD ＝∠BQF ，∴∠DEQ ＝∠DQE ，∴DE ＝DQ ，∴ED ＝DQ ＝BP ＝t ，∴PQ ＝10−2t ．又∵△PNQ ∽△BMD ， ∴BM PN BD PQ =，∴6410210PN t =-，∴PN ＝)5t -，∴S △PEQ ＝21EQ ·PN ＝⨯⨯t 5221)5t -=2255-+；第7题解图（3）存在.此时t 的值为1s 或4s .S △BCD ＝21CD ·BM ＝21×4×46＝86， 若S △PEQ =252S △BCD ， 则有2646255-+=252×86, 解得t 1＝1，t 2＝4，∴当t=1或4时，S △PEQ =252S △BCD ； （4）五边形PFCDE 的面积不发生变化.理由如下：在△PDE 和△FBP 中，∵DE ＝BP ＝t ，PD ＝BF ＝10−t ，∠PDE ＝∠FBP ，∴△PDE ≌△FBP （SAS ）．∴S 五边形PFCDE ＝S △PDE ＋S 四边形PFCD ＝S △FBP ＋S 四边形PFCD ＝S △BCD ＝86,∴在运动过程中，五边形PFCDE 的面积不变．8. 如图．在△ABC 中．AB ＝AC ＝5 cm ，BC ＝6 cm ，AD 是BC 边上的高．点P 由C 出发沿CA 方向匀速运动．速度为1 cm /s ．同时，直线EF 由BC 出发沿DA 方向匀速运动,速度为1 cm /s ，EF//BC ，并且EF 分别交AB 、AD 、AC 于点E ，Q ，F ，连接PQ ．若设运动时间为t （s ）（0＜t ＜4），解答下列问题：（1）当t 为何值时，四边形BDFE 是平行四边形？（2）设四边形QDCP 的面积为y （cm 2），求出y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使S 四边形QDCP ：S △ABC ＝9：20？若存在，求出此时t 的值；若不存在，说明理由；（4）是否存在某一时刻t ，使点Q 在线段AP 的垂直平分线上？若存在，求出此时点F 到直线PQ 的距离h ；若不存在，请说明理由．第8题图解：（1）如解图①中，连接DF ，第8题解图①∵AB ＝AC ＝5，BC =6，AD ⊥BC ，∴BD ＝CD ＝3，在Rt △ABD 中，AD ＝223-5＝4，∵EF//BC ，∴△AEF ∽△ABC ， ∴ADAQ BC EF =， ∴446t EF -=， ∴EF ＝23（4−t ）， ∵EF//BD ，∴EF ＝BD 时，四边形EFDB 是平行四边形， ∴23（4−t ）＝3， ∴t ＝2，∴t ＝2s 时，四边形EFDB 是平行四边形；（2）如解图②中，作PN ⊥AD 于N ，第8题解图②∵PN //DC ， ∴AC AP DC PN =， ∴553t PN -=， ∴PN ＝53（5-t ）， ∴y ＝21DC ·AD −21AQ ·PN ＝6−21（4−t ） ·53（5−t ）＝6−（t t 10271032-＋6）=t t 10271032+-（0＜t ＜4）； （3）存在.理由：由题意（t t 10271032+-）：12＝9：20， 解得t ＝3或6（舍去）；∴当t ＝3s 时，S 四边形QDCP ：S △ABC ＝9：20；（4）存在．理由如下：如解图③，作QN ⊥AC 于N ，作FH ⊥PQ 于H ．第8题解图③∵QA ＝QP ，QN ⊥AP ，∴AN ＝NP ＝21AP ＝21（5−t ），由题意cos ∠CAD ＝AQ AN C A AD =， ∴()544521=--t t ， ∴t ＝37， ∴t ＝37s 时，点Q 在线段AP 的垂直平分线上． ∵sin ∠FPH ＝53=PF FH ， ∵PA ＝5−37＝38，AF ＝AQ ÷122554=， ∴PF ＝127， ∴FH ＝207． ∴点F 到直线PQ 的距离h ＝207．9. 如图，BD 是正方形ABCD 的对角线，BC ＝2，动点P 从点B 出发，以每秒1个单位长度的速度沿射线BC 运动，同时动点Q 从点C 出发，以相同的速度沿射线BC 运动，当点P 出发后，过点Q 作QE ⊥BD ，交直线BD 于点E ，连接AP 、AE 、PE 、QE ，设运动时间为t （秒）．（1）请直接写出动点P 运动过程中，四边形APQD 是什么四边形？（2）请判断AE ，PE 之间的数量关系和位置关系，并加以证明；（3）设△EPB 的面积为y ，求y 与t 之间的函数关系式；（4）直接写出△EPQ 的面积是△EDQ 面积的2倍时t 的值．第9题图解：（1）四边形APQD 是平行四边形；【解法提示】∵四边形ABCD 是正方形，P 、Q 速度相同， ∴∠ABE ＝∠EBQ ＝45°，AD ∥BQ ，AD ＝BC ＝2，BP ＝CQ ， ∴BC ＝AD ＝PQ ，∴四边形APQD 是平行四边形.（2）AE ＝PE ，AE ⊥PE ；理由如下：∵EQ ⊥BD ，∴∠PQE ＝90°−45°＝45°，∴∠ABE ＝∠EBQ ＝∠PQE ＝45°，∴BE ＝QE ，在△AEB 和△EPQ 中，AB PQ ABE PQE BE QE =⎧⎪∠=∠⎨⎪=⎩，∴△AEB ≌△EPQ （SAS ），∴AE ＝PE ，∠AEB ＝∠PEQ ，∴∠AEP ＝∠BEQ ＝90°，∴AE ⊥PE ；（3）过点E 作EF ⊥BC 于点F ，如解图①所示：BQ ＝t ＋2，EF ＝22+t ， ∴y ＝21×22+t ×t ，即y ＝t t 41212+；第9题解图①（4）△EPQ 面积是△EDQ 面积的2倍时t 的值为1或3.【解法提示】分两种情况：① 当P 在BC 延长线上时，作PM ⊥QE 于M ，如解图②所示：第10题解图②∵PQ ＝2，∠BQE ＝45°，∴PM ＝22PQ ＝2，BE ＝QE ＝22BQ ＝22（t ＋2）， ∴DE ＝BE −BD ＝22（t ＋2）−22＝22t -2, ∵△EPQ 的面积是△EDQ 面积的2倍， ∴21×22（t ＋2）×2＝2×21（22t −2）×22（t ＋2）， 解得t ＝3或t ＝−2（舍去），∴t ＝3；②当P 在BC 边上时，解法同①，此时DE ＝2-22t ， ∵△EPQ 的面积是△EDQ 面积的2倍， ∴21×22（t ＋2）×2＝2×21（2-22t ）×22（t ＋2）， 解得：t ＝1或t ＝−2（舍去），∴t ＝1；综上所述，△EPQ 的面积是△EDQ 面积的2倍时t 的值为：1或3．。

初二动态几何问题一.动态几何问题涉及的几种情形动态几何问题就其活动对象而言,有：1.点动（有单动点型.多动点型）.2.线动（重要有线平移型.扭转型）.线动本质就是点动,即点动带动线动,进而还会产生形动,因而线动型几何问题可以经由过程转化成点动型问题来求解.3.形动（就其活动情势而言,有平移.扭转.翻折.滚动）二.解决动态几何问题的根本思虑计谋与剖析办法：动态型问题分解了代数.几何中较多的常识点,解答时要特别留意以下七点:1.掌控活动变更的情势及进程;2.思虑活动初始状况时几何元素的关系,以及可求出的几何量;3.动中取静：（最重要的一点）要擅长在“动”中取“静”（让图形和各个几何量都“静”下来）,抓住变更中的“不变量”和不变关系为“领导”,求出相干的常量或者以含有变量的代数式暗示相干的几何量;4.找等量关系：应用面积关系.类似三角形的性质.勾股定理.特别图形等的几何性质及互相关系,找出根本的等量关系式;5.列方程：将相干的常量和含有变量的代数式代入等量关系树立方程或函数模子;(某些几何元素的变更会带来其它几何量的变更,所以在求变量之间的关系时,平日树立函数模子或不等式模子求解.在解决有关特别点.特别值.特别地位关系问题时常联合图形树立方程模子求解)6.是否以及怎么分类评论辩论：将变更的几何元素按标题指定的活动路径活动一遍,从动态的角度去剖析不雅察可能消失的情形,看图形的外形是否转变,或图形的有关几何量的盘算办法是否转变,以明白是否须要依据活动进程中的特别地位分类评论辩论解决,7.肯定变更分界点：若需分类评论辩论,要以活动到达的特别点为分界点,画出与之对应情形相吻合的图形,找到情形产生转变的时刻,肯定变更的规模分类求解.例：如图,有一边长为5cm的正方形ABCD和等腰三角形△RQR,PQ=PR=5cm,QR=8cm,点B.C.Q.R在统一条直线ι上,当C.Q两点重应时开端,t秒后正方形ABCD与等腰△PQR重合部分的面积为.解答下列问题：（1）当t=3秒时,求S的值;（2）当t=5秒时,求S的值;（3）当5秒≤t≤8秒时,求S与t的函数关系式,并求出S的最大值.【要点导航】经由过程实验操纵——不雅察猜测——科学论证,使我们体验和学到了发明.获得常识的进程和办法. 实验操纵摸索——懂得题意.实验操纵是根本包管,不雅察猜测.摸索结论是症结,论证猜测的结论是落实. 【典例精析】例1取一张矩形纸片进行折叠,具体操纵进程如下：第一步：先把矩形ABCD 半数,折痕为MN ,如图1;第二步：再把B 点叠在折痕线MN 上,折痕为AE ,点B 在MN 上的对应点为B ',得R t △AB 'E ,如图2;第三步：沿EB '线折叠得折痕EF ,使A 点落在EC 的延伸线上,如图3．应用睁开图4探讨： （1）△AEF 是什么三角形？证实你的结论;（2）对于任一矩形,按照上述办法可否折出这种三角形？请解释你的来由．例2 已知：在△ABC 中,∠BAC =90°,M 为BC 中点．操纵：将三角板的90°角的极点与点M 重合,并绕着点M 扭转,角的双方分离与边AB .AC 订交于点E .F ．（1）探讨1：线段BE .EF .FC 是否能组成三角形？假如可以组成三角形,那么是什么外形的三角形？请证实你的猜测．（2）探讨2：若转变成：“角的双方分离与边AB .直线AC 订图 1 图 2图 3图4CM交于点E .F ．”其它前提都不变的情形下,那么结论是否还消失？请画出对应的图形并请证实你的猜测． 【练习】1.★★★如图,在正方形ABCD 中,点E 在边AB 上（点E与点A .B 不重合）,过点E 作FG ⊥DE ,FG 与边BC 订交于点F,与边DA 的延伸线订交于点G ．（1）操纵：由几个不合的地位,分离测量BF .AG .AE 的长,从中你能发明BF .AG .AE 的数目之间具有如何的关系？并证实你所得到的结论;（2）贯穿连接DF ,假如正方形的边长为2,设DFG的面,并写出函数的界说域;（3）假如正方形的边长为2,FG求点C 到直线DE 的距离．2.★★★操纵：将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角极点P 在对角线AC上滑动,直角的一边始终经由点B ,另一边与射线DC 订交于点Q ． 探讨：设A .P 两点间的距离为x ．（1）当点Q 在边CD 上时,线段PQ 与线段PB 之间有如何的大小关系？试证实你不雅察得到结论;GFD ACBD ACB供实验操纵用（2）当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数解析式,并写出函数的界说域;（3）当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形？假如可能,指出所有能使△PCQ 成为等腰三角形的点Q 的地位,并求出响应的x 的值;假如不成能,试解释来由．（图5.图6.图7的外形大小雷同,图5供操纵.实验用,图6和图7备用）3.★★★在△ABC 中,AB =AC ,CG ⊥BA 交BA 的延伸线于点G ．一等腰直角三角尺按如图1所示的地位摆放,该三角尺的直角极点为F ,一条直角边与AC 边在一条直线上,另一条直角边正好经由点B ．（1）在图1中请你经由过程不雅察.测量BF 与CG 的长度,猜测并写出BF 与CG 知足的数目关系,然后证实你的猜测;（2）当三角尺沿AC 偏向平移到图2所示的地位时,一条直角边仍与AC 边在统一向线上,另一条直角边交BC 边于点D ,过点D 作DE ⊥BA 于点E ．此时请你经由过程不雅察.测量DE .DF 与CG 的长度,猜测并写出DE ＋DF 与CG 之间知足的数目关系,然后证实你的猜测;（3）当三角尺在（2）的基本上沿AC 偏向持续平移到图3所DC B图5DAC B图6DACB图7图1示的地位（点F在线段AC上,且点F与点C不重合）时,（2）中的猜测是否仍然成立？（不必解释来由）4.★★如图,在平面直角坐标系中,直线l是第一.三象限的角等分线．实验与探讨：（1）由图不雅察易知A（0,2）关于直线l为（2,0）,请在图平分离标明B(5,3) .C(-2,5) 关于直线l的对,并写出他们的坐标：归纳与发明：（2）联合图形不雅察以上三组点的坐标,你会发明：坐标平面内任一点P(a,b)关于第一.三象限的角等分线l的对称点;应用与拓广：（3）已知两点D(1,-3).E(-1,-4),试在直线l上肯定一点Q,使点Q到D.E两点的距离之和最小,并求出Q点坐标．摸索性问题摸索性问题是指命题中缺乏必定的前提或无明白的结论,须要经由揣摸,填补并加以证实的题型．摸索性问题一般有三种类型：（1）前提摸索型问题;（2）结论摸索型问题;（3）摸索消失型问题．前提摸索型问题是指所给问题中结论明白,须要完整前提的标题;结论摸索型问题是指标题中结论不肯定,不独一,或标题结论须要类比,引申推广,或标题给出特例,要经由过程归纳总结出一般结论;摸索消失型问题是指在必定的前提下,需摸索发明某种数学关系是否消失的标题．前提摸索【要点导航】“摸索”是人类熟悉客不雅世界进程中最活泼.最活泼的思维活动,摸索性问题消失于一切学科范畴之中,数学中的“前提摸索”题型,是指命题中缺乏必定的题设,需经由揣摸.填补并加以证实的命题,因而必须应用题设大胆猜测.剖析.比较.归纳.推理,由结论去摸索未赐与的前提.因为题型新鲜.分解性强.构造奇特,此类问题的一般解题思绪并没有固定模式或套路,因而具体操纵时要更重视数学思惟办法的分解应用．【典例精析】例1如图,,垂1．（1）证实△CMG≌△NBP;（2）设BE=x,四边形MGBN的面积为y,求y关于x式,并写出界说域．（3长．（4）联络PG ,,求BE 的长;假如不克不及,请解释来由．（5）联络AC .AF .CF ,求证△ACF 的面积为定值． 〖思绪剖析〗1．第（3BE 的长． 2PBG 始终是45°,而∠BPG 和∠PGB 有可能为90°,要分情形评论辩论．3．第（5）小题即可用割补法求也可用应用AC ∥BF 将△ACF 的面积转化为△ABC 的面积．例2在等边△ABC 的双方AB .AC 地点直线上分离有两点M .N ．D 为△ABC 外一点,且∠MDN ＝60°,∠BDC ＝120°,BD ＝DC ． 探讨：当M .N 分离在直线AB .AC 上移动时,BM .NC .MNABC 的周长L 的关系．,当点,且DM （2）如图2所示,点M 且当时,猜测（1; （3） 如图3所示,当M .N 分离在边AB .CA 的延伸线上时,若AN ＝2,则Q ＝（用含有L 的式子暗示）．C图1 C 图2C图3【练习】1.★★★如图1所示,直线AB 交x 轴于点A （A ,0）,交y 轴于点B （0,B ）,且A .B 知足2b (4)0a a ++-=．（1）如图1,若C 的坐标为（－1,0）,且AH ⊥BC 于点H ,AH 交OB 于点P ,试求点P 的坐标;（2）如图2,衔接OH ,求证：∠OHP ＝45°;（3）如图3,若点D 为AB 的中点,点M 为y 轴正半轴上一动点,衔接MD ,过D 作DN ⊥DM 交x 轴于N 点,当M 点在y 轴正半轴上活动的进程中,式子S △BDM －S △ADN 的值是否产生转变,如产生转变,求出该式子的值的变更规模;若不转变,求该式子的值．2. ★★★已知BD .CE 分离是ABC △的AC 边.AB 边上的高,M 是BC 边的中点,分离联络MD .ME .DE ．（1）当︒<∠90BAC 时,垂足D .E 分离落在边AC .AB 上,如图1．求证：EM DM =．(2) 当︒>∠90BAC 时,垂足D .E 分离落在边AC .AB 地点的直线上,如图2,问（1）中的结论是否依旧成立？无需解释来由,直接写出答案即可;若︒=∠135BAC ,试断定DEM △的外形,简写解答进程． （3）设BAC ∠的度数为x ,DME ∠的度数为y ,求y 与x 之间的函数关系式．3.★★★如ABOy xN MD 图3ABCH P Oyx图2x yOP H CBA图1 ABC（备用图）ABCDM E图2ABCDE图1图1,已知∠ABC =90°,△ABE 是等边三角形,点P 为射线BC 上随意率性一点（点P 与点B 不重合）,贯穿连接AP ,将线段AP 绕点A 逆时针扭转60°得到线段AQ ,贯穿连接QE 并延伸交射线BC 于点F .（1）如图2,当BP =BA 时,∠EBF =°,猜测∠QFC =°;（2）如图1,当点P 为射线BC 上随意率性一点时,猜测∠QFC 的度数,并加以证实;（3）已知线段AB设BP 点Q 到射线BC 的距离为y ,求y摸索性问题是指命题中缺乏必定的前提或无明白的结论,须要经由揣摸,填补并加以证实的题型．摸索性问题一般有三种类型：（1）前提摸索型问题;（2）结论摸索型问题;（3）摸索消失型问题．前提摸索型问题是指所给问题中结论明白,须要完整前提的标题;结论摸索型问题是指标题中结论不肯定,不独一,或标题结论须要类比,引申推广,或标题给出特例,要经由过程归纳总结出一般结论;摸索消失型问题是指在必定的前提下,需摸索发明某种数学关系是否消失的标题．摸索型问题具有较强的分解性,因而解决此类问题用到了所学过的全部初中数学常识．经经常应用到的常识是：一元一次方程.平面直角坐标系.正.反比例和一次函数的求法（图象及其性质）.图图2ABEQPF C直角三角形的性质.四边形（特别）的性质.等．个顶用几何图形的某些特别性质：勾股定理.类似三角形对应线段成比例等来构造方程是解决问题的重要手腕和门路．是以温习中既要看重基本常识的温习,又要增强变式练习和数学思惟办法的研讨,切实进步剖析问题.解决问题的才能． 【典例精析】例 1 如图1,在△ABC 中,∠ACB = 90°,AC =BC ,AB = 8,CD ⊥AB ,垂足为点D ．M 为边AB 上随意率性一点,点N 在射线CB 上（点N 与点C 不重合）,且MC = MN ,NE ⊥AB ,垂足为点E ．当点M 在边AB 上移动时,试摸索线段ME 的长是否会转变？解释你的来由． 〖思绪剖析〗射线CB 包含线段CB 和线段CB 的延伸线两部分,点N 在射线CB 上活动时,可证实△CMD 和△MEN 全等,所以线段ME 的长始终和线段CD 相等,所以不会转变长度．例2如图,已知在正方形ABCD 中,AB = 2,P 是边BC 上的随意率性一点,E 是边BC 延伸线上一点,联络AP ．过点P 作PF ⊥AP ,与∠DCE 的等分线CF 订交于点F ．联络AF ,与边CD 订交于点G ,联络PG ．（1）求证：AP = FP ;（2）摸索线段BP .DG .PG 之间的数目关系,并给出证实进程;（3）当BP 取何值时,PG // CF ． 〖思绪剖析〗ABC图1D NM EBA CD EPFGC F P M DB ADM AB CP F EA BED MC1．过点F 作FH ⊥BC ,联合所给前提无法证实△ABP 和△PHF 全等．在边AB 上截取线段AH ,使AH = PC ,即可证实△AHP ≌△PCF ．2．由第（1）小题的结论得△APF 是等腰直角三角形,所以∠PAF =45°,将△ADG 绕点A 顺时针扭转90°后,BP 与DG 联络成一条线段,经由过程全等三角形可证BP 与DG 的和等于PG ．3．当PG // CF 时,△PCG 是等腰直角三角形,由第（2）小题结论得PG =DG +BP ,在R t △PCG 中,由勾股定理可求得BP 的长． 【练习】第 天 ,年 月 日1.★★已知：在△ABC 中,AB =AC ,点P 在直线BC 上,PD ⊥AB 于点D ,PE ⊥AC 于点E ,BH 是△ABC 的高．（1）当点P 在边BC 上时,求证：PD +PE =BH（2）当点P 在边BC 的延伸线上时,试摸索PD .PE 和BH 之间的数目关系．2.★★★已知等边△ABC 和点P ,设点P 到△ABC 三边AB .AC .BC的距离分离为H 1,H 2,H 3,△ABC 的高为H ．“若点P 在一边BC 上如图（1）,此时H 3＝0可得结论：H 1＋H 2＋H 3＝H ．”请直策应用上述信息解决下列问题：当点P 在△ABC 内如图（2）,以及点P 在△ABC 外如图（3）这两种情形时,上述结论是否成立？若成立,请予以证实;若不成立,H 1,H 2,H 3与H 之间又有如何的关系,请写出你的猜测,图1图2图33.★★★已知在正△ABC 中,AB =4,点M 是射线AB 上的随意率性一点（点M 与点A .B 不重合）,点N 在边BC 的延伸线上,且AM = CN ．联络MN ,交直线AC 于点D ．设AM = x ,CD = y ．（1）如图,当点M 在边AB 上时,求y 关于x 的函数解析式,并写出自变量x 的取值规模．（2）当点M 在边AB 上,且四边形BCDM 的面积等于△DCN 面积的4倍时,求x 的值．（3）过点M 作ME ⊥AC ,垂足为点E ．当点M 在射线AB 上移动时,线段DE 的长是否会转变？请证实你的结论．4.★★★在R t △ABC 中,∠C =900,∠A =300,AB =4,将一个300角的极点P 放在AB 边上滑动,保持300角的一边平行于BC ,且交边AC 于点E ,300角的另一边交射线BC 于点D ,联络ED ．（1）如图1,当四边形PBDE 为等腰梯形时,求AP 的长;（2）四边形PBDE 有可能为平行四边形吗？若可能,求出PBDE 为平行四边形时AP 的长;若不成能,解释来由;（3）若D 在BC 边上（不与B .C 重合）,试写出线段AP 取值规模.5.★★★在梯形ABCD 中,AD //BC ,AB=CD=AD =5cm ,BC =11cm ,点P从点D 动身沿DA 边以每秒1cm 的速度移动,点Q 从点B 动身,沿BC 边以每秒2cm 的速度移动（当点P 到达点A 时,点P 与点Q 同时停滞移动）,假设点P 移动的时光为x （秒）,四边形ABQP 的面积为y （平方厘米）.ABCMNDABCPED300（图1）（1）求y 关于x 的函数解析式,并写出它的界说域;（2）在移动的进程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;（3）在移动的进程中,是否消失x 使得PQ =AB ,若消失求出所有的x 的值,若不消失请解释来由6.★★★★如图,平面直角坐标系中,O是坐标原点,（1;（24个单位得到直线BC ,直线BCB .C ,如点D 在直线BC 上,在平面直角坐标系中求一点P ,使以O .B .D .P 为极点的四边形是菱形．7.★★★★如图1,x 轴.y 轴交于点A.B ,点C 是线段AB 的中点,点D 在线段OC 上,点D 的纵坐标为4．（1）求点C 的坐标和直线AD 的解析式;（2）P 是直线AD 上的点,请你找一点Q ,使以O.A.P.Q 这四个点为极点的四边形是菱形,写出所有知足前提的点Q 的坐标． 猜测证实Q【要点导航】此类问题平日由一个特别图形到一般情形,引出一系列探讨的问题．阅历对一些命题和结论的猜测.证实.推广的进程,领会常识之间的内涵接洽,感触感染特别到一般.数形联合等数学思惟,对学生的想象.思维.归纳.剖析都有较高的请求．此类标题变式多,证实方法也不尽雷同,可以说是出色纷呈．借题施展,拓宽视野,如许做不但有助于学生分解而灵巧的应用常识,并且能不竭进步学生自力探讨问题解决的才能,更有助于造就学生思维的深入性与批评性.【典例精析】例1如图1,已知点D在AC上,△ABC和△ADE都是等腰直角三角形,点M为EC的中点．（1）求证：△BMD为等腰直角三角形．（2）将△ADE绕点A如图2,（1）中的“△BMD为等腰直角三角形”是否仍然成立？请解释来由．（3A如图3,（1）中来由）．（4）我们是否可以猜测,A随意率性扭转必定的角度,如图4,（1）中的均成立？ABCDEM图1ABCDEM图2ABCDE M图3ABCDE M图4〖思绪剖析〗1． 应用直角三角形斜边中线性质和三角形的表里角和定理不难证实DM 与BM 垂直且相等．2．将△ADE 绕点A,加倍延伸DM ,可构造出全等三角形,等腰直角三角形．3．将△ADE 绕点A 随意率性扭转必定的角度时,可以D .M .B例2点A .B .C 在统一向线上,在直线AC衔接AF ,CE ．取AF .CE的中点M .N ,衔接BM ,BN , MN ．（1,（如图1）,三角形．（2,若BA =BE ,BC =BF ,（如图2）,,（3）若将（2B 扭转必定角度,（如图3）,其他前提不变,那么（2）中的结论是否成立？ 若成立,给出你的证实;若不成立,写出准确的结论并给出证实．〖思绪剖析〗1．△ABF 和△EBC 可看作绕点B 扭转90°后可重合的两个三角形,BM 和BN 是对应斜边上的中线,夹角为90°,ABCEFM N图1 A B CEFMN图2ABCEFMN3腰直角三角形．2．∠MBN可看作是两个全等三角形△ABF和△EBC对应边上的中线,它们的夹角∠MBN和对应边的夹角∠ABE和∠FBC相等．3．要证实∠MBN和∠FBC相等,只要证实∠FBM和∠CBN相等,所以要证实△MFB和△NCB全等．〔练习】1.★★★如图1,四边形ABCD,将极点为A的角绕着极点A顺时针扭转,若角的一条边与DC的延伸线交于点F,角的另一条边与CB的延伸线交于点E,衔接EF．（1）若四边形ABCD为正方形,当∠EAF=45°时,有EF=DF－BE．请你思虑若何证实这个结论（只思虑,不必写出证实进程）;（2）如图2,假如在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,当∠EAFBAD时,EF与DF.BE之间有如何的数目关系？请写出它们之间的关系式（只需写出结论）;（3）如图3,假如四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAFBAD时,EF与DF.BE之间有如何的数目关系？请写出它们之间的关系式并赐与证实．（4）在（3）中,若BC=4,DC=7,CF=2,求△CEF的周长（直接写出成果即可）．2.ABCD的边AB上任取一点E,作EF⊥AB交BDEABCDEF 图2ABCDEF图3于点F,取FD的中点G,衔接EG.CG,如图1,易证EG=CG且EG⊥CG．（1）将△BEF绕点B逆时针扭转90°,如图2,则线段EG和CG有如何的数目关系和地位关系？请直接写出你的猜测．（2）将△BEF绕点B逆时针扭转180°,如图3,则线段EG和CG实．3.ABCDEF,（1EG（2）将图1中△BEF绕B点逆时针扭转45º,如图2所示,取DF中点G,衔接EG,CG．你在（1）中得到的结论是否产生变更？写出你的猜测并加以证实．（3）将图1中△BEF绕B点扭转随意率性角度,如图3所示,再衔接响应的线段,问（1）中的结论是否仍然成立？（不请求证实）4.,点D.E.F分离为边AB,M DMN为等边三角形（点M的地位转变时,△DMN也随之整体移动）．（1）如图1,当点M在点B左侧时,请你贯穿连接EN,并断定D图1D图2DD图1D图2FBACE图3DEN与MF有如何的数目关系？点F是否在直线NE上？请写出结论,并解释来由;（2）如图2,当点M在BC上时,其它前提不变,（1）的结论中EN与MF的数目关系是否仍然成立? 若成立,请应用图2证实;若不成立,请解释来由;（3）如图3,若点M在点C右侧时,请你断定（1）的结论中EN 与MF的数目关系是否仍然成立? 若成立,请直接写出结论;若不成（图2）。

动态几何定值问题【考题研究】数学因运动而充满活力，数学因变化而精彩纷呈。

动态题是近年来中考的的一个热点问题，以运动的观点探究几何图形的变化规律问题，称之为动态几何问题，随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题，就其运动对象而言，有点动、线动、面动三大类，就其运动形式而言，有轴对称（翻折）、平移、旋转（中心对称、滚动）等，就问题类型而言，有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。

解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况。

以动态几何问题为基架而精心设计的考题，可谓璀璨夺目、精彩四射。

【解题攻略】动态几何形成的定值和恒等问题是动态几何中的常见问题，其考点包括线段（和差）为定值问题；角度（和差）为定值问题；面积（和差）为定值问题；其它定值问题。

解答动态几何定值问题的方法，一般有两种：第一种是分两步完成：先探求定值. 它要用题中固有的几何量表示.再证明它能成立.探求的方法，常用特殊位置定值法，即把动点放在特殊的位置，找出定值的表达式，然后写出证明.第二种是采用综合法，直接写出证明.【解题类型及其思路】在中考中，动态几何形成的定值和恒等问题命题形式主要为解答题。

在中考压轴题中，动态几何之定值（恒等）问题的重点是线段（和差）为定值问题，问题的难点在于准确应用适当的定理和方法进行探究。

【典例指引】类型一【线段及线段的和差为定值】【典例指引1】已知：△ABC是等腰直角三角形，∠BAC＝90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C交于点E．（1）如图1，当∠CA ′D ＝15°时，作∠A ′EC 的平分线EF 交BC 于点F ． ①写出旋转角α的度数； ②求证：EA ′+EC ＝EF ；（2）如图2，在（1）的条件下，设P 是直线A ′D 上的一个动点，连接PA ，PF ，若AB＝2，求线段PA +PF 的最小值．（结果保留根号） 【举一反三】如图（1），已知∠=90MON ,点P 为射线ON 上一点，且=4OP ，B 、C 为射线OM 和ON 上的两个动点（OC OP >），过点P 作PA ⊥BC ，垂足为点A ，且=2PA ，联结BP ．（1）若12PAC ABOPS S ∆=四边形时，求tan BPO ∠的值； （2）设PC x =，ABy BC=求y 与x 之间的函数解析式，并写出定义域； （3）如图(2)，过点A 作BP 的垂线，垂足为点H ，交射线ON 于点Q ，点B 、C 在射线OM 和ON 上运动时，探索线段OQ 的长是否发生变化？若不发生变化，求出它的值。

武汉市中考数学复习专题——动态几何问题（含答案）春去秋来，花开花落，物转星移，世间万物每时每刻都处于运动变化、相互联系、相互转化中，事物的本质特征只有在运动中方能凸现出来．动态几何问题，是指以几何知识和图形为背景，渗入运动变化观点的一类问题，常见的形式是：点在线段或弧线上运动、图形的翻折、平移、旋转等，解这类问题的基本策略是：1．动中觅静这里的“静”就是问题中的不变量、不变关系，动中觅静就是在运动变化中探索问题中的不变性．2．动静互化“静”只是“动”的瞬间，是运动的一种特殊形式，动静互化就是抓住“静”的瞬间，使一般情形转化为特殊问题，从而找到“动”与“静”的关系．3．以动制动以动制动就是建立图形中两个变量的函数关系，通过研究运动函数，用联系发展的观点来研究变动元素的关系．注：几何动态既是一类问题，也是一种观点与思维方法，运用几何动态的观点，可以把表面看来不同的定理统一起来，可以找到探求几何中的最值、定值等问题的方法；更一般情况是，对于一个数学问题，努力去发掘更多结论，不同解法，通过弱化或强化条件来探讨结论的状况等，这就是常说的“动态思维”．第二十七讲动态几何问题透视春去秋来，花开花落，物转星移，世间万物每时每刻都处于运动变化、相互联系、相互转化中，事物的本质特征只有在运动中方能凸现出来．动态几何问题，是指以几何知识和图形为背景，渗入运动变化观点的一类问题，常见的形式是：点在线段或弧线上运动、图形的翻折、平移、旋转等，解这类问题的基本策略是：1．动中觅静这里的“静”就是问题中的不变量、不变关系，动中觅静就是在运动变化中探索问题中的不变性．2．动静互化“静”只是“动”的瞬间，是运动的一种特殊形式，动静互化就是抓住“静”的瞬间，使一般情形转化为特殊问题，从而找到“动”与“静”的关系．3．以动制动以动制动就是建立图形中两个变量的函数关系，通过研究运动函数，用联系发展的观点来研究变动元素的关系．注：几何动态既是一类问题，也是一种观点与思维方法，运用几何动态的观点，可以把表面看来不同的定理统一起来，可以找到探求几何中的最值、定值等问题的方法；更一般情况是，对于一个数学问题，努力去发掘更多结论，不同解法，通过弱化或强化条件来探讨结论的状况等，这就是常说的“动态思维”．【例题求解】【例1】如图，把直角三角形ABC 的斜边AB 放在定直线上，按顺时针方向在l 上转动两次，使它转到A ″B ″C ″的位置，设BC=1，AC=3，则顶点A 运动到点A ″的位置时，点A 经过的路线与直线l 所围成的面积是．(黄冈市中考题)思路点拨解题的关键是将转动的图形准确分割．Rt ΔABC 的两次转动，顶点A 所经过的路线是两段圆弧，其中圆心角分别为120°和90°，半径分别为2和3，但该路线与直线l 所围成的面积不只是两个扇形面积之和．【例2】如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作AA ′⊥AB ，BB′⊥AB ，且AA ′=AP ，BB ′=BP ，连结A ′B ′，当点P 从点A 移到点B 时，A ′B ′的中点的位置()A ．在平分AB 的某直线上移动B ．在垂直AB 的某直线上移动C ．在AmB 上移动D ．保持固定不移动(荆州市中考题)⌒动态几何问题透视春去秋来，花开花落，物转星移，世间万物每时每刻都处于运动变化、相互联系、相互转化中，事物的本质特征只有在运动中方能凸现出来．动态几何问题，是指以几何知识和图形为背景，渗入运动变化观点的一类问题，常见的形式是：点在线段或弧线上运动、图形的翻折、平移、旋转等，解这类问题的基本策略是： 1．动中觅静这里的“静”就是问题中的不变量、不变关系，动中觅静就是在运动变化中探索问题中的不变性．2．动静互化“静”只是“动”的瞬间，是运动的一种特殊形式，动静互化就是抓住“静”的瞬间，使一般情形转化为特殊问题，从而找到“动”与“静”的关系． 3．以动制动以动制动就是建立图形中两个变量的函数关系，通过研究运动函数，用联系发展的观点来研究变动元素的关系．注：几何动态既是一类问题，也是一种观点与思维方法，运用几何动态的观点，可以把表面看来不同的定理统一起来，可以找到探求几何中的最值、定值等问题的方法；更一般情况是，对于一个数学问题，努力去发掘更多结论，不同解法，通过弱化或强化条件来探讨结论的状况等，这就是常说的“动态思维”． 【例题求解】【例1】 如图，把直角三角形ABC 的斜边AB 放在定直线上，按顺时针方向在l 上转动两次，使它转到A ″B ″C ″的位置，设BC=1，AC=3，则顶点A 运动到点A ″的位置时，点A 经过的路线与直线l 所围成的面积是 ．(黄冈市中考题)思路点拨 解题的关键是将转动的图形准确分割．Rt ΔABC 的两次转动，顶点A 所经过 的路线是两段圆弧，其中圆心角分别为120°和90°，半径分别为2和3，但该路线与直线l 所围成的面积不只是两个扇形面积之和．【例2】如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作AA ′⊥AB ，BB ′⊥AB ，且AA ′=AP ，BB ′=BP ，连结A ′B ′，当点P 从点A 移到点B 时，A ′B ′的中点的位置( ) A ．在平分AB 的某直线上移动 B ．在垂直AB 的某直线上移动C ．在AmB 上移动D ．保持固定不移动(荆州市中考题)⌒思路点拨画图、操作、实验，从中发现规律．【例3】如图，菱形OABC的长为4厘米，∠AOC＝60°，动点P从O出发，以每秒1厘米的速度沿O→A→B路线运动，点P出发2秒后，动点Q从O出发，在OA上以每秒1厘米的速度，在AB上以每秒2厘米的速度沿O→A→B路线运动，过P、Q两点分别作对角线AC的平行线．设P点运动的时间为x秒，这两条平行线在菱形上截出的图形(图中的阴影部分)的周长为y厘米，请你回答下列问题：(1)当x=3时，y的值是多少?(2)就下列各种情形：①0≤x≤2；②2≤x≤4；③4≤x≤6；④6≤x≤8．求y与x之间的函数关系式．(3)在给出的直角坐标系中，用图象表示(2)中的各种情形下y与x的关系．(吉林省中考题)思路点拨本例是一个动态几何问题，又是一个“分段函数”问题，需运用动态的观点，将各段分别讨论、画图、计算．注：动与静是对立的，又是统：一的，无论图形运动变化的哪一类问题，都真实地反映了现实世界中数与形的变与不变两个方面，从辩证的角度去观察、探索、研究此类问题，是一种重要的解题策略．建立运动函数关系就更一般地、整体-地把握了问题，许多相关问题就转化为求函数值或自变量的值．【例4】 如图，正方形ABCD 中，有一直径为BC 的半圆，BC=2cm ，现有两点E 、F ，分别从点B 、点A 同时出发，点E 沿线段BA 以1m ／秒的速度向点A 运动，点F 沿折线A —D —C 以2cm ／秒的速度向点C 运动，设点E 离开点B 的时间为2 (秒)． (1)当t 为何值时，线段EF 与BC 平行?(2)设1<t <2，当t 为何值时，EF 与半圆相切?(3)当1≤t <2时，设EF 与AC 相交于点P ，问点E 、F 运动时，点P 的位置是否发生变化?若发生变化，请说明理由；若不发生变化，请给予证明，并求AP ：PC 的值． (江西省中考题)思路点拨 动中取静，根据题意画出不同位置的图形，然后分别求解，这是解本例的基本策略，对于(1)、(2)，运用相关几何性质建立关于t 的方程；对于(3)，点P 的位置是否发生变化，只需看PCAP是否为一定值．注：动态几何问题常通过观察、比较、分析、归纳等方法寻求图形中某些结论不变或变化规律，而把特定的运动状态，通过代数化来定量刻画描述也是解这类问题的重要思想．【例5】 ⊙O 1与⊙O 2相交于A 、B 两点；如图(1)，连结O 2 O 1并延长交⊙O 1于P 点，连结PA 、PB 并分别延长交⊙O 2于C 、D 两点，连结C O 2并延长交⊙O 2于E 点．已知⊙O 2的半径为R ，设∠CAD=α．(1)求：CD 的长(用含R 、α的式子表示)；(2)试判断CD 与PO 1的位置关系，并说明理由；(3)设点P ′为⊙O 1上(⊙O 2外)的动点，连结P ′A 、P ′B 并分别延长交⊙O 2于C ′、D ′，请你探究∠C ′AD ′是否等于α? C ′D ′与P ′O l 的位置关系如何?并说明理由．(济南市中考题)思路点拨 对于(1)、(2)，作出圆中常见辅助线；对于(3)，P 点虽为OO l 上的一个动点，但⊙O 1、⊙O 2一些量(如半径、AB)都是定值或定弧，运用圆的性质，把角与孤联系起来．⌒学力训练1．如图， ΔABC 中，∠C=90°，AB=12cm ，∠ABC=60°，将ΔABC 以点B 为中心顺时针旋转，使点C 旋转到AB 延长线上的D 处，则AC 边扫过的图形的面积是 cm (π=3.14159…，最后结果保留三个有效数字)． (济南市中考题) 2．如图，在Rt Δ ABC 中，∠C=90°，∠A=60°，AC=3 cm ，将ΔABC 绕点B 旋转至ΔA'BC'的位置，且使A 、B 、C'三点在同一条直线上，则点A 经过的最短路线的长度是 cm ．(黄冈市中考题)3．一块等边三角形的木板，边长为l ，现将木板沿水平线翻滚，那么B 点从开始至结束走过的路径长度为( ) A ．23π B ．34πC ．4D ．232π+(烟台市中考题)4．把ΔABC 沿AB 边平移到ΔA'B'C'的位置，它们的重叠部分的面积是ΔABC 的面积的一半，若AB=2，则此三角形移动的距离AA'是( )A ．12-B ．22C ．1D ．21(荆门市中考题)5．如图，正三角形ABC 的边长为63厘米，⊙O 的半径为r 厘米，当圆心O 从点A 出发，沿着线路AB —BC —CA 运动，回到点A 时，⊙O 随着点O 的运动而移动． (1)若r=3厘米，求⊙O 首次与BC 边相切时AO 的长；(2)在O 移动过程中，从切点的个数来考虑，相切有几种不同的情况?写出不同的情况下，r 的取值范围及相应的切点个数；(3)设O 在整个移动过程中，在ΔABC 内部，⊙O 未经过的部分的面积为S ，在S>0时，求关于r 的函数解析式，并写出自变量r 的取值范围．(江西省中考题)6．已知：如图，⊙O 韵直径为10，弦AC=8，点B 在圆周上运动(与A 、C 两点不重合)，连结BC 、BA ，过点C 作CD ⊥AB 于D ．设CB 的长为x ，CD 的长为y ． (1)求y 关于x 的函数关系式；当以BC 为直径的圆与AC 相切时，求y 的值； (2)在点B 运动的过程中，以CD 为直径的圆与⊙O 有几种位置关系，并求出不同位置时y 的取值范围；(3)在点B 运动的过程中，如果过B 作BE ⊥AC 于E ，那么以BE 为直径的圆与⊙O 能内切吗?若不能，说明理由；若能，求出BE 的长．(太原市中考题)7．如图，已知A 为∠POQ 的边OQ 上一点，以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点，且∠MAN=∠POQ=α(α为锐角)．当∠MAN 以点A 为旋转中心，AM 边从与AO 重合的位置开始，按逆时针方向旋转(∠MAN 保持不变)时，M 、N 两点在射线OP 上同时以不同的速度向右平移移动．设OM=x ，ON= (y >x ≥0)，ΔAOM 的面积为S ，若cos α、OA 是方程02522=+-z z 的两个根．(1)当∠MAN 旋转30°(即∠OAM=30°)时，求点N 移动的距离； (2)求证：AN 2=ON ·MN ；(3)求y 与x 之间的函数关系式及自变量x 的取值范围； (4)试写出S 随x 变化的函数关系式，并确定S 的取值范围．(河北省中考题)8．已知：如图，梯形ABCD 中，AD ∥BC ，AB=CD=3cm ，∠C ＝60°，BD ⊥CD ． (1)求BC 、AD 的长度；(2)若点P 从点B 开始沿BC 边向点C 以2cm ／s 的速度运动，点Q 从点C 开始沿CD 边向点D 以1cm ／s 的速度运动，当P 、Q 分别从B 、C 同时出发时，写出五边形ABPQD 的面积S 与运动时间t 之间的函数关系式，并写出自变量t 的取值范围(不包含点P 在B 、C 两点的情况)；(3)在(2)的前提下，是否存在某一时刻t ，使线段PQ 把梯形ABCD 分成两部分的面积比为1：5？若存在，求出t 的值；若不存在，请说明理由．(青岛市中考)9．已知：如图①，E 、F 、G 、H 按照AE=CG ，BF=DH ，BF ＝nAE(n 是正整数)的关系，分别在两邻边长a 、na 的矩形ABCD 各边上运动． 设AE=x ，四边形EFGH 的面积为S ．(1)当n=l 、2时，如图②、③，观察运动情况，写出四边形EFGH 各顶点运动到何位置，使?(2)当n=3时，如图④，求S 与x 之间的函数关系式(写出自变量x 的取值范围)，探索S 随x 增大而变化的规律；猜想四边形EFGH 各顶点运动到何位置，使ABCD S S 矩形21； (3)当n=k (k ≥1)时，你所得到的规律和猜想是否成立?请说明理由．(福建省三明市中考题)10．如图1，在直角坐标系中，点E 从O 点出发，以1个单位／秒的速度沿x 轴正方向运动，点F 从O 点出发，以2个单位／秒的速度沿y 轴正方向运动，B(4，2)，以BE 为直径作⊙O 1．(1)若点E 、F 同时出发，设线段EF 与线段OB 交于点G ，试判断点G 与⊙O 1的位置关系，并证明你的结论；(2)在(1)的条件下，连结FB ，几秒时FB 与⊙O 1相切?(3)如图2，若E 点提前2秒出发，点F 再出发，当点F 出发后，E 点在A 点左侧时，设BA ⊥x 轴于A 点，连结AF 交⊙O 1于点P ，试问PA ·FA 的值是否会发生变化?若不变，请说明理由，并求其值；若变化，请求其值的变化范围．(武汉市中考题)参考答案。

2020年中考数学热点专练八动态几何问题（江苏版）（解析版）专题导读动态几何问题，是近年来的热点问题.它几乎成了每个城市中考试卷中的亮点，拿到一套试卷，总是习惯先看看有没有关于动态几何的问题.动态几何问题也就是关于图形运动的一类问题，它主要是牵扯到图形的三种变换：平移、旋转、轴对称及动点问题.当然考查图形的运动问题有小题，也有大题，小题主要分布在选择和填空的最后一两个题，也就是小压轴题，解答题中也会有关于图形的运动问题，主要有两类，一类是关于平移、旋转、轴对称的作图，这个比较简单，我们这里就不说了；另一类就是我们介绍的重点一一研究图形在运动过程中产生的一些图形性质上的变化和不变的情况.这几乎成了压轴题基本上共同的特点.中考要求中考要求课程标准和中考说明都要求学生要具备一定的用运动观点分析问题的能力.学会在运动变化中寻求不变的图形性质.学会运用函数的观点研究关于图形运动中性质的变化情况.专题集训考向1图形的运动与最值1.（2019江苏省连云港市）如图，在矩形ABCD中，AB=4,AD=3,以点C为圆心作。

与直线相切，点P是QC±一个动点，连接AP交于点T,则业的最大值是AT2.（2019江苏省无锡市）如图，在AABC中，AB=AC=5,BC=4逐，D为边AB上一动点（3点除外），以CD为一边作正方形CDEF,连接8E,则ABDE面积的最大值为.3.（2019江苏省宿迁市）如图，ZMAN^60°,若△ABC的顶点3在射线AM上，且A3=2,点。

在射线AN上运动，当AABC是锐角三角形时，BC的取值范围是.4.（2019江苏省宿迁市）如图，正方形ABCQ的边长为4,E为BC上一点，且BE=1,F为AB边上的一个动点，连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为.5.(2019江苏省扬州市)如图，己知等边△ABC的边长为8,点F是边上的一个动点(与点A、B不重合).直线1是经过点P的一条直线，把△ABC沿直线1折叠，点B的对应点是点B'.(1)如图1,当PB=4时，若点可恰好在AC边上，则菌，的长度为；(2)如图2,当PB=5时，若直线1〃AC,则33,的长度为；(3)如图3,点P在AB边上运动过程中，若直线1始终垂直于AC,AACB'的面积是否变化？若变化，说明理由；若不变化，求出面积；(4)当PB=6时，在直线1变化过程中，求可面积的最大值.6.(2019江苏省苏州市)已知矩形ABCD AB=5cm,点F为对角线AC上的一点，且AP =26cm.如图①，动点M从点A出发，在矩形边上沿着的方向匀速运动(不包含点C).设动点M的运动时间为I(s),A4PM的面积为S(enF),S与f的函数关系如图②所示:(1)直接写出动点M的运动速度为cm/s,BC的长度为cm-,(2)如图③，动点M重新从点A出发，在矩形边上，按原来的速度和方向匀速运动.同时，另一个动点N从点£＞出发，在矩形边上沿着D t C t B的方向匀速运动，设动点N的运动速度为v(cm/s).已知两动点M、N经过时间x(s)在线段BC上相遇(不包含点C),动点N相遇后立即停止运动，记此时AARW与AZJRV的面积为5]（＜?麻）,$2（伽2）.①求动点N运动速度v（cm/s）的取值范围；②试探究S] .S?是否存在最大值.若存在，求出S|・S2的最大值并确定运动速度时间x的值;若不存在，请说明理由.(B®)7.（2019江苏省扬州市）如图，四边形A3CD是矩形，A3=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,ZG=90°.点M在线段AB上，且AM=a,点P沿折线AQ-DG运动，点Q沿折线BC-CG运动（与点G不重合），在运动过程中始终保持线段PQ//AQ.设PQ与AB之间的距离为x.（1）若a=12.①如图1,当点F在线段AD上时，若四边形AMQF的面积为48,则x的值为；②在运动过程中，求四边形AMQP的最大面积；（2）如图2,若点P在线段ZJG上时，要使四边形AMQP的面积始终不小于50,求a的取值范围.考向2动点与函数的结合问题1.(2019江苏省连云港市)如图，在平面直角坐标系xOy中，抛物线L：y^x+bx+c过点C(0,-3),与抛物线£2：-lx2-旦t+2的一个交点为A,且点A的横坐标为2,点22P、Q分别是抛物线3、3上的动点.(1)求抛物线3对应的函数表达式；(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形，求出点F的坐标；(3)设点R为抛物线3上另一个动点，且CA平分ZPCR.若OQ//PR,求出点。

《动态几何问题》专题突破训练（附答案）1．如图，在直角三角形ABC 中，∠ACB =90°，AB =5cm ，BC =4cm ．动点P 从点A 出发，沿线段AB 向终点B 以5cm /s 的速度运动，同时动点Q 从点A 出发沿射线AC 以5cm /s 的速度运动，当点P 到达终点时，点Q 也随之停止运动；连接PQ ，设∠APQ 与∠ABC 重叠部分图形的面积为S （cm 2），点P 运动的时间为t （s ）（t ＞0）．（1）直接写出AC = cm ；（2）当点A 关于直线PQ 的对称点A '落在线段BC 上时，求t 的值；（3）求S 与t 之间的函数关系式；（4）若M 是PQ 的中点，N 是AB 的中点，当MN 与BC 平行时，t = ；当MN 与AB 垂直时，t = ．2．如图，矩形ABCD 中，P 是边AD 上的一动点，联结BP 、CP ，过点B 作射线交线段CP 的延长线于点E ，交边AD 于点M ，且使得ABE CBP =∠∠，如果2AB =，5BC =，AP x =，PM y =（1）求y 关于x 的函数解析式，并写出它的定义域；（2）当4AP =时，求 tan EBP ∠；（3）如果EBC ∆是以EBC ∠为底角的等腰三角形，求AP 的长A-，点3．如图，平行四边形ABCO位于直角坐标系中，O为坐标原点，点(8,0)()C BC交y轴于点.D动点E从点D出发，沿DB方向以每秒1个单位长度的速度3,4终点B运动，同时动点F从点O出发，沿射线OA的方向以每秒2个单位长度的速度运动，当点E运动到点B时，点F随之停止运动，运动时间为t（秒）．（1）用t的代数式表示：BE=________，OF=________（2）若以A，B，E，F为顶点的四边形是平行四边形时，求t的值．（3）当BEF恰好是等腰三角形时，求t的值．4．在∠ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作∠ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE为多少？说明理由；（2）设∠BAC=α，∠BCE=β．①如图2，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；②当点D在直线BC上移动，则α，β之间有怎样的数量关系？请直接写出你的结论，不需证明．5．问题情境：如图1，已知正方形ABCD与正方形CEFG，B、C、G在一条直线上，M是AF的中点，连接DM，EM．探究DM，EM的数量关系与位置关系．小明的思路是：小明发现AD//EF，所以通过延长ME交AD于点H，构造∠EFM和∠HAM全等，进而可得∠DEH是等腰直角三角形，从而使问题得到解决，请你参考小明同学的思路，探究并解决下列问题：（1）猜想图1中DM、EM的数量关系，位置关系．（2）如图2，把图1中的正方形CEFG绕点C旋转180°，此时点E在线段DC的延长线上，点G落在线段BC上，其他条件不变，（1）中结论是否成立？请说明理由；（3）我们可以猜想，把图1中的正方形CEFG绕点C旋转任意角度，如图3，（1）中的结论（“成立”或“不成立”）拓展应用：将图1中的正方形CEFG绕点C旋转，使D，E，F三点在一条直线上，若AB＝13，CE＝5，请画出图形，并直接写出MF的长．6．如图，已知抛物线y＝﹣x2+bx+c经过点A（﹣1，0），B（3，0），与y轴交于点C，点P 是抛物线上一动点，连接PB，PC．（1）求抛物线的解析式；（2）如图1，当点P在直线BC上方时，过点P作PD上x轴于点D，交直线BC于点E．若PE＝2ED，求∠PBC的面积；（3）抛物线上存在一点P，使∠PBC是以BC为直角边的直角三角形，求点P的坐标．7．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB ∠＝ °，线段BD 、CE 之间的数量关系是 ；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，AC ＝AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．8．如图，∠O 的半径为5，弦BC ＝6，A 为BC 所对优弧上一动点，∠ABC 的外角平分线AP 交∠O 于点P ，直线AP 与直线BC 交于点E ．（1）如图1，①求证：点P 为BAC 的中点；②求sin∠BAC 的值；（2）如图2，若点A 为PC 的中点，求CE 的长；（3）若∠ABC 为非锐角三角形，求PA •AE 的最大值．9．如图1，已知∠ABC 中，∠ACB ＝90°，AC ＝BC ＝6，点D 在AB 边的延长线上，且CD ＝AB ．（1）求BD 的长度；（2）如图2，将∠ACD 绕点C 逆时针旋转α（0°＜α＜360°）得到∠A'CD'．①若α＝30°，A'D'与CD 相交于点E ，求DE 的长度；②连接A'D 、BD'，若旋转过程中A'D ＝BD'时，求满足条件的α的度数．（3）如图3，将∠ACD 绕点C 逆时针旋转α（0°＜α＜360°）得到∠A'CD'，若点M 为AC 的中点，点N 为线段A'D'上任意一点，直接写出旋转过程中线段MN 长度的取值范围．10．如图，P 是等边ABC 内的一点，且5PA =，4PB =，3PC =，将APB △绕点B 逆时针旋转，得到CQB △．（1）求点P 与点Q 之间的距离；（2）求BPC ∠的度数；（3）求ABC 的面积ABC S．11．如图，在矩形ABCD 中，6AB cm =，8BC cm =，如果点E 由点B 出发沿BC 方向向点C 匀速运动，同时点F 由点D 出发沿DA 方向向点A 匀速运动，它们的速度分别为2/cm s 和1/cm s ，FQ BC ⊥，分别交AC ，BC 于点P 和Q ，设运动时间为()04ts t <<．（1）连接EF ，若运动时间t =_______s 时，EF =；（2）连接EP ，当EPC 的面积为23cm 时，求t 的值；（3）若EQP ADC ∽△△，求t 的值．12．如图，边长为ABCD 中，P 是对角线AC 上的一个动点（点P 与A 、C 不重合），连接BP ，将BP 绕点B 顺时针旋转90°得到BQ ，连接QP ，QP 与BC 交于点E ，其延长线与AD （或AD 延长线）交于点F ．（1）连接CQ ，证明：CQ AP =；（2）设AP x =，CE y =，试写出y 关于x 的函数关系式，并写出自变量x 的取值范围； （3）试问当P 点运动到何处时，PB PE +的值最小，并求出此时CE 的长．（画出图形，直接写出答案即可）13．已知：O 是ABC ∆的外接圆，且,60,AB BC ABC D =∠=︒为O 上一动点． （1）如图1，若点D 是AB 的中点，求DBA ∠的度数．（2）过点B 作直线AD 的垂线，垂足为点E ．①如图2，若点D 在AB 上．求证CD DE AE =+．②若点D 在AC 上，当它从点A 向点C 运动且满足CD DE AE =+时，求ABD ∠的最大值．14．抛物线239344y x x =--与x 轴交于点A ，与y 轴交于点B ．线段OA 上有一动点P (不与O A 、重合)，过点P 作y 轴的平行线交直线AB 于点C ，交抛物线于点M （1）求直线AB 的解析式；（2）点N 为线段AB 下方抛物线上一动点，点D 是线段AB 上一动点；①若四边形CMND 是平行四边形，证明：点M N 、横坐标之和为定值；②在点P N D 、、运动过程中，平行四边形CMND 的周长是否存在最大值？若存在，求出此时点D 的坐标，若不存在，说明理由15．如图，在平面直角坐标系中，点C 在x 轴上，90,10cm,6cm OCD D AO OC CD ︒∠=∠====．（1）请求出点A 的坐标．（2）如图（2），动点P Q 、以每秒1cm 的速度分别从点O 和点C 同时出发，点P 沿OA AD DC 、、运动到点C 停止，点Q 沿CO 运动到点O 停止，设P Q 、同时出发t 秒． ①是否存在某个时间t （秒），使得OPQ △为直角三角形？若存在，请求出值；若不存在，请说明理由．②若记POQ △的面积为()2cm y ，求()2cm y 关于t （秒）的函数关系式． 16．已知，点O 是等边ABC 内的任一点，连接OA ，OB ，OC ．（∠）如图1所示，已知150AOB ∠=︒，120BOC ∠=︒，将BOC 绕点C 按顺时针方向旋转60︒得ADC ．①求DAO ∠的度数：②用等式表示线段OA ，OB ，OC 之间的数量关系，并证明；（∠）设AOB α∠=，BOC β∠=．①当α，β满足什么关系时，OA OB OC ++有最小值？并说明理由；②若等边ABC 的边长为1，请你直接写出OA OB OC ++的最小值．17．如图，在正方形ABCD 中，AB =4，动点P 从点A 出发，以每秒2个单位的速度，沿线段AB 方向匀速运动，到达点B 停止．连接DP 交AC 于点E ，以DP 为直径作∠O 交AC 于点F ，连接DF 、PF ．（1）则∠DPF 是 三角形；（2）若点P 的运动时间t 秒．①当t 为何值时，点E 恰好为AC 的一个三等分点；②将∠EFP 沿PF 翻折，得到∠QFP ，当点Q 恰好落在BC 上时，求t 的值．18．已知四边形ABCD 为矩形，对角线AC 、BD 相交于点O ，AD AO =．点E 、F 为矩形边上的两个动点，且60EOF ∠=︒．（1）如图1，当点E 、F 分别位于AB 、AD 边上时，若75OEB ∠=︒，求证：AD BE =；（2）如图2，当点E 、F 同时位于AB 边上时，若75OFB ∠=︒，试说明AF 与BE 的数量关系；（3）如图3，当点E 、F 同时在AB 边上运动时，将OEF 沿OE 所在直线翻折至OEP ，取线段CB 的中点Q ．连接PQ ，若()20AD a a =>，则当PQ 最短时，求PF 之长．19．如图，在∠ABC中，AB＝BC＝AC＝12cm，点D为AB上的点，且BD＝34AB，如果点P在线段BC上以3cm/s的速度由B点向终点C运动，同时，点Q在线段CA上由C点向终点A运动．当一点到达终点时，另一点也随之停止运动．（1）如（图一）若点Q的运动速度与点P的运动速度相等，经过1s后，∠BPD与∠CQP是否全等，请说明理由．（2）如（图二）若点Q的运动速度与点P的运动速度相等（点P不与点B和点C重合），连接点A与点P，连接点B与点Q，并且线段AP，BQ相交于点F，求∠AFQ的度数．（3）若点Q的运动速度为6cm/s，当点Q运动几秒后，可得到等边∠CQP？20．如图，Rt∠ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．（1）若∠BPQ与∠ABC相似，求t的值；（2）试探究t为何值时，∠BPQ是等腰三角形；（3）试探究t为何值时，CP＝CQ；（4）连接AQ，CP，若AQ∠CP，求t的值．21．如图1，在正方形ABCD 中，4AB m =，点P 从点D 出发，沿DA 向点A 匀速运动，速度是1/cm s ，同时，点Q 从点A 出发，沿AB 方向，向点B 匀速运动，速度是2/cm s ，连接PQ 、CP 、CQ ，设运动时间为()(02)t s t <<．()1是否存在某一时刻，使得//PQ BD 若存在，求出t 的值；若不存在，说明理由； ()2设PQC △的面积为()2S cm ，求S 与t 之间的函数关系式；()3如图2，连接AC ，与线段PQ 相交于点M ，是否存在某一时刻t ，使QCM S ：4PCM S =：5？若存在，直接写t 的值；若不存在，说明理由．22．如图，在 RtΔABC 中，∠C=90°，BC=5cm ，tanA 512=．点 M 在边 AB 上，以 2 cm/s 的速度 由点B 出发沿BA 向点A 匀速运动；同时点N 在边AC 上，以1 cm/s 的速度由A 出发沿AC 向点C 匀速运动．当点M 到达A 点时，点M ，N 同时停止运动．连接MN ，设点M 运动的时间为t (单位：s)．（1）求AB 的长；（2）当t 为何值时，ΔAMN 的面积为∠ABC 面积的326； （3）是否存在时间t ，使得以A ，M ，N 为顶点的三角形与ΔABC 相似？若存在，求出时间t 的值；若不存在，请说明理由．23．如图，抛物线y ＝ax 2+bx+3与x 轴交于A ，B 两点，且点B 的坐标为(2，0)，与y 轴交于点C ，抛物线对称轴为直线x 12=-．连接AC ，BC ，点P 是抛物线上在第二象限内的一个动点．过点P 作x 轴的垂线PH ，垂足为点H ，交AC 于点Q ．过点P 作PG∠AC 于点G ． （1）求抛物线的解析式．（2）求PQG 周长的最大值及此时点P 的坐标．（3）在点P 运动的过程中，是否存在这样的点Q ，使得以B ，C ，Q 为顶点的三角形是等腰三角形？若存在，请写出此时点Q 的坐标；若不存在，请说明理由．24．如图，直线1:1l y kx =+与x 轴交于点D ，直线2:l y x b =-+与x 轴交于点A ，且经过定点(1,5)B -，直线1l 与2l 交于点(2,)C m ．（1）求k 、b 和m 的值；（2）求ADC ∆的面积；（3）在x 轴上是否存在一点E ，使BCE ∆的周长最短？若存在，请求出点E 的坐标；若不存在，请说明理由；（4）若动点P 在线段DA 上从点D 开始以每秒1个单位的速度向点A 运动，设点P 的运动时间为t 秒．是否存在t 的值，使ACP ∆为等腰三角形？若存在，直接写出t 的值；若不存在，清说明理由．25．如图，已知抛物线2()30y ax bx a =++≠与x 轴交于点(1,0)A 和点(3,0)B -，与y 轴交于点C ．（1）求抛物线的解析式；（2）设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使CMP ∆为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由； （3）作直线BC ，若点(,0)D d 是线段BM 上的一个动点（不与B 、M 重合），过点D 作x 轴的垂线交抛物线于点F ，交BC 于点E ，当BDE CEF S S ∆∆=时，求d 的值．26．正方形ABCD 和等腰Rt DEF △共顶点D ，90DEF ∠=︒，DE EF =，将DEF 绕点D 逆时针旋转一周．（1）如图1，当点F 与点C 重合时，若2AD =，求AE 的长；（2）如图2，M 为BF 中点，连接AM 、ME ，探究AM 、ME 的关系，并说明理由； （3）如图3，在（2）条件下，连接DM 并延长交BC 于点Q ，若22AD DE ==，在旋转过程中，CQ 的最小值为_________．27．综合与探究 如图，抛物线245y x bx c =++经过点()0,4A ，()10B ,，与x 轴交于另一点C （点C 在点B 的右侧），点()P m n ,是第四象限内抛物线上的动点．（1）求抛物线的函数解析式及点C 的坐标；（2）若APC △的面积为S ，请直接写出S 关于m 的函数关系表达式，并求出当m 的值为多少时，S 的值最大？最大值为多少？（3）是否存在点P ，使得PCO ACB ∠=∠？若存在，求出点P 的坐标；若不存在，请说明理由．28．某学校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程： 操作发现：（1）如图1，分别以AB 和AC 为边向∠ABC 外侧作等边∠ABD 和等边∠ACE ，连接BE ､CD ，请你完成作图并证明BE =CD ．（要求：尺规作图，不写作法但保留作图痕迹）类比探究：（2）如图2，分别以AB 和AC 为边向∠ABC 外侧作正方形ABDE 和正方形ACFG ，连接CE ､BG ，则线段CE ､BG 有什么关系？说明理由．灵活运用：（3）如图3，在四边形ABCD 中，AC 、BD 是对角线，AB =BC ，∠ABC =60°，∠ADC =30°，AD =3，BD =5，求CD 的长．参考答案1．（1）3；（2）38t =；（3）当305t <≤时，210S t =；当315t <≤时，215309S t t =-+-；（4）38；58．2．（1）4y x x =-．定义域为25x <≤；（2）34；（3）4或53+ 3．（1）5－t ，2t ；（2）3t =或133t =；（3）53t =或910t = 4．（1）90°；（2）①α＋β＝180°；②点D 在直线BC 上移动，α＋β＝180°或α＝β．5．（1）DM∠EM ，DM ＝ME ；（2）结论成立；（3）成立；拓展应用： 6．（1）y ＝﹣x 2+2x +3；（2）3；（3）点P 的坐标为（1，4）或（﹣2，﹣5）7．（1）60BD CE ，＝；（2）45CEB BD ∠︒＝，；（3）CE 的长为或48．（1）①证明；②3sin 5BAC ∠=；（2）CE =；（3）80.9．（1）﹣（2）；②45°或225°；（3）﹣＋310．（1）4PQ =；（2）150BPC ∠=︒；（3）9ABC S =． 11．（1）23；（2）2；（3）212．（1）见解析；（2）2(06)y x x =+<<；（3）P 位置如图所示，此时PB PE +的值最小，6CE =-13．（1）30DBA ∠=；（2）①；②当点D 运动到点I 时ABI ∠取得最大值，此时30ABD ∠=．14．（1）334y x =-；（2）①证明；②存在；点D 的坐标为111111,,3434⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭；． 15．（1）(8,6)A ．（2）①存在，40 s 9t =或者50 s 9t =．②233(010)10S t t t =-+<<． 16．（1）①90°；②线段OA ，OB ，OC 之间的数量关系是OA 2+OB 2=OC 2，证明；（2）①当α=β=120°时，OA+OB+OC 有最小值．证明；②线段OA+OB+OC17．(1)等腰直角;(2)①当t 为1时，点E 恰好为AC 的一个三等分点；．18．（1）证明；（2）2AF BE =；（3）.2FP a =19．（1）BPD CQP ≌；（2）60︒（3）4320．（1）1或3241；（2）23或89或6457；（3）329-；（4）78． 21．()1存在，43t =；()2228(02)S t t t =-+<<；()3存在，1t = 22．（1）13cm ；（2）t=2或92s ；（3）存在，15637t =或16938t =s23．（1）y 12=-x 212-x+3；（2）)9108，P(32-，218)；（3）存在，Q 1(，+3)，Q 2(﹣1，2)24．（1）12k =，4b =，2m =；（2）6；（3存在，8(7E ，0)；（4）存在，6-4或2．25．（1）223y x x =--+；（2）存在，P (-或(1,-或(1,6)-或5(1,)3-；（3）d =26．（1）AE =（2）AM ME =，AM ME ⊥；（3）227．（1）2424455x x y -+=；点C 的坐标为（5，0）；（2）当m ＝52时，S 的值最大，最大值为252；（3）存在点P ，使得使得∠PCO ＝∠ACB ．点P 的坐标为（2，－125）. 28．（1）；（2）CE=BG ；（3）CD=4。

微重点　立体几何中的动态问题“动态”问题是高考立体几何问题最具创新意识的题型，它渗透了一些“动态”的点、线、面等元素，给静态的立体几何题赋予了活力，题型更新颖．同时，由于“动态”的存在，也使立体几何题更趋多元化，将立体几何问题与平面几何中的解三角形问题、多边形面积问题以及解析几何问题之间建立桥梁，使得它们之间灵活转化．知识导图考点一：动点轨迹问题考点二：折叠、展开问题考点三：最值、范围问题考点分类讲解考点一：动点轨迹问题规律方法　解决与几何体有关的动点轨迹问题的方法(1)几何法：根据平面的性质进行判定．(2)定义法：转化为平面轨迹问题，用圆锥曲线的定义判定或用代数法进行计算．(3)特殊值法：根据空间图形线段长度关系取特殊值或位置进行排除．1(2024·浙江温州·一模)如图，所有棱长都为1的正三棱柱ABC -A 1B 1C 1，BE =2EC，点F 是侧棱AA 1上的动点，且AF =2CG，H 为线段FB 上的动点，直线CH ∩平面AEG =M ，则点M 的轨迹为()A.三角形(含内部)B.矩形(含内部)C.圆柱面的一部分D.球面的一部分【答案】A【分析】根据题意首先保持H 在线段FB 上不动(与F 重合)，研究当点F 运动时M 的轨迹为线段MN ，再根据H 点在线段FB 上运动的轨迹即可得出点M 的轨迹为△MNE 及其内部的所有点的集合.【详解】如下图所示：首先保持H 在线段FB 上不动，假设H 与F 重合根据题意可知当F 点在侧棱AA 1上运动时，若F 点在A 1点处时，G 为CC 1的中点，此时由AF =2CG 可得满足FM =2MC，当F 点运动到图中F 1位置时，易知AF 1 =2CG 1，取AG 1∩CF 1=P ，可得F 1P =2PC ，取棱AC 上的点N ，满足AN =2NC，根据三角形相似可得M ,N ,P 三点共线，当点F 在侧棱AA 1上从A 1点运动到A 点时，M 点轨迹即为线段MN ；再研究当点H 在线段FB 上运动，当点H 在线段FB 上从点F 运动到点B 时，M 点的轨迹是线段ME ，当点H 在线段F 1B 上从点F 1运动到点B 时，M 点的轨迹是线段PE ，因此可得，当点F 是侧棱AA 1上运动时，H 在线段FB 上运动时，点M 的轨迹为△MNE 及其内部的所有点的集合；即可得M 的轨迹为三角形(含内部).故选：A2(多选)(23-24高三上·贵州安顺·期末)如图，在棱长为2的正方体ABCD -A 1B 1C 1D 1中，点E 、F 、G 、H 分别为棱CC 1、C 1D 1、A 1D 1、AB 的中点，点M 为棱A 1B 1上动点，则()A.点E 、F 、G 、H 共面B.GM +MH 的最小值为1+5C.点B 到平面AB 1C 的距离为233D.DE ⊥A 1H【答案】ACD【分析】根据题意建立空间之间坐标系，利用平面向量基本定理可对A 判断，利用向量的垂直表示可对D 判断；利用正方体面展开图可对B 判断；利用等体积法可对C 判断.【详解】如图，以D 为原点，建立空间直角坐标系，则D 0,0,0 ，E 0,2,1 ，F 0,1,2 ，G 1,0,2 ，H 2,1,0 ，对A ：EF =0,-1,1 ，EG =1,-2,1 ，EH =2,-1,-1 ，设EF =λEG +μEH ，即0,-1,1 =λ1,-2,1 +μ2,-1,-1 ，解得λ=23，μ=-13，所以EF ,EG ,EH共面，故A 正确．对B ：将正方体沿AB 剪开展开如下图，连接GH 交A 1B 1于一点，此点为M 点，此时GM +MH 为最小值32+22=13，故B 错误；对C ：由等体积法可知V B -AB 1C =V B 1-ABC ，即13·S △AB 1C ·d =13·S △ABC ·BB 1 ，由S △AB 1C =12×2×2×sin π3=32，S △ABC =12×2×2=2，求解得d =233，故C 正确.对D ：D 0,0,0 ，A 12,0,2 ，DE =0,2,1 ，A 1H=0,1,-2 DE ·A 1H =2-2=0，则DE ⊥A 1H ，所以DE ⊥A 1H ，故D 正确.故选：ACD .3(2023·贵州·一模)如图，已知正方体ABCD -A 1B 1C 1D 1的棱长为2，M ，N ，P 分别为棱AA 1,CC 1,AD 的中点，Q 为该正方体表面上的点，若M ，N ，P ，Q 四点共面，则点Q 的轨迹围成图形的面积为．【答案】33【分析】根据题意找出点Q 的轨迹围成图形为正六边形PENFGM 即可求解.【详解】如图，取CD ,B 1C 1,A 1B 1的中点分别为EFG ，则点Q 的轨迹围成图形为正六边形PENFGM ，且边长为面对角线的一半，即2，所以点Q 的轨迹围成图形的面积为6×122×2 2-222=33，故答案为:3 3.4(2023·宁波联考)正方体ABCD -A 1B 1C 1D 1的棱长为1，点P 满足BP =λBC+μ-→BB 1(λ，μ∈R )，则下列说法正确的有()A.若λ+μ=1，则A 1P ⊥AD 1B.若λ+μ=1，则三棱锥A 1-PDC 1的体积为定值C.若点P 总满足PA ⊥BD 1，则动点P 的轨迹是一条直线D.若点P 到点A 的距离为3，则动点P 的轨迹是一个面积为π的圆【答案】ABC【解析】对于A ，因为BP =λBC +μ-→BB 1(λ，μ∈R )且λ+μ=1，由向量基本定理可知，点B 1，C ，P 共线，如图，连接AD1，A 1C ，BC 1，B 1C ，在正方体ABCD -A 1B 1C 1D 1中，B 1C ⊥BC 1，A 1B 1⊥平面BB 1C 1C ，因为BC 1⊂平面BB 1C 1C ，所以A 1B 1⊥BC 1，又B 1C ∩A 1B 1=B 1，所以BC 1⊥平面A 1B 1C ，在BC 1上任取一点P ，连接A 1P ，则A 1P ⊂平面A 1B 1C ，所以BC 1⊥A 1P ，在正方体ABCD -A 1B 1C 1D 1中，因为AB ∥D1C 1，且AB =D 1C 1，所以四边形ABC 1D 1为平行四边形，所以AD 1∥BC 1，则AD 1⊥A 1P ，故选项A 正确；对于B ，如图，连接A 1C 1，C 1D ，A 1D ，B 1C ，因为BP =λBC+μ-→BB 1(λ，μ∈R )且λ+μ=1，由向量基本定理可知点B 1，C ，P 共线，即点P 在直线B 1C 上，在正方体ABCD -A 1B 1C 1D 1中，因为A 1B 1∥DC ，且A 1B 1=DC ，所以四边形A 1B 1CD 为平行四边形，所以A 1D ∥B 1C ，A 1D ⊂平面A 1C 1D ，BC 1⊄平面A 1C 1D ，所以B 1C ∥平面A 1C 1D ，则直线B 1C 上任意一点到平面A 1C 1D 的距离相等，又因为△A 1C 1D 的面积为一定值，所以三棱锥A 1-PDC 1的体积为定值，故选项B 正确；对于C ，如图，连接AC ，BD ，AB1，BD 1，B 1C ，B 1D 1，在正方体ABCD -A 1B 1C 1D 1中，AC ⊥BD ，BB 1⊥平面ABCD ，因为AC ⊂平面ABCD ，所以BB 1⊥AC ，又BB 1∩BD =B ，所以AC ⊥平面BB 1D 1D ，BD 1⊂平面BB 1D 1D ，所以AC ⊥BD 1，同理AB 1⊥BD 1，又AB 1∩AC =A ，所以BD 1⊥平面AB 1C ，因为点P 满足BP =λBC +μ-→BB 1(λ，μ∈R )，所以点P 在侧面BB 1C 1C 所在的平面上运动，且PA ⊥BD 1，所以动点P 的轨迹就是直线B 1C ，故选项C 正确；对于D ，因为点P 到点A 的距离为3，所以点P 的轨迹是以A 为球心，3为半径的球面与平面BB 1C 1C 的交线，即点P 的轨迹为小圆，设小圆半径为r ，因为球心A 到平面BB 1C 1C 的距离为1，则r =(3)2-1=2，所以小圆的面积S =πr 2=2π，故选项D 错误考点二：折叠、展开问题规律方法　画好折叠、展开前后的平面图形与立体图形，抓住两个关键点：不变的线线关系、不变的数量关系．1(2024·河南·模拟预测)为体现市民参与城市建设、共建共享公园城市的热情，同时搭建城市共建共享平台，彰显城市的发展温度，某市在中心公园开放长椅赠送点位，接受市民赠送的休闲长椅.其中观景草坪上一架长椅因其造型简单别致，颇受人们喜欢(如图1).已知AB 和CD 是圆O 的两条互相垂直的直径，将平面ABC 沿AB 翻折至平面ABC ，使得平面ABC ⊥平面ABD (如图2)此时直线AB 与平面C BD 所成角的正弦值为()A.13B.33C.22D.32【答案】B【分析】根据给定条件，建立空间直角坐标系，利用空间向量求出线面角的正弦值.【详解】依题意，OC ⊥AB ,OD ⊥AB ，而平面ABC ⊥平面ABD ，平面ABC ∩平面ABD =AB ，又OC ⊂平面ABC ,OD ⊂平面ABD ，则OC ⊥平面ABD ，OD ⊥OC ，因此直线OD ,OB ,OC 两两垂直，以点O 为原点，直线OD ,OB ,OC 分别为x ,y ,z 轴建立空间直角坐标系，令圆半径OD =1，则O (0,0,0),D (1,0,0),B (0,1,0),C (0,0,1)，OB =(0,1,0),BC=(0,-1,1),BD =(1,-1,0)，设平面C BD 的一个法向量n =(x ,y ,z )，则n ⋅BC=-y +z =0n ⋅BD=x -y =0，令y =1，得n =(1,1,1)，设直线AB 与平面C BD 所成的角为θ，则sin θ=|cos ‹n ,OB ›|=|n ⋅OB ||n ||OB |=11×3=33，所以直线AB 与平面C BD 所成角的正弦值为33.故选：B2(22-23高三上·浙江·开学考试)如图，矩形ABCD 中，AD =2,AB =3,AE =2EB，将△ADE 沿直线DE 翻折成△A 1DE ，若M 为线段A 1C 的点，满足CM =2MA 1，则在△ADE 翻折过程中(点A 1不在平面DEBC 内)，下面四个选项中正确的是()A.BM ⎳平面A 1DEB.点M 在某个圆上运动C.存在某个位置，使DE ⊥A 1CD.线段BA 1的长的取值范围是5,3【答案】ABD【分析】由已知，选项A ，在DC 上取一点N ，令CN =2ND ，可通过面面平行的判定定理证明平面BMN ∥平面ADE ，从而证明BM ∥平面A 1DE ；选项B ，可通过∠A 1DE =∠MNB =π4,NM =43，EB =22，借助余弦定理可知BM 为定值，从而确定M 点的轨迹；选项C ，可先假设DE ⊥A 1C 成立，然后借助线面垂直的判定定理和性质定理得到DE ⊥CH ，然后在△DHC 中，利用勾股定理验证是否满足，即可做出判断；选项D ，可通过点A 1运行轨迹，分别找出最大值和最小值点，然后求解即可做出判断.【详解】如上图所示，在DC 上取一点N ，令CN =2ND，连接NB ，在矩形ABCD 中，AB =CD 且AB ∥CD ，又因为AE =2EB ，CN =2ND，所以EB =ND 且EB ∥ND ，所以四边形EBND 为平行四边形，所以NB ∥ED ，又因为NB ⊄平面ADE ，DE ⊂平面ADE ，所以NB ∥平面ADE ，又因为CN =2ND ，CM =2MA 1，所以NM ∥A 1D ，又因为NM ⊄平面ADE ，DA 1⊂平面ADE ，所以NM ∥平面ADE ，又因为NM ∩NB =N 且NM 、NB ⊂平面BMN ,所以平面BMN ∥平面ADE ，又因为MB ⊂平面BMN ,所以BM ∥平面A 1DE ，选项A 正确；由NB ∥ED ，NM ∥A 1D ，AD =AE =2,可得∠A 1DE =∠MNB =π4,由CN =2ND ，CM =2MA 1 可知，NM =23A 1D =43，而EB =ND =22，由余弦定理可知，BM 为定值，而B 为定点，故M 在以B 为圆心，BM 为半径的圆上运动，故选项B 正确；取ED 的中点H ，连接HA 1、HC ，在△A 1DE 中，AD =AE =2，所以DE ⊥A 1H ，假设DE ⊥A 1C 成立，A 1H 、A 1C ⊂平面A 1HC ,所以DE ⊥平面A 1HC ，又因为CH ⊂平面A 1HC ，所以DE ⊥CH ，而，在△DHC 中，DH =2，DC =3，CH =5，所以∠DHC ≠π2，故DE ⊥CH 不成立，所以假设不成立，该选项C 错误；在DC 上取一点A 2，令DA 2 =2A 2C，在△ADE 翻折过程中, 线段BA 1的最大值是A 1与A 点重合，此时BA 1=3，线段BA 1的最小值是A 1与A 2点重合，此时BA 1=5，又因为点A 1不在平面DEBC 内，所以线段BA 1的长的取值范围是5,3 ，选项D 正确；故选：ABD3(2024高三·全国·专题练习)如图1，在等边△ABC 中，点D 、E 分别为边AB 、AC 上的动点且满足DE ⎳BC ，记DEBC=λ.将△ADE 沿DE 翻折到△MDE 的位置，使得平面MDE ⊥平面DECB ，连接MB ，MC ，如图2，N 为MC 的中点．(1)当EN ⎳平面MBD 时，求λ的值．(2)随着λ的值的变化，二面角B -MD -E 的大小是否改变？若是，请说明理由；若不是，请求出二面角B -MD -E 的正弦值．【答案】(1)λ=12(2)不是，255【分析】(1)取MB 的中点为P ，连接DP ，PN ，推出NP ∥BC ，证明NEDP 为平行四边形，利用比例关系求解即可．(2)取DE 的中点O ，如图建立空间直角坐标系，求出平面BMD 的法向量，平面EMD 的法向量，利用空间向量的数量积求解二面角的余弦函数值然后求解即可．【详解】(1)如图，取MB 的中点P ，连接DP ，PN ．因为N 为MC 的中点，所以NP ⎳BC ，NP =12BC ．又DE ⎳BC ，所以NP ⎳DE ，即N ，P ，D ，E 四点共面．因为EN ⎳平面MBD ，EN ⊂平面NEDP ，平面NEDP ∩平面MBD =DP ，所以EN ⎳DP ，即四边形NEDP 为平行四边形，所以NP =DE ，即DE =12BC ，所以λ=12．(2)取ED 的中点O ，连接MO ，则MO ⊥DE ．因为平面MDE ⊥平面DECB ，平面MDE ∩平面DECB =DE ，MO ⊂平面MDE ，所以MO ⊥平面DECB ．如图，建立空间直角坐标系，不妨设BC =2，则M 0,0,3λ ，D λ,0,0 ，B 1,31-λ ,0 ，所以MD =λ,0,-3λ ，DB =1-λ,31-λ ,0 ．设平面MBD 的一个法向量为m=(x ,y ,z )，则MD ⋅m=λx -3λz =0,DB ⋅m =1-λ x +31-λ y =0,即x =3z ,x =-3y , 令x =3，所以m =3,-1,1 ．由题意可知n=(0,1,0)为平面MDE 的一个法向量．设二面角B -MD -E 的平面角为θ，则cos θ =cos m ,n =m ⋅n m n =55，因此sin θ=1-cos 2θ=255，所以二面角B -MD -E 的正弦值为255．4(2023·邵阳模拟)如图所示，在矩形ABCD 中，AB =3，AD =1，AF ⊥平面ABCD ，且AF =3，点E 为线段CD (除端点外)上的动点，沿直线AE 将△DAE 翻折到△D ′AE ，则下列说法中正确的是()A.当点E 固定在线段CD 的某位置时，点D ′的运动轨迹为球面B.存在点E ，使AB ⊥平面D ′AEC.点A 到平面BCF 的距离为32D.异面直线EF 与BC 所成角的余弦值的取值范围是1313，1010【答案】　D【解析】选项A ，当点E 固定在线段CD 的某位置时，线段AE 的长度为定值，AD ′⊥D ′E ，过D ′作D ′H ⊥AE 于点H ，H 为定点，D ′H 的长度为定值，且D ′H 在过点H 与AE 垂直的平面内，故D ′的轨迹是以H 为圆心，D ′H 为半径的圆，故A 错误；选项B ，无论E 在CD (端点除外)的哪个位置，AB 均不与AE 垂直，故AB 不与平面AD ′E 垂直，故B 错误；选项C ，以AB ，AD ，AF分别为x ，y ，z 轴的方向建立如图所示的空间直角坐标系，则A (0,0,0)，F (0,0,3)，B (3，0,0)，C (3，1,0)．BC =(0,1,0)，BF =(-3，0,3)，AB =(3，0,0)，设平面BCF 的法向量为n =(x ，y ，z )，则n ·BC=y =0，n ·BF =-3x +3z =0， 取n =(3，0,1)，则点A 到平面BCF 的距离d =n ·ABn=32，故C 错误；选项D ，设E (3λ，1,0)，λ∈(0,1)，BC=(0,1,0)，EF=-3λ，-1，3 ，设EF 与BC 所成的角为θ，则cos θ=EF ·BCEF BC=13λ2+10∈1313，1010 ，故D 正确．考点三：最值、范围问题规律方法　在动态变化过程中产生的体积最大、距离最大(小)、角的范围等问题，常用的解题思路是(1)直观判断：在变化过程中判断点、线、面在何位置时，所求的量有相应最大、最小值．(2)函数思想：通过建系或引入变量，把这类动态问题转化为目标函数，从而利用代数方法求目标函数的最值．1(多选)(2023·鞍山模拟)如图，正方体ABCD -A 1B 1C 1D 1的棱长为1，P 是线段BC 1上的动点，则下列结论正确的是()A.四面体PA 1D 1A 的体积为定值B.AP +PC 的最小值为22C.A 1P ∥平面ACD 1D.直线A 1P 与AC 所成的角的取值范围是0，π3【答案】ACD【解析】对于A ，由正方体可得平面DAA 1D 1∥平面BCC 1B 1，且B ，P ∈平面BCC 1B 1，所以点B 到平面DAA 1D 1的距离等于点P 到平面DAA 1D 1的距离，所以四面体PA 1D 1A 的体积V P -A 1D 1A =VB -A 1D 1A =13S △A 1D 1A ×1=13×12×1×1×1=16，所以四面体PA 1D 1A 的体积为定值，故A 正确；对于B ，当P 与B 重合时，AP +PC =AB +BC =2<22，所以AP +PC 的最小值不为22，故B 错误；对于C ，连接A 1C 1，A 1B ，由正方体可得AA 1=CC 1，AA 1∥CC 1，所以四边形AA 1C 1C 是平行四边形，所以AC ∥A 1C 1，因为AC ⊂平面ACD 1，A 1C 1⊄平面ACD 1，所以A 1C 1∥平面ACD 1，同理可得BC 1∥平面ACD 1因为A 1C 1∩BC 1=C 1，A 1C 1，BC 1⊂平面A 1C 1B ，所以平面A 1C 1B ∥平面ACD 1，因为A 1P ⊂平面A 1C 1B ，所以A 1P ∥平面ACD 1，故C 正确；对于D ，因为AC ∥A 1C 1，所以∠PA 1C 1(或其补角)为直线A 1P 与AC 所成的角，由图可得当P 与B 重合时，此时∠PA 1C 1最大为π3，当P 与C 1重合时，此时∠PA 1C 1最小为0，所以直线A 1P 与AC 所成的角的取值范围是0，π3，故D 正确．2(2023·青岛模拟)三面角是立体几何的基本概念之一，而三面角余弦定理是解决三面角问题的重要依据．三面角P -ABC 是由有公共端点P 且不共面的三条射线PA ，PB ，PC 以及相邻两射线间的平面部分所组成的图形，设∠APC =α，∠BPC =β，∠APB =γ，二面角A -PC -B 为θ，由三面角余弦定理得cos θ=cos γ-cos α·cos βsin α·sin β.在三棱锥P -ABC 中，PA =6，∠APC =60°，∠BPC =45°，∠APB =90°，PB +PC=6，则三棱锥P -ABC 体积的最大值为()A.2724B.274C.92D.94【答案】C【解析】如图所示，作BD 垂直于CP 于点D ，设点B 在平面APC 中的射影为M ，连接BM ，MD ，由题意得V P -ABC =13·S △APC·BM .设二面角A -PC -B 为θ，则cos θ=0-12×2232×22=-33，θ∈(0，π)，∴sin ∠BDM =63，BM =BD ·sin ∠BDM =63BD =63·PB ·sin ∠BPC =33·PB ，S △APC =12·PA ·PC ·sin ∠APC =332·PC ，∴V P -ABC =13·S △APC ·BM =12·PB ·PC =12·PB (6-PB )=-12PB 2+3PB=-12(PB -3)2+92，当PB =3时，V P -ABC 的最大值为92.3(23-24高三下·北京·开学考试)正方体ABCD -A 1B 1C 1D 1的棱长为1，动点M 在线段CC 1上，动点P 在平面A 1B 1C 1D 1上，且AP ⊥平面MBD 1.线段AP 长度的取值范围是()A.1,2B.62,3 C.62,2 D.62+∞ 【答案】C【分析】根据题意，建立空间直角坐标系，结合空间向量的坐标运算，代入计算，即可得到结果.【详解】以D 为坐标原点，以DA ,DC ,DD 1分别为x ,y ,z 轴的正半轴，建立如图所示的空间直角坐标系，设P a ,b ,1 ，M 0,1,t 0≤t ≤1 ，则A 1,0,0 ,B 1,1,0 ,D 10,0,1 ，则AP =a -1,b ,1 ,BD 1 =-1,-1,1 ,MD 1=0,-1,1-t ，因为AP ⊥平面MBD 1，所以AP ⊥BD 1,AP ⊥MD 1，即AP ⋅BD 1=1-a -b +1=0AP ⋅MD 1 =-b +1-t =0 ，解得a =t +1b =1-t ，所以AP =t ,1-t ,1 ，所以AP =t 2+1-t 2+1=2t -12 2+32，又0≤t ≤1，所以当t =12时，即M 是CC 1的中点时，AP 取得最小值62，当t =0或1，即M 与点C 或C 1重合时，AP取得最大值2，所以线段AP 长度的取值范围为62,2.故选：C4(2023·黑龙江哈尔滨·三模)已知四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ,PD =AD ，点E 是线段PB 上的动点，则直线DE 与平面PBC 所成角的最大值为()A.π6B.π4C.π3D.π2【答案】C【分析】根据题意，建立空间直角坐标系，结合空间向量的坐标运算即可得到结果.【详解】由题意，因为ABCD 为正方形，且PD ⊥底面ABCD ，以D 为原点，DA ,DC ,DP 所在直线分别为x ,y ,z 轴，建立如图所示空间直角坐标系，设PD =AD =1，则D 0,0,0 ,B 1,1,0 ,C 0,1,0 ,P 0,0,1 ，所以PB =1,1,-1 ,PC =0,1,-1 ，设PE =λPB ，λ∈0,1 ，则PE =λ,λ,-λ ，所以E λ,λ,1-λ ，即DE =λ,λ,1-λ ，设平面PBC 的法向量为n=x ,y ,z ，则n ⋅PB=x +y -z =0n ⋅PC=y -z =0，解得x =0,y =z ，取y =z =1，所以平面PBC 的一个法向量为n=0,1,1 ，设直线DE 与平面PBC 所成角为θ，则sin θ=cos <n ,DE> =n ⋅DEn DE =12×2λ2+1-λ2=12×3λ-132+23，因为y =sin θ,θ∈0,π2单调递增，所以当λ=13时，sin θ=32最大，此时θ=π3，即直线DE 与平面PBC 所成角的最大值为π3.故选:C强化训练一、单选题1(2023·云南保山·二模)已知正方体ABCD -A 1B 1C 1D 1，Q 为上底面A 1B 1C 1D 1所在平面内的动点，当直线DQ 与DA 1的所成角为45°时，点Q 的轨迹为()A.圆B.直线C.抛物线D.椭圆【答案】C【分析】建系，利用空间向量结合线线夹角分析运算.【详解】以点D 为原点，DA ，DC ，DD 1为x ，y ，z 的正方向，建立空间直角坐标系，设正方体棱长为1，则D 0,0,0 ,A 11,0,1 ，设Q x ,y ,1 ，可得DQ =x ,y ,1 ，DA 1 =1,0,1 ，因为直线DQ 与DA 1的所成角为45°，则cos45°=DQ ⋅DA 1 DQ ⋅DA 1=x +1x 2+y 2+1×2=22，化简可得y 2=2x ，所以点Q 的轨迹为抛物线.故选：C .2(2023·全国·三模)在平面直角坐标系中，P 为圆x 2+y 2=16上的动点，定点A -3,2 ．现将y 轴左侧半圆所在坐标平面沿y 轴翻折，与y 轴右侧半圆所在平面成2π3的二面角，使点A 翻折至A ，P 仍在右侧半圆和折起的左侧半圆上运动，则A ，P 两点间距离的取值范围是()A.13,35B.4-13,7C.4-13,35D.13,7【答案】B【分析】设A 所在平面为α，圆的另一半所在平面为β，若P ∈α，则P ,A ,O 三点共线时，以及P 在圆的下端点时，分别取到A ，P 两点间距离的最值；若P ∈β，设P 4cos α,4sin α ，利用两点间的距离公式结合A 到β的距离，以及三角函数的有界性取到最值，进而得出答案．【详解】设A 所在平面为α，圆的另一半所在平面为β，若P ∈α，则P ,A ,O 三点共线时，PA 有最小值P 1A =R -OA =4-13；当P 在圆的下端点时，取到最大值P 2A =-3-02+2+4 2=32+62=35，即PA ∈4-13,35 ；若P ∈β，设P 4cos α,4sin α ，A 在β上的投影为距离为A 1，则A 到β面距离为AA 1 =-3 sin π3=332，又A 到y 轴的距离为3，∴A 1到y 轴的距离为9-274=32，而A 1到x 轴的距离为2，则PA =32+4cos α2+2-4sin α 2+3322=29+2035cos α-45sin α =29+20sin φ-α ，其中α∈-π2,π2 ，sin φ=35,cos φ=45，故PA min =13，当且仅当α=-π2时成立；PAmax =7，当且仅当α=φ-π2时成立；即PA ∈13,7 ；综上可得，PA∈4-13,7 ，故选：B3(2024·全国·模拟预测)如图，已知矩形ABCD 中，E 为线段CD 上一动点(不含端点)，记∠AED =α，现将△ADE 沿直线AE 翻折到△APE 的位置，记直线CP 与直线AE 所成的角为β，则()A.cos α>cos βB.cos α<cos βC.cos α>sin βD.sin α<cos β【答案】B【分析】利用空间向量夹角余弦公式和向量数量积公式得到cos β=CE+EPcos αCP，由三角形三边关系得到cos β>cos α，求出答案.【详解】AB 选项，cos β=CP ⋅EA CP ⋅EA =CE +EP⋅EA CP ⋅EA =CE ⋅EA +EP ⋅EA CP ⋅EA=CE ⋅EA cos α+EP ⋅EA cos α CP ⋅EA =CE +EP ⋅EA cos αCP ⋅EA =CE +EP cos αCP，因为CE +EP >CP ，所以CE +EPCP>1，所以cos β>cos α，A 错误，B 正确；由于y =cos x 在x ∈0,π2上单调递减，故β<α，不确定cos α,sin β和sin α,cos β的大小关系，CD 错误.故选：B ．4(2023·上海宝山·二模)在空间直角坐标系O -xyz 中,已知定点A 2,1,0 ,B 0,2,0 和动点C 0,t ,t +2 t ≥0 .若△OAC 的面积为S ,以O ,A ,B ,C 为顶点的锥体的体积为V ,则VS的最大值为()A.2155 B.155 C.4155 D.455【答案】C【分析】由已知OA =2,1,0 ,0B =0,2,0 ,OC =0,t ,t +2 ,设直线OA 的单位方向向量为u ,根据空间向量公式求出C 到直线OA 的距离,得到△OAC 的面积为S ,根据锥体体积公式得到以O ,A ,B ,C 为顶点的锥体的体积为V ,利用分离常数法和基本不等式求解即可得到最大值.【详解】由已知OA =2,1,0 ,0B =0,2,0 ,OC=0,t ,t +2 ,设直线OA 的单位方向向量为u ,则u =255,55,0,所以C 到直线OA 的距离h =OC 2-OC ⋅u 2=t 2+t +2 2-t 25=9t 2+20t +205,所以S =12×5×9t 2+20t +205=9t 2+20t +202,V =13S △OAB ⋅t +2 =13×12×2×2×t +2 =2t +2 3,则V S =2t +239t 2+20t +202=43⋅t +229t 2+20t +20=49⋅9t 2+36t +369t 2+20t +20=49⋅9t 2+20t +20+16t +169t 2+20t +20=49⋅1+16⋅t +19t 2+20t +20,令m =t +1m ≥1 ,则t =m -1,所以t +19t 2+20t +20=m 9m -1 2+20m -1 +20=m 9m 2+2m +9=19m +9m +2≤129m ⋅9m +2=120,当且仅当9m =9m即m =1时等号成立,所以V S≤49×1+16×120=4515,即V S的最大值为4515.故选:C .5(23-24高三上·河北衡水·阶段练习)正三棱柱ABC -A 1B 1C 1中，AB =2,AA 1=3,O 为BC 的中点，M 为棱B 1C 1上的动点，N 为棱AM 上的动点，且MN MO =MOMA ，则线段MN 长度的取值范围为()A.364,7 B.62,477C.34,477D.3,6【答案】B【分析】根据正三棱柱建立空间直角坐标系，设动点坐标，结合线线关系求线段MN 的表达式，利用函数求最值即可.【详解】因为正三棱柱ABC -A 1B 1C 中,O 为BC 的中点，取B 1C 1中点Q ，连接OQ ，如图，以O 为原点，OC ,OA ,OQ 为x ,y ,z 轴建立空间直角坐标系，则O 0,0,0 ,A 0,3,0 ,B 1-1,0,3 ,C 11,0,3 ，因为M 是棱B 1C 1上一动点，设M a ,0,3 ，且a ∈[-1,1]，所以OM ⋅OA=a ,0,3 ⋅0,3,0 =0，则OA ⊥OM ，因为ON ⊥AM ，且MN MO =MOMA 所以在直角三角形OMA 中可得：△OMN ~△AMO即MN =MO 2MA=a 2+3a 2+3 2+3 2=a 2+3a 2+6，于是令t =a 2+6,t ∈6,7 ，所以a 2+3a 2+6=t 2-3t =t -3t ，t ∈6,7 ，又符合函数y =t -3t 为增增符合，所以在t ∈6，7 上为增函数，所以当t =6时，t -3tmin =6-36=62，即线段MN 长度的最小值为62，当t =7时，t -3tmax=7-37=477，即线段MN 长度的最大值为477，故选：B .【点睛】关键点睛：1.找到△OMN ~△AMO ，再利用函数单调性求出最值.2.建系，设出动点M a ,0,3 ，利用空间向量法求出ON ⊥AM ，再结合线线关系求线段MN 的表达式，利用函数求最值即可.6(23-24高三下·山西·阶段练习)在棱长为4的正方体ABCD -A 1B 1C 1D 1中，E 是CD 的中点，F 是CC 1上的动点，则三棱锥A -DEF 外接球半径的最小值为()A.3B.23C.13D.15【答案】C【分析】取AE 的中点G ，根据题意分析可知：三棱锥A -DEF 外接球的球心O 在过G 垂直于平面ABCD 的直线上，设GO =n ,CF =m ∈0,4 ，建系，结合空间两点距离公式可得n =m 2+4m，进而利用基本不等式运算求解.【详解】连接AE ，取AE 的中点G ，可知G 为△ADE 的外心，过G 作平面ABCD 的垂线，可知三棱锥A -DEF 外接球的球心O 在该垂线上，设GO =n ,CF =m ∈0,4 ，以D 为坐标原点，DA ,DC ,DD 1分别为x ,y ,z 轴，建立空间直角坐标系，则D 0,0,0 ,A 4,0,0 ,E 0,2,0 ,G 2,1,0 ,O 2,1,n ,F 0,4,m ，因为OD =OF ，即4+1+n 2=4+9+m -n 2，整理得n =m 2+4m≥2m 2⋅4m =22，当且仅当m 2=4m，即m =22时，等号成立，所以三棱锥A -DEF 外接球半径的最小值为4+1+8=13.故选：C .【点睛】关键点点睛：根据题意分析可知三棱锥A -DEF 外接球的球心O 在过G 垂直于平面ABCD 的直线上，再以空间直角坐标系为依托，分析求解.7(2023·陕西咸阳·模拟预测)如图，点P 是棱长为2的正方体ABCD -A 1B 1C 1D 1的表面上一个动点，则以下不正确的是()A.当P 在平面BCC 1B 1上运动时，四棱锥P -AA 1D 1D 的体积不变B.当P 在线段AC 上运动时，D 1P 与A 1C 1所成角的取值范围是π3,π2C.使直线AP 与平面ABCD 所成的角为45o 的点P 的轨迹长度为π+42D.若F 是A 1B 1的中点，当P 在底面ABCD 上运动，且满足PF ⎳平面B 1CD 1时，PF 长度的最小值是5【答案】D【分析】由底面正方形ADD 1A 1的面积不变，点P 到平面AA 1D 1D 的距离不变，可判定A 正确；以D 为原点，建立空间直角坐标系，设P (x ,2-x ,0)，则D 1P =(x ,2-x ,-2),A 1C 1=(-2,2,0)，结合向量的夹角公式，可判定B 正确；由直线AP 与平面ABCD 所成的角为45°，作PM ⊥平面ABCD ，得到点P 的轨迹，可判定C 正确；设P (m ,m ,0)，求得平面CB 1D 1的一个法向量为n=(1,-1,-1)，得到FP =2(x -1)2+6，可判定D 错误.【详解】对于A 中：底面正方形ADD 1A 1的面积不变，点P 到平面AA 1D 1D 的距离为正方体棱长，所以四棱锥P -AA 1D 1D 的体积不变，所以A 选项正确；对于B 中：以D 为原点，DA ,DC ,DD 1所在的直线分别为x 轴、y 轴和z 轴，建立空间直角坐标系，可得A 1(2,0,2),D 1(0,0,2),C 1(0,2,2)，设P (x ,2-x ,0),0≤x ≤2，则D 1P =(x ,2-x ,-2),A 1C 1 =(-2,2,0)，设直线D 1P 与A 1C 1所成角为θ，则cos θ=cos D 1P ,A 1C 1 =D 1P ⋅A 1C 1D 1P A 1C 1 =x -1(x -1)2+3，因为0≤x -1 ≤1，当x -1 =0时，可得cos θ=0，所以θ=π2；当0<x -1 ≤1时，cos θ=x -1(x -1)2+3=11+3x -12≤12，所以π3≤θ<π2，所以异面直线D 1P 与A 1C 1所成角的取值范围是π3,π2，所以B 正确；对于C 中：因为直线AP 与平面ABCD 所成的角为45°，若点P 在平面DCC 1D 1和平面BCC 1B 1内，因为∠B 1AB =45°,∠D 1AD =45°最大，不成立；在平面ADD 1A 1内，点P 的轨迹是AD 1=22；在平面ABB 1A 1内，点P 的轨迹是AB 1=22；在平面A 1B 1C 1D 1时，作PM ⊥平面ABCD ，如图所示，因为∠PAM =45°，所以PM =AM ，又因为PM =AB ，所以AM =AB ，所以A 1P =AB ，所以点P 的轨迹是以A 1点为圆心，以2为半径的四分之一圆，所以点P 的轨迹的长度为14×2π×2=π，综上，点P 的轨迹的总长度为π+42，所以C 正确；对于D 中，由B 1(2,2,2),D 1(0,0,2),C (0,2,0),F (2,1,2)，设P (m ,n ,0),0≤m ≤2,0≤n ≤2，则CB 1 =(2,0,2),CD 1 =(0,-2,2),FP=(m -2,n -1,-2)设平面CB 1D 1的一个法向量为n=(a ,b ,c )，则n ⋅CD 1=-2b +c =0n ⋅CB 1=2a +2c =0，取a =1，可得b =-1,c =-1，所以n=(1,-1,-1)，因为PF ⎳平面B 1CD ，所以FP ⋅n=(m -2)-(n -1)+2=0，可得n =m +1，所以FP=(m -2)2+(n -1)2+4=2m 2-4m +8=2(m -1)2+6≥6，当x =1时，等号成立，所以D 错误.故选：D .【点睛】方法点拨：对于立体几何的综合问题的解答方法：(1)、立体几何中的动态问题主要包括：空间动点轨迹的判断，求解轨迹的长度及动角的范围等问题；(2)、解答方法：一般时根据线面平行，线面垂直的判定定理和性质定理，结合圆或圆锥曲线的定义推断出动点的轨迹，有时也可以利用空间向量的坐标运算求出动点的轨迹方程；(3)、对于线面位置关系的存在性问题，首先假设存在，然后再该假设条件下，利用线面位置关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论，则否定假设；(4)、对于探索性问题用向量法比较容易入手，一般先假设存在，设出空间点的坐标，转化为代数方程是否有解的问题，若由解且满足题意则存在，若有解但不满足题意或无解则不存在.8(2023·吉林长春·模拟预测)四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥CD，2AB =BC=CD，BC⊥CD，侧面A1ABB1为正方形，设点O为四棱锥A1-CC1DD外接球的球心，E为DD1上的动点，则直线AE与OB所成的最小角的正弦值为()A.55B.255C.265D.15【答案】D【分析】建立空间直角坐标系，确定各点坐标，设球心O1,h,1 2，根据OA=OC得到h=34，设E2,0,a，根据向量的夹角公式结合二次函数性质计算最值得到答案.【详解】如图所示：以CD,CB,CC1分别为x,y,z轴建立空间直角坐标系，设AB=1，则A1,2,0，C0,0,0，B0,2,0，球心O在平面CDD1C1的投影坐标为1,0,1 2，则设球心O1,h,12，则OA =OC ，即1-12+h -2 2+122=12+h 2+122，解得h =34，则O 1,34,12.设E 2,0,a ，a ∈0,1 ，EA =-1,2,-a ，OB =-1,54,-12，cos EA ,OB=EA ⋅OB EA ⋅OB =1+52+12a a 2+5⋅355=72+12a a 2+5⋅354=14+2a 35×a 2+5设7+a =t ，则a =7-t ，t ∈7,8 ，则14+2a 35×a 2+5=2t35×t 2-14t +54=235×541t-7542+554，当t =547时，有最大值为235×554=265，此时直线AE 与OB 所成的角最小，对应的正弦值为1-2652=15.故选：D【点睛】关键点睛：本题考查了立体几何中的异面直线夹角问题，外接球问题，意在考查学生的计算能力，空间想象能力和综合应用能力，其中建立空间直角坐标系可以简化运算，是解题的关键.二、多选题9(23-24高三下·江苏苏州·开学考试)在正方体ABCD -A 1B 1C 1D 1中，点M 为棱AB 上的动点，则()A.平面ABC 1D 1⊥平面A 1DMB.平面BCD 1⎳平面A 1DMC.A 1M 与BC 1所成角的取值范围为π4,π3D.A 1M 与平面ABC 1D 1所成角的取值范围为π6,π4【答案】ACD【分析】由面面垂直的判定定理可判断A 选项；取点M 与点B 重合，可判断B 选项；以点D 为坐标原点，DA 、DC 、DD 1所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法可判断CD 选项.【详解】对于A 选项，因为四边形AA 1D 1D 为正方形，则A 1D ⊥AD 1，在正方体ABCD -A 1B 1C 1D 1中，AB ⊥平面AA 1D 1D ，A 1D ⊂平面AA 1D 1D ，则A 1D ⊥AB ，因为AB ∩AD 1=A ，AB 、AD 1⊂平面ABC 1D 1，所以，A 1D ⊥平面ABC 1D 1，因为A 1D ⊂平面A 1DM ，故平面ABC 1D 1⊥平面A 1DM ，A 对；对于B 选项，当点M 与点B 重合时，平面BCD 1与平面A 1DM 有公共点，B 错；对于CD 选项，以点D 为坐标原点，DA 、DC 、DD 1所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，不妨设正方体的棱长为1，则A 1,0,0 、B 1,1,0 、C 0,1,0 、D 0,0,0 、A 11,0,1 、B 11,1,1 、C 10,1,1 、D 10,0,1 ，设点M 1,m ,0 ，其中0≤m ≤1，A 1M =0,m ,-1 ，BC 1 =-1,0,1 ，所以，cos A 1M ,BC 1 =A 1M ⋅BC 1A 1M ⋅BC 1 =12m 2+1 ∈12,22 ，设A 1M 与BC 1所成角为α，其中0≤α≤π2，则12≤cos α≤22，可得π4≤α≤π3，所以，A 1M 与BC 1所成角的取值范围为π4,π3，C 对；对于D 选项，由A 选项可知，平面ABC 1D 1的一个法向量为DA 1 =1,0,1 ，则cos A 1M ,DA 1 =A 1M ⋅DA 1A 1M ⋅DA 1 =12m 2+1 ∈12,22 ，设A 1M 与平面ABC 1D 1所成角为β，则0≤β≤π2，则12≤sin β≤22，可得π6≤β≤π4，所以，A 1M 与平面ABC 1D 1所成角的取值范围为π6,π4，D 对.故选：ACD .10(2023·全国·模拟预测)如图①，四边形ABCD 是两个直角三角形拼接而成，AB =1，BD =2，∠ABD =∠C =90°，∠BDC =45°.现沿着BD 进行翻折，使平面ABD ⊥平面BCD ，连接AC ，得到三棱锥A -BCD (如图②)，则下列选项中正确的是()A.平面ABC ⊥平面ACDB.二面角B -AD -C 的大小为60°C.异面直线AD 与BC 所成角的余弦值为33D.三棱锥A -BCD 外接球的表面积为π【答案】ABC【分析】A 选项，面面垂直⇒线面垂直⇒CD ⊥平面ABC ⇒平面ABD ⊥平面ACD ；B 、C 选项，建立空间直角坐标系，利用直线方向向量和平面法向量求解；D 选项，三棱锥的外接球，寻求斜边中点(球心位置).【详解】A 项，平面ABD ⊥平面BCD ，交线为BD ，AB ⊥BD ，AB ⊂平面ABD ，所以AB ⊥平面BCD ，因为CD ⊂平面BCD ，所以AB ⊥CD .又BC ⊥CD ，且AB ∩BC =B ，所以CD ⊥平面ABC .因为CD ⊂平面ACD ，所以平面ABC ⊥平面ACD ，选项A 正确.C 选项，以B 为原点，过B 在平面BCD 内作BD 的垂线为x 轴，直线BD 为y 轴，直线AB 为z 轴，建立空间直角坐标系，则B 0,0,0 ,A 0,0,1 ,C 22,22,0,D 0,2,0 ，则AC =22,22,-1 ，AD =0,2,-1 ,BC =22,22,0.易知平面ABD 的一个法向量为n 1=1,0,0 .设平面ACD 的法向量为n2=x ,y ,z ，则n 2⋅AC =0,n 1⋅AD=0, 即22x +22y -z =0,2y -z =0,取z =2，则x =1,y =1，则n 2=1,1,2 ，由图可知二面角B -AD -C 为锐角，则二面角B -AD -C 的余弦值为cos n 1,n 2=n 1⋅n 2 n 1 n 2 =11×2=12，即二面角B -AD -C 的大小为60°，选项B 正确；cos AD ,BC =AD ⋅BCAD BC =0,2,-1 ⋅22,22,0 3×1=33，选项C 正确；D 项，取AD 的中点N ，因为△ABD 与△ACD 都是直角三角形，所以点N 到A ，B ，C ，D 的距离相等，即为三棱锥A -BCD 外接球的球心，球半径为32，则三棱锥A -BCD 外接球的表面积为4π×322=3π，选项D 错误.故选：ABC .11(2023·全国·模拟预测)如图1，矩形B 1BCC 1由正方形B 1BAA 1与A 1ACC 1拼接而成．现将图形沿A 1A 对折成直二面角，如图2．点P (不与B 1,C 重合)是线段B 1C 上的一个动点，点E 在线段AB 上，点F 在线段A 1C 1上，且满足PE ⊥AB ，PF ⊥A 1C 1，则()。

动态几何与函数问题【例1】如图①所示，直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移，平移后的直线l与x轴交于点D，与y轴交于点E.（1）将直线l向右平移，设平移距离CD为t（t≥0），直角梯形OABC被直线l扫过的面积（图中阴影部份）为s，s关于t的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，且NQ平行于x轴，N点横坐标为4，求梯形上底AB的长及直角梯形OABC的面积.（2）当24<<时，求S关于t的函数解析式.t【思路分析】本题虽然不难，但是非常考验考生对于函数图像的理解。

很多考生看到图二的函数图像没有数学感觉，反应不上来那个M点是何含义，于是无从下手。

其实M点就表示当平移距离为2的时候整个阴影部分面积为8，相对的，N点表示移动距离超过4之后阴影部分面积就不动了。

脑中模拟一下就能想到阴影面积固定就是当D移动过了0点的时候.所以根据这么几种情况去作答就可以了。

第二问建立函数式则需要看出当24<<时，阴t影部分面积就是整个梯形面积减去△ODE的面积，于是根据这个构造函数式即可。

动态几何连带函数的问题往往需要找出图形的移动与函数的变化之间的对应关系，然后利用对应关系去分段求解。

【解】（1）由图（2）知，M点的坐标是（2，8）∴由此判断：24，；==A B O A∵N点的横坐标是4，N Q是平行于x轴的射线，∴4C O=∴直角梯形O A B C 的面积为：()()112441222A BO C O A +⋅=+⨯=..... (3分)（2）当24t <<时，阴影部分的面积=直角梯形O A B C 的面积-O D E∆的面积 (基本上实际考试中碰到这种求怪异图形面积的都要先想是不是和题中所给特殊图形有割补关系)∴1122S O D O E=-⋅ ∵142O D O D tO E==-，∴()24O E t =- .∴()()()21122441242St t t =-⨯-⋅-=--284S t t =-+-.【例2】已知：在矩形A O B C 中，4O B =，3O A =．分别以O B O A ，所在直线为x 轴和y 轴，建立如图所示的平面直角坐标系．F 是边B C 上的一个动点（不与B C ，重合），过F 点的反比例函数(0)k y k x=>的图象与A C 边交于点E ．（1）求证：A O E △与B O F △的面积相等；（2）记O E F E C F S S S =-△△，求当k 为何值时，S 有最大值，最大值为多少？ （3）请探索：是否存在这样的点F ，使得将C E F △沿E F 对折后，C 点恰好落在O B 上？若存在，求出点F 的坐标；若不存在，请说明理由．【思路分析】本题看似几何问题，但是实际上△AOE 和△FOB 这两个直角三角形的底边和高恰好就是E,F 点的横坐标和纵坐标，而这个乘积恰好就是反比例函数的系数K 。