有关二分法计算线性方程根的问题
- 格式:docx
- 大小:51.27 KB
- 文档页数:6


《数值分析》实验报告实验一方程求根一、实验目的:掌握二分法、Newton法、不动点迭代法、弦截法求方程的根的各种计算方法、并实施程序调试和运行,学习应用这些算法于实际问题。
二、实验内容:二分法、Newton法、不动点迭代法、弦截法求方程的根、程序的调试和运行,给出实例的计算结果。
观察初值对收敛性的影响。
三、实验步骤:①、二分法:定义:对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
实现方法:首先我们设一方程400*(x^4)-300*(x^3)+200*(x^2)-10*x-1=0,并求其在区间[0.1,1]上的根,误差限为e=10^-4。
PS:本方法应用的软件为matlab。
disp('二分法')a=0.1;b=1;tol=0.0001;n0=100;fa=400*(a.^4)-300*(a.^3)+200*(a.^2)-10*a-1;for i=1:n0 p=(a+b)/2;fp=400*(p.^4)-300*(p.^3)+200*(p.^2)-10*p-1;if fp==0||(abs((b-a)/2)<tol)disp('用二分法求得方程的根p=')disp(p)disp('二分迭代次数为:')disp(i)break;end;if fa*fp>0 a=p;else b=p;end;end;if i==n0&&~(fp==0||(abs((b-a)/2)<tol)) disp(n0) disp('次二分迭代后没有求出方程的根')end;程序调试:运行结果:用二分法求得方程的根p=0.1108二分迭代次数为:14②Newton法定义:取定初值x0,找到函数对应的点,然后通过该点作函数切线,交x轴,得到新的横坐标值,然后找函数对应的点,做切线,得到新的横坐标值,重复上述步骤,多次迭代,直到收敛到需要的精度。

函数方程的近似根一.实验课题用二分法和牛顿迭代法(包括弦截法)编程求方程sinx-x*x/2=0的实根,要求误差不超过0。
0001。
输出迭代次数,初始值和根的近似值。
二.解决方法(a).二分法求方程的根,首先应该知道根的大概位置或大致范围,就是要确定一个区间(a,b),使f(x)=0在这个区间内只有一个根,区间(a,b)称为有根区间。
有根区间(a,b)内的任何一个值都可以作为方程根的初始近似值。
确定有根区间的方法,主要根据连续函数的一个性质:设f(x)在[a,b]上连续,f(a)*f(b)<0,则方程杂(a,b)内至少有一个根。
用二分法求实根x的思路,就是反复将含有x的区间一分为二,通过判断函数杂各个小区间端点处的符号,逐步对折缩小有根区间,直到区间缩小到容许误差范围之内,然后取最终小区间的中点作为实根x的近似值。
(b).牛顿法牛顿法是求解方程的一种重要的迭代法,其实质是将原方程线性化后获得一个迭代函数的方法。
记[a,b]为方程f(x)=0的根的存在区间,取区间[a,b]内的一点,对f(x)用微分中值定理,近似的有f(x)=f(x(0))+f’(x(0))*(x-x(0))令f(x(0)+f’(x(0))*(x-x(0))=0,显然这是一个线性方程。
解此方程,并设f’(x)不等于零,得到f(x)=0的近似根x(0)-f(x(0))/f’(x(0))记为x(1),即x(1)为方程的一个近似根x(1)=x(0)-f(x(0))/f’(x(0))为改善根近似程度,反复实施这一过程,得到牛顿迭代公式x(k+1)=x(k)-f(x(k))/f’(x(k))这相当于选择迭代函数F(x)=x-f(x)/f’(x)为避免复杂函数计算导f’(x)的困难,常用差分形式f(x(k))-f(x(k-1))/(x(k)-x(k-1)) 代替导数f’(x(k)),这样迭代公式的形式成为x(k+1)=x(k)-(x(k)-x(k-1))*f(x(k))/(f(x(k))-f(x(k-1))) 三.编程a)画图程序plot(x,zeros(size(x)))>> hold off>> grid>> x=0:0.001:2;>> plot(x,fun1(x),'r')>> hold on>> plot(x,zeros(size(x)))>> hold off>> gridfunction y1=fun1(x)y1=sin(x)-x.^2.*0.5;b)二分法程序function c=dicho(a,b)n=50;detra=0.0001;k=0;c=(a+b)*0.5;while abs(a-b)>detraif fun1(c)==0,break,endif fun1(a)*fun1(c)<0,b=c;else a=c;endk=k+1;if k>n,k,error('fail')else c=(a+b)*0.5;endend['Iterative time =',int2str(k)]c)牛顿法程序function [y,k]=newton(x0,n)y(1)=x0;detra=0.0001;k=1;t=x0-(sin(x0)-x0.^2*0.5)/(cos(x0)-x0);while abs(t-x0)>detrax0=t;k=k+1;y(k)=t;t=x0-(sin(x0)-x0.^2./2)./(cos(x0)-x0);if (k-1)>n error('n is full'), endendk=k-1;四.结果与结论1.二分法程序>> c=dicho(1,2)ans =Iterative time =14c =1.40442.牛顿法程序>> [y,k]=newton(1,50)y =1.0000 1.7428 1.4641 1.4070 1.4044k =4由此可见二分法案求根比较慢,牛顿法较快。

用二分法求方程的近似解知识点二分法是一种常用的求方程近似解的数值计算方法,运用这种方法可以找到函数方程f(x)=0在给定区间[a,b]上的一个根。
本文将对二分法的原理、步骤及其应用进行详细介绍。
一、原理二分法的原理基于数学中的零点定理,也叫做中间值定理。
该定理表明:如果一个连续函数f(x)在区间[a,b]上有f(a)和f(b)异号,即f(a)·f(b)<0,则在该区间内至少存在一个根。
基于这一定理,我们可以通过不断将给定区间一分为二,并判断中点函数值与零的位置关系,从而确定新的区间,直到满足精度要求或者迭代次数达到指定值。
这样可以在给定的精度范围内逐步缩小根的位置。
二、步骤下面是使用二分法求解方程根的一般步骤:1.选择一个区间[a,b],确保f(a)·f(b)<0。
这样可以保证函数在区间[a,b]内至少有一个根。
2.计算区间中点m=(a+b)/23.计算函数在中点处的值f(m)。
4.判断f(m)和0的关系:a.如果f(m)等于0,那么m就是方程的一个根;b.如果f(m)与f(a)异号,那么存在根的区间变为[a,m],重复步骤2-4;c.如果f(m)与f(b)异号,那么存在根的区间变为[m,b],重复步骤2-45.重复步骤2-4,直到达到所需的精度要求或者迭代次数达到指定值。
三、应用二分法在解决方程问题中有广泛的应用,特别是对于无法用解析法求解的非线性方程、高次多项式等复杂函数,二分法可以提供一个近似解。
此外,二分法还可以用于其他数值计算问题。
例如,在一些求极值的问题中,我们可以通过求解函数导数方程的根来找到极值点。
这时,同样可以使用二分法来近似求解。
四、注意事项在使用二分法求解方程时,需要注意以下几点:1.确保函数在给定区间上是连续且有定义的。
2.选择合适的初始区间[a,b]。
如果起始区间过大,则可能导致求解时间过长;如果起始区间过小,则可能无法找到根。
通常情况下,可以通过分析函数图像或者利用已知的条件进行初步估计。

高中数学如何求解二分法和牛顿迭代法方程在高中数学中,求解方程是一个重要的内容,而二分法和牛顿迭代法是两种常用的求解方程的方法。
本文将介绍这两种方法的原理、应用以及解题技巧,并通过具体的例题来说明其考点和解题思路。
一、二分法的原理和应用二分法是一种通过不断缩小搜索范围来逼近方程根的方法。
其基本原理是将待求解的区间不断二分,判断根是否在左半区间还是右半区间,并将搜索范围缩小至根的附近。
具体步骤如下:1. 确定初始区间[a, b],使得f(a)与f(b)异号;2. 计算区间中点c=(a+b)/2;3. 判断f(c)与0的关系,若f(c)=0,则c为方程的根;若f(c)与f(a)异号,则根在区间[a, c]内,否则根在区间[c, b]内;4. 重复步骤2和步骤3,直到满足精度要求或找到根。
二分法的应用非常广泛,例如在求解函数的零点、解方程、求解最优化问题等方面都有应用。
下面通过一个具体的例题来说明二分法的应用和解题技巧。
例题1:求方程x^3-2x-5=0的根。
解题思路:1. 首先我们需要确定初始区间[a, b],使得f(a)与f(b)异号。
根据题目中的方程,可以取a=1,b=2,计算f(1)=-6和f(2)=1,满足条件;2. 计算区间中点c=(a+b)/2=1.5;3. 计算f(c)=f(1.5)=-1.375,与0的关系异号,说明根在区间[1, 1.5]内;4. 重复步骤2和步骤3,不断缩小搜索范围,直到满足精度要求或找到根。
通过不断迭代,我们可以得到方程的根为x=1.709。
这个例题展示了二分法的基本思路和解题技巧,通过不断缩小搜索范围,我们可以逼近方程的根。
二、牛顿迭代法的原理和应用牛顿迭代法是一种通过不断迭代逼近方程根的方法,其基本原理是利用函数的切线来逼近根的位置。
具体步骤如下:1. 确定初始点x0;2. 计算函数f(x)在x0处的导数f'(x0);3. 计算切线的方程y=f(x0)+f'(x0)(x-x0);4. 求切线与x轴的交点x1,即x1=x0-f(x0)/f'(x0);5. 重复步骤2到步骤4,直到满足精度要求或找到根。

一、概述二分法是一种常见的数值计算方法,在许多数学问题中都有广泛的应用。
然而,二分法却有一个令人困惑的现象,即当使用二分法寻找函数的根时,有时算法会收敛到一个错误的解。
这种现象被称为二分法悖论,在数值计算领域引起了广泛的讨论和研究。
在本文中,我们将使用现代数学方法解释二分法悖论,并探讨其背后的数学原理。
二、二分法的基本原理在介绍二分法悖论之前,首先需要了解二分法的基本原理。
二分法是一种求解方程根的经典算法,其基本思想是将定义域分割成两部分,然后确定目标值所在的那一部分,再对该部分继续进行分割,直到找到目标值或者满足一定的精度要求为止。
在数值计算中,二分法通常被用来求解函数的零点,即找到函数的根所对应的横坐标。
三、二分法的应用三、一、在实际工程问题中,二分法被广泛应用于求解非线性方程、求解最优化问题和求解微分方程等。
在计算机图形学中,我们常常需要对曲线和曲面进行求交,而二分法可以高效地求解曲线和曲面的交点。
在金融学中,二分法也常被用来计算期权的定价和风险价值。
在生物医学工程领域,二分法则可以用来估计人体组织的材料特性和生物学参数。
四、二分法悖论的实例四、一、尽管二分法在许多应用中表现出色,但在一些情况下却会出现令人困惑的现象。
考虑函数f(x)=x^3-2x-5,在区间[1,2]上使用二分法寻找根时,算法会不断迭代,最终发现无法找到根。
这种情况违反了二分法应该能够找到函数根的基本原则,称为二分法悖论。
五、现代数学方法解释二分法悖论现代数学方法能够对二分法悖论进行深入的解释和分析。
在实际应用中,二分法常常需要与计算机浮点数进行交互,而浮点数的表示精度有限,在对浮点数进行运算时会引入误差。
这些误差可能导致二分法在收敛过程中出现偏离期望的结果。
函数本身的性质,如导数的变化率和函数的凹凸性,也会影响二分法的收敛行为。
六、避免二分法悖论的方法六、一、尽管二分法悖论令人困扰,但通过一些方法和技巧,我们可以在实际应用中避免或减少这种现象的发生。
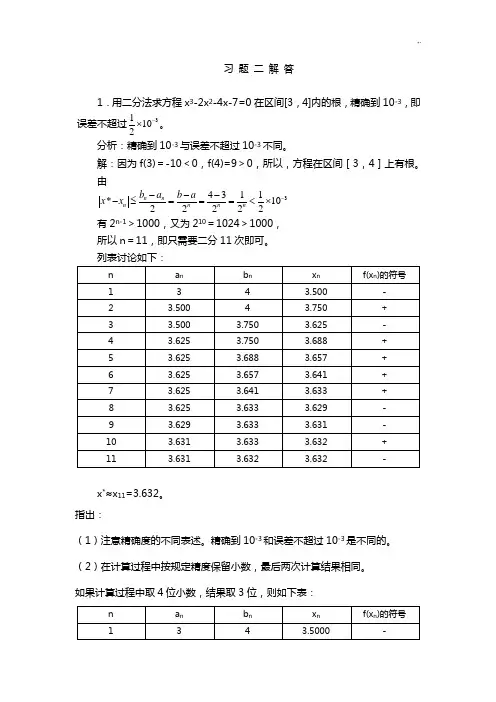
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。

二分法、试位法,牛顿法求方程的根二分法、试位法和牛顿法是求解方程根的常用数值方法。
一、二分法二分法是一种简单而有效的数值方法,它通过不断将区间一分为二来逼近方程的根。
它的基本思想是,如果在一个闭区间[a, b]内,函数f(x)在a和b两点的函数值f(a)和f(b)异号,那么函数在[a, b]内至少存在一个根。
算法步骤如下:1.初始化区间[a, b]和误差容限ε。
2.计算区间中点c=(a+b)/2。
3.如果f(c)=0或者(b-a)/2<ε,则停止迭代,c即为近似的根。
4.如果f(c)与f(a)异号,则根在[a, c]内,将b=c,否则根在[c,b]内,将a=c。
5.回到步骤2。
二、试位法试位法也是一种通过逼近来求解方程根的方法。
与二分法不同,试位法通过计算函数在两个点之间的插值点来逼近根。
它的基本思想是,如果在一个闭区间[a, b]内,函数f(x)在两个点a和b之间有一个变号点c,则函数在[a, b]内至少存在一个根。
算法步骤如下:1.初始化区间[a, b]和误差容限ε。
2.计算函数在区间[a, b]上的插值点c。
3.如果f(c)=0或者(b-a)/2<ε,则停止迭代,c即为近似的根。
4.如果f(c)与f(a)异号,则根在[a, c]内,将b=c,否则根在[c,b]内,将a=c。
5.回到步骤2。
三、牛顿法牛顿法又称为牛顿-拉弗森方法,它是一种通过不断迭代逼近根的方法。
牛顿法基于函数的局部线性近似,通过求导数来计算函数在当前近似根附近的切线与x轴的交点作为新的近似根。
算法步骤如下:1.初始化初始近似根x0和误差容限ε。
2.计算函数在当前近似根x的导数f'(x)。
3.如果f'(x)为0,则停止迭代,x即为近似的根。
4.计算函数在当前近似根x的函数值f(x)。
5.如果|f(x)|<ε,则停止迭代,x即为近似的根。
6.计算新的近似根x=x-f(x)/f'(x)。

方程求根的数值方法数值方法是一种求解方程根的近似方法,它通过一系列计算和迭代来逼近方程的根。
这些方法常用于无法通过代数方法求得解析解的复杂方程,或者是当方程没有明确的解析解时。
在这篇文章中,我们将讨论三种常用的数值方法:二分法、牛顿法和割线法。
二分法是一种基于零点定理的根查找方法。
零点定理指出,如果一个函数在区间[a,b]的两个端点处取得正负值,那么这个函数在这个区间内至少存在一个根。
二分法的基本思想是将区间二分,并判断根是否在分割后的子区间内。
具体步骤如下:1.选择一个初始区间[a,b],使得f(a)和f(b)异号。
2.计算区间中点c=(a+b)/23.如果f(c)等于0或者f(c)的绝对值小于给定的误差限,那么c是近似的根。
4.如果f(c)和f(a)异号,那么根在左半区间[a,c]内;否则,根在右半区间[c,b]内。
5.重复步骤2到4,直到找到满足条件的近似根。
二分法的优点是简单易懂,收敛速度较快;缺点是每次迭代只能减少一半的区间长度。
牛顿法是一种迭代法,通过对函数f(x)的一阶导数进行线性逼近,来求得方程f(x)=0的根。
具体步骤如下:1.选择一个初始近似根x0。
2.计算函数f(x)在x=x0处的导数f'(x0)。
3.计算线性逼近方程的解x1=x0-f(x0)/f'(x0)。
4.如果f(x1)的绝对值小于给定的误差限,那么x1是近似的根。
5.否则,令x0=x1,重复步骤2到4,直到找到满足条件的近似根。
牛顿法的优点是收敛速度快,通常是二次收敛;缺点是对于一些特殊的函数,可能会出现发散或者陷入局部最优解的情况。
割线法是对牛顿法的改进,它通过将区间的两个端点连接起来,构建一条割线来逼近方程的根。
具体步骤如下:1.选择两个初始近似根x0和x1,使得f(x0)和f(x1)异号。
2.计算割线的斜率k=(f(x1)-f(x0))/(x1-x0)。
3.计算线性逼近方程的解x2=x1-f(x1)/k。

数学二分法的原理及应用原理数学二分法是一种常见的数值计算方法,用于求解方程的近似解。
其基本思想是将问题的解空间逐步缩小,通过多次迭代来逼近方程的解。
二分法的原理可以简单地概括为以下几个步骤: 1. 确定解空间的起始范围,即确定一个包含解的区间; 2. 求解区间的中点,并计算中点处的函数值; 3. 判断中点处函数值与目标值的关系,从而确定解所在的区间; 4. 将新的解区间作为起始范围,然后重复步骤2和步骤3,直到满足迭代停止条件。
应用二分法在各个领域都有广泛的应用,下面列举了几个具体的应用场景。
数值计算数值计算中常常需要求解非线性方程的近似解。
通过二分法可以有效地逼近方程的解,从而提供计算的准确性和效率。
例如,二分法可以用于求解多项式的根、方程的解以及函数的零点等。
统计学在统计学中,二分法可以用于确定分位数。
分位数是指将一个集合或分布按照大小划分为几个部分的值,常用于衡量数据的离散程度。
通过二分法可以有效地找到给定百分比的分位数。
优化问题二分法可以应用于求解优化问题。
在一些特定情况下,优化问题可以被转化为求解方程的形式。
通过二分法,可以逐步逼近最优解的取值范围,从而提高求解效率。
数据库查询在数据库查询中,二分法可以用于实现高效的索引查找。
通过将数据按照某种大小顺序进行排序,然后使用二分法进行查找,可以大大提高查询的效率。
二分法在数据库索引的构建和维护中也有广泛应用。
图像处理在图像处理中,二分法可以用于图像分割和边缘检测。
通过将图像的灰度值进行二分,可以将不同的区域分割开来,从而实现对图像的分割和边缘的提取。
在以上应用中,二分法的原理是一致的,即通过逐步缩小解空间来逼近问题的解。
具体应用场景根据问题的特点进行相应的调整和优化,以提高计算的精度和效率。
总之,数学二分法作为一种常见的数值计算方法,在各个领域都有着广泛的应用。
通过了解二分法的原理和相应的应用场景,可以更好地理解和应用这一数学方法。
二分法、不动点迭代法和牛顿迭代法是数值计算中常用的三种求根方法。
它们在不同的数学领域及实际问题中有着广泛的应用。
本文将对这三种方法进行介绍和比较。
一、二分法1. 原理二分法是一种基于区间不断缩小的求根方法。
其原理是通过在函数值的两个不同点处得到异号的情况下缩小区间来逼近实根。
具体过程为:首先确定一个区间[a,b],使得f(a)和f(b)异号,然后将区间一分为二,取中点c=(a+b)/2,若f(c)为零或在一定误差范围内,则c即为所求的根;否则,根据f(a)和f(c)的符号确定新的区间[a,c]或[c,b],重复上述步骤,直到满足要求。
2. 特点二分法的优点是简单易实现,对于连续且单调函数一定能收敛。
但其缺点是收敛速度较慢,尤其在根附近时迭代次数较多。
二、不动点迭代法1. 原理不动点迭代法是求解方程f(x)=0的一种迭代方法,通过将方程变换为x=g(x),其中g(x)为连续函数,然后通过不断地迭代计算得到方程的根。
具体过程为:给定一个初始近似值x0,通过不断迭代计算xn+1=g(xn)来逼近实根。
2. 特点不动点迭代法的优点是迭代过程简单,不需要对函数进行求导。
但其缺点是收敛性有一定要求,不是所有的g(x)函数都能得到收敛结果。
三、牛顿迭代法1. 原理牛顿迭代法是一种通过不断线性化函数来逼近方程根的方法。
其原理是通过对函数f(x)进行泰勒展开,并取展开式的线性部分来进行迭代计算。
具体过程为:给定一个初始近似值x0,通过不断迭代计算xn+1=xn-f(xn)/f'(xn)来逼近实根。
2. 特点牛顿迭代法的优点是收敛速度较快,在根附近有二次收敛性。
但其缺点是需要对函数进行求导,且初始值的选取对迭代结果有一定影响。
二分法、不动点迭代法和牛顿迭代法都是求解方程根的有效方法,各有其优缺点和适用范围。
在实际应用中,根据问题的特性和计算要求来选择适当的方法,以达到准确和高效的求解目的。
4. 比较与应用通过对二分法、不动点迭代法和牛顿迭代法的介绍,我们可以对它们进行比较与应用。
《数值分析》实验报告一**: **学号: PB********实验一一、实验名称方程求根二、实验目的与要求:通过对二分法和牛顿法作编程练习和上机运算,进一步体会它们在方程求根中的不同特点;比较二者的计算速度和计算精度。
三、实验内容:通过对二分法和牛顿迭代法作编程练习和上机运算,进一步体会它们在方程求根中的不同特点 。
(一)二分法算法:给定区间[a,b],并设f (a )与f (b )符号相反,取δ为根的容许误差,ε为值的容许误差。
(1)令c=(a+b)/2(2)如果(c-a)< δ或)(c f <ε,则输出c ,结束;否则执行(3)(3)如果f(a)f(c)<0,则令)()(,c f b f c b ←←;否则,则令)()(,c f a f c a ←←,重复(1),(2),(3)。
(二)牛顿迭代法:给定初值0x ,ε为根的容许误差,η为)(x f 的容许误差,N 为迭代次数的容许值。
(1)如果)(x f <η或迭代次数大于N ,则算法结束;否则执行(2)。
(2)计算)('/)(0001x f x f x x -=(3)若 < 或 < ,则输出 ,程序结束;否则执行(4)。
(4)令 = ,转向(1)。
四、实验题目与程序设计1、二分法3.1.1、用二分法求方程a. f(x)= x x tan 1--在区间[0,π/2]上的根,c. f(x)=6cos 22-++-x e x x 在区间[1,3]上的根。
源程序:3.1.1.a#include<stdio.h>#include<math.h>void main(){float a,b;double c,y,z;printf("plese input two number a and b:\n");scanf("%f%f",&a,&b);c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);while(fabs(b-a)>0.00001|| fabs(y)>0.00001){z=1/a-tan(a);if(z*y<0)b=c;elsea=c;c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);}x x 01-ε)(1x f ηx 1x 0x 1}输入0 1.5707563( /2~1.5705563)得到下表:由上表可以看出刚开始时f(c)取值幅度很大,但是经过一段历程之后,幅度变得平缓甚至基本接近与零,我们认为,x=0.8603是方程的根,结果与实际想要得到的值相当接近。
二分法求方程一、引言在数学中,解方程是一个重要的问题。
对于一些简单的方程,可以通过代数方法来求解。
但是对于一些复杂的方程,代数方法可能无法得到精确解,需要使用数值方法来求解。
本文将介绍二分法求解方程的方法。
二、二分法原理二分法又称折半法,是一种在有序数组中查找某一特定元素的搜索算法。
其基本思想是:将有序数组从中间分开成两部分,如果要查找的元素比中间元素大,则在右半部分继续查找;如果要查找的元素比中间元素小,则在左半部分继续查找;如果要查找的元素恰好等于中间元素,则直接返回。
三、二分法求解方程步骤1. 确定区间首先需要确定一个包含根的区间[a, b]。
通常情况下,可以通过观察函数图像或者利用初值定理来确定一个大致的区间。
2. 求出区间中点将区间[a, b]从中点m=(a+b)/2处划分成两个子区间[a, m]和[m, b]。
3. 判断根所在子区间计算f(m)的值,并与0进行比较。
如果f(m)=0,则m即为方程的解;如果f(m)>0,则根在子区间[a, m]中;如果f(m)<0,则根在子区间[m, b]中。
4. 缩小区间根据上一步的判断结果,将包含根的子区间作为新的搜索区间,重复步骤2和步骤3,直到找到满足精度要求的解。
四、二分法求解方程示例假设要求解方程x^3-2x-5=0在[2, 3]内的一个近似解。
1. 确定区间观察函数图像可知,方程在[2, 3]内有且仅有一个实根。
2. 求出区间中点m=(a+b)/2=2.53. 判断根所在子区间f(m)=m^3-2m-5=-1.875<0,因此根在子区间[m, b]=[2.5, 3]中。
4. 缩小区间重复步骤2和步骤3:m=(a+b)/2=2.75f(m)=m^3-2m-5=1.015625>0,因此根在子区间[a, m]=[2, 2.75]中。
m=(a+b)/2=2.375f(m)=m^3-2m-5=-0.6484375<0,因此根在子区间[m, b]=[2.375, 2.75]中。
数值计算方法实验报告数值计算方法实验报告引言:数值计算方法是一种通过数学模型和计算机算法来解决实际问题的方法。
在科学研究和工程应用中,数值计算方法被广泛应用于求解方程、优化问题、模拟仿真等领域。
本实验报告将介绍数值计算方法的基本原理和实验结果。
一、二分法求根二分法是一种通过不断折半缩小搜索区间来求解方程根的方法。
在实验中,我们选取了一个简单的方程f(x) = x^2 - 4 = 0来进行求根实验。
通过不断将搜索区间进行二分,我们可以逐步逼近方程的根。
实验结果表明,通过二分法,我们可以得到方程的根为x = 2。
二、牛顿迭代法求根牛顿迭代法是一种通过不断逼近方程根的方法。
在实验中,我们同样选取了方程f(x) = x^2 - 4 = 0进行求根实验。
牛顿迭代法的基本思想是通过对方程进行线性近似,求得近似解,并不断迭代逼近方程的根。
实验结果表明,通过牛顿迭代法,我们可以得到方程的根为x = 2。
三、高斯消元法求解线性方程组高斯消元法是一种通过变换线性方程组的系数矩阵,将其化为上三角矩阵的方法。
在实验中,我们选取了一个简单的线性方程组进行求解实验。
通过对系数矩阵进行行变换,我们可以将其化为上三角矩阵,并通过回代求解得到方程组的解。
实验结果表明,通过高斯消元法,我们可以得到线性方程组的解为x = 1,y = 2,z = 3。
四、插值与拟合插值与拟合是一种通过已知数据点来构造函数模型的方法。
在实验中,我们选取了一组数据点进行插值与拟合实验。
通过拉格朗日插值多项式和最小二乘法拟合,我们可以得到数据点之间的函数模型。
实验结果表明,通过插值与拟合,我们可以得到数据点之间的函数关系,并可以通过该函数模型来进行预测和拟合。
结论:数值计算方法是一种通过数学模型和计算机算法来解决实际问题的方法。
通过本次实验,我们学习了二分法求根、牛顿迭代法求根、高斯消元法求解线性方程组以及插值与拟合的基本原理和应用。
这些方法在科学研究和工程应用中具有广泛的应用前景。
数学中的代数方程求根算法研究在数学中,代数方程是一种常见的数学问题,求解代数方程的根是解决这类问题的关键。
代数方程求根算法的研究,旨在寻找一种高效准确的方法来解决各种类型的代数方程,从而拓展数学的应用领域。
本文将探讨几种经典的代数方程求根算法,并分析它们的优缺点。
一、牛顿法是代数方程求根中最为常用的算法之一。
它基于函数的局部线性近似,通过迭代逼近来求得方程的根。
具体的步骤是:1. 选择一个初始近似解。
2. 利用初始解求出函数在该点的导数。
3. 根据函数和导数的关系,计算出下一个近似解。
4. 不断迭代,直到近似解的变化很小或满足预设的精度要求。
牛顿法的优点是收敛速度快,但也有一些问题需要注意。
首先,初始近似解的选择对结果有较大影响,可能会导致陷入局部最小值。
其次,如果函数在某些地方的导数为零,牛顿法会失效。
因此,为了保证算法的可靠性,需要对函数进行充分的了解和分析。
二、二分法是另一种常见的代数方程求根算法。
它利用函数值的符号变化来缩小根的范围,直到满足精度要求。
具体的步骤是:1. 选择一个区间,在该区间的两个端点的函数值异号。
2. 将区间平分,得到中点,并计算中点的函数值。
3. 根据函数值的符号变化,确定新的区间。
4. 不断重复步骤2和步骤3,直到满足精度要求。
二分法的优点是简单易懂,收敛性可证明且较为稳定。
然而,它的收敛速度较慢,特别是当根的数量较多或者根的范围较大时,需要较多的迭代次数。
三、拉格朗日插值法也可以应用于代数方程求根中。
该方法基于多项式插值的思想,通过构造一个插值多项式来逼近函数,然后求取多项式的根。
具体的步骤是:1. 根据给定的数据点,构造一个插值多项式。
2. 求取插值多项式的根。
拉格朗日插值法的优点是对函数进行拟合较好,近似精度较高。
但它也存在一些问题,如插值多项式的次数过高会引发龙格现象,造成插值误差较大。
另外,构造插值多项式需要已知的数据点,如果数据点不准确或者缺失,会导致结果的不准确性。
吉林化工学院
专业:
班级:
学号:
姓名:
有关二分法计算线性方程根的问题
1、二分法求解的提出及其背景
由于实际问题的需要,我们经常需要寻求函数的零点(即的根),对于为一次或二次函数,我们有熟知的公式解法(二次时,称为求根公式).我国古代数学家已比较系统地解决了部分方程求解的问题,在《九章算术》,北宋数学家贾宪的《黄帝九章算法细草》,南宋数学家秦九韶的《数书九章》中均有记载.在十六世纪,已找到了三次和四次函数的求根公式,人们曾经希望得到一般的五次以上代数方程的根式解,但经过长期的努力仍无结果.1824年,挪威年轻数学家阿贝尔(N. H. Abel,1802-1829)成功地证明了五次以上一般方程没有根式解.1828年,法国天才数学家伽罗瓦(E.Galois,1811-1832)巧妙而简洁地证明了存在不能用开方运算求解的具体方程.人们认识到高于4次的代数方程不存在求根公式,因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题。
求解非线性方程的数值解有二分法、迭代法、牛顿—雷扶生方法、正割法和抛物线法。
下面我们就来讨论二分法求解非线性方程数值解的问题。
2、在求解过程中需要用到的定理:
1、(1)设f(x)于[a,b]上连续;
(2)且f(a)•f(b)<0;
则存在有x*∈(a,b),使f(x*)于(a,b)内存在实的零点。
2、给定方程f(x)=0,设f(x)于[a,b]上连续,且f(a)•f(b)<0,则由二分法产生的序列{x k }收敛于方程f(x)=0的根x*,且具有性质
|x k-x*|≦(b-a)/2k(k=1,2,3,…)
3、二分法的描述:
设有非线性方程f(x=0),其中,f(x)为[a,b]上的连续函数且设f(a)•f(b)<0(不妨设该方程在[a,b]内仅有一个实根)。
二分法具体方法如下:
运用上述定理2,设ε>0为给定精度要求,则由|xk-x*|≦(b-a)/2k<ε得半分次数k>[㏑(b-a)-㏑ε]/㏑2.
记a1=a,b1=b;
第一步:k=1,计算x1=(a1+b1)/2及f(x1),如果f(a1)·f(x1)<0则根一定在[ a1,x1]≡[a2,b2]内,否则根一定在区间[x1,b1] ≡[a2,b2]内(若f(x)=0,则x1=x*)。
于是到长度缩小一半的含根区间[a2,b2],即f(a2)·f(b2)<0,且b2-a2=1/2(b1-a1)
第k步分半计算:重复上述计算过程,设已完成第1步,…,第k-1步分半计算得到含根区间[a1, b1] ⊃[a2,b2] ⊃…⊃[a k,b k]且满足:
(1) f(a k )·f(a k)<0,即x*∈[a k,b k];
(2) b k-a k=1/(2k-1);
现进行第k步分部计算:
(3) 计算x k=( a k+ b k)/且有|x k-x*|≦(b-a)/2=1/2k(b-a)
(4) 确定新的含根区间[a k+1,b k+1],即如果f(a k)·f(b k)<0,则根一定在
[a k+1,b k+1]= [a k,b k]内,否则根一定在区间[a k+1,b k+1]=[ x k,, b k],且有b k+1-a k+1=1/2k(b-a).
由上述二分法得到一序列{x k},即可得x*=lim k→∞X k,这个值即为f(x)=0的实根,根据题目要求的精度ε可以求出它的近似解。
4、二分法示意图如下:
5、程序设计:
#include<stdio.h>
#include<math.h>
double funx( double x)
{
return(x*x*x*x*x*x-x-1);} //给出要求的方程。
double fun(float m,float n) // 定义功能函数,通过循环找出在所给精度的
{ 范围内根所在的区间。
double r;
r=(m+n)/2;
while(fabs(m-n)>0.000001) //确定精度不超过0.000001
{ if(funx(r)==0) return r;
if(funx(r)*funx(n)<0)
m=r;
else
n=r;
r=(m+n)/2;}
return r;
}
main()
{
double root ;
float m,n;
printf("plese input two number m n:\n");
scanf("%f%f",&m,&n);
root =fun(m,n); // 调用功能函数。
printf("%f\n",root);// 输出方程的根。
}
所测试的题目是fx=x6-x-1于[1,2]内的一个实根,且要求精确到小数点后第三位。
得到的结果如下:
6、论文分析
二分法的优点是方法简单,易于理解,且对f(x)只要求连续即可。
可用二分法求出f(x)=0于[a,b]内的全部的实根。
但二分法不能求复根及偶数重根。
对于用C语言编程解决二分法求解的问题,显然它没有用Excle那么方便,
而且用C语言编程得到的结果不能看到求解过程中的每一个结果,而用Excle求解可以看到全部的借。
对于此论文中所用到的程序,它只适用于给出一个题目,如果要用来求其他题目的解,则必须对程序中的部分代码进行修改,有点不太方便,需要进行修改优化。
关键字:二分法求解方程的根,C语言编程。