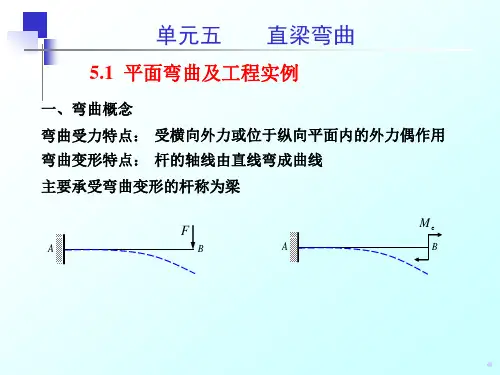
(x) 由边界条件确定。
常见的约束状况与边界条件
1. 固定端条件(位移边界) 挠度和转角等于零
y(x,t) 0 y '(x,t) 0
(x) 0
'(x) 0 x 0,l
2. 简支端(铰支)(位移、力混界)
挠度和弯矩等于零
y(x,t) 0 M (x,t) 0
(x) 0
EIy"(x) 0
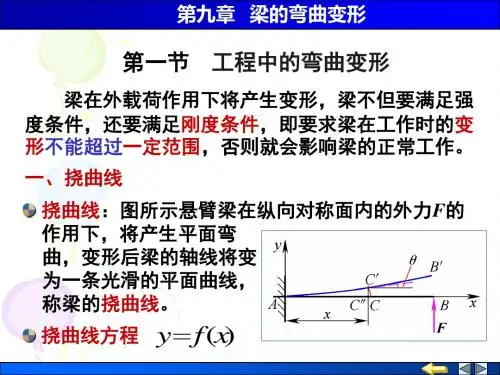
伯努利-欧拉梁(Bernoulli-Euler Beam)
y x,t 距原点 x处的截面在 t 时刻的横向位移
微段受力分析
FS , M 截面上的剪力和弯矩
l
(
x)
2 t
y
2
微段的惯性力
f x,t 微段所受的外力
l
(
x)
2 t
y
2
动力平衡关系由达朗贝尔原理得
l (x)
2 y t 2
dx
Fs
解:固定端:(0) 0 '(0) 0
自由端: 弯矩为零,剪力与质量惯性力平衡
EI "(l) 0 EIl m02 l
利用相同的方法,得频率方程:
cos lchl 1 l sin lcoshl cos l sinh l
其中: m0 为集中质量与梁质量之比
m m Sl 为梁质量
说明:
以上分析中没有考虑剪切变形和截面转动惯量的影响, 因此以上有关梁的分析只适用于细长梁(梁的长度大于梁 高度5倍以上) 若梁为非细长梁,必须考虑剪切变形和截面转动惯量的影响
Fs
Fs x
dx
f
( x, t )dx
l
(
x)
2 t
y
2
Fs x
f (x,t)