线性回归方程——非线性方程转化为线性方程.docx

编号032 §9.1.2 线性回归方程目标要求1、结合具体实例，了解一元线性回归模型的含义．2、结合具体实例，了解模型参数的统计意义．3、结合具体实例，了解最小二乘原理，掌握一元线性回归模型参数的最小二乘估计方法．4、结合具体实例，会使用相关的统计软件．5、针对实际问题，会用一元线性回归模型进行预测．学科素养目标本章内容是在学生已经学习过必修课程中的统计知识和概率知识的基础上，通过对典型案例的研究，了解和使用一些常用统计分析方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用，从而形成运用统计的观点认识客观事物的习惯．在本章教学中，应突出对学生应用意识的培养，不能只限于要求学生会解书本上的习题，还要关注学生应用与解决实际问题的能力．应引导、鼓励学生从现实生活中发现问题，并能自觉地运用所学的统计方法加以理解，应尽量给学生提供一定的实践活动机会，可结合数学建模活动，选择一个案例，要求学生亲自实践．重点难点重点：一元线性回归模型参数的最小二乘估计方法； 难点：用一元线性回归模型进行预测．教学过程基础知识点 1．线性回归模型我们将y ＝___________称为线性回归模型． 2．线性回归方程与最小二乘法(1)线性回归方程：直线＝__________称为线性回归方程．其中__称为回归截距，__称为回归系数，__称为回归值． (2)，的计算公式＝∑i ＝1n（x i －x）（y i －y ）∑i ＝1n（x i －x ）2＝________________ ，＝______________.【课前小题演练】题1．关于回归分析，下列说法错误的是( ) A ．回归分析是研究两个具有相关关系的变量的方法 B ．散点图中，解释变量在x 轴，响应变量在y 轴 C ．回归模型中一定存在随机误差 D ．散点图能明确反映变量间的关系题2．根据如下样本数据：x2 3 4 5 6Y 4 2.5 －0.5 －2 －3得到的经验回归方程为＝x＋，则( )A．＞0，＞0 B．＞0，＜0C．＜0，＞0 D．＜0，＜0题3．已知变量x，Y之间具有线性相关关系，其散点图如图所示，则其经验回归方程可能为( )A．＝1.5x＋2 B．＝－1.5x＋2C．＝1.5x－2 D．＝－1.5x－2题4．若某地财政收入x与支出Y满足经验回归方程＝x＋＋e i(单位：亿元)(i＝1，2，…)，其中＝0.8，＝2，|e i|<0.5，如果今年该地区财政收入10亿元，年支出预计不会超过( )A．10亿元B．9亿元C．10.5亿元D．9.5亿元题5．若施肥量x(kg)与水稻产量Y(kg)的经验回归方程为＝5x＋250，当施肥量为80 kg时，预计水稻产量约为________kg.题6．某种产品的广告费用支出x与销售额Y(单位：百万元)之间有如下的对应数据：x/百万元 2 4 5 6 8Y/百万元30 40 60 50 70(1)画出散点图；(2)求经验回归方程；(3)试预测广告费用支出为10百万元时，销售额多大？【当堂巩固训练】题7．已知x，y的取值如表所示：x234 5y 2.2 3.8 5.5m若y与x线性相关，且回归直线方程为＝1.46x－0.61，则表格中实数m的值为( )A．7.69 B．7.5 C．6.69 D．6.5题8．某药厂为了了解某新药的销售情况，将2019年2至6月份的销售额整理如下：月份 2 3 4 5 6 销售额(万元)1925353742根据2至6月份的数据可求得每月的销售额y 关于月份x 的线性回归方程＝x ＋为( )(参考公式及数据：＝∑i ＝1nx i y i －n x y∑i ＝1n x 2i －n （x ）2，＝y －x ，∑i ＝15x i y i ＝690，∑i ＝15x 2i ＝90)A ．＝5.8x ＋8.4B ．＝8.4x ＋5.8C ．＝6x －9D ．＝4x ＋31.6题9．登山族为了了解某山高y (km )与气温x (℃)之间的关系，随机统计了4次山高与相应的气温，并制作了对照表：气温x (℃) 18 13 10 －1 山高y (km )24343864由表中数据，得到线性回归方程＝－2x ＋()∈R ，由此请估计出山高为72(km )处气温的度数为( )A ．－10B ．－8C ．－4D ．－6题10．根据如下的样本数据：x 1 2 3 y2.133.9得到的回归方程为＝bx ＋a ，则直线ax ＋by －3＝0经过定点( ) A ．(－1，－2) B ．(－1，2) C ．(1，－2)D ．(1，2)题11．某同学在研究学习中，收集到某制药厂今年5个月甲胶囊生产产量(单位：万盒)的数据如表所示：x (月份) 1 2 3 4 5 y (万盒)55668若x ，y 线性相关，线性回归方程为＝0.7x ＋，则以下为真命题的是( ) A ．x 每增加1个单位长度，则y 一定增加0.7个单位长度 B ．x 每增加1个单位长度，则y 必减少0.7个单位长度C．当x＝6时，y的预测值为8.1万盒D．线性回归直线＝0.7x ＋经过点(2，6)题12．下列说法：①设有一个回归方程＝3－5x，变量x增加一个单位时，y平均增加5个单位；②线性回归方程＝x＋必过()x，y；③设某地女儿身高y对母亲身高x的一个回归直线方程是＝34.92＋0.78x，则方程中的＝34.92可以解释为女儿身高不受母亲身高变化影响的部分．其中正确的个数是( )A．0 B．1 C．2 D．3题13．(多选题．．．)两个相关变量x，y的5组对应数据如表：x8.3 8.6 9.9 11.1 12.1y 5.9 7.8 8.1 8.4 9.8根据表格，可得回归直线方程＝x＋，求得＝0.78.据此估计，以下结论正确的是( )A．x＝10 B．y＝9C．＝0.2 D．当x＝15时，＝11.95题14．(多选题．．．)已知x与y之间的几组数据如表：x 1 2 3 4 5 6y0 2 1 3 3 4假设根据表格数据所得线性回归直线方程为＝x＋，若某同学根据上表中的前两组数据()1，0和()2，2求得的直线方程为y＝b′x＋a′，则以下结论正确的是( )参考公式：＝∑i＝1nx i y i－n x y∑i＝1nx2i－n（x）2，＝y－b x .A．a′＝－2 B．b′＝2 C．>b′ D．>a′【综合突破拔高】题15．对于指数曲线y＝ae bx，令U＝ln y，c＝ln a，经过非线性回归分析后，可转化的形式为( ) A．U＝c＋bx B．U＝b＋cxC．y＝c＋bx D．y＝b＋cx题16．若一函数模型为y ＝sin 2α＋2sinα＋1，为将y 转化为t 的经验回归方程，则需作变换t 等于( ) A ．sin 2αB ．(sinα＋1)2C ．⎝ ⎛⎭⎪⎫sin α＋12 2D ．以上都不对题17．在生物学上，有隔代遗传的现象．已知某数学老师的体重为62 kg ，他的曾祖父、祖父、父亲、儿子的体重分别为58 kg 、64 kg 、58 kg 、60 kg .如果体重是隔代遗传，且呈线性相关，根据以上数据可得解释变量x 与预报变量的回归方程为＝x ＋，其中＝0.5，据此模型预测他的孙子的体重约为( ) A ．58 kgB ．61 kgC ．65 kgD ．68 kg题18．(多选题．．．)月亮公转与自转的周期大约为30天，阴历是以月相变化为依据．人们根据长时间的观测，统计了月亮出来的时间y (简称“月出时间”，单位：小时)与天数x (x 为阴历日数，x ∈N *，且0≤x ≤30)的有关数据，如表，并且根据表中数据，求得y 关于x 的线性回归方程为＝0.8x ＋．x 2 4 7 10 15 22 y8.19.41214.418.524其中，阴历22日是分界线，从阴历22日开始月亮就要到第二天(即23日0：00)才升起．则( ) A ．样本点的中心为()10，14.4 B ．＝6.8C ．预报月出时间为16时的那天是阴历13日D ．预报阴历27日的月出时间为阴历28日早上4：00题19．对某台机器购置后的运行年限x (x ＝1，2，3，…)与当年利润Y 的统计分析知x ，Y 具备线性相关关系，经验回归方程为＝10.47－1.3x ，估计该台机器最为划算的使用年限为______年．题20．以模型y ＝ce kx 去拟合一组数据时，为了求出非经验回归方程，设z ＝ln y ，其变换后得到经验回归方程＝0.3x ＋4，则c ＝________.题21．为了响应中央号召，某日深圳环保局随机抽查了本市市区汽车尾气排放污染物x (单位：ppm )与当天私家车路上行驶的时间y (单位：小时)之间的关系，从某主干路随机抽取10辆私家车，已知x 与y 之间具有线性相关关系，其回归直线方程为＝0.3x －0.4，若该10辆车中有一辆私家车的尾气排放污染物为6(单位：ppm )，据此估计该私家车行驶的时间为________小时．题22．某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月4日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下数据：日期 12月1日12月2日12月3日12月4日温差 11 13 12 8 发芽数(颗)26322617根据表中12月1日至12月3日的数据，求得线性回归方程＝x ＋中的＝－8，则求得的＝________；若用12月4日的数据进行检验，检验方法如下：先用求得的线性回归方程计算发芽数，再求与实际发芽数的差，若差值的绝对值不超过2颗，则认为得到的线性回归方程是可靠的，则求得的线性回归方程________(填“可靠”或“不可靠”).题23．如表为收集到的一组数据：x 21 23 25 27 29 32 35 Y711212466115325试建立Y 与x 之间的回归方程．题24．宿州市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定：所有主干道路凡机动车途经十字路口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人，违反者将被处以100元罚款，记3分的行政处罚．如表是本市一主干路段监控设备所抓拍的5个月内，机动车驾驶员“不礼让行人”行为统计数据：月份x 1 2 3 4 5 违章驾驶员人数y1151101009085(1)若x 与y 之间具有很强的线性相关关系，请利用所给数据求违章驾驶员人数y 与月份x 之间的回归直线方程＝x ＋；(2)预测该路段8月份的“不礼让行人”违章驾驶员的人数．参考公式：＝∑i ＝1nx i y i －n x ·y∑i ＝1nx 2i －n （x）2，＝y －x ，参考数据：∑i ＝15x i y i ＝1 420.编号032 §9.1.2 线性回归方程目标要求1、结合具体实例，了解一元线性回归模型的含义．2、结合具体实例，了解模型参数的统计意义．3、结合具体实例，了解最小二乘原理，掌握一元线性回归模型参数的最小二乘估计方法．4、结合具体实例，会使用相关的统计软件．5、针对实际问题，会用一元线性回归模型进行预测．学科素养目标本章内容是在学生已经学习过必修课程中的统计知识和概率知识的基础上，通过对典型案例的研究，了解和使用一些常用统计分析方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用，从而形成运用统计的观点认识客观事物的习惯．在本章教学中，应突出对学生应用意识的培养，不能只限于要求学生会解书本上的习题，还要关注学生应用与解决实际问题的能力．应引导、鼓励学生从现实生活中发现问题，并能自觉地运用所学的统计方法加以理解，应尽量给学生提供一定的实践活动机会，可结合数学建模活动，选择一个案例，要求学生亲自实践．重点难点重点：一元线性回归模型参数的最小二乘估计方法； 难点：用一元线性回归模型进行预测．教学过程基础知识点 1．线性回归模型我们将y ＝a ＋bx ＋ε称为线性回归模型． 2．线性回归方程与最小二乘法(1)线性回归方程：直线＝＋x 称为线性回归方程．其中称为回归截距，称为回归系数，称为回归值．(2)，的计算公式＝∑i ＝1n（x i －x ）（y i －y ）∑i ＝1n（x i －x ）2＝___∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n （x）2___ ，＝__y －x __.【课前小题演练】题1．关于回归分析，下列说法错误的是( ) A ．回归分析是研究两个具有相关关系的变量的方法 B ．散点图中，解释变量在x 轴，响应变量在y 轴 C ．回归模型中一定存在随机误差 D ．散点图能明确反映变量间的关系【解析】选D .用散点图反映两个变量间的关系时，存在误差． 题2．根据如下样本数据：x 2 3 4 5 6Y 4 2.5 －0.5 －2 －3得到的经验回归方程为＝x＋，则( )A．＞0，＞0 B．＞0，＜0C．＜0，＞0 D．＜0，＜0【解析】选B.由题干表中的数据可得，变量Y随着x的增大而减小，则＜0，又回归方程为＝x＋经过(2，4)，(3，2.5)，可得＞0.题3．已知变量x，Y之间具有线性相关关系，其散点图如图所示，则其经验回归方程可能为( )A．＝1.5x＋2 B．＝－1.5x＋2C．＝1.5x－2 D．＝－1.5x－2【解析】选B.设经验回归方程为＝x＋，由题干中散点图可知变量x，Y之间负相关，经验回归直线在Y轴上的截距为正数，所以<0，>0，因此方程可能为＝－1.5x＋2.题4．若某地财政收入x与支出Y满足经验回归方程＝x＋＋e i(单位：亿元)(i＝1，2，…)，其中＝0.8，＝2，|e i|<0.5，如果今年该地区财政收入10亿元，年支出预计不会超过( )A．10亿元B．9亿元C．10.5亿元D．9.5亿元【解析】选C.＝0.8×10＋2＋e i＝10＋e i，因为|e i|<0.5，所以9.5＜<10.5.题5．若施肥量x(kg)与水稻产量Y(kg)的经验回归方程为＝5x＋250，当施肥量为80 kg时，预计水稻产量约为________kg.【解析】把x＝80代入经验回归方程可得其预测值＝5×80＋250＝650(kg).答案：650题6．某种产品的广告费用支出x与销售额Y(单位：百万元)之间有如下的对应数据：x/百万元 2 4 5 6 8Y/百万元30 40 60 50 70(1)画出散点图；(2)求经验回归方程；(3)试预测广告费用支出为10百万元时，销售额多大？【解析】(1)散点图如图所示：(2)列出下表，并用科学计算器进行有关计算：i 1 2 3 4 5 合计 x i 2 4 5 6 8 25 y i 30 40 60 50 70 250 x i y i 60 160 300 300 560 1 380 x 2i416253664145所以x ＝255 ＝5，y ＝2505＝50，∑i ＝15x 2i ＝145，∑i ＝15x i y i ＝1 380.于是可得＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x 2＝1 380－5×5×50145－52×5＝6.5，＝y －x ＝50－6.5×5＝17.5. 所以所求的经验回归方程为＝6.5x ＋17.5.(3)根据上面求得的经验回归方程，当广告费用支出为 10百万元时，＝6.5×10＋17.5＝82.5(百万元)，即广告费用支出为10百万元时，销售额大约为82.5百万元． 【当堂巩固训练】题7．已知x ，y 的取值如表所示：x 2 3 4 5 y2.23.85.5m若y 与x 线性相关，且回归直线方程为＝1.46x －0.61，则表格中实数m 的值为( ) A ．7.69 B ．7.5 C ．6.69 D ．6.5 【解析】选D .因为x ＝2＋3＋4＋54 ＝72， y ＝2.2＋3.8＋5.5＋m 4 ＝11.5＋m 4，所以11.5＋m 4 ＝1.46×72－0.61，解得m ＝6.5.题8．某药厂为了了解某新药的销售情况，将2019年2至6月份的销售额整理如下：月份 2 3 4 5 6 销售额(万元)1925353742根据2至6月份的数据可求得每月的销售额y 关于月份x 的线性回归方程＝x ＋为( )(参考公式及数据：＝∑i ＝1nx i y i －n x y∑i ＝1n x 2i －n （x ）2，＝y －x ，∑i ＝15x i y i ＝690，∑i ＝15x 2i ＝90)A ．＝5.8x ＋8.4B ．＝8.4x ＋5.8C ．＝6x －9D ．＝4x ＋31.6【解析】选A .由表格中的数据得x ＝2＋3＋4＋5＋65＝4，y ＝19＋25＋35＋37＋425＝31.6，所以＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5（x）2＝690－5×4×31.690－5×42＝5.8， ＝31.6－5.8×4＝8.4，因此，y 关于x 的线性回归方程为＝5.8x ＋8.4.题9．登山族为了了解某山高y (km )与气温x (℃)之间的关系，随机统计了4次山高与相应的气温，并制作了对照表：气温x (℃) 18 13 10 －1 山高y (km )24343864由表中数据，得到线性回归方程＝－2x ＋()∈R ，由此请估计出山高为72(km )处气温的度数为( )A ．－10B ．－8C ．－4D ．－6【解析】选D .由题意可得x ＝10，y ＝40，所以＝y ＋2x ＝40＋2×10＝60.所以＝－2x ＋60，当＝72时，有－2x ＋60＝72，解得x ＝－6. 题10．根据如下的样本数据：x 1 2 3 y2.133.9得到的回归方程为＝bx ＋a ，则直线ax ＋by －3＝0经过定点( ) A ．(－1，－2)B ．(－1，2)C ．(1，－2)D ．(1，2)【解析】选D .由所给数据得x ＝2，y ＝3，3i 1=∑(x i －x )(y i －y )＝1.8，3i 1=∑(x i －x )2＝2，所以b ＝0.9，a ＝3－0.9×2＝1.2，所以直线ax ＋by －3＝0方程为1.2x ＋0.9y －3＝0，过点(1，2). 题11．某同学在研究学习中，收集到某制药厂今年5个月甲胶囊生产产量(单位：万盒)的数据如表所示：x (月份) 1 2 3 4 5 y (万盒)55668若x ，y 线性相关，线性回归方程为＝0.7x ＋，则以下为真命题的是( ) A ．x 每增加1个单位长度，则y 一定增加0.7个单位长度 B ．x 每增加1个单位长度，则y 必减少0.7个单位长度 C ．当x ＝6时，y 的预测值为8.1万盒 D ．线性回归直线＝0.7x ＋经过点(2，6)【解析】选C .由＝0.7x ＋，得x 每增(减)一个单位长度，y 不一定增加(减少)0.7，而是大约增加(减少)0.7个单位长度，故选项A ，B 错误；由已知表中的数据，可知x ＝1＋2＋3＋4＝55 ＝3，y ＝5＋5＋6＋6＋85＝6，则回归直线必过点(3，6)，故D 错误；将(3，6)代入回归直线＝0.7x ＋，解得＝3.9，即＝0.7x ＋3.9，令x ＝6，解得＝0.7×6＋3.9＝8.1万盒． 题12．下列说法：①设有一个回归方程＝3－5x ，变量x 增加一个单位时，y 平均增加5个单位； ②线性回归方程＝x ＋必过()x ，y ；③设某地女儿身高y 对母亲身高x 的一个回归直线方程是＝34.92＋0.78x ，则方程中的＝34.92可以解释为女儿身高不受母亲身高变化影响的部分． 其中正确的个数是( ) A ．0 B ．1 C ．2 D ．3【解析】选C .设有一个回归方程＝3－5x ，变量x 增加一个单位时，y 平均减少5个单位，故①错；线性回归方程＝x ＋必过样本中心点()x ，y ，故②正确；设某地女儿身高y 对母亲身高x 的一个回归直线方程是＝34.92＋0.78x ，当x ＝0时，＝34.92， 方程中的＝34.92可以解释为女儿身高不受母亲身高变化影响的部分，故③正确． 题13．(多选题．．．)两个相关变量x ，y 的5组对应数据如表：x 8.3 8.6 9.9 11.1 12.1 y5.97.88.18.49.8根据表格，可得回归直线方程＝x ＋，求得＝0.78.据此估计，以下结论正确的是( )A ．x ＝10B ．y ＝9C ．＝0.2D ．当x ＝15时，＝11.95【解析】选AC .易求得x ＝10，y ＝8⇒＝y －x ＝8－0.78×10＝0.2，所以＝0.78x ＋0.2. x ＝15⇒＝0.78×15＋0.2＝11.90.题14．(多选题．．．)已知x 与y 之间的几组数据如表：x 1 2 3 4 5 6 y21334假设根据表格数据所得线性回归直线方程为＝x ＋，若某同学根据上表中的前两组数据()1，0 和()2，2 求得的直线方程为y ＝b ′x ＋a ′，则以下结论正确的是()参考公式：＝∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n （x）2，＝y －b x . A ．a ′＝－2 B ．b ′＝2 C ．>b ′ D ．>a ′【解析】选ABD .因为某同学根据前两组数据()1，0 和()2，2 求得的直线方程为y ＝b ′x ＋a ′，所以b ′＝2，a ′＝－2，根据题意得：x ＝3.5，y ＝136，∑i ＝16x i y i ＝0＋4＋3＋12＋15＋24＝58，∑i ＝16x 2i ＝1＋4＋9＋16＋25＋36＝91，所以＝∑i ＝16x i y i －6x y∑i ＝16x 2i －6（x）2＝57 ，＝y －x ＝136 －57 ×72 ＝－13 ，所以<b ′，>a ′. 【综合突破拔高】题15．对于指数曲线y ＝ae bx ，令U ＝ln y ，c ＝ln a ，经过非线性回归分析后，可转化的形式为( ) A ．U ＝c ＋bx B ．U ＝b ＋cx C ．y ＝c ＋bxD ．y ＝b ＋cx【解析】选A .由y ＝ae bx 得ln y ＝ln (ae bx )， 所以ln y ＝ln a ＋ln e bx ，所以ln y ＝ln a ＋bx ，所以U ＝c ＋bx .题16．若一函数模型为y ＝sin 2α＋2sinα＋1，为将y 转化为t 的经验回归方程，则需作变换t 等于( ) A ．sin 2αB ．(sinα＋1)2C ．⎝⎛⎭⎪⎫sin α＋12 2D ．以上都不对 【解析】选B .因为y 是关于t 的经验回归方程，实际上就是y 是关于t 的一次函数，又因为y ＝(sin α＋1)2，若令t ＝(sin α＋1)2，则可得y 与t 的函数关系式为y ＝t ，此时变量y 与变量t 是线性相关关系． 题17．在生物学上，有隔代遗传的现象．已知某数学老师的体重为62 kg ，他的曾祖父、祖父、父亲、儿子的体重分别为58 kg 、64 kg 、58 kg 、60 kg .如果体重是隔代遗传，且呈线性相关，根据以上数据可得解释变量x 与预报变量的回归方程为＝x ＋，其中＝0.5，据此模型预测他的孙子的体重约为( ) A ．58 kgB ．61 kgC ．65 kgD ．68 kg【解析】选B .由于体重是隔代遗传，且呈线性相关， 则取数据(58，58)，(64，62)，(58，60)，得x ＝58＋64＋583 ＝60，y ＝58＋62＋603 ＝60，即样本点的中心为(60，60)，代入＝x ＋， 得＝60－0.5×60＝30，则＝0.5x ＋30， 取x ＝62，可得＝0.5×62＋30＝61 kg . 故预测他的孙子的体重约为61 kg .题18．(多选题．．．)月亮公转与自转的周期大约为30天，阴历是以月相变化为依据．人们根据长时间的观测，统计了月亮出来的时间y (简称“月出时间”，单位：小时)与天数x (x 为阴历日数，x ∈N *，且0≤x ≤30)的有关数据，如表，并且根据表中数据，求得y 关于x 的线性回归方程为＝0.8x ＋．x 2 4 710 15 22 y8.19.41214.418.524其中，阴历22日是分界线，从阴历22日开始月亮就要到第二天(即23日0：00)才升起．则( ) A ．样本点的中心为()10，14.4 B ．＝6.8C ．预报月出时间为16时的那天是阴历13日D ．预报阴历27日的月出时间为阴历28日早上4：00 【解析】选AD .x ＝2＋4＋7＋10＋15＋226＝10，y ＝8.1＋9.4＋12＋14.4＋18.5＋246＝14.4，故样本点的中心为()10，14.4 ，选项A 正确；将样本点的中心()10，14.4 代入＝0.8x ＋得＝6.4，故选项B 错误；因为＝0.8x ＋6.4，当y ＝16时，求得x ＝12，月出时间为阴历12日，选项C 错误；因为阴历27日时，即x ＝27，代入＝0.8×27＋6.4＝28，日出时间应该为28日早上4：00，选项D 正确． 题19．对某台机器购置后的运行年限x (x ＝1，2，3，…)与当年利润Y 的统计分析知x ，Y 具备线性相关关系，经验回归方程为＝10.47－1.3x ，估计该台机器最为划算的使用年限为______年． 【解析】当年利润小于或等于零时应该报废该机器， 当y ＝0时，令10.47－1.3x ＝0，解得x ≈8， 故估计该台机器最为划算的使用年限为8年． 答案：8题20．以模型y ＝ce kx 去拟合一组数据时，为了求出非经验回归方程，设z ＝ln y ，其变换后得到经验回归方程＝0.3x ＋4，则c ＝________. 【解析】由题意，得ln (ce kx )＝0.3x ＋4，所以ln c ＋kx ＝0.3x ＋4，所以ln c ＝4，所以c ＝e 4. 答案：e 4题21．为了响应中央号召，某日深圳环保局随机抽查了本市市区汽车尾气排放污染物x (单位：ppm )与当天私家车路上行驶的时间y (单位：小时)之间的关系，从某主干路随机抽取10辆私家车，已知x 与y 之间具有线性相关关系，其回归直线方程为＝0.3x －0.4，若该10辆车中有一辆私家车的尾气排放污染物为6(单位：ppm )，据此估计该私家车行驶的时间为________小时．【解析】由＝0.3x －0.4，令x ＝6，代入可得＝0.3×6－0.4＝1.4.所以估计该私家车行驶的时间为1.4小时． 答案：1.4题22．某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月4日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下数据：日期 12月1日 12月2日12月3日12月4日温差 11 13 12 8 发芽数(颗)26322617根据表中12月1日至12月3日的数据，求得线性回归方程＝x ＋中的＝－8，则求得的＝________；若用12月4日的数据进行检验，检验方法如下：先用求得的线性回归方程计算发芽数，再求与实际发芽数的差，若差值的绝对值不超过2颗，则认为得到的线性回归方程是可靠的，则求得的线性回归方程________(填“可靠”或“不可靠”).【解析】由题得x ＝11＋13＋123 ＝12，y ＝26＋32＋263 ＝28，所以样本中心点为(12，28)，所以28＝×12－8，所以＝3；因为＝3x －8，所以12月4日的估计值为＝3×8－8＝16，又|17－16|＝1，没有超过2，所以求得的线性回归方程可靠． 答案：3 可靠题23．如表为收集到的一组数据：x 21 23 25 27 29 32 35 Y711212466115325试建立Y 与x【解析】作出散点图，如图．从散点图中可以看出x 与Y 不具有线性相关关系，根据已有知识可以发现样本点分布在某一条指数函数曲线的周围．令Z ＝ln Y ，则变换后的样本点分布在直线＝x ＋的周围，这样就可以利用线性经验回归模型来建立非线性经验回归方程了，数据可以转化为：x 21 232527 29 32 35 Z1.9462.3983.0453.1784.1904.7455.784求得经验回归方程为＝0.272x －3.849， 所以＝e0.272x －3.849.题24．宿州市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定：所有主干道路凡机动车途经十字路口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人，违反者将被处以100元罚款，记3分的行政处罚．如表是本市一主干路段监控设备所抓拍的5个月内，机动车驾驶员“不礼让行人”行为统计数据：月份x 1 2 3 45 违章驾驶员人数y1151101009085(1)若x 与y 之间具有很强的线性相关关系，请利用所给数据求违章驾驶员人数y 与月份x 之间的回归直线方程＝x ＋；(2)预测该路段8月份的“不礼让行人”违章驾驶员的人数．参考公式：＝∑i ＝1nx i y i －n x ·y∑i ＝1nx 2i －n （x）2，＝y －x ，参考数据：∑i ＝15x i y i ＝1 420.【解析】(1)由表中数据得：x ＝15()1＋2＋3＋4＋5 ＝3，y ＝15()115＋110＋100＋90＋85 ＝100，＝∑i ＝15x i y i－5x·y∑i＝15x2i－5（x）2＝1 420－5×3×10055－45＝－8，＝y－x＝100＋8×3＝124.所以y与x之间的回归直线方程为＝－8x＋124；(2)由(1)得，＝－8x＋124，令x＝8，得＝－8×8＋124＝60，预测该路段8月份的“不礼让行人”违章驾驶员人数为60人．。

线性回归方程——非线性方程转化为线性方程例1．(2015·高考全国卷Ⅰ)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近8年的宣传费x i 和年销售量y i (i =1,2,⋯,8)数据作了初步处理，得到下面的散点图及一些统计量的值.x̅ y ̅ w ̅46.6 563 6.8289.81.61469108.8表中w i =√x i ，w ̅ =18 ∑w i 8i=1，，I ）根据散点图判断，y =a +bx 与y =c +d √x ，哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型（给出判断即可，不必说明理由）；，II ）根据（I ）的判断结果及表中数据，建立y 关于x 的回归方程；（III ）已知这种产品的年利润z 与x ，y 的关系为z =0.2y −x ，根据（II ）的结果回答下列问题： （i ）年宣传费x =49时，年销售量及年利润的预报值是多少？ （ii ）年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据(u 1,v 1) (u 2,v 2) ，…，(u n ,v n ) 其回归直线v =α+βu 的斜率和截距的最小二乘估计分别为：β̂=∑(u i −u)(v i −v)ni=1∑(u i −u)2ni=1，α̂=v −β̂u . 【答案】(Ⅰ)y =c +d √x 适宜作为年销售量y 关于年宣传费x 的回归方程类型；(Ⅱ)y ̂=100.6+68√x ；(Ⅲ)(i)答案见解析；(ii)46.24千元.【解析】（I ）由散点图可以判断，y =c +d √x 适宜作为年销售量y 关于年宣传费x 的回归方程类型. （II ）令w =√x ，先建立y 关于w 的线性回归方程，由于d̂=∑(w i −w)(y i −y)8i=1∑(w i −w)28i=1=108.81.6=68，∴ĉ=y −d ̂w =563−68×6.8=100.6， ∴y 关于w 的线性回归方程为y ̂=100.6+68w ， 因此y 关于x 的回归方程为y ̂=100.6+68√x .（III ）(ⅰ)由（II ）知，当x =49时，年销售量y 的预报值y ̂=100.6+68√49=576.6， 年利润z 的预报值为ẑ=576.6×0.2−49=66.32.，ⅱ）根据（II ）的结果知，年利润z 的预报值ẑ=0.2(100.6+68√x)−x =−x +13.6√x +20.12， 所以当√x =13.62=6.8，即x =46.24时，ẑ取得最大值. 故年宣传费为46.24千元时，年利润的预报值最大.例2．某地级市共有200000中小学生，其中有7%学生在2017年享受了“国家精准扶贫”政策，在享受“国家精准扶贫”政策的学生中困难程度分为三个等次：一般困难、很困难、特别困难，且人数之比为5:3:2，为进一步帮助这些学生，当地市政府设立“专项教育基金”，对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。

（整理）计量经济学第四章⾮线性回归模型的线性化第四章⾮线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是⾮线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述⾮线性回归模型是⽆法⽤最⼩⼆乘法估计参数的。

可采⽤⾮线性⽅法进⾏估计。

估计过程⾮常复杂和困难，在20世纪40年代之前⼏乎不可能实现。

计算机的出现⼤⼤⽅便了⾮线性回归模型的估计。

专⽤软件使这种计算变得⾮常容易。

但本章不是介绍这类模型的估计。

另外还有⼀类⾮线性回归模型。

其形式是⾮线性的，但可以通过适当的变换，转化为线性模型，然后利⽤线性回归模型的估计与检验⽅法进⾏处理。

称此类模型为可线性化的⾮线性模型。

下⾯介绍⼏种典型的可以线性化的⾮线性模型。

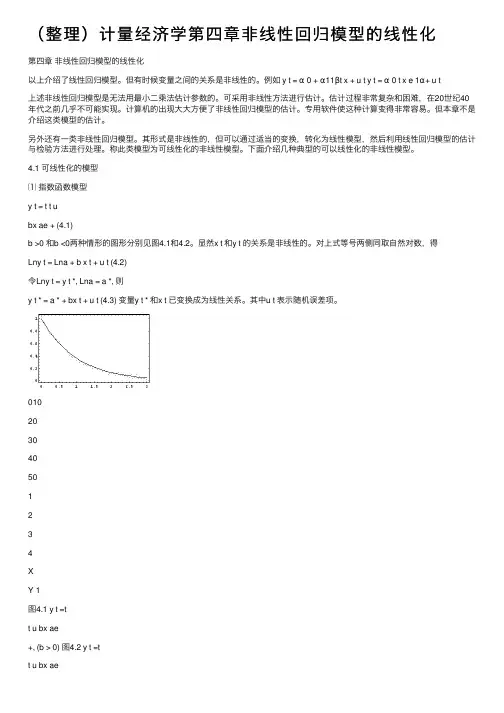
4.1 可线性化的模型⑴指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是⾮线性的。

对上式等号两侧同取⾃然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表⽰随机误差项。

010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =t+, (b < 0)⑵对数函数模型y t = a + b Ln x t+ u t(4.4)b>0和b<0两种情形的图形分别见图4.3和4.4。

x t和y t的关系是⾮线性的。

令x t* = Lnx t, 则y t = a + b x t* + u t(4.5)变量y t和x t* 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6) b取不同值的图形分别见图4.5和4.6。

掌握非线性回归函数 nlinfit polyfit lsqcurvefit
非线性回归( nonlinear regression )
前面假定因变量和自变量之间的相关关系可以 用线性方程来近似地反映，但是，在现实生活中， 非线性关系是大量存在的，在许多场合，非线性 与 第 的回归函数比线性回归函数更能够正确地反映客 非 五 观现象之间的相互联系。
非线性回归( nonlinear regression )
非线性回归通常需要猜测未知的初始值，然后 反复迭代，每次迭代都会修正当前的估计值，直至 算法收敛为止。但是，如果设定的参数初始值不当 则计算难以收敛，无法求得正确结果(或陷入局部 与第 非 五 最优)，在实际应用当中，对大多数用户来说，给 线 讲 出(猜出)恰当的初始值是件相当困难的事 。
线 性 回 归 讲 一 元 多 元 线 性 回 归
2
非线性回归模型是回归函数关于未知参数具有 非线性结构的回归模型，模型的拟合一般很困难。 处理非线性回归的通行方法是，通过变量变换， 将非线性回归转化为 y f ( x1 , x2 ,..., xn ) 线性回归，然后用线 ~ N (0, 2 ) 性回归方法处理。
首先: 编写被调M函数文件reacfun.m
function yhat=reacfun(b,x) x1=x(:,1); x2=x(:,2); x3=x(:,3); yhat=(b(1)*x2-x3/b(5))./(1+b(2)*x1+b(3)*x2+b(4)*x3);
然后: 导入数据并利用nlinfit进行非线性回归
与 非 线 性 回 归 第 五 讲 一 元 应用：试估计氢255、n-戊烷230和异戊烷70时的该 多 元 物质的反应速度？f(255,130,70) % ans = 2.4895 线 性 回 归

School of Microelectronics and Solid-State Electronics
3
第五章 回归分析方法
回归分析处理的是变量与变量间的关系。变量 间常见的关系有两类：确定性关系与相关关系。
变量间的相关关系不能用完全确切的函数形式表 示，但在平均意义下有一定的定量关系表达式，寻 找这种定量关系表达式就是回归分析的主要任务。
1
第五章 回归分析方法
5.1 一元线性回归
5.1.1 引言
确定关系
变量之间的关系
相关关系
S πr 2
确定性关系
身高和体重 相关关系
相关关系的特征是: 变量之间的关系很难用一
种精确的方法表示出来.
School of Microelectronics and Solid-State Electronics
回归分析便是研究变量间相关关系的一门学科 。它通过对客观事物中变量的大量观察或试验获 得的数据，去寻找隐藏在数据背后的相关关系，
给出它们的表达形式——回归函数的估计。
School of Microelectronics and Solid-State Electronics
4
第五章 回归分析方法
8
第五章 回归分析方法
如何制订含碳量的控制标准？
为达到以上质量控制要求，就需要制定该合 金钢冶炼中含碳量的工艺控制标准，也即要 确定在冶炼中应将含碳量控制在什么范围内 ，可以有99%的把握使抗拉强度和延伸率这两 项指标都达到要求。 这是一个典型的产品质量控制问题，可以使 用回归分析方法求解。
School of Microelectronics and Solid-State Electronics

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载线性回归方程——非线性方程转化为线性方程地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容线性回归方程——非线性方程转化为线性方程例1．(2015·高考全国卷Ⅰ)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z （单位：千元）的影响，对近8年的宣传费xi和年销售量yii=1,2,⋯,8数据作了初步处理，得到下面的散点图及一些统计量的值.表中wi=xi ，w =18 i=18wi．（I）根据散点图判断，y=a+bx与y=c+dx，哪一个适宜作为年销售量y关于年宣传费x的回归方程类型（给出判断即可，不必说明理由）；（II）根据（I）的判断结果及表中数据，建立y关于x的回归方程；（III）已知这种产品的年利润z与x，y的关系为z=0.2y-x ，根据（II）的结果回答下列问题：（i）年宣传费x=49时，年销售量及年利润的预报值是多少？（ii）年宣传费x为何值时，年利润的预报值最大？附：对于一组数据(u1,v1),(u2,v2)，…，(un,vn),其回归直线v=α+βu 的斜率和截距的最小二乘估计分别为：β=i=1n(ui-u)(vi-v)i=1n(ui-u)2，α=v-βu.【答案】(Ⅰ)y=c+dx适宜作为年销售量y关于年宣传费x的回归方程类型；(Ⅱ)y=100.6+68x；(Ⅲ)(i)答案见解析；(ii)46.24千元.【解析】（I）由散点图可以判断，y=c+dx适宜作为年销售量y关于年宣传费x的回归方程类型.（II）令w=x，先建立y关于w的线性回归方程，由于d=i=18(wi-w)(yi-y)i=18(wi-w)2=108.81.6=68，∴c=y-dw=563−68×6.8=100.6，∴y关于w的线性回归方程为y=100.6+68w，因此y关于x的回归方程为y=100.6+68x.（III）(ⅰ)由（II）知，当x=49时，年销售量y的预报值y=100.6+6849=576.6，年利润z的预报值为z=576.6×0.2-49=66.32.（ⅱ）根据（II）的结果知，年利润z的预报值z=0.2(100.6+68x)-x=-x+13.6x+20.12，所以当x=13.62=6.8，即x=46.24时，z取得最大值. 故年宣传费为46.24千元时，年利润的预报值最大.例2．某地级市共有200000中小学生，其中有7%学生在2017年享受了“国家精准扶贫”政策，在享受“国家精准扶贫”政策的学生中困难程度分为三个等次：一般困难、很困难、特别困难，且人数之比为5:3:2，为进一步帮助这些学生，当地市政府设立“专项教育基金”，对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。

第2章 辅导机械系统机械旋转系统如图所示。

为一圆柱体被轴承支撑并在黏性介质中转动。

当力矩作用于系统时，产生角位移。

求该系统的微分方程式。

解 根据牛顿第二定律，系统的诸力矩之和为22s )()()(T -T (t)dtt d J t T t d θ=- 式中：J ——转动系统的惯性矩；扭矩)()(T s t K t θ=， K ——扭簧的弹性系数； 黏性摩擦阻尼力矩dtt d B t T d )()(θ=，B因此该系统的运动方程式为)()()()(22t T tK dt t d B dt td J =++θθθ （2－2）电气系统电气系统的基本元件是电阻、电容、电感以及电动机等，支配电气系统的基本定律是基尔霍夫电路定律。

图为一具有电阻－电感－电容的无源网络，求以电压u 为输入，u c 为输出的系统微分方程式。

解 根据基尔霍夫电路定律，有 C u R i dtdiL t u +⋅+⋅=)( 而 dtdu Ci c=，则上式可写成如下形式 22u dt du RC dt u d LCC cc =++ （2－3）上式表示了RLC 电路的输入量和输出量之间的关系。

编写控制系统微分方程的一般步骤为：(l) 首先确定系统的输入量和输出量；(2) 将系统划分为若干个环节，确定每一环节的输入量和输出量。

确定输入量和输出量时，应使前一环节的输出量是后一环节的输入量。

(3) 写出每一环节(或元件)描述输出信号和输入信号相互关系的运动方程式；找出联系输出量与输入量的内部关系，并确定反映这种内在联系的物理规律。

而这些物理定律的数学表达式就是环节(或元件)的原始方程式。

在此同时再做一些数学上的处理，如非线性函数的线性化。

考虑忽略一些次要因素。

使方程简化的可能性和容许程度。

(4) 消去中间变量，列出各变量间的关系式。

设法消去中间变量，最后得到只包含输入量和输出量的方程式。

于是，就得到所要建立的元件或系统的数学模型了。

非线性数学模型的线性化1、一般运动方程式化为增量方程式的步骤 以下式为例)()()()(22t ky dt t dy B dtt y d M t F ++= (1) 确定额定点，写出静态方程式：设额定点为(F 。

• 多元线性回归方程的评价
评价回归方程的优劣、好坏可用确定系 数R2和剩余标准差Sy,x1,2..p 。 Sy,x1,2. p ＝SQRT（SS误差／n-p-1） 如用于预测，重要的是组外回代结果。
回归方程中自变量的选择
• 多元线性回归方程中并非自变量越多越 好，原因是自变量越多剩余标准差可能 变大；同时也增加收集资料的难度。故 需寻求“最佳”回归方程，逐步回归分 析是寻求“较佳”回归方程的一种方法。
• 逐步引入－剔除法（stepwise selection) 先规定两个阀值F引入和F剔除，当候选变 量中最大F值＞＝F引入时，引入相应变量； 已进入方程的变量最小F＜＝F剔除时，剔 除相应变量。如此交替进行直到无引入 和无剔除为止。（ 因素分析 • 调整混杂因素的作用 • 统计预测
2、偏回归系数的显著性检验：目的是检验回 归模型中自变量的系数是否为零，等价于总 体优势比OR是否为零。 H0：B等于零 H1：B不等于零 A、wald检验： B、Score test: C、likelihood ratio test(wald chi-square test):
回归模型中自变量的筛选
logistic回归模型参数的意义
优势比（odds ratio, OR)：暴露人群发病优势与非暴露 人群发病优势之比。
P(1) / [1-p(1)] OR= ——————— P(0) / [1-p(0)]
Ln(oR)=logit[p(1)]-logit[p(0)]=(B0+B×1) －(B0+B×0)=B 可见 B 是暴露剂量增加一个单位所引起的对数优势的增 量，或单位暴露剂量与零剂量死亡优势比的对数。eB就 是两剂量死亡优势比。常数项B0是所有变量 X等于零时 事件发生优势的对数。

线性回归方程——非线性方程转化为线性方程例1．(2015·高考全国卷Ⅰ)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近8年的宣传费x i 和年销售量y i (i =1,2,⋯,8)数据作了初步处理，得到下面的散点图及一些统计量的值.x̅ y ̅ w ̅46.6 563 6.8289.81.61469108.8表中w i =√x i ，w ̅ =18∑w i 8i=1．（I ）根据散点图判断，y =a +bx 与y =c +d √x ，哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型（给出判断即可，不必说明理由）；（II ）根据（I ）的判断结果及表中数据，建立y 关于x 的回归方程；（III ）已知这种产品的年利润z 与x ，y 的关系为z =0.2y −x ，根据（II ）的结果回答下列问题： （i ）年宣传费x =49时，年销售量及年利润的预报值是多少？ （ii ）年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据(u 1,v 1),(u 2,v 2)，…，(u n ,v n ),其回归直线v =α+βu 的斜率和截距的最小二乘估计分别为：β̂=∑(u i −u)(v i −v)ni=1∑(u i −u)2ni=1，α̂=v −β̂u . 【答案】(Ⅰ)y =c +d √x 适宜作为年销售量y 关于年宣传费x 的回归方程类型；(Ⅱ)y ̂=100.6+68√x ；(Ⅲ)(i)答案见解析；(ii)46.24千元.【解析】（I ）由散点图可以判断，y =c +d √x 适宜作为年销售量y 关于年宣传费x 的回归方程类型.（II ）令w =√x ，先建立y 关于w 的线性回归方程，由于d ̂=∑(w i −w)(y i −y)8i=1∑(w i −w)28i=1=108.81.6=68， ∴ĉ=y −d ̂w =563−68×6.8=100.6， ∴y 关于w 的线性回归方程为y ̂=100.6+68w ， 因此y 关于x 的回归方程为y ̂=100.6+68√x .（III ）(ⅰ)由（II ）知，当x =49时，年销售量y 的预报值y ̂=100.6+68√49=576.6， 年利润z 的预报值为ẑ=576.6×0.2−49=66.32.（ⅱ）根据（II ）的结果知，年利润z 的预报值ẑ=0.2(100.6+68√x)−x =−x +13.6√x +20.12， 所以当√x =13.62=6.8，即x =46.24时，ẑ取得最大值. 故年宣传费为46.24千元时，年利润的预报值最大.例2．某地级市共有200000中小学生，其中有7%学生在2017年享受了“国家精准扶贫”政策，在享受“国家精准扶贫”政策的学生中困难程度分为三个等次：一般困难、很困难、特别困难，且人数之比为5:3:2，为进一步帮助这些学生，当地市政府设立“专项教育基金”，对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。

第九章 非线性模型的线性化标准线性模型：因变量与自变量以及参数均呈线性关系。

非标准线性模型：因变量与自变量不呈线性关系，但与参数呈线性关系。

非线性模型：因变量与参数都不呈线性关系。

§5.1 非标准线性模型的线性化因变量与自变量不呈线性关系，但与参数呈线性关系。

一． 多项式函数模型：形如2012k k y x x x u ββββ=+++⋅⋅⋅⋅⋅++的模型可通过代换s z x s =， 1,2,,s k =⋅⋅⋅⋅ 线性化（标准化）后，得01122k k y z z z u ββββ=+++⋅⋅⋅⋅⋅++二． 双曲函数模型：形如011y u x ββ=++的模型可通过代换1z x=线性化，得 01y z u ββ=++三． 半对数函数模型和双对数函数模型：形如01ln y x u ββ=++或01ln y x u ββ=++的模型称为半对数模型； 形如01ln ln y x u ββ=++的模型称为双对数模型。

可分别采用变换 ln y y *=或ln x x *=进行标准化，01y x u ββ*=++；01y x u ββ*=++；01y x u ββ**=++§5.2 非线性模型的标准化一． 非线性模型的变换（间接代换）：对某些非线性模型施以适当的变换，可化为标准线性模型。

研究柯布-道格拉斯生产函数模型：1． 柯布-道格拉斯生产函数模型：u Q AL K e βα=其中Q 代表产出，L 表示劳动力投入，K 表示资本的投入。

L 和K 是生产要素；u 是随机干扰项，A ，α和β是参数。

对于道格拉斯生产函数，一般要求满足“规模报酬不变”。

所谓规模报酬是指：在一定技术水平条件下，由生产规模的变动（要素投入量的变动）引起的产出量变动。

“规模报酬不变”是所有要素投入量按同比例变动，产出量也按相同比例变动。

一般， 设生产函数(,)Q f L K =，0λ> (,)f L K λλ(,)f L K λ= 不变规模报酬（又称为一阶齐次性）(,)f L K λλ(,)f L K λ> 递增规模报酬(,)f L K λλ(,)f L K λ< 递减规模报酬对于柯布-道格拉斯生产函数模型，有()()u u Q A L K AL K e e βαββααλλλλ+==所以，当 1αβ+= 不变规模报酬 （1βα=-）1αβ+> 递增规模报酬1αβ+< 递减规模报酬2．标准化：模型 u Q AL K e βα=首先，两边取对数ln ln ln ln Q A L K u αβ=+++然后作如下变换ln y Q =，1ln L x =，2ln x K =，ln a A =（要求u 满足假定，且1x ，2x 无多重共线性）则，12y a x x u αβ=+++，并且可用OLS 估计其参数，这样原模型的样本回归方程为Q A L K αβ∧∧∧∧=，其中，α∧和β∧是参数α和β的无偏估计量；y Q e ∧∧=，a A e ∧∧=，不是无偏估计量。

非线性系统的线性化处理方法,√j}/Z非线性系大连晨光科技开发邮王士和Tp~?/,2.在各种电气设备,自动控制装置,检查与测线段联结,用于分f与”0,则得到分段线性量用仪器仪表中经常碰到线性或近似线性系统.但是,在很多情况下,也会碰到非线性系统问题关于线性系统的理论分析与计算方法在许多文献中已有讨论但是,非线性系统的理论分析与计算方法在近二十年来一直引起人们的关注还有许多线性系统问题尚待讨论.本文试图就非线性系统中一些分支问题,探讨若干处理方法这里讨论的是稳态情况下若干种非线性问题的处理方法:1.线性化法(或分段线性化法);2.函数化法(或分段函数化法),或称经验公式法;3.数字化法等等.‘一,线性化法(或分段线性化法)假设有一含非线性铁心的电路.其磁化曲线具有图1a所示形状.由图可以看出,这是非线性的但是,如果通过原点至急剧弯曲部分画一条斜线oa代替oa弯曲线时,在理论分析与计算上可以得到符合工程实际需要的分析结论与计算结果.这一类处理工程计算的方法.称谓线性化法.H图1如果将磁化曲线画分成若干段.如图1b所……示.将O1,12,23,34,蛎,56各弯曲段甩近似直线n《■气开曩》(199鼍蹄Io-●)化法显然.它比线性化法更逼真一步.在工程分析与计算上将给出更满意的结果.二,函数化法(或分段函数化法)函数化法是将非线性特性曲线近似地用一个经验公式表达,用来分析各种工程技术问题. 显然,它能够给出的计算精确度决定于经验公式与实际曲线逼近程度例如.图l给出的磁化曲线可以用下式表示,即B:,(H)(1)或H一()(2)详见参考文献1中表1—1所示由各作者给出的磁化曲线经验公式.分段函数法是将非线性曲线分割成若干段,然后对各小段分别用某一函数表示.用这些表达式分析与处理各种技术问题.显然,比前一种方法更逼真一步.但是,应用上会带来许多麻烦.计算机的出现,给解决这类工程问题带来了方便.可以看出,分段线性化方法可视作分段函数法的一个特倒.三,数字化方法数字化方法实际上是将一连续变化的非线性特性曲线实施离散化,将其储存在计算机内, 根据计算程序需要随时调用(详见文献2)以上讨论了非线性系统的直接处理方法.主要用于:非线性元件,非线性线路非线性控制,测量与检查等系统的分析与计算.下面讨论若干间接处理方法四,非线性系统的线性变换法图2中的A环节是一个非线性元件或网路,B环节是另一个非线性元件或网络.此方法的基本思想是A环节在系统中无法直接应用其非线性输入一输出特性用B环节具有另一种非线性输入输出特性来补偿.如果B环节设一25—._,●计合理.可使总的输入一输出特性线性化,如图3所示.因此B环节称作对-A环节的整直环节(或元件).设A环节具有非缉眭函数关系X2= f.(x),B环节具有另_非线性爵数关系Xa—f(x).经过综合后.得到总的输入一输出特性为X.一c.X+线性关系.这就是通过整直环节(或元件)B将非线性环节(或元件)A的菲线性系统实现线性化的线性变换法.如果得到图3的直线,再进行技术处理就很方便.例如.如欲得到X一O时.xf一0{在x正向增加时x也正向增加.只需要在B环节后再增设一级移位倒向环节C就可H实现如图4,5趼示,网?I警l3—26I4瞄5五,非线性系统的补偿网路法非线性元件(或装置)采用线性R,L,C或非线性半导体器件等组成元件或网路可以对其非线性逐段地进行朴偿,以l达到更精确的变换, 例如,目前工业上应用的热电偶上采用的各种温度一电压线性变换网路等.六,非线性系统的数字化处理方法此方法与第四章相似,只是将非线性元件(或装置)输出的模拟量用集成电路(模片)交换成数字量,即进行A/D转换.但此数字量尚须经过专用单片机(例如EPROM或EEPR0M)处理之后,才能整直,送给数字显示器或其他控制部件.这时显示器的指示量与非线性元件(或装置)的输入量呈线性关系,关于其它特殊类型的非线性元件(或装胃=)的非线性特性需要根据要求进行线性化,例如, 开关控制元件对发电机进行电压自动调整等需要特殊处理,而不一定要求对其作线性化处理, 关于这些问题,可参考文献3,4.综上所述.在遇到非线性系统问题时.可以参考上面提出的方法进行处理当然.还可根据不同的具体问题提出新的处理方法,对于这方面的具体理论和技术工作,不仅需要对控制系统及其控制的对象有深刻的了解.而且还要有丰富的元器件的理论与实际知识.参考文献[1]王士和缩自动电礁装置,大连铁道学院, 1985[2:张冠生主编电器学,规被】:业m版社】980_l3]扬自厚主编自动控制原理,精金1:业出暖社,198O[4]蔡尚峰主编.自动控制理沧,机被业m版社,198l[5]尤德裴主编数字化酬量技术眨但器.机械】= 业出版社1980[6]常健生缩.捡j羹I与转换技术.机被丁=业m版社,1981[7]王士和郭永波带热电阻捡渊播的解舟折法电杂志】99o3[8]王士和孝章武王常有智艟化湿度控制倥●气开善》(1995N0_4)。

非线性回归方程公式详解一、非线性回归的定义和方程1、非线性回归非线性回归是回归函数关于未知回归系数具有非线性结构的回归。

常用的处理方法有回归函数的线性迭代法、分段回归法、迭代等。

非线性回归分析的主要内容与线性回归分析相似。

2、回归分析对具有相关关系的两个变量进行统计分析的方法叫回归分析。

其基本步骤是：（1）画散点图；（2）求回归直线方程；（3）用回归直线方程作预报。

3、回归直线如果具有相关关系的两个变量的一组数据(x1,y1)(x1,y1)，(x2,y2)(x2,y2)，⋯⋯，(xn,yn)(xn,yn)大致分布在一条直线附近，那么我们称这样的变量之间的关系为线性相关关系，这条直线就是回归直线，记为yˆ=bˆx+aˆy^=b^x+a^。

4、回归直线方程的求法——最小二乘法设具有线性相关关系的两个变量xx，yy的一组观察值为(xi,yi)(xi,yi)(i=1,2,⋯,n)(i=1,2,⋯,n)，则回归直线方程yˆ=bˆx+aˆy^=b^x+a^的系数为bˆ=b^=∑ni=1(xi−x¯¯¯)(yi−y¯¯¯)∑ni=1(xi−x¯¯¯)2=∑ni=1(xi−x¯)(yi−y¯)∑ni=1(xi−x¯)2=∑ni=1xiyi−nx¯¯¯y¯¯¯∑ni=1x2i−nx¯¯¯2∑ni=1xiyi−nx¯ y¯∑ni=1xi2−nx¯2，aˆ=y¯¯¯−bˆx¯¯¯a^=y¯−b^x¯，其中(xi,yi)(xi,yi)为样本数据，x¯¯¯=x¯=1n∑ni=1xi1n∑ni=1xi，y¯¯¯=y¯=1n∑ni=1yi1n∑ni=1yi为样本平均数。

=1
^
^
6.435
所以 =
≈2.12, =3.55-2.12×2.55≈-1.86,
3.035
所以模型 y=m
^
+n 的回归方程为 =2.12
-1.86.
6
2
(2) ∑ ( -) =(-2.65)2+(-1.55)2+0.652+0.352+1.652+1.552≈15.1,
=1
所以 r1=
r2=
5.55
2.2× 15.1
6.435
3.035× 15.1
≈
=
5.55
33.22
6.435
45.83
≈
≈
5.55
≈0.964,
5.76
6.435
≈0.951,
6.77
因为r1更接近1,所以模型y=2.52ln x-0.99的拟合效果更好,则次年2月净利
润为y≈2.52ln 14-0.99≈5.6(万元).
业情况进行调查统计,得到的数据如下:
2ቤተ መጻሕፍቲ ባይዱ
4
6
月份x
净利润
0.9
2.0
4.2
y/万元
8
10
12
3.9
5.2
5.1
(1)设 μi=ln xi,vi= .试建立 y 关于 x 的非线性回归方程 y=aln x+b 和
y=m +n(保留 2 位小数);
(2)从相关系数的角度确定哪一个模型的拟合效果更好,并据此预测次年2
c=ln a,则μ=bv+c;
(2)指数曲线:y=aebx,两边取对数可得ln y=ln a+bx,令μ=ln y,c=ln a,则

D(X)= 2 X X X X X t t 1 t 2
2 X X X X1X 2 1 t 1 2 X X X X2Xt 2 1 2
协方差阵传播率
E X E (( X 12 )) 随机向量X的数学期望E(X)是由E(X)= E (X ) t 定义的，它具有如下性质：

则有
A ( k ) X ( k 1) L ( k ) R
(k )
ε 0
（6）
在式（6）中，将 换成估值形式 ，用 代表 的最或然误差 （又称为 的改正数），则有
V 1( k ) (k ) V 2 V (k ) n
(D(L1)+D(L2)+·· ·+D(Ln)).

n
2
如果D(L1)=D(L2)=·· ·=D(Ln)=σ2,则上式为 D(x)= 令
D (x)
,

n
=σx，则有 σx=
式中σ和σx分别为观测值和算术平均值的标准差，标准 差在测量中称为中误差。
二.协方差及其传播律
1.协方差的概念及定义
设有线性函数 z=f1x+f2y， 令x，y的真误差为⊿x，⊿y，则z的真误差⊿z 为 ⊿z=f1 ⊿x+f2 ⊿y. ⊿y
ξ
1
（3）n个随机变量之和的数学期望，等 于各随机变量数学期望之和，即 E(ξ1+ξ2+·· n)=E(ξ1)+E(ξ2)+·· ξ ). ·+ξ ·+E随机变量的线性函数 F=α1ξ1+α2ξ2+·· αnξn= ·+ 的数学期望为 E( )= α1E(ξ )+ α2E(ξ2)+·· α E(ξn). ·+

物理图像中从‘非线性’到‘线性’的转化•线性关系和非线性关系
物理量y随x的变化规律若是一次函数，则y-x图像就是直线，也就是说y随x线性变化，如匀变速直线运的速度公式中
v和t就是线性的，而匀变速直线运动的位移公式中
x和t之间是二次函数关系，x-t图像是抛物线，也就是说x随t的变化是非线性的。

•从非线性到线性的转化
为便于分析和研究，物理学中常把物理量之间的非线性关系转化为线性关系，如---探究加速和质量的关系---实验中，为便于直观的探究加速度a和质量m的定量关系，我们往往根据数据画a-(1/m)图象，而不是画a-m图象。

分析相关问题时，首先要根据物理规律写出两个量之间的原始函数关系，然后通过数学变换，把非线性的关系转化为相应的线性关系，找出直线的斜率、截距等代表的物理意义，最后结合图象数据即可求解相关问题。

•应用示例
例题1 利用函数图象是一种解决物理问题的常用方法。

某同学利用传感器探究一玩具车沿某一路段做直线运动的性质，从t＝0时刻开始计时得到了（x/t）一t的图象如图所示，由此可知（）
A．玩具车做速度为﹣3m/s的匀速直线运动
B．玩具车做变加速直线运动
C．玩具车做匀加速直线运动，初速度大小为2m/s
D．玩具车做匀加速直线运动，加速度大小为1.5m/s2
例题2 某实验小组设计了如图甲所示的电路测量某电池的电动势E 和内阻r，图中R为电阻箱（0﹣999.9Ω），电流表A可看做理想电表。

根据测量数据作出（1/I）—R象如图乙所示。

若该图线的斜率为k，纵轴截距为b，则该电池的电动势E＝____；内阻r＝____（用k和b表示）。

7
1.0066 err = 0.0066 k= 5 y= 1.3270e-004 p1 = 1.0033 err = 0.0033 k= 6 y= 3.3211e-005 p1 = 1.0017 err = 0.0017 k= 7 y= 8.3074e-006 p1 = 1.0008 err = 8.3157e-004 k= 8 y= 2.0774e-006 p1 = 1.0004 err = 4.1596e-004 k= 9 y= 5.1943e-007 p1 = 1.0002 err = 2.0802e-004 k= 10 y=
3
6
function y=f(x); y=x^3-3*x+2; 再用 M-文件写一个名为 df.m 的文件定义函数的微商 df ( x) 3x 2 3 。 function y=df(x) y=3*x^2-3; 然后再 MATLAB 的命令窗口输入： newton('f','df',1.2,10^(-6),10) 结果为： p0 = 1.2000 ans = 0.1280 p1 = 1.1030 err = 0.0970 k= 1 y= 0.0329 p1 = 1.0524 err = 0.0507 k= 2 y= 0.0084 p1 = 1.0264 err = 0.0260 k= 3 y= 0.0021 p1 = 1.0133 err = 0.0131 k= 4 y= 5.2963e-004 p1 =
解 先按照二分法的基本原理编写二分发的 MATLAB 程序（程序命名为： HalfInterval.m） ， 编程如下： function root=HalfInterval(f,a,b,eps) if(nargin==3) eps=1.0e-4 end f1=subs(sym(f),findsym(sym(f)),a); f2=subs(sym(f),findsym(sym(f)),b); if(f1==0) root=a; end if(f2==0) root=b; end if(f1*f2>0) disp('两端点函数值乘积大于 0！ '); return; else root=FindRoots(f,a,b,eps); end function r=FindRoots(f,a,b,eps) f_1=subs(sym(f),findsym(sym(f)),a); f_2=subs(sym(f),findsym(sym(f)),b); mf=subs(sym(f),findsym(sym(f)),(a+b)/2); if(f_1*mf>0) t=(a+b)/2; r=FindRoots(f,t,b,eps); else if(f_1*mf==0) r=(a+b)/2; else if(abs(b-a<=eps))

（3） 半对数模型
半对数模型指的是应变量和解释变量中一个为对 数形式而另一个为线性的模型。
被解释变量为对数形式的称为对数-线性模型 （log-lin model）。
解释变量为对数形式的称为线性-对数模型（linlog model）。
我们先介绍对数-线性模型，其形式如下：
ln Y t 01Xtut
例：美国咖啡需求：1970-1980
美国咖啡消费（Y）与平均真实零售价格（X） 数据，（X=名义价格/食品与饮料的消费者价 格指数，1967年=100），求咖啡消费函数。
散点图：确定函数形式：Y-X; lnY-lnX 建立模型：lnY=+lnX+i 参数估计：
lnde d ˆ m 0.a7-n 0 7.7 25c3elnpri
这一部分我们要关注的是（1）如何将非线性模型转变为 线性模型；（2）转变后，偏回归系数的含义。
一、模型的类型与变换
1、非线性回归模型与变量的直接置换法
当变量是非线性的，参数之间是线性时，可 以利用变量直接代换的方法将模型线性化。
因此，关于解释变量的非线性问题都可以通 过变量置换变成线性问题。
对于以下形式的非线性方程，我们可以直接 进行变量代换转换为线性方程：
则可将原模型化为标准的线性回归模型
Yi*Xi*ui
7
（2） 多项式回归模型
多项式回归模型通常用于描述生产成本函数，其一 般形式为：
Y i 0 1 X i 2 X i 2 .. .P . X i P . u .i
其中，Y表示总成本，X表示产出，P为多项式的阶 数，一般不超过四阶。
多项式回归模型中，解释变量X以不同幂次出现在 方程的右端。这类模型也仅存在变量非线性，因而很容 易线性化，可用OLS法估计模型。