信息论与编码复习
- 格式:doc
- 大小:1.93 MB
- 文档页数:15


“信息论与编码”总复习1.消息、信号、信息的含义、定义及区别。
信息是指各个事物运动的状态及状态变化的方式。
消息是指包含信息的语言,文字和图像等。
信号是消息的物理体现。
消息是信息的数学载体、信号是信息的物理载体信号:具体的、物理的消息:具体的、非物理的信息:非具体的、非物理的同一信息,可以采用不同形式的物理量来载荷,也可以采用不同的数学描述方式。
同样,同一类型信号或消息也可以代表不同内容的信息2.信息的特征与分类。
1接收者在收到信息之前,对其内容是未知的,所以信息是新知识,新内容;2信息是能使认识主体对某一事物的未知性或不确定性减少的有用知识;3信息可以产生,也可以消失,同时信息可以被携带,被存储及处理;4信息是可以量度的,信息量有多少的差别。
3.狭义信息论、广义信息论、一般信息论研究的领域。
狭义信息论:信息论是在信息可以量度的基础上,对如何有效,可靠地传递信息进行研究的科学。
它涉及信息量度,信息特性,信息传输速率,信道容量,干扰对信息传输的影响等方面的知识。
广义信息论:信息是物质的普遍属性,所谓物质系统的信息是指它所属的物理系统在同一切其他物质系统全面相互作用(或联系)过程中,以质、能和波动的形式所呈现的结构、状态和历史。
包含通信的全部统计问题的研究,除了香农信息论之外,还包括信号设计,噪声理论,信号的检测与估值等。
概率信息:信息表征信源的不定度,但它不等同于不定度,而是为了消除一定的不定度必须获得与此不定度相等的信息量4.信息论的起源、历史与发展。
⏹1924年,Nyquist提出信息传输理论;⏹1928年,Hartly提出信息量关系;⏹1932年,Morse发明电报编码;⏹1946年,柯切尼柯夫提出信号检测理论;⏹1948年,Shannon提出信息论,“通信中的数学理论”—现代信息论的开创性的权威论文,为信息论的创立作出了独特的贡献。
5.通信系统的物理模型(主要框图),各单元(方框)的主要功能及要解决的主要问题。

第1章 概论1. 信号(适合信道传输的物理量)、信息(抽象的意识/知识,是系统传输、转换、处理的对象)和消息(信息的载体)定义;相互关系:(1信号携带消息,是消息的运载工具(2信号携带信息但不是信息本身(3同一信息可用不同的信号来表示(4同一信号也可表示不同的信息。
2. 通信的系统模型及目的:提高信息系统可靠性、有效性和安全性,以达到系统最优化.第2章 信源及信息量1. 单符号离散信源数学模型2. 自信息量定义:一随机事件发生某一结果时带来的信息量I(xi)=- log2P(xi)、单位:bit 、物理意义:确定事件信息量为0;0概率事件发生信息量巨大、性质:I(xi)非负;P(xi)=1时I(xi)=0;P(xi)=0时I(xi)无穷;I(xi)单调递减;I(xi)是随机变量。
3. 联合自信息量:I(xiyi)=- log2P(xiyj) 物理意义:两独立事件同时发生的信息量=各自发生的信息量的和、条件自信息量:I(xi/yi)=- log2P(xi/yj);物理意义:特定条件下(yj 已定)随机事件xi 所带来的信息量。
三者关系:I(xi/yi)= I(xi)+ I(yi/xi)= I(yi)+ I(xi/yi)4. 熵:定义(信源中离散消息自信息量的数学期望)、单位(比特/符号)、物理意义(输出消息后每个离散消息提供的平均信息量;输出消息前信源的平均不确定度;变量的随机性)、计算:(H(X)=-∑P(xi)log2 P(xi)) 1)连续熵和离散的区别:离散熵是非负的2)离散信源当且仅当各消息P 相等时信息熵最大H (X )=log 2 n 。
3)连续信源的最大熵:定义域内的极值.5.条件熵H(Y/X) = -∑∑P(xiyj) log2P(yj/xi),H (X /Y )= -∑∑P(xiyj) log2P(xi/yj) 、物理意义:信道疑义度H(X/Y):信宿收到Y 后,信源X 仍存在的不确定度,有噪信道传输引起信息量的损失,也称损失熵。


1、通信系统模型的组成,及各部分的功能。
答:信源,产生消息的源,消息可以是文字,语言,图像。
可以离散,可以连续。
随机发生。
编码器,信源编码器:对信源输出进行变换(消去冗余,压缩),提高信息传输的有效性。
信道编码器:对信源编码输出变换(加入冗余),提高抗干扰能力,提高信息传输的可靠性。
调制器:将信道编码输出变成适合信道传输的方式信道,信号从发端传到收端的介质干扰源,系统各部分引入的干扰,包括衰落,多径,码间干扰,非线性失真,加性噪声译码器,编码器的逆变换信宿,信息的接收者2、消息,信号,信息三者之间的关系答:关系:信息---可以认为是具体的物理信号、数学描述的消息的内涵,即信号具体载荷的内容、消息描述的含义。
信号---则是抽象信息在物理层表达的外延;消息---则是抽象信息在数学层表达的外延。
3、信源的分类答:分类:单消息(符号)信源:离散信源;连续变量信源。
平稳信源。
无/有记忆信源。
马尔可夫信源。
随机波形信源。
离散信源:信源可能输出的消息数是有限的或可数的,而且每次只输出其中一个消息。
可以用一维离散型随机变量X来描述这个信源输出的消息。
这个随机变量X的样本空间就是符号集A;而X的概率分布就是各消息出现的先验概率,信源的概率空间必定是一个完备集。
连续变量信源:数据取值是连续的,但又是随机的。
可用一维的连续型随机变量X来描述这些消息。
这种信源称为连续信源,其数学模型是连续型的概率空间:4、自信息的含义:当事件ai发生以前,表示事件ai发生的不确定性,当事件ai发生以后表示事件ai所含有(所提供)的信息量。
5、互信息含义:信源发送消息ai,而由于干扰,在接收端收到的为消息bj ,此时获得的信息量——互信息,即最初的不确定性减去尚存在的不确定性。
6、离散单符号信源熵的物理含义:熵是随机变量的随机性的描述。
熵是信源输出消息前随机变量平均不确定性的描述。
信源熵H(X)是表示信源输出后每个消息/符号所提供的平均信息量。

一、填空题1. 设信源X 包含4个不同离散消息,当且仅当X 中各个消息出现的概率为___1/4___时,信源熵达到最大值,为__2__,此时各个消息的自信息量为__2 __。
2.如某线性分组码的最小汉明距dmin=4,则该码最多能检测出___3____个随机错,最多能纠正__1____个随机错。
3.克劳夫特不等式是唯一可译码___存在___的充要条件。
4.平均互信息量I(X;Y)与信源熵和条件熵之间的关系是___(X;Y)=H(X)-H(X/Y )___。
5._信源___提高通信的有效性,_信道____目的是提高通信的可靠性,_加密__编码的目的是保证通信的安全性。
6.信源编码的目的是提高通信的 有效性 ,信道编码的目的是提高通信的 可靠性 ,加密编码的目的是保证通信的 安全性 。
7.设信源X 包含8个不同离散消息,当且仅当X 中各个消息出现的概率为__1/8__时,信源熵达到最大值,为___3____。
8.自信息量表征信源中各个符号的不确定度,信源符号的概率越大,其自信息量越_小___。
9.信源的冗余度来自两个方面,一是信源符号之间的__相关性__,二是信源符号分布的__不均匀性__。
10.最大后验概率译码指的是 译码器要在已知r 的条件下找出可能性最大的发码 作为译码估值 ,即令 =maxP( |r)_ __。
11.常用的检纠错方法有__前向纠错___、反馈重发和混合纠错三种。
二、单项选择题1.下面表达式中正确的是(A )。
A.∑=j i j x y p 1)/( B.∑=i i j x y p 1)/( C.∑=j j j iy y x p )(),(ω D.∑=ii j i x q y x p )(),( 2.彩色电视显像管的屏幕上有5×105 个像元,设每个像元有64种彩色度,每种彩度又有16种不同的亮度层次,如果所有的彩色品种和亮度层次的组合均以等概率出现,并且各个组合之间相互独立。

1第1章 概论1. 信号(适合信道传输的物理量)、信息(抽象的意识/知识,是系统传输、转换、处理的对象)和消息(信息的载体)定义;相互关系:(1信号携带消息,是消息的运载工具(2信号携带信息但不是信息本身(3同一信息可用不同的信号来表示(4同一信号也可表示不同的信息。
2. 通信的系统模型及目的:提高信息系统可靠性、有效性和安全性,以达到系统最优化.第2章 信源及信息量1. 单符号离散信源数学模型2. 自信息量定义:一随机事件发生某一结果时带来的信息量I(xi)=-log2P(xi)、单位:bit 、物理意义:确定事件信息量为0;0概率事件发生信息量巨大、性质:I(xi)非负;P(xi)=1时I(xi)=0;P(xi)=0时I(xi)无穷;I(xi)单调递减;I(xi)是随机变量。
3. 联合自信息量:I(xiyi)=- log2P(xiyj) 物理意义:两独立事件同时发生的信息量=各自发生的信息量的和、条件自信息量:I(xi/yi)=- log2P(xi/yj);物理意义:特定条件下(yj 已定)随机事件xi 所带来的信息量。
三者关系:I(xi/yi)= I(xi)+ I(yi/xi)= I(yi)+ I(xi/yi)4. 熵:定义(信源中离散消息自信息量的数学期望)、单位(比特/符号)、物理意义(输出消息后每个离散消息提供的平均信息量;输出消息前信源的平均不确定度;变量的随机性)、计算:(H(X)=-∑P(xi)log2 P(xi)) 1)连续熵和离散的区别:离散熵是非负的2)离散信源当且仅当各消息P相等时信息熵最大H (X )=log 2 n 。
3)连续信源的最大熵:定义域内的极值. 5.条件熵H(Y/X) = -∑∑P(xiyj) log2P(yj/xi),H (X /Y )= -∑∑P(xiyj) log2P(xi/yj) 、物理意义:信道疑义度H(X/Y):信宿收到Y 后,信源X 仍存在的不确定度,有噪信道传输引起信息量的损失,也称损失熵。

信息论与编码复习
去年考点(部分):
简答题:香农第一定理P106、香农第二定理P141
计算题:马尔可夫信源P37、香农编码P110、霍夫曼编码P111、费诺编码P115、平均错误概率P131(例6.3)、例5.10。
重点:
第二章:本章为基础性内容,主要是理解专业词语的含义,记住公式,可参考笔记。
第三章:
重点3.3节,特别是马尔可夫信源P37~P40,会画状态转移图,会求状态转移概率矩阵(例3.5 P38、例3.6 P40)。
第四章:
各种信道容量的计算P58(例4.1、4.2、4.3)、离散对称信道的判别和信道容量计算P61~P64。
第五章:
定长码、码的分类P91、定长码及定长编码定理P94、编码效率P97、Kraft和McMillan不等式、唯一可译码存在条件P100、编码效率及剩余度P108、变长码编码(例 5.5 P108、例5.6 P110、例5.7 P112、例5.8 P115、例5.9 P116)。
第六章:
最大后验概率译码准则、极大似然译码规则P131、平均错误概率P131(例6.3 P131)、编码效率P150、线性分组码P150(例6.6 、6.7、6.8 P154、例5.10 P161)。

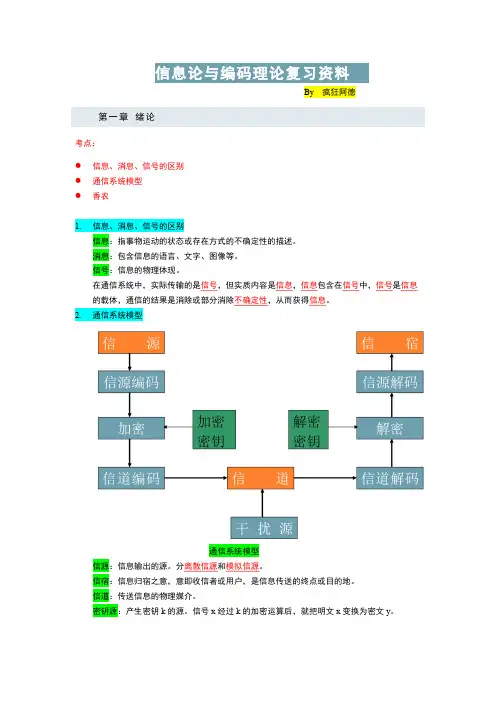

信息论与编码复习总结题型:填空、解答、计算1、编码:无失真与限失真信源编码定理编码分为信源编码和信道编码,其中信源编码又分为无失真和限失真三大定理:无失真信源编码定理(第一极限定理)(可逆)信道编码定理(第二极限定理)限失真信源编码定理(第三极限定理)(不可逆)Shannon(香农)信息论:在噪声环境下,可靠地、安全地、有效地传送信息理论。
通信系统模型方框图:信道的种类很多,如电信中常用的架空明线、同轴电缆、波导、光纤、传输电磁波的空间等都是信道。
也可以从信道的性质或其传送的信号情况来分类,例如:无干扰信道和有干扰信道、恒参信道和变参信道、离散信道(Discrete Channel)和连续信道(Continuous Channel)、单用户信道和多用户信道等。
信源的描述:通过概率空间描述平稳包含齐次,而齐次不包含平稳(重要,第二章计算题)定义:若齐次马尔可夫链对一切i,j存在不依赖于i的极限,则称其具有遍历性,p j称为平稳分布(如下)设有一齐次马尔可夫链,其状态转移矩阵为P,其稳态分布为w j=p(s j)自信息量的特性:p(x i)=1,I(x i)=0; p(x i)=0,I(x i)=∞;非负性;单调递减性;可加性;定义:联合概率空间中任一联合事件的联合(自)信息量为:定义:对于给定离散概率空间表示的信源,在出现y事件后所提供有关事件x的信息量定义互信息,单位为比特信道模型:二进制离散信道BSC;离散无记忆信道DMC;波形信道信源编码器的目的:是使编码后所需的信息传输率R尽量小。
信源编码:主要任务就是减少冗余,提高编码效率。
唯一可译码:(任意有限长的码元序列,只能被唯一地分割成一个个的码字,便称为唯一可译码){0,10,11}为唯一可译码,任意有限长码序列:100111000。
(分类)即时码和非即时码变长编码定理:(解答,重要)???1、平均码长:2、根据信源各个符号的统计特性,如概率大的符号用短码,概率小的用较长的码,使得编码后平均码长降低,从而提高编码效率。
“信息论与编码”总复习*****************************************************************************简要***************************************************************************** 第二章 信源与信息熵1.每次只发出一个符号代表一个消息的信源叫做发出单个符号的无记忆信源。
2.由一系列符号组成,这种用每次发出1组含2个以上符号序列来代表一个信息的信源叫做发出符号序列的信源。
3.信源发出的序列的统计性质与时间的推移无关,是平稳的随机序列。
4.当信源的记忆长度为m+1时,该时刻发出的符号与前m 个符号有关联性,而与更前面的符号无关,这种有记忆信源叫做m 阶马尔可夫信源。
若上述条件概率与时间起点无关,则信源输出的符号序列可看成齐次马尔可夫链,这样的信源叫做齐次马尔可夫信源。
5.例题:稳态分布概率|稳定后的符号概率分布:符号条件概率矩阵:1/22/33/44/5⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦j i 1/21/3[p(s |s )]=1/41/5状态转移概率矩阵1/20001/32/33/40004/5⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦j i 1/20[p(s |s )]=1/41/50令各稳态分布概率为W1,W2,W3,W4:1131124W W W =+ 2131324W W W =+ 3241135W W W =+ 4242435W W W =+ 12341W W W W +++= 得稳态分布的概率:W1=3/35 W2=6/35 W3=6/35 W4=4/7稳定后的符号概率分布:11131616149()(|)()2353354355735i i i p a p a s p s ==⨯+⨯+⨯+⨯=∑ 221326364426()(|)()2353354355735i i ip a p a s p s ==⨯+⨯+⨯+⨯=∑6.定义具有概率为()i p x 的符号i x 的自信息量为:()log ()i i I x p x =-7.自信息量具有下列特性:(1)()1,()0i i p x I x ==(2)()0,()i i p x I x ==∞(3)非负性(4)单调递减性(5)可加性8.信源熵是在平均意义上来表征信源的总体特征,它是信源X 的 函数,一般写成H (X )。
信息论与编码期末复习(基本上涵盖了所有考点,有了这份资料,期末绝不会挂科)1填空题1、信息论研究的主要问题是如何提高信息传输系的性和性,对应这两个性能数字通讯系统量化指标分别为和。
2、若给定离散概率空间[X,p(x)]表示的信源,则该信源中的信源消息(事件)x的自信息量可表I(x)=;该信源平均自信息量(即信源的熵)可表示为H(X)=E[I(x)]= 。
3、在离散联合概率空间[XY,P(xy)] 上随机变量I(xy) 的数学期望H(XY)= ,若集合X与集合Y相互独立,则H(XY)= 。
4、若给定离散联合概率空间[XY,P(xy)],则x与y之间的互信息量I(x;y)= ;平均互信息量可用熵和条件熵表示即I(X;Y)= = ,其中条件熵H(X|Y)通常称为熵,条件熵H(Y|X) 称为____________熵;若集合X与集合Y相互独立,则H(X|Y) = ,H(Y|X) = ,平均互信息量I(X;Y)= 。
5、离散信源的冗余度是R表示信源消息的可压缩____________,设信源符号集的最大熵为Ho,实际熵为H∞,则冗余度R可表示为______________;信源编码目的就是通过减少或消除信源____________来提高信息传输效率,因此信源编码亦称__________性编码,而信道编码则称__________性编码。
6、对于连续随机变量,在峰值功率受限于P m的条件下,取得最大相对熵的最佳概率密度函数是一个恒值即W opt(x)=_________,称W(x)为__________分布,这时最大相对熵H cmax=__________。
7、对于平均功率受限,均值不为零的一维连续随机变量的方差为定值时,其取得最大相熵的最佳概率密度函数为_________ ,最大相对熵H cmax=__________。
正态分布,即Wopt(x)=8、假设任一随机变量X与一正态分布随机变量具有相同的相对熵Hc,则其等效正态分布的随机变量X的熵功率为P=;可以用信号平均功率和熵功率的相对差值_________来表示连续信源的冗余度。
填空1.人们研究信息论的目的是为了 高效、可靠、安全 地交换和利用各种各样的信息。
2.信息的 可度量性 是建立信息论的基础。
3.统计度量 是信息度量最常用的方法。
4.熵 是香农信息论最基本最重要的概念。
5.事物的不确定度是用时间统计发生 概率的对数 来描述的。
6.单符号离散信源一般用随机变量描述,而多符号离散信源一般用 随机矢量 描述。
7.一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为 其发生概率对数的负值 。
8.自信息量的单位一般有 比特、奈特和哈特 。
9.必然事件的自信息是 0 。
10.不可能事件的自信息量是 ∞ 。
11.两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 。
12.数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量 趋于变小 。
13. 离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 。
14. 离散平稳有记忆信源的极限熵,=∞H )/(lim 121-∞→N N N X X X X H 。
15. 对于n 元m 阶马尔可夫信源,其状态空间共有 n m 个不同的状态。
16. 一维连续随即变量X 在[a ,b]区间内均匀分布时,其信源熵为 log 2(b-a ) 。
17.平均功率为P 的高斯分布的连续信源,其信源熵,H c (X )=eP π2log 212。
18.对于限峰值功率的N 维连续信源,当概率密度 均匀分布 时连续信源熵具有最大值。
19.对于限平均功率的一维连续信源,当概率密度 高斯分布 时,信源熵有最大值。
20.若一离散无记忆信源的信源熵H (X )等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为 3 。
21.若把掷骰子的结果作为一离散信源,则其信源熵为 log 26 。
22.同时掷两个正常的骰子,各面呈现的概率都为1/6,则“3和5同时出现”这件事的自信息量是 log 218(1+2 log 23)。
“信息论与编码”复习
1.消息、信号、信息的含义、定义及区别。
信息是指各个事物运动的状态及状态变化的方式。
消息是指包含信息的语言,文字和图像等。
信号是消息的物理体现。
消息是信息的数学载体、信号是信息的物理载体
信号:具体的、物理的
消息:具体的、非物理的
信息:非具体的、非物理的
同一信息,可以采用不同形式的物理量来载荷,也可以采用不同的数学描述方式。
同样,同一类型信号或消息也可以代表不同内容的信息
2.信息的特征与分类。
1接收者在收到信息之前,对其内容是未知的,所以信息是新知识,新内容;
2信息是能使认识主体对某一事物的未知性或不确定性减少的有用知识;
3信息可以产生,也可以消失,同时信息可以被携带,被存储及处理;
4信息是可以量度的,信息量有多少的差别。
3.狭义信息论、广义信息论、一般信息论研究的领域。
狭义信息论:信息论是在信息可以量度的基础上,对如何有效,可靠地传递信息进行研究的科学。
它涉及信息量度,信息特性,信息传输速率,信道容量,干扰对信息传输的影响等方面的知识。
广义信息论:信息是物质的普遍属性,所谓物质系统的信息是指它所属的物理系统在同一切其他物质系统全面相互作用(或联系)过程中,以质、能和波动的形式所呈现的结构、状态和历史。
包含通信的全部统计问题的研究,除了香农信息论之外,还包括信号设计,噪声理论,信号的检测与估值等。
概率信息:信息表征信源的不定度,但它不等同于不定度,而是为了消除一定的不定度必须获得与此不定度相等的信息量
4.信息论的起源、历史与发展。
⏹1924年,Nyquist提出信息传输理论;
⏹1928年,Hartly提出信息量关系;
⏹1932年,Morse发明电报编码;
⏹1946年,柯切尼柯夫提出信号检测理论;
⏹1948年,Shannon提出信息论,“通信中的数学理论”—现代信息论的开创性的权
威论文,为信息论的创立作出了独特的贡献。
5.通信系统的物理模型(主要框图),各单元(方框)的主要功能及要解决的主要问题。
信源的核心问题是它包含的信息到底有多少,怎样将信息定量地表示出来,即如何确定信息量。
信宿需要研究的问题是能收到或提取多少信息。
信道的问题主要是它能够传送多少信息,即信道容量的多少。
6.通信的目的?要解决的最基本问题?通信有效性的概念。
提高通信有效性的最根本途径?通信可靠性的概念。
提高通信可靠性的最根本途径?通信安全性的概念,提高通信安全性的最根本途径?
通信系统的性能指标主要是有效性,可靠性,安全性和经济性。
通信系统优化就是使这些指标达到最佳。
从提高通信系统的有效性意义上说,信源编码器的主要指标是它的编码效率,即理论上所需的码率与实际达到的码率之比。
提高通信有效性的最根本途径是信源编码。
减少冗余。
提高可靠性:信道编码。
增加冗余。
提高安全性:加密编码。
7.随机事件的不确定度和它的自信息量之间的关系及区别?单符号离散信源的数学模型,自信息量、条件自信息量、联合自信息量的含义?
信源符号不确定度:具有某种概率的信源符号在发出之前,存在不确定度,不确定度表征该符号的特性。
符号的不确定度在数量上等于它的自信息量,两者的单位相同,但含义不同:
•不确定度是信源符号固有的,不管符号是否发出;
•自信息量是信源符号发出后给予收信者的;
•为了消除该符号的不确定度,接受者需要获得信息量。
自信息量
条件自信息量:
联合自信息量:
8.信息量的性质?含义?分别从输入端、输出端和系统总体来理解互信息量的含义。
自信息量指的是该符号出现后,提供给收信者的信息量。
9. 各种熵(信源熵,条件熵,联合熵(共熵),等)的含义及其关系。
信源熵:
条件熵:
疑义度:
噪声熵:
联合熵:
10. 信源熵的基本性质与定理及其理解?
•熵的性质
对称性
非负性
确定性
香农辅助定理
最大熵定理
条件熵小于无条件熵
信源熵和平均自信息量两者在数值上是相等的,但含义并不同。
信源熵表征信源的平均不确定度,平均自信息量是消除信源不确定度所需要的信息的量度。
信源熵是在平均意义上来表征信源的总体特性,它是信源X的函数,而X是指随机变量的整体(包括概率空间)。
信源给定,概率空间就给定,信源熵就是一个确定值。
小结:信源熵H(X)的三种物理含义:
表示信源输出后,每个离散消息所提供的平均信息量。
表示信源输出前,信源的平均不确定度。
反映了变量X的随机性。
11. 平均互信息量的定义及物理意义?疑义度及噪声熵?
12. 平均互信息量的性质及理解?
13. 平均互信息量关于信源概率和信道转移概率的凸性定理。
14. 最大离散熵定理及理解。
16. 数据处理定理及其含义。
17. 信源的种类(详细分类)?各举出几个例子。
按时间和幅度分类:
离散信源单符号离散信源文字,数字,数据等
离散序列信源
连续信源连续幅度信源话音,图像,图形等
随机波形信源
按符号之间的关系:
无记忆信源发出单个符号的无记忆信源
发出符号序列的无记忆信源
有记忆信源发出符号序列的有记忆信源
发出符号序列的马尔可夫信源
18. 离散平稳信源的定义,平均符号熵,极限熵的定义,含义与理解。
信源所发符号序列的概率分布与时间的起点无关,这种信源我们称之为多符号离散平稳信源。
19.马尔可夫信源的定义,含义及其极限熵?
当信源的记忆长度为m+1时,该时该发出的符号与前m个符号有关联性,而与更前面的符号无关。
马尔可夫链极限熵:
为了使马尔可夫链最后达到稳定,成功之路遍历的马尔可夫链,还必须满足两个条件:
平稳信源的概率分布特性具有时间推移不变性,而齐次马氏链只要求转移概率具有推移不变性,因此一般情况下平稳包含齐次,但齐次不包含平稳。
20. 信源的冗余度的定义和含义?为什么有些信源有冗余度?冗余度的计算。
冗余度,表示给定信源在实际发出消息时所包含的多余信息。
它来自两个方面,一是信源符号间的相关性;二是信源符号分布的不均匀性.
21. 连续信源的熵的定义?
连续信源的不确定度应为无穷大,是相对熵,或叫差熵。
在取两熵之间的差时才具有信息的所有特性。
22. 几种特殊连续信源的熵。
幅度连续的单个符号信源熵
波形信源熵
24. 信源输出值受限的最大连续熵定理。
限峰功率最大熵定理:对于定义域为有限的随机变量X,当它是均匀分布时,具有最
大熵。
25. 信源输出的平均功率受限的最大连续熵定理。
限平均功率最大熵定理:对于相关矩阵一定随机变量X,当它是正态分布时具有最大
熵。
H c(X) = 1/2 ln()
28. Shannon第一定理—离散无失真信源编码定理(定长和变长)及含义?
克劳夫特不等式只是用来说明唯一可译码是否存在,并不能作为唯一可译码的判据。
29. 信道的数学模型和分类?
30. 信息传输速率R的定义?信道转移概率、信道矩阵和信道容量C的定义?几种离散无噪信道的C?
31. 强对称,对称,准对称信道的含义及其C?
式中,m为信道输出符号集中符号的数目。
强对称信道:
或:
32. 离散信道容量的一般计算方法及其步骤?
33.连续信道,连续信道的C的定义。
连续单符号加性信道:多维无记忆加性连续信道:
34. 香农公式的含义?
由香农公式得到的值是其信道的下限值。
35 Shannon第二定理(信道编码定理)及其含义?
35. 对信源编码器有些什么基本要求?编码效率的定义?如何提高编码效率?
36. 什么是最佳编码?说出Shannon、Fano和Huffman编码的基本方法和主要特点。
37. 理解Huffman编码是最佳编码?38. 游程编码相关定义与步骤?
39. 算术编码(非分组码)相关定义与步骤?
40.简要说明下面几种译码准则:(1)最优译码准则;(2)最大似然译码准则
BSC信道的最大似然译码可以简化为信道的最大似然译码可以简化为最最小汉明距离译码小汉明距离译码。
41.信源与信道达到匹配的含义以及如何实现?信道剩余度的概念及计算?
42.失真函数、平均失真度的定义及其含义?
失真函数定义:
推广-〉L长序列:平均失真度:
43.信息率失真函数R(D)的定义、性质及其含义?R(D)与C的比较?
对于给定信源,在平均失真不超过失真限度D的条件下,信息率容许压缩的最小值为R(D)。
如果选取对压缩更为有利的编码方案,则压缩的效果可能更好。
但是一旦超过最小互信息这个极限值,就是R(D)的数值,那么失真就要超过失真限度。
如果需要压缩的信息率更大,则可容忍的平均失真就要大。
信息率失真函数R(D)性质:
44.Shannon第三定理及其含义?
45.常用哪些差错控制的方法?主要特点?
46.纠错编码的分类(从不同的角度)?。