第四次习题课(maxwell方程)
- 格式:ppt
- 大小:858.50 KB
- 文档页数:16




maxwell方程组微分形式Maxwell方程组微分形式是描述电磁场在给定介质中的行为的方程组。
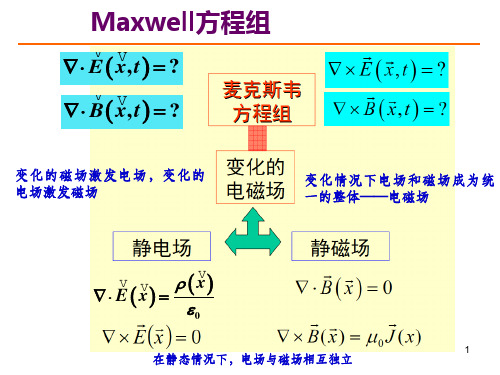
它由四个方程组成:1. 高斯定律(Gauss's law):$\nabla \cdot \mathbf{E} =\frac{\rho}{\varepsilon_0}$,其中$\nabla \cdot \mathbf{E}$表示电场$\mathbf{E}$的散度,$\rho$表示电荷密度,$\varepsilon_0$表示真空中的介电常数。
2. 高斯磁定律(Gauss's law for magnetism):$\nabla \cdot\mathbf{B} = 0$,其中$\nabla \cdot \mathbf{B}$表示磁场$\mathbf{B}$的散度。
3. 法拉第电磁感应定律(Faraday's law of electromagnetic induction):$\nabla \times \mathbf{E} = -\frac{\partial\mathbf{B}}{\partial t}$,其中$\nabla \times\mathbf{E}$表示电场$\mathbf{E}$的旋度,$\frac{\partial\mathbf{B}}{\partial t}$表示磁场$\mathbf{B}$随时间的变化率。
4. 麦克斯韦-安培定律(Ampère-Maxwell law):$\nabla \times \mathbf{B} = \mu_0\mathbf{J} + \mu_0\varepsilon_0\frac{\partial\mathbf{E}}{\partial t}$,其中$\nabla \times\mathbf{B}$表示磁场$\mathbf{B}$的旋度,$\mu_0$表示真空中的磁导率,$\mathbf{J}$表示电流密度,$\frac{\partial\mathbf{E}}{\partial t}$表示电场$\mathbf{E}$随时间的变化率。

maxwell方程式麦克斯韦方程组(Maxwell's equations)是英国物理学家詹姆斯·克拉克·麦克斯韦在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。
它由四个方程组成:描述电荷如何产生电场的高斯定律、论述磁单极子不存在的高斯磁定律、描述电流和时变电场怎样产生磁场的麦克斯韦-安培定律、描述时变磁场如何产生电场的法拉第感应定律。
从麦克斯韦方程组,可以推论出电磁波在真空中以光速传播,并进而做出光是电磁波的猜想。
麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。
从这些基础方程的相关理论,发展出现代的电力科技与电子科技。
詹姆斯·克拉克·麦克斯韦,出生于苏格兰爱丁堡,英国物理学家、数学家。
经典电动力学的创始人,统计物理学的奠基人之一。
1831年6月13日生于苏格兰爱丁堡,1879年11月5日卒于剑桥。
1847年进入爱丁堡大学学习数学和物理,毕业于剑桥大学。
他成年时期的大部分时光是在大学里当教授,最后是在剑桥大学任教。
1873年出版的《论电和磁》,也被尊为继牛顿《自然哲学的数学原理》之后的一部最重要的物理学经典。
麦克斯韦被普遍认为是对物理学最有影响力的物理学家之一。
没有电磁学就没有现代电工学,也就不可能有现代文明。
麦克斯韦的主要贡献是建立了麦克斯韦方程组,创立了经典电动力学,并且预言了电磁波的存在,提出了光的电磁说。
麦克斯韦是电磁学理论的集大成者。
他出生于电磁学理论奠基人法拉第提出电磁感应定理的1831年,后来又与法拉第结成忘年之交,共同构筑了电磁学理论的科学体系。
物理学历史上认为牛顿的经典力学打开了机械时代的大门,而麦克斯韦电磁学理论则为电气时代奠定了基石。
电磁场中的麦克斯韦方程组练习题及解答电磁场中的麦克斯韦方程组练习题及解答文中,我们将探讨电磁场中的麦克斯韦方程组,并给出相应的练习题及解答。
一、麦克斯韦方程组简介麦克斯韦方程组是电动力学的基本方程,描述了电磁场的行为和规律。
它由四个方程组成,分别是:1. 高斯定律2. 麦克斯韦-法拉第定律3. 安培环路定律4. 波恩定律下面我们将逐一介绍这四个方程。
1. 高斯定律麦克斯韦方程组中的第一个方程是高斯定律,它描述了电场与电荷之间的关系。
数学表达式为:∮E·dA = 1/ε₀∫ρdV其中,∮E·dA表示电场E沿闭合曲面的通量,ρ表示电荷密度,ε₀为真空电容率。
2. 麦克斯韦-法拉第定律麦克斯韦-法拉第定律描述了磁场的变化与电场的关系,数学表达式为:∮B·ds = μ₀(I + ε₀∂∅/∂t)在上式中,∮B·ds表示磁场B沿闭合回路的环路积分,I表示穿过该回路的电流,∂∅/∂t表示电场的变化率,μ₀为真空磁导率。
3. 安培环路定律安培环路定律描述了磁场的产生与电流的关系,数学表达式为:∮B·ds = μ₀∫J·dA在上式中,∮B·ds表示磁场B沿闭合回路的环路积分,J表示电流密度,∫J·dA表示电流通过曲面的总量。
4. 波恩定律波恩定律描述了电磁感应现象,即磁场的变化会在闭合回路中引起电流的产生。
数学表达式为:∮E·ds = -∂∅/∂t在上式中,∮E·ds表示电场E沿闭合回路的环路积分,∂∅/∂t表示磁通量的变化率。
二、练习题及解答1. 高斯定律练习题考虑一个半径为R的球体,球心处有一个电荷Q。
求该电荷产生的电场在球体表面上的总通量。
解答:根据高斯定律,我们有∮E·dA = 1/ε₀∫ρdV,又因为球体内电荷密度为零,故只需考虑球体表面。
球面上的面积元素为dA = R²sinθdθdφ。
麦克斯韦方程组及其解法麦克斯韦方程组被公认为经典电磁学的基石,它描述了电场、磁场与电荷之间的关系,并且包含了电磁波的传播规律。
数学上,麦克斯韦方程组是四个偏微分方程,它们分别是高斯定理、安培定理、法拉第电磁感应定律和法拉第电磁感应定律的推论。
本文将介绍麦克斯韦方程组的物理及数学意义,以及解法与应用。
1. 麦克斯韦方程组的物理意义麦克斯韦方程组描述了电磁学的基本规律,其中最重要的是法拉第电磁感应定律和安培定理。
法拉第电磁感应定律表示一个变化的磁场可以在一个导体中产生感应电场,而安培定理则说明电流会产生磁场。
这两个定律统一了电场和磁场的产生原理,引出了电磁波传播的概念。
此外,高斯定理用于衡量一个电场的大小,而法拉第电磁感应定律则可以解释电磁感应现象。
麦克斯韦方程组的物理意义可以总结为电磁现象之间的相互作用。
2. 麦克斯韦方程组的数学理解麦克斯韦方程组是四个偏微分方程,写成数学形式如下:\begin{align}\mathrm{div}\;\mathbf{E} &= \frac{\rho}{\varepsilon_0} \\\mathrm{div}\;\mathbf{B} &= 0 \\\mathrm{curl}\;\mathbf{E} &= -\frac{\partial\mathbf{B}}{\partial t} \\\mathrm{curl}\;\mathbf{B} &=\mu_0\mathbf{J}+\varepsilon_0\mu_0\frac{\partial\mathbf{E}}{\partial t}\end{align}其中 $\mathbf{E}$ 表示电场,$\mathbf{B}$ 表示磁场,$\rho$ 表示电荷密度,$\mathbf{J}$ 表示电流密度,$\varepsilon_0$ 表示真空介质中的电容率,$\mu_0$ 表示真空中的磁导率。
Mawell教学讲解课件.一、教学内容本课件基于《电磁学》教材第四章“麦克斯韦方程组及其应用”,详细内容涵盖:麦克斯韦方程组的数学表达形式及其物理意义,边界条件的应用,以及静态电磁场和时变电磁场的分析和计算。
二、教学目标1. 理解并掌握麦克斯韦方程组的四个基本方程及其衍生形式。
2. 能够运用麦克斯韦方程组分析和解决实际电磁问题。
3. 掌握电磁波的产生与传播,理解电磁波在现代科技中的应用。
三、教学难点与重点教学难点:麦克斯韦方程组的理解与应用,特别是时变电磁场问题的分析。
教学重点:麦克斯韦方程组的推导,以及各个方程的物理意义。
四、教具与学具准备1. 电磁学实验器材:电流表、电压表、导线、电容和电感元件。
2. 多媒体教学设备,用于展示电磁场模拟动画。
3. 学生用计算器、笔记本、教材。
五、教学过程1. 实践情景引入:通过简单的电磁感应实验,引导学生思考电磁场的变化规律。
2. 理论讲解:详细讲解麦克斯韦方程组的四个方程,每个方程通过例题进行讲解。
例题1:计算一个简单闭合回路的磁通量变化。
例题2:分析一个平面电磁波的传播特性。
3. 随堂练习:布置与例题难度相近的练习题,学生现场解答,教师及时反馈。
4. 互动讨论:针对麦克斯韦方程组的应用,组织学生讨论其在现实生活中的应用案例。
六、板书设计1. 麦克斯韦方程组的四个基本方程。
2. 例题的详细解题步骤。
3. 随堂练习的关键步骤提示。
七、作业设计1. 作业题目:计算给定线圈中的感应电动势,并分析其与线圈半径、线速度的关系。
描述一个均匀磁场中平面电磁波的传播特点。
2. 答案:作业答案将提供详细的计算步骤和最终结果。
八、课后反思及拓展延伸1. 反思:通过学生作业和随堂练习的反馈,调整教学方法,加强学生对难点的理解。
2. 拓展延伸:鼓励学生探索麦克斯韦方程组在现代通信技术中的应用,例如无线充电技术、光纤通信等。
组织课外阅读和小组讨论,拓宽学生视野。
重点和难点解析:1. 麦克斯韦方程组的理解与应用。