压缩弹簧设计

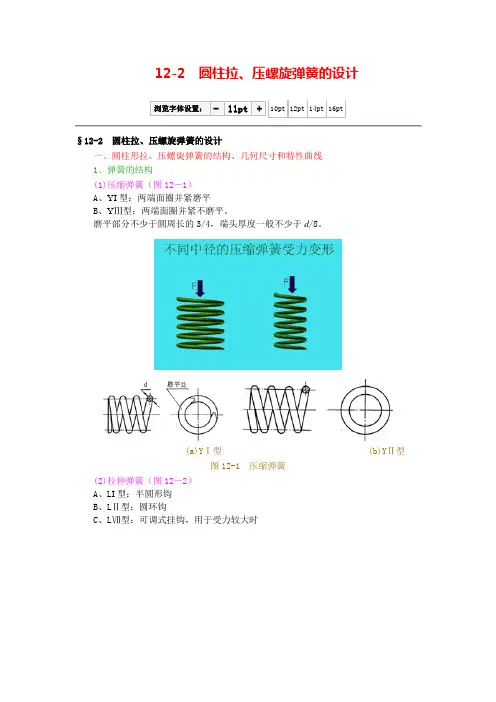
12-2 圆柱拉、压螺旋弹簧的设计浏览字体设置：- 11pt + 10pt 12pt 14pt 16pt§12-2 圆柱拉、压螺旋弹簧的设计一、圆柱形拉、压螺旋弹簧的结构、几何尺寸和特性曲线1、弹簧的结构(1)压缩弹簧（图12－1）A、YI型：两端面圈并紧磨平B、YⅢ型：两端面圈并紧不磨平。

磨平部分不少于圆周长的3/4，端头厚度一般不少于d/8。

(a)YⅠ型(b)YⅡ型图12-1 压缩弹簧(2)拉伸弹簧（图12－2）A、L I型：半圆形钩B、LⅡ型：圆环钩C、LⅦ型：可调式挂钩，用于受力较大时图12-2 拉伸弹簧2、主要几何尺寸弹簧丝直径d、外径D、内径、中径、节距p、螺旋升角 、自由高度(压缩弹簧)或长度(拉伸弹簧)，如图12-3。

此外还有有限圈数n，总圈数，几何尺寸计算公式见表12-1。

(a) (b)图12-3 圆柱形拉、压螺旋弹簧的参数弹簧指数C：弹簧中径D2和簧丝直径d的比值即：C=D2/d。

弹簧丝直径d相同时，C值小则弹簧中径D2也小，其刚度较大。

反之则刚度较小。

通常C值在4～16范围内，可按表12-2选取。

表12-2 圆柱螺旋弹簧常用弹簧指数C弹簧直径d/mm0.2～0.40.5～1 1.1～2.2 2.5～67～1618～42C7～145～125～104～104～84～63、特性曲线弹簧所受载荷与其变形之间的关系曲线称为弹簧的特性曲线。

(1)压缩弹簧其特性曲线如图12-4所示。

图中H0为弹簧未受载时的自由高度。

F min为最小工作载荷，它是使弹簧处于安装位置的初始载荷。

在F min的作用下，弹簧从自由高度H0被压缩到H1，相应的弹簧压缩变形量为λmin。

在弹簧的最大工作载荷F max作用下，弹簧的压缩变形量增至λmax。

图中F lim为弹簧的极限载荷，在其作用下，弹簧高度为H lim，变形量为λlim，弹簧丝应力达到了材料的弹性极限。

此外，图中的h=λmax-λmin，称为弹簧的工作行程。

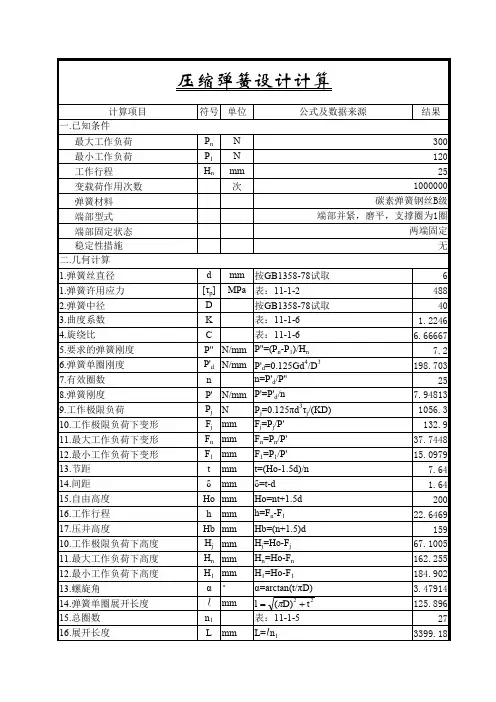
弹簧设计计算已知条件：弹簧自由长度H0=796.8mm弹簧安装长度L1=411mm 弹簧工作长度L2=227mm弹簧中径D=22.3mm弹簧直径d=3.2mm弹簧螺距P=12mm弹簧有效圈数n=66弹簧实际圈数n1=68计算步骤：（1）初步考虑采用油淬火-回火硅锰弹簧钢丝60Si2MnA C 类，抗拉强度1716-1863MPa ，切变模量G=79GPa ，弹性模量E=206GPa 。

取b σ=1716MPa 。

（2）压缩弹簧许用切应力p τ=(0.4~0.47) b σ=(0.4~0.47)*1716MPa=686.4~806.52MPa取p τ=686.4MPa 。

（3）由于弹簧刚度尚未可知，但是弹簧的中径、直径、有效圈数都已知。

2.33.22==d D C =6.9688（计算值在5~8之间） 6.9688615.046.9688416.96884615.04414+-⨯-⨯=+--=C C C K =1.2139 弹簧的最大工作压缩量Fn=795-227=568mm由公式348DP F Gd n n n =可得最大工作载荷34343.226685682.3798⨯⨯⨯⨯==nD F Gd P n n = 803.5758N 弹簧刚度663.2282.37983434'⨯⨯⨯==n D Gd P =1.4147N/mm 节距t=662.35.1795)2~1(0⨯-=-n d H =11.9727≈12 计算出来的自由高度H0=nt+1.5d=66*12+1.5*3.2=796.8mm压并高度Hb=(n+1.5)d=(66+1.5)*3.2=216mm弹簧最小工作载荷时的压缩量F1=795-411=384mm 则最小工作载荷3431413.226683842.3798⨯⨯⨯⨯==nD F Gd P =543.2625N 螺旋角α=arctan(t/πD )=arctan(12/(3.14*22.3))= 0.1696弧度= 9.7174°弹簧展开长度L=1696.0cos 683.22cos 1⨯⨯=παπDn = 4833.3mm ≈4833mm 弹簧压并高度H b ≤n 1*d max =68*（3.2+0.03）=219.64，取值216mm弹簧压并时的变形量为796.8-216=580.8mm弹簧压并时的载荷为Fa=580.8*1.4147=821.6578N（4）螺旋弹簧的稳定性、强度和共振的验算高径比b=H0/D=796.8/22.3=35.7309>0.4n B c P H P C P >=0' 不稳定系数C B =0.02==0'H P C P B c 0.02*1.4147*796.8=22.5447N<n P =803.5758N 所以必须设置导杆。

压缩弹簧设计参数1.弹簧材料：选择合适的弹簧材料是设计过程中的第一步。

常用的材料包括高碳钢、合金钢和不锈钢等。

不同材料的强度和刚度不同，可以根据需要选择适合的材料。

2.弹簧直径：弹簧的直径是指弹簧线圈的直径，也称为线径。

直径的选择会影响到弹簧的刚度和负载能力。

通常情况下，直径越大，弹簧的刚度和负载能力越大。

3.弹簧长度：弹簧的长度是指弹簧线圈的高度。

长度的选择也会影响到弹簧的刚度和负载能力。

一般来说，长度越大，弹簧的刚度和负载能力越大。

4.弹性系数：弹性系数也称为弹簧常数，是衡量弹簧刚度的指标。

它可以通过计算或实验进行确定。

对于同一种弹簧材料，直径和长度的不同会影响到弹性系数的大小。

5.负载要求：压缩弹簧通常用于承受外部负载。

根据负载的要求，可以计算出弹簧的最大、最小和平均负载值。

设计中需要考虑弹簧的负载能力，确保其在工作过程中不会发生塑性变形或失效。

6.工作环境：弹簧的工作环境也是设计中需要考虑的因素。

比如温度、湿度、腐蚀性等因素都会对弹簧的性能和寿命产生影响。

选择合适的材料和表面处理方法可以提高弹簧的耐久性。

7.安全系数：在设计弹簧时，需要考虑弹簧的安全系数。

安全系数是指实际负载与设计负载之比。

通常情况下，设计时应保证弹簧的负载能力远远大于实际负载，以确保弹簧在使用过程中的安全性。

8.加工工艺：对于弹簧的制造和加工工艺也需要进行设计考虑。

常见的加工方法包括冷镦拉伸和热处理等。

合理的制造和加工工艺将会影响到弹簧的质量和性能。

在压缩弹簧设计过程中，需要综合考虑以上参数，进行材料选择、尺寸计算和加工工艺设计等。

通过合理的设计，可以确保弹簧的工作性能和使用寿命，满足实际应用的需求。

矩形圆周压缩弹簧-概述说明以及解释1.引言概述部分介绍了矩形圆周压缩弹簧的基本概念和相关要点。

可以按照以下内容进行编写：1.1 概述矩形圆周压缩弹簧是一种特殊的弹簧结构，其形状呈矩形圆周状。

相比传统的圆柱形弹簧，矩形圆周压缩弹簧具有更大的压缩面积和更高的刚度。

矩形圆周压缩弹簧的设计原理是通过将金属带或板材弯曲成特定的矩形圆周形状，然后将其连接成闭合环形。

这种设计使得弹簧在受力时可以承受更大的压缩力，并且能够提供更高的刚度和稳定性。

矩形圆周压缩弹簧在工程领域有广泛的应用。

它可以用于缓冲、减震、支撑和传递力量等多种机械装置中。

在汽车制造、航空航天、电子设备和工业机械等领域，矩形圆周压缩弹簧往往是不可或缺的组成部分。

在本文中，我们将详细探讨矩形圆周压缩弹簧的定义、设计原理和应用领域。

通过对其特点和性能的分析，我们希望能够更好地理解和应用矩形圆周压缩弹簧，并为其进一步的研究提供一定的指导方向。

通过以上内容，可以简明扼要地介绍矩形圆周压缩弹簧的基本概念和意义。

接下来的文章结构部分可以进一步详细介绍各个方面的内容。

1.2文章结构1.2 文章结构本文分为三个主要部分：引言、正文和结论。

每个部分的内容和目标如下：引言部分将概述矩形圆周压缩弹簧的基本概念和其在工程领域中的应用。

我们将简要介绍矩形圆周压缩弹簧的定义、设计原理和应用领域，以便读者对该主题有一个整体的了解。

正文部分将深入探讨矩形圆周压缩弹簧的定义、设计原理和应用领域。

我们将详细介绍矩形圆周压缩弹簧的结构、工作原理和性能特点。

此外，我们还将探讨其在各个工程领域中的具体应用，包括机械、汽车、航空航天等领域。

通过对矩形圆周压缩弹簧的深入研究，我们可以更好地理解其在工程中的实际应用和优势。

结论部分将总结矩形圆周压缩弹簧的特点和应用，并展望未来对该领域的进一步研究。

我们将回顾矩形圆周压缩弹簧的优势和限制，并提出在设计和制造方面的改进建议。

同时，我们还将强调矩形圆周压缩弹簧在未来工程发展中的重要性和潜在应用前景。

圆柱螺旋压缩（拉伸）弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。

由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。

圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青•(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。

因此在设计弹簧时，务必使其工作应力在弹性极限范围内。

在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。

为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系(右图b)。

这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。

对拉伸弹簧，如图<圆柱螺旋拉伸弹簧的特性曲线>所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。

右图a中的H0是压缩弹簧在没有承受外力时的自由长度。

弹簧在安装时，通常预加一个压力F min，使它可靠地稳定在安装位置上。

F min称为弹簧的最小载荷(安装载荷)。

在它的作用下，弹簧的长度被压缩到H1其压缩变形量为λmin。

F max为弹簧承受的最大工作载荷。

在F max作用下，弹簧长度减到H2，其压缩变形量增到λmax。

λmax与λmin的差即为弹簧的工作行程圆柱螺旋压缩弹簧的特性曲线h,h=λmax-λmin。

F lim为弹簧的极限载荷。

在该力的作用下，弹簧丝内的应力达到了材料的弹性极限。

弹簧设计计算步骤
线径d=φ 1.8mm内径Di=14mm
有效卷数Na=40总卷数Nt=42
左 座卷数Nzl=1左座研削补正系数Gnl=0（有研削=-0.75、右 座卷数Nzr=1右座研削补正系数Gnr=0（有研削=-0.75、横弹性系数G=68500（SW-C、SWP-A、SWP-B =78500N/mm2
SUS304-WPB =68500N/mm2
SUS631J1-WPC =73500N/mm2 )
弹性系数k=0.56972N/mm k＝G*d4/（8*Na*（Di+d）3）
提供的力N=40N发生形变的长度L=70.2
形变时长度L1=190mm自由时的长度L0=260
密着高度Hs=75.6mm
密着时荷重Ps=105.176N
弹簧系数C=8.77778C=(Di+d)/d
注：弹簧系数C数值，必须符合下面要求。

压力修正系数k= 1.16649k=（4C-1)/(4C-4)+0.615/C
压缩容许压力∫emax=850注：∫emax具体数值，根据材料，从下面表格读取。

最大允许荷重Pmax=105.62Pmax=∫emax*∏*d 3/(8*(Di+d)*k)
荷重比
Rp=
37.87%
注：Rp的数值必须在20%-80%之间，才能说明弹簧设
（有研削=-0.75、无研削=0）
（有研削=-0.75、无研削=0）材料，从下面表格读取。

才能说明弹簧设计合理。

% 圆柱螺旋压缩弹簧设计计算% M文件中的表16-3和表16-5见参考文献[1]% 已知条件：最小和最大弹簧载荷、工作行程、剪切弹性模量、许用应力、最小内径F1=500;F2=1200;h=60;G=7.85e4;sigma=1420;D1_min=50;% 1-按照强度条件确定弹簧丝直径% 由于弹簧丝材料强度与它的直径相关，需要采用试算法ds=input(' 试选弹簧丝直径(mm) ds = ');sigma_b=input(' 按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = ');tau_p=0.45*sigma_b;fprintf(' 许用剪切应力tau_p = %3.4f MPa \n',tau_p);Cj=D1_min/ds+1;fprintf(' 计算弹簧指数Cj = %3.4f \n',Cj);C=input(' 按照表16-5，选择弹簧指数C = ');Kq=(4*C-1)/(4*C-4)+0.615/C;fprintf(' 计算曲度系数Kq = %3.4f \n',Kq);dj=sqrt(8*Kq*F2*C/(pi*tau_p));fprintf(' 计算簧丝直径dj = %3.4f mm \n',dj);if dj>dsdisp ' 不安全，需要重选弹簧丝直径'elsedisp ' 安全'd=ds; % 确定弹簧丝直径end第1次试算：试选弹簧丝直径(mm) ds = 6按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = 1420许用剪切应力tau_p = 639.0000 MPa计算弹簧指数Cj = 9.3333按照表16-5，选择弹簧指数C = 9计算曲度系数Kq = 1.1621计算簧丝直径dj = 7.0721 mm不安全，需要重选弹簧丝直径第2次试算：试选弹簧丝直径(mm) ds = 7按照表16-3，选择弹簧丝强度极限(MPa) sigma_b = 1370许用剪切应力tau_p = 616.5000 MPa计算弹簧指数Cj = 8.1429按照表16-5，选择弹簧指数C = 8计算曲度系数Kq = 1.1840计算簧丝直径dx = 6.8520 mm安全% 2-按照刚度条件确定弹簧工作圈数Kj=(F2-F1)/h;fprintf(' 计算弹簧刚度Kj = %3.4f N/mm \n',Kj);nj=G*d/(8*C^3*Kj);fprintf(' 计算弹簧圈数nj = %3.4f \n',nj);n=input(' 选取弹簧工作圈数n = ');n2=input(' 选取弹簧支承圈数n2 = ');n1=n+n2;fprintf(' 弹簧总圈数n1 = %3.4f \n',n1);% 计算弹簧的刚度和变形量Kp=G*d/(8*C^3*n);f1=F1/Kp;f2=F2/Kp;fprintf(' 弹簧实际刚度Kp = %3.4f N/mm \n',Kp);fprintf(' 弹簧最小变形量f1 = %3.4f mm \n',f1);fprintf(' 弹簧最大变形量f2 = %3.4f mm \n',f2);计算结果：计算弹簧刚度Kj = 11.6667 N/mm计算弹簧圈数nj = 11.4990选取弹簧工作圈数n = 12选取弹簧支承圈数n2 = 2弹簧总圈数n1 = 14.0000弹簧实际刚度Kp = 11.1796 N/mm弹簧最小变形量f1 = 44.7243 mm弹簧最大变形量f2 = 107.3383 mm% 3-弹簧稳定性校核D2=C*d;fprintf(' 弹簧中径D2 = %3.4f mm \n',D2);delta=input(' 选取相邻两圈弹簧丝间隙系数delta = ');t=(1+delta)*d+f2/n; % 圆柱螺旋压缩弹簧fprintf(' 弹簧节距t = %3.4f mm \n',t);Y=input(' 选取弹簧端部结构类型Y = '); % 弹簧端部结构类型:1或是2if Y==1H0=n*t+(n2-0.5)*d;elseif Y==2H0=n*t+(n2+1)*d;endfprintf(' 弹簧自由高度H0 = %3.4f mm \n',H0);b=H0/D2;fprintf(' 弹簧高径比 b = %3.4f \n',b);% 采用3次样条插值确定圆柱螺旋弹簧不稳定系数CbDBZC=input(' 选取弹簧端部支承类型DBZC = '); % 弹簧端部支承类型:1、2、3 switch DBZCcase 1 % 1-弹簧两端固定支承bx=[5.3 5.4 5.5 5.75 6 6.5 7 7.5 8 8.5 9 10];Cby=[0.80 0.65 0.60 0.45 0.40 0.325 0.265 0.225 0.19 0.165 0.145 0.125];case 2 % 2-弹簧一端固定、一端自由支承bx=[3.7 3.85 4 4.5 5 5.5 6 6.5 7 8 9 10];Cby=[0.80 0.60 0.50 0.31 0.24 0.20 0.17 0.15 0.13 0.105 0.08 0.075];case 3 % 3-弹簧两端自由支承bx=[2.6 2.8 3 3.5 4 4.5 5 5.5 6 7 8 9 10];Cby=[0.8 0.5 0.4 0.27 0.21 0.15 0.12 0.09 0.075 0.05 0.04 0.03 0.025]; endCb=interp1(bx,Cby,b,'spline'); % 3次样条插值fprintf(' 弹簧不稳定系数Cb = %3.4f \n',Cb);% 绘制圆柱螺旋弹簧不稳定系数Cb线图plot(bx,Cby,'ro',bx,Cby);grid on;xlabel('\bf\it b');ylabel('\bf\it Cb');title('\bf 弹簧不稳定系数线图');switch DBZCcase 1gtext('\bf 1-弹簧两端固定支承')case 2gtext('\bf 2-弹簧一端固定、一端自由支承')case 3gtext('\bf 3-弹簧两端自由支承')endFc=Cb*Kp*H0;fprintf(' 弹簧稳定临界载荷Fc = %3.4f N \n',Fc);if Fc<F2disp ' 弹簧工作不稳定，需要改变参数或是加装导向装置'elsedisp ' 弹簧工作稳定'end计算结果：弹簧中径D2 = 56.0000 mm选取相邻两圈弹簧丝间隙系数delta = 0.15弹簧节距t = 16.9949 mm选取弹簧端部结构类型Y = 1弹簧自由高度H0 = 214.4383 mm弹簧高径比 b = 3.8293选取弹簧端部支承类型DBZC = 3弹簧不稳定系数Cb = 0.2278弹簧稳定临界载荷Fc = 546.0792 N弹簧工作不稳定，需要改变参数或是加装导向装置。

弹簧设计理论陈晓华 2009年5月一、 压簧设计 1、压簧的结构分类图1 压缩弹簧的结构压缩弹簧特点：弹簧节距p 在自由状态下，各圈之间应留有适当的间隙，以便弹簧受到压缩时，有产生相应变形的可能。

为了使弹簧在压缩后仍能保持一定的弹性，在设计时还应考虑在最大载荷作用下，各圈之间仍能保留一定的弹性，各圈之间仍能保留一定的间隙1δ，其推荐值为：mm d 2.01.01≥=δ，其中d 为弹簧直径。

压簧的两个端面圈应与邻圈并紧（无间隙），只起支撑作用，不参与变形，故称为死圈。

当弹簧的工作圈数7≤n 时，弹簧每端的死圈约为0.75圈；当弹簧的工作圈数n ＞7时，弹簧每端的死圈约为1～1.75圈。

压簧端部结构的形式最常用的形式有两种：1）两端并紧磨平；2）两端并紧不磨平。

在重要场合采用第一种，以保证两端支撑端面与弹簧的轴线垂直，从而使弹簧受力时不致歪斜。

弹簧丝直径d ≤0.5mm 时，弹簧的两端面可不需磨平。

弹簧丝直径d ＞0.5mm 时，弹簧的两端面则需要磨平，磨平部分应不少于圆周长的3/4。

端头厚度一般不小于d /8，端面的粗糙度不能低于Ra 3.2μm 。

2、压弹簧特性图2压缩弹簧的载荷——变形图其中 d ——弹簧丝直径（mm ）D 、D 1、D 2——弹簧的中径、内径、大径（mm ）P j ——试验载荷，为测定时允许承受的最大载荷（N ）F 1、F 2、…、F n ——在P 1、P 2、…、P n 的作用下，弹簧的变形量（mm ）H 1、H 2、…、H n ——在P 1、P 2、…、P n 的作用下，弹簧的高度（长度）mm H 0——弹簧的自由高度（即自由长度）为了保证载荷与变形的可靠性，要求弹性变形量应在试验载荷下变形量的20%～80%之间，即要求：0.2 P j ≤P 1、2、…、n ≤0.8 P j在特殊需要保证弹簧刚度时，工作载荷应在试验载荷下变形量的30%～70%之间。

3、计算公式(1)弹簧螺旋升角（见图4）Dtarctgπα= 压缩弹簧螺旋升角一般应在5°～9°范围内选取。

压缩弹簧设计计算公式
常见的弹簧刚度计算公式有以下几种：
1. Hooke定律：
弹簧刚度（K）=受力（F）/变形量（ΔL）
弹簧刚度也可以表示成：K=Gd^4/8ND^3，其中G为弹簧材料的剪切模量，d为弹簧线径，D为弹簧的均衡直径，N为弹簧的圈数。

2.圈数公式：
弹簧刚度（K）=Gd^4/8ND^3
弹簧圈数（N）=(Gd^4/8KD^3)+1
弹簧线径（d）=(8NKD^3)/(G)
3.线径公式：
弹簧刚度（K）=Gd^4/8ND^3
弹簧线径（d）=((8NKF)/(πG))^0.25
弹簧圈数（N）=(Gd^4/8KD^3)+1
以上的公式是根据Hooke定律和圈数公式、线径公式推导得出的。

其中，G为弹簧材料的剪切模量，d为弹簧线径，D为弹簧的均衡直径，N为弹簧的圈数，K为弹簧刚度，F为受力，ΔL为变形量。

在实际应用中，根据不同的设计需求和实际情况，可以选择合适的公式进行计算。

同时，由于弹簧经常在循环载荷下工作，还需考虑弹簧的疲劳寿命等因素，以保证弹簧的使用安全和可靠性。

因此，在进行压缩弹簧
设计时，应结合实际情况和经验进行综合考虑，并且需要进行相关的试验和验证。

此外，弹簧设计还需要考虑其他因素，如预缩量、自由长度、受力方式等。

因此，以上给出的公式只是设计中的一部分，还需要根据具体情况进行综合考虑和修改。

总结起来，压缩弹簧设计计算公式主要包括Hooke定律、圈数公式和线径公式，这些公式基于弹簧刚度的定义，用于计算弹簧的物理性能。

在实际应用中，需要根据具体情况选择和修改适合的公式，并结合其他因素进行综合设计。

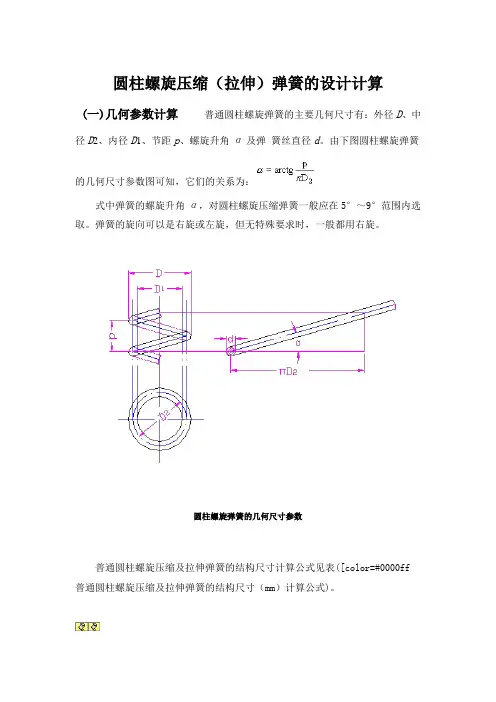
圆柱螺旋压缩（拉伸）弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。

由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。

圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式参数名称及代号计算公式备注压缩弹簧拉伸弹簧中径D2D2=Cd 按普通圆柱螺旋弹簧尺寸系列表取标准值内径D1D1=D2-d外径D D=D2+d旋绕比C C=D2/d 压缩弹簧长细比b b=H0/D2b在1～5.3的范围内选取自由高度或长度H0H0≈pn+(1.5～2)d（两端并紧，磨平）H0≈pn+(3～3.5)d（两端并紧，不磨H0=nd+钩环轴向长度平）工作高度或长度H1,H2,…,H nH n=H0-λn H n=H0+λnλn--工作变形量有效圈数n根据要求变形量按式（16-11）计算n≥2总圈数n1n1=n+(2～2.5)（冷卷）n1=n+(1.5～2)（YII型热卷）n1=n拉伸弹簧n1尾数为1/4,1/2,3/4整圈。

推荐用1/2圈节距p p=(0.28～0.5)D2p=d轴向间距δδ=p-d展开长度L L=πD2n1/cosαL≈πD2n+钩环展开长度螺旋角αα=arct g(p/πD2) 对压缩螺旋弹簧，推荐α=5°～9°质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。

因此在设计弹簧时，务必使其工作应力在弹性极限范围内。

在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。

弹簧设计参数名称与代号压缩螺旋弹簧弹簧直径d/mm由强度计算公式确定弹簧中径D2/mm D2=Cd弹簧内径D1/mm D1=D2-d弹簧外径D/mm D=D2+d弹簧指数C C=D2/d 一般4≤C≤6螺旋升角g/° 对压缩弹簧，推荐g＝5°～9°有效圈数n由变形条件计算确定一般n>2总圈数n1压缩n1＝n＋(2~2.5)；拉伸n1＝nn1＝n＋(1.5～2)( YⅠ型热卷)；n1的尾数为1/4、1/2、3/4或整圈，推荐1/2圈自由高度或长度H0/mm两端圈磨平n1＝n＋1.5时，H0＝np+d n1＝n＋2时，H0＝np+1.5dn1＝n＋2.5时，H0＝np+2d两端圈不磨平n1＝n＋2时，H0＝np+3dn1＝n＋2.5时，H0＝np+3.5d工作高度或长度Hn/mm Hn＝H0－ln节距p/mm间距d/mm d＝p－d压缩弹簧高径比b b＝H0/D2展开长度L/mm L=pD2n1/cosg弹簧弹力计算公式：压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；弹簧常数公式（单位：kgf/mm）：K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ） G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300；磷青铜线G=4500 ；黄铜线G=3500 d=线径Do=OD=外径 Di=ID=内径 Dm=MD=中径=Do-d N=总圈数 Nc=有效圈数=N-2 弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）＝（８０００×２４）／（８×２０３×３．５）＝０．５７１ｋｇｆ／ｍｍ拉力弹簧拉力弹簧的k值与压力弹簧的计算公式相同。

压缩弹簧–类型及设计计算•压缩弹簧在压缩时会存储机械能，而在移除负载时会释放机械能。

•虽然压缩弹簧通常由弹簧钢制成，但它们也可能包含碳，镁，镍，铬，锡，铜，钨和铝。

•不同的材料会为压缩弹簧产生不同程度的弹性和能量存储能力。

•罗伯特·胡克（Robert Hooke）早在1676年就引入了一个公式来计算弹簧所施加的力，该力与弹簧的伸长成比例。

压缩弹簧是专门设计用于承受轴向压缩负载的机械设备。

它们通常还可以扩展以及旋转到一个点。

通常，压缩弹簧在施加压缩负载时可以存储机械能。

一旦消除了载荷，它们就会恢复其原始形状和大小，并经历弹性变形。

这种独特的存储势能的能力以及相对简单和便宜的特点使得压缩弹簧在非常广泛的应用中具有无价的价值。

从机械键盘按钮，床垫和圆珠笔到枪支和汽车悬架减震器。

自15世纪第一批压缩弹簧用于发条机构以来，我们一直在使用压缩弹簧。

压缩弹簧的类型压缩弹簧可以具有许多不同的几何形状。

最普遍的是螺旋弹簧或螺旋弹簧。

这种形状优于其他形状，因为它可以进行无缝的高压缩，并且还可以扩展到一个点。

由于使用较少的材料来满足压缩载荷吸收的需要，因此重量也更轻。

最后，螺旋弹簧的形状使这种类型的弹簧具有相对较大的弹簧常数（稍后会对此进行更多介绍）。

此类别进一步分为子类别，包括：自由长度（L）是弹簧在不受任何压缩时的总长度，而有效长度（na）和总螺旋（n）分别是存储和释放机械能的线圈数和总线圈（至少两个专用于弹簧的末端/底部）。

另一个重要的形态特性是风向，可以是左风或右风。

弹簧所施加的力与其伸长成正比，这一定律是由罗伯特·胡克（Robert Hooke）于1676年制定并引入的，距最初的弹簧开始使用仅几年。

Hooke向世界介绍了公式：“ F = -kx”，其中F是弹簧力，x是伸出距离，k是每个弹簧都不同的弹簧常数–由制造商通过实验确定，或者由用户使用公式：“ k = Gd 4 /[8 3Dna]”。

圆柱压缩弹簧端部解释
圆柱压缩弹簧是一种常见的机械弹簧，它通常由圆柱形弹簧线圈组成，用于吸
收和储存机械能。

在弹簧的端部设计上有着重要的作用，下面将就圆柱压缩弹簧端部进行解释。

圆柱压缩弹簧的端部通常包括两种设计，一种是封闭端，另一种是开口端。

封
闭端是指弹簧的两端线圈环绕在一起，形成一个封闭的圆环。

这种设计可以防止弹簧线圈的松动和脱落，提高弹簧的稳定性和使用寿命。

而开口端则是弹簧的两端线圈分开，不连接在一起，这种设计通常用于需要弹簧两端连接其他机械部件的情况，比如固定在支架上。

在圆柱压缩弹簧的端部设计中，还需要考虑弹簧的端部形状和处理方式。

一般
来说，端部的形状可以是平面、圆形、方形等，不同的形状会影响弹簧的受力性能和安装方式。

此外，端部的处理方式也很重要，常见的处理方式包括研磨、热处理、喷砂等，这些处理可以提高弹簧的表面光洁度和耐磨性，延长弹簧的使用寿命。

除了端部的设计和处理，圆柱压缩弹簧的端部还需要考虑弹簧的连接方式。

弹
簧的端部通常需要连接其他机械部件，常见的连接方式包括焊接、压制、固定螺栓等。

在选择连接方式时，需要考虑弹簧的受力方向和工作环境，以确保连接牢固和安全。

总的来说，圆柱压缩弹簧的端部设计是弹簧制造中的重要环节，端部的设计和
处理会直接影响弹簧的受力性能、稳定性和使用寿命。

通过合理的端部设计和处理，可以提高弹簧的性能和可靠性，满足不同工程的需求。

压缩弹簧尺寸及参数表压缩弹簧是一种常用的弹簧类型，广泛应用于各个行业和领域。

压缩弹簧的尺寸和参数表是根据具体要求和设计需要确定的，下面是一个示例，详细介绍了压缩弹簧的尺寸和参数表。

1.弹簧直径（D）：指弹簧线径的两倍，即弹簧外径。

直径的选择应根据设计的应用环境和弹簧的承载能力来确定。

2. 弹簧线径（d）：指弹簧线的直径。

线径的大小决定了弹簧的刚度和承载能力，一般使用在0.1mm到50mm之间。

3.弹簧活动圈数（N）：指弹簧未压缩时的圈数。

活动圈数的选择主要根据设计的工作行程和力的需求来确定。

4.弹簧自由长度（L0）：指弹簧未受任何外力压缩时的长度。

自由长度的选择应根据设计的工作行程和弹簧特性来确定。

5.弹簧刚度（K）：指单位长度的弹簧力。

刚度的选择主要取决于设计的要求和应用环境，可以根据所需的力量和变形程度来确定。

6.弹簧承载力（F）：指弹簧能够承载的最大力量。

承载力的选择应根据设计的工作负荷和应力安全因素来确定。

7.弹簧工作行程（S）：指弹簧压缩过程中的总行程。

工作行程的选择应根据设计的要求和应用环境来确定，需要考虑到弹簧的变形和寿命等因素。

8.弹簧材料：弹簧的材料选择应根据设计的要求和应用环境来确定，常见的材料有钢丝、不锈钢、合金钢等。

9.弹簧表面处理：根据具体的要求和应用环境，可以对弹簧进行表面处理，如镀铜、镀锌、电镀等。

10.弹簧质量要求：对于一些高精度要求的应用场合，如汽车发动机、航天器等，对弹簧的质量有严格的要求，如轴向力偏差、弹簧截面形状和尺寸公差等。

总结：以上是关于压缩弹簧尺寸和参数表的一些内容。

压缩弹簧的尺寸和参数选取是根据具体的设计要求和应用环境来确定的，需要综合考虑弹簧的承载能力、刚度、工作行程等因素。

在选择和设计压缩弹簧时，应该遵循弹簧设计原理和相关标准，并进行合理的参数计算和选取，以确保弹簧的性能和可靠性。