1015指数型函数的对称平移与绝对值函数图像).

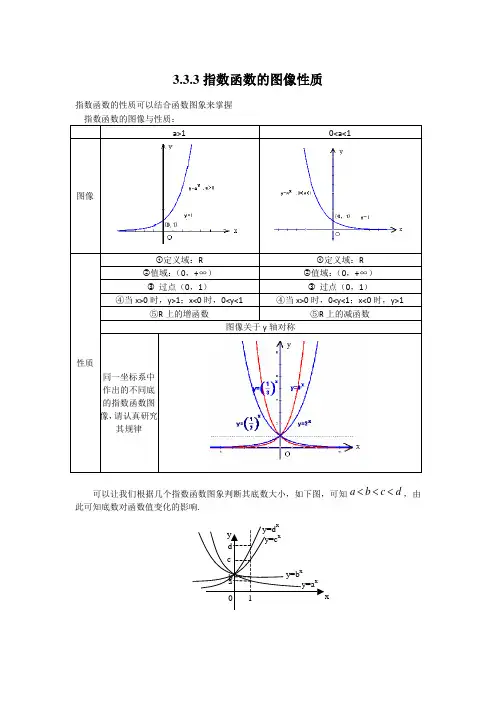
指数函数图象及性质应用指数函数是数学中的一种常见函数形式，其表达式为y = a^x，其中a是一个常数且大于0且不等于1，x可以是任意实数。

指数函数的图象具有如下几个特点：1. 定义域与值域: 指数函数的定义域是所有的实数x，而其值域则是大于0的所有实数。

2. 增长性: 当底数a大于1时，指数函数随着自变量x的增大而增大；当底数a 在0和1之间时，指数函数随着自变量x的增大而减小。

这表明指数函数的增长性取决于其底数a的大小。

3. 奇偶性: 当底数a为正数时，指数函数是奇函数；当底数a为负数时，指数函数是偶函数。

这是因为指数函数的自变量x发生变化时，函数值会发生对称变化。

4. 渐近线: 当x趋于负无穷时，指数函数的值趋于0；当x趋于正无穷时，指数函数的值趋于正无穷。

这意味着指数函数图象有两条渐近线：x轴和y轴。

5. 零点: 指数函数不存在实数零点，即该函数的值不会等于0。

这是因为指数函数的底数a不等于1，所以不可能存在x使得a^x=0。

指数函数在实际中有很多重要的应用。

以下是其中一些常见的应用：1. 经济与金融: 指数函数在经济学和金融学中广泛应用。

例如，人口增长模型可以使用指数函数来描述，其中底数a表示每年的人口增长率。

另外，指数函数还可以用于计算财富的增长，例如复利计算。

2. 自然科学: 指数函数在物理学、化学和生物学等自然科学领域中也有广泛的应用。

例如，放射性衰变过程可以使用指数函数来描述，其中底数a表示衰减的速率。

另外，指数函数还可以用于描述反应动力学和细胞生长等现象。

3. 电子技术: 指数函数在电子技术中起着重要的作用。

例如，放大器的电压增益可以使用指数函数来表示，其中底数a表示放大器的增益系数。

另外，电路中的充电和放电过程也可以使用指数函数来描述。

4. 计算机科学: 指数函数在计算机科学中有广泛的应用。

例如，指数函数可以用于表示算法的时间复杂度，其中底数a表示算法的增长速度。

另外，指数函数还可以用于表示数据结构的增长率，例如二叉树的高度。

指数函数的像和性质指数函数是高中数学中非常重要的一类函数，其像和性质具有一定的规律和特点。

本文将通过对指数函数的定义、图像、性质等方面的介绍，探讨指数函数的像和性质。

一、指数函数的定义指数函数是形如y = a^x的函数，其中a为常数且大于0且不等于1，x为自变量，y为因变量。

在指数函数中，底数a决定了函数的性质及其图像的形状。

二、指数函数的图像1. 当0 < a < 1时，指数函数的图像呈现出上凸形状，随着x的增加，y值逐渐减小。

即指数函数的图像在y轴的正半轴上逐渐趋近于零。

2. 当a > 1时，指数函数的图像呈现出下凸形状，随着x的增加，y值逐渐增大。

即指数函数的图像在y轴的正半轴上逐渐趋近于正无穷大。

3. 指数函数的图像经过点(0, 1)，即当x为0时，y的值为1。

4. 指数函数的图像都在y轴的负半轴上不存在定义，即当x小于零时，y无定义。

三、指数函数的性质1. 零次指数函数性质：a^0 = 1，其中a为常数且大于0且不等于1。

即任何非零实数的0次方均为1。

2. 同底数相乘性质：a^m * a^n = a^(m+n)，其中a为常数且大于0且不等于1，m和n为任意实数。

即同底数的指数相乘等于底数不变、指数相加的情况。

3. 同底数相除性质：a^m / a^n = a^(m-n)，其中a为常数且大于0且不等于1，m和n为任意实数且n不等于0。

即同底数的指数相除等于底数不变、指数相减的情况。

4. 幂运算性质：(a^m)^n = a^(m*n)，其中a为常数且大于0且不等于1，m和n为任意实数。

即指数函数的幂运算等于指数相乘的情况。

综上所述，指数函数的像和性质与底数和指数相关。

通过对指数函数的定义、图像、性质的了解，我们可以更好地理解和应用指数函数。

指数函数在数学、自然科学、经济学等领域都有重要的应用，不仅能够描述自然界中的现象，还能够解决实际问题，具有重要的意义和价值。

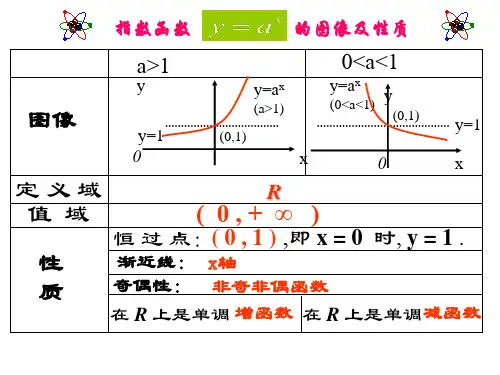
指数函数性质及图像指数函数定义为y=a^x(a>0,a1)，其中，x 为“指数”，a 为“底数”，y 为“值”。

指数函数可以用于描述一定规律的大小之间的变化关系。

从数学上讲，指数函数属于多项式函数中的特例，其特点是当变量 x加 1，函数值 y 会翻倍或减半，而不像多项式函数那样只会减少很小的数量，比如，当 x 从 0加到 1，y 会从 a^0加到 a^1。

指数函数的性质有如下几点：（1）变量 x指数函数中的未知数，而 a是指数函数中的常量；（2）当 a > 1，指数函数单调递增；当 a < 1，指数函数单调递减；当 a = 1，指数函数是线性函数；（3）任意两个底数不一样的指数函数互不相等，但两个有着相同底数的指数函数则相等；（4）指数函数可以增加或减少的极限是无穷大或无穷小；（5）指数函数是可导函数，其导数可以由变量 x决定，只有当x 为正数或0时其导数才有意义，如当 x 为正数时，其导数为 a^x * ln(a)；（6）对于指数函数而言，当其变量 x大时，其函数值 y 会越大，也就是说随着 x增大，y按照指数函数变化，而不像线性函数那样按照简单的等比数列变化。

二、指数函数的图像指数函数的图像只有在二维坐标系内才能看到，在二维坐标系内，指数函数的图像具有以下几个特点：（1）指数函数图像与底数 a正比，因此，当 a > 1，图像的斜率增大，而 a < 1，斜率减小；（2）指数函数的图像是一条弯曲的曲线；（3）指数函数的变量 x 与底数 a取值有关，当 a = 1，x值大小范围为所有实数；当 a > 1，x取值范围是所有正数；当 a < 1，x取值范围是所有负数；（4）指数函数的图像不会交叉，即，它的定义域和值域是相同的；（5）指数函数的图像没有不连续的部分，它表示的是一个连续的函数。

三、指数函数的应用指数函数的性质和图像有着广泛的应用，下面介绍几个比较常见的指数函数的应用：（1）指数函数在金融中有着重要的应用，例如，可以通过指数函数来计算投资利息、通货膨胀率等；（2）指数函数可以用来描述物理数据，例如压强温度曲线、热变形速度温度曲线等；（3）指数函数在社会学、政治科学和投票学中也有着广泛的用途，它可以帮助我们进行统计分析和预测社会变化；（4）指数函数也可以用来模拟电路中的电流电压曲线、正弦波等。

指数函数图像与性质（2）(图像对称、平移与绝对值函数图像)一、函数图像间的对称性对称。

的图像关于与函数、函数______212y A xx y ⎪⎭⎫ ⎝⎛== 若___)(,2)(=-=x f x f x则， 这两个函数的图像关于____对称。

抽象化：函数对称。

的图像关于与____)()(y x f y x f -==回顾：①轴对称。

）关于）与点（点（y ,,y x y x -②对称。

）关于）与点（点（____,,y x y x -③对称。

）关于）与点（点（____,,y x y x --扩展为函数性质： 对称。

的图像关于与____)()(y x f y x f -==对称。

的图像关于与____)()(y x f y x f -==对称。

的图像关于与____)()(y x f y x f --==对称。

的图像关于与函数、函数)(33y B x x y --==别、自对称与他对称的区C（1）轴对称。

于是偶函数，本身图像关函数y y 2x = （2）轴对称。

的图像关于与函数函数y 212y xx y ⎪⎭⎫ ⎝⎛== 二、函数图像的平移图像。

分别画出这两个函数的则函数、已知____,)1(,2)(A =-=x f x f x发现：函数y =)1(-x f 的图像相当于把函数y =)(x f 的图像向____移动____个单位。

类似：函数y =)1(+x f 的图像相当于把函数y =)(x f 的图像向____移动____个单位。

图像。

分别画出这两个函数的则函数、已知____,1)(,2)(B =-=x f x f x发现：函数y =1)(-x f 的图像相当于把函数y =)(x f 的图像向____移动____个单位。

那么：函数y =1)(+x f 的图像相当于把函数y =)(x f 的图像向____移动____个单位。

C 、。

）的对称轴为则函数为偶函数已知________2(,)(-x f x f。

关于指数函数与对数函数的问题一、指数函数底数对指数函数的影响：①在同一坐标系内分别作函数的图象，易看出：当a>l时，底数越大，函数图象在第一象限越靠近y轴；同样地，当0<a<l时，底数越小，函数图象在第一象限越靠近x轴．②底数对函数值的影响如图．③当a>0，且a≠l时，函数与函数y=的图象关于y轴对称。

利用指数函数的性质比较大小：若底数相同而指数不同，用指数函数的单调性比较：若底数不同而指数相同，用作商法比较；若底数、指数均不同，借助中间量，同时要注意结合图象及特殊值二、对数函数底数对函数值大小的影响：1.在同一坐标系中分别作出函数的图象，如图所示，可以看出：当a>l时，底数越大，图象越靠近x轴，同理，当O<a<l时，底数越小，函数图象越靠近x轴．利用这一规律，我们可以解决真数相同、对数不等时判断底数大小的问题．2.类似地，在同一坐标系中分别作出的图象，如图所示，它们的图象在第一象限的规律是：直线x=l把第一象限分成两个区域，每个区域里对数函数的底数都是由右向左逐渐减小，比如分别对应函数，则必有对数函数的图象与性质：三、对数函数与指数函数的对比：(1)对数函数与指数函数互为反函数，它们的定义域、值域互换，图象关于直线y=x对称．(2)它们都是单调函数，都不具有奇偶性．当a>l时，它们是增函数；当O<a<l时，它们是减函数．(3)指数函数与对数函数的联系与区别：四、关于同底指数函数与对数函数的交点问题一、1a >时方程x log a a x =的解 先求如图3所示曲线x log y a y a x ==与相切时a 的值。

设曲线x log y a y a x==与相切于点M （00x ,x ），由于曲线xa y =在点M 处的切线斜率为1，所以⎪⎩⎪⎨⎧==⎪⎩⎪⎨⎧===1a ln a ,x a 1|)'a (,x a 0000x 0x x x x0x 即所以a ln 1a x a ln 1,x a a ln 100x 0=⎪⎩⎪⎨⎧==则即ex ,e a ,a ln 1e 0e 1===此时所以。