专训“化斜为直”构造直角三角形的方法

解直角三角形的方法和技巧直角三角形是三角形中最为基础和重要的一类三角形，因为它具有很多特殊的性质和应用。

解直角三角形的方法和技巧在数学的学习过程中非常重要，本文将为大家介绍10条关于解直角三角形的方法和技巧，并展开详细描述。

一、勾股定理勾股定理是解直角三角形最基本的定理，也是解直角三角形的最快捷的方法。

勾股定理的公式为：a² + b² = c²。

a和b表示直角边，c表示斜边。

当已知a和b的长度时，可以通过计算c的长度来确定直角三角形的大小和形状。

勾股定理非常广泛地应用于工程、科学和数学等领域，可以帮助我们计算物体的大小、距离和位置等。

二、正弦定理正弦定理也是解直角三角形的一种基本方法，它是一个三角形中的三角函数，公式为：a/sinA = b/sinB = c/sinC。

a、b、c分别表示三角形任意两边和斜边，A、B、C表示这些边对应的角度。

如果已知了两个长度和一个角度，则可以通过正弦定理计算第三个长度。

正弦定理的应用十分广泛，可以帮助我们计算三角形的任意边的长度。

三、余弦定理余弦定理也是解直角三角形的一种基本方法，它也是一个三角形中的三角函数，公式为：c² = a² + b² - 2abcosC。

a、b表示三角形中两个边的长度，c表示斜边的长度，C表示斜边对应的角度。

如果已知了两个长度和一个角度，则可以通过余弦定理计算第三个长度。

余弦定理也是应用广泛的一个数学公式，可以帮助我们计算三角形的任意边的长度。

四、正切定理正切定理也是解直角三角形的一种基本方法，它是一个三角形中的三角函数，公式为：tanA = a/b或tanB = b/a。

a、b分别表示三角形中的两个直角边，A、B是它们对应的角度。

通过正切定理可以求得角度的大小或两直角边的比例。

五、特殊直角三角形的知识特殊直角三角形是指那些具有特殊边长和角度的直角三角形。

其中最为常见的是边长为3、4、5的特殊直角三角形。

典中点勾股定理专训4 巧用勾股定理判定直角的六种方法◐名师点金◑说明垂直的方法：1.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.2.等腰三角形中“三线合一”.3.直角三角形的判定.在几何中,我们常常先说明垂直,再利用垂直的性质来解相关问题。

典例剖析：某校把一块三角形的废地开辟为植物园,如图,测得AC=80m,BC=60m,AB=100m 。

(1)若人口E 在边AB 上,且与A,B 的距离相等.求从入口E 到出口C 的最短路线的长(提示直角三角形斜边上的中线等于斜边的一半);(2)若线段CD 是一条水渠,且点D 在边AB 上,点D 距点A 多远时,水渠最短?解题秘方:解实际生活中的问题,需先将实际问题通过建立数学模型转化为数学问题,再利用数学知识进行解答.本题中:已知△ABC 中,AC=80m,BC=60m ，AB=100m 。

(1)若AE=EB,求CE 的长； (2)若CD ⊥AB,求AD 的长。

方法1：利用三边的数量关系证明直角1.如图,在正方形ABCD 中,F 为DC 的中点,E 为BC 上一点,且CE=41BC ，求证:∠AFE 是直角.方法2：利用转化为三角形法构造直角三角形2.如图,在四边形ABCD 中,∠B=90°,AB=3，BC=4，CD=12，AD=13.求ABCD S 四边形.方法3：利用倍长中线法构造直角三角形3.如图,在△ABC 中,D 为边BC 的中点,AB=5,AD=6,AC=13.求证AB ⊥AD方法4：利用化分散为集中法构造直角三角形4.如图,在等腰直角三角形ABC 的斜边上取两点M,N,使∠MCN=45°,设AM=a,MN=x,BN=b,判断以x,a,b 为边长的三角形的形状。

方法5：利用“三线合一”法构造直角三角形5. 如图,在△ABC 中,CA=CB,∠ACB=90°,D 为AB 的中点,M,N 分别为AC,BC 上的点,且DM ⊥DN.求证:22CN CM 2AB ）（+=方法6：利用轴对称的性质构造直角三角形6.如图,在Rt △ABC 中,∠B=90°,AB=3,AC=5,将△ABC 折叠,使点B 恰好落在边AC 上,与点B'重合,AM 为折痕,则MB'的长为多少?。

专题训练(八) 解直角三角形常见的七种方法►方法一已知两边解直角三角形1．在△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，根据下面的条件解直角三角形．(1)b＝6，c＝2 2；(2)a＝4，b＝4 3.2．如图8－ZT－1，已知AD为△BAC的角平分线，且AD＝2，AC＝3，∠C＝90°，求BC的长及AB的长．图8－ZT－1►方法二已知一边和一个锐角解直角三角形3．在△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，根据下列条件解直角三角形．(1)∠A＝60°，a＝6；(2)∠A＝30°，b＝10 3.4．已知：如图8－ZT －2，在Rt △ABC 中，∠C ＝90°，AC ＝3，D 为BC 边上一点，且BD ＝2AD ，∠ADC ＝60°，求△ABC 的周长．(结果保留根号)图8－ZT －2► 方法三 已知一边和一锐角的三角函数值解直角三角形5．2018·自贡改编如图8－ZT －3，在△ABC 中，CH ⊥AB 于点H ，BC ＝12，tan A ＝34，∠B ＝30°；求AC 和AB 的长．图8－ZT －36．如图8－ZT －4，在△ABC 中，∠ACB ＝90°，sin A ＝45，BC ＝8，D 是AB 的中点，过点B 作直线CD 的垂线，垂足为E .(1)求线段CD 的长； (2)求cos ∠DBE 的值．图8－ZT －4►方法四“化斜为直法”解三角形7．如图8－ZT－5，在△ABC中，∠A＝30°，∠B＝45°，AC＝2 3.求AB的长．图8－ZT－58．如图8－ZT－6，在△ABC中，CD是边AB上的中线，∠B是锐角，且sin B＝22，tan A＝12，AC＝3 5.(1)求∠B的度数及AB的长；(2)求tan∠CDB的值．图8－ZT －6► 方法五 “参数法”解直角三角形9．2018·马鞍山一模如图8－ZT －7，在△ABD 中，AC ⊥BD 于点C ，BC CD ＝32，E 是AB的中点，tan D ＝2，CE ＝1，求sin ∠ECB 的值和AD 的长．图8－ZT －7► 方法六 “等角代换法”解直角三角形10．2018·当涂县六校联考如图8－ZT －8，在四边形ABCD 中，AC ，BD 是它的对角线，相交于点O ，∠ABC ＝∠ADC ＝90°，∠BCD 是锐角，BD ＝BC .求证：sin ∠BCD ＝BD AC.图8－ZT －8► 方法七 “等比代换法”解直角三角形11．如图8－ZT －9所示，在平面直角坐标系xOy 中，直线AB 与x 轴、y 轴分别交于点B ，A ，与反比例函数的图象交于点C ，D ，CE ⊥x 轴于点E ，tan ∠ABO ＝12，OB ＝4，OE ＝2.(1)求该反比例函数的表达式；(2)求直线AB对应的函数表达式．图8－ZT－9教师详解详析1．解：(1)在Rt △ABC 中，由勾股定理，得a ＝c 2－b 2＝8－6＝ 2. ∵tan B ＝b a ＝62＝3，∴∠B ＝60°，∴∠A ＝90°－∠B ＝30°.(2)∵在△ABC 中，∠C ＝90°，a ＝4，b ＝4 3， ∴c ＝a 2＋b 2＝8.∵sin A ＝a c ＝48＝12，∴∠A ＝30°，∴∠B ＝90°－∠A ＝60°.2．解：∵AD ＝2，AC ＝3，∠C ＝90°， ∴cos ∠CAD ＝AC AD ＝32，∴∠CAD ＝30°.∵AD 为△BAC 的角平分线， ∴∠BAC ＝2∠CAD ＝60°，∴BC ＝AC ·tan ∠BAC ＝3×tan60°＝3×3＝3. ∵△ABC 是直角三角形，∴AB ＝BC 2＋AC 2＝9＋3＝2 3.3．解：(1)∠B ＝90°－∠A ＝90°－60°＝30°. ∵sin A ＝a c ，∴c ＝6sin60°＝632＝4 3.∵sin B ＝bc，∴b ＝4 3×sin30°＝4 3×12＝2 3.(2)∠B ＝90°－∠A ＝90°－30°＝60°. ∵tan A ＝ab，∴a ＝10 3×tan30°＝10 3×33＝10. ∵sin A ＝a c ，∴c ＝10sin30°＝1012＝20.4．解：在Rt △ADC 中，∵sin ∠ADC ＝ACAD ，∴AD ＝AC sin ∠ADC ＝3sin60°＝2，∴BD ＝2AD ＝4. ∵tan ∠ADC ＝ACDC ，∴DC ＝AC tan ∠ADC ＝3tan60°＝1，∴BC ＝BD ＋DC ＝5.在Rt △ABC 中，AB ＝AC 2＋BC 2＝2 7，∴△ABC 的周长＝AB ＋BC ＋AC ＝2 7＋5＋ 3. 5．解：在Rt △BCH 中，∵BC ＝12，∠B ＝30°， ∴CH ＝12BC ＝6，BH ＝BC 2－CH 2＝6 3.在Rt △ACH 中，tan A ＝34＝CHAH ，∴AH ＝8，∴AC ＝AH 2＋CH 2＝10，6．解：(1)在△ABC 中，∵∠ACB ＝90°， ∴sin A ＝BC AB ＝45.又∵BC ＝8，∴AB ＝10.∵D 是AB 的中点，∴CD ＝12AB ＝5.(2)在Rt △ABC 中，∵AB ＝10，BC ＝8， ∴AC ＝AB 2－BC 2＝6.∵D 是AB 的中点，∴BD ＝5，S △BDC ＝S △ADC ，∴S △BDC ＝12S △ABC ，即12CD ·BE ＝12·12AC ·BC ，∴BE ＝6×82×5＝245.在Rt △BDE 中，cos ∠DBE ＝BE BD ＝2455＝2425.7．解：过点C 作CD ⊥AB 于点D ，∴∠ADC ＝∠BDC ＝90°. ∵∠B ＝45°， ∴∠BCD ＝∠B ＝45°， ∴CD ＝BD .∵∠A ＝30°，AC ＝2 3， ∴CD ＝3， ∴BD ＝CD ＝ 3.由勾股定理，得AD ＝AC 2－CD 2＝3，答：AB 的长是3＋ 3.8．解：(1)如图，过点C 作CE ⊥AB 于点E .设CE ＝x .在Rt △ACE 中，∵tan A ＝CE AE ＝12，∴AE ＝2x ，∴AC ＝x 2＋（2x ）2＝5x ， ∴5x ＝3 5，解得x ＝3，∴CE ＝3，AE ＝6.在Rt △BCE 中，∵sin B ＝22，∴∠B ＝45°， ∴△BCE 为等腰直角三角形， ∴BE ＝CE ＝3，∴AB ＝AE ＋BE ＝9. (2)∵CD 是边AB 上的中线， ∴BD ＝12AB ＝4.5，∴DE ＝BD －BE ＝4.5－3＝1.5， ∴tan ∠CDE ＝CE DE ＝31.5＝2，即tan ∠CDB 的值为2. 9．解：∵AC ⊥BD ， ∴∠ACB ＝∠ACD ＝90°. ∵E 是AB 的中点，CE ＝1， ∴BE ＝CE ＝1，AB ＝2CE ＝2，∴∠B ＝∠ECB . ∵BC CD ＝32， ∴设BC ＝3x ，则CD ＝2x . 在Rt △ACD 中，tan D ＝2， ∴ACCD＝2， ∴AC ＝4x .在Rt △ACB 中，由勾股定理，得AB ＝AC 2＋BC 2＝5x ， ∴sin ∠ECB ＝sin B ＝AC AB ＝45.由AB ＝2，得x ＝25，∴AD ＝AC 2＋CD 2＝（4x ）2＋（2x ）2＝2 5x ＝2 5×25＝4 55.10．证明：如图，过点B 作AD 的垂线BE 交DA 的延长线于点E ，延长CB 与DA 交于点F .∵∠ABC ＝∠ADC ＝90°，∴∠ADC ＋∠ABC ＝180°，∠FBA ＝∠FDC ， ∴∠BCD ＋∠BAD ＝180°， ∠EAB ＝∠BCD .∵∠F ＝∠F ，∠FBA ＝∠FDC ， ∴△FBA ∽△FDC ，∴FB FD ＝F AFC ，∴FB F A ＝FD FC. ∵∠F ＝∠F ，∴△FBD ∽△F AC ，∴∠FDB ＝∠BCA . ∵∠BED ＝∠ABC ＝90°， ∴△BED ∽△ABC ，∴BD AC ＝BEAB＝sin ∠EAB ＝sin ∠BCD ， 即sin ∠BCD ＝BDAC.11．解：(1)∵OB ＝4，OE ＝2， ∴EB ＝OB ＋OE ＝6. ∵tan ∠ABO ＝AO OB ＝12＝CEEB ，∴CE ＝3，AO ＝2，∴A (0，2)，B (4，0)，C (－2，3)． 设反比例函数的表达式为y ＝kx .∵点C 在反比例函数的图象上， ∴将点C (－2，3)代入，得k ＝－6， 即反比例函数的表达式为y ＝－6x.(2)设直线AB 对应的函数表达式为y ＝k 1x ＋b .将A (0，2)，B (4，0)代入y ＝k 1x ＋b ，可得b ＝2，k 1＝－12，∴直线AB 对应的函数表达式为y ＝－12x ＋2.。

化“斜”为“直”转化思想在数学中应用十分的广泛，我们在解决数学问题时，常将陌生的问题转化为熟悉的问题，将复杂的问题转化为简单的问题，从而使问题获得解决，在解直角三角形时，许多问题中并不见直角三角形，而是通过构造直角三角形，即化“斜”为“直”的方法，将问题转化. 下面举例予以说明.例1 如图1，在四边形ABCD中，DC⊥BC，若AB=100，∠A=45°，∠ABD=75°，∠CBD=30°，求BC的长.【分析】此题含有两个三角形，其中一个不是直角三角形，可通过添加适当的辅助线（一般不破坏已知的特殊角），即过点B作BE⊥AD，垂足为E，从而化“斜”为“直”，将条件集中到Rt△ABE中来解决.解：过点B作BE⊥AD，垂足为E，在Rt△ABE中，∠A=45°，AB=100，sin45°=，所以BE=100×sin45°=50，∠ABE=45°，∵∠ABD=75°，∴∠DBE=∠CBD=30°，又BD=BD，∴△BCD ≌△BED，∴BC=BE=50.例2 如图2，在△ABC中，∠A=90°，AB=AC，D是AC 上的一点，且CD=3AD，求tan∠DBC的值.【分析】要求的∠DBC在斜三角形中，而tan∠DBC的值不能从给定的直角三角形中得到，故需将其转化到直角三角形中，作辅助线DE⊥BC，构造Rt△DBE来求tan∠DBC的值.在条件中没有给出有关线段的长度，于是将已知条件中的CD=3AD中的AD用参数k来表示，并对其“设而不求”，这是一种常用的方法，这样让字母来参与运算，应用方便.解：过点D作DE⊥BC，垂足为E，并设AD=k，DC=3k，则AB=AC=4k，因为∠A=90°，所以BC=AC=4k，又因为∠C=45°，所以∠EDC=45°，DE=EC，在Rt△DEC中，sin45°=，所以DE=3k×sin45°=k，所以EC=DE=k，所以BE=BC-EC=4k-k=k，所以在Rt△DBE中，tan∠DBC==.例3 已知，如图3，某班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC，他们首先在A点处测得建筑物CD的顶部D点的仰角为25°，然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′. 已知建筑物AB的高度为30米，求两建筑物的水平距离AC. （精确到0.1米）【分析】解题的关键是依据题意，通过作垂线构造两个直角三角形，利用三角函数将有关数据有机地联系起来.解：如图，过点D作DH⊥AB，垂足为H，设AC=x，在Rt△ACD中，∠ACD=90°，∠DAC=25°，所以CD=AC tan∠DAC=xtan25°，在Rt△BDH中，∠BHD=90°.∠BDH=15°30′，所以BH=DHtan15°30′=AC tan15°30′=xtan15°30′，又因CD=AH，AH+HB=AB，所以x（tan25°+tan15°30′）=30.所以x=≈40.3（米）.答：两建筑物的水平距离AC为40.3米.说明：解直角三角形的实际问题要注意两个转化：一是将实际问题转化为数学问题，二是将数学问题转化为解直角三角形问题. 此外掌握仰角、俯角的概念和一些特殊角的三角函数值也是解题的关键.小试身手要在宽为28 m的海堤公路的路边安装路灯. 路灯的灯臂长为3 m，且与灯柱成120°的角（如图4所示），路灯采用圆锥形灯罩，灯罩的轴线与灯臂垂直. 当灯罩的轴线通过公路路面的中线时，照明效果最理想. 问：应设计多高的灯柱，才能取得最理想的照明效果？（精确到0. 01 m，≈1.732）（作者单位：江苏省泗洪县第一实验学校）。

“高对于含有特殊角的斜三角形(锐角三角形和钝角三角形)的计算问题,直接求解往往比较困难,这时我们可以通过作高,将原三角形分割成含有特殊角的直角三角形,“化斜为直”后,即可轻松获解.例1（2010云南玉溪）在玉溪州大河旁边的路灯杆顶上有一个物体，它的抽象几何图形如图1，若60ABC10,AC4,AB=∠==, 求B、C两点间的距离.分析:△ABC是一个普通三角形，由于∠ABC=60°，考虑构造以∠ABC为内角的直角三角形，过A点作AD⊥BC于点D，BC被分成BD、CD两部分，分别解相应的三角形即可。

解：过A点作AD⊥BC于点D，在Rt△ABD中，∵∠ABC=60°，∴∠BAD=30°.∵AB=4,∴BD=2, ∴AD=23.在Rt△ADC中，AC=10，∴CD=22ADAC-=12100-=222 .∴BC=2+222 . 答：B、C两点间的距离为2+222.点评:作AD⊥BC于点D，将△ABC分成两个Rt△ABD和Rt△ADC是解本题的关键.例2（2010广西柳州）如图2，从热气球P上测得两建筑物A B、的底部的俯角分别为45°和30°，如果A B、两建筑物的距离为90m，P点在地面上的正投影恰好落在线段AB上，求热气球P的高度．（结果精确到0.01m1.7321.414）分析:过点P作PC⊥AB,PC即为所求，本题可以用方程思想，设PC=x,分别在直角三角形△APC和△BPC中，表示出AC=x,BC=x,即可列出方程：x=90,求出x．解：过点P作PC⊥AB设PC=x，在Rt △APC中，∠A=45°，所以，AC=PC= x在Rt △BPC中，∠B=30°，所以，tanB=tan30°=3，所以，BC=x∵AB=90∴C图2 45°30°解得：-45≈32.94答：热气球P 的高度约为32.94m.点评:在直角三角形中，选用恰当的三角函数求出有关的量或用含有未知数的式子表示有关的量进行求解。

证直角三角形的方法
证明一个三角形是直角三角形的方法有多种，主要有以下几种：
1. 利用勾股定理：如果一个三角形的三条边满足a^2 + b^2 = c^2，其中a, b,
c 分别为三角形的三边长度，那么这个三角形就是直角三角形。

2. 利用三角函数：如果一个三角形的两条边的长度a, b 和它们之间的夹角θ满足sin(θ) = a/c 或者sin(θ) = b/c，那么这个三角形就是直角三角形。

3. 利用相似三角形性质：如果一个三角形的两个内角分别为30度和60度，或者45度和45度，那么这个三角形就是直角三角形。

这是因为这些角度具有特殊的三角函数值，能够满足之前提到的三角函数条件。

4. 利用角平分线性质：如果一个三角形的一个角的角平分线与另外两条边相交，且与这两条边的交点分别到这两条边的距离为相等的长度，那么这个三角形就是直角三角形。

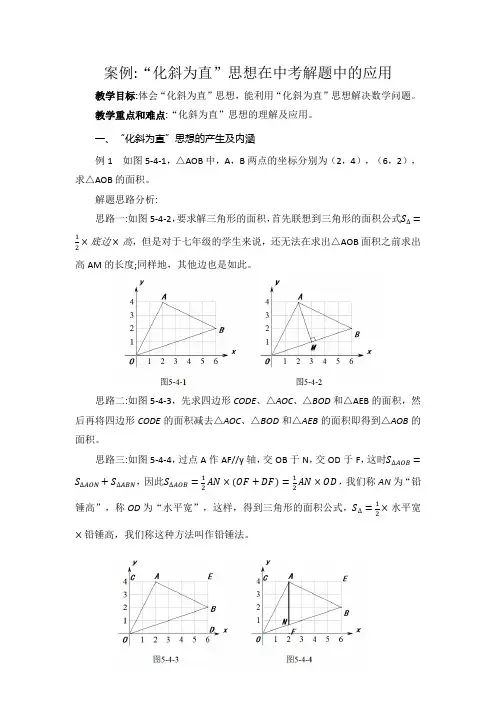
案例:“化斜为直”思想在中考解题中的应用教学目标:体会“化斜为直”思想，能利用“化斜为直”思想解决数学问题。

教学重点和难点:“化斜为直”思想的理解及应用。

一、“化斜为直”思想的产生及内涵例1 如图5-4-1，△AOB中，A，B两点的坐标分别为（2，4），（6，2），求△AOB的面积。

解题思路分析:思路一:如图5-4-2，要求解三角形的面积，首先联想到三角形的面积公式S∆=12×底边×高，但是对于七年级的学生来说，还无法在求出△AOB面积之前求出高AM的长度;同样地，其他边也是如此。

思路二:如图5-4-3，先求四边形CODE、△AOC、△BOD和△AEB的面积，然后再将四边形CODE的面积减去△AOC、△BOD和△AEB的面积即得到△AOB的面积。

思路三:如图5-4-4，过点A作AF//y轴，交OB于N，交OD于F，这时S∆AOB=S∆AON+S∆ABN，因此S∆AOB=12AN×(OF+DF)=12AN×OD，我们称AN为“铅锤高”，称OD为“水平宽”，这样，得到三角形的面积公式，S∆=12×水平宽×铅锤高，我们称这种方法叫作铅锤法。

问题解决反思:在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系。

点A（x1，y1）和B（x2，y2）如果满足AB //x轴（y1=y2）.则A、B两点间的距离公式由AB=√(x1−x2)2+(y1−y2)2变为AB=|x1−x2|,而点C（x3，y3）（不在直线AB上）到直线AB的距离为d=|y1−y3|；同样地如果AB//y轴，也有类似的结论。

结论: 在解决以平面直角坐标系为背景的问题中，我们往往可以通过“竖直方向”或者“水平方向”的线段关系解析倾斜的线段关系。

我们称这种解决思想为“化斜为直”思想。

在前面的案例中，思路一无法达成是因为在初中学段缺乏直接研究倾斜直线（线段）的利器，而思路二和思路三能顺利达成就是因为它们不去求各条倾斜的边长，把问题转化为求各条水平方向、竖直方向的线段的长度。

专训2“化斜为直”构造直角三角形的方法名师点金：锐角三角函数是在直角三角形中定义的，解直角三角形的前提是在直角三角形中进行，对于非直角三角形问题，要注意观察图形特点，恰当作辅助线，将其转化为直角三角形来解．无直角、无等角的三角形作高1．如图，在△ABC中，已知BC＝1＋3，∠B＝60°，∠C＝45°，求AB的长．(第1题)有直角、无三角形的图形延长某些边2．如图，在四边形ABCD中，AB＝2，CD＝1，∠A＝60°，∠D＝∠B＝90°，求四边形ABCD的面积．(第2题)有三角函数值不能直接利用时作垂线3．如图，在△ABC 中，点D 为AB 的中点，DC ⊥AC ，sin ∠BCD ＝13，求tan A 的值．(第3题)求非直角三角形中角的三角函数值时构造直角三角形4．如图，在△ABC 中，AB ＝AC ＝5，BC ＝8.若∠BPC ＝12∠BAC ，求tan ∠BPC 的值．(第4题)答案1．解：如图，过点A 作AD ⊥BC ，垂足为点D.设BD ＝x ，在Rt △ABD 中，AD ＝BD·tan B ＝x·tan 60°＝3x.在Rt △ACD 中，∵∠C ＝45°，∴∠CAD ＝90°－∠C ＝45°，∴∠C ＝∠CAD ，∴CD ＝AD ＝3x.∵BC ＝1＋3，∴3x ＋x ＝1＋3，解得x ＝1，即BD ＝1.在Rt △ABD 中，∵cos B ＝BD AB， ∴AB ＝BD cos B ＝1cos 60°＝2.(第1题)(第2题)2．解：如图，延长BC ，AD 交于点E.∵∠A ＝60°，∠B ＝90°，∴∠E ＝30°.在Rt △ABE 中，BE ＝AB tan E ＝2tan 30°＝23， 在Rt △CDE 中，EC ＝2CD ＝2，∴DE ＝EC·cos 30°＝2×32＝ 3. ∴S 四边形ABCD ＝S Rt △ABE －S Rt △ECD ＝12AB·BE －12CD·ED ＝12×2×23－12×1×3＝332. 点拨：本题看似是四边形问题，但注意到∠B ＝90°，∠A ＝60°，不难想到延长BC ，AD 交于点E ，构造出直角三角形，将所求问题转化为直角三角形问题来解决．3．解：如图，过点B 作BE ⊥CD ，交CD 的延长线于点E.∵点D 是AB 的中点，∴AD ＝DB.又∵∠ACD ＝∠BED ＝90°，∠ADC ＝∠BDE ，∴△ACD ≌△BED ，∴CD ＝DE ，AC ＝BE.在Rt △CBE 中，sin ∠BCE ＝BE BC ＝13，∴BC ＝3BE. ∴CE ＝BC 2－BE 2＝22BE ，∴CD ＝12CE ＝2BE ＝2AC. ∴tan A ＝CD AC ＝2AC AC＝ 2. 点拨：构造直角三角形，把所要求的量与已知量建立关系是解题的关键．(第3题)(第4题)4．解：如图，过点A 作AE ⊥BC 于点E ， ∵AB ＝AC ＝5，∴BE ＝12BC ＝12×8＝4，∠BAE ＝12∠BAC. ∵∠BPC ＝12∠BAC ，∴∠BPC ＝∠BAE. 在Rt △BAE 中，由勾股定理得AE ＝AB 2－BE 2＝52－42＝3，∴tan ∠BPC ＝tan ∠BAE ＝BE AE ＝43.。

重庆数学中考专题：几何图形的相关证明及计算类型五：构造直角三角形方法点拨：（1）若三角形两边相等，且一边所对的角为45°，即为等腰直角三角形，可考虑过直角顶点向斜边作垂线构造直角三角形；（2）若遇到中点可想到若一条边上的中线等于该边的一般的三角形为直角三角形，构造直角三角形。

例：如图1，已知△ABC中，∠ABC=45°，点E为AC上的一点，连接BE，在BC上找一点G，使得AG=AB，AG交BE于K．（1）若∠ABE=30°，且∠EBC=∠GAC，BK=4，求AC的长度．（2）如图2，过点A作DA⊥AE交BE于点D，过D、E分别向AB所在的直线作垂线，垂足分别为点M、N，且NE=AM，若D为BE的中点，证明：DG=2AG．针对演练：如图，四边形为矩形，连接，点在边上。

（1）如图1，若，求的面积；（2）如图2，延长至点使得，连接并延长交于点，过点作于点，连接，求证：；2、(2017• 重庆模拟)已知△ABC和△ADE都是等边三角形,点B,D,E同一在一条直线上.(1)如图1,当AC⊥DE,且 AD=2时,求线段BC的长度;(2)如图2,当且CD⊥BE时,取线段BC的中点F,线段DC的中点G,连接DF,EG,求证:DF=EG2、如图1，在Rt△ABC中，∠ACB=90°，D为CB上一点，且满足CD=CA，连接AD．过点C作CE⊥AB于点E．（1）若AB=10，BD=2，求CE的长；（2）如图2，若点F是线段CE延长线上一点，连接FD，若∠F=30°，求证：3、如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC 上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE(1)若∠EBD=15°,求∠ADF;(2)求证:BE-AE=DF备用图4、如图，在等腰直角△ABC中，AB=AC，∠BAC=90°，点D为AC上一点，连接BD，过C点作BD的垂线交BD的延长线于点E，连接AE，过点A作AF⊥AE交BD于点F，连接CF.5、如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC的延长线上，连接AD，过点B作BE⊥AD。

指向核心素养的中考专题复习课教学改进研究——以“‘化斜为直’在平面直角坐标系中的应用”为例
何珠瑜;杨文
【期刊名称】《中学数学教学参考》
【年(卷),期】2024()5
【摘要】"化斜为直"是解决平面直角坐标系中函数问题的重要思想方法之一。

以直线的斜率与直角三角形中的边角关系为起点,引导学生通过构建直角三角形,通过化"斜"为"直"、化陌生为熟悉、化未知为已知实现知识的迁移应用。

【总页数】3页(P60-62)
【作者】何珠瑜;杨文
【作者单位】四川省成都市七中育才学校;四川省成都市七中育才学校华兴分校【正文语种】中文
【中图分类】G63
【相关文献】
1.——以"平面直角坐标系"一课为例基于学科核心素养的概念教学
2.核心素养下的中考数学专题复习例题及作业设计研究——以“与圆有关的位置关系”专题复习课为例
3.知识“点”,方法“线”,思想“面”——九年级《平面直角坐标系中的“点”》专题复习课教学实录
4.基于基本图形教学的专题复习课——平面直角坐标系中的图形变换(翻折)
5.基于“336”互动教学模式的初中数学教学策略探究——以《平面直角坐标系》复习课为例
因版权原因，仅展示原文概要，查看原文内容请购买。

专训2 “化斜为直”构造直角三角形的方法名师点金:锐角三角函数是在直角三角形中定乂的，解直角三角形的称提是在直角三角形中进行, 对于非直角三角形问题，要注意观察图形特点，恰当作捕助线，将其转化为直角三角形来解. ［龙徐・！无宣角.无等角的三角形作高L 如图，在△ABC 中•已知 BC=1+71 ZB=6O\ ZC=45% 求 AB 的长.［方济Z 有直角、无三角形的图形延长某些边2.如图，在四边形 ABCD 中，AB=2, CD=1, ZA=60^ ZD=ZB=90。

，求四边 形ABCD 的而积.魏壬有三角函数值不能直接利用时作垂线3.如图，在^ABC 中，点D 为AB 的中点，DC 丄AC, sht ZBCD=^,求他” A 的值.::多決4求非直角三角形中角的三角函数值时构造直角三角形4.如图，在△ABC 中，AB=AC=5, BC = &若ZBPC=^ZBAC,求 tan ZBPC 的值.14答案1.解：如图，过点A 作AD 丄BC,垂足为点D ・设 BD=X,在 /?『△ ABD 中，AD=BD-tan B=x- tan 60°=75x ・ 在 /??AACD 中，7ZC=45^•••ZCAD=90°-ZC=45Q,•••ZC=ZCAD, •••CD=AD=伍.TBC=1+皿 Wx+x=l+e 解得X=lr 即BD=1・RD在 /??AABD 中，7ewB=^,cos 60° 2・AR 7在心MBE 中，BEr ；^=^=2©,在 /?rACDE 中，EC = 2CD=2,.*.DE=EC CO 5 30^=2X^=A /3.111 13AS w 边形 ABCD=SRrABE —S R 小 ECD =T AB ・BE —云 D ・ED=2X2X2萌—2X 1 点拨：本题看似是四边形问题，但注意到ZB=90\ ZA=60。

，不难想到延长BC, AD 交于点E,构造出宜角三角形，将所求问题转化为直角三角形问题来解决.3.解：如图，过点B 作BE 丄CD.交CD 的延长线于点E「点D 是AB 的中点，•••AD=DB ・又TZACD=ZBED=90°, ZADC=ZBDE ・AAACD^ABED, ACD=DE> AC=BEBE 1在心^CBE 中.M«ZBCE=g^=矛•••BC=3BE ・ACE=^/B C--BE-=2A /2BE.2.解：如图, ••'ZA=60°,延长BC, AD 交于点E ・ZB=90°, •••ZE=30°・/.CD=|CE=V2BE=V2AC点拨：构造直角三角形，把所要求的量与已知量建立关系是解题的关键.4.解：如图，过点A作AE丄BC于点E.VAB=AC=5.•••BE=-BC=2X8=4, ZBAEpZBAC.VZBPC=^ZBAC, •••ZBPC=ZBAE・在RfMAE中，由勾股；4^理得AE=^/A B2-BE2=>/52_42=3,/.tan ZBPC=Z«/i ZBAE=||=|。