相对论质点力学方程
- 格式:ppt
- 大小:2.94 MB
- 文档页数:2

狭义相对论中力学的基本方程全文共四篇示例,供读者参考第一篇示例:狭义相对论是物理学中的一个分支,描述了高速运动的物体和引力场中的物体之间的相互作用。
在狭义相对论中,力学是一个重要的研究领域,它涉及物体的运动和受力情况。
在狭义相对论中,力学的基本方程是描述物体受力和运动的数学公式。
本文将介绍狭义相对论中力学的基本方程。
我们需要了解狭义相对论的基本原理。
狭义相对论是由爱因斯坦在1905年提出的,它与经典力学和牛顿力学有着本质上的不同。
在狭义相对论中,时间和空间是相互联系的,物体的运动速度越快,时间的流逝速度就越慢。
质量也受速度影响,质量随着速度的增加而增加。
这些原理对力学方程的推导和理解具有重要意义。
在狭义相对论中,最基本的力学公式是质点的动力学方程,即狭义相对论的牛顿第二定律。
这个方程描述了物体的加速度与受力之间的关系。
在经典力学中,牛顿第二定律可以写成F=ma,其中F是物体所受的合力,m是物体的质量,a是物体的加速度。
在狭义相对论中,这个公式需要进行修正,考虑到了速度的影响。
质点的动力学方程可以写成:F = dp/dt其中F是物体所受的合力,p是物体的动量,t是时间。
这个方程描述了力对物体动量的影响。
在狭义相对论中,动量与速度有关,动量可以表示为p=mv,其中m是物体的质量,v是物体的速度。
动力学方程可以进一步展开为:F = d(mv)/dt = m(dv/dt) + v(dm/dt)这个方程描述了力对速度的影响,考虑了速度的变化对质量的影响。
当物体的速度接近光速时,质量变化会导致动量的变化,从而影响物体的受力情况。
除了动力学方程,狭义相对论中还有能量方程和动量守恒定律。
能量方程描述了物体的能量与受力之间的关系,可以写成:E = mc^2其中E是物体的能量,m是物体的质量,c是光速。
这个方程描述了质量和能量之间的等价关系,也是相对论力学中的基本方程之一。
动量守恒定律描述了物体在瞬时碰撞过程中动量守恒的原理。

狭义相对论公式及证明单位符号单位符号坐标: m (x, y, z) 力: N F(f)时间: s t(T) 质量:kg m(M)位移: m r 动量:kg*m/s p(P)速度: m/s v(u) 能量: J E加速度: m/s^2 a 冲量:N*s I长度: m l(L) 动能:J E k路程: m s(S) 势能:J E p角速度: rad/s ω力矩:N*m M角加速度:rad/s^2α功率:W P一:牛顿力学(预备知识)(一):质点运动学基本公式:(1)v=dr/dt, r=r0+∫rdt(2)a=dv/dt, v=v0+∫adt(注:两式中左式为微分形式,右式为积分形式)当v不变时,(1)表示匀速直线运动。
当a不变时,(2)表示匀变速直线运动。
只要知道质点的运动方程r=r(t),它的一切运动规律就可知了。
(二):质点动力学:(1)牛一:不受力的物体做匀速直线运动。
(2)牛二:物体加速度与合外力成正比与质量成反比。
F=ma=mdv/dt=dp/dt(3)牛三:作用力与反作与力等大反向作用在同一直线上。
(4)万有引力:两质点间作用力与质量乘积成正比,与距离平方成反比。
F=GMm/r2,G=6.67259*10-11m3/(kg*s2)动量定理:I=∫Fdt=p2-p1(合外力的冲量等于动量的变化)动量守恒:合外力为零时,系统动量保持不变。
动能定理:W=∫Fds=E k2-E k1(合外力的功等于动能的变化)机械能守恒:只有重力做功时,E k1+E p1=E k2+E p2(注:牛顿力学的核心是牛二:F=ma,它是运动学与动力学的桥梁,我们的目的是知道物体的运动规律,即求解运动方程r=r(t),若知受力情况,根据牛二可得a,再根据运动学基本公式求之。
同样,若知运动方程r=r(t),可根据运动学基本公式求a,再由牛二可知物体的受力情况。
)二:狭义相对论力学:(注:γ=1/sqr(1-u2/c2),β=u/c, u为惯性系速度。





第五篇相对论第一章狭义相对论第一节狭义相对论产生的背景【知识框架】一、狭义相对论产生的背景绝对时空理论和力学相对性原理;麦克斯韦电磁理论与旧物理学原理的矛盾。
二、迈克尔孙-莫雷实验迈克尔孙-莫雷实验;对迈克尔孙-莫雷实验零结果的解释。
【核心内容】一、狭义相对论产生的背景1.绝对时空理论和力学相对性原理(1)绝对时空理论①绝对空间绝对空间是指长度的量度与参考系无关。
②绝对时间绝对时间是指时间的量度和参考系无关。
注:同样两点间的距离或同样的前后两个事件之间的时间,无论在哪个惯性系中测量都是一样的;时间和空间的量度是相互独立的。
(2)力学相对性原理牛顿相对性原理或力学相对性原理,又称伽利略不变性是指在任何惯性系中观察,同一力学现象将按同样的形式发生和演变。
2.麦克斯韦电磁理论与旧物理学原理的矛盾在电磁感应现象中,只是磁体和线圈的相对运动决定线圈内产生的感生电动势。
对于不同的惯性系,电磁现象的基本规律的形式是一样的吗?如果用伽利略变换对电磁现象的基本规律进行变换,发现这些规律对不同的惯性系并不具有相同的形式。
就这样,伽利略变换和电磁现象符合相对性原理的设想发生了矛盾。
在这个问题中,光速的数值起了特别重要的作用。
以c 表示在某一参考系S 中测得的光在真空中的速率,以c′表示在另一参考系S′中测得的光在真空的速率,如果根据伽利略变换,就应该有c′=c±u式中u 为S′相对于S 的速度,他前面的正负号由c 和u 的方向相反或相同而定。
但是麦克斯韦的电磁场理论给出的结果与此不相符,该理论给出的光在真空中的速率c =其中,ε0=6.85×10-12C 2·N -1·m -2(或F/m),μ0=1.26×10-6N·s 2·C -2(或H/m)是两个电磁学常量。
将这两个值代入上式,可得c=2.99×108m/s。
这就是说任何参考系内测的光在真空中的速率都应该是这一数值。



1广义相对论:R_uv-1/2×R×g_V=κ×T_V2狭义相对论:S(R4,ηαβ)三个。
相对速度公式:△v=| v1-v2 |/√(1-v1v2/c^2)4相对长度公式L=Lo*√(1-v^2/c^2)Lo5相对质量公式M=Mo/√(1-v^2/c^2)Mo6相对时间公式t=to*√(1-v^2/c^2)to7质能方程E=mc^2相对论是一个关于时空和引力的理论,主要由爱因斯坦创立。
根据研究对象的不同,可以分为狭义相对论和广义相对论。
相对论和量子力学给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
相对论极大地改变了人类对宇宙和自然的“常识”概念,提出了“同时相对论”、“四维时空”、“弯曲时空”等新概念。
然而,近年来,人们对物理理论的分类有了新的认识。
经典物理和非经典物理按其理论是否确定来划分,即“非经典=量子”。
从这个意义上说,相对论仍然是一个经典理论。
扩展信息:狭义相对论与广义相对论的区别传统上,在爱因斯坦提出相对论的早期,人们用非惯性参照系作为狭义相对论和广义相对论分类的标志。
随着相对论的发展,这种分类方法越来越暴露出它的缺点:参照系与观察者有关,利用这样一个相对的物理对象对物理理论进行分类被认为不能反映问题的本质。
目前,人们普遍认为狭义相对论与广义相对论的区别在于所讨论的问题是否涉及引力(弯曲时空),即狭义相对论只处理没有引力效应或可忽略不计的问题,而广义相对论则讨论引力效应。
物理学。
在相对论的语言中,狭义相对论的背景时空是平坦的,即四维平凡流型与Min的度量相匹配,其曲率张量为零,也称为最小时空;广义相对论的背景时空是弯曲的,其曲率张量不为零。
单位符号坐标:m (x, y, z)力:N F(f)时间:s t(T)质量:kg m(M)位移:m r 动量: kg*m/s p(P)速度:m/s v(u)能量:J E加速度:m/s^2 a 冲量:N*s Ixx:m l(L)动能:J Ek路程:m s(S)势能:J Ep角速度:rad/s ω力矩:N*m M角加速度:rad/s^2α功率:W P一:xx力学(预备知识)(一):质点运动学基本公式:(1)v=dr/dt, r=r0+∫rdt(2)a=dv/dt,v=v0+∫adt(注:两式中左式为微分形式,右式为积分形式)当v不变时,(1)表示匀速直线运动。
当a不变时,(2)表示匀变速直线运动。
只要知道质点的运动方程r=r(t),它的一切运动规律就可知了。
(二):质点动力学:(1)xx:不受力的物体做匀速直线运动。
(2)xx:物体加速度与合外力xx与质量成反比。
F=ma=mdv/dt=dp/dt(3)xx:作用力与反作与力等大反向作用在同一直线上。
(4)万有引力:两质点间作用力与质量乘积成正比,与距离平方成反比。
F=GMm/r2,G=6.67259*10-11m3/(kg*s2)动量定理:I=∫Fdt=p2-p1(合外力的冲量等于动量的变化)动量守恒:合外力为零时,系统动量保持不变。
动能定理:W=∫Fds=Ek2-Ek1(合外力的功等于动能的变化)机械能守恒:只有重力做功时,Ek1+Ep1=Ek2+Ep2(注:牛顿力学的核心是牛二:F=ma,它是运动学与动力学的桥梁,我们的目的是知道物体的运动规律,即求解运动方程r=r(t),若知受力情况,根据牛二可得a,再根据运动学基本公式求之。
同样,若知运动方程r=r(t),可根据运动学基本公式求a,再由牛二可知物体的受力情况。
)二:狭义相对论力学:(注:γ=1/sqr(1-u2/c2),β=u/c, u为惯性系速度。
)(一)基本原理:(1)相对性原理:所有惯性系都是等价的。
相对论公式大全一、狭义相对论基本公式。
1. 洛伦兹变换公式。
- 坐标变换。
- 在两个相对做匀速直线运动的惯性系S(x,y,z,t)和S'(x',y',z',t')中,设S'系相对于S系沿x轴正方向以速度v运动,且当t = t'=0时两坐标系原点重合。
- x'=(x - vt)/(√(1-frac{v^2)){c^{2}}}- y' = y- z'=z- t'=(t-frac{v)/(c^2)x}{√(1 - (v^2))/(c^{2)}}- 其逆变换为:- x=(x'+vt')/(√(1-frac{v^2)){c^{2}}}- y = y'- z = z'- t=(t'+frac{v)/(c^2)x'}{√(1-(v^2))/(c^{2)}}- 速度变换。
- 在上述两个惯性系中,设物体在S系中的速度分量为u_x,u_y,u_z,在S'系中的速度分量为u_x',u_y',u_z'。
- u_x'=frac{u_x-v}{1-frac{u_xv}{c^2}}- u_y'=frac{u_y√(1-(v^2))/(c^{2)}}{1-frac{u_xv}{c^2}}- u_z'=frac{u_z√(1-(v^2))/(c^{2)}}{1-frac{u_xv}{c^2}}- 逆变换为:- u_x=frac{u_x'+v}{1 +frac{u_x'v}{c^2}}- u_y=frac{u_y'√(1-(v^2))/(c^{2)}}{1+frac{u_x'v}{c^2}}- u_z=frac{u_z'√(1-(v^2))/(c^{2)}}{1+frac{u_x'v}{c^2}}2. 时间延缓效应(钟慢效应)公式。
相对论中的向心力
在相对论中,向心力是指一个质点在曲线运动中体验到的力,使其朝向运动轨迹的中心点。
根据相对论的观点,运动物体会经历时空的弯曲,因此,在曲线运动中,质点将受到向心力的作用。
向心力的大小由质点的质量和速度来决定,具体表达式为:
F = mv²/R
其中,F是向心力,m是质点的质量,v是质点的速度,R是曲线运动的半径。
根据这个公式可以看出,当质点的速度增加或者半径减小时,向心力将变大。
需要注意的是,在相对论中,向心力不是一个真正的力,而是因为时空的弯曲所产生的一种效应。
这与牛顿力学中的向心力概念有所不同。
在相对论中,向心力只是描述质点在曲线运动中的力效果,而并不是由一个真正的力源产生的力。
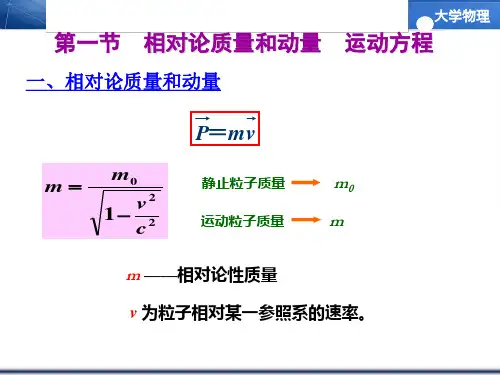
相对论质量方程全文共四篇示例,供读者参考第一篇示例:相对论质量方程是相对论中的一个基本公式,描述了当一个物体运动时其质量会发生变化。
这个方程是爱因斯坦在提出狭义相对论的基础上,通过研究能量和动量之间的关系得出的。
在传统物理学中,质量被认为是一个固定不变的量,而相对论质量方程则揭示了物体的质量会随着其速度的变化而发生变化的事实。
相对论质量方程的表示形式为:\[ m = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \]\(m\) 代表物体的相对论质量,\(m_0\) 代表物体的静止质量,\(v\) 代表物体的速度,\(c\) 代表光速。
从这个公式中我们可以看出, 当物体的速度接近光速时,其相对论质量将趋近于无穷大,这也意味着能够以光速运动的物体的质量将无限增加。
相对论质量方程的推导过程涉及到许多复杂的数学和物理概念,但可以通过简单的例子来理解其基本原理。
假设有一个静止的质量为1 千克的物体,如果它以0.8 光速运动,根据相对论质量方程我们可以计算出其相对论质量为这意味着当物体以0.8 光速运动时,其质量将增加为原来的1.67 倍。
这种相对论质量的增加是因为物体的运动能量被转化为了质量,符合质能等价原理的基本思想。
相对论质量方程的重要性在于揭示了物体的质量和速度之间的关系,并为研究高速运动物体和引力场中的物体提供了重要的理论基础。
在实际应用中,相对论质量方程在核反应和粒子加速器等领域发挥着重要作用,帮助科学家们理解物质的本质和力量的本质。
相对论质量方程是相对论物理学中一个重要的基础公式,帮助我们理解物质运动的本质和宇宙中的基本规律。
通过深入研究和应用这个方程,我们可以更深入地了解物理学的奥秘,为人类认识宇宙和改变世界提供了强大的理论工具。
【2000字】第二篇示例:相对论质量方程是相对论中基本的物理方程之一,它描述了质量随着物体运动速度的增加而变化的情况。
相对论质量方程的提出和发展,对于我们理解物质的运动规律和能量转化过程有着重要意义。
相对论质量方程全文共四篇示例,供读者参考第一篇示例:相对论质量方程是相对论物理中非常重要的一个概念,它描述了质量随速度变化的规律。
在相对论物理中,质量不再是一个不变的量,而是一个与速度相关的量。
这个概念是由爱因斯坦在提出狭义相对论的过程中引入的,它揭示了质量与能量之间的关系和质量随速度增加而增加的规律。
在经典物理学中,质量是一个固定不变的量,它只取决于物体的性质和组成。
一个质量为1千克的物体,不管它处于静止状态还是运动状态,它的质量都是不变的。
但是在相对论物理中,质量不再是一个固定不变的量,而是一个动态的变量,它随着速度的增加而变化。
相对论质量方程可以用数学公式表示为:\[m = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\]m是相对论质量,\(m_0\)是静止质量,v是物体相对于观察者的速度,c是光速。
从这个公式可以看出,当物体的运动速度接近光速时,相对论质量会变得非常大,接近无穷大。
这说明质量不再是一个固定的量,而是一个随速度变化的变量。
这个现象被称为“质量增加效应”,它解释了为什么质子在高速环境下会变得更重。
相对论质量方程的推导主要依赖于狭义相对论的基本原理,即光速不变原理。
根据这个原理,光速在所有惯性参考系中都是不变的,不受观察者的运动状态影响。
在相对论物理中,质量与速度之间的关系必须遵守光速不变原理。
实际上,相对论质量方程不仅适用于物体的质量,还适用于它的能量。
根据质能关系公式\(E=mc^2\),能量与质量也是密切相关的。
相对论质量方程不仅描述了质量与速度之间的关系,还揭示了能量与质量之间的等价性。
相对论质量方程的应用非常广泛,它在核物理、粒子物理、宇宙学等领域中都有重要的意义。
在加速器实验中,科学家们可以通过测量粒子在高速碰撞中的质量增加效应来验证相对论质量方程的正确性。
在宇宙学中,相对论质量方程也有助于解释夸克星、黑洞等天体中的奇特现象。
第二篇示例:相对论质量方程,也称为质能关系,是相对论力学中的一个基本方程,描述了能量和质量之间的关系。