依据全等三角形的旋转难题

初二数学全等三角形双等腰旋转 易错题难题质量专项训练一、全等三角形双等腰旋转1．在正方形ABCD 中，对角线AC 、BD 交于点O ，以BC 为斜边作直角三角形BCP ，连接OP ．（1）如图所示，易证：2CP BP OP =+；（2）当点P 的位置变换到如第二幅图和第三幅图所示的位置时，线段CP 、BP 、OP 之间又有怎样的数量关系？请写出你的猜想，并对第二幅图加以证明．答案：（1）见解析；（2）第二幅图：，第三幅图：【分析】（1）在CP 上截取CE=BP ，连接OE ，记OB 与CP 交于点F ，根据正方形的性质证明，得到是等腰直角三角形，所以有，从而证得；（2）第二幅图的证解析：（1）见解析；（2）第二幅图：2BP CP OP =+，第三幅图：2BP CP OP +=【分析】 （1）在CP 上截取CE=BP ，连接OE ，记OB 与CP 交于点F ，根据正方形的性质证明()OCE OBP SAS ≅，得到EOP △是等腰直角三角形，所以有2PE OP =，从而证得2CP CE PE BP OP =+=；（2）第二幅图的证明过程类似（1）中的证明过程，在BP 上截取BE=CP ，连接OE ，记OC 与BP 交于点F ，证明()OBE OCP SAS ≅，得到OEP 是等腰直角三角形，可以证得2BP CP OP =+；第三幅图的结论是2BP CP OP +=，证明方法一样是构造三角形全等，由()OBE OCP SAS ≅可以证出结论．【详解】解：（1）如图，在CP 上截取CE=BP ，连接OE ，记OB 与CP 交于点F ，∵四边形ABCD 是正方形，∴OB=OC ，90BOC ∠=°，∵BP CP ⊥，∴90BOC BPC ∠=∠=︒，∵OFC PFB ∠=∠，∴OCE OBP ∠=∠，在OCE △和OBP 中，OC OB OCE OBP CE BP =⎧⎪∠=∠⎨⎪=⎩，∴()OCE OBP SAS ≅，∴OE OP =，COE BOP ∠=∠，∵BOC BOE COE ∠=∠+∠，EOP BOE BOP ∠=∠+∠，∴90EOP BOC ∠=∠=︒，∴EOP △是等腰直角三角形， ∴2PE OP =， ∴2CP CE PE BP OP =+=；（2）第二幅图：2BP CP OP =+， 第三幅图：2BP CP OP +=， 证明第二幅图的结论：如图，在BP 上截取BE=CP ，连接OE ，记OC 与BP 交于点F ，同（1）中证明()OCE OBP SAS ≅的过程证明()OBE OCP SAS ≅，同理OEP 是等腰直角三角形， ∴2EP OP =， ∴2BP BE EP CP OP =+=；第三幅图的证明过程是：如图，延长PB 至点E ，使BE=CP ，证明()OBE OCP SAS ≅，得到OEP 是等腰直角三角形， ∴2EP OP =， ∵EP EB BP CP BP =+=+， ∴2OP CP BP =+．【点睛】本题考查全等三角形的性质和判定，等腰直角三角形的性质和进行的性质，解题的关键是掌握这些性质定理进行证明求解，并且学会构成全等三角形的方法．2．（1）如图①，在直角ABC 中，90BAC ∠=︒，AB AC =，点D 为BC 边上一动点（与点B 不重合），连接AD ，将ABD △绕点A 逆时针旋转90︒，得到ACE △，那么,CE BD 之间的位置关系为__________，数量关系为__________；（2）如图②，在ABC 中，90BAC ∠=︒，AB AC =，D ，E （点D ，E 不与点B ，C 重合）为BC 上两动点，且45DAE ∠=︒．求证：222BD CE DE +=．（3）如图③，在ABC 中，120CAB ∠=︒，AB AC =，60DAE ∠=︒，33BC =+，D ，E （点D ，E 不与点B ，C 重合）为BC 上两动点，若以,,BD DE EC 为边长的三角形是以BD 为斜边的直角三角形时，求BE 的长．答案：（1）CE ⊥BD ；CE=BD ；（2）见解析；（3）．【分析】（1）根据，AD=AE ，运用SAS 证明，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE 、BD 之间的关系；（2）把绕点解析：（1）CE ⊥BD ；CE=BD ；（2）见解析；（3）BE 23=+．【分析】 （1）根据D CAE BA ∠=∠，AD=AE ，运用SAS 证明ABD ACE ≅，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE 、BD 之间的关系；（2）把ACE 绕点A 顺时针旋转90︒，得到 ABG ，连接DG ，由SAS 得到ADG ADE ≅，可得DE=DG ，即可把EF 、BE 、FC 放到一个直角三角形中，从而根据勾股定理即可证明；（3）把AEC 绕点A 顺时针旋转120︒，得到AFB ，可得AF=AE ，ABF ACB ∠=∠，EC=BF ，EAF 120∠=︒，由SAS 可证ADE ADF ≅，可得DF=DE ，由以BD 、DE 、EC 为边的三角形是直角三角形，分两种情况讨论，由直角三角形的性质可求解．【详解】解：（1）CE 与BD 位置关系是CE ⊥BD ，数量关系是CE=BD∵ABD △绕点A 逆时针旋转90︒，得到ACE △∴DAE 90BAC ∠=∠=︒∴D 90DAC BA ∠=︒-∠，CAE 90DAC ∠=︒-∠∴D CAE BA ∠=∠∵BA=CA ，AD=AE∴ABD ACE ≅∴ACE 45B ∠=∠=︒且CE=BD∵ACB 45B ∠=∠=︒∴ECB=4545=90∠︒+︒︒，即CE ⊥BD故答案为：CE ⊥BD ；CE=BD ；（2）如图②，把ACE 绕点A 顺时针旋转90︒，得到ABG ，连接DG ，则ACE ABG ≅∴AG=AE ，BG=CE ，ABG ACF 45∠=∠=︒∵BAC 90∠=︒，GAE 90∠=︒∴GAD DAE 45∠=∠=︒在ADG 和ADE 中，AG AE GAD DAE AD AD =⎧⎪∠=∠⎨⎪=⎩∴ADG ADE ≅∴ED=GD∵GBD 90∠=︒ ∴222BD BG DG +=即222BD EC DE +=（3）如图③，把AEC 绕点A 顺时针旋转120︒，得到AFB ，∴AEC AFB ≅∴AF=AE ，ABF ACB ∠=∠，EC=BF ，EAF 120∠=︒∵CAB 120∠=︒，AB=AC∴ABC ACB ABF 30∠=∠=∠=︒∴FBD 60∠=︒∵EAF 120∠=︒，EAD 60∠=︒∴DAE DAF 60∠=∠=︒，且AF=AE ，AD=AD∴ADE ADF ≅∴DF=DE∵以BD 、DE 、EC 为边的三角形是直角三角形∴以BD 、DF 、BF 为边的三角形是直角三角形∴BDF 是直角三角形若BDF 90∠=︒，且FBD 60∠=︒ ∴BF=2BD=EC ，DF 3BD DE == ∵(BC BD DE EC BD 2BD 33333BD BD =++=++==+∴BD 1= ∴DE 3=∴BE BD DE 13=+=若BFD 90∠=︒，且FBD 60∠=︒∴BD=2BF=2EC ，DF 3BF DE ==∵()BC BD DE EC 2BF BF 33333BF BF =++=++=+=+∴BF 1=∴BD=2，DE 3=∴BE 23=+【点睛】此题是几何变换综合题，考查了等腰三角形的性质、全等三角形的判定和性质、旋转的性质、勾股定理，添加恰当辅助线构造全等三角形是本题的关键．3．如图，ABC 是等腰直角三角形，90,ACB ∠=︒分别以,AB AC 为直角边向外作等腰直角ABD △和等腰直角,ACE G 为BD 的中点，连接,,CG BE ,CD BE 与CD 交于点F ．（1）证明：四边形ACGD 是平行四边形；（2）线段BE 和线段CD 有什么数量关系，请说明理由；（3）已知2,BC =求EF 的长度(结果用含根号的式子表示)．答案：（1）见解析；（2）BE=CD ，理由见解析；（3）EF= ．【分析】（1）利用等腰直角三角形的性质易得BD=2BC ，因为G 为BD 的中点，可得BG=BC ，由∠CGB=45°，∠ADB=45得AD ∥解析：（1）见解析；（2）BE =CD ，理由见解析；（3）EF 3105【分析】（1）利用等腰直角三角形的性质易得BD=2BC ，因为G 为BD 的中点，可得BG=BC ，由∠CGB=45°，∠ADB=45得AD ∥CG ，由∠CBD+∠ACB=180°，得AC ∥BD ，得出四边形ACGD 为平行四边形；（2）利用全等三角形的判定证得△DAC ≌△BAE ，由全等三角形的性质得BE=CD ；首先证得四边形ABCE 为平行四边形，再利用全等三角形的判定定理得△BCE ≌△CAD ，易得∠CBE=∠ACD ，由∠ACB=90°，易得∠CFB=90°，得出结论．（3）先证明△DBF 是直角三角形，再利用勾股定理进行计算，即可求出答案．【详解】解：（1）∵△ABC 和△ABD 都是等腰直角三角形∴∠CAB =∠ABD = 45°，BD 2AB 22BC =2BC =2AC∴AC ∥BD又∵G 为BD 的中点，∴BD =2DG ，∴AC =DG ，AC ∥DG∴四边形ACGD 为平行四边形；（2）BE =CD ，理由如下∵△AEC 和△ABD 都是等腰直角三角形AE =AC ，AB =AD∠EAB =∠EAC +∠CAB =90°+45°=135°，∠CAD =∠DAB +∠BAC =90°+45°=135°，∴∠EAB =∠CAD ，在△DAC 与△BAE 中，AD AB CAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩，∴△DAC ≌△BAE ，∴BE =CD ；（3） ∵△DAC ≌△BAE∴∠AEB=∠ACD又∵∠EAC=90°∴∠EFC=∠DFB=90°∴ △DBF 是直角三角形∵BC，∴BD根据勾股定理得CD， ∴11••22CD BF BC BD = ∴12=12•∴BF∴EF =BE -BF =CD -BF【点睛】 本题主要考查了等腰直角三角形的性质，平行四边形和全等三角形的判定及性质定理，综合运用各种定理是解答此题的关键．4．已知，ABC 中，AB AC =，2BAC α∠=︒，点D 为BC 边中点，连接AD ，点E 为AD 的中点，线段CE 绕点E 顺时针旋转2α︒得到线段EF ，连接FC ，FD ． （1）如图1，当60BAC ∠=︒时，请直接写出DF DC的值；（2）如图2，当90BAC ∠=︒时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请写出正确的结论，并说明理由；（3）如图3，当2BAC α∠=︒时，请直接写出DF DC的值(用含α的三角函数表示)．答案：（1）；（2）不成立，，理由见解析；（3）．【分析】（1）如图1（见解析），先根据中位线定理得出，再根据旋转的性质、等边三角形的性质得出，，，然后根据三角形全等的判定定理与性质可得，由此即可得出解析：（1）12；（2）不成立，22DF DC =3）sin DF DC α=︒． 【分析】（1）如图1（见解析），先根据中位线定理得出12EG DC =，再根据旋转的性质、等边三角形的性质得出EC FC =，CD CG =，DCF GCE ∠=∠，然后根据三角形全等的判定定理与性质可得DF EG =，由此即可得出答案；（2）如图2（见解析），先根据中位线定理、等腰三角形的三线合一得出90AEM ∠=︒，再根据等腰直角三角形的性质得出ACE BCF ∠=∠，22AC CE BC CF ==，然后根据相似三角形的判定与性质可得CBF CAE ∠=∠，22AE BF =，从而可得AE AM BF BD =，最后根据相似三角形的判定与性质可得90BFD AEM ∠=∠=︒，据此利用正弦三角函数值即可得；（3）如图3（见解析），参照题（2）的思路，先根据相似三角形的判定与性质得出,90CBF CAE BFD AEN α∠=∠=︒∠=∠=︒，再在Rt BFD 中，利用正弦三角函数值即可得．【详解】 （1）如图1，取AC 的中点G ，连接EG ，则12CG AC =点E 为AD 的中点EG ∴是ACD 的中位线12EG DC ∴=，即12EG DC = 由旋转的性质可知，EC EF =，60FEC ∠=︒CEF ∴是等边三角形60ECF ∴∠=︒，EC FC =AB AC =，60BAC ∠=︒ABC ∴是等边三角形60,ACB AC BC ∴∠=︒=点D 为BC 边中点1122CD BC AC CG ∴=== 60ECF ECD DCF ∠=∠+∠=︒，60ACB ECD GCE ∠=∠+∠=︒ DCF GCE ∴∠=∠在DCF 和GCE 中，CD CG DCF GCE FC EC =⎧⎪∠=∠⎨⎪=⎩()DCF GCE SAS ∴≅DF EG ∴=12DF EG DC DC ∴==； （2）不成立，2DF DC =，理由如下： 如图2，连接BF ，取AC 的中点M ，连接EM∵E 是AD 的中点∴//EM BC∴AEM ADC ∠=∠∵AB AC =ABC ∴是等腰三角形∵D 是BC 中点, 2BAC α∠=︒∴AD BC ⊥，12CAD BAC α∠=∠=︒，BD DC = ∴90ADC ∠=︒∴90AEM ∠=︒当90BAC ∠=︒时，则90CEF ∠=︒ABC ∴和CEF △为等腰直角三角形∴45ACB ECF ∠=∠=︒，即45ECD ACE ECD BCF ∠+∠=∠+∠=︒∴ACE BCF ∠=∠，cos 452AC CE BC CF ==︒= ∴ACE BCF ~ ∴90452CBF CAE α︒∠=∠=︒==︒，2AE AC BF BC ==∵12122AC AM BD BC == ∴AE AM BF BD = ∴BDF AME ~ ∴90BFD AEM ∠=∠=︒在Rt BFD 中，sin DF DF CBF BD DC ∠==，即sin 45DF DC ︒=则2DF DC =； （3）sin DF DC α=︒，求解过程如下： 如图3，连接BF ，取AC 的中点N ，连接EN参照（2），同理可得：12CAD BAC α∠=∠=︒，BD DC =，90AEN ADC ∠=∠=︒ 当2BAC α∠=︒时，则2CEF α∠=︒AB AC =，EC EF =（旋转的性质）ABC ∴和EFC 为等腰三角形 ∴1(180)902ACB ABC BAC α∠=∠=︒-∠=︒-︒ 1(180)902ECF EFC CEF α∠=∠=︒-∠=︒-︒ 90ACB ECF α∴∠=∠=︒-︒ABC EFC ∴~AC CE BC CF∴= 又,ACB ECD ACE ECF ECD BCF ∠=∠+∠∠=∠+∠ ∴ACE BCF ∠=∠∴ACE BCF ~∴CBF CAE α∠=∠=︒，AE AC BF BC =∵1212ACAN AC BDBCBC==∴AE ANBF BD=∴BDF ANE~∴90BFD AEN∠=∠=︒在Rt BFD中，sinDF DFCBFBD DC∠==即sinDFDCα=︒．【点睛】本题考查了等腰三角形的性质、旋转的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点，通过作辅助线，构造全等三角形和相似三角形是解题关键．5．已知在矩形ABCD中，∠ADC的平分线DE与BC边所在的直线交于点E，点P是线段DE上一定点（其中EP<PD）（1）如图1，若点F在CD边上（不与D重合），将∠DPF绕点P逆时针旋转90°后，角的两边PD、PF分别交射线DA于点H、G．①求证：PG=PF；②探究：DF、DG、DP之间有怎样的数量关系，并证明你的结论．（2）拓展：如图2，若点F在CD的延长线上（不与D重合），过点P作PG⊥PF，交射线DA于点G，你认为（1）中DE、DG、DP之间的数量关系是否仍然成立？若成立，给出证明；若不成立，请写出它们所满足的数量关系式，并说明理由．答案：（1）①详见解析；②DG+DF=DP；（2）不成立，数量关系式应为：DG-DF=DP【解析】【分析】（1）①根据矩形性质证△HPG≌△DPF（ASA），得PG=PF；②由①知，△HPD为等腰直解析：（1）①详见解析；2；（2）不成立，数量关系式应为：DG-2【解析】【分析】（1）①根据矩形性质证△HPG≌△DPF（ASA），得PG=PF；②由①知，△HPD为等腰直角三角形，△HPG≌△DPF，根据直角三角形性质可得2DP；（2）过点P作PH⊥PD 交射线DA于点H，得到△HPD为等腰直角三角形，证△HPG≌△DPF，得HG=DF，DH=DG-HG=DG-DF，2DP．【详解】（1）①∵由矩形性质得∠GPF=∠HPD=90°，∠ADC=90°，∴∠GPH=∠FPD，∵DE平分∠ADC，∴∠PDF=∠ADP=45°，∴△HPD为等腰直角三角形，∴∠DHP=∠PDF=45°，在△HPG和△DPF中，∵PHG PDF PH PDGPH FPD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△HPG≌△DPF（ASA），∴PG=PF；②结论：2DP，由①知，△HPD为等腰直角三角形，△HPG≌△DPF，∴2DP，HG=DF，∴HD=HG+DG=DF+DG，∴DG+DF=2DP；（2）不成立，数量关系式应为：DG-DF=2DP，如图，过点P作PH⊥PD交射线DA于点H，∵PF⊥PG，∠GPF=∠HPD=90°，∴∠GPH=∠FPD，∵DE平分∠ADC，且在矩形ABCD中，∠ADC=90°，∴∠HDP=∠EDC=45°，得到△HPD为等腰直角三角形，∴∠DHP=∠EDC=45°，且PH=PD，2DP，∴∠GHP=∠FDP=180°-45°=135°，在△HPG和△DPF中，∵GPH FPDGHP FDP PH PD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△HPG≌△DPF，∴HG=DF，∴DH=DG-HG=DG-DF，∴2DP．【点睛】考核知识点：矩形性质的运用,等腰直角三角形.综合运用全等三角形判定和等腰直角三角形性质是关键.6．[发现]：（1）如图1．在△ABC中，AB=AC，∠BAC=90°，过点A作AH⊥BC于点H，求证：AH=12 BC．[拓展]：（2）如图2．在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE=90°，点D、B、C在同一条直线上，AH为△ABC中BC边上的高，连接CE．则∠DCE的度数为________，同时猜想线段AH、CD、CE之间的数量关系，并说明理由．[应用]：（3）在图3、图4中．在△ABC中，AB=AC，且∠BAC=90°，在同一平面内有一点P，满足PC=1，PB=6，且∠BPC=90°，请求出点A到BP的距离．答案：（1）证明见解析；（2）∠DCE的度数为90°，CE+2AH=CD，理由见解析；（3）或．【分析】发现：根据同角的余角相等可得∠CAH=∠B，根据AAS证明三角形全等，再根据全等三角形的对应边相解析：（1）证明见解析；（2）∠DCE的度数为90°，CE+2AH=CD，理由见解析；（3）5 2或72．【分析】发现：根据同角的余角相等可得∠CAH=∠B，根据AAS证明三角形全等，再根据全等三角形的对应边相等即可得结论；拓展：证明△ADB≌△AEC，即可得∠DCE的度数为90°，线段AH、CD、CE之间的数量关系；应用：如图3，过点A作AH⊥BP于点H，连接AP，过A作AD垂直于AP，交PB于点D，可得△APC≌△ADB，得BD=CP=1，根据DP=BP-BD=6-1=5，AH⊥DP，即可得点A到BP的距离；同理如图4，过点A作AH⊥BP于点H，连接AP，将△APC绕点A顺时针旋转90度到△ADB，可得DP=BP+BD=6+1=7，进而可得点A到BP的距离．【详解】解：发现：（1）证明：∵AH⊥BC，∠BAC=90°，∴∠AHC=90°=∠BAC．∴∠BAH+∠CAH=90°，∠BAH+∠B=90°．∴∠CAH=∠B ，在△ABH 和△CAH 中，CAH B AHC BHA AB CA ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ABH ≌△CAH ．（AAS ）．∴BH=AH ，AH=CH ．∴AH=12BC． 拓展：∠DCE 的度数为90°，线段AH 、CD 、CE 之间的数量关系为：CE+2AH=CD ，理由如下：∵∠DAB+∠BAE=90°，∠EAC+∠BAE=90°，∴∠DAB=∠EAC ，∵AD=AE ，AB=AC ，∴△ADB ≌△AEC （SAS ），∴∠ABD=∠ACE ，∵AB =AC ，∠BAC =90°∴∠ABC=∠ACB=45°，∴∠ABD=135°，∴∠DCE=90°；∵D 、B 、C 三点共线，∴DB+BC=CD ，∵DB=CE ，AH=12BC ， ∴CE+2AH=CD ．应用：点A 到BP 的距离为：52或72． 理由如下：如图3，过点A 作AH ⊥BP 于点H ，连接AP ，作∠PAD=90°，交BP 于点D ，∴∠BAC=∠DAP=90°，∴∠BAD=∠CAP ，∵∠BDA=∠APC=90°+∠APD ，∴△APC ≌△ADB （AAS ），∴BD=CP=1，∴DP=BP-BD=6-1=5，∵AH ⊥DP ，∴AH=12DP=52； 如图4，过点A 作AH ⊥BP 于点H ，作∠PAD=90°，交PB 的延长线于点D ，∴∠BAC=∠DAP=90°，∴∠BAD=∠CAP ，∵∠BAC=90°，∠BPC=90°，∴∠ACP+∠ABP=180°，∴∠ACP=∠ABD ，∵AB=AC ，∴△APC ≌△ADB （AAS ），∴BD=CP=1 ∴DP=BP+BD=6+1=7．∵AH ⊥DP ，∴AH=12DP=72． 综上所述：点A 到BP 的距离为：52或72． 【点睛】本题考查了三角形综合题，解决本题的关键是掌握全等三角形的判定与性质．7．如图，锐角ABC 中，分别以AB 、AC 为边向外作等腰直角ABE △和等腰直角ACD △，使AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，可以通过全等三角形的知识证得BD 与CE 相等．（1）如图，锐角ABC 中分别以AB 、AC 为边向外作等腰ABE △和等腰ACD △，AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，试猜想BD 与CE 的数量关系，并说明理由．（2）如图，在中ABC ，45ACB ∠=︒，以AB 为直角边，A 为直角顶点向外作等腰直角ABD △，连接CD ，若2,3AC BC ==，求CD 的长．（3）如图，在四边形中ABCD ，60,15,8,ADC BC AB AD CD ∠=︒===，求BD 的最大值．答案：（1），证明见解析；（2）；（3）23．【分析】（1）由等腰三角形的性质解得，继而可证及，再由全等三角形对应边相等解题；（2）过A 作交于点，连接，先证明是等腰直角三角形，得到 ，，再证明，由全解析：（1）BD CE =，证明见解析；（2）13；（3）23．【分析】（1）由等腰三角形的性质解得,,AE AB AD AC BAE CAD ==∠=∠，继而可证EAC BAD ∠=∠及(SAS)EAC BAD ≌，再由全等三角形对应边相等解题；（2）过A 作AE AC ⊥交BC 于点E ，连接DE ，先证明EAC 是等腰直角三角形，得到 AE AC =，DAE BAC ∠=∠，再证明(SAS)DAE BAC ≌，由全等三角形的性质得到3,45DE BC DEA BCA ==∠=∠=︒，接着在等腰直角三角形EAC 中，由勾股定理解得22222EC AC AE AC =+=，最后在Rt DEC △中，由勾股定理即可解得CD 的长； （3）先证明ACD △为等边三角形，再由等边三角形的性质可得，,60AC CD ACD =∠=︒将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转的性质得815DE AB BC EC ====，，继而证明BCE 是等边三角形，由等边三角形的性质得到75BE BC ==，最后根据三角形三边关系解题即可．【详解】解：（1）∵ABE △和ACD △是等腰三角形，,,AE AB AD AC BAE CAD ∴==∠=∠，BAE BAC CAD BAC ∴∠+∠=∠+∠，即：EAC BAD ∠=∠，在EAC 中BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩，(SAS)EAC BAD ∴≌，CE BD ∴=；（2）如图（1）所示，过A 作AE AC ⊥交BC 于点E ，连接DE ，45,ACB AE AC ∠=︒⊥，90EAC ∴∠=︒，EAC ∴△是等腰直角三角形，AE AC ∴=，又ABD 是等腰直角三角形，,90AB AD BAD ∴=∠=︒，90BAD EAC ∴∠=∠=︒，BAD BAE EAC BAE ∴∠+∠=∠+∠，即：DAE BAC ∠=∠，在DAE △和BAC 中,AD AB DAE BAC AE AC =⎧⎪∠=∠⎨⎪=⎩(SAS)DAE BAC ∴≌，3,45DE BC DEA BCA ∴==∠=∠=︒，在等腰直角三角形EAC 中，45AEC ∠=︒，90DEC DEA AEC ∴∠=∠+∠=︒，由勾股定理得：22222EC AC AE AC =+=.在Rt DEC △中，由勾股定理得： 229413CD DE EC =+=+=；（3）,60AD CD ADC =∠=︒，∴ACD △为等边三角形，,60AC CD ACD ∴=∠=︒，如图（2）所示，将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转性质可得∶815DE AB BC EC ====，60BCE ∠=︒，∴BCE 是等边三角形，∴75BE BC ==，又∴BE DE BD +≥， 即158BD BE DE ≤+=+，即23BD ≤，∴BD 的最大值为 23．【点睛】本题考查全等三角形的判定与性质、旋转、勾股定理、等边三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．8．（1）问题发现：如图①，ABC 与ADE 是等边三角形，且点B ，D ，E 在同一直线上，连接CE ，求BEC ∠的度数，并确定线段BD 与CE 的数量关系．（2）拓展探究：如图②，ABC 与ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，且点B ，D ，E 在同一直线上，AF BE ⊥于点F ，连接CE ，求BEC ∠的度数，并确定线段AF ，BF ，CE 之间的数量关系．答案：（1）的度数为，线段与之间的数量关系是；（2）．【分析】（1）首先根据和均为等边三角形，可得，，，，据此判断出．然后根据全等三角形的判定方法，判断出≌，即可判断出，．进而判断出∠BEC 的度数为6 解析：（1）BEC ∠的度数为60︒，线段BD 与CD 之间的数量关系是BD CE =；（2）BF CE AF =+．【分析】（1）首先根据ABC 和ADE 均为等边三角形，可得AB AC =，AD AE =，60BAC DAE ∠=∠=︒，60ADE AED ∠=∠=︒，据此判断出BAD CAE ∠=∠．然后根据全等三角形的判定方法，判断出ABD △≌ACE △，即可判断出BD CE =，DBA CEA ∠=∠．进而判断出∠BEC 的度数为60°即可；（2）首先根据ABC 和ADE 均为等腰直角三角形，可得AB AC =，AD AE =，90BAC DAE ∠=∠=︒，45ADE AED ∠=∠=︒，据此判断出BAD CAE ∠=∠．然后根据全等三角形的判定方法，判断出ABD △≌ACE △，即可判断出,BD CE =ADB AEC ∠=∠．进而判断出∠BEC 的度数为90°即可；最后根据90DAE ∠=︒，AD AE =，AF DE ⊥，得到AF DF EF ==于是得到结论．【详解】解：（1）因为ABC 和ADE 均为等边三角形，所以AB AC =，AD AE =，60BAC DAE ∠=∠=︒，60ADE AED ∠=∠=︒， 所以BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠．在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，所以ABD △≌ACE △，所以BD CE =，DBA CEA ∠=∠．因为点B ，D ，E 在同一直线上，所以18060120ADB ∠=︒-︒=︒，所以120AEC ∠=︒，所以1206060BEC AEC AED ∠=∠-∠=︒-︒=︒．综上可得，BEC ∠的度数为60︒，线段BD 与CD 之间的数量关系是BD CE =． （2）因为ABC 和ADE 均为等腰直角三角形，所以AB AC =，AD AE =，90BAC DAE ∠=∠=︒，45ADE AED ∠=∠=︒， 所以BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠．在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，所以ABD △≌ACE △，所以BD CE =，ADB AEC ∠=∠．因为点B ，D ，E 在同一直线上，所以18045135ADB ∠=︒-︒=︒，所以135AEC ∠=︒，所以1354590BEC AEC AED ∠=∠-∠=︒-︒=︒．因为90DAE ∠=︒，AD AE =，AF DE ⊥，易证AF DF EF ==，所以BF BD DF CE AF =+=+．9．如图，已知Rt △ABC 中，AB=AC=2，点D 为直线BC 上的动点（不与B 、C 重合），以A 为直角顶点作等腰直角三角形ADE （点A ，D ，E 按逆时针顺序排列），连结CE ． （1）当点D 在线段BC 上运动时，①求证：BD=CE ；②请探讨四边形ADCE 的面积是否有变化；（2）当点D 在直线BC 上运动时，直接写出CD ，CB 与CE 之间的数量关系．答案：（1）①见解析；②四边形ADCE 的面积不变；（2）当点D 在线段BC 上时，CB=CE ＋CD ；当点D 在点C 右侧时，CB = CE －CD ；当点D 在点B 左侧时，CB= CD －CE【分析】（1）①根据等腰解析：（1）①见解析；②四边形ADCE 的面积不变；（2）当点D 在线段BC 上时，CB=CE ＋CD ；当点D 在点C 右侧时，CB = CE －CD ；当点D 在点B 左侧时，CB= CD －CE【分析】（1）①根据等腰直角三角形的性质可得AB=AC ，AD=AE ，∠BAC=∠DAE=90°，从而得出∠BAD=∠CAE ，然后利用SAS 即可证出△BAD ≌△CAE ，从而得出BD=CE ；②根据直角三角形的面积公式即可求出S △ABC ，然后根据全等三角形的性质可得S △BAD =S △CAE ，然后根据S 四边形ADCE =S △CAE ＋S △ADC 和等量代换即可得出结论；（2）根据点D 的位置分类讨论，分别画出对应的图形，根据（1）①中证全等的方法和全等三角形的性质即可推出结论．【详解】解：（1）①∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ，AD=AE ，∠BAC=∠DAE=90°∴∠BAD ＋∠DAC=90°，∠CAE ＋∠DAC=90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE ；②∵已知Rt △ABC 中，AB=AC=2，∴S △ABC=12AB·AC=2 ∵△BAD ≌△CAE∴S △BAD =S △CAE ∴S 四边形ADCE =S △CAE ＋S △ADC =S △BAD ＋S △ADC = S △ABC =2∴四边形ADCE 的面积不变；（2）当点D 在线段BC 上时，如下图所示由（1）①的结论知BD=CE∴CB=BD ＋CD= CE ＋CD ；当点D 在点C 右侧时，如下图所示∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ，AD=AE ，∠BAC=∠DAE=90°∴∠BAD －∠DAC=90°，∠CAE －∠DAC=90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE∴CB=BD －CD= CE －CD ；当点D 在点B 左侧时，如下图所示∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ，AD=AE ，∠BAC=∠DAE=90°∴∠BAD=∠DAC －90°，∠CAE=∠DAC － 90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE∴CB= CD －BD = CD －CE ．综上所述：当点D 在线段BC 上时，CB=CE ＋CD ；当点D 在点C 右侧时，CB = CE －CD ；当点D 在点B 左侧时，CB= CD －CE ．【点睛】此题考查的是等腰直角三角形的性质、全等三角形的判定及性质和三角形的面积公式，掌握等腰直角三角形的性质、全等三角形的判定及性质、分类讨论的数学思想和三角形的面积公式是解决此题的关键．10．如图所示，点A 是线段BC 上一点，ABD ∆和ACE ∆都是等边三角形.（1）连结BE ，CD ，求证：BE CD =；（2）如图所示，将ABD ∆绕点A 顺时针旋转得到AB D ''∆.①当旋转角为______度时，边AD '落在AE 上；②在①的条件下，延长DD '交CE 于点P ，连结BD '，CD '.当线段AB 、AC 满足什么数量关系时，BDD '∆与CPD '∆全等？并给予证明.答案：（1）详见解析；（2）①；②当时，与全等.【分析】根据等边三角形的性质可得，，，然后求出，再利用“边角边”证明和全等，根据全等三角形对应边相等即可得证；求出，即可得到旋转角度数；当时，与全等解析：（1）详见解析；（2）①60︒；②当2AC AB =时，BDD '∆与CPD '∆全等.【分析】()1根据等边三角形的性质可得AB AD =，AE AC =，60BAD CAE ∠∠==，然后求出BAE DAC ∠∠=，再利用“边角边”证明BAE 和DAC 全等，根据全等三角形对应边相等即可得证； ()2①求出DAE ∠，即可得到旋转角度数；②当2AC AB =时，'BDD 与'CPD 全等.根据旋转的性质可得''AB BD DD AD ===，然后得到四边形'ABDD 是菱形，根据菱形的对角线平分一组对角可得''30ABD DBD ∠∠==，菱形的对边平行可得//DP BC ，根据等边三角形的性质求出AC AE =，60ACE ∠=，然后根据等腰三角形三线合一的性质求出''30PCD ACD ∠∠==，从而得到'''''30ABD DBD BDD ACD PDC ∠∠∠∠∠=====，然后利用“角边角”证明'BDD 与'CPD 全等．【详解】()1证明：ABD 和ACE 都是等边三角形．AB AD ∴=，AE AC =，60BAD CAE ∠∠==，BAD DAE CAE DAE ∠∠∠∠∴+=+，即BAE DAC ∠∠=，在BAE 和DAC 中，AB AD BAE DAC AE AC ∠∠=⎧⎪=⎨⎪=⎩，BAE ∴≌()DAC SAS ，BE CD ∴=；()2①当旋转角为60°时，边AD '落在AE 上.理由如下：60BAD CAE ∠∠==，18060260DAE ∠∴=-⨯=，边'AD 落在AE 上，∴旋转角60DAE ∠==．故答案为60．②当2AC AB =时，'BDD 与'CPD 全等．理由如下：由旋转可知，'AB 与AD 重合，''AB BD DD AD ∴===，∴四边形'ABDD 是菱形，11''603022ABD DBD ABD ∠∠∠∴===⨯=，//DP BC ， ACE 是等边三角形，AC AE ∴=，60ACE ∠=，2AC AB =，2'AE AD ∴=，11''603022PCD ACD ACE ∠∠∠∴===⨯=， 又//DP BC ，''''''30ABD DBD BDD ACD PCD PDC ∠∠∠∠∠∠∴======，在'BDD 与'CPD 中，DBD PCD BD CD BD D PD C ∠=∠⎧⎪=⎨⎪∠='∠''''⎩'， 'BDD ∴≌()'CPD ASA ．【点睛】本题考查了全等三角形的判定与性质，等边三角形的性质，以及旋转的性质，综合性较强，但难度不大，熟练掌握等边三角形的性质与全等三角形的判定时提到过．二、全等三角形手拉手模型11．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB ∠＝ °，线段BD 、CE 之间的数量关系是 ；（2）拓展探究： 如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．解析：（1）60BD CE ，＝；（2）452CEB BD CE ∠︒＝，＝，理由见解析；（3）CE 的长为2或2【分析】（1）证明ACE ABD ≌，得出CE ＝BD ，AEC ADB ∠=∠，即可得出结论； （2）证明ACE ABD ∽，得出AEC ADB ∠=∠，2BD CE =，即可得出结论； （3）先判断出2BD CE =，再求出210AB =：①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出AP ＝DP ＝AE ＝2，再根据勾股定理求出，BP ＝6，得出BD ＝4；②当点E 在点D 下方时，同①的方法得，AP ＝DP ＝AE ＝1，BP ＝6，进而得出BD ＝BP +DP ＝8，即可得出结论．【详解】解：（1）ABC 为等腰三角形，60AC BC ACB ∠︒＝，＝，∴ABC 是等边三角形，同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAEAD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒＝≌（）故答案为：60CEB BD CE ∠=︒=；．（2）45CEB BD ∠︒＝，，理由如下：在等腰三角形ABC 中，AC ＝BC ，90ACB ∠︒＝，45AB CAB ∴∠︒，＝ ，同理，45AD ADE DAE ∠∠︒，＝＝， ∴AE AC AD AB =，DAE CAB ∠∠＝， EAC DAB ∴∠∠＝，ACE ABD ∴∽ ，∴BD AD CE AE==∴AEC ADB BD ∠∠＝，，点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒＝＝135AEC ∴∠︒＝45CEB AEC AED ∴∠∠-∠︒＝＝；（3）由（2）知，ACE ABD ∽，BD ∴，在Rt ABC中，AC ＝AB ∴＝，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ，DE BD ⊥，PDE AED APD ∴∠∠∠＝＝，∴四边形APDE 是矩形，AE DE ＝ ，∴矩形APDE 是正方形，2AP DP AE ∴＝＝＝，在Rt APB △中，根据勾股定理得，226BP AB AP -＝＝，4BD BP AP ∴-＝＝，222CE BD ∴＝＝； ②当点E 在点D 下方时，如图④同①的方法得，AP ＝DP ＝AE ＝2，BP ＝6，∴BD ＝BP +DP ＝8，22CE BD ∴＝＝4， 综上CE 的长为22或42．【点睛】本题是几何变换的综合题，主要考查了旋转的性质，全等三角形的判定和定理，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出三角形ACE 和三角形ABD 相似是关键．12．已知：在△ABC 中，∠BAC=90°，AB=AC ，点D 为直线BC 上一动点(点D 不与B 、C 重合)．以AD 为边作正方形ADEF ，连接CF ．（1）如图1，当点D 在线段BC 上时，请直接写出线段BD 与CF 的数量关系： ； （2）如图2，当点D 在线段BC 的延长线上时，其它条件不变，若AC=2，CD=1，则CF= ；（3）如图3，当点D 在线段BC 的反向延长线上时，且点A 、F 分别在直线BC 的两侧，其它条件不变：①请直接写出CF 、BC 、CD 三条线段之间的关系： ；②若连接正方形对角线AE 、DF ，交点为O ，连接OC ，探究△AOC 的形状，并说明理由．解析：（1）BD=CF ；（2）221；（3）①CD=CF+BC ，②等腰三角形，见解析【分析】（1）△ABC 是等腰直角三角形，利用SAS 即可证明△BAD ≌△CAF ；（2）同（1）相同，利用SAS 即可证得△BAD ≌△CAF ，从而证得BD=CF ，即可得到CF=CD+BC ，然后求出答案；（3）中的①与（1）相同，可证明BD=CF ，又点D 、B 、C 共线，故：CD=BC+CF ； ②由（1）猜想并证明BD ⊥CF ，从而可知△FCD 为直角三角形，再由正方形的对角线的性质判定△AOC 三边的特点，再进一步判定其形状．【详解】解：（1）证明：∵∠BAC=90°，AB=AC ，∴∠ABC=∠ACB=45°，∵四边形ADEF 是正方形，∴AD=AF ，∠DAF=90°，∵∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°，∴∠BAD=∠CAF ，在△BAD 和△CAF 中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAF （SAS ），∴BD=CF ，（2）与（1）同理，证△BAD ≌△CAF ；∴BD=CF ，∴CF=BC+CD ，∵AC=AB=2，CD=1， ∴22222BC =+=∴CF=221；（3）①BC 、CD 与CF 的关系：CD=BC+CF理由：与（1）同法可证△BAD ≌△CAF ，从而可得：BD=CF ，即：CD=BC+CF②△AOC 是等腰三角形理由：与（1）同法可证△BAD ≌△CAF ，可得：∠DBA=∠FCA ，又∵∠BAC=90°，AB=AC ，∴∠ABC=∠ACB=45°，则∠ABD=180°-45°=135°，∴∠ABD=∠FCA=135°∴∠DCF=135°-45°=90°∴△FCD 为直角三角形．又∵四边形ADEF 是正方形，对角线AE 与DF 相交于点O ，∴OC=12DF ， ∴OC=OA ∴△AOC 是等腰三角形．【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点，一般情况下，要证明两条线段相等，就得证明这两条线段所在的两个三角形全等，关键是掌握图形特点挖掘题目所隐含的条件．13．（1）小迪同学在学习圆的内接正多边形时，发现：如图1，若P 是圆内接正三角形ABC 的外接圆的BC 上任一点，则60APB ∠=︒，在PA 上截取PM PC =，连接MC ，可证明MCP ∆是_______（填“等腰”、“等边”或“直角”）三角形，从而得到=PC MC ，再进一步证明PBC ≅_______，得到=PB MA ，可证得：．（2）小迪同学对以上推理进行类比研究，发现：如图2，若P 是圆内接正四边形ABCD 的外接圆的BC 上任一点，则APB APD ∠=∠= °，分别过点,B D 作BM AP ⊥于M 、⊥DN AP 于N ．（3）写出,PB PD 与PA 之间的数量关系，并说明理由．解析：（1）等边，MAC △；（2）45；（3）2BP DP AP +．【分析】（1）由ABC 是正三角形；=AC AC 可得60APC ABC ∠=∠=︒，即可判定MCP 是等边三角形；再根据AAS 可判定PBC MAC ≅，由此得解；（2）根据圆周角和弧的关系即可得出45APB APD ∠=∠=︒；（3）由（2）得DNP、BMP均为等腰直角三角形，即2BM PM BP==，DN PN==；再由AAS定理可判定ABM DAN≅，可知BM AN=，继而可得AP BM NP=+，由此即可得出结论．【详解】解：（1）∵ABC是正三角形；AC AC=，∴60APC ABC∠=∠=︒，又∵PM PC=，∴MCP是等边三角形；∴=PC MC，60PMC PCM∠=∠=︒，∵120AMC∠=︒，又∵60APB∠=︒；∴120BPC∠=︒，∵PC PC=，∴PBC PAC∠=∠，在PBC和MAC△中，PBC PACBPC AMCBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴PBC MAC≅（AAS）∴BP AM=，∵AP AM MP BP PC=+=+，即AP BP PC=+，故答案为：（1）等边，MAC△；（2）∵四边形ABCD是圆内接正四边形，∴90m mAB AD︒==，∴45APB APD∠=∠=︒，故答案为45；（3）∵BM AP⊥、⊥DN AP，45APB APD∠=∠=︒，∴22BM PM BP DN PN DP====，，又∵90PAB PAD∠+∠=︒，90ADN PAD∠+∠=︒，∴MAB ADN∠=∠，在ABM和DAN中，。

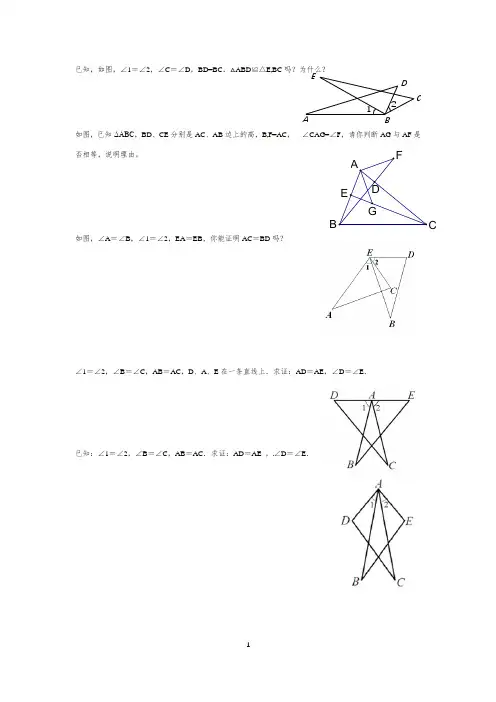
已知，如图，∠1＝∠2，∠C ＝∠D ，BD=BC ，△ABD ≌△E BC 吗？为什么？如图，已知ΔABC ，BD 、CE 分别是AC 、AB 边上的高，B F=AC ， ∠CAG=∠F ，请你判断AG 与AF 是否相等，说明理由。

如图，∠A ＝∠B ，∠1＝∠2，EA ＝EB ，你能证明AC ＝BD 吗？∠1＝∠2，∠B ＝∠C ，AB ＝AC ，D 、A 、E 在一条直线上．求证：AD ＝AE ，∠D ＝∠E ．已知：∠1＝∠2，∠B ＝∠C ，AB ＝AC ．求证：AD ＝AE ，∠D ＝∠E ．ABCDE1 2两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90∘，B，C，E在同一条直线上，连接DC.(1)请找出图2中与△ABE全等的三角形,并给予证明(2)证明：DC⊥BE.如图,在Rt△ABC中,∠ACB=90∘,点D. F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90∘后得CE，连接EF.(1)求证：△BCD≌△FCE；(2)若EF∥CD，求∠BDC的度数。

如图，在正方形ABCD中，△PBC、△QCD是两个等边三角形，PB与DQ交于M，BP与CQ交于E，CP与DQ交于F. 求证：PM=QM.如图,已知长方形ABCD,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB，MD. (1)求证：BE=DC；(2)求证：∠MBE=∠MDC如图所示，已知△ABC和△DCE均是等边三角形，点B，C，E在同一条直线上，AE与BD与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC，FG，其中正确结论的个数是（）①AE=BD；②AG=BF；③FG∥BE；④∠BOC=∠EOC．如图，△ABD与△ACE均为正三角形，且AB＜AC，则BE与CD之间的大小关系是（）如图，在▱ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF，EF，则以下四个结论一定正确的是（）①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边三角形；④CG⊥AE．已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=．下列结论：①△APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD+S△APB=1+；⑤S正方形ABCD=4+．其中正确结论的序号是（）如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF．求证：DE=BF．如图，△ABC中，AB=AC，延长BC至D，使CD=BC，点E在边AC上，以CE，CD为邻边做▱CDFE，过点C作CG∥AB交EF于点G，连接BG，DE．（1）∠ACB与∠GCD有怎样的数量关系？请说明理由；（2）求证：△BCG≌△DCE．如图所示、△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上．（1）求证：△AOC≌△BOD；（2）若AD=1，BD=2，求CD的长．如图，△ACD和△BCE都是等腰直角三角形，∠ACD=∠BCE=90°，AE交CD于点F，BD分别交CE、AE 于点G、H．试猜测线段AE和BD的数量和位置关系，并说明理由．已知：如图，点C是线段AB的中点，CE=CD，∠ACD=∠BCE，求证：AE=BD．已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过E点作AC的垂线，交CD的延长线于点F．求证：AB=FC．如图，分别以Rt△ABC的直角边AC，BC为边，在Rt△ABC外作两个等边三角形△ACE和△BCF，连接BE，AF．求证：BE=AF．如图，已知，等腰Rt△OAB中，∠AOB=90°，等腰Rt△EOF中，∠EOF=90°，连接AE、BF．求证：（1）AE=BF；（2）AE⊥BF．如图，在△ABD和△ACE中，有下列四个等式：（1）AB=AC；（2）AD=AE；（3）∠1=∠2；（4）BD=CE．请你以其中三个等式作为题设，余下的作为结论，写出一个真命题．（要求写出已知，求证及证明过程）如图，P是等边三角形ABC内的一点，连接PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连接CQ．（1）观察并猜想AP与CQ之间的大小关系，并证明你的结论；（2）若PA：PB：PC=3：4：5，连接PQ，试判断△PQC的形状，并说明理由．如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．（1）求证：△ACE≌△BCD；（2）若AD=5，BD=12，求DE的长．如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过E点作EF⊥AE交∠DCE 的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由．如图，△ABC是等腰直角三角形，其中CA=CB，四边形CDEF是正方形，连接AF、BD．（1）观察图形，猜想AF与BD之间有怎样的关系，并证明你的猜想；（2）若将正方形CDEF绕点C按顺时针方向旋转，使正方形CDEF的一边落在△ABC的内部，请你画出一个变换后的图形，并对照已知图形标记字母，题（1）中猜想的结论是否仍然成立？若成立，直接写出结论，不必证明；若不成立，请说明理由．正方形ABCD和正方形AEFG有一公共点A，点G．E分别在线段AD、AB上（如图（1）所示），连接DF、BF．（1）求证：DF=BF，（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG、BE（如图（2）所示），在旋转过程中，请猜想线段DG、BE始终有什么数量关系和位置关系并证明你的猜想．（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°，求证：①AC=BD；②∠APB=60度；（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为_______；∠APB的大小为_______；（3）如图③，在△AOB和△COD中，若OA=k•OB，OC=k•OD（k＞1），∠AOB=∠COD=α，则AC与BD 间的等量关系式为_______；∠APB的大小为_______．如图，四边形ABCD是边长为a的正方形，点G，E分别是边AB，BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F．（1）证明：∠BAE=∠FEC；（2）证明：△AGE≌△ECF；（3）求△AEF的面积．如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连结BE、EC．试猜想线段BE和EC的数量及位置关系，并证明你的猜想．△DAC, △EBC均是等边三角形，AE,BD分别与CD,CE交于点M,N,求证：（1）AE=BD (2)CM=CN (3) △CMN为等边三角形（4）MN∥BC已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2），其中结论正确的个数是（）如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．（1）求证：CE=CF；（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？已知，如图，△ABC和△ECD都是等腰直角三角形，∠ACD=∠DCE=90°，D为AB边上一点．求证：BD=AE．某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．（1）求证：△ADE≌△ABF；已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF（1）如图1，当点D在线段BC上时．求证CF+CD=BC；（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；①请直接写出CF，BC，CD三条线段之间的关系；②若正方形ADEF的边长为2，对角线AE，DF相交于点O，连接OC．求OC的长度．。

G F E D C BA全等三角形——旋转问题一、知识梳理：把图形G 绕平面上的一个定点O 旋转一个角度θ，得到图形G '，这样的由图形G 到G '变换叫做旋转变换，点O 叫做旋转中心，θ叫做旋转角，G '叫做G 的象；G 叫做G '的原象，无论是什么图形，在旋转变换下，象与原象是全等形．很明显，旋转变换具有以下基本性质：①旋转变换的对应点到旋转中心的距离相等； ②对应直线的交角等于旋转角．旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上，其功能还是把分散的条件相对集中，以便于诸条件的综合与推演．二、典型例题：例1、如图，有四个图案，它们绕中心旋转一定的角度后，都能和原来的图案相互重合，其中有一个图案与其余三个图案旋转的角度不同，它是_____________．及时练习：如图，同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的， 其中菱形AEFG 可以看成是把菱形ABCD 以A 为中心_____________。

A ．顺时针旋转60°得到B ．顺时针旋转120°得到C ．逆时针旋转60°得到D ．逆时针旋转120°得到例2、如图，C 是线段BD 上一点，分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE ,AD 交CE 于F ，BE 交AC 于G ，则图中可通过旋转而相互得到的三角形对数有___________。

A ．1对B ．2对C ．3对D ．4对KGFEDC BA及时练习：如图，B ，C ，E 三点共线，且ABC ∆与DCE ∆是等边三角形，连结BD ，AE 分别交AC ，DC 于M ，N 点．求证：CM CN =．NMEDCBAP DC B A 例3、如图，四边形ABCD 、DEFG 都是正方形，连接AE 、CG ．求证：AE CG =．G FE DCBA及时练习：如图，点C 为线段AB 上一点，ACM ∆、CBN ∆是等边三角形，D 是AN 中点，E 是BM 中点，求证：CDE ∆是等边三角形．M DNECBA例4、如图，等边三角形ABC ∆与等边DEC ∆共顶点于C 点．求证：AE BD =．DECBA及时练习：如图，D 是等边ABC ∆内的一点，且BD AD =，BP AB =，DBP DBC ∠=∠，问BPD ∠的度数是否一定，若一定，求它的度数；若不一定，说明理由．例5、如图，等腰直角三角形ABC 中，90B =︒∠，AB a =，O 为AC 中点，EO OF ⊥．求证：BE BF +为定值． OB ECF A及时练习：如图，正方形OGHK 绕正方形ABCD 中点O 旋转，其交点为E 、F ，求证：AE CF AB +=．54321OHBE DK G CFA例6、E 、F 分别是正方形ABCD 的边BC 、CD 上的点，且45EAF =︒∠，AH EF ⊥，H为垂足，求证：AH AB =．CHF E D B A及时练习：如图，正方形ABCD 的边长为1，点F 在线段CD 上运动，AE 平分BAF ∠交BC 边于点E ．⑴求证：AF DF BE =+．⑵设DF x =(01x ≤≤)，ADF ∆与ABE ∆的面积和S 是否存在最大值？若存在，求出此时x 的值及S ．若不存在，请说明理由．FEDC BA例7、请阅读下列材料：已知：如图1在Rt ABC ∆中，90BAC ∠=︒，AB AC =，点D 、E 分别为线段BC 上两动点，若45DAE ∠=︒．探究线段BD 、DE 、EC 三条线段之间的数量关系．小明的思路是：把AEC ∆绕点A 顺时针旋转90︒，得到ABE '∆，连结E D '， 使问题得到解决．请你参考小明的思路探究并解决下列问题：⑴ 猜想BD 、DE 、EC 三条线段之间存在的数量关系式，并对你的猜想给予证明； ⑵ 当动点E 在线段BC 上，动点D 运动在线段CB 延长线上时，如图2，其它条件不变，⑴中探究的结论是否发生改变？请说明你的猜想并给予证明．图1ABCDE图2AB CDE及时练习：(1)如图，在四边形ABCD 中，AB ＝AD ，∠B ＝∠D ＝90︒，E 、F 分别是边BC 、CD 上的点，且∠EAF=12∠BAD ．求证：EF ＝BE +FD;FED CBA(2) 如图，在四边形ABCD 中，AB ＝AD ，∠B+∠D ＝180︒，E 、F 分别是边BC 、CD上的点，且∠EAF=12∠BAD ， (1)中的结论是否仍然成立？不用证明．FEDCB A三、课堂练习：1. 如下图，在线段AE 同侧作两个等边三角形ABC ∆和CDE ∆(120ACE ∠<°)，点P 与点MPM BC DEA PD CB A 分别是线段BE 和AD 的中点，则CPM ∆是_____________。

全等三角形作为初中数学中的一个重要知识点，转变换是其中的一个重要应用。

旋转变换是指将一个图形围绕一个固定点进行旋转后得到另一个图形的变换。

在三角形的旋转变换中，我们常用的是以三角形某一个顶点为旋转中心，将整个三角形围绕该点旋转一定角度，再得到一个全等三角形。

本文将教大家如何应用全等三角形的旋转变换。

一、基本概念在进行旋转变换时，我们首先需要了解几个基本概念，这些概念将帮助我们更好地理解旋转变换。

1.旋转中心：旋转中心是指在旋转变换中被旋转的图形围绕的点。

在三角形旋转变换中，我们通常将三角形的某个顶点作为旋转中心。

2.旋转角度：旋转角度指的是图形围绕旋转中心顺时针或逆时针旋转的角度。

在三角形旋转变换中，我们通常使用角度制来表示旋转角度。

3.旋转方向：旋转方向分为顺时针和逆时针两种，根据具体问题来决定采用哪种旋转方向。

二、旋转变换的规律在进行旋转变换时，我们需要掌握一定的规律，这样才能更加准确地进行计算、解题。

1.旋转后对应的点与原点的距离相等在三角形的旋转变换中，旋转后的三角形中点的位置与原三角形中对应点的位置相同，且距离相等。

因此，我们可以通过计算原三角形中对应点与旋转三角形中对应点之间的距离来确定旋转角度。

2.旋转角度相等在三角形的旋转变换中，旋转角度相等，也就是说，如果我们将一个三角形绕不同的顶点旋转，保持其它条件不变，那么我们得到的三角形是全等的。

这个规律对于解决一些旋转变换问题非常有用。

三、应用全等三角形的旋转变换下面我们将通过一些例题来说明如何应用全等三角形的旋转变换。

例题1已知 AB=AC，P为三角形ABC内部一点，且∠CBP = 30°，∠BCP = 75°。

求∠APB 和∠APC 的度数值。

解析：我们可以通过旋转变换来求解该问题。

具体步骤如下：1.以点B为旋转中心，将△BCP绕B点逆时针旋转105°，得到△B'DP。

2.连接AD，可知△B'DA ≌△BCA 。

全等三角形专题——三角形的旋转、翻折与线段的截长补短经典例题透析类型一：由角平分线想到构造全等不管轴对称图形还是两个图形轴对称，我们不难发现对应点与轴上一点（此点作为顶点）组成的角被轴平分，根据这一特点，在做题中如果遇到角平分线我们就会联想到，以角平分线为轴构造对称（全等），从而把角、线段转移达到解题目的．1．如图1，等腰梯形ABCD中，AD∥BC，∠DBC=45°，翻折梯形ABCD，使点B与点D重合，折痕分别交AB、BC于点F、E．若AD=2，BC=8．求BE的长．图 1 图 2 解析：由题意得△BFE≌△DFE，∴ BE=DE，在△BDE中，ED=BE，∠DBE=45°，∴∠BDE=∠DBE=45°，∴∠DEB=90°，即DE⊥BC，在等腰梯形中，AD=2，BC=8，过A作AG⊥BC，交BC于G，如图2，四边形AGED是矩形∴ GE=AD=2，在Rt△ABG和Rt△DCE中，AB=DC，AG=DE，∴ Rt△ABG≌Rt△DCE，∴ BG=CE，∴2．如图3，已知△ABC中，AB=AC，∠B=2∠A 求证：，∴ BE=5．图 3 图 4解析：如图4，作∠B的平分线交AC于D，则∠A=∠ABD，∠BDC=2∠A=∠C∴ AD=BD=BC作BM⊥AC于M，则CM=DM．3．如图5，已知梯形ABCD中，AB∥CD，AD＞BC，求证：AC＞BD图 5 图 6 解析：如图6，作DE∥AC，DF∥BC，交BA或延长线于点E、F，四边形ACDE和四边形BCDF都是平行四边形．∴ DE=AC，DF=BC，AE=CD=BF作DH⊥AB于H，根据勾股定理∵ AD＞BC，AD＞DF∴ AH＞FH，EH＞BH∴ DE＞BD，即AC＞BD.4．如图7，已知△ABC中，AD⊥BC，AB+CD=AC+BD．求证：AB=AC．，，，图 7解析：设AB、AC、BD、，CD分别为b、c、m、n，则c+n=b+m，c-b=m-n，∵ AD⊥BC，根据勾股定理，得∴，，∵ c+b＞m+n，∴ c-b=0即c=b，∴ AB=AC．，类型二：勾股定理的逆定理的运用5．如图8，P是正△ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A旋，则点P与点之间的距离为________，∠APB=________．转后，得到图 8 图 9解析：如图9，连结所以所以三角形则在三角形所以6．如图10，已知∠ABC=30°，∠ADC=60°，AD=DC．求证：是等边三角形，中是直角，．．．，是由旋转得到的，所以. ≌. ．图 10 图 11解析：如图11，显然△ADC是等边三角形，以BC为边向右侧作等边三角形，则BC=BE，连接AE，则可证明△BCD≌△ACE，所以AE=DB，∠ABC+∠CBE=90°，根据勾股定理有，即．7．如图12，D为等腰△ABC的腰AB上的一点，E为另一腰AC延长线上的一点，且BD=CE，则A．DE=BC B．DE＞BCC．DE＜BC D．DE与BC大小关系决定于∠A的大小．图 12 图 13解析：如图13，分别过D和E点作到BC边的垂线，交BC及其延长线于G和H．则根据，可得到△BDG≌△ECH. 所以BG=CH．所以BC=GH．显然DE＞GH. 所以DE＞BC.8．如图14，已知等边△ABC内有一点N，ND⊥BC，NE⊥AB，NF⊥AC，D、E、F都是，，那垂足，M是△ABC中异于N的另一点，若么与的大小关系是________．图 14 图 15 解析：如图15，作M到正三角形的各边上的高，根据面积相等的关系，有分别化简为所以．，，，而根据直角三角形斜边与直角边的关系有，．所以有9．如图16，梯形ABCD中，AD∥BC，E是AB的中点，CE恰好是平分∠BCD，若AD=3，． BC=4，则CD的长是A．5 B．6 C．7 D．8图 16 图 17解析：如图17，延长CE交DA的延长线于F，则容易证明△BEC≌△AEF，于是可得到∠DCE=∠BCE=∠AFE，所以△FCD是等腰三角形，所以CD=AD+AF=7．10．如图18，在等腰直角△ABC中，∠BAC=90°，AD∥BC，在AD上取一点E，使∠EBC=30°，则BE和BC的大小关系是（）A．BE＞BC B．BE＜BC C．BE=BC D．不确定图 18解析：作△ABC的高h，那么BC=2h．而BE=2h．所以BE=BC．11．已知三角形的两条边长分别为a=5，b=4，它们的高分别为，那么该三角形的面积是________．解析：根据三角形的面积公式，可知所以或，所以．，若，而根据，可得到．如果所以，则结合，结合．，可得到，得到，矛盾．，所以，所以三角形的面积为。

专题07 全等三角形旋转、一线三等角模型【中考考向导航】目录【直击中考】 (1)【考向一 全等三角形旋转模型】 (1)【考向二 全等三角形一线三等角模型】 (6)【直击中考】【考向一 全等三角形旋转模型】 例题：（2022·山东菏泽·菏泽一中校考模拟预测）如图①，在ABC 中，90A ∠=︒，AB AC =，点D ，E 分别在边AB ，AC 上，且AD AE =．则CE BD =．现将ADE 绕点A 顺时针方向旋转，旋转角为()0180αα︒<<︒．如图②，连接CE ，BD ．(1)如图②，请直接写出CE 与BD 的数量关系．(2)将ADE 旋转至如图③所示位置时，请判断CE 与BD 的数量关系和位置关系，并加以证明．(3)在旋转的过程中，当BCD △的面积最大时，α=______．（直接写出答案即可）【变式训练】 一、选择题1．（2022·重庆璧山·统考一模）如图，在正方形ABCD 中，将边BC 绕点B 逆时针旋转至点BC '，若90CC D '∠=︒，2CC '=，则线段BC '的长度为（ ）A ．2B ．52C ．6D ．52．（2022·四川南充·模拟预测）如图，在Rt ABC △中，90BAC ∠=︒，AB AC =，直角EPF ∠的顶点P 是BC的中点，将EPF ∠绕顶点P 旋转，两边PE ，PF 分别交AB ，AC 于点E ，F ．下列四个结论：①AE CF =；②PEF 是等腰直角三角形；③EF AP =；④12ABC AEPF S S =四边形△．在EPF ∠旋转过程中，上述四个结论始终正确的有（ ）A ．①②③B ．②③④C ．①③④D ．①②④3．（2022秋·全国·九年级专题练习）如图，在矩形ABCD 中，DE 平分ADC ∠交BC 于点E ，点F 是CD 边上一点（不与点D 重合）．点P 为DE 上一动点，PE PD <，将DPF ∠绕点P 逆时针旋转90°后，角的两边交射线DA 于H ，G 两点，有下列结论：①DH DE =；②DP DG =；③2DG DF DP +=；④DP DE DH DC ⋅=⋅，其中一定正确的是（ ）A ．①②B ．②③C ．①④D ．③④ 二、填空题4．（2022·广西贺州·统考中考真题）如图，在平面直角坐标系中，OAB 为等腰三角形，5OA AB ==，点B到x 轴的距离为4，若将OAB 绕点O 逆时针旋转90︒，得到OA B ''△，则点B '的坐标为__________．5．（2022·江苏无锡·模拟预测）笑笑将一副三角板按如图所示的位置放置，DOE 的直角顶点O 在边BC 的中点处，其中90,45A DOE B ∠=∠=︒∠=︒，60D ∠=︒，DOE 绕点O 自由旋转，且OD ，OE 分别交AB ，AC 于点M ，N ，当4AN =，2NC =时，MN 的长为______．6．（2022·广东广州·统考中考真题）如图，在矩形ABCD 中，BC =2AB ，点P 为边AD 上的一个动点，线段BP 绕点B 顺时针旋转60°得到线段BP '，连接PP ' ，CP '．当点P ' 落在边BC 上时，∠PP 'C 的度数为________； 当线段CP ' 的长度最小时，∠PP 'C 的度数为________三、解答题7．（2022·山东日照·校考二模）在ABC ∆中，AB AC =，BAC α∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接DB ，DC ．(1)如图1，当60α=︒时，①求证：PA DC =；②求DCP ∠的度数；(2)如图2，当120α=︒时，请直接写出PA 和DC 的数量关系．(3)当120α=︒时，若6AB =，31BP =，请直接写出点D 到CP 的距离为8．（2022·河北保定·校考一模）如图1，等腰直角三角形ABC 中，∠A ＝90°，AB ＝AC ＝102cm ，D 为AB边上一点，tan ∠ACD ＝15，点P 由C 点出发，以2cm /s 的速度向终点B 运动，连接PD ，将PD 绕点D 逆时针旋转90°，得到线段DQ ，连接PQ ．(1)填空：BC ＝ ，BD ＝ ；(2)点P 运动几秒，DQ 最短；(3)如图2，当Q 点运动到直线AB 下方时，连接BQ ，若S △BDQ ＝8，求tan ∠BDQ ；(4)在点P 运动过程中，若∠BPQ ＝15°，请直接写出BP 的长．9．（2022秋·九年级单元测试）如图，正方形ABCD 和正方形CEFG （其中BD >2CE ），直线BG 与DE 交于点H ．(1)如图1，当点G 在CD 上时，请直接写出线段BG 与DE 的数量关系和位置关系；(2)将正方形CEFG 绕点C 旋转一周．①如图2，当点E 在直线CD 右侧时，求证：2BH DH CH -=；②当∠DEC ＝45°时，若AB ＝3，CE ＝1，请直接写出线段DH 的长．10．（2022·全国·九年级专题练习）如图，在ABC 与DEF 中，90ACB EDF ∠=∠=︒，,BC AC ED FD ==，点D 在AB 上．(1)如图1，若点F 在AC 的延长线上，连接AE ，探究线段AF 、AE 、AD 之间的数量关系，并证明你的结论；(2)如图2，若点D 与点A 重合，且32AC =，4DE =，将DEF 绕点D 旋转，连接BF ，点G 为BF 的中点，连接CG ，在旋转的过程中，求32CG BG +的最小值； (3)如图3，若点D 为AB 的中点，连接BF 、CE 交于点M ，CE 交AB 于点N ，且::7:9:10BC DE ME ＝，请直接写出ND CN 的值．11．（2022·内蒙古通辽·模拟预测）综合实践问题情境在图1所示的直角三角形纸片ABC 中，O 是斜边AB 的中点．数学老师让同学们将ABC 绕中点O 做图形的旋转实验，探究旋转过程中线段之间的关系．解决问题（1）“实践小组”的同学们将ABC 以点O 为中心按逆时针旋转，当点A 的对应点A '与C 重合时，BC 与它的对应边B C ''交于点D ．他们发现：OD B C '⊥．请你帮助他们写出证明过程．数学思考（2）在图2的基础上，“实践小组”的同学们继续将ABC 以点O 为中心进行逆时针旋转，当AB 的对应边A B AB ''⊥时，设A B ''与BC 交于点F ，B C ''与AB 交于点E ．他们认为ED FD AC +=．他们的认识是否正确？请说明理由．再探发现（3）解决完上面两个问题后，“实践小组”的同学们在图3中连接OD ，他们认为DF ，DE 与OD 也具有一定的数量关系．请你写出这个数量关系______．（不要求证明）【考向二 全等三角形一线三等角模型】例题：（2023·全国·九年级专题练习）感知：数学课上，老师给出了一个模型：如图1，点A 在直线DE 上，且90BDA BAC AEC ∠=∠=∠=︒，像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型．应用：(1)如图2，Rt ABC △中，90，ACB CB CA ∠=︒=，直线ED 经过点C ，过A 作AD ED ⊥于点D ，过B 作BE ED ⊥于点E ．求证：BEC CDA ≌．(2)如图3，在ABC 中，D 是BC 上一点，90，，CAD AC AD ∠=︒=，23DBA DAB AB ∠=∠=，求点C 到AB 边的距离．(3)如图4，在ABCD 中，E 为边BC 上的一点，F 为边AB 上的一点．若，10，6DEF B AB BE ∠=∠==，求EF DE 的值．【变式训练】一、选择题1．（2022秋·八年级课时练习）如图，在∠ABC 中，AB ＝AC ＝9，点E 在边AC 上，AE 的中垂线交BC 于点D ，若∠ADE ＝∠B ，CD ＝3BD ，则CE 等于（ ）A ．3B ．2C ．94D ．92 二、解答题2．（2022秋·广东惠州·八年级校考期中）如图1，90ACB AC BC AD CE BE CE ∠==⊥⊥，，，，垂足分别为D ，E ．(1)若 2.5cm 1.7cm AD DE ==，，求BE 的长．(2)在其它条件不变的前提下，将CE 所在直线变换到ABC 的外部（如图2），请你猜想AD DE BE ，，三者之间的数量关系，并证明你的结论；(3)如图3，将（1）中的条件改为：在ABC 中，AC BC =，D ，C ，E 三点在同一条直线上，并且有BEC ADC BCA α∠=∠=∠=，其中α为任意钝角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．3．（2022秋·云南昭通·八年级校考期末）在ABC 中，90o ACB AC BC ∠＝，＝，直线MN 经过点C ，且AD MN ⊥于D ，BE MN ⊥于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：①ACD CEB ≌；②DE AD BE ＝＋．(2)当直线MN 绕点C 旋转到图2的位置时，求证：DE AD BE -＝；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE AD BE 、、具有怎样的等量关系？请写出这个等量关系，并加以证明．4．（2022秋·全国·八年级专题练习）已知，在ABC 中，AB AC =，D A E ，，三点都在直线m 上，且9DE cm BDA AEC BAC =∠=∠=∠，．(1)如图①，若AB AC ⊥，则BD 与AE 的数量关系为 ___________，CE 与AD 的数量关系为 ___________；(2)如图②，判断并说明线段BD ，CE 与DE 的数量关系；(3)如图③，若只保持7BDA AEC BD EF cm ∠=∠==，，点A 在线段DE 上以2cm/s 的速度由点D 向点E 运动，同时，点C 在线段EF 上以cm /s x 的速度由点E 向点F 运动，它们运动的时间为s t （）．是否存在x ，使得ABD △与EAC 全等？若存在，求出相应的t 的值；若不存在，请说明理由．5．（2022秋·八年级课时练习）【问题解决】（1）已知∠ABC 中，AB =AC ，D ，A ，E 三点都在直线l 上，且有∠BDA =∠AEC =∠BAC ．如图①，当∠BAC =90°时，线段DE ，BD ，CE 的数量关系为：______________；【类比探究】（2）如图②，在（1）的条件下，当0°<∠BAC <180°时，线段DE ，BD ，CE 的数量关系是否变化，若不变，请证明：若变化，写出它们的关系式；【拓展应用】（3）如图③，AC =BC ，∠ACB =90°，点C 的坐标为（-2，0），点B 的坐标为（1，2），请求出点A 的坐标．。

例谈“旋转法”构造全等三角形,外显解题思路与技巧证明三角形全等是解决线段与角相等或和、差、倍、分关系的重要方法，应用“全等三角形”来解题时，通常需要添加辅助线，而很多同学在寻找辅助线的添法时往往感到无从下手，这也是很多学生认为几何比较难的重要原因.平移、旋转和翻折是图形运动中的三种全等变换，经过全等变换后的图形与原图形是全等的. 因此，我们可以借助全等变换的方法帮助我们识别复杂图形中的全等图形，同时我们还可以利用全等变换将分散的条件集中，从而寻求添加辅助线的方法. 本文主要从图形旋转的角度，通过几个具体的例题分析来谈谈什么时候构造旋转，怎样构造旋转，同时如何从学生的角度探索辅助线的叙述方法，从而帮助我们有效的解决问题，现呈现出来，希望得到指正.1. 旋转对应线段例1 已知如图1（1），以△ABC的AB，AC为边向三角形外作等边△ABD，△ACE，连接CD，BE相交于点O.求证：OA平分∠DOE.解析本题是旋转的基本模型，要证OA平分∠DOE，即证∠DOA = ∠EOA.可证∠DOA与∠EOA所在的三角形全等，或者证明∠DOA与∠EOA和同角（或等角）相等.由题目条件易知：AD = AB，∠DAC = ∠BAE，AC = AE，所以△DAC ≌△BAE.即△DAC绕点A逆时针旋转60°与△BAE重合.所以可旋转三角形的重要线段（或对应线段），从而构造三角形全等.方法1 （构造对应高相等）如图1（2），过点A作AP ⊥CD于点P，AQ⊥BE于点Q，则∠APD = ∠AQB = 90°. 因为△DAC ≌△BAE，所以∠ADP = ∠ABQ，AD = AB，所以△ADP ≌△ABQ，所以AP = AQ，又AO = AO，所以△APO ≌△AQO（HL）. 所以∠DOA = ∠EOA，即OA 平分∠DOE.方法2 （构造一般对应线段）如图1（3），在线段BE 上截取BF = DO，因为△DAC ≌△BAE，所以∠ADO = ∠ABF，AD = AB，所以△ADO ≌△ABF，所以∠DOA = ∠BFA，AO = BF，所以∠EOA = ∠BFA. 所以∠DOA = ∠EOA，即OA 平分∠DOE.说明：△DAC绕点A逆时针旋转60°与△BAE重合，在旋转过程中，两个三角形的对应元素始终相等，线段AO 作为△DAC中的线段，在旋转过程中必有某线段AF与之对应，因此可构造△ADO ≌△ABF. 但是我们在叙述辅助线的时候，不易在BE上取点F，使得AF = AO，所以要变换辅助线的叙述方法，在线段BE上截取BF = DO.拓展：如图2，以△ABC的AB、AC为边向三角形外正方形ABDE、ACFG，连接CE交AB于点H，连接BG交CE于点O.求证：（1）BG⊥CE；（2）OA平分∠EOG .说明：还可以向外构造正五边形得到类似的结论.2. 旋转等腰三角形的顶角例2 如图3（1），△ABC是正三角形，△BDC是等腰三角形，且∠BDC = 120°，以点D为顶点作∠MDN = 60°，分别交AB、AC于M、N，连接MN.（1）探索线段BM、CN、MN的数量关系，并加以证明；（2）当M、N分别在边AB、CA的延长线上时，其他条件不变，如图3（2），探索BM、CN、MN之间的数量关系，并给出证明.分析（1）如图3（2），从△BDC是等腰三角形入手，可以将△BDM绕点D旋转120°，则点B落在点C，点M 落在点E，点N、C、E共线，然后证明△MDN ≌△EDN 即可.（2）如图3（4），同理将△BDM绕点D旋转120°，则点B落在点C，点M落在点F，点A、F、C，在共线，然后证明△MDN ≌△FDN即可.解析（1）MN = BM + CN. 如图3（2），延长NC到E，使得CE = BM . 因为△BDC是等腰三角形，且∠BDC = 120°，所以BD = CD，∠DBC = ∠DCB = 30°.又因为△ABC是正三角形，所以∠ABC = ∠ACB = 60°，所以∠MBD = ∠ECD = 90°，所以△BMD ≌△CED （SAS），所以DM = DE，∠BDM = ∠CDE. 因为∠MDN = 60°，∠BDC = 120°，所以∠MDN = ∠EDN = 60°，所以△MDN ≌△EDN（SAS），所以MN = EN. 所以MN = CE + CN，即MN = BM + CN.（2）MN = CN - BM. 如图3（4），在CN上截取CF = BM，由（1）可知∠MBD = ∠FCD = 90°，BD = CD，所以△BMD ≌△CFD（SAS）. 所以DM = DF，∠BDM = ∠CDF，所以∠MDN = ∠FDN = 60°，所以△MDN ≌△FDN（SAS），所以MN = FN. 所以MN = CN - CF，即MN = CN - BM.说明：△BDM绕点D旋转120°，则点B落在点C，点M落在点E，因为∠NCD + ∠ECD = 180°，因此点N、C、E共线. 本题说明点共线比较容易，而当我们在旋转后，证明共线问题较困难时，我们可借鉴本题解析中的方法，转变角度，变换辅助线的叙述方法，来回避共线问题的证明.总结当然，利用“旋转法”添加辅助线的题型还很多，例如旋转30°、60°、90°、120°、150°、180°等. 只要我们心中有“旋转”的思想，在具体问题中注意变换辅助线的方法，通常都会使问题迎刃而解.。

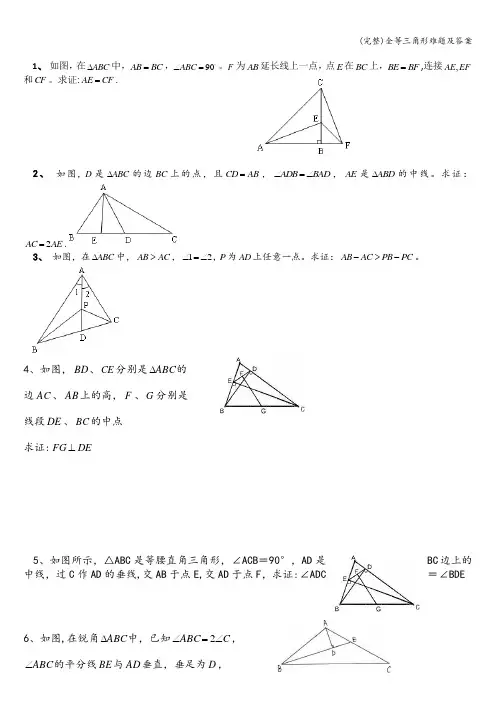
1、 如图，在ABC ∆中，AB BC =，90ABC ∠=。

F 为AB 延长线上一点，点E 在BC 上，BE BF =,连接,AE EF 和CF 。

求证:AE CF =.2、 如图,D 是ABC ∆的边BC 上的点，且CD AB =，ADB BAD ∠=∠，AE 是ABD ∆的中线。

求证：2AC AE =.3、 如图，在ABC ∆中，AB AC >，12∠=∠,P 为AD 上任意一点。

求证：AB AC PB PC ->-。

4、如图，BD 、CE 分别是ABC ∆的边AC 、AB 上的高，F 、G 分别是线段DE 、BC 的中点求证:DE FG ⊥5、如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线,交AB 于点E,交AD 于点F ，求证:∠ADC＝∠BDE6、如图,在锐角ABC ∆中，已知C ABC ∠=∠2,ABC ∠的平分线BE 与AD 垂直，垂足为D ，若cm BD 4=，求AC 的长参考答案1、 思路分析：可以利用全等三角形来证明这两条线段相等，关键是要找到这两个三角形.以线段AE 为边的ABE ∆绕点B 顺时针旋转90到CBF ∆的位置，而线段CF 正好是CBF ∆的边，故只要证明它们全等即可。

解答过程：90ABC ∠=，F 为AB 延长线上一点∴90ABC CBF ∠=∠=在ABE ∆与CBF ∆中AB BC ABC CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴ABE CBF ∆≅∆(SAS)∴AE CF =。

解题后的思考：利用旋转的观点，不但有利于寻找全等三角形，而且有利于找对应边和对应角。

小结：利用三角形全等证明线段或角相等是重要的方法，但有时不容易找到需证明的三角形。

这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。

2、 思路分析：要证明“2AC AE =”，不妨构造出一条等于2AE 的线段，然后证其等于AC 。

旋转已知，如图，三角形ABC是等腰直角三角形，∠ACB=90°，F是AB的中点，直线l经过点C，分别过点A、B作l的垂线，即AD⊥CE,BE⊥CE，（1）如图1，当CE位于点F的右侧时，求证：△ADC≌△CEB；（2)如图2，当CE位于点F的左侧时，求证:ED=BE—AD；（3）如图3,当CE在△ABC的外部时，试猜想ED、AD、BE之间的数量关系,并证明你的猜想．考点:全等三角形的判定与性质．专题：证明题；探究型．分析：(1）利用同角的余角相等得出∠CAD=∠BCE，进而根据AAS证明△ADC≌△CEB．（2）根据AAS证明△ADC≌△CEB后，得其对应边相等，进而得到ED=BE—AD．（3）根据AAS证明△ADC≌△CEB后，得DC=BE，AD=CE，又有ED=CE+DC，进而得到ED=AD+BE．解答：（1)证明：∵AD⊥CE，BE⊥CE，∴∠ADC=∠CEB=90°．∵∠ACD+∠ECB=90°，∠CAD+∠ACD=90°，∴∠CAD=∠BCE（同角的余角相等）．在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ，∴△ADC≌△CEB(AAS）．（2)证明：∵AD⊥CE，BE⊥CE，∴∠ADC=∠CEB=90°．∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°，∴∠CAD=∠BCE（同角的余角相等)．在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ，∴△ADC≌△CEB（AAS）．∴DC=BE，AD=CE．又∵ED=CD—CE,∴ED=BE-AD．（3）ED=AD+BE．证明:∵AD⊥CE，BE⊥CE,∴∠ADC=∠CEB=90°．∵∠ACD+∠ECB=90°，∠CAD+∠ACD=90°，∴∠CAD=∠BCE（同角的余角相等）．在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ，∴△ADC≌△CEB(AAS）．∴DC=BE,AD=CE．又∵ED=CE+DC，∴ED=AD+BE．点评：本题考查了全等三角形的判定和性质;利用全等三角形的对应边相等进行等量交换，证明线段之间的数量关系,这是一种很重要的方法，注意掌握3。

专题6类比探究—图形旋转中三角形全等题型知识归纳几何类比探究题是近几年中招考试的必考题型，目前位于解答题的最后一题，分值为11分或12分．主要考查方式有求线段长，求角度，判断图形形状，判断两条线段的数量关系和位置关系并证明，考查知识点主要涉及特殊三角形，勾股定理，四边形的判定与性质，全等、相似三角形的判定及性质，二次函数等，综合性较强。

本专题主要对类比探究—图形旋转中三角形全等题型进行总结，对其解法进行归纳总结，所选题型为近几年期末考试中的常考题型。

解题思路总结图形的类比探究常以三角形、四边形为背景，与翻折、旋转相结合，考查三角形全等或相似的性质与判定，难度较大．此类题目第一问相对简单，后面的问题需要结合第一问的方法进行类比解答．根据其特征大致可分为：几何变换类比探究问题、旋转综合问题、翻折类问题等。

解决此类问题要善于将复杂图象分解为几个基本图形，通过添加副主席补全或构造基本图形，借助转化、方程、数形结合、分类讨论等数学思想解决几何证明问题，计算则把几何与代数知识综合起来，渗透数形结合思想，考查学生分析问题的能力、逻辑思维和推理能力.常考题型专练一、解答题1.如图1，△ABC和△DCE都是等边三角形．探究发现（1）△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由．拓展运用（2）若B、C、E三点不在一条直线上，∠ADC＝30°，AD＝3，CD＝2，求BD的长．（3）若B、C、E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为1和2，求△ACD的面积及AD 的长．2.在△ABC中，∠BAC＝90°，点O是斜边BC上的一点，连接AO，点D是AO上一点，过点D分别作DE AB∥，DF AC∥，交BC于点E、F．（1）如图1，若点O为斜边BC的中点，求证：点O是线段EF的中点．（2）如图2，在（1）的条件下，将△DEF绕点O顺时针旋转任意一个角度，连接AD，CF，请写出线段AD和线段CF的数量关系，并说明理由．（3）如图3，若点O是斜边BC的三等分点，且靠近点B，当∠ABC＝30°时，将△DEF绕点O顺时针旋转任意一个角度，连接AD、BE、CF，请求出BEAD的值．3.在等腰直角三角形ABC中,∠ACB＝90°,AC＝BC,D是AB边上的中点，Rt△EFG的直角顶点E在AB边上移动.(1)如图1，若点D与点E重合且EG⊥AC、DF⊥BC，分别交AC、BC于点M、N，易证EM＝EN；如图2，若点D与点E重合，将△EFG绕点D旋转，则线段EM与EN的长度还相等吗?若相等请给出证明，不相等请说明理由；(2)将图1中的Rt△EGF绕点O顺时针旋转角度α(0∘＜α＜45∘).如图2，在旋转过程中,当∠MDC＝15∘时，连接MN，若AC＝BC＝2，请求出写出线段MN的长；(3)图3,旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合)，当AB＝3AE时，线段EM与EN 的数量关系是________；当AB＝m·AE时，线段EM与EN的数量关系是__________.4.(1)问题发现：如图1，在等边ABC ∆中，点D 为BC 边上一动点，//DE AB 交AC 于点E ，将AD 绕点D 顺时针旋转60︒得到DF ，连接CF ．则AE 与FC 的数量关系是_____，ACF ∠的度数为______．(2)拓展探究：如图2，在 Rt ABC ∆中，90ABC ∠=︒，60ACB ∠=︒，点D 为BC 边上一动点，//DE AB 交AC 于点E ，当∠ADF=∠ACF=90°时，求AE FC 的值．(3)解决问题：如图3，在ABC ∆中，:BC AB m =，点D 为BC 的延长线上一点，过点D 作//DE AB 交AC 的延长线于点E ，直接写出当ADF ACF ABC ∠=∠=∠时AE FC 的值．5.在等边△ABC 中，点D 是BC 边上一点，点E 是直线AB 上一动点，连接DE，将射线DE 绕点D 顺时针旋转120°，与直线AC 相交于点F ．（1）若点D 为BC 边中点．①如图1，当点E 在AB 边上，且DE AB ⊥时，请直接写出线段DE 与DF 的数量关系________；②如图2，当点E 落在AB 边上，点F 落在AC 边的延长线上时，①中的结论是否仍然成立？请结合图2说明理由；（2）如图3，点D 为BC 边上靠近点C 的三等分点．当:3:2AE BE =时，直接写出CF AF 的值．6.在ABCD 中，BAD ∠=α，以点D 为圆心，适当的长度为半径画弧，分别交边AD 、CD 于点M 、N ，再分别以M 、N 为圆心，大于 MN 的长为半径画弧，两弧交于点K ，作射线DK ，交对角线AC 于点G ，交射线AB 于点E ，将线段EB 绕点E 顺时针旋转α得线段EP ．（1）如图1，当120α=︒时，连接AP ，线段AP 和线段AC 的数量关系为；（2）如图2，当90α=︒时，过点B 作BF EP ⊥于点F ，连接AF ，请求出∠FAC 的度数，以及AF ，AB ，AD 之间的数量关系，并说明理由；（3）当120α=︒时，连接AP ，若13BE AB =，请直接写出线段AP 与线段DG 的比值．7.在数学兴趣小组活动中，小亮进行数学探究活动．（1）△ABC是边长为3的等边三角形，E是边AC上的一点，且AE=1，小亮以BE为边作等边三角形BEF，如图（1）所示．则CF的长为．（直接写出结果，不说明理由）（2）△ABC是边长为3的等边三角形，E是边AC上的一个动点，小亮以BE为边作等边三角形BEF，如图（2）所示．在点E从点C到点A的运动过程中，求点F所经过的路径长．思路梳理并填空：当点E不与点A重合时，如图，连结CF，∵△ABC、△BEF都是等边三角形∴BA=BC，BE=BF，∠ABC=∠EBF=60°∴①∠ABE+=∠CBF+；∴∠ABE=∠CBF∴△ABE≌△CBF∴∠BAE=∠BCF=60°又∠ABC=60°∴∠BCF=∠ABC∴②______∥______；当点E在点A处时，点F与点C重合．当点E在点C处时，CF=CA．∴③点F所经过的路径长为．（3）△ABC是边长为3的等边三角形，M是高CD上的一个动点，小亮以BM为边作等边三角形BMN，如图（3）所示．在点M从点C到点D的运动过程中，求点N所经过的路径长．（4）正方形ABCD的边长为3，E是边CB上的一个动点，在点E从点C到点B的运动过程中，小亮以B为顶点作正方形BFGH，其中点F，G都在直线AE上，如图（4）．当点E到达点B时，点F，G，H与点B重合．则点H所经过的路径长为．（直接写出结果，不说明理由）8．如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；（3）拓展延伸把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值．。

旋转背景下三角形全等的相关问题全等三角形是两个三角形最简单、最常见的关系。

它不仅是学习相似三角形、平行四边形、圆等知识的基础，并且是证明线段相等、角相等的常用方法，也是证明两线互相垂直、平行的重要依据。

平移、旋转、翻折是图形运动中的全等变换，经过全等变换后的图形与原图形是全等的，经过旋转得到的图形与原图形全等。

因此我们可以借助全等变换的方法帮助我们在复杂的图形中找到全等的三角形，同时还可以利用全等变换将分散的条件集中，从而寻求利用三角形全等解决问题的方法。

1、线的旋转例1、如图1（1），在△ABC 中，AB=AC ，∠BAC=90°，AN 是过点A 的任一直线，BD ⊥AN 于D ，CE ⊥AN 于E.求证：BD=AE（2）若将直线AN 绕点A 沿顺时针方向旋转，使它经过△ABC 内部，再作BD ⊥AN D ，CE ⊥AN 于E ，如图1（2）、图1（3），原结论是否不变，请说明理由。

分析：本题为图形旋转证明三角形全等的基本题型，在直线AN 旋转的过程中，∠BAD=∠ACE 与∠ABD=∠CAE 的结论始终是成立的，由同角的余角相等及三角形内角和等于180°的定理可证明（证明方法不唯一）。

由已知条件AB=AC ，可证明△ABD ≌△CAE(A.A.S)，从而证明BD=AE 。

该结论对图（2）、图（3）仍然成立。

说明：此题为直线旋转，条件不变得到全等，△ABD ≌△CAE 始终成立，求证线段BD=AE 与线段AD=CE 方法相同，是需要掌握的基本题型。

图1（1）NEDCBA图1（2）NEDCBAA图1（3）NEDCB拓展：条件不变，求证线段DE 、BD 、CE 之间的等量关系，说明：结论虽然会因为直线AN 位置的不同而不同，但证明方法都是由证△ABD ≌△CAE 入手。

2、图形的旋转例2、如2（1）中，△AOB 与△COD 均是等腰直角三角形，∠AOB=∠COD=90°.（1） 在图2（1）中，AC 与BD 相等吗，有怎样的位置关系？请说明理由。

图1CB图2CB 第12-13讲 全等三角形旋转综合题例1．如图1，△ABC 是正三角形，△BDC 是等腰三角形，BD=CD ，∠BDC=1200，以D 为顶点作一个600角，角的两边分别交AB 、AC 边于M 、N 两点，连接MN. （1）探究BM 、MN 、NC 之间的关系，并说明理由. （2）若△ABC 的边长为2，求△AMN 的周长.（3）若点M 、N 分别是射线AB 、CA 上的点，其他条件不变，此时（1）中的结论是否还成立，在图2中画出图形，并说明理由.练：在等边三角形ABC 的两边AB 、AC 所在直线上分别由两点M,N,D 为ABC ∆外一点，且︒=∠︒=∠120,60BDC MDN ,BD=CD.探究：当点M,N 分别在直线AB ，AC 上移动时，BM,NC,MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系。

（1）如图（1），当点M 、N 在边AB 、AC 上，且DM=DN 时，BM 、NC 、MN 之间的数量关系是_________；此时_______=LQ(2)如图（2），当点M 、N 在边AB 、AC 上，且DM ≠DN 时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明。

（3）如图（3），当点M 、N 分别在边AB 、CA 的延长线上时，若x AN =，则Q=______(用L x ,表示)（3）(2)(1)例2．如图1，E 、F 分别在正方形ABCD 的边BC 、CD 上，且∠EAF ＝45°。

（1）请猜测线段EF 、BE 、DF 之间的等量关系并证明。

（2）变式：如图2，E 、F 分别在四边形ABCD 的边BC 、CD 上，∠B ＋∠D ＝180°，AB ＝AD ，∠EAF ＝12∠BAD ，则线段BE 、EF 、FD 的等量关系又如何？请加以证明。

（3）应用：在条件（2）中，若∠BAD ＝120°，AB ＝AD ＝1，BC ＝CD （如图3），求此时△CEF 的周长。

1、如图13－1，一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图13－2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 满足的数量关系，并证明你的猜想；（2）若三角尺GEF 旋转到如图13－3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．2、如图，在Rt△ABC 和Rt△DEF 中，∠ABC=90°，AB=4，BC=6，∠DEF=90°，DF=EF=4.3、(1)移动△DEF，使边DE 与AB 重合(如图1)，再将△DEF 沿AB 所在直线向左平移，使点F 落在AC 上(如图2)，求BE 的长；(2)将图2中的△DEF 绕点A 顺时针旋转，使点F 落在BC 上，连接AF(如图3).请找出图中的全等三角形，并说明它们全等的理由(不再添加辅助线，不再标注其他字母).4、(本题10分)填空或解答：点B 、C 、E 在同一直线上，点A 、D 在直线CE 的同侧，AB ＝AC ，EC ＝ED ，∠BAC ＝∠CED ，直线AE 、BD 交于点F 。

(1)如图①，若∠BAC ＝60°，则∠AFB ＝_________；如图②，若∠BAC ＝90°，则∠AFB ＝_________； (2)如图③，若∠BAC ＝α，则∠AFB ＝_________(用含α的式子表示)；(3)将图③中的△ABC 绕点C 旋转(点F 不与点A 、B 重合)，得图④或图⑤。

在图④中，∠AFB 与∠α的数量关系是________________；在图⑤中，∠AFB 与∠α的数量关系是________________。

全等三角形的的性质与判定难题50道1．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），⋯，按此方式依次操作，则第6个正六边形的边长为( )A ．511()32a ⨯B ．511()23a ⨯C ．611()32a ⨯D ．611()23a ⨯2．如图，在等边ABC ∆中，点D ，E 分别在边BC ，AC 上，且//DE AB ，过点E 作EF DE ⊥，交BC 的延长线于点F ，（1）求F ∠的度数；（2）若3CD =，求DF 的长．3．数学课上，李老师出示了如下的题目：“在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED EC =，如图，试确定线段AE 与DB 的大小关系，并说明理由”． 小敏与同桌小聪讨论后，进行了如下解答： （1）特殊情况，探索结论当点E 为AB 的中点时，如图1，确定线段AE 与DB 的大小关系，请你直接写出结论：AEDB （填“>”，“ <”或“=” )． （2）特例启发，解答题目解：题目中，AE 与DB 的大小关系是：AE DB （填“>”，“ <”或“=” )．理由如下：如图2，过点E 作//EF BC ，交AC 于点F ．（请你完成以下解答过程） （3）拓展结论，设计新题在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED EC =．若ABC ∆的边长为1，2AE =，求CD 的长（请你直接写出结果）．4．如图，过等边ABC ∆的边AB 上一点P ，作P E A C ⊥于E ，Q 为BC 延长线上一点，且PA CQ =，连PQ 交AC 边于D ． （1）求证：PD DQ =；（2）若ABC ∆的边长为1，求DE 的长．5．如图所示，已知等边ABC ∆的边长为a ，P 是ABC ∆内一点，//PD AB ，//PE BC ，//PF AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++= ，并证明你的猜想．6．如图，已知ABC ∆和CDE ∆均为等边三角形，且点B 、C 、D 在同一条直线上，连接AD 、BE ，交CE 和AC 分别于G 、H 点，连接GH ．（1）请说出AD BE =的理由； （2）试说出BCH ACG ∆≅∆的理由；（3）试猜想：CGH ∆是什么特殊的三角形，并加以说明．7．如图，已知ABC ∆是边长为6cm 的等边三角形，动点P ，Q 同时从A 、B 两点出发，分别沿AB 、BC 方向匀速运动，其中点P 运动的速度是1/cm s ，点Q 运动的速度是2/cm s ，当点Q 运动到点C 时，P ，Q 都停止运动．（1）出发后运动2s 时，试判断BPQ ∆的形状，并说明理由；那么此时PQ 和AC 的位置关系呢？请说明理由；（2）设运动时间为t ，BPQ ∆的面积为S ，请用t 的表达式表示S ．8．已知：在等边ABC ∆中，点D 、E 、F 分别为边AB 、BC 、AC 的中点，点G 为直线BC 上一动点，当点G 在CB 延长线上时，有结论“在直线EF 上存在一点H ，使得DGH ∆是等边三角形”成立（如图①)，且当点G 与点B 、E 、C 重合时，该结论也一定成立． 问题：当点G 在直线BC 的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．9．已知点C 为线段AB 上一点，分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆，且CA CD =，CB CE =，ACD BCE ∠=∠，直线AE 与BD 交于点F ，（1）如图1，若60ACD ∠=︒，则AFB ∠= ；如图2，若90ACD ∠=︒，则AFB ∠= ；如图3，若120ACD ∠=︒，则AFB ∠= ；（2）如图4，若ACD α∠=，则AFB ∠= （用含α的式子表示）；（3）将图4中的ACD ∆绕点C 顺时针旋转任意角度（交点F 至少在BD 、AE 中的一条线段上），变成如图5所示的情形，若ACD α∠=，则AFB ∠与α的有何数量关系？并给予证明．10．如图1，ABC ∆为等边三角形，面积为S ．1D 、1E 、1F 分别是ABC ∆三边上的点，且11112AD BE CF AB ===，连接11D E 、11E F 、11F D ，可得△111D E F 是等边三角形，此时△11AD F 的面积114S S =，△111D E F 的面积114S S =． （1）当2D 、2E 、2F 分别是等边ABC ∆三边上的点，且22213AD BE CF AB ===时如图2，①求证：△222D E F 是等边三角形；②若用S 表示△22AD F 的面积2S ，则2S = ；若用S 表示△222D E F 的面积2S '，则2S '= ．（2）按照上述思路探索下去，并填空：当n D 、n E 、n F 分别是等边ABC ∆三边上的点，11n n n AD BE CF AB n ===+时，(n 为正整数）△n n n D E F 是 三角形；若用S 表示△n n AD F 的面积n S ，则n S = ；若用S 表示△n n n D E F 的面积n S '，则n S '= ．11．如图，在等边ABC ∆的三边上分别取点D 、E 、F ，使AD BE CF ==． （1）试说明DEF ∆是等边三角形；（2）连接AE 、BF 、CD ，两两相交于点P 、Q 、R ，则PQR ∆为何种三角形？试说明理由．12．如图所示，一个六边形的六个内角都是120︒，其中连续四边的长依次是1、9、9、5．求这个六边形的周长．13．如图，已知D 是ABC ∆的边BC 上的一点，CD AB =，BDA BAD ∠=∠，AE 是ABD ∆的中线．（1）若60B ∠=︒，求C ∠的值； （2）求证：AD 是EAC ∠的平分线．14．如图，ABC ∆为等边三角形，BD 平分ABC ∠交AC 于点D ，//DE BC 交AB 于点E ． （1）求证：ADE ∆是等边三角形．（2）求证：12AE AB =．15．如图．在等边ABC ∆中，ABC ∠与ACB ∠的平分线相交于点O ，且//OD AB ，//OE AC ． （1）试判定ODE ∆的形状，并说明你的理由；（2）线段BD 、DE 、EC 三者有什么关系？写出你的判断过程．16．如图，ABC ∆是等边三角形，DF AB ⊥，DE CB ⊥，EF AC ⊥，求证：DEF ∆是等边三角形．17．用三根火柴棒可以搭成一个等边三角形，你能用9根火柴搭出5个等边三角形吗？ 18．如图，ABC ∆是等边三角形，AD 是高，并且AB 恰好是DE 的垂直平分线． 求证：ADE ∆是等边三角形．19．如图，60AOB ∠=︒，OC 平分AOB ∠，C 为角平分线上一点，过点C 作CD OC ⊥，垂足为C ，交OB 于点D ，//CE OA 交OB 于点E ． （1）判断CED ∆的形状，并说明理由；（2）若3OC=，求CD的长．20．如图，在ABC∆中，AB AC=，120BAC∠=︒，D、F分别为AB、AC的中点，且DE AB⊥，FG AC⊥，点E、G在BC上，18BC cm=，求线段EG的长．（提示：需要添加辅助线）21．已知，如图，ABC∆是正三角形，D，E，F分别是各边上的一点，且AD BE CF==．请你说明DEF∆是正三角形．22．如图所示，DEF∆是等边三角形，且123∠=∠=∠，试问：ABC∆是等边三角形吗？请说明理由．23．如图，ABC∆为等边三角形，BD平分ABC∠，//DE BC．（1）求证：ADE∆是等边三角形；（2）求证：12AE AB=．24．如图ABC∆是等边三角形（1）如图①，//∆是等边三角形；DE BC，分别交AB、AC于点D、E．求证：ADE（2）如图②，ADE∆仍是等边三角形，点B在ED的延长线上，连接CE，判断BEC∠的度数及线段AE、BE、CE之间的数量关系，并说明理由．25．如图，E是AOB⊥，C、D是垂足，连接CD ∠的平分线上一点，EC OB⊥，ED OA交OE于点F，若60∠=︒．AOB（1）求证：OCD∆是等边三角形；（2）若5EF=，求线段OE的长．26．如图，ABCBCD CBE∠=∠=︒，BAC∆中，60∠=︒，点D、E分别在AB、AC上，30 BE、CD相交于点O，OG BC+=．OE OD OG⊥于点G，求证：227．如图，在ABC∠=∠=︒，EBC E∠，60∆中，AB AC=，D、E是ABC∆内两点，AD平分BAC若30=，则BC=cm．DE cmBE cm=，228．如图，已知ABC=，∆为等边三角形，D为BC延长线上的一点，CE平分ACD∠，CE BD 求证：ADE∆为等边三角形．29．如图，ABC∆∠=︒，DE与ABC ∆为等边三角形，D为BC边上一点，以AD为边作60ADE的外角平分线CE交于点E，连接AE，且CE BD∆是等边三角形．=．求证：ADE30．如图，在ABC+=．求ABD∠=︒，BD DC AB ∆中，AB AC=，D是三角形外一点，且60证：60∠=︒．ACD31．如图，在等边ABCOD AB，//OE AC．∠与ACB∠的平分线相交于点O，且//∆中，ABC（1）求证：ODE∆是等边三角形．（2）线段BD、DE、EC三者有什么数量关系？写出你的判断过程．（3）数学学习不但要能解决问题，还要善于提出问题．结合本题，在现有的图形上，请提出两个与“直角三角形”有关的问题．（只要提出问题，不需要解答）32．已知：如图，在ABC∠=︒，BD是中线，延长BC至点E，使C E C D=．A=，60∆中，AB AC求证：DB DE=．33．如图，ABD∆和BCD∆均是边长为2的等边三角形，E、F分别是AD、CD上的两个动点，且满足2+=．AE CF（1）求证：BDE BCF∆≅∆；（2）判断BEF∆的形状，并说明理由．34．已知：如图，四边形ABCD中，AB BC CD DA a∠=︒，M为BC上====，120BAD的点(M不与B、C重合），若AMN∆有一角等于60︒．（1）当M 为BC 中点时，则ABM ∆的面积为 （结果用含a 的式子表示）； （2）求证：AMN ∆为等边三角形；（3）设AMN ∆的面积为S ，求出S 的取值范围（结果用含a 的式子表示）．35．如图，点O 是等边ABC ∆内一点，110AOB ∠=︒，BOC α∠=，将B O C ∆绕点C 按顺时针方向旋转60︒得ADC ∆，连接OD ． （1）COD ∆是什么三角形？说明理由；（2）若21AO n =+，21AD n =-，2(OD n n =为大于1的整数），求α的度数； （3）当α为多少度时，AOD ∆是等腰三角形？36．已知：如图，ABC ∆、CDE ∆都是等边三角形，AD 、BE 相交于点O ，点M 、N 分别是线段AD 、BE 的中点． （1）求证：AD BE =； （2）求DOE ∠的度数；（3）求证：MNC ∆是等边三角形．37．已知：在AOB ∆和COD ∆中，OA OB =，OC OD =．（1）如图①，若60AOB COD ∠=∠=︒，求证：①AC BD =②60APB ∠=︒．（2）如图②，若A O B C O D α∠=∠=，则AC 与BD 间的等量关系式为 ，APB ∠的大小为 （直接写出结果，不证明）38．如图，ABC ∆是等边三角形，D 是AC 上一点，BD CE =，12∠=∠，试判断ADE ∆形状，并证明你的结论．39．等边ABC ∆边长为6，P 为BC 上一点，含30︒、60︒的直角三角板60︒角的顶点落在点P 上，使三角板绕P 点旋转．（1）如图1，当P 为BC 的三等分点，且PE AB ⊥时，判断EPF ∆的形状；（2）在（1）问的条件下，FE 、PB 的延长线交于点G ，如图2，求EGB ∆的面积； （3）在三角板旋转过程中，若2CF AE ==，()CF BP ≠，如图3，求PE 的长．40．为了使同学们更好地解答本题，我们提供了思路点拨，你可以依照这个思路填空，并完成本题解答的全过程，当然你也可以不填空，只需按照解答的一般要求，进行解答即可． 如图，已知AB AD =，60BAD ∠=︒，120BCD ∠=︒，延长BC ，使C E C D =，连接DE ，求证：BC DC AC +=． 思路点拨：（1）由已知条件AB AD=，60BAD∠=︒，可知：ABD∆是三角形；（2）同理由已知条件120BCD∠=︒得到DCE∠=，且CE CD=，可知；（3）要证BC DC AC+=，可将问题转化为两条线段相等，即=；（4）要证（3）中所填写的两条线段相等，可以先证明⋯．请你完成证明过程：41．已知ABC∆是等边三角形，点P是AC上一点，PE BC⊥于点E，交AB于点F，在CB 的延长线上截取BD PA=，PD交AB于点I，PA nPC=．（1）如图1，若1n=，则EBBD=，FIED=；（2）如图2，若60EPD∠=︒，试求n和FIED的值；（3）如图3，若点P在AC边的延长线上，且3n=，其他条件不变，则EBBD=．（只写答案不写过程）42．如图ABC∆为等边三角形，直线//a AB，D为直线BC上任一动点，将一60︒角的顶点置于点D处，它的一边始终经过点A，另一边与直线a交于点E．（1）若D恰好在BC的中点上（如图1)求证：ADE∆是等边三角形；（2）若D为直线BC上任一点（如图2)，其他条件不变，上述（1）的结论是否成立？若成立，请给予证明；若不成立，请说明理由．43．如图，在等边ABC=，点P从点C出发沿CB边向点B点以2/cm s的速AB cm∆中，9度移动，点Q点从B点出发沿BA边向A点以5/cm s速度移动．P、Q两点同时出发，它们移动的时间为t秒钟．（1）你能用t表示BP和BQ的长度吗？请你表示出来．（2）请问几秒钟后，PBQ∆为等边三角形？（3）若P、Q两点分别从C、B两点同时出发，并且都按顺时针方向沿ABC∆三边运动，请问经过几秒钟后点P与点Q第一次在ABC∆的哪条边上相遇？44．如图：在ABC⊥于Q．==，AE CD∆中，AB BC AC=，AD与BE相交于点P，BQ AD求证：①ADC BEA∆≅∆；②2=．BP PQ45．如图1，点B是线段AD上一点，ABC∆分别是等边三角形，连接AE和CD．∆和BDE（1）求证：AE CD=；（2）如图2，点P、Q分别是AE、CD的中点，试判断PBQ∆的形状，并证明．46．如图：已知ABC∆是等边三角形，D、E、F分别是AB、AC、BC边的中点，M是直线BC上的任意一点，在射线EF上截取EN，使EN FM=，连接DM、MN、DN．（1）如图①，当点M在点B左侧时，请你按已知要求补全图形，并判断DMN∆是怎样的特殊三角形（不要求证明）；（2）请借助图②解答：当点M在线段BF上（与点B、F不重合），其它条件不变时，（1）中的结论是否依然成立？若成立，请证明；若不成立，请说明理由；（3）请借助图③解答：当点M在射线FC上（与点F不重合），其它条件不变时，（1）中的结论是否仍然成立？不要求证明．47．如图，ABC∆是等边三角形，点D、E、F分别是线段AB、BC、CA上的点，（1）若AD BE CF∆是等边三角形吗？试证明你的结论；==，问DEF（2）若DEF∆是等边三角形，问AD BE CF==成立吗？试证明你的结论．48．如图，已知ABC=，连∆为等边三角形，延长BC到D，延长BA到E，并且使AE BD 接CE，DE．求证：EC ED=．49．如图，已知ABC ∆与ACD ∆都是边长为2的等边三角形，如图有一个60︒角的三角板绕着点A 旋转分别交BC 、CD 于点P 、Q 两点（不与端点重合）． （1）试说明：PAQ ∆是等边三角形； （2）求四边形APCQ 的面积；（3）填空：当BP = 时，APQ S ∆最小．50．如图，A 、B 、C 三点在同一直线上，ABM ∆和BCN ∆是正三角形，P 是AN 中点，Q 是CM 中点．求证：BPQ ∆是正三角形．全等三角形的的性质与判定难题50道参考答案与试题解析一．选择题（共1小题）1．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），⋯，按此方式依次操作，则第6个正六边形的边长为( )A ．511()32a ⨯B ．511()23a ⨯C ．611()32a ⨯D ．611()23a ⨯【解答】解：连接AD 、DF 、DB ． 六边形ABCDEF 是正六边形，ABC BAF AFE ∴∠=∠=∠，AB AF =，120E C ∠=∠=︒，EF DE BC CD ===， 30EFD EDF CBD BDC ∴∠=∠=∠=∠=︒， 120AFE ABC ∠=∠=︒， 90AFD ABD ∴∠=∠=︒，在Rt ABD ∆和RtAFD 中 AF ABAD AD =⎧⎨=⎩Rt ABD Rt AFD(HL)∴∆≅∆， 1120602BAD FAD ∴∠=∠=⨯︒=︒，60120180FAD AFE ∴∠+∠=︒+︒=︒， //AD EF ∴，G 、I 分别为AF 、DE 中点，////GI EF AD ∴，60FGI FAD ∴∠=∠=︒，六边形ABCDEF 是正六边形，QKM ∆是等边三角形， 60EDM M ∴∠=︒=∠，ED EM ∴=，同理AF QF =， 即AF QF EF EM ===， 等边三角形QKM 的边长是a ，∴第一个正六边形ABCDEF 的边长是13a ，即等边三角形QKM 的边长的13，过F 作FZ GI ⊥于Z ，过E 作EN GI ⊥于N ， 则//FZ EN ， //EF GI ，∴四边形FZNE 是平行四边形，13EF ZN a ∴==，11112236GF AF a a ==⨯=，60FGI ∠=︒（已证）， 30GFZ ∴∠=︒，11212GZ GF a ∴==，同理112IN a =， 1111123122GI a a a a ∴=++=，即第二个等边三角形的边长是12a ，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是1132a ⨯；同理第第三个等边三角形的边长是1122a ⨯，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是111322a ⨯⨯；同理第四个等边三角形的边长是111222a ⨯⨯，第四个正六边形的边长是11113222a ⨯⨯⨯；第五个等边三角形的边长是11112222a ⨯⨯⨯，第五个正六边形的边长是1111132222a ⨯⨯⨯⨯；第六个等边三角形的边长是1111122222a ⨯⨯⨯⨯，第六个正六边形的边长是111111322222a ⨯⨯⨯⨯⨯， 即第六个正六边形的边长是511()32a ⨯，故选：A ．二．解答题（共49小题）2．如图，在等边ABC ∆中，点D ，E 分别在边BC ，AC 上，且//DE AB ，过点E 作EF DE ⊥，交BC 的延长线于点F ，（1）求F ∠的度数；（2）若3CD =，求DF 的长．【解答】解：（1）ABC ∆是等边三角形，60B ∴∠=︒， //DE AB ，60EDC B ∴∠=∠=︒，EF DE ⊥，90DEF ∴∠=︒，9030F EDC ∴∠=︒-∠=︒；（2）60ACB ∠=︒，60EDC ∠=︒，EDC∴∆是等边三角形．∴==，ED DC3∠=︒，F90∠=︒，30DEF∴==．DF DE263．数学课上，李老师出示了如下的题目：“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED EC=，如图，试确定线段AE与DB的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE =DB（填“>”，“<”或“=”)．（2）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE DB（填“>”，“<”或“=”)．理由如下：如图2，过点E作//EF BC，交AC于点F．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED EC∆的边=．若ABC 长为1，2AE=，求CD的长（请你直接写出结果）．【解答】解：（1）故答案为：=．（2）过E作//EF BC交AC于F，等边三角形ABC，∴∠=∠=∠=︒，AB AC BC==，ABC ACB A60AFE ACB∴∠=∠=︒，60∠=∠=︒，AEF ABC60即60∠=∠=∠=︒，AEF AFE A∴∆是等边三角形，AEFAE EF AF ∴==，60ABC ACB AFE ∠=∠=∠=︒，120DBE EFC ∴∠=∠=︒，60D BED FCE ECD ∠+∠=∠+∠=︒，DE EC =，D ECD ∴∠=∠，BED ECF ∴∠=∠，在DEB ∆和ECF ∆中DEB ECF DBE EFC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，DEB ECF ∴∆≅∆，BD EF AE ∴==，即AE BD =，故答案为：=．（3）解：1CD =或3，理由是：分为两种情况：①如图1过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，则//AM EN ，ABC ∆是等边三角形，1AB BC AC ∴===，AM BC ⊥， 1122BM CM BC ∴===， DE CE =，EN BC ⊥，2CD CN ∴=，//AM EN ，AMB ENB ∴∆∆∽， ∴AB BM BE BN=， ∴11221BN=-， 12BN ∴=， 13122CN ∴=+=， 23CD CN ∴==；②如图2，作AM BC ⊥于M ，过E 作EN BC ⊥于N ，则//AM EN ，ABC ∆是等边三角形，1AB BC AC ∴===，AM BC ⊥，1122BM CM BC ∴===， DE CE =，EN BC ⊥，2CD CN ∴=，//AM EN ， ∴AB BM AE MN=， ∴1122MN=， 1MN ∴=，11122CN ∴=-=，21CD CN ∴==，即3CD =或1．4．如图，过等边ABC ∆的边AB 上一点P ，作P E A C ⊥于E ，Q 为BC 延长线上一点，且PA CQ =，连PQ 交AC 边于D ．（1）求证：PD DQ =；（2）若ABC ∆的边长为1，求DE 的长．【解答】（1）证明：如图，过P 做//PF BC 交AC 于点F ，AFP ACB ∴∠=∠，FPD Q ∠=∠，PFD QCD ∠=∠ABC ∆为等边三角形，60A ACB ∴∠=∠=︒，60A AFP ∴∠=∠=︒，APF ∴∆是等边三角形；AP PF =，AP CQ =，PF CQ ∴=PFD QCD ∴∆≅∆，PD DQ ∴=．（2）APF ∆是等边三角形，PE AC ⊥，AE EF ∴=，PFD QCD ∆≅∆，CD DF ∴=，12DE EF DF AC =+=， 1AC =，12DE =． 5．如图所示，已知等边ABC ∆的边长为a ，P 是ABC ∆内一点，//PD AB ，//PE BC ，//PF AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++= a ，并证明你的猜想．【解答】解：PD PE PF a ++=．理由如下：如图，延长EP 交AB 于G ，延长FP 交BC 于H ，//PE BC ，//PF AC ，ABC ∆是等边三角形，60PGF B ∴∠=∠=︒，60PFG A ∠=∠=︒，PFG ∴∆是等边三角形，同理可得PDH ∆是等边三角形，PF PG ∴=，PD DH =，又//PD AB ，//PE BC ，∴四边形BDPG是平行四边形，∴=，PG BD∴++=++==．PD PE PF DH CH BD BC a故答案为a．6．如图，已知ABC∆均为等边三角形，且点B、C、D在同一条直线上，连接AD、∆和CDEBE，交CE和AC分别于G、H点，连接GH．（1）请说出AD BE=的理由；（2）试说出BCH ACG∆≅∆的理由；（3）试猜想：CGH∆是什么特殊的三角形，并加以说明．【解答】解：（1）ABC∆均为等边三角形∆和CDE=∴=，EC DCAC BC∠=∠=︒ACB ECD60∴∠=∠ACD ECBACD BCE∴∆≅∆∴=；AD BE（2）ACD BCE∆≅∆∴∠=∠CBH CAGACB ECD∠=∠=︒，点B、C、D在同一条直线上60∴∠=∠=∠=︒ACB ECD ACG60又AC BC=ACG BCH∴∆≅∆；（3）CGH∆是等边三角形，理由如下：ACG BCH∆≅∆∴=（全等三角形的对应边相等）CG CH又60∠=︒ACG∴∆是等边三角形（有一内角为60度的等腰三角形为等边三角形）；CGH7．如图，已知ABC∆是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1/cm s，cm s，点Q运动的速度是2/当点Q运动到点C时，P，Q都停止运动．（1）出发后运动2s时，试判断BPQ∆的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；（2）设运动时间为t，BPQ∆的面积为S，请用t的表达式表示S．【解答】解：（1）BPQ∆是等边三角形，//PQ AC，（2分）运动至2s时，2AP=，4BQ=，BP AB AP BQ∴=-==（4分）4又ABC∆是边长为6cm的等边三角形∴∠=︒B60∴∆是等边三角形（6分）BPQ∴∠=∠=︒60BPQ A∴．//PQ AC（2）过Q作QH AB⊥于H，=，30∠=︒，BQHBQ t2∴=，QH=．（10分）BH t=-BP t6213(6)3(6)2S t t t t ∴=-=-=+． （12分）8．已知：在等边ABC ∆中，点D 、E 、F 分别为边AB 、BC 、AC 的中点，点G 为直线BC上一动点，当点G 在CB 延长线上时，有结论“在直线EF 上存在一点H ，使得DGH ∆是等边三角形”成立（如图①)，且当点G 与点B 、E、C 重合时，该结论也一定成立． 问题：当点G 在直线BC 的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．【解答】证明：连接DE 、EF 、DF ．（1）当点G 在线段BE 上时，如图①，在EF 上截取EH 使EH BG =．D 、E 、F 是等边ABC ∆三边中点，DEF ∴∆、DBE ∆也是等边三角形且12DE AB BD ==． 在DBG ∆和DEH ∆中，60DB DE DBG DEH BG EH =⎧⎪∠=∠=︒⎨⎪=⎩，()DBG DEH SAS ∴∆≅∆，DG DH ∴=．BDG EDH ∴∠=∠．60BDE GDE BDG ∠=∠+∠=︒，60GDH GDE EDH ∴∠=∠+∠=︒∴在直线EF 上存在点H 使得DGH ∆是等边三角形．（2）当点G 在射线EC 上时，如图②，在EF 上截取EH 使EH BG =．由（1）可证DBG DEH ∆≅∆．DG DH ∴=，BDG EDH ∠=∠．60BDE BDG EDG ∠=∠-∠=︒，60GDH EDH EDG ∴∠=∠-∠=︒．∴在直线EF 上存在点H 使得DGH ∆是等边三角形．（3）当点G 在BC 延长线上时，如图③，与（2）同理可证，结论成立．综上所述，点G 在直线BC 上的任意位置时，该结论成立．9．已知点C 为线段AB 上一点，分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆，且CA CD =，CB CE =，ACD BCE ∠=∠，直线AE 与BD 交于点F ，（1）如图1，若60ACD ∠=︒，则AFB ∠= 120︒ ；如图2，若90ACD ∠=︒，则AFB ∠= ；如图3，若120ACD ∠=︒，则AFB ∠= ；（2）如图4，若ACDα∠=（用含α的式子表示）；∠=，则AFB（3）将图4中的ACD∆绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），变成如图5所示的情形，若ACDα∠与α的有何数量关系？并给予∠=，则AFB证明．【解答】解：（1）如图1，CA CD∠=︒，ACD=，60所以ACD∆是等边三角形．∠=∠=︒，ACD BCE=，60CB CE所以ECB∆是等边三角形．AC DC∠=∠+∠，BCD BCE DCE∠=∠+∠，=，ACE ACD DCE又ACD BCE∠=∠，∴∠=∠．ACE BCDAC DC=，=，CE BC∴∆≅∆．ACE DCB∴∠=∠．EAC BDC∠是ADFAFB∆的外角．∴∠=∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒AFB ADF FAD ADC CDB FAD ADC EAC FAD ADC DAC120．如图2，AC CD=，∠=∠=︒，EC CBACE DCB=，90∴∆≅∆．ACE DCB∴∠=∠，AEC DBC又FDE CDB∠=︒，DCB∠=∠，9090EFD ∴∠=︒．90AFB ∴∠=︒．如图3，ACD BCE ∠=∠，ACD DCE BCE DCE ∴∠-∠=∠-∠．ACE DCB ∴∠=∠．又CA CD =，CE CB =，ACE DCB ∴∆≅∆．EAC BDC ∴∠=∠．180180(180)120BDC FBA DCB ACD ∠+∠=︒-∠=︒--∠=︒， 120FAB FBA ∴∠+∠=︒．60AFB ∴∠=︒．故填120︒，90︒，60︒．（2）ACD BCE ∠=∠，ACD DCE BCE DCE ∴∠+∠=∠+∠．ACE DCB ∴∠=∠．CAE CDB ∴∠=∠．DFA ACD ∴∠=∠．180180180AFB DFA ACD α∴∠=︒-∠=︒-∠=︒-．（3）180AFB α∠=︒-；证明：ACD BCE α∠=∠=，则ACD DCE BCE DCE ∠+∠=∠+∠， 即ACE DCB ∠=∠．在ACE ∆和DCB ∆中AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，则()ACE DCB SAS ∆≅∆．则CBD CEA ∠=∠，由三角形内角和知EFB ECB α∠=∠=． 180180AFB EFB α∠=︒-∠=︒-．10．如图1，ABC ∆为等边三角形，面积为S ．1D 、1E 、1F 分别是ABC ∆三边上的点，且。

全等三角形角6090旋转 易错题难题提优专项训练试题一、全等三角形角6090旋转1．数学课上，王老师出示了问题：如图1，AC ，BD 是四边形ABCD 的对角线，若60ACB ACD ABD ADB ∠=∠=∠=∠=︒，则（1）线段BC ，CD ，AC 三者之间存在等量关系为：______________________； （2）经过思考：小丽、小明和小亮三位同学分别展示了三种正确的思路：如图2，在AC 上取一点E ，使CE CB =，连接BE ；如图3，延长CB 到E ，使BE CD =，连接AE ；如图4，将ABC ∆绕着点A 逆时针旋转60︒．在此基础上，请你选择一种合适的方法证明上述等量关系．（3）小强同学提出：如图5，如果把“60ACB ACD ABD ADB ∠=∠=∠=∠=︒”改为“45ACB ACD ABD ADB ∠=∠=∠=∠=︒”，其它条件不变，那么线段BC ，CD ，AC 三者之间有何等量关系？针对小强提出的问题，请你写出结论，并给出证明．2．如图，在等腰ABC 中，AC ＝AB ，∠CAB ＝90°，E 是BC 上一点，将E 点绕A 点逆时针旋转90°到AD ，连接DE 、CD ．（1）求证：ABE ACD △≌△；（2）当BC ＝6，CE ＝2时，求DE 的长．3．（1）如图1，在正方形ABCD 中，点E 、F 分别是BC 、CD 边上的动点，且∠EAF ＝45°，求证：EF ＝DF+BE ．（2）如图2，在正方形ABCD 中，如果点E 、F 分别是CB 、DC 延长线上的动点，且∠EAF ＝45°，则EF 、BE 、DF 之间数量关系是什么？请写出证明过程．（3）如图1，若正方形ABCD 的边长为6，AE ＝35，求AF 的长．4．如图1，ABC 与CDE △都是等腰直角三角形，直角边AC ，CD 在同一条直线上，点M 、N 分别是斜边AB 、DE 的中点，点P 为AD 的中点，连接AE ，BD ，PM ，PN ，MN ．（1）观察猜想：图1中，PM 与PN 的数量关系是______，位置关系是______．（2）探究证明：将图1中的CDE △绕着点C 顺时针旋转()090αα︒<<︒，得到图2，AE 与MP 、BD 分别交于点G 、H ，判断PMN 的形状，并说明理由；（3）拓展延伸：把CDE △绕点C 任意旋转，若4AC =，2CD =，请直接写出PMN 面积的最大值． 5．已知，四边形ABCD 中，,,,120,60AB AD BC CD BA BC ABC MBN ︒︒⊥⊥=∠=∠=，MBN ∠绕B 点旋转，它的两边分别交,AD DC （或它们的延长线）于E ，F ．当MBN ∠绕B 点旋转到AE CF =时，如图（1），易证：AE CF EF +=．当MBN ∠绕B 点旋转到AE CF ≠时，在图（2）和图（3）中这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段,,AE CF EF 又有怎样的数量关系？请写出你的猜想，不需证明．6．如图，BC 为等边△ABM 的高，AB ＝52，点P 为射线BC 上的动点（不与点B ，C 重合），连接AP ，将线段AP 绕点P 逆时针旋转60°，得到线段PD ，连接MD ，BD ． （1）如图①，当点P 在线段BC 上时，求证：BP ＝MD ；（2）如图②，当点P 在线段BC 的延长线上时，求证：BP ＝MD ；（3）若点P 在线段BC 的延长线上，且∠BDM ＝30°时，请直接写出线段AP 的长度．7．如图1，已知△ABC 是边长为8的等边三角形，∠EBD ＝30°，BE ＝DE ，连接AD ，点F 为AD 的中点，连接EF ．将△BDE 绕点B 顺时针旋转．（1）如图2，当点E 位于BC 边上时，延长DE 交AB 于点G ．①求证：BG ＝DE ；②若EF ＝3，求BE 的长；（2）如图3，连接CF ，在旋转过程中试探究线段CF 与EF 之间满足的数量关系，并说明理由．8．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 是BC 上一动点、连接AD ，过点A 作AE AD ⊥，并且始终保持AE AD =，连接CE ，（1）求证：ABD ACE ≅；（2）若AF 平分DAE ∠交BC 于F ，①探究线段BD ，DF ，FC 之间的数量关系，并证明；②若3BD =，4CF =，求AD 的长，9．在Rt ABC 中，ACB =∠90°，30A ∠=︒，点D 是AB 的中点，连结CD ．（1）如图①，BC 与BD 之间的数量关系是_________，请写出理由；（2）如图②，若P 是线段CB 上一动点（点P 不与点B 、C 重合），连结DP ，将线段DP 绕点D 逆时针旋转60°，得到线段DF ，连结BF ，请猜想BF ，BP ，BD 三者之间的数量关系，并证明你的结论；（3）若点P 是线段CB 延长线上一动点，按照（2）中的作法，请在图③中补全图形，并直接写出BF ，BP ，BD 三者之间的数量关系．10．已知90ACD ∠=︒，MN 是过点A 的直线，AC DC =，DB MN ⊥于点B ，如图（1）所示.易证BD AB 2CB +=，过程如下：过点C 作CE CB ⊥于点C ，与MN 交于点E90ACB BCD ∠+∠=︒，90ACB ACE ∠+∠=︒，BCD ACE ∴∠=∠.四边形ACDB 内角和为360︒，180BDC CAB ∴∠+∠=︒.180EAC CAB ∠+∠=︒，EAC BDC ∴∠=∠.又AC DC =，ACE DCB ∴∆≅∆，AE DB ∴=，CE CB =，ECB ∴∆为等腰直角三角形BE 2CB ∴=.又BE AE AB =+，BE BD AB ∴=+，BD AB 2CB ∴+=.（1）当MN 绕A 旋转到如图（2）所示和如图（3）所示两个位置时，BD 、AB 、CB 满足什么样关系式，请写出你的猜想，并对如图所示给予证明.（2）MN 在绕点A 旋转过程中，当30BCD ∠=︒，2BD =时，则CD =______，CB =______.【参考答案】***试卷处理标记，请不要删除一、全等三角形角6090旋转1．（1）BC CD AC +=；（2）见解析；（3）2BC CD AC +=，见解析【分析】（1）与（2）中的证明一证法一样；（2）添加不同的辅助线证明一：如图2，在AC 上取一点E ，使CE CB =，连接BE ；证明二：延长CB 到E ，使BE CD =，连接AE ；证明三：将ABC ∆绕着点A 逆时针旋转60︒，分别证明两三角形全等，再根据全等三角形的性质及等量代换即可得证；（3）先证出ABE ADC ∠=∠，再证明ABE ∆≌ADC ∆，最后利用勾股定理得出结果．【详解】（1）BC CD AC +=；（2）3种证明方法均可证明一：如图2，在AC 上取一点E ，使CE CB =，连接BE∵60ACB ∠=︒，∴BCE ∆为等边三角形，∴,60BE BC CE CBE ==∠=︒，又∵60ABD ADB ∠=∠=︒，∴ABD ∆为等边三角形，∴AB BD =，60ABE EBD DBC ∠=︒-∠=∠，在ABE ∆和DBC ∆中,AB BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩，∴ABE ∆≌DBC ∆，∴AE CD =∴BC CD CE AE AC +=+=；证明二：如图3，延长CB 到E ，使BE CD =，连接AE若AC 与BD 交于O 点，∵60ABD ACD ∠=∠=︒，AOB DOC ∠=∠∴12∠=∠，∴31160ACB ∠=∠+∠=∠+︒，2260ADC ADB ∠=∠+∠=∠+︒，∴3ADC ∠=∠在AEB ∆和ACD ∆中，,3AB AD ADC BE CD =⎧⎪∠=∠⎨⎪=⎩，∴AEB ∆≌ACD ∆∴AE AC =，而60ACE ∠=︒，∴ACE ∆为等边三角形，∴CE AC =又∵CE BC BE BC CD =+=+，∴AC BC CD =+．证明三：如图4：将ABC ∆绕着点A 逆时针旋转60︒．由旋转的性质得：ADE ∆≌ABC ∆，∴AE AC =，BC DE =又∵60ACE ∠=︒，∴ACE ∆为等边三角形，∴AC CE =，∴CE CD DE CD BC =+=+，∴AC BC CD =+（3）线段BC ，CD ，AC 三者的等量关系为： 2BC CD AC +=．证明：延长CB 到E ，使BE CD =，连接AE ，∵45ABD ACD ∠=∠=︒，∴AB AD =，180454590BAD ∠=︒-︒-︒=︒∵45ACB ACD ∠=∠=︒，∴454590BCD ∠=︒+︒=︒在四边形ABCD 中，180BAD BCD ∠+∠=︒，∴180ABC ADC ∠+∠=︒又∵180ABC ABE ∠+∠=︒，∴ABE ADC ∠=∠在ABE ∆和ADC ∆中，,AB AD ABE ADC BE CD =⎧⎪∠=∠⎨⎪=⎩，∴ABE ∆≌ADC ∆，∴AE AC =，∵45ACB ∠=︒，∴45E ACB ∠=∠=︒，∴90EAC ∠=︒， ∴CE =，∵CE BC BE BC CD =+=+， ∴BC CD +=． 【点睛】不同考查了全等三角形的判定，四边形的内角和，等腰三角形的判定和性质，解本题的关键是构造全等三角形，是一道综合性较强的题目．2．（1）见解析；（2）【分析】（1）根据E 点绕A 点逆时针旋转90°到AD ，可得AD ＝AE ，∠DAE ＝90°，进而可以证明△ABE ≌△ACD ；（2）结合（1）△ABE ≌△ACD ，和等腰三角形的性质，可得∠DCE ＝90°，再根据勾股定理即可求出DE 的长．【详解】（1）证明：∵E 点绕A 点逆时针旋转90°到AD ，∴AD ＝AE ，∠DAE ＝90°，∵∠CAB ＝90°，∴∠DAC ＝∠EAB ，∵AC ＝AB ，∴△ABE ≌△ACD （SAS ）；（2）∵等腰△ABC 中，AC ＝AB ，∠CAB ＝90°，∴∠ACB ＝∠ABC ＝45°，∵△ABE ≌△ACD ，∴BE ＝CD ，∠DCA ＝∠ABE ＝45°，∴∠DCE ＝90°，∵BC ＝6，CE ＝2，∴BE ＝4＝CD ，∴DE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、等腰直角三角形的性质，解决本题的关键是综合运用以上知识．3．（1）见解析；（2）EF ＝DF ﹣BE ，见解析；（3）【分析】（1）把△ABE 绕点A 顺时针旋转90°至△ADG ，由“SAS”可证△EAF ≌△GAF ，可得出EF ＝FG ，则结论得证；（2）将△ABE绕点A顺时针旋转90°至△ADM，根据SAS可证明△EAF≌△MAF，可得EF ＝FM，则结论得证；（3）由全等三角形的性质可得AE＝AG＝35，EF＝FG，BE＝DG，由勾股定理可求DG的长，FD的长，AF的长．【详解】（1）把△ABE绕点A顺时针旋转90°至△ADG，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），∴EF＝FM＝DF﹣DM＝DF﹣BE；（3）如图，由（1）可得AE ＝AG ＝35EF ＝FG ，BE ＝DG ，∵DG 2245363AG AD -=-=，∴BE ＝DG ＝3，∴EC ＝BC ﹣BE ＝3，∵EF 2＝EC 2+CF 2，∴（DF+3）2＝9+（6﹣DF ）2，∴DF ＝2，∴AF 22AD DF +436+10．【点睛】本题考查了全等三角形的判定和性质，勾股定理，旋转等知识，此题为半角模型，∠EAF 是∠BAD 的一半，故命名半角模型，半角模型必旋转，再证全等即可．4．（1）PM PN =，PM PN ⊥；（2）PMN 的形状为等腰直角三角形，理由见解析；（3）PMN 的面积的最大值为92． 【分析】（1）延长AE 交BD 于点H ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（2）设AE 交BC 于⊙O ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（3）易证ΔPMN 是等腰直角三角形，PM=12BD ，当B 、C 、D 共线时，BD 的值最大，进而求解．【详解】解：（1）如图1，延长AE 交BD 于点H ，∵ΔACB 和ΔECD 是等腰直角三角形，∴AC=BC ，EC=CD ，∠ACB=∠ECD=90°，∴∠ACB+∠BCE=∠ECD+∠BCE ，∴∠ACE=∠BCD ，∴ΔACE ≌ΔBCD （SAS ），∴AE=BD ，∠CAE=∠CBD ，又∵∠AEC=∠BEH ，∴∠BHA=∠ACE=90°，∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴PM=12BD ，PM//BD ，PN=12AE ，PN//AE ， ∴PM=PN ，∴PM ⊥AH ，∴PM ⊥PN ．（2）如图中，设AE 交BC 于O ．∵ACB △和ECD 是等腰直角三角形，∴AC BC =，EC CD =，90ACB ECD ∠=∠=︒∴ACB BCE ECD BCE ∠+∠=∠+∠∴ACE BCD ∠=∠.∴ACE BCD ≅∴AE BD =，CAE CBD ∠=∠又∵AOC BOE ∠=∠，CAE CBD ∠=∠，∴90BHO ACO ∠=∠=︒∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴12PM BD =，//PM BD ； PN AE =，//PN AE .∴PM PN =∴180MGE BHA ∠+∠=︒∴90MGE ∠=︒∴90MPN ∠=︒∴PM PN ⊥（3）PMN 的面积的最大值为92． 由（2）可知PMN 是等腰直角三角形，12PM BD =， ∴当BD 的值最大时，PM 的值最大，PMN 的面积最大，∴当B 、C 、D 共线时，BD 的最大值6BC CD =+=，∴3PM PN ==，∴PMN 的面积的最大值193322=⨯⨯=． 【点睛】 本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质和判定定理，掌握旋转全等三角形模型，是解题的关键．5．图（2）成立，图（3）不成立；图（2）中有AE CF EF +=，理由见解析；在图（3）中，有结论EF AE CF =-，理由见解析【分析】根据已知可以利用SAS 证明△ABE ≌△CBF ，从而得出对应角相等，对应边相等，从而得出∠ABE ＝∠CBF ＝30°，△BEF 为等边三角形，利用等边三角形的性质及边与边之间的关系，即可推出AE +CF ＝EF ．同理图2可证明是成立的，图3不成立．【详解】解：∵AB ⊥AD ，BC ⊥CD ，AB ＝BC ，AE ＝CF ，在△ABE 和△CBF 中，90AB BC A C AE CF =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABE ≌△CBF （SAS ）；∴∠ABE ＝∠CBF ，BE ＝BF ；∵∠ABC ＝120°，∠MBN ＝60°，∴∠ABE ＝∠CBF ＝30°，∴AE ＝12BE ，CF ＝12BF ； ∵∠MBN ＝60°，BE ＝BF ，∴△BEF 为等边三角形；∴AE +CF ＝12BE +12BF ＝BE ＝EF ； 图2成立，图3不成立．证明图2．延长DC 至点K ，使CK ＝AE ，连接BK ，在△BAE 和△BCK 中，90AB CB A BCK AE CK =⎧⎪∠=∠=︒⎨⎪=⎩则△BAE ≌△BCK ，∴BE ＝BK ，∠ABE ＝∠KBC ，∵∠FBE ＝60°，∠ABC ＝120°，∴∠FBC +∠ABE ＝60°，∴∠FBC +∠KBC ＝60°，∴∠KBF ＝∠FBE ＝60°，在△KBF 和△EBF 中，BK BE KBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩∴△KBF ≌△EBF ，∴KF ＝EF ，∴KC +CF ＝EF ，即AE +CF ＝EF ．图3不成立，AE 、CF 、EF 的关系是AE ﹣CF ＝EF ．理由如下：延长DC 至G ，使CG ＝AE ，同理可知，△BAE≌△BCG（SAS），∴BE＝BG，∠ABE＝∠GBC，∠GBF＝∠GBC﹣∠FBC＝∠ABE﹣∠FBC＝120°+∠FBC﹣60°﹣∠FBC＝60°，∴∠GBF＝∠EBF，∵BG＝BE，∠GBF＝∠EBF，BF＝BF，∴△GBF≌△EBF，∴EF＝GF，∴AE﹣CF＝CG﹣CF＝GF＝EF．【点睛】本题几何变换综合题，考查的是全等三角形的判定和性质，正确作出辅助性、掌握全等三角形的判定定理和性质定理是解题的关键．6．（1）证明见解析；（2）证明见解析；（3）AP＝52【分析】（1）由旋转定理，可得AP＝DP，结合∠APD＝60°，可推导出△APD是等边三角形；再通过角度之间加减关系，推导出∠BAP＝∠MAD，结合等边△ABM的性质，可证明△BAP≌△MAD，即完成BP＝MD证明；（2）由旋转定理，可得AP＝DP，结合∠APD＝60°，可推导出△APD是等边三角形；再通过角度之间加减关系，推导出∠BAP＝∠MAD，结合等边△ABM的性质，可证明△BAP≌△MAD，即完成BP＝MD证明；（3）由△BAP≌△MAD和BC为等边△ABM的高，计算得∠DBM＝60°，从而证明点D在BA的延长线上，再利用Rt△BMD和特殊角度三角函数，计算得到答案．【详解】（1）如图①，连接AD∵△ABM是等边三角形∴AB＝AM，∠BAM＝60°由旋转的性质可得：AP＝DP，∠APD＝60°∴△APD是等边三角形∴PA＝PD＝AD，∠PAD＝∠BAM＝60°∴∠BAP＝∠BAC﹣∠CAP，∠MAD＝∠PAD﹣∠CAP ∴∠BAP＝∠MAD∵AB AMBAP MADAP AD=⎧⎪∠=∠⎨⎪=⎩∴△BAP≌△MAD（SAS）∴BP＝MD；（2）如图②，连接AD∵△AMB是等边三角形∴AB＝AM，∠BAM＝∠AMB＝60°由旋转的性质可得：AP＝DP，∠APD＝60°∴△APD是等边三角形∴PA＝PD＝AD，∠PAD＝∠BAM＝60°∴∠BAP＝∠BAC+∠CAP，∠MAD＝∠PAD+∠CAP ∴∠BAP＝∠MAD在△BAP与△MAD中∵AB AMBAP MADAP AD=⎧⎪∠=∠⎨⎪=⎩∴△BAP≌△MAD（SAS）∴BP＝MD；（3）∵BC为等边△ABM的高∴∠ABC＝30°∵△BAP≌△MAD∴∠ABP＝∠AMD＝30°∴∠BMD＝∠AMB+∠AMD＝90°∴∠BMD＝90°∵∠BDM＝30°∴∠DBM＝60°∴点D在BA的延长线上如图③∵∠BDM＝30°,∠BMD＝90°∴BD＝2BM＝2∴AD＝BD﹣AB＝2∵PA＝PD＝AD∴AP＝AD＝2．【点睛】本题考察了全等三角形、旋转、特殊角度三角函数等知识点；求解的关键在于结合图形，熟练掌握运用等边三角形、旋转的性质，推导证明全等三角形和直角三角形，并运用特殊角度三角函数计算得到答案．7．（1）①见解析；②2；（2）EC3EF，EC⊥EF，见解析【分析】（1）①想办法证明△BEG是等边三角形即可解决问题；②利用三角形的中位线定理求出AG，再求出BG即可解决问题．（2）结论：EC3，EC⊥EF．延长DF交CA的延长线于M，延长FE到K，使得EK＝EF，连接AK，CK，CF，在FM上截取FN＝DF，连接BN．证明图中，红色三角形全等，推出△CFK是等边三角形即可解决问题．【详解】（1）①证明：如图2中，∵△ABC是等边三角形，∴∠ABC＝60°，∵EB＝ED，∴∠EBD＝∠EDB＝30°，∴∠GBD＝∠ABC+∠EBD＝90°，∴∠BGD＝60°，∴△BEG是等边三角形，∴BG＝BE，∴BG＝ED．②解：由①可知，BG＝GE＝BE＝DE，又∵AF＝DF，∴AG＝2EF＝6，∵AB＝8，∴BG＝AB﹣AG＝8﹣6＝2，∴BE＝BG＝2．（2）结论：EC3，EC⊥EF．理由：如图2中，延长DF交CA的延长线于M，延长FE到K，使得EK＝EF，连接AK，CK，CF，在FM上截取FN＝DF，连接BN．∵FB＝FD＝FN，∴∠DBN＝90°，∵∠DBF＝30°，∴∠FBN＝60°，∴△FBN是等边三角形，∴BN＝BF，∵∠ABC＝∠NBF＝60°，∴∠ABN＝∠CBF，∵AB＝BC，∴△ABN≌△CBF（SAS），∴AN＝CF，∵FN＝DF，AE＝ED，∴EF∥AN，AN＝2EF，∵2EF＝FK，∴AN＝FK，AN∥FK，∴四边形ANFK是平行四边形，∴AK∥DM，AK＝FN＝BN，∴∠CAK＝∠M，∵∠AOM＝∠BON，∠OAM＝∠BNO＝120°，∴∠M＝∠OBN，∴∠ABN＝∠CAK，∵AB＝AC，∴△ABN≌△CAK（SAS），∴AN ＝CK ，∴CF ＝CK ＝FK ，∴△CFK 是等边三角形，∠CFE ＝60°∵2EF ＝FK ，∴CE ⊥FK ，∵∠EFC ＝60°，∴tan ∠CFE ＝EC EF ＝3， ∴EC ＝3EF ，EC ⊥EF ．【点睛】本题主要考查了三角形的综合应用，准确应用等边三角形的性质进行分析是关键． 8．（1）见详解（2）①结论：222BD FC DF +=，证明见详解②35【分析】（1）根据SAS ，只要证明BAD CAE ∠=∠即可解决问题；（2）①结论：222BD FC DF +=．连接EF ，进一步证明90ECF ∠=︒，DF EF =，再利用勾股定理即可得证；②过点A 作AG BC ⊥于点G ，在Rt ADG 中求出AG 、DG 即可求解．【详解】解：（1）∵AE AD ⊥∴90DAC CAE ∠+∠=︒∵90BAC ∠=︒∴90DAC BAD ∠+∠=︒∴BAD CAE ∠=∠∴在ABD △和ACE △中 AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴ABD △≌ACE △()SAS（2）①结论：222BD FC DF +=证明：连接EF ，如图：∵ABD △≌ACE △∴B ACE ∠=∠，BD CE =∴90ECF BCA ACE BCA B ∠=∠+∠=∠+∠=︒∴222FC CE EF +=∴222FC BD EF +=∵AF 平分DAE ∠∴DAF EAF ∠=∠∴在DAF △和EAF △中AD AE DAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴DAF △≌EAF △()SAS∴DF EF =∴222FC BD DF +=即222BD FC DF +=②过点A 作AG BC ⊥于点G ，如图：∵由①可知222223425DF BD FC =+=+= ∴5DF =∴35412BC BD DF FC =++=++=∵AB AC =，AG BC ⊥ ∴1112622BG AG BC ===⨯= ∴633DG BG BD =-=-= ∴在Rt ADG 中，22223635AD DG AG =+=+=故答案是：（1）见详解（2）①结论：222BD FC DF +=，证明见详解②35【点睛】本题考查了全等三角形的判定和性质、直角三角形的判定和性质以及角平分线的性质．综合性较强，属中档题，学会灵活应用相关知识点进行推理证明．9．（1）BC BD =，理由见解析；（2）BF BP BD +=，证明见解析；（3）BF BP BD +=．【分析】（1）利用含30的直角三角形的性质得出12BC AB =，即可得出结论； （2）同（1）的方法得出BC BD =进而得出BCD ∆是等边三角形，进而利用旋转全等模型易证DCP DBF ∆≅∆，得出CP BF =即可解答；（3）同（2）的方法得出结论．【详解】解：（1）90ACB ∠=︒，30A ∠=︒，60CBA ∴∠=︒，12BC AB =， 点D 是AB 的中点，BC BD ∴=，故答案为：BC BD =；（2）BF BP BD +=，理由：90ACB ∠=︒，30A ∠=︒，60CBA ∴∠=︒，12BC AB =， 点D 是AB 的中点，BC BD ∴=，DBC ∴∆是等边三角形，60CDB ∴∠=︒，DC DB =，线段DP 绕点D 逆时针旋转60︒，得到线段DF ，60PDF ∴∠=︒，DP DF =，CDB PDB PDF PDB ∴∠-∠=∠-∠，CDP BDF ∴∠=∠，在DCP ∆和DBF ∆中， DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，DCP DBF ∴∆≅∆，CP BF ∴=，CP BP BC +=，BF BP BC ∴+=，BC BD =，BF BP BD ∴+=；（3）如图③，BF BD BP =+，理由：90ACB ∠=︒，30A ∠=︒，60CBA ∴∠=︒，12BC AB =， 点D 是AB 的中点，BC BD ∴=，DBC ∴∆是等边三角形，60CDB ∴∠=︒，DC DB =，线段DP 绕点D 逆时针旋转60︒，得到线段DF ，60PDF ∴∠=︒，DP DF =，CDB PDB PDF PDB ∴∠+∠=∠+∠，CDP BDF ∴∠=∠，在DCP ∆和DBF ∆中， DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，DCP DBF ∴∆≅∆，CP BF ∴=，CP BC BP =+，BF BC BP ∴=+，BC BD =，BF BD BP ∴=+．【点睛】此题是三角形综合题，主要考查了含30的直角三角形的性质，等边三角形的判定，全等三角形的判定和性质，旋转的性质，解本题的关键是判断出DCP DBF ∆≅∆，是一道中等难度的中考常考题．10．（1）详见解析；（2）2CD =，31CB =31【解析】【分析】 ()1过点C 作CE CB ⊥于点C ，与MN 交于点E ，证明ACE ≌DCB ，则ECB 为等腰直角三角形，据此即可得到2BE CB =，根据BE AB AE =-即可证得；()2过点B 作BH CD ⊥于点H ，证明BDH 是等腰直角三角形，求得DH 的长，在直角BCH 中，利用直角三角形中30的锐角所对的直角边等于斜边的一半，即可求得．【详解】解：()1如图()2：2AB BD CB -=．证明：过点C 作CE CB ⊥于点C ，与MN 交于点E ，90ACD ∠=， 90ACE DCE ∠∠∴=-，90BCD ECD ∠∠=-，BCD ACE ∠∠∴=．DB MN ⊥，90CAE AFC ∠∠∴=-，90D BFD ∠∠=-，AFC BFD ∠∠=，CAE D ∠∠∴=，又AC DC =，ACE ∴≌DCB ，AE DB ∴=，CE CB =，ECB ∴为等腰直角三角形， 2BE CB ∴=．又BE AB AE =-，BE AB BD ∴=-， 2AB BD CB ∴-=．如图()3：2BD AB CB -=．证明：过点C 作CE CB ⊥于点C ，与MN 交于点E ，90ACD ∠=， 90ACE ACB ∠∠∴=+，90BCD ACB ∠∠=+，BCD ACE ∠∠∴=．DB MN ⊥， 90CAE AFB ∠∠∴=-，90D CFD ∠∠=-，AFB CFD ∠∠=，CAE D ∠∠∴=，又AC DC =，ACE ∴≌DCB ，AE DB ∴=，CE CB =，ECB ∴为等腰直角三角形， 2BE CB ∴=．又BE AE AB =-，BE BD AB ∴=-， 2BD AB CB ∴-=．()2MN 在绕点A 旋转过程中，有两种情况：i .如图（1）：易证ACE ≌DCB ，CE CB =，ECB ∴为等腰直角三角形，45AEC CBD ∠∠∴==，过D 作.DH CB ⊥则DHB 为等腰直角三角形．2BD BH =，1BH DH ∴==．直角CDH 中，30DCH ∠=，22CD DH ∴==，3CH =31CB CH HB ∴=+=ii .如图（2）：过D 作DH CB ⊥交CB 延长线于H ．同理可得，2CD =，31CB CH HB =-=．【点睛】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，全等三角形的性质是全等三角形的对应边相等，对应角相等．。

课题概述八年级学生虽然已经在七年级学习了平行线与相交线，但是平行线与相交线的证明很简单，本学期学习连续学习《三角形》，《全等三角形》，《轴对称》三章，图形变化较多，学生在寻找图形边角关系上还存在问题，证明也有一定难度，只能见一个图形硬性记一个图形，所以本节课设计意图就是将看似分隔的图形通过几何画板的演示整合到一起，形成一个图形的不同变换形式，而实质是不变的，从而帮助学生理解图形的内在联系。

对于以后学习旋转规律图形也会有相当大的帮助。

学习目标阐述（1）通过观察图形的变化过程，探究发现图形变化的实质，从而抓住本质规律，找到证明全等的条件．（2）通过观察几何画板的图形变换的演示，将看似分割的图形整合到一起，抓住事物本质．完成目标（1）的标志是：学生能用旋转的角度理解两个三角形能重合，所以全等，进而理解边角关系，找到证明条件。

完成目标（2）的标志是：学生发挥想象力和创意移动点C，B位置，发现不同图形式可以整合到一起，从而将图形统一，抓住图形本质。

学习者特征分析学生在八年级上学期刚刚学习了《三角形》，《全等三角形》和《轴对称》三章，三大章几何连在一起学习，学生的几何体系还没有建立起来，还不能熟练辨析图形之间的关系，对于图形的变换还比较陌生，对于判定两个三角形全等方法的选择以及利用等边三角形证明两个三角形全等也还有一定难度。

教学策略选择与教学活动设计教学策略：八年级学生好奇心强，对新鲜事物感到新奇，创意无限，喜欢探索。

几何画板的动态演示过程，能激发学生的学习兴趣，帮助学生发现并理解图形的变化过程及变换的实质，让学生能够更积极主动地探索新知。

教学活动设计教师创设背景，由学生发挥想象和创意改变图形，发现图形规律和内在联系，并由学生尝试总结规律，给出证明。

教学资源与工具的设计和使用八年级上册数学课本几何画板V5.05演示正方形旋转过程，通过观察发现题目本质，引导学生观察P点的变化范围，其轨迹像在荡秋千，引导学生观察P在AE’上，P标最大，需使直线AE’倾斜程度最大，那么倾斜NMD ECBA 教学评价与反馈设计1.如图，四边形ACDE,BCMN 为正方形，AM_____BD, ∠MAC_____∠BDC(填<，=，>)第1题 第2题2.如图，在ABC 中，D 在AB 上，且ΔCAD 和ΔCBE 都是等边三角形，（1）DE______AB ，（2）∠EDB=_________°3. 如图，已知△ABC 是等边三角形，E 是AC 延长线上任一点，选择一点D ，使得△CDE 是等边三角形，如 果M 是线段AD 的中点，N 是线段BE 的中点.则∠CMN=_____________°第3题 第4题4.已知：如图，△ABC 和△ADE 是有公共顶点的等腰直角三角形. 求证：BD=CE 且BD ⊥CE总结与帮助放飞学生的心灵，尊重学生独特的体验探究学习是一种发现学习，具有深刻的问题性、广泛的参与性、丰富的实践性和开放性。

全等三角形与旋转问题专题练习全等三角形与旋转问题专题练中考要求：掌握旋转变换的概念和性质，能够灵活应用旋转变换解决问题。

知识点睛：基本知识：旋转变换是指将一个图形绕平面上的一个定点旋转一个角度，得到一个新的图形，这个过程叫做旋转变换。

旋转中心是旋转的定点，旋转角是旋转的角度，原图形叫做原象，新图形叫做象。

在旋转变换下，原象和象是全等的。

旋转变换具有以下基本性质：①旋转变换的对应点到旋转中心的距离相等；②对应直线的交角等于旋转角。

旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上，可以将分散的条件集中，便于条件的综合和推导。

重点：本节的重点是全等三角形的概念、性质及其判定。

全等三角形的性质是证明三角形问题的基础，也是学好本章的关键。

同时，全等三角形的判定也是本章的重点，特别是在直角三角形中，HL判定是整个直角三角形的重点。

难点：本节的难点是全等三角形性质和判定定理的灵活应用。

为了能熟练地应用性质定理及其推论，要把性质定理和推论的条件和结论弄清楚，哪几个是条件，决定哪个结论，如何用数学符号表示，即书写格式，都要在讲练中反复强化。

例题精讲：例1】如图，有四个图案，它们绕中心旋转一定的角度后，都能和原来的图案相互重合，其中有一个图案与其余三个图案旋转的角度不同，它是哪一个？解析】选择A。

例2】如图，万花筒是由三块等宽等长的玻璃片围成的，其中菱形AEFG可以看成是把菱形ABCD以A为中心逆时针旋转120°得到的。

则以菱形AEFG为一侧的等边三角形AKF可以看成是把以菱形ABCD的一条对角线为一边的等边三角形旋转了多少度得到的？解析】选择D。

例3】如图，C是线段BD上一点，分别以BC、CD为边在BD同侧作等边三角形ABC和等边三角形CDE，AD交CE于F，BE交AC于G，则图中可通过旋转而相互得到的三角形对数有多少对？解析】选择C。

例4】已知：如图，点C为线段AB上一点，∆ACM、∆CBN是等边三角形。