机械学基础第03章
- 格式:ppt
- 大小:15.97 MB
- 文档页数:10

直线的投影[教学目标与要求]一、知识与能力1、掌握直线的投影特性和三面投影;2、掌握各种位置直线的投影特性和求作方法;2、能根据投影正确判断直线段的空间位置。
二、学习方法与素质养成学生自行演示观察,积累感性知识,自觉培养学习能力,学会学习,善于学习,温故知新,举一反三。
[教学重点]直线的三面投影、各种位置直线的投影特性,直线三面投影的求作方法。
[难点分析]直线的命名与空间位置的判别。
[分析学生]1、在学习点的投影的基础上,直线的投影入门不难,难点在于直线的空间位置多样化,初学者对空间直线的各种位置、命名不易把握,容易产生混淆和初记困难。
在教师讲授、演示的基础上,仍需学生通过自己借助于铅笔等直观道具演示观察,来强化感性认识,同时进行反复练习,达到熟练掌握。
[教学设计思路]教学方法:讲练法、演示法、归纳法。
[教学资源]机械制图网络课程,圆规、三角板、教杆等。
[教学安排]2学时(90分钟)。
教学步骤:讲课与演示交叉进行,讲课与练习交叉进行,最后进行归纳。
[教学过程]一、复习回顾(15~10分钟)1、简述点的投影规律,求作点的三面投影的方法,判断重影点的可见性。
2、讲评作业批改情况,纠错。
3、提问教材P.74思考题5、6。
4、预习检测:直线的空间位置有几种?直线段的投影特性是什么?点的投影和直线的投影有什么联系?二、导入新课简述本课主要内容、要点、作用和地位,展示并确认教学目标和要求。
直线的投影是平面投影的基础,也是学习平面立体投影的基础。
三、新课教学(70~80分钟)1、直线的三面投影教师结合教具演示,讲授直线的投影特性和空间位置,在此基础上讲授直线的三面投影,指导学生自己演示、观察直线的三面投影,并讨论归纳其投影特性。
在讲直线的命名时,应引导学生分析直线空间位置及命名的唯一性,增强学生的动手动脑的主动性和探究性学习的兴趣,提高学习成效。
2、直线三面投影的求作教师讲授演示在各种不同条件下,平行线、垂直线、一般位置直线的求作方法,指导学生根据直线的投影特性,利用排除法快速判定其空间位置的技巧。

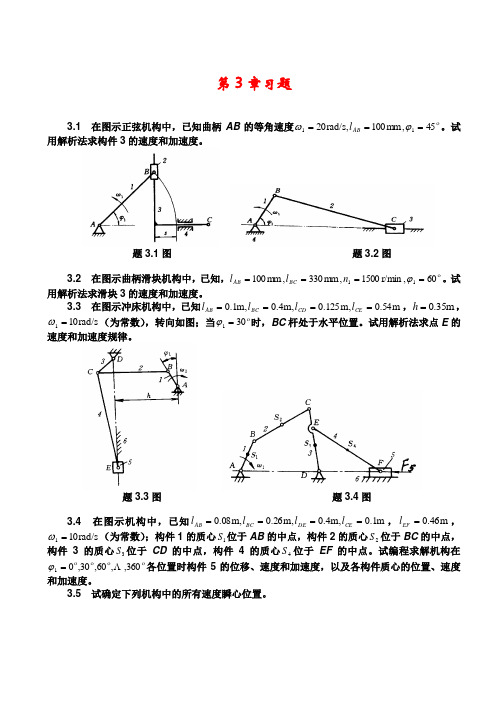
第3章习题3.1 在图示正弦机构中,已知曲柄AB 的等角速度 45,m m 100,rad/s 2011===ϕωAB l 。
试用解析法求构件3的速度和加速度。
题3.1图 题3.2图3.2 在图示曲柄滑块机构中,已知, 60,r/min 1500,mm 330,mm 10011====ϕn l l BC AB 。
试用解析法求滑块3的速度和加速度。
3.3 在图示冲床机构中,已知m 54.0,m 125.0,m 4.0,m 1.0====CE CD BC AB l l l l ,m 35.0=h ,rad/s 101=ω(为常数),转向如图;当 301=ϕ时,BC 杆处于水平位置。
试用解析法求点E 的速度和加速度规律。
题3.3图 题3.4图3.4 在图示机构中,已知m 1.0,m4.0,m 26.0,m 08.0====CE DE BC AB l l l l ,m 46.0=EF l ,rad/s 101=ω(为常数);构件1的质心1S 位于AB 的中点,构件2的质心2S 位于BC 的中点,构件3的质心3S 位于CD 的中点,构件4的质心4S 位于EF 的中点。
试编程求解机构在 360,,60,30,01=ϕ各位置时构件5的位移、速度和加速度,以及各构件质心的位置、速度和加速度。
3.5 试确定下列机构中的所有速度瞬心位置。
题3.5图3.6 在图示凸轮机构中,已知 90,mm 80,mm 22,mm 501====ϕAC OA l l r ,凸轮1的角速度rad/s 101=ω,逆时针方向转动。
试用瞬心法求从动件2的角速度2ω。
题3.6图 题3.7图3.7 图示齿轮连杆组合机构,试用瞬心法求齿轮1与齿轮3的角速度之比31/ωω。
3.8 在图示四杆机构中,已知rad/s 10,m m 125,m m 90,m m 651=====ωBC AD CD AB l l l l ,顺时针转动。
试用瞬心法求:1) 当 15=ϕ时,点C 的速度C v ;2) 当 15=ϕ时,构件BC 上(即BC 线上或其延长线上)速度最小的一点E 的位置及其速度值;3) 当0=C v 时角ϕ的值。

复习要点第01章 机构的组成及平面连杆机构1) 两构件通过点、线或面接触组成运动副,按照接触特性,通常分为低副和高副两类。
P2下列运动副中,按照接触特性,可认为低副的是(D )。
2) 平面机构自由度的计算公式为:32L H W n P P =--机构具有确定运动的条件是:W > 0且W 等于原动件个数。
p4 计算图中所示运动机构的自由度数: 解1:在活塞泵机构中,有4个活动构件,n=4;有5个低副,P L =5;有1个高副,P H =1。
机构的自由度:W = 3 n - 2 P L - PH = 3 × 4 - 2 × 5 - 1 = 1该机构具有 1 个原动件(曲柄),故原动件数与机构自由度相等,机构具有确定的运动。
解2:机构中有7个活动构件, n = 7; A 、B 、C 、D 四处都是三个构件汇交的复合铰链,各有两个回转副,故P L = 10。
由式(1-1)可得 W = 3 × 7 - 2 × 10 = 1W 与机构原动件个数相等。
当原动件8 转动时, 圆盘中心E 将确定地沿直线EE ′移动。
解3:机构中的滚子有一个局部自由度。
顶杆与机架在E 和E ′组成两个导路平行的移动副,其中之一为虚约束。
C 处是复合铰链。
现将滚子与顶杆焊成一体,去掉移动副E ′,并在C 点注明回转副的个数。
得n = 7, P L = 9 (7个回转副和2个移动副), P H = 1, 故由式(1-1)得W = 3 n - 2 P L - P H = 3 × 7 - 2 × 9 - 1 = 2 此机构的自由度等于2,有两个原动件。
A B CD3) 按照铰链四杆机构的连架杆是曲柄还是摇杆,可将铰链四杆机构分为三种基本型式:曲柄摇杆机构、双曲柄机构和双摇杆机构。
P74) 极位夹角θ与行程速比系数K 的关系是: p11(180)/(180)180(1)/(1)K K K θθθ=︒+︒-⇒=︒-+5) 曲柄存在的条件是:1)最短杆与最长杆长度之和小于或等于其余两杆长度之和;2)在曲柄摇杆机构中,曲柄是最短杆。


教案首页课程名称农业机器人任课教师李玉柱第3章机器人运动学和动力学计划学时 3教学目的和要求:1.概述,齐次坐标与动系位姿矩阵,了解平移和旋转的齐次变换;2.机器人的运动学方程的建立与求解*;3.机器人的动力学*重点:1.机器人操作机运动学方程的建立及求解;2.工业机器人运动学方程3.机器人动力学难点:1. 机器人动力学方程及雅可比矩阵基本原理思考题:1.简述齐次坐标与动系位姿矩阵基本原理。
2.连杆参数及连杆坐标系如何建立?3.机器人动力学方程及雅可比矩阵基本原理是什么?第3章机器人运动学和动力学教学主要内容:3.2 齐次坐标与动系位姿矩阵3.3 齐次变换3.4 机器操作机运动学方程的建立与求解3.5 机器人运动学方程3.6 机器人动力学本章将主要讨论机器人运动学和动力学基本问题。
先后引入了齐次坐标与动系位姿矩阵、齐次变换,通过对机器人的位姿分析,介绍了机器人运动学方程;在此基础上有对机器人运动学方程进行了较为深入的探讨。
3.1 概述机器人,尤其是关节型机器人最有代表性。
关节型机器人实质上是由一系列关节连接而成的空间连杆开式链机构,要研究关节型机器人,必须对运动学和动力学知识有一个基本的了解。
分析机器人连杆的位置和姿态与关节角之间的关系,理论称为运动学,而研究机器人运动和受力之间的关系的理论则是动力学。
3.2 齐次坐标与动系位姿矩阵3.2.1 点的位置描述在关节型机器人的位姿控制中,首先要精确描述各连杆的位置。
为此,先定义一个固定的坐标系,其原点为机器人处于初始状态的正下方地面上的那个点,如图3-1(a)所示。
记该坐标系为世界坐标系。
在选定的直角坐标系{A}中,空间任一点P的位置可以用3×1的位置向量A P表示,其左上标表示选定的坐标系{A},此时有A P=XYZ P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦式中:P X、P Y、P Z—点P在坐标系{A}中的三个位置坐标分量,如图3-1(b)。
3.2.2 齐次坐标将一个n维空间的点用n+1维坐标表示,则该n+1维坐标即为n维坐标的齐次坐标....。