导热数值解法基础
- 格式:ppt
- 大小:3.17 MB
- 文档页数:48

名词解释这些名词解释都是学长自己从传热学课本中总结的,课本上有的基本上都在这里。
绪论:1.传热学:传热学是研究温差作用下热量传递过程和传递速率的科学。
2.热传递:自然界和生产过程中,在温差的作用下,热量自发地由高温物体传递到低温物体的物理现象。
3.导热(热传导):是指物体各部分五项队位移或不同物体直接接触时依靠分子、原子及自由电子等微观粒子热运动而进行的热量传递现象。
(固液气中均可发生,但是在引力场的作用下,单纯的导热一般只发生在密实的固体中)4.热流密度q:单位时间内,通过物体单位横截面积上的热量——W/㎡。
5.热导率(导热系数):单位厚度的物体具有单位温度差时,在它单位面积上每单位时间的导热量——W/(m*K)。
6.导热热阻:温度差的情形下,导热过程中,物体抵抗传热的能力——K/W。
7.对流(热对流):在流体内部,仅依靠流体的宏观运动传递热量的现象称为热对流。
8.对流传热:工程上,流体在与它温度不同的壁面上流动时,两者间产生的热量交换,传热学中将这一过程称为“对流传热”过程。
9.表明面传热系数h:单位面积上,流体与壁面之间在单位温差下及单位时间内所能传递的热量——W/(㎡*K)。
10.对流传热热阻:温度差的情形下,对流过程中,物体抵抗传热的能力——K/W。
11.辐射(热辐射):依靠物体表面对外发射可见和不可见的射线(电磁波,或者说光子)传递热量。
12.辐射力E:物体表面每单位时间、单位面积对外辐射的热量成为辐射力。
13.辐射传热:物体间靠热辐射进行的热量传递称为辐射传热。
14.传热过程:工程中所遇到的冷热两种流体隔着固体壁面的传热,即热量从壁一侧的高温流体通过壁传给另一侧低温流体的过程,称为传热过程。
15.传热系数K:单位时间、单位壁面积上,冷热流体间温差为1K时所传递的热量——W/(㎡*K)。
16.单位面积传热热阻:温度差的情形下,传热过程中,单位面积物体抵抗传热的能力——K/W。
第一章:导热理论基础1.温度场:温度场是指某一时刻物体的温度在空间上的分布,一般来说,它是时间和空间的函数。






导热问题数值解法初次研究对物理物体的数值求解的基本思想可以概括为:把原有的时间、空间坐标系中连续的物理量的场,如导热问题的温度场,用有限个离散点上的值的集合来代替,通过求解按一定方法建立起来的关于这些值的代数方程,来获得离散点上的值。
这些离散点上的被求解物理量的值的集合称为该物理量的数值解。
物理模型在四个输气的管道中间有一个各边长为10厘米的薄铁片,求导热其达到稳态后,这块铁片的温度分布。
四个输气管道里的气体温度是恒值分别为100℃、200℃、500℃、1000℃。
因此,可以看成是二维矩形域内的稳态、无内热源、常物性的导热问题。
建立数学模型描写物理问题的微分方程称为控制方程,导热微分方程为:22220t t xy∂∂+=∂∂ (1)其四个边界分别为第一类边界条件,1234t =1005002001000===℃、t ℃、t ℃、t ℃。
区域离散化用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为需要确定温度值的空间位置,称为节点。
相邻两节点的距离称为步长,记为x ∆、y ∆。
本模型x 、y 方向是各自均分的,各自为100个子区域。
节点的位置以该节点在两个方向上的标号m 、n 来表示。
每一个节点都可以看成是以它为中心的一个小区域的代表,由相邻的两节点连接的中垂线构成。
为叙述方便,我们把节点所代表的小区域称为元体。
数学模型离散化它的建立是数值求解过程中的重要环节,主要有泰勒级数展开法及热平衡法两种,取节点(m ,n )及其临点为例。
泰勒级数展开法以节点(m ,n )处的二阶偏导数为例用这种方法来导出其差分表达式。
对节点(1,)m n +及(1,)m n -分别写出函数t 对(m ,n )的泰勒级数展开式:2233441,,,,,,2342624m n m n m nm nm nm nt x t x t xtt t xx xxx +∂∆∂∆∂∆∂=+∆++++∂∂∂∂ (2)2233441,,,,,,2342624m n m n m n m nm nm nt x t x t xtt t xxxxx-∂∆∂∆∂∆∂=-∆+-++∂∂∂∂ (3)将式(2)、(3)相加得24421,1,,,,24212m n m n m n m nm nt xtt t t x xx+-∂∆∂+=+∆++∂∂ (4) 将(4)式改写成2,2m n t x∂∂的表达式,有21,,1,2,222()m n m n m n m nt t t t O x xx+--+∂=+∆∂∆ (5)这是用三个离散点上的值来计算二阶导数2,2m nt x∂∂的严格的表达式,其中符号2()O x ∆表示未明确写出的级数余项中x ∆的最低阶数为2。



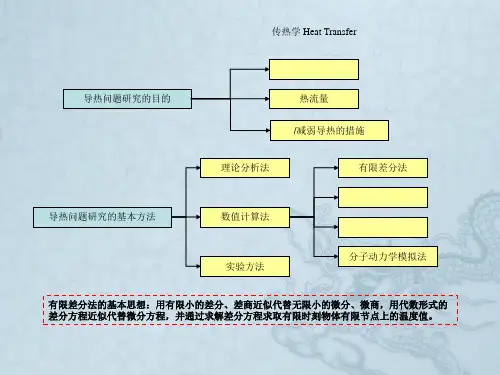
导热问题的数值求解方法数值解法的基本思想是用空间和时间区域内有限个离散点(称为节点)上温度的近似值,代替物体内实际的连续温度分布,然后由导热方程和边界条件推导出各节点温度间的相互关系的代数方程组(称为离散方程),求解此方程组,得到节点上的温度值,此即物体中温度场的解。
只要节点分布的足够稠密,数值解就有足够的精度。
求解导热问题的数值方法有有限差分法及有限元法,近几年又发展了边界元法和有限分析法。
数值方法适用于求解各种导热问题,不管物体的几何形状有多复杂,不管线性或非线性问题,都能使用。
由于计算机的飞速发展,计算技术软件发展也很快,数值方法的的地位越来越重要。
1 数值求解的基本思路及稳态导热内节点离散方程的建立一、 解法的基本思路1、基本思路:数值解法的求解过程可用框图4-1表示。
由此可见:1)物理模型简化成数学模型是基础;2)建立节点离散方程是关键;3)一般情况微分方程中,某一变量在某一坐标方向所需边界条件的个数等于该变量在该坐标方向最高阶导数的阶数。
二、稳态导热中位于计算区域内部的节点离散方程的建立方法1、基本方法方法:①泰勒级数展开法;②热平衡法。
1)泰勒级数展开法如图4-3所示,以节点(m,n)处的二阶偏导数为例,对节点(m+1,n)及(m-1,n)分别写出函数t 对(m,n)点的泰勒级数展开式:对(m+1,n):+∂∂∆+∂∂∆+∂∂∆+∂∂∆+=+444333,222,,,12462x t x x t x x t x x t x t t n m n m n m n m (a )对(m-1,n ):+∂∂∆+∂∂∆-∂∂∆+∂∂∆-=-444333,222,,,12462x t x x t x x t x x t xt t n m n m n m n m (b )(a )+(b )得: +∂∂∆+∂∂∆+=+-+444,222,,1,1122x t x x t x t t t n m n m n m n m 变形为n m x t,22∂∂的表示式得:n m x t,22∂∂)(0222,1,,1x x t t t nm n m n m ∆+∆+-=-+ 上式是用三个离散点上的值计算二阶导数n m x t ,22∂∂的严格表达式,其中:)(02x ∆―― 称截断误差,误差量级为2x ∆在数值计算时,用三个相邻节点上的值近似表示二阶导数的表达式即可,则相应的略去)(02x ∆。