【配套K12】内蒙古鄂尔多斯市东胜区八年级数学下册 18 平行四边形 18.1 平行四边形 18.1.2 平行四边形的判

内蒙古鄂尔多斯市东胜区八年级数学下册 18 平行四边形导学案（无答案）（新版）新人教版1 / 41内蒙古鄂尔多斯市东胜区八年级数学下册 18 平行四边形导学案（无答案）（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（内蒙古鄂尔多斯市东胜区八年级数学下册 18 平行四边形导学案（无答案）（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快 业绩进步，以下为内蒙古鄂尔多斯市东胜区八年级数学下册 18 平行四边形导学案（无答案）（新版）新人教版的全部内容。

2 / 42第十八章:平行四边形班级 小组 姓名一、学习目标：目标A ：进一步理解平行四边形、矩形、菱形、正方形的概念及其相互联系. 目标B ：掌握平行四边形、矩形、菱形、正方形的性质和判定.二、问题引领目标A ：进一步理解平行四边形、矩形、菱形、正方形的概念及其相互联系.1、根据条件判定它是什么图形,并在括号内填出，在四边形ABCD 中，对角线AC 和BD 相交于点O:（1）AB ＝CD ，AD ＝BC （ ） (2）∠A＝∠B＝∠C＝90° ( ） (3)AB ＝BC,四边形ABCD 是平行四边形 （ ） (4)OA ＝OC ＝OB ＝OD ，AC⊥BD （ )（5）AB ∥CD ， ∠A＝∠C （ )2、菱形的两条对角线长分别是6厘米和8厘米，则菱形的边长为 ____ 厘米。

3、顺次连结矩形ABCD 各边中点所成的四边形是 _ .4、若正方形ABCD 的对角线长10厘米,那么它的面积是 ______ 平方厘米。

5、平行四边形、矩形、菱形、正方形中，轴对称图形有：___________________6、平行四边形、矩形、菱形、正方形之间的关系:目标B:掌握平行四边形、矩形、菱形、正方形的性质和判定.1、性质和判定平行四边形 矩形 菱形正方形 性 质边________平行且相等 ____平行且相等 ____平行，____相等_____平行，____相等角 __________相等______都是直角 __________相等 ________都是直角 对角线互相__________ 互相__________互相______，且每条对角线平分一组____互相______且____，每条对角线平分一组_____________判定1两组对边分别________的四边形2、两组对边分别_______的四边形； 3、一组对边__________的四边形4、两组对角分别__________的四边1、有__________的四边形;2、有一个角是直角的________3、________相等的平行四边1、四边___的四边形；2、对角线________的平行四边形；3、有一组邻边_____的平行四边形.4、对角线_________的四边形。

内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.2 特殊的平行四边形18.2.2 菱形（第1课时）菱形的性质教案（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.2 特殊的平行四边形18.2.2 菱形（第1课时）菱形的性质教案（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.2 特殊的平行四边形18.2.2 菱形（第1课时）菱形的性质教案（新版）新人教版的全部内容。

菱形的性质课题菱形的性质课时第1课时课型新授课作课时间教学内容分析本节课探究菱形的性质.教学目标1.回顾复习矩形的性质，哪些是区别于平行四边形的性质.2.回顾复习三线合一，线段垂直平分线的知识。

3.经历菱形性质的探究过程，掌握菱形的两条性质.重点难点菱形性质的探求过程。

教学策略选择与设计先回顾复习矩形的性质，三线合一，线段垂直平分线的知识，为本节课做铺垫。

然后经历菱形的性质的探究过程,培养学生动手实验、观察推理的意识，在探究菱形的性质的活动中获得成功的体验。

学生学习方法记忆总结法,探究分析法教具三角板教学过程教师活动学生活动设计意图【知识准备】1.矩形的性质与一般平行四边形的性质的区别主要表现在__角__和__对角线__两个方面，其判定也主要从这两个方面来寻求条件.2.在等腰三角形中，__顶角的平分__线、__底边上的高__线、__底边上的中__线三线合一.3.如图所示,在四边形ABCD中，AB＝AD，CB＝CD，则直线AC是线段BD的__垂直平分线_，依据是_与一条线段两个端点距离相等的点,在这条线段的垂直平分线上_，即AC__⊥__BD，且BO__＝__DO。

三、教学策略
（一）情景创设
情景创设在教学过程中起着至关重要的作用，它能够激发学生的学习兴趣，提高学生的学习积极性。在教学平行四边形的过程中，我设计了以下几种情景：
1.生活情景：以实际生活中的场景为背景，提出与平行四边形相关的问题，让学生感受到平行四边形与生活的紧密联系。
2.探究情景：引导学生观察、操作几何图形，让学生在实践中发现平行四边形的性质和规律。
3.如何判断一个四边形是平行四边形？请同学们思考并分享自己的方法。
（三）小组合作
小组合作是一种重要的教学策略，它能够培养学生的团队协作能力，提高学生的沟通能力。在教学平行四边形的过程中，我组织了以下几种小组合作活动：
1.小组讨论：让学生在小组内讨论平行四边形的性质和判定方法，分享自己的观点和经验。
2.小组竞赛：设计一些有关平行四边形的题目，进行小组间的竞赛，激发学生的学习兴趣和团队协作精神。
（三）学生小组讨论
学生小组讨论是教学过程中的重要环节，它能够培养学生的团队协作能力和表达能力。在学生小组讨论环节，我设计了以下几个问题：
1.平行四边形有哪些性质？请同学们以小组为单位，进行讨论并分享自己的观点。
2.如何判断一个四边形是平行四边形？请同学们以小组为单位，思考并分享自己的方法。
（四）总结归纳
3.问题情景：提出具有挑战性和引导性的问题，激发学生的思考，引导学生深入探究平行四边形的性质和判定方法。
（二）问题导向
问题导向教学策略是一种以问题为主线，引导学生主动探究、解决问题的教学方法。在教学平行四边形的过程中，我设计了以下几个问题：
1.什么是平行四边形？请同学们举例说明。
2.平行四边形有哪些性质？请同学们通过观察、操作来探究。
讲授新知是教学过程中的核心环节，它能够帮助学生系统地掌握知识。在讲授平行四边形的性质和判定方法时，我采用了以下方法：

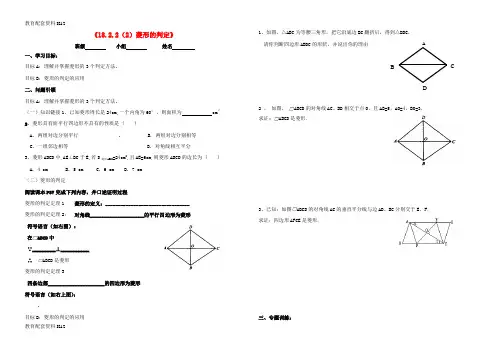
《18.2.2（2）菱形的判定》班级 小组 姓名一、学习目标：目标A ：理解并掌握菱形的3个判定方法。

目标B ：菱形的判定的应用 二、问题引领目标A ：理解并掌握菱形的3个判定方法。

（一）知识链接1、已知菱形周长是24cm,一个内角为60°，则面积为 cm ２2、菱形具有而平行四边形不具有的性质是 ( )A. 两组对边分别平行B. 两组对边分别相等C. 一组邻边相等D. 对角线相互平分3、菱形ABCD 中,AE ⊥BC 于E,若S 菱形ABCD =24cm 2,且AE=6cm,则菱形ABCD 的边长为 ( )A. 4 cmB. 5 cmC. 6 cmD. 7 cm（二）菱形的判定阅读课本P57完成下列内容，并口述证明过程菱形的判定定理1 菱形的定义：_________________________________菱形的判定定理2： 对角线_____________________的平行四边形为菱形符号语言（如右图）:在ABCD 中∵_________⊥___________∴ABCD 是菱形菱形的判定定理3四条边都______________________的四边形为菱形 符号语言（如右上图）：目标B ：菱形的判定的应用 1、如图，△ABC 为等腰三角形，把它沿底边BC 翻折后，得到△DBC ， 请你判断四边形ABDC 的形状，并说出你的理由2 、 如图，ABCD 的对角线AC 、BD 相交于点O ，且AB=5，AO=4，BO=3. 求证: ABCD 是菱形．3、已知：如图ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F ．求证：四边形AFCE 是菱形．三、专题训练：B1、在四边形ABCD 中，对角线AC 、BD 交于点O ，从（1）AB ＝CD ；（2）AB∥CD ；（3）OA ＝OC ；（4）OB ＝OD ；（5）AC ⊥BD ；（6）AC 平分∠BA D 这六个条件中，选择合适的3个条件_______________________________可证出四边形ABCD 是菱形.（请写出所有不同情况）2、一个平行四边形的一条边长是9，两条对角线的长分别是12和65，这是一个特殊的平行四边形吗？为什么？求出它的面积。

内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.1 平行四边形（第1课时）平行四边形的性质教案（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.1 平行四边形（第1课时）平行四边形的性质教案（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.1 平行四边形（第1课时）平行四边形的性质教案（新版）新人教版的全部内容。

平行四边形的性质课题平行四边形的性质课时第1课时课型复习课作课时间教学内容分析本节课复习平行四边形边角性质的应用。

教学目标1. 通过例题，巩固平行四边形的定义。

2。

能够根据平行四边形的性质，求角度和边长。

3。

结合三角形全等知识,探究平行四边形边、角性质的综合运用。

4. 能够根据平行线间距离，计算平行四边形的面积。

重点难点能够根据平行四边形的性质进行简单的推理和计算。

教学策略选择与设计能根据定义探究平行四边形的性质。

求角度和边长。

再结合三角形全等知识，探究平行四边形边、角性质的综合运用。

最后，能够根据平行线间距离，计算平行四边形的面积。

学生学习方法应用法，分析法，探究法教具三角板教学过程教师活动学生活动设计意图【知识点1】利用平行四边形的定义解题平行四边形的定义有两层意思：①是四边形；②两组对边分别平行.这两个条件缺一不可。

平行四边形的定义既是性质，又是判定方法:①由定义可知平行四边形的两组对边分别平行；②由定义可知只要四边形中有两组对边分别平行，那么这个四边形就是平行四边形。

解：∵ 四边形ABCD是矩形 C ∴AC与BD相等且互相平分 B ∴ OA=OB ∵ ∠AOB=60° ∴ △AOB是等边三角形 ∴ OA=AB=4(㎝) ∴ 矩形的对角线长 AC=BD=2OA=8(㎝) 4
60°
运用性质 解决问题
A 解： ∵四边形ABCD是矩形， ∴ OA=OB ∵ ∠AOD=120°∴ ∠AOB=60°
O
C
猜想1：矩形的四个角都是直角．
2.对角线AC和BD的长度有什么关系？
猜想2：矩形的对角线相等．
探究性质
命题：矩形的四个角都是直角．
已知：如图，四边形ABCD是平行四边形, ∠A=90° 求证：∠A=∠B=∠C=∠D=90° 证明： ∵四边形ABCD是平行四边形 A D ∠A=90° ∴ ∠A=∠C
矩形与四边形、平行四边形有什么关系？
两组对边 分别平行
四边形 平行四边形 平行 四边形 一个角 是直角
四边形
矩形
矩形
练一练
已知：如图BE、CF是△ABC的两条高， M为BC的中点，分别连ME、MF
1 求证： (1)ME= BC (2)ME=MF 2 A
E
F
B M
C
可以明智的运用知识，再现你的魅力！
C
四个学生正在做投圈游戏,他们分别站在一 个矩形的四个顶点处，目标物放在对角线的交 点处,这样的队形对每个人公平吗?为什么？ A D
O
B 公平,因为OA=OC=OB=OD C
问题：矩形ABCD中,对角线AC、 A BD相交于点O.我们观察Rt△ABD， ┛ 在Rt△ABD中，OA是斜边BD上的 中线，OA与BD有什么数量关系？
B
∠B = ∠D
C
∠A +∠B = 180° ∴ ∠A=∠B=∠C=∠D=90° 即矩形的四个角都是直角

课题18.1.2平行四边形的判定(2) 课时第2课时课型复习课作课时间教学内容分析本节课复习一组对边平行且相等的四边形是平行四边形的判定方法.教学目标1. 通过例题，复习利用一组对边平行且相等判定四边形是平行四边形。

2. 在探究运动型问题中，会判定一个四边形是平行四边形，关键是把运动的问题转化为静止的问题.3. 通过例题，复习综合利用判定和性质解决平行四边形问题。

重点难点利用判定和性质解决平行四边形问题。

教学策略选择与设计通过例题，复习利用一组对边平行且相等判定四边形是平行四边形。

再通过探究运动型问题，培养学生的发散思维能力和逻辑思维能力. 最后通过例题，综合利用判定和性质解决平行四边形问题。

学生学习方法分析法，讨论法教具三角板内蒙古呼和浩特市赛罕区八年级数学下册18平行四边形18.1平行四边形18.1.2平行四边形的判定2第2课时教案新版新人教版05142168教学过程教师活动学生活动设计意图【知识点1】利用一组对边平行且相等判定四边形是平行四边形。

平行四边形的五种判定方法三种方法都与边有关系：(1)一种是对边的位置关系(两组对边分别平行的四边形是平行四边形)；(2)一种是对边的数量关系(两组对边分别相等的四边形是平行四边形)；(3)一种是对边的数量与位置关系(一组对边平行且相等的四边形是平行四边形).所以利用对边关系判定平行四边形的方法多且较简单，一般思路是：证明两组对边分别平行；或两组对边分别相等；或一组对边平行且相等.例：如图，已知BE∥DF，∠ADF＝∠CBE，AF＝CE.求证：四边形DEBF是平行四边形.证明：∵BE∥DF，∴∠AFD＝∠CEB，又∵∠ADF＝∠CBE，AF＝CE，∴△ADF≌△CBE，∴DF＝BE，∵BE∥DF，BE＝DF，∴四边形DEBF是平行四边形.【知识点2】平行四边形的判定的探究题平行四边形是一类特殊的四边形，并且它是学习矩形、菱形和正方形的基础.在有关平行四边形判定的探究型问题中，要会判定一个四边形是平行四边形，解决运动型问题的关键是把运动的问题转化为静止的问题.运动变化题，这类题的解决技巧是把“运动”的“静止”下来，以静制动，同时注意不同的情况.例：如图所示，已知在四边形ABCD中，AD∥BC(AD＞BC)，BC＝6 cm，点P从A点以1 cm/s的速度向D点出发，同时点Q从C点以2 cm/s的速度向B点出发，设运动时间为t秒，问t为何值时，四记忆观察分析利用对边关系判定平行四边形的方法多且较简单，一般思路是：证明两组对边分别平行；或两组对边分别相等；或一组对边平行且相等.应用巩固因题而定，有时候需要利用三角形的方法解决平行四边形问题.探究提高，感受生活中的数学。

首先，关于平行四边形性质的推理过程，我意识到需要更加注重引导学生通过观察、分析、归纳来理解这些性质。在课堂上，我尝试通过丰富的实例和图示来让学生感受这些性质的产生，但感觉还可以做得更好。今后，我打算多设计一些具有启发性的问题，让学生在自主探索中理解和掌握这些性质。
其次，我发现学生们在平行四边形判定方法的灵活运用方面还有待提高。在讲授过程中，我强调了四种判定方法，但课后反馈显示，部分学生在面对具体问题时，仍然不知道如何选择合适的方法。针对这个问题，我打算在接下来的课程中，增加一些具有针对性的练习，让学生在实际操作中学会灵活运用判定方法。
三、教学难点与重点
1.教学重点
（1）平行四边形的性质：熟练掌握平行四边形的对边平行且相等、对角相等、对角线互相平分等性质，并能运用这些性质解决相关问题。
举例：在解决实际问题时，如求平行四边形的周长、面积等，学生需要运用性质来简化计算过程。
（2）平行四边形的判定方法：熟悉并掌握对边平行且相等、对角线互相平分、一组对边平行且相等、两组对边分别相等四种判定方法。
同学们，今天我们将要学习的是《平行四边形周考》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要判断一个四边形是否为平行四边形的情况？”（如建筑设计、地图绘制等）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索平行四边形的奥秘。
2.平行四边形的判定方法：熟悉使用对边平行且相等、对角线互相平分、一组对边平行且相等、两组对边分别相等四种方法判定平行四边形。
3.特殊平行四边形：了解矩形、菱形、正方形的定义及性质，并掌握它们的判定方法。
4.平行四边形周长、面积的计算：熟练运用公式计算平行四边形的周长和面积。

HGFEAB C D平行四边形的判定〔3〕班级 小组 姓名一、学习标：目标A ：探索并掌握三角形中位线的定义及性质 目标B ：三角形中位线性质应用 二、问题引领问题A ：三角形中位线定义及性质1.，如图，D 、E 分别是△ABC 的边AB 、AC 的中点. 求证：DE ∥BC, 且DE=21BC.2.归纳：(1)三角形中位线定义：连接三角形两边中点的线段叫三角形的_________________(2)三角形中位线定理：三角形的中位线_________于三角形的___________,并且等于第三边的__________. 符号语言：∵_______________________________∴___________________________________3.思考：一个三角形共有几条中位线？____ 问题B ：三角形中位线的应用例1：如图，在四边形ABCD 中，E,F,G,H 分别是AB,BC,CD,DA 的中点. 求证：四边形EFGH 是平行四边形【归纳】顺次连接任意一个四边形各边的中点所得的四边形叫做中点四边形.任意四边形的中点四边形是 .三、训练测评训练A:三角形中位线性质1.三角形各边分别是3cm 、5cm 、6c m,那么连结各边中点所围成的三角形的周长 是 cm.2.在ΔABC 中，M,N 分别是AB,AC 的中点，且∠A+∠B=120°，那么∠ANM= .3. 三角形三边长分别为a,b,c 它的三条中位线组成一个新的三角形，这个新三角形的三条中位线又组成一个小三角形，这个小三角形的三条中位线又组成一个新小三角形，那么最小的三角形的周图18.1-15ED AC第2题D E A B C 第1题D C A O B 第3题E GFD A C B 长是〔 〕 A.21(a+b+c) B. 61 (a+b+c) C. 81(a+b+c) D. 41(a+b+c) 4. 等腰三角形的两条中位线的长分别为3和5，那么等腰三角形的周长为 5. 如图，ΔABC 中，D,E,F 分别是AB,AC,BC 的中点.〔1〕假设EF=5cm,那么AB= cm;假设BC=9cm,那么DE= cm; (2)中线AF 与中位线DE 有什么特殊关系？证明你的猜测.6.：E 为□ABCD 中DC 边的延长线上一点，且CE=DC,连接AE,分别交BC 、BD 于点F 、G ，连接AC 交BD 于O,连接OF.求证：AB= 2 OF四：课堂小结：__________________________________________________班级 小组 姓名五．课时作业.1.如图，要测量A,B 两点之间的距离，在O 点设桩，分别取OA 的中点C ，OB 的中点D,测得CD=24m,那么AB 的长为 .2.如图，在ΔABC 中，AB=AC=6，BC=8，AE 平分∠BAC 交BC 于点E,点D 为AB 的中点，连接DE,那么ΔBDE 的周长为〔 〕 A.7+5 B.10 C.4+25 D.123.如图，在四边形ABCD 中，AD=BC,E,F,G 分别是AB,CD,AC 的中点. 求证：ΔEFG 是等腰三角形4.如图，在□ABCD 中，EF ∥AB 交BC 于E,交AD 于F,连结AE,BF 交于点M,连结CF,DE 交于点N,求证：〔1〕MN ∥AD;(2)MN=21AD第5题EDB第6题G FOACN MADF第7题MBC【能力提升】5.如图，ΔABC 中，AB=8，AC=12，AM 平分∠BAC,BM ⊥AM 于点M,N 是BC 的中点，求MN 的长.。

18.1.2 平行四边形的判定（1）学习目标：会综合运用平行四边形的判定方法和性质来解决问题。

重点及难点：平行四边形的判定方法和性质的灵活应用知识点归纳：1.平行四边形的对边，对角之间的关系：(1) 平行四边形的对边平行且相等.(2) 平行四边形的对角相等.(3) 平行四边形的邻角互补.2.平行四边形的判定方法：(1) 两组对边分别相等的四边形是平行四边形.(2) 两组对角分别相等的四边形是平行四边形.(3) 对角线互相平分的四边形是平行四边形.针对训练：1.如图，已知AD∥BC，要使四边形ABCD为平行四边形，需要添加的条件是___ _____________.(只需填写一个2.下列能判定一个四边形为平行四边形的条件是( )A.一组对边平行，另一组对边相等B.一组对边平行，一组对角互补C.一组对角相等，一组邻角互补D.一组对角相等，另一组对角互补3.如图，E，F是平行四边形ABCD对角线BD上的两点，请你添加一个适当的条件：____四边形AECF是平行四边形4. 如图，下列判断正确的是（）A．若AB=CD，且AD∥BC，则四边形ABCD是平行四边形B．若AD=BC，且AB∥CD，则四边形ABCD是平行四边形C．若AB=CD，且AB∥CD，则四边形ABCD是平行四边形D．以上判断都对5. 下列说法，属于平行四边形判定方法的有（）①两组对边分别平行的四边形；②平行四边形的对角线互相平分；③两组对边分别相等的四边形；④两条对角线互相平分的四边形.A．6个 B．5个 C．4个 D．3个6. 把两个全等的非等腰三角形拼成平行四边形，可拼成的不同平行四边形的个数为（）A．1 B．2 C．3 D．47. 如图所示，在□ABCD中，E，F分别是对角线BD上的两点，且BE=DF，要证明四边形AECF是平行四边形，最简单的方法是根据来证明.8 . 如图，AB∥EF∥CD，AD∥MN∥BC，则图中共有平行四边形( )A.6个B.7个C.8个D.9个9. 如图所示，在△ABC中，AB＝AC＝8，D是BC上一动点(点D与点B，C不重合)，且DE∥AB，DF∥AC，则四边形DEAF的周长是( )A.24B.18C.16 D10. 如图，在▱ABCD中，点E，F是对角线AC上的两点，且AE＝CF.求证：∠EBF＝∠11. 如图，四边形ABCD是平行四边形，E，F为对角线AC上两点，连接ED，EB，FD，FB.给出以下结论：①BE∥DF；②BE＝DF；③AE＝CF.请你从中选取一个作条件，使∠1＝∠2成立，并给出证明.12. 如图所示，BD是▱ABCD的对角线，AE⊥BD于点E，CF⊥BD于点F.求证：四边形AECF是平行四边形.13. 如图，已知AB，CD相交于点O，AC∥DB，AO＝BO，E，F分别是OC，OD的中点，求证：四边形AEBF是平行四边形.14. 如图所示，在▱ABCD中，E，F，G，H分别是四条边上的点，且AE＝CF，BG＝DH. 求证：EF与GH互相平分.15. 如图，在△ABC中，∠ACB＝90°，D是BC的中点，DE⊥BC，CE∥AD，若AC＝2，CE＝4，求四边形ACEB的周长。

内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.1 平行四边形18.1.1 平行四边形的性质（2）（第3课时）教案（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.1 平行四边形18.1.1 平行四边形的性质（2）（第3课时）教案（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.1 平行四边形18.1.1 平行四边形的性质（2）（第3课时）教案（新版）新人教版的全部内容。

18。

1.1 平行四边形的性质课题18。

1。

1 平行四边形的性质（2)课时第3课时课型习题课作课时间教学内容分析本节课学习平行四边形的对角线性质的应用。

教学目标1.利用平行四边形的对角线性质求线段长度2.利用平行四边形的对角线性质进行简单的证明题。

3.利用平行四边形的对角线互相平分确定边的取值范围4.能综合运用平行四边形的对角线性质解决平行四边形的有关计算问题。

重点难点平行四边形的对角线性质的应用教学策略选择与设计引导学生观察、分析，使传授的数学知识成为学生自己思考获得的结果，从而抓住了重点，突破了难点。

让学生深刻地理解平行四边形的对角线性质.同时通过练习进行针对性的巩固,体会该性质在具体问题中的应用。

针对学生回答时存在的问题，教师可以采取学生间互相纠错，必要时教师再予以矫正学生学习方法观察法，分析法，引导法，讨论法教具三角板教学过程教师活动学生活动设计意图1. 平行四边形的对角线一定具有的性质是（）A.相等 B .互相平行C.互相垂直D.互相垂直且相等2。

《18.2.1（2）矩形的判定》班级 小组 姓名一、学习目标：目标A ：理解并掌握矩形的3个判定方法。

目标B ：矩形的判定的应用 二、问题引领目标A ：理解并掌握矩形的3个判定方法。

（一）知识链接1、 矩形具有而平行四边形不一定具有的性质是___________ (1)对边平行且相等 (2)对角线互相平分 (3)对角相等 (4)对角线相等 (5)4个角都是900(6)轴对称图形 2、矩形ABCD 的对角线AC 、BD 相交于点O ， ∠AOB=600， OA=3， 则ＡＣ＝_____,AB=__________（二）矩形的判定:阅读课本P54—55完成下列内容（口述证明过程） 矩形的判定定理1：(定义）有一个角是__________的_______________是矩形 符号语言（如右图）：矩形的判定定理2：_________________的平行四边形是矩形 已知：如右上图，平行四边形ABCD 中，AC=BD 。

求证：四边形ABCD 是矩形矩形的判定定理3：有三个角是__________的四边形是矩形（口述证明过程） 符号语言：目标B ：矩形的判定的应用1、已知 ：ABCD 的对角线AC 、BD 相交于点O ，△AOD 是等边三角形，AD=4 cm ，求这个平行四边形的面积（结果保留根号）.2、如图，在平行四边形ABCD 中，E ，F 为BC 上两点，且BE=CF ，AF=DE 。

求证：（1）△ABF≌△DCE； （2）四边形A BCD 是矩形。

3、如图，点B 为直线PC 上一点，BD,BE 分别是∠ABC 与∠ABP 的角平分线，AE ⊥BE 于E, AD ⊥BD 于D.求证：四边形AEBD 是矩形。

A DCBOCA DOBBACD E P三、专题训练：1、在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是（ ）．A ．测量对角线是否相互平分B ．测量两组对边是否分别相等C ．测量一组对角是否都为直角D ．测量其中三角形是否都为直角 2、能判断四边形是矩形的条件是（ ）A 、两条对角线互相平分B 、两条对角线相等C 、两条对角线互相平分且相等D 、两条对角线互相垂直。

内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.2 特殊的平行四边形18.2.2 菱形（第3课时）菱形的性质教案（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.2 特殊的平行四边形18.2.2 菱形（第3课时）菱形的性质教案（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为内蒙古呼和浩特市赛罕区八年级数学下册18 平行四边形18.2 特殊的平行四边形18.2.2 菱形（第3课时）菱形的性质教案（新版）新人教版的全部内容。

菱形的性质课题菱形的性质课时第3课时课型习题课作课时间教学内容分析本节课学习菱形的性质的应用。

教学目标1.通过习题，巩固利用菱形的性质进行计算.2.通过习题，巩固利用菱形的性质进行证明.3.通过习题,巩固利用菱形的性质解决实际问题。

重点难点菱形的性质的应用。

教学策略选择与设计通过针对性练习题，巩固利用菱形的性质进行计算和证明，培养学生的逻辑推理能力，掌握菱形的两条性质.在练习设计上，遵循由浅入深、循序渐进的原则，使学生发现问题、解决问题的能力得到进一步提升。

学生学习方法分析法，计算法,巩固应用法教具三角板教学过程教师活动学生活动设计意图一、选择题1。

如图所示，在菱形ABCD中，AB＝5,∠BCD＝120°，则对角线AC的长是( D ）A。

20 B。

15 C。

10 D。

52。

如图，菱形ABCD的两条对角线相交于点O，若AC＝6，BD＝4，则菱形ABCD的周长是( C)A。

24 B.16 C.4 错误! D.2错误!3。

13.已知：如图，在四边形ABCD中，AB∥CD，对角线AC，BD相交于点O，BO＝DO.
求证：四边形ABCD是平行四边形.
14.如图，E，F是四边形ABCD的对角线AC上的两点，且AE＝CF，BE＝DF，BE∥DF.
求证：四边形ABCD是平行四边形 .
15.如图，在▱ABCD中，点E，F在对角线BD上，且BE＝DF.求证：(1)AE＝CF；
18.1.2平行四边形的判定
课题
18.1.2平行四边形的判定(2)
课时
第3课时
课型
习题课
作课时间
教学
内容
分析
本节课学习一组对边平行且相等的四边形是平行四边形的判定方法.
教学
目标
1.通过习 题，掌握一组对边平行且相等的四边形是平行四边形的判定方法.
2.根据不同条件能正确地选择判定方法，熟悉掌握平行四边形判定的五种方法。
4.如图，平行四边形ABCD中，A E＝CF，M，N分别是DE，BF的中点.
求证：四边形MFNE是平行四边形.
板
书
设
计
18.1.2平行四边形的判定(2)
13.已知：如图所示，在四边形ABCD中，AB∥CD，对角线AC，BD相交于点O，BO＝DO.
求证：四边形ABCD是平行四边形.
证明：∵AB∥CD，
(2)四边形AECF是平行四边形.
16.如图，已知▱ABCD，过点A作AM⊥BC于点M，交BD于点E，过点C作CN⊥AD于点N，交BD于点F，连接AF，CE.求证：四边形AECF是平行四边形.
通过练习题，使学生掌握平行四边形的判定方法，并会综 合运用平行四边形的判定方法和性质来解决问题.
作业
3.已知：如图，在平行四边形ABCD中，AE，CF分别是∠DAB，∠BCD的平分线.求证：四边形AFCE是平行四边形.

图18－2－167
A.1 B.2 C. D.
二、填空题
5.如图，四边形ABCD的对角线互相垂直，且OB＝OD，请你添加一个适当的条件：答案不唯一，如OA＝OC或AD＝BC或AD∥BC或AB＝BC，使四边形ABCD成为菱形(只需添加一个即可).
6.一个平行四边形的一条边长为3，两条对角线的长分别为4和2 ，则它的面积为___4 __.
(1)在图中画出线段DE和DF；
(2)连接EF，则线段AD和EF互相垂直平分，这是为什么？
解：(1)如图，画出线段DE和DF.
(2)如图，连接EF.
∵DE∥AB，DF∥AC，
∴∠FAD＝∠EDA，
四边形AEDF是平行四边形.
∵AD是△ABC的角平分线，
∴∠FAD＝∠EAD，
∴∠EAD＝∠EDA，
∴EA＝ED，
∴∠ACF＝∠AFC，
∴AF＝AC，
∴▱ACGF为菱形.
教学反思
四条边相等的四边形是菱形
9.如图，CE是△ABC外角∠ACD的平分线，AF∥CD交CE于点F，FG∥AC交CD于点G.
求证：四边形ACGF是菱形.
证明：∵AF∥CD，FG∥AC，
∴四边形ACGF为平行四边形.
∵CE是△ABC外角∠ACD的平分线，
∴∠ACF＝∠FCG.
∵AF∥CG，
∴∠AFC＝∠FCG，
(1)求证：四边形DBFE是平行四边形；
(2)当△ABC满足什么条件时，四边形DBEF是菱形？为什么？
板
书
设
计
菱形的判定
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直，并且每一条对角线平分一组对角

教学
策略
选择
与设计
通过类比学习激发学生的好奇心和求知欲，引入本节课要研究的内容.引导学生认识判定定理与性质定理是互逆定理后，可以让学生独立思考，逐步锻炼学生的推理论证能力。通过例题和练习题教学使学生掌握利用菱形的判定定理解决一些简单的问题.
学生
学习
方法
类比法，分析法，练习法
教具
三角板
教学过程
教师活动
口答
记忆
口答
思考
猜想
探究分析
观察思考
对比学习理解
通过类比学习激发学生的好奇心和求知欲，引入本节课要研究的内容.
探究推导菱形的判定方法。
教师活动
学生活动
设计意图
总结：对角线互相垂直的平行四边形是菱形.
课堂设计：组织学生以小组合作的方式独立完成“对角线互相垂直的平行四边形是菱形”的证明，并进行全班交流.
应用迁移、
巩固提高
作业
课本60第6题。
板
书
设
计
菱形的判定
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直，并且每一条对角线平分一组对角
菱形的四条边都相等
菱形的
判定
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四条边相等的四边形是菱形
例：如图，▱ABCD的对角线AC，B D相交于点O， 且AB＝5，AO＝4，BO＝3.
【探究2】如图，先画两条等长的线段AB，AD，然后分别以B，D为圆心，AB长为半径画弧，两弧交点为C，连接BC，CD.得到的四边形ABCD是菱
形吗？请说明理由.Fra bibliotek总结：四条边相等的四边形是菱形.

图18.1-7A第4题B平行四边形的判定（1）班级 小组 姓名一、学习标：目标A ：探索并掌握平行四边形判定的方法 目标B ：平行四边形判定的应用. 二、问题引领问题A ：平行四边形的判定方法 1．复习：平行四边形的性质有哪些？ 2、猜测：如何判断一个四边形是平行四边形？ 3、如何证明你的猜测？4.归纳：平行四边形的判定方法判定1： 的四边形是平行四边形 符号语言： 在四边形ABCD 中，∵_______________________________∴___________________________________判定2： 的四边形是平行四边形 符号语言： 在四边形ABCD 中，∵_______________________________∴_______________________________判定3： 的四边形是平行四边形 符号语言： 在四边形ABCD 中，∵_______________________________∴_______________________________问题B ：平行四边形判定的应用例1:如图，□ABCD 的对角线AC 、BD 相交于点O ，E 、F 是AC 上的两点，并且AE=CF.求证：四边形BFDE 是平行四边形.你还有其他证明方法吗？例2：如图，在□ABCD 中，点E,F 分别在BC,AD 上，且AF=CE.求证：四边形AECF 是平行四边形三、专题训练CCC F E DAOCB第3题ACB训练A:平行四边形的判定1.在平行四边形ABCD 中，∠A ：∠B ：∠C ：∠D 的值可能是( )A.1：2：3：4B.2：2：3：3C.2：3：2：3D.2：3：3：2 2.一个四边形的边长依次是a 、b 、c 、d ，且a 2+b 2+c 2+d 2=2ac+2bd ，则这个四边形是 。

训练B:平行四边形判定的应用3.如图，□ABCD 的对角线AC 、BD 相交于点O ，E 、F 分别是OA,OC 的中点. 求证：BE=DF4.如图，四边形ABCD 是平行四边形，BE 平分∠ABC 交AD 于E ，DF 平分∠ADC 交BC 于点F.求证：四边形BFDE 是平行四边形四、课堂小结：_____________________________班级 小组 姓名五、课堂作业1.不能判定四边形ABCD 是平行四边形的是( ) A.AB=CD ,AD=BC B.∠A=∠C, ∠B=∠D C. AB=CD,AD ∥BC D. AB ∥CD, AD ∥BC2. 已知：如图，△ABC ，BD 平分∠ABC ，DE ∥BC ，EF ∥AC ，求证：BE=CF3. 如图，□ABCD 的对角线AC 、BD 交于点O ，E 、F 在AC 上，G,H 在BD 上，且AF=CE,BH=DG.求证：GF ∥HE【能力提升】已知如图，□ABCD 的对角线AC 、BD 相交于点O ，E,F 分别为OB 、OD 的中点，过O 任作一直线分别交AB 、CD 于G 、H. 求证：GF ∥EH第5题B。