小升初数学-圆与扇形
- 格式:docx
- 大小:1.40 MB
- 文档页数:8

小升初几何问题总复习一、小升初考试热点及命题方向圆和立体几何近两年虽然不是考试热点,但在小升初考试中也会时常露面。
因为立体图形考察学生的空间想象能力,可以反映学生的本身潜能;而另一方面,初中很多知识点都是建立在空间问题上,所以可以说学校考察立体也是为初中选拔知识链接性好的学生。
二、2015年考点预测2015年的小升初考试如果考察圆与立体几何,不会难度太大,只需掌握我们本讲中所介绍的几类基本题型,就可成功在握。
考试热点将会出现在诸如水位问题和三维视图问题等题型。
三、典型例题解析1 与圆和扇形有关的题型【例1】(★★)如下图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等。
求扇形所在的圆面积。
【解】:等腰三角形的角为45度,则扇形所在圆的面积为扇形面积的8倍。
而扇形面积为等腰三角形面积:S=1/2×10×10=50。
则:圆的面积为400。
【例2】(★★★)草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?【解】:(此题十分经典)如右上图所示,羊活动的范围可以分为A,B,C三部分,所以羊活动的范围是【例3】(★★)在右图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差。
【解】:我们只要看清楚阴影部分如何构成则不难求解。
左边的阴影是大扇形减去小扇形,再扣除一个长方形中的不规则白色部分,而右边的阴影是长方形扣除这块不规则白色部分,那么它们的差应为大扇形减去小扇形,再减去长方形。
则为:π/4×4×4-π/4×2×2-4×2=3×3.14-8=1.42。
【例4】(★★★)如图,ABCD 是正方形,且FA=AD=DE=1,求阴影部分的面积。
(取π=3)【解】:先看总的面积为1/4的圆,加上一个正方形,加上一个等腰直角三角形,然后扣除一个等腰直角三角形,一个1/4圆,一个45度的扇形。
扇形和圆的组合图形的面积学生姓名年级学科授课教师日期时段核心内容扇形和圆的组合图形的面积课型一对一/一对N 教学目标掌握扇形和圆的组合图形的面积的计算重、难点1、会利用平面图形的周长和面积公式求平面图形的周长和面积。
2、会用割、补、分解、代换、增加辅助线等方法,将复杂问题变得简单。
课首沟通和学生交谈。
了解学生对圆的认识,对各计算公式是否掌握。
知识导图课首小测1.一个圆形花坛的半径是3m,它的面积是多少平方米?(已知圆的半径,求圆的面积)2.圆形花坛的直径是20m,它的面积是多少平方米?(已知圆的直径,求圆的面积)3.一个圆形蓄水池的周长是25.12m,这个蓄水池的占地面积是多少?(已知圆的周长,求圆的面积)4.求下图扇形的面积。
导学一:运用代换法将复杂的图形转化为简单的规则图形例 1. 图1中右半部分阴影面积比左半部分阴影面积大33平方厘米,AB=60厘米,CB垂直AB,求BC的长。
我爱展示1.如图1-1所示,两个圆的圆心分别为O1、O两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO1O的面积。
2.如图1-2,所示,求右半部分阴影面积比左半部分阴影面积大多少平方厘米。
3.如图1-3:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少平方厘米?导学二:巧用各基本图形的计算公式求解知识点讲解 1:把R2看成一个整体例 1. 图2中已知阴影部分的面积是20平方分米,求环形的面积。
我爱展示1.下图中正方形的面积是8平方米,圆的面积是多少平方米?2.已知下图2-2中阴影部分三角形的面积是5平方米,求圆的面积。
3.已知下图2-3中阴影部分三角形的面积是7平方米,求圆的面积。
知识点讲解 2:从局部到整体,从整体到局部,牢记公式,巧妙应用。
例 1. 如图3,半圆S1的面积是14.13平方厘米,圆S2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?我爱展示1.下图3-1中,△ABC是等腰直角三角形,以为半径的圆弧交延长线于点,已知阴影部分的面积是求。
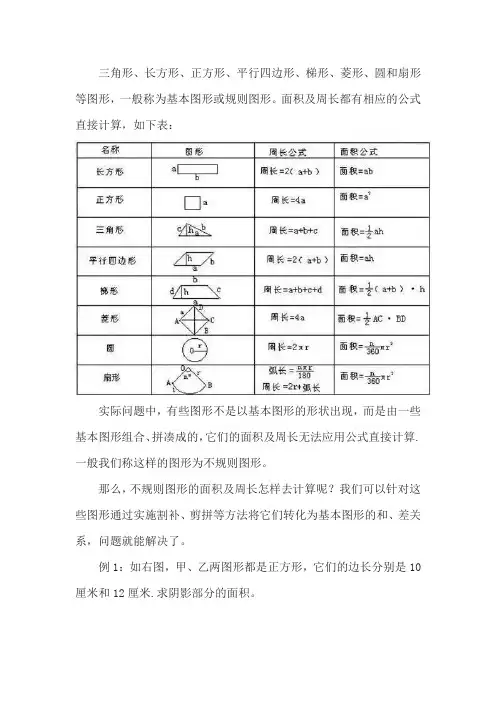
三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
面积及周长都有相应的公式直接计算,如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。

沪教版六年级(上)小升初题单元试卷:第4章圆和扇形(03)一、选择题(共10小题)1. 如图,大圆的周长与两个小圆的周长和比较()A.大圆的周长长B.两个小圆的周长和长C.一样长D.无法判定2. 如图,大半圆的周长()两个小半圆的周长之和。
A.=B.>C.<3. 一个正方形的边长和圆的半径相等,已知正方形的面积是20平方米,圆的面积是()平方米。
A.无法解答B.62.8C.12.56D.15.74. 小圆和大圆的半径比是2:3,那么小圆和大圆的面积比是()A.2:3B.4:9C.无法判断5. 圆的半径扩大到原来的2倍,则它的面积扩大到原来的()倍。
A.2B.4C.6D.86. 小圆直径是3厘米,大圆半径是6厘米,小圆的面积是大圆面积的()A.14B.18C.1167. 小圆直径是3,大圆半径是6,小圆的面积是大圆面积的()A.12B.14C.18D.1168. 一个圆的半径扩大3倍,面积扩大()倍。
A.3B.6C.99. 设C为圆的周长,则Cπ×12=()A.圆的半径B.圆的直径C.圆的面积D.圆的周长10. 在长5厘米,宽3厘米的长方形中,画一个最大的半圆,这个半圆的周长是厘米。
()A.9.42B.18.84C.14.42D.12.85二、填空题(共16小题)在同一圆中,周长总是直径的π倍。
________.半径是2分米的圆,周长和面积相等。
________.(判断对错)在长为10厘米,宽为8厘米的长方形中画一个最大的圆,这个圆的半径是________,面积是________.在纸片上将圆规两脚间的距离定为4cm,画出的圆的面积是50.24cm2,如果把这个圆平均分成若干份。
剪拼成一个近似的长方形,这个近似长方形的长是12.56cm.要剪一个面积是9.42平方分米的圆形纸片,至少要面积是________平方分米的正方形纸片。
若两个圆的半径比是1:2,则它们的面积比是1:2________.(判断对错)大圆的直径是小圆直径的2倍,大圆的周长是小圆周长的________倍,小圆的面积是大圆的________.两圆相比,周长小的面积一定小。

第二讲ﻩ几何之圆与扇形教学目标组合图形的面积计算,除了直线型面积计算“五大模型”(已在暑假班重点精讲),跟圆有关的曲线型面积也是得别重要的组成部分。
其中,尤以结合情境的曲线形面积计算为最常答案提示:地球赤道长:22 3.14640040192r π=⨯⨯=(千米),所以绳长40192千米; 一般我们会想对于4万多千米来说,仅仅延长1米,会有多大的间隔?即使有间隔,恐怕也只能在显微镜下才能看见!让我们来计算一下吧!假如绳长加上1米变为40192001米,则有:40192001264000000.159π÷-≈(米),大约为16厘米,差不多有一支铅笔长。
简直不可思议!利用“加、减”思想解答问题【例1】 (资源杯试题)如图,两个正方形摆放在一起,其中大正方形边长为12,小正方形边长为4,那么阴影部分面积是多少?(π取3)分析:ABCD ABF 1361084S S S π=+-==阴影面积梯形三角形圆[巩固](5年级春季所学题目)计算下列各图阴影部分的面积。
(π取3)想 挑 战 吗 ?捆地球的绳子假设地球上即无山,又无海,完全像一个大圆球,现在想用一根很长很长的绳子,沿着赤道用绳子捆上一圈,问绳长多少?如果绳长加上1米,绳子围成一个大圆圈之后,就要离开赤道一段距离,形成围绕地球的一个等距离的圆环,问圆环和地球之间的间隔有多大?(已知地球半径约为6400千米,π取3.14分析:因为是回忆之前学习过的内容,所以大部分题目教师只要帮助学生找到方法即可,过程可以课下完成!但对于(3),希望教师再次讲解!如果班上孩子多数没有学过,或忘记了,酌情讲解!(1)1122=--阴影部分面积大圆面积小圆面积三角形面积221114244=10222ππ••-••-••=(2)22314444+2416044π=+-••=阴影部分面积正方形个圆个圆=(+)(3)法1:如右图所示,过B做BD 垂直于A C,我们就容易得到BD =AD=DC,所以BD=3,三角形ABC 的面积=3×6÷2=9, 阴影部分面积=扇形面积-三角形ABC 的面积=4.5×3-9=4.5 ; 法2 :直角三角形的三边有一个特殊的关系,那就是著名的勾股定 理:如右图所示,三角形AB C是直角三角形,最长边是AC ,较短 的两条边是AB 、BC ,那么有222AC AB BC =+.反之, 若三角形中有222AC AB BC =+,那么这个三角形就是直角三角形,且A C边为最大边,所对的角是直角.最经典的直角三角形三边为:3、4、5 (222534=+).B A在题目中,三角形AB C是等腰直角三角形,所以有222AC AB BC =+,且AB=BC,则2222112AB 6AB 18ABC =AB BC AB 922⨯==••=•=,,三角形的面积,阴影部分面积=扇形面积-三角形ABC 的面积=4.5×3-9=4.5 ; 法3:对称的补出另一半,很容易得到答案.(4)阴影部分面积= 一半小圆+ 一半中圆 + 三角形 – 一半大圆 ;因为5×5=4×4+3×3 ,三角形是直角三角形,阴影面积为:3×4÷2=6 .[巩固](5年级春季所学题目)(西城区三帆中学选拔考题)如右图,两个正方形边长分别是10和6,求阴影部分的面积。

圆与扇形1、分别以一个边长为2厘米的等边三角形的三个顶点为圆心,以2厘米为半径画弧,得到下图.那么,阴影图形的周长是厘米.(取3.14)2、有7根直径都是5分米的圆柱形木头,现用绳子分别在两处把它们捆绑在一起,其切面如下图所示,至少需要绳子分米.(取3.14)3、把同一段铁丝围成一个正方形后,又改围成一个圆形,发现按照面积公式得出的二者面积之比为4:5,那么在计算圆面积时,圆周率丌的取值为。
4、如下图所示,已知圆环的面积是141.3平方厘米,那么阴影部分的面积是平方厘米.(取3.14)5、如下图所示,弧IFD与JED是分别以A、B为圆心、以AD、BD为半径的圆弧,已知AD1=DB=DC=4厘米,且AGDHB、AFC与BEC分别是三条直线段.线段IA、FG、CD、EH、JB都分别垂直于AB.请问图中阴影部分的面积是多少?(取)6、如下图所示的半圆的直径BC=8厘米,AB=AC,D是AC的中点,则阴影部分的面积是.(取3.14)7、如下图所示,ABCD是边长为10厘米的正方形,且AB是半圆的直径,则阴影部分的面积是平方厘米.(取3.14)8、下图中正方形ABCD及DCEG的面积均为64平方厘米,EFG则为一半圆,F是弧EFG的中点.请问阴影部分的面积为多少平方厘米?(3.14)9、半径为10、20、30的三个扇形如下图放置,是的倍,10、如下图所示,图中的曲线是用半径长度的比为2:1.5:o.5的6条半圆曲线连成的,问:涂有阴影的部分与未涂阴影的部分的面积比是多少?11、有三个同心圆,它们的半径之比是3:4:5,如果大圆的面积是100平方厘米,那么中圆与小圆所构成的圆环的面积是A.20平方厘米B.28平方厘米C.36平方厘米D.60平方厘米12、下图是两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%.问:大圆的面积是多少?13、下图中五个相同的圆的圆心连线构成一个边长为10厘米的正五边形.求五边形内阴影部分的面积.=3.14)14、如下图所示,已知圆心是O,半径r=9厘米,∠1=∠2=15°,那么阴影部分的面积是平方厘米。

圆练习题1一、填空。
1、一个圆的周长是50。
24厘米,它的直径是()厘米,面积是()平方厘米。
2、一个环形,内圆半径是4厘米,外圆直径是12厘米。
这个环形的面积是()平方厘米。
3、一个长方形,长12厘米,宽8厘米,从它上剪下一个最大的圆形,这个圆形的周长是()厘米,面积是()平方厘米。
4、要从一个边长是6米的正方形上剪下一个最大圆形,剪掉的面积是()平方米,这个正方形的利用率是()。
5、在操场上画一个直径是10米的半圆,它的周长是()米,面积是()平方米。
6、一个长方形和圆形的面积相等,已知圆的半径是5厘米,长方形的长是()厘米,宽是()厘米,周长是()厘米,面积是()平方厘米。
7、():()=圆周率。
二、判断。
(1)通过圆心的线段叫做圆的直径。
()(2)半径是直径的一半。
()(3)任何一个圆的周长都是它直径的3.14倍。
()(4)圆的半径扩大2倍,面积和周长都扩大2倍。
()(5)面积相等的两个圆周长一定相等。
()三、选择。
1、把一个圆分成32等份,剪开后可以拼成一个近似的()。
A、长方形B、平行四边形C、梯形2、小明拿出一张长13厘米,宽9厘米的长方形手工纸,剪一些半径为2厘米的圆,他最多可以剪()个。
A、 6B、10C、113、从3块面积相等的正方形钢板上,分别冲下1个、4个和9个圆片,如图,哪种剩下的钢板面积大?()A、第一种B、第二种C 、第三种 D、一样大4、把一个半径为r的圆对折,得到的半圆的周长是()。
再对折得到的扇形的周长是()如果再对折,得到的扇形的周长是()。
A、21πr + 2r B、41πr + 2rC、πr+2rD、πr +d5、用3根同样长的铁丝分别围城正方形、长方形和圆,面积最大的是( )A 、 正方形B 、 圆C 、 长方形 6、正方形、长方形和圆的面积相等,它们中( )的周长最长。
A 、 圆B 、正方形C 、长方形 7、大圆的直径是6厘米,小圆的半径是1.5厘米,大圆的周长是小圆周长的( A )倍,小圆面积是大圆面积的( )。

7.扇形统计图【知识点睛】1.扇形统计图的特点:扇形统计图是用整个圆的面积表示总数,用院内的扇形面积表示各部分数量占总数的百分比.2.读懂扇形统计图:(1)获取信息的方法:运用综合、对比等多种观察方法,可以从扇形统计图中获取信息,还可以利用这些信息提出相应的问题.(2)扇形统计图的优点:它可以清楚地表示出部分数量与总数、部分数量与部分数量之间的关系.3.利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数应用题的解题思路和解题方法进行解答.【小题狂做】一.选择题(共1小题)1.(2018秋•深圳期末)如图是六(1)班“我最喜欢的科目”统计图.六(1)班有50人,最喜欢数学的有()人.A.10B.12C.16D.9【解答】解:50×32%=16(人)答:最喜欢数学的有16人.故选:C.二.填空题(共8小题)2.(2019•萧山区模拟)(1)如果用整幅图表示某小学共有学生800人,那么B表示该小学三四年级有学生240人.(2)如果用A表示“城乡手拉手,爱心传真情”活动中一二年级共捐书600本,那么C 代表的五六年级共捐书1080本.【解答】解:(1)800×30%=240(人)答:B表示该小学三四年级有学生240人.(2)90÷360=25%600÷25%=2400(本)2400×(1﹣25%﹣30%)=2400×45%=1080(本)答:C代表的五六年级共捐书1080本.故答案为:240,1080.3.(2019春•泗洪县期中)如图是六年一班期中数学成绩统计图,请根据下列信息解答相关问题.(1)不合格率为5%.(2)已知得优的有12人,全班有40人.(3)得良的比得合格的多6人.【解答】解:(1)1﹣(25%+30%+40%)=1﹣95%=5%答:不合格率为5%.(2)12÷30%=40(人)答:已知得优的有12人,全班有40人.(3)40×(40%﹣25%)=40×15%=6(人)答:得良的比得合格的多6人.故答案为:5,40,6.4.(2019春•南京月考)下面是新街生态园三种蔬菜种植面积的扇形统计图.(1)已知草莓园的面积是126平方米,三种蔬菜的总面积是225平方米.(2)黄瓜园的面积是67.5平方米,西红柿比草莓少75%.【解答】解:(1)126÷56%=225(平方米)答:三种蔬菜的总面积是225平方米.(2)225×30%=67.5(平方米)(56%﹣14%)÷56%=42%÷56%=0.75=75%答:黄瓜园的面积是67.5平方米,西红柿比草莓少75%.故答案为:225,67.5,75.5.(2019春•沛县月考)如图是一件毛线衣中各种材质占总质量的统计图,根据右图回答问题.(1)棉的含量占这件衣服的7%.(2)羊毛的含量最多,棉的含量最少.(3)兔毛含量比涤纶少占总数的17%.(4)这件毛衣重200克,羊毛有120克,兔毛有16克.如果羊毛含量120克,那么棉含量是14克.【解答】解:(1)答:棉的含量占这件衣服的7%.(2)答:羊毛的含量最多,棉的含量最少.(3)25%﹣8%=17%答:兔毛含量比涤纶少占总数的17%.(3)200×60%=120(克)200×8%=16(克)120÷60%×7%=200×7%=14(克)答:羊毛有120克,兔毛有16克.棉含量是14克.故答案为:7,羊毛,棉,17,120,16,14.6.(2018秋•郑州期末)如图的扇形统计图清楚地表示参加各社团人数与总人数之间的关系.【解答】解:如图如图的扇形统计图清楚地表示参加各社团人数与总人数之间的关系.故答案为:各社团人数,总人数.7.(2018秋•定西期末)如图:是某校六年级学生某次数学竞赛的成绩统计图,若获得优秀成绩有60人,那么全年级有200人,本次竞赛不及格10人.【解答】解:60÷30%=60÷0.3=200(人);200×(1﹣30%﹣40%﹣25%)=200×5%=200×0.05=10(人);答:全年级有200人,本次竞赛不及格的有10人.故答案为:200、10.8.(2019•吴川市模拟)一块菜地种植了4种蔬菜,分布情况如图.若油菜的种植面积是420m2.则(1)黄瓜的种植面积是630平方米;(2)芹菜的种植面积比油菜少105平方米.【解答】解(1)420÷20%×(1﹣15%﹣20%﹣35%)=2100×30%=630(m2)答:黄瓜的种植面积是630平方米.(2)420÷20%×(20%﹣15%)=2100×5%=105(m2)答:芹菜的种植面积比油菜少105平方米.故答案为:630,105.9.(2019春•雁塔区期末)六年级同学血型情况如图.AB型的占8%;如果O型的共有60人,那么六年级共有150人;A型的有42人.【解答】解:1﹣28%﹣24%﹣40%=8%60÷40%=150(人)150×28%=42(人)答:AB型的占8%;六年级共有150人;A型的有42人.故答案为:8,150,42.三.计算题(共1小题)10.(2018秋•河北区期末)看图回答问题如图是实验小学图书室藏书情况统计图(1)已知故事书有120本,这个图书室共藏书400本.(2)这个图书室科技书的本书占藏书总数的20%.(3)这个图书室的科技书比文艺书少80本.【解答】解:(1)120÷30%=400(本)答:这个图书室共藏书400本.(2)1﹣30%﹣40%﹣10%=20%答:这个图书室科技书的本书占藏书总数的20%.(3)400×(40%﹣20%)=400×20%=80(本)答:这个图书室的科技书比文艺书少80本.故答案为:400,20,80.四.应用题(共6小题)11.(2018秋•卢龙县期末)第三小学购买一批新书,数量如图所示.算一算,这个学校一共购进多少图书?【解答】解:320÷(1﹣50%﹣30%)=320÷20%=320÷0.2=1600(本)答:这个学校一共购进1600本图书.12.(2018秋•乳源县期末)如图是张叔叔家2017年的生活开支情况统计图.如果张叔叔家2017年购买服装用去了9750元,那么购买食品用去多少元?【解答】解:9750÷15%×35%=65000×35%=22750(元)答:购买食品用去22750元.13.(2018秋•黄埔区期末)如图是六年级学生“最喜欢球类运动”的统计图(1)喜欢其他球类的人数占全班人数的几分之几?(2)六年级学生共有300人,喜欢乒乓球的有多少人?比喜欢足球的人数多多少人?【解答】解:(1)1﹣19%﹣25%﹣32%﹣18%=56%﹣32%﹣18%=6%=答:喜欢其他球类的人数占全班人数的.(2)300×32%=96(人)300×18%=54(人)96﹣54=42(人)答:喜欢乒乓球的有96人,比喜欢足球的人数多42人.14.(2018秋•河东区期末)滨河学校对学生吃早餐的情况进行了调查,结果全校每天都坚持吃早餐的人数为360人,那么全校偶尔吃早餐的有多少人?【解答】解:360÷80%﹣360=450﹣360=90(人)答:全校偶尔吃早餐的有90人.15.(2018秋•河西区期末)下面是妙想根据妈妈去年一年购买的三种水果情况制成的扇形统计图,看图填空并回答问题:(1)橘子的质量占三种水果总质量的22%;(2)如果橘子的质量是44千克,那么这三种水果的总质量是多少千克?【解答】解:1﹣41%﹣37%=22%;答:橘子的质量占三种水果总质量的22%.(2)44÷22%=44÷0.22=200(千克);答:这三种水果的总质量是200千克.故答案为:22.16.(2018秋•盘龙区期末)一块菜地四种蔬菜的种植面积分布情况如下:①你获得哪些信息请逐条写下来.②如果种植黄瓜的面积有90平方米,你能提出哪些用百分数解决的问题?并解答.【解答】解:①可以获得的信息有:黄瓜的种植面积占总面积的30%;油菜的种植面积占总面积的20%;芹菜的种植面积占总面积的15%;西红柿的种植面积占总面积的35%.②可以选择下面其中的一、两个问题:问题一:种植的总面积是多少平方米?90÷30%=300(平方米)答:种植的总面积是300平方米.问题二:油菜的种植面积是多少平方米?300×20%=60(平方米)答:油菜的种植面积是60平方米.问题三:芹菜的种植面积是多少平方米?300×15%=45(平方米)答:芹菜的种植面积是45平方米.问题四:西红柿的种植面积是多少平方米?300×35%=105(平方米)答:西红柿的种植面积是105平方米.五.解答题(共5小题)17.(2018秋•抚宁区期末)李大伯在一块地里种植蔬菜,下面统计图分别统计了2014年四种蔬菜的收入情况和近四年来种植蔬菜的收入情况.(1)2014年种植萝卜的收入是多少元?(2)2013年的收入比2012年增加了百分之几?【解答】解:(1)4×(1﹣35%﹣20%﹣21%)=4×24%=4×0.24=0.96(万元),0.96万元=9600(元);答:2014年种植萝卜的收入是9600元.(2)(3﹣2.3)÷2.3=0.7÷2.3≈0.304=30.4%;答:2013年的收入比2012年增加了30.4%.18.(2018秋•天河区期末)为开展阳光体育活动,坚持让中小学生“每天锻炼1小时”,调查组随机调查了600名学生,调查内容是“每天锻炼的时间”,所得数据制成了以下的扇形统计图和条形统计图.(1)把扇形统计图中的括号和条形统计图补充完整.(2)锻炼时间不超过1小时的人数与超过1小时的人数比为1:2.【解答】解:(1)600﹣75﹣375=150(人)75÷600=12.5%375÷600=62.5%150÷600=25%如图:(2)75:150=1:2答:锻炼时间不超过1小时的人数与超过1小时的人数比为1:2.故答案为:1;2.19.(2018秋•中山市期末)光明小学对六年级全体学生进行了血型统计,王老师根据统计数据制作了一幅扇形统计图和一幅条形统计图.(1)光明小学六年级共有学生400人.(2)根据以上数据,把扇形统计图和条形统计图补充完整.【解答】解:(1)92÷23%=400(人)答:光明小学六年级共有学生400人.(2)400﹣92﹣100﹣168=40(人)光明小学六年级学生有AB型血40人1﹣23%﹣42%﹣10%=25%光明小学B型血人数占25%完成扇形统计图、条形统计图如下:故答案为:400.20.(2018秋•阿克苏市期末)六(1)班参加课外活动的情况统计如下:先算出六(1)班学生的总人数,再将统计图和统计表填写完整.【解答】解:(8+10)÷(1﹣64%)=18÷0.36=50(人)音乐组占总人数的百分比:8÷50×100%=0.16×100%=16%美术组占总人数的百分比:10÷50×100%=0.2×100%=20%体育组的人数:50﹣8﹣10=32(人)统计表如下:统计图如下:21.(2018秋•白云区期末)下面是红英学校美术小组血型情况统计表.血型A型B型O型AB型人数(人)2201414(1)算出B型和O型人数各占总人数的百分之多少?(2)请根据统计表补充完整扇形统计图.(3)请提出一个数学问题并解答.【解答】解:(1)2+20+14+14=50(人)B型人数占总人数的:20÷50=0.4=40%;O型人数占总人数的:14÷50=0.28=28%;(2)作图如下:(3)红英学校美术小组B型人数比A型人数多多少人?20﹣2=18(人),答:红英学校美术小组B型人数比A型人数多18人.。

小升初数学总复习专题分类训练卷圆、组合图形的面积第一部分知识梳理字母意义:O 圆心,r 半径,d 直径,π 圆周率,C 周长,S 面积特征:同一圆内,所有的半径、直径都分别相等,直径等于半径的2倍对称性:圆是轴对称图形,圆的直径所在的直线是圆的对称轴1.圆圆的周长计算公式:C=πd=2πr ,半圆周长计算公式:C半圆=πr+2r=(π+2)r圆的面积计算公式推导过程:将圆沿着直径等分成若干个扇形(偶数份),再拼成一个近似的长方形(分成的扇形越多,越接近长方形),长方形的长相当于圆的周长一半(πr),宽相当与圆的半径,圆的面积等于长方形的面积。
所以:S圆=S长方形=πr×r=πr2概念:两个半径不等的同心圆之间的部分称之为圆环。
各部分名称:①外圆:圆环中较大的圆叫做外圆,其半径通常用R表示。
2.圆环②内圆:圆环中较小的圆叫做内圆,其半径通常用r表示。
③环宽:外圆到内圆的距离叫做环宽环宽=R—r圆环的面积计算方法:外圆的面积与内圆的面积之差是圆环的面积。
即:S圆环=S外圆—S内圆,S圆环=π(R2 —r2)弧:圆上任意两点间的部分叫做弧3.扇形圆心角:弧的两个端点与圆心连结,所得两条半径的夹角叫圆心角扇形:由圆心角的两条半径和圆心角所对的弧组成的图形叫扇形割补(平移)法组合图形的面积加减法计算策略1 旋转、对称法4.组合图形的要求阴影先求空白面积计算包含与排除组合图形的面积总面积=两部分面积和-重叠部分面积计算策略2 巧添辅助线等积转化(代换)第二部分精讲点拨例1判断下列各题是否正确:(1)圆的周长是直径的3.14倍。
()(2)圆是轴对称图形,直径是圆的对称轴。
()(3)世界上第一位把圆周率精确到七位小数的人物是祖冲之。
()举一反三:1.填空题:(1)经过圆心并且两端都在圆上的线段叫做圆的(),圆有()条直径。
(2)圆的面积推导公式是:将圆分成若干个扇形,再拼成一个近似的长方形,长方形的长相当于圆的(),长方形的宽相当于圆的(),所以圆的面积公式为()。

第一讲 图形面积本次阴影专题是在阴影专题(一)的基础上加深对三角形的认识,再引入圆形阴影部分。
1、r 2的运用 涉及圆的面积有:圆的面积公式S 圆=πr 2; 扇形面积公式S 扇=360n πr 2 “月牙形”面积公式S 月牙=0.285 r 2; “风筝形”面积公式S 风筝=0.215 r 2通过以上公式,我们发现一个共同的特点,即在计算圆的阴影面积时,从本质上讲,我们不用求出r 的值,只要求出r 2是多少,把r 2作为一个整体,即可求解。
这是学习圆的阴影面积时首先需要掌握的。
2、割补法 学习圆的阴影面积时,有一个解题办法非常重要,它是“割补法”。
很多看似无法解的问题,运用割补法,解起来非常巧妙、简洁。
3、“容斥”原理 在例题中讲解。
总体看,与三角形相比,求圆的阴影面积,变化不多,题型较为简单。
因此本讲仍将把三角形阴影面积的求法做为学习重点,继续运用“等底等高,高相等底倍数”的办法解题,达到熟练掌握的程度,同时学习用代数法、等分法、旋转法、割补法、填补法等方法解题。
[关键词]:r 2的运用 割补法 代数法例1、如图,三角形ABC 的面积是1平方厘米,且BE=2EC ,F 是CD 的中点。
那么阴影部分的面积是多少平方厘米?例2、如图正方形ABCD 的边长为10cm ,EC=2BE ,求阴影部分面积?例3、如图正方形边长10厘米,E 、F 、H 分别为三边中点,阴影四边形面积是多少平方厘米?H例4、如图:有一张斜边为22厘米的红色直角三角形纸片,一张斜边为36厘米的蓝色直角三角形的纸片,一张黄色正方形纸片,拼成一个直角三角形,红、蓝两张三角形纸片的面积之和为多少平方厘米?例5、如图所示四边形ABCD,线段BC长为6厘米,角ABC为直角,角BCD为135o,而且点A到边CD的垂线AE的长为12厘米,线段ED的长为5厘米,求四边形ABCD的面积。
例6、有红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间互相叠放,如图所示。

一、几何图形的相关概念及基本公式1、点、线、面、体;直线、射线、线段、角;长方形(体)、正方形(体)、平行四边形、三角形、题型、多边形、圆与扇形、圆柱、圆锥、轴对称图形2、平面图形的周长、面积公式,立体图形的侧面积、表面积、体积公式3、定理、结论:三角形内角和、三角形三边关系、勾股定理、一笔画、格点图形面积公式(毕克定理)4、几何计数二、巧求周长和面积1、通过平移、旋转、翻折(对称)、割补等手段将图形转化成比较好求的形状2、利用差不变原理将图形转化3、利用面积之比与边长之比的关系解题三、几何五大模型1、等高模型及变型(如一半模型、鸟头模型等)2、风筝模型(也叫蝴蝶模型)3、相似三角形(金字塔模型、沙漏模型)4、题型比例关系(题型蝴蝶模型)5、燕尾模型四、长方体正方体及侧面展开图、圆柱圆锥【例 1】如图,阴影部分是正方形,则最大长方形的周长是_ _____厘米.知识框架例题精讲3 几何10答案: 30【练习】 如图7-20,在直角梯形ABCD 中,三角形ABE 和三角形CDE 都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD 的面积是多少?答案: 200平方厘米【例 2】 如图,有一块长方形的草坪,长20米,宽10米,现要在草坪上铺设两条宽1米的小路,则剩下草坪的面积是________平方米.答案: 171【练习】 一块矩形场地被一条路隔成甲、乙两块,甲乙的面积之比为3:8,尺寸如图,甲的面积是____。
21122乙甲答案: 60【例 3】 如图,一个梯形,面积为45,AB=10,高为6,则△AOB 的面积是___________.OCDA答案: 20【练习】如图,梯形ABCD的上底AD长5厘米,下底BC长12厘米,腰CD的长为8厘米,过B点向CD作出的垂线BE的长为9厘米,那么梯形ABCD的面积是多少?答案: 51平方厘米【例 4】已知如图,求阴影部分的面积(π取3.14)44答案: 4.56【练习】求图中阴影部分的面积。
小升初数学必会的10种图形求面积解题法!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
它们的面积及周长都有相应的公式直接计算,具体如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。
一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下:例1如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF 的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米。
解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法1相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
小升初数学专题练习:圆一、选择题1.圆的半径有()A. 一条B. 4条C. 无数2.圆的大小与圆的( )无关。
A. 半径B. 直径C. 圆心3.如图,以大圆的半径为直径画一个小圆,大圆的周长是小圆周长的( )倍。
A. 2B. 4C. 6D. 84.一个半圆,半径是r ,它的周长是()。
A. B. C.5.图形中,阴影部分是扇形的是()。
A. B. C. D.6.把一根长1.884米的铁条,弯成一个铁环(接头处不计),铁环的直径是()A. 0.7米B. 0.6米C. 0.5米D. 0.8米7.下图是在一张边长为a的正方形纸片中剪去一个半圆,那么剩下部分的周长是()。
A. 3a+πaB.C.D. 3a+πa÷28.已知一个长方形,长是10cm,宽是8cm,则从中剪一个最大的圆,则圆的半径是()厘米。
A. 4厘米B. 8厘米C. 5厘米D. 10厘米9.如图,大圆内画一个最大的正方形,正方形内画一个最大的圆…,如此画下去,共画了4个圆.那么,最大的圆的面积是最小的圆的()倍.A. 2B. 4C. 8D. 16二、判断题10.半圆的周长就是它所在圆周长的一半。
11.圆中最长的线段是直径。
12.把一张圆形纸片从不同方向折叠,折痕都经过圆心。
13.用4个圆心角都是90。
的扇形,一定可以拼成一个圆.14.如果正方形的周长和圆的周长相等,那么正方形面积一定小于圆面积。
三、填空题15.汽车的车轮滚动一周,所行的路程是车轮的________。
16.计算下圆的周长,请记住这些常用数据.d=8厘米,c=________厘米17.________决定圆的位置,________决定圆的大小。
18.通过圆心,并且两端都在圆上的线段叫做________ ,用字母________表示。
19.填表。
20.汽车车轮的半径为0.3米,车轮向前滚动50圈,前进了________米.21.圆的位置是由________决定,圆的大小是由________决定.22.一个半圆图形,它的对称轴是这个圆的________。
小学六年级数学圆的练习题及答案小学六年级数学圆的练题及答案圆是小学数学的重要内容之一,与圆锥、圆柱、扇形等几何图形有联系。
在小升初考试中,圆相关问题主要出现在选择题和填空题中,解答题相对较少,多以求阴影部分面积为主。
只有掌握好这部分知识,才能为以后初中、高中的数学几何研究打下坚实的基础。
一、填空。
1.一个车轮的直径为50cm,车轮转动一周,大约前进多少米?答案:周长为πd,所以车轮转动一周前进π×50≈157.08cm。
2.在一张长8厘米,宽12厘米的长方形纸上画一个最大的圆,这个圆的直径是多少?面积是多少?周长是多少?答案:最大圆的直径为长方形的短边,即8cm;面积为πr²,即16π≈50.27平方厘米;周长为πd,即8π≈25.13厘米。
3.一个环形的外圆直径是10cm,内圆直径是8cm,它的面积是多少平方厘米?答案:环形的面积为外圆面积减去内圆面积,即πR²-πr²,其中R为外圆半径,r为内圆半径。
所以环形的面积为(π×5²-π×4²)≈9.42平方厘米。
4.一个圆的半径扩大2倍,它的周长扩大几倍?面积扩大几倍?答案:半径扩大2倍,周长也扩大2倍,面积扩大4倍。
5.用一根12.56厘米的铁丝弯成一个圆形铁环,铁环的直径是多少?面积是多少平方厘米?答案:铁环的直径为铁丝长度,即12.56厘米;面积为πr²,其中r为半径,即(12.56/π/2)²≈5.02平方厘米。
7.一个圆的半径扩大2倍,它的周长扩大几倍?面积扩大几倍?答案:半径扩大2倍,周长也扩大2倍,面积扩大4倍。
8.圆是由一条围成的。
圆是一个图形,它有一条对称轴,圆的任意一条直径所在的直线都是圆的对称轴。
9.圆有一条直径,有一条半径。
叫做直径,用字母表示d;叫做半径,用字母表示r。
10.当圆规两脚间的距离为5厘米时,画出圆的周长是多少厘米?答案:圆的周长为2πr,所以当圆规两脚间的距离为5厘米时,画出的圆的周长为10π≈31.42厘米。
小升初数学专项练习一线名师严选内容,逐一攻克☆基本概念、基本原理、基础技能一网打尽☆点拨策略思路,侧重策略指导,拓宽眼界思路☆7.扇形统计图【小升初考点归纳】1.扇形统计图的特点:扇形统计图是用整个圆的面积表示总数,用院内的扇形面积表示各部分数量占总数的百分比.2.读懂扇形统计图:(1)获取信息的方法:运用综合、对比等多种观察方法,可以从扇形统计图中获取信息,还可以利用这些信息提出相应的问题.(2)扇形统计图的优点:它可以清楚地表示出部分数量与总数、部分数量与部分数量之间的关系.3.利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数应用题的解题思路和解题方法进行解析.【经典例题】一.选择正确的答案,把序号填在括弧中(共6小题)1.(2018春•徐州期末)如图是某家庭旅游支出情况统计,这项支出占全部支出的()A.25%B.40%C.90%【解析】解:90÷360=0.25=25%,答:旅游支出占全部支出的25%.故选:A.2.(2018•衢州)在一个有40名学生的班级里选举班长(每人投一票),选举结果如表:下面()图表示了这一结果.张明10小豆20杨杨5丽丽5A.B.C.D.【解析】解:张明:10÷40=0.25=25%;小豆:20÷40=0.5=50%;杨杨:5÷40=0.125=12.5%;丽丽:5÷40=0.125=12.5%;图A,没有表示50%的扇形,不符合题意;图B,有表示50%的扇形,表示25%的扇形和12.5%的扇形,符合题意;图C,4个扇形都表示25%,互符合题意;图D,没有表示50%的扇形,不符合题意;故选:B.3.(2018春•相山区期末)如图是某小学六(1)班学生上网时间统计图.六(1)班不上网的有30人,全班共有()人.A.30B.40C.50D.60【解析】解:1﹣(30%+10%)=1﹣40%=60%30÷60%=50(人)答:全班共有50人.故选:C.4.(2018•泉州)如图是甲、乙两个班男、女生人数分布统计图,其中说法正确的是()A.两个班的人数一样多B.乙班的男生人数比女生多40%C.甲班的女生人数占全班的D.甲班的女生人数一定比乙班的女生多【解析】解:由分析得:A.两个班的人数一样多,这种说法是错误的.B.乙班男生占全班人数的70%,女生占全班人数的30%,男生人数比女生人数多全班人数的40%,而不是男生人数比女生多40%,因此,乙班的男生人数比女生多40%.这种说法是错误的.C.因为40%=,所以甲班的女生人数占全班的.这种说法是正确的.D.虽然甲班女生人数占全班人数的40%,乙班女生人数占全班人数的30%,但是两个班的人数不一定一样多,所以甲班的女生人数一定比乙班的女生多.这种说法是错误的.故选:C.5.(2018•太仓市)画统计图时,要根据信息的特点来画.在下面的信息中,适合用扇形统计图的是()A.六年级一班女同学的身高B.芳芳6﹣12岁的身高变化C.大豆的营养成分【解析】解:根据统计图的特点可知:画统计图时,要根据信息的特点画.A、六年级一班女同学的身高,适合用条形统计图表示;B、芳芳6﹣12岁的身高变化,适合用折线统计图表示;C、大豆的营养成分,适合用扇形统计图表示;故选:C.6.(2018•鼓楼区)六(1)班共有48名同学,期末推选一名优秀毕业生,投票选举结果如表中,下面()图能大体表示出这个结果姓名小红小刚小芳小军票数241248A.B.C.【解析】解:24+12+8+4=48小红:24÷48=50%;小刚:12÷48=25%;小芳:4÷48≈8%;小军:8÷48≈17%;只有A答案能表示出投票结果;故选:A.二.将正确答案填写在横线上(共10小题)7.(2019春•简阳市期中)扇形统计图是中,圆表示总量,各个扇形表示部分量占总量的百分比.【解析】解:扇形统计图中,圆表示总量,各扇形表示部分量占总量的百分比.故答案为:总量、部分量占总量的百分比.8.(2019•郴州模拟)如图是某校六年级全体学生某次数学竞赛成绩的统计图.“不及格”部分的扇形圆心角是18度.【解析】解:360×(1﹣30%﹣40%﹣25%)=360×5%=360×0.05=18(度),答:.“不及格”部分的扇形圆心角是18度.故答案为:18.9.(2019•武侯区)(1)妙想家其他支出占家庭总支出的12%?(2)如果伙食水电支出2700元,那么文化支出1320元.【解析】解:(1)答:妙想家其他支出占家庭总支出的12%.(2)2700÷45%×22%=2700÷0.45×0.22=6000×0.22=1320(元),答:文化支出1320元.故答案为:12%;1320.10.(2018秋•临河区期末)如图是对某校六年级(1)班60名同学就“能不能主动帮助家长做家务”的情况的调查结果.主动的有18人;从不主动的有15人;偶尔主动的比主动的多9人.【解析】解:60×30%=18(人);60×25%=15(人);60×(45%﹣30%)=60×0.15=9(人);答:主动帮助家长做家务的有18人,从不主动帮助家长做家务的有15人,偶尔主动比主动的多9人.故答案为:18、15、9.11.(2018秋•醴陵市期末)某学校六年级某次考试中,成绩情况如图所示:不及格人数为20人,六年级总共有200人,良好有70人,良好人数比优秀人数少12.5%.【解析】解:20÷(1﹣40%﹣35%﹣15%)=20÷10%=20÷0.1=200(人);200×35%=200×0.35=70(人);(40%﹣35%)÷40%=5%÷40%=0.05÷0.4=0.125=12.5%;答:六年级总共有200人,良好的有70人,良好人数比优秀人数少12.5%.故答案为:200、70、12.5.12.(2018春•泰兴市期末)鼓楼商场根据今年端午节最热销的三种粽子的销量制作了一张扇形统计图,请仔细看图填空.蛋黄粽占三种粽子总数的15%,据统计蛋黄粽卖出了210个,那么绿豆粽卖掉了840个,火腿粽的销量比绿豆粽少490个.【解析】解:1﹣60%﹣25%=15%;210÷15%=210÷0.15=1400(个),1400×60%=1400×0.6=840(个),1400×25%=1400×0.25=350(个),840﹣350=490(个),答:蛋黄粽占三种粽子总数的15%,绿豆粽卖掉了840个,火腿粽的销量比绿豆粽少490个.故答案为:15、840、490.13.(2018•杭州模拟)下面分别是关于四(3)班学生的综合等级评定情况统计表和统计图,但由于沾上污渍使成绩优秀的数据看不清楚,只知道等级评定为“优”的女生比男生多2人.根据所给的信息可以知道,四(3)班一共有14人得了“优”,其中女生有8人.【解析】解:总人数:(2+1)÷6%=50(人)得优的人数和:50﹣12﹣9﹣6﹣6﹣2﹣1=14(人)其中女生:(14+2)÷2=8(人)答:四(3)班一共有14人得了“优”,其中女生有8人.故答案为:14;814.(2017秋•涟源市校级期末)下面是某学校教师喜欢看的节目统计图.(1)喜欢《走进科学》的老师占全体老师人数的32%.(2)喜欢大风车节目和新闻联播节目的人数差不多.(3)喜欢焦点访谈节目的人数最少.如果该学校有150名老师,那么喜欢新闻联播的老师有42人.【解析】解:(1)1﹣15%﹣25%﹣28%=32%;答:喜欢《走进科学》的老师占全体老师人数的32%.(2)喜欢大风车占25%,喜欢新闻联播的占28%,所以喜欢大风车节目和喜欢新闻联播节目的人数差不多.(3)150×28%=150×0.28=42(人);答:喜欢焦点访谈节目的人数最少,喜欢新闻联播的老师有42人.故答案为:32;大风车、新闻联播;焦点访谈;42.15.(2017秋•涟源市期末)绿荫小学共种树木160棵,各种树木种植情况如图.那么杉树有64棵,杨树有72棵,柳树有24棵.【解析】解:160×40%=160×0.4=64(棵);160×45%=160×0.45=72(棵);160×15%=160×0.15=24(棵);答:杉树有64棵、杨树有72棵、柳树有24棵.故答案为:64、72、24.16.(2018•乐昌市)根据扇形统计图和统计表提供的信息填表.黑兔/只白兔/只灰兔/只合计/只1565490300【解析】解:90÷30%=90÷0.3=300(只);300×52%=300×0.52=156(只);300×18%=300×0.18=54(只);故答案为:156、54、300.三.应用题(共1小题)17.(2019春•东台市校级期中)如图是某农场各种农作物种植面积统计图,看图回答问题.(1)已知粮食作物比经济作物多260公顷,这个农场一共耕种土地多少公顷?(2)经济作物耕种多少公顷?【解析】解:(1)260÷(60%﹣34%)=260÷26%=260÷0.26=1000(公顷),答:这个农场一共耕种土地1000公顷.(2)1000×34%=1000×0.34=340(公顷),答:经济作物耕种340公顷.四.解析题(共5小题)18.(2018秋•西山区期末)如图是林场育苗基地树苗情况统计图.(1)已知柳树有3500棵,这些树苗的总数是多少棵?(2)槐树和杨树分别有多少棵?(3)松树比柏树多百分之几?【解析】解:(1)3500÷25%=14000(棵)答:这些树苗的总数是14000棵.(2)14000×17%=2380(棵)14000×33%=4620(棵)答:槐树有2380棵,杨树有4620棵.(3)(15%﹣10%)÷10%5%÷10%=50%答:松树比柏树多50%.19.(2018秋•深圳期末)据不完全统计,2014年深圳市城市垃圾中可回收再生资源构成如图.(1)电子垃圾是8.4万吨,深圳市城市垃圾中可回收再生资源共多少万吨?(2)2014年全市可回收再生资源的回收量实际约为265万吨,请计算可回收再生资源的回收率.(百分号前保留整数)(3)谈谈你对垃圾分类的看法或建议.【解析】解:(1)8.4÷2%=420(万吨)答:深圳市城市垃圾中可回收再生资源共420万吨.(2)265÷420×100%≈0.63×100%=63%答:可回收再生资源的回收率约为63%.(3)我的看法与建议:在当今这个社会,大多数人类只重视经济和物质的发展,却渐渐忘记了环境是直接受害者,而人类是间接受害者.只有少部分的人意识到要走可持续发展的路线.环保问题已经成为全球关注和面对的问题,关系到整个人类发展的将来.作为世界主人的我们,已经不能对此视而不见.一次次惨不忍睹的自然灾害,已经向我们传递了警戒信息.我们不能在做些有损自然而对自己无利的行为了.因此,在这个资源贫乏,能源紧缺,环境日益恶化的现代,我们应该保护环境,并以此展开更多的环保行动,通过一点点的微薄的努力,让人类从熟视无睹到彻底明白这一重要性.人类才是破坏环境的真凶,我们要保护自己,保护我们无可被任何东西取代的环境.20.(2018秋•阿克苏市期末)如图是小明一家三口五一旅游的各项费用统计图.其中A表示食宿费用,B表示路费,C表示购物费用.(1)这是扇形统计图.(2)图中A、B、C三部分的比是9:6:5.(3)已知食宿费用是1350元,路费是多少元?【解析】解:(1)这是扇形统计图.(2)1﹣25%﹣30%=45%A、B、C三部分的比:45%:30%:25%=9:6:5.(3)总费用:1350÷45%=3000(元)路费:3000×30%=900(元)答:路费是900元.故答案为:扇形;9:6:5.21.(2019•集美区模拟)如图是六年级一班学生喜欢的电视节目统计图.(1)喜欢《走进科学》的同学人数占全班人数的38%.(2)喜欢《焦点访谈》的人数相当于喜欢《大风车》人数的60%,如果全班有100人,那么,喜欢《大风车》的有25人,新闻联播有22人.【解析】解:(1)1﹣15%﹣25%﹣22%=38%答:喜欢《走进科学》的同学人数占全班人数的38%.(2)15%÷25%=60%100×25%=25(人)100×22%=22(人)答:喜欢《焦点访谈》的人数相当于喜欢《大风车》人数的60%,如果全班有100人,那么,喜欢《大风车》的有25人,喜欢《新闻联播》的有22人.故答案为:38,60,25,22.22.(2018秋•湟源县期末)看图解决问题.(1)喜欢足球的人数占六年级人数的百分之几?(2)如果喜欢跳绳的人数为36人,那么六年级共有多少人?【解析】解:(1)1﹣15%﹣12.5%﹣22.5%﹣30%=20%答:喜欢足球的人数占六年级人数的20%.(2)36÷15%=240(人)答:六年级共有240人.。
小升初专项练习几何图形圆与立体图形引言:立体图形是近两年来小生初的考察新热点,由于立体图形考察学生的空间想象能力,更反映学生的本身潜能,所以越来越受到学校的欢迎;而另一方面,初中很多知识点都是建立在空间问题上,所以可以说学校考察立体也是为初中选拔知识链接性好的学生。
【典型题目解析】:一、圆与扇形阴影部分的面积【例1】.(★★★)在图中,一个圆的圆心是O,半径r=9厘米,∠1=∠2=15º。
那么阴影部分的面积是多少平方厘米?(π取3.14.)【例2】、(★★★★)如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径都是1。
求阴影部分的面积。
【例3】(★★★)草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?【例4】求图中阴影部分的面积(单位:厘米)。
【例5】求图中阴影部分的面积(单位:厘米)。
【分析】阴影部分通过翻折移动位置后,构成了一个新的图形(如图所示)。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×42×1/4-4×4÷2÷2=8.56(平方厘米)【例6】如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求O的面积。
长方形ABO1【分析】因为两圆的半径相等,所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图19-10右图所示)。
所以3.14×12×1/4×2=1.57(平方厘米)【例7】如图所示,图中圆的直径AB是4厘米,平行四边形ABCD的面积是7平方厘米,∠ABC=30度,求阴影部分的面积(得数保留两位小数)。
【分析】阴影部分的面积等于平行四边形的面积减去扇形AOC的面积,再减去三角形BOC的面积。
半径:4÷2=2(厘米)扇形的圆心角:180-(180-30×2)=60(度)扇形的面积:2×2×3.14×60/360≈2.09(平方厘米)三角形BOC的面积:7÷2÷2=1.75(平方厘米)7-(2.09+1.75)=3.16(平方厘米)【例8】如图所示,求图中阴影部分的面积。
与圆和扇形的周长、面积相关的几何问题,将所求的对象进行适当的移动、分割或拼补以简化计算是常用的方法.
1.如图17-1,有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周率π取3.1416,那么花瓣图形的面积是多少平方厘米?
【分析与解】如下图,添上部分辅助线,有花瓣的面积为4个边长为2的小正方形面
积加上4个的面积减去4个的面积,即加上
31
441
42
⨯-⨯=个半径为1的圆的面积.
所以花瓣组成的图形的面积为4×2×2+1×1×1 7π≈16+3.1416=19.1416平方厘米.
2.如图17-2,一套绞盘和一组滑轮形成一个提升机构,其中盘A直径为10厘米,盘B直径为40厘米,盘C直径为20厘米.问:A顺时针方向转动一周时,重物上升多少厘米?( π取3.14.)
【分析与解】 A 顺时针转一周时,C 顺时针转12周,同轴的B 也顺时针转1
2
周,从而绳索被拉动的距离等于B 的半个圆周长即π×20≈62.8,这时重物应该上升去1
2
×62.8=31.4.
所以重物上升31.4厘米.
3.图17-3为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?
【分析与解】 将这卷纸展开后,它的侧面可以近似的看成一个长方形,它的长度就等于面积除以宽.这里的宽就是纸的厚度,而面积就是一个圆环的面积. 因此
纸的长度 ()22 3.1410093.1410 3.1437143.50.040.04
⨯-⨯-⨯≈
≈==纸卷侧面积纸的厚度(厘米) 所以,这卷纸展开后大约71.4米.
4. 如图
17-4,大小两圆的相交部分(即阴影区域)的面积是大圆面积的
4
15
,是小圆面积的3
5
.如果量得小圆的半径是5厘米,那么大圆半径是多少厘米?
【分析与解】 小圆的面积为2525ππ⨯=,则大小圆相交部分面积为325155
ππ⨯=,那么
大圆的面积为422515154ππ÷=,而2251515422
=⨯,所以大圆半径为7.5厘米.
5.如图17-5,在18×8的方格纸上,画有1,9,9,8四个数字.那么,图中的阴影面积占整
个方格纸面积的几分之几?
【分析与解】我们数出阴影部分中完整的小正方形有8+15+15+16=54个,其中部分有6+6+8=20个,部分有6+6+8=20个,而1个和1个正好组成一个完整的小正方形,所以阴影部分共包含54+20=74个完整小正方形,而整个方格纸包含8×18=144个完整小正方形.
所以图中阴影面积占整个方格纸面积的
74
144
,即
37
72
.
6.如图17-6,用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?
【分析与解】有小圆直径的3倍为大圆的直径,所以小圆的面积是大圆的
2
11
39
⎛⎫
=
⎪
⎝⎭
,现在
剪去7个小圆,它们的面积和为
17
7
99
⨯=,所以剩下的角料的面积为大圆面积的
72
1
99
-=.
即所余下的边角料的总面积是36×2
9
=8平方厘米.
7.如图17-7,已知大正方形的面积是22平方厘米,那么小正方形的面积是多少平方厘米?
【分析与解】如下左图所示,设DC=x,则2x=22,而小正方形FGHI的边长为HI,我们虽然知
道大正方形内圆的半径EO为1
2
x,则直径FH为x,却不易求出小正方形边长FG.
但是,我们将小正方形内的等腰直角三角形FGH 割补至FIG 'V ,则得到的大三角形FHG 'V 是以FH 为直角边的等腰直角三角形,所以其面积为212x ,即为1
2
×22=11. 所以小正方形的面积是11平方厘米.
8.图17-8是一个直径是3厘米的半圆,AB 是直径.让A 点不动,把整个半圆逆时针转60o ,此时B 点移动到C 点,如图17-9所示.那么图中阴影部分的面积是多少平方厘米?(π取3.14.)
【分析与解】 有图中阴影部分面积等于以AC 为直径的半圆,以AC 为半径的60o 扇形的面
积和减去以AB 为直径的半圆面积,所以面积相等.
那么阴影部分的面积等于以AC 为半径的60o 扇形的面积,即260
3360
π⨯⨯≈1.5×3.14=4.71平方厘米.
9.如图17-10,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率π取近似值
227
.
【分析与解】 原题图中的左边部分可以割补至如下图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求. 因为四分之一大圆的半径为7,所以其面积为
221122
77447
π⨯⨯≈⨯⨯=38.5.
四分之一大圆内的等腰直角三角形ABC 的面积为
1
2
×7×7=24.5,所以阴影部分的面积为38.5-24.5=14.
10.如图17-11,等腰直角三角形的一腰的长是8厘米,以它的两腰为直径分别画了两个半圆,那么阴影部分的面积共有多少平方厘米?(π取3.14)
【分析与解】 如下图,我们将原题中阴影部分分成①、②、③、④4个部分,并且这4个部分的面积相等.
有②、③部分的面积和为二分之一圆的面积与其内等腰直角三角形的面积差. 二分之一圆的面积为1
442
π⨯⨯⨯≈8×3.14=25.12.其内等腰直角的底为8,高为4,所以其面积为
1
2
×8×4=16,所以②、③部分的面积和为25.12-16=9.12(平方厘米). 而①、②、③、④四部分的面积和为②、③部分的面积和的2倍,即为9.12×2=18.24(平方厘米).
所以,原题中阴影部分的面积共有18.24平方厘米.
11.图17-12中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?
【分析与解】 方法一:如下图所示
可以将每个圆内的阴影部分拼成一个正方形,而这个正方形与图17-12中的正方形形状、大小相同.
每个正方形的面积为(1×1÷2) ×4=0.5×4=2平方厘米,所以阴影部分的总面积为2×4=8平方厘米.
方法二:我们可以将图中空白部分分成8个形状相同、面积相等的小图形
其在圆内的位置如下图,有弓形
部分面积为
1
4
圆马等腰直角三角形ABO 的面积差,即为
2111
111 3.140.50.285424
π⨯⨯-⨯⨯≈⨯-=.
原题图中的整个图形的面积为四个圆的面积减去公共的4个
的面积,即8个
的面积,而阴影部分面积又是整个图形面积减去4个的面积,即8个
的面积.
那么,原题图中阴影部分面积为4个圆面积减去16个的面积.
所以,原题图中阴影部分总面积为241160.2854 3.14 4.56π⨯⨯-⨯≈⨯-=8(平方厘米).
12.如图17-13,三角形ABC 是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,AB 长40厘米.求BC 的长度.(π取3.14)
【分析与解】 图中半圆的直径为AB ,所以其面积为21202
π⨯⨯≈200×3.14=628.
有空白部分③与①的面积和为628,又②-①=28,所以②、③部分的面积和628+28=656.
有直角三角形ABC 的面积为12×AB×BC=1
2
×40×BC=656.所以BC=32.8厘米.
13.图17-14中阴影部分的面积是多少平方厘米?(π取3.14)
【分析与解】 如下图,为了方便说明标上字母,并称曲线四边形BCFE 的面积为“①”.
将扇形ABC 的面积称为“大扇形”,扇形CDF 的面积称为“小扇形”,长方形BCDE 的面积称为“长方形”.
阴影部分面积=大扇形-①,①=长方形-小扇形.
所以有阴影部分面积=大扇形-(长方形-小扇形)=大扇形+小扇形-长方形.
2211
522529 3.1441044
ππ⨯⨯+⨯⨯-⨯≈⨯÷-=12.765(平方厘米).
14.求图17-15中阴影部分的面积.(π取3.14)
【分析与解】 我们只用将两个半径为10厘米的四分之一圆减去空白的①、②部分面积和即可,其中①、②面积相等.
易知①、②部分均是等腰直角三角形,但是①部分的直角边AB 的长度未知.单独求①部分面积不易,于是我们将①、②部分平移至一起,如下图所示,则①、②部分变为一个以AC 为直角边的等腰直角三角形,而AC 为四分之一圆的半径,所以有AC=10.
两个四分之一圆的面积和为2121050 3.144
π⨯⨯⨯≈⨯=157,而①、②部分的面积和为12
×
10×10=50,所以阴影部分的面积为157-50=107(平方厘米).
15.平面上有7个大小相同的圆,位置如图17-16所示.如果每个圆的面积都是10,那么阴影部分的面积是多少?
【分析与解】 题中阴影部分面积可以视为一个完整的圆与6个阴影部分的面积
和.
而图形①可以通过割补得到图形②而图形②是一个圆心角为60o的扇形,即1 6
圆.
所以,原题图中阴影部分面积为1个完整圆与6个1
6
圆,即2个圆的面积.
即原题图中阴影部分面积为2×10=20.。