用向量法证明欧拉线问题
- 格式:pdf
- 大小:77.16 KB
- 文档页数:1

欧拉角方向向量欧拉角欧拉角是一种描述物体在空间中旋转的方法,它由三个角度组成,分别是绕x轴旋转的角度、绕y轴旋转的角度和绕z轴旋转的角度。
欧拉角可以用于描述飞机、船舶、火箭等运动物体的姿态。
欧拉角的表示方法有很多种,其中最常见的是XYZ欧拉角、ZYX欧拉角和ZXZ欧拉角。
XYZ欧拉角XYZ欧拉角又称为固定轴顺序(Fixed Axis Order)欧拉角,表示先绕x轴旋转、再绕y轴旋转、最后绕z轴旋转。
这种表示方法常用于飞机和船舶等物体的姿态描述。
ZYX欧拉角ZYX欧拉角与XYZ欧拉角相反,表示先绕z轴旋转、再绕y轴旋转、最后绕x轴旋转。
这种表示方法常用于机器人和游戏中的人物姿态描述。
ZXZ欧拉角ZXZ欧拉角表示先绕z轴旋转一个固定的量,然后绕新的x轴和原来的z轴重合,再沿着新x轴方向进行第二次旋转,最后沿着新z轴方向进行第三次旋转。
这种表示方法常用于对称物体的姿态描述。
欧拉角的问题欧拉角虽然简单易懂,但是存在万向锁问题和奇异性问题。
万向锁问题指的是在某些情况下,欧拉角无法准确描述物体的姿态,导致物体出现不可预测的旋转。
例如当绕x轴旋转90度后,再绕y轴旋转时,会出现无法区分绕z轴正方向还是负方向旋转的情况。
奇异性问题指的是在某些情况下,欧拉角会出现奇异点,导致无法准确描述物体的姿态。
例如当绕x轴旋转90度后,在绕y轴旋转0度或180度时就会出现奇异点。
因此,在实际应用中,通常使用四元数或方向余弦矩阵等更为复杂但更为准确的方法来描述物体的姿态。
方向向量方向向量是指从原点指向某个点或者从一个点指向另一个点所形成的矢量。
方向向量可以用来表示物体在空间中朝着哪个方向移动或者朝着哪个方向面对。
表示方法方向向量可以用三个数值来表示,分别是x方向上的分量、y方向上的分量和z方向上的分量。
例如(1,0,0)表示x轴正方向。
在计算机图形学中,通常使用单位向量来表示方向向量,即长度为1的矢量。
这样可以简化计算,并且使得不同长度的矢量具有相同的方向。

欧理线三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线,且外心到重心的距离等于垂心到重心距离的一半。
莱昂哈德·欧拉于1765年在它的著作《三角形的几何学》中首次提出定理:三角形的重心在欧拉线上,即三角形的重心、垂心和外心共线。
他证明了在任意三角形中,以上四点共线。
欧拉线上的四点中,九点圆圆心到垂心和外心的距离相等,而且重心到外心的距离是重心到垂心距离的一半。
欧拉线的证法1作△ABC的外接圆,连结并延长BO,交外接圆于点D。
连结AD、CD、AH、CH、OH。
作中线AM,设AM交OH于点G’∵ BD是直径∴ ∠BAD、∠BCD是直角∴ AD⊥AB,DC⊥BC∵ CH⊥AB,AH⊥BC∴ DA‖CH,DC‖AH∴ 四边形ADCH是平行四边形∴ AH=DC∵ M是BC的中点,O是BD的中点∴ OM= 1/2DC∴ OM= 1/2AH∵ OM‖AH∴ △OMG’ ∽△HAG’∴AG’/MG’=AH/MO=2/1∴ G’是△ABC的重心∴ G与G’重合∴ O、G、H三点在同一条直线上如果使用向量,证明过程可以极大的简化,运用向量中的坐标法,分别求出O G H 三点的坐标即可.欧拉线的证法2设H,G,O,分别为△ABC 的垂心、重心、外心。
连接AG 并延长交BC 于D, 则可知D 为BC 中点。
连接OD ,又因为O 为外心,所以OD⊥BC。
连接AH 并延长交BC 于E,因H 为垂心,所以 AE⊥BC。
所以OD//AE ,有∠ODA=∠EAD。
由于G 为重心,则GA:GD=2:1。
连接CG 并延长交BA 于F,则可知F 为AB 中点。
同理,OF//CM.所以有∠OFC=∠MCF连接FD ,有FD 平行AC,且有DF:AC=1:2。
FD 平行AC ,所以∠DFC=∠FCA,∠FDA=∠CAD,又∠OFC=∠MCF,∠ODA=∠EAD,相减可得∠OFD=∠HCA,∠ODF=∠EAC,所以有△OFD∽△HCA,所以OD:HA=DF:AC=1:2;又GA:GD=2:1所以OD:HA=GA:GD=2:1又∠ODA=∠EAD,所以△OGD∽△HGA。

欧拉线的向量证法欧拉线的向量证法是一种证明欧拉线存在的方法。
欧拉线是指连接一个三角形的垂心、重心和外心所形成的直线。
这条直线通常被认为是三角形的重要性质之一,因为它连接了三角形的三个关键点,并且具有一些重要的几何性质。
这篇文章将讨论欧拉线的向量证法。
欧拉线的向量证法的关键在于证明欧拉线存在于一个三维向量空间中。
我们可以将一个三角形三个关键点的坐标表示为向量,并将欧拉线表示为这些向量的线性组合。
然后,我们可以使用向量运算证明这个线性组合的结果是一个常向量,这个常向量就是欧拉线。
具体地,我们可以定义向量OA、OB和OC分别表示三角形的三个关键点。
然后,我们可以构造向量OH,表示垂心O到三角形所在平面的垂线。
向量OG表示重心G到三角形所在平面的垂线。
最后,向量OA、OB和OC的平均向量OM表示外接圆心O到三角形所在平面的垂线。
现在我们需要找到一个向量倍数,将OH、OG和OM相加后可以得到一个常向量。
我们可以首先证明OH、OG和OM在同一平面内,并且通过欧拉线的定义,这个平面必须与三角形所在平面垂直。
因此,我们可以用叉乘来证明一个向量与这个平面垂直。
这可以通过叉乘OH和OG,OG和OM,以及OH和OM来完成。
然后,我们可以相互叠加OH、OG和OM,找出它们之间的线性关系。
最后,我们将这个线性关系表示为向量倍数,并证明这个线性组合的结果是一个常向量,表示欧拉线。
简而言之,欧拉线的向量证法是一种通过向量运算来证明欧拉线存在的方法。
这种方法非常优雅,因为它基于三角形的几何关系和向量空间的基本性质。
这个方法可以帮助我们更好地理解欧拉线的几何性质,并将其应用到更广泛的研究领域。

欧拉线问题欧拉线是高中数学常见的信息题类的考点,其原理很简单:三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心的距离之半”,这条直线叫做三角形的欧拉线,只需要掌握图形特点即可轻松求解等腰三角形中的欧拉线(中垂线)1.数学巨星欧拉(LeonhardEuler,1707~1783)在1765年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心的距离之半”,这条直线被后人称之为三角形的欧拉线.若已知△ABC的顶点B(-1,0),C(0,2),且AB=AC,则△ABC的欧拉线方程为()A.2x-4y-3=0B.2x+4y+3=0C.4x-2y-3=0D.2x+4y-3=0【答案】D【分析】根据题意得出△ABC的欧拉线方程为线段BC的垂直平分线,再根据点B和点C的坐标求出线段BC 的垂直平分线即可.【详解】由B(-1,0),C(0,2),得线段BC中点的坐标为-1 2 ,1,所以线段BC的斜率k BC=2,所以线段BC垂直平分线的方程为:y-1=-12x+12,即2x+4y-3=0,又因为AB=AC,所以△ABC的外心、中心、垂心都在线段△ABC的垂直平分线上,所以△ABC的欧拉线方程为2x+4y-3=0,故选:D.2.瑞士著名数学家欧拉在1765年得出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为“欧拉线”.在平面直角坐标系中作△ABC,AB=AC,点B-1,3,点C4,-2,圆M:(x+3)2+y2= 4,P x0,y0是“欧拉线”上一点,过P可作圆的两条线切,切点分别为D,E.则下列结论正确的是()A.△ABC的“欧拉线”方程为y=x-1B.圆M上存在点N,使得∠MPN=π6C.四边形PDME面积的最大值为4D.直线DE恒过定点【答案】ABD【分析】由题意求出BC中点为D的坐标,根据欧拉线的定义求出欧拉线的方程即直线AD的方程,再利用圆和圆的切线的性质判断各选项即可.【详解】设BC中点为D,因为AB=AC,所以AD⊥BC,因为k BC=3+2-1-4=-1,所以k AD=1,且x D=-1+42=32,y D=3-22=12,所以D32,12,由题意可得欧拉线为直线AD,则欧拉线的方程为y-12=x-32即y=x-1,A正确;由圆的切线性质可得∠MPD≥∠MPN,设P(a,a-1),则PM2=(a+3)2+(a-1)2=2a2+4a+10,在△MPD中由正弦定理得PMsin∠PDM=PDsin∠MPD,所以sin∠MPD=PD×sin∠PDMPM=22a2+4a+10,由二次函数的性质得当a=-42×2=-1时2a2+4a+10取最小值8,所以sin∠MPD=22a2+4a+10≤22,即∠MPD的最大值为π4,所以∠MPN≤π4,所以圆M上存在点N,使得∠MPN=π6,B正确;由圆的切线的定义可知PD⊥MD,PE⊥ME,PD=PE,所以S PDME=S△PMD+S△PME=12×PD×MD+12×PE×ME=2PD,又因为PD=PM2-4,且PM min=-3-112+(-1)2=22,所以PD min=4即四边形PDME面积的最小值为4,C错误;设P(a,a-1),因为PD⊥MD,PE⊥ME,所以P,D,M,E四点共圆,其中PM为直径,设PM中点Ha-32,a-12,则PH=a-a-322+a-1-a-122=a2+2a+52,所以圆H为x-a-3 22+y-a-122=a2+2a+52即x2+y2-(a-3)x-(a-1)y-3a=0,所以DE为圆M和圆H的相交弦,两圆方程相减得DE方程为(a+3)x+(a-1)y+5+3a=0,即a(x+y+3)+3x-y+5=0,由x+y+3=03x-y+5=0解得DE过定点(-2,-1),D正确;故选:ABD3.瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.在非等边△ABC中,AB=AC,点B坐标为-1,1,点C坐标为3,-3,且其“欧拉线”与圆M:x2+y2=r2r>0相切,则△ABC的“欧拉线”方程为,圆M的半径r=.【答案】y=x-22【分析】分析可知△ABC 的“欧拉线”为线段BC 的中垂线,求出线段BC 的中垂线方程,可得出△ABC 的“欧拉线”方程,利用圆心到“欧拉线”的距离等于圆的半径可求得r 的值,即可得解.【详解】线段BC 的中点为M 1,-1 ,在非等边△ABC 中,AB =AC ,所以,△ABC 的“欧拉线”为线段BC 的中垂线,k BC =1+3-1-3=-1,所以,△ABC 的“欧拉线”方程为y +1=x -1,即y =x -2,由已知,圆M 与直线y =x -2相切,故r =212+12= 2.故答案为:y =x -2;2.普通三角形中的欧拉线4.数学家欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理:三角形的外心、垂心和重心都在同一直线上.这条直线被后人称为三角形的欧拉线.已知△ABC 的顶点分别为A 0,2 ,B -1,0 ,C 4,0 ,则△ABC 的欧拉线方程为()A.4x -3y -6=0B.3x +4y +3=0C.4x +3y -6=0D.3x +4y -3=0【答案】C【分析】先求出△ABC 的重心坐标,由k AB ⋅k AC =-1得出△ABC 为直角三角形,外心为斜边中点,进而求出外心坐标,由于外心和重心在同一直线上,根据外心和重心的坐标即可得出答案.【详解】因为△ABC 的顶点分别为A 0,2 ,B -1,0 ,C 4,0 ,所以△ABC 的重心为G 1,23 ,因为k AB =2,k AC =-12,所以k AB ⋅k AC =-1,所以AB ⊥AC ,所以△ABC 的外心为BC 的中点D 32,0 ,因为三角形的外心、垂心和重心都在同一直线上,所以△ABC 的欧拉线为直线GD ,所以△ABC 的欧拉线方程为y -023-0=x -321-32,即4x +3y -6=0,故选:C .5.欧拉于1765年在他的著作《三角形的几何学》中首次提出定理:三角形的重心、垂心和外心共线,这条线称之为三角形的欧拉线.已知A 0,2 ,B 4,2 ,C a ,-1 ,且△ABC 为圆x 2+y 2+Ex +Fy =0内接三角形,则△ABC 的欧拉线方程为.【答案】y =1/y -1=0【分析】首先将点的坐标代入圆的方程,即可求出E 、F ,从而得到圆心坐标即△ABC 的外心坐标,再确定△ABC的重心坐标,即可得解.【详解】依题意22+2F=042+22+4E+2F=0,解得E=-4F=-2,所以圆x2+y2-4x-2y=0,即x-22+y-12=5,故圆心坐标为2,1,即△ABC的外心坐标为2,1,又△ABC的重心坐标为a+43,1 ,又点2,1、a+4 3,1均在直线y=1上,所以△ABC的欧拉线方程为y=1.故答案为:y=16.瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中,△ABC满足AC=BC,顶点A-1,0、B1,2,且其“欧拉线”与圆M:x+52+y2=r2r>0相切.(1)求△ABC的“欧拉线”方程;(2)若圆M与圆x2+y-a2=2有公共点,求a的范围.【答案】(1)x+y-1=0(2)a∈-7,7【分析】(1)由等腰三角形三线合一知△ABC的欧拉线即为AB的垂直平分线,根据与直线AB垂直得到斜率,结合过中点得到所求直线方程;(2)由直线与圆相切得到圆M的圆心和半径,由两圆有公共点得到两圆的位置关系进而得到关于a的不等式,解不等式即可得到a的取值范围.【详解】(1)因为AC=BC,所以△ABC是等腰三角形,由三线合一得:△ABC的外心、重心、垂心均在边AB 的垂直平分线上,设△ABC的欧拉线为l,则l过AB的中点,且与直线AB垂直,由A-1,0、B1,2可得:AB的中点D1-12,0+22,即D0,1 ,由k AB=2-01--1=1,得k l=-1,故l的方程为y-1=-x即x+y-1=0;(2)因为l与圆M:x+52+y2=r2相切,故圆心M-5,0,r=|6|1+1=32,圆x2+y-a2=2的圆心坐标为0,a,半径r1=2,则要想圆M与圆x2+y-a2=2有公共点,则两圆外切、相交或内切,只需两圆圆心的距离小于等于半径之和,大于等于半径之差的绝对值,即32-2≤-52+a2≤32+2,故22≤25+a2≤42,解得a∈-7,7.。

三角形的四心三角形的四心是指三角形的重心、外心、内心、垂心。
等边三角形的四心重合。
一、三角形的重心三角形的重心是三角形三条中线的交点。
三角形的三条中线必交于一点已知:△ABC的两条中线AD、CF相交于点O,连结并延长BO,交AC于点E。
三角形的三条中线必交于一点求证:AE=CE证明:延长OE到点G,使OG=OB∵OG=OB,∴点O是BG的中点又∵点D是BC的中点∴OD是△BGC的一条中位线∴AD∥CG∵点O是BG的中点,点F是AB的中点∴OF是△BGA的一条中位线∴CF∥AG∵AD∥CG,CF∥AG,∴四边形AOCG是平行四边形∴AC、OG互相平分,∴AE=CE三角形的重心的性质1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/35.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
6.重心是三角形内到三边距离之积最大的点。
二、三角形的外心三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
三角形的三条垂直平分线必交于一点三角形的三条垂直平分线必交于一点已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O求证:O点在BC的垂直平分线上证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO∵EO垂直平分AC,∴AO=CO∴BO=CO即O点在BC的垂直平分线上三角形的外心的性质1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
解析几何中的欧拉定理欧拉定理(Euler's Theorem)是数学中的一个重要定理,源于欧拉的研究。
该定理是描述三维空间中点、线、面三种基本几何对象之间的关系的公式,也称为多面体公式。
欧拉定理被广泛应用于几何学、拓扑学、物理学等领域,是研究空间几何结构的一个基础定理。
欧拉定理的正式陈述是:一个立体图形的顶点数与面数的差再加上边数等于2。
即:V - E + F = 2,其中V代表立体图形的顶点数,E代表立体图形的边数,F代表立体图形的面数。
该定理适用于所有的多面体,包括正则多面体、不规则多面体以及任意多面体。
为了理解欧拉定理,我们需要先了解一些基本的几何概念。
在三维空间中,点、线、面是最基本的几何对象。
点是空间中最基本的单位,没有形状、大小等特征;线是由两个点之间的直线连接而成的,具有长度但没有宽度和高度;面是由至少三个非共线点连接而成的平面几何图形,具有面积和形状。
欧拉定理可以通过一个简单的例子来进行解释。
我们考虑一个正四面体,即一个具有四个等大的面,每个面都是一个正三角形的立体图形。
这个正四面体有4个顶点、6条边和4个面。
插入这些数字后,欧拉定理的方程变为:4 - 6 + 4 = 2。
这个式子成立,证明欧拉定理在这种情况下成立。
我们可以通过把这个正四面体的一个顶点通过线段连接到另一个顶点的方式来创造一个新的多面体。
新多面体的顶点数是原来的顶点数加1,即5个。
新多面体的边数是原来的边数加4,即10条。
新多面体的面数是原来的面数加4,即8个。
把这些数字带入欧拉定理的方程中,得到:5 - 10 + 8 = 2。
这个式子同样成立,证明欧拉定理适用于新创建的多面体。
欧拉定理的证明是一项相对简单的数学运算,但是定理本身具有非常广泛的应用范围。
它可以用于计算多面体的面积、体积、对称性等各种基本性质。
在几何学中,欧拉定理是刻画空间多面体拓扑结构的基础工具。
在物理学中,欧拉定理被应用于描述空间物体的运动状态。
欧拉角方向向量一、引言欧拉角是用来描述物体在三维空间中旋转的一种方法。
它由三个连续的旋转角度组成,通常分别表示绕三个坐标轴的旋转。
方向向量则表示了一个向量在三维空间中的方向。
在本文中,我们将探讨欧拉角和方向向量的概念、应用以及它们之间的关系。
二、欧拉角的定义和表示方法2.1 欧拉角的定义欧拉角是一种用于描述物体在三维空间中旋转的方法。
它由三个连续的旋转角度组成,分别表示绕三个坐标轴的旋转。
2.2 欧拉角的表示方法欧拉角可以用不同的表示方法进行描述,常见的有以下几种:1.Tait-Bryan角:也称为航向-俯仰-滚转角,分别表示绕z轴、y轴和x轴的旋转。
2.XYZ欧拉角:分别表示绕x轴、y轴和z轴的旋转。
3.ZYX欧拉角:分别表示绕z轴、y轴和x轴的旋转。
不同的表示方法有各自的优缺点,选择适合特定场景的表示方法非常重要。
三、方向向量的定义和表示方法3.1 方向向量的定义方向向量是指在三维空间中的一个向量,它表示了一个向量的方向。
3.2 方向向量的表示方法方向向量可以用坐标表示法进行描述,也可以用单位向量进行表示。
坐标表示法中,方向向量的每个分量表示了向量在各个坐标轴上的投影。
单位向量表示法则是将方向向量除以其长度,使其成为长度为1的向量。
四、欧拉角与方向向量之间的关系欧拉角和方向向量之间存在着紧密的联系。
在欧拉角的表示方法中,我们可以通过欧拉角获得一个旋转矩阵。
旋转矩阵可以将一个向量从参考坐标系中旋转到新坐标系中。
而方向向量可以被视为一个在三维空间中的向量,我们同样可以用一个矩阵将其旋转到新坐标系中。
因此,我们可以使用欧拉角的旋转矩阵来将一个方向向量进行旋转。
这样我们就可以通过欧拉角来描述一个方向向量在空间中的旋转。
五、欧拉角和方向向量的应用欧拉角和方向向量在许多领域中都有重要的应用。
在计算机图形学中,欧拉角被广泛用于描述物体的旋转。
通过欧拉角的旋转矩阵,我们可以方便地对物体进行旋转操作,从而实现动画效果或者模拟真实物体的运动。
多面体欧拉定理:
定理简单多面体的顶点数V、棱数E及面数F间有关系对于简单多面体,有著名的欧拉公式:V—E+F=2简单多面体即表面经过连续变形可以变为球面的多面体。
欧拉定理:
定理简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2;
公式描述了简单多面体中顶点数、面数、棱数之间特有的规律。
定理的证明:
分析:以四面体ABCD为例.
将它的一个面BCD去掉,再使它变为平面图形,四面体的顶点数V、棱数E 与剩下的面数F1变形后都没有变(这里F1=F-1)。
因此,要研究V、E 和F的关系,只要去掉一个面,将它变形为平面图形即可。
只需平面图形证明:V+F1-E=1;
(1)去掉一条棱,就减少一个面,V+F1-E的值不变。
例如去掉BC,就减少一个面ABC。
同理,去掉棱CD、BD,也就各减少一个面ACD、ABD,由于V、F1—E的值都不变,因此V+F1-E的值不变;
(2)再从剩下的树枝形中,去掉一条棱,就减少一个顶点,V+F1-E的值不变.例如去掉CA,就减少一个顶点C.同理去AD就减少一个顶点D,最后剩下AB.
在以上变化过程中,V+F1—E的值不变,V+F1-E=2—0—1=1,所以 V+F—E= V+F1-E+1=2。
对任意的简单多面体,运用这样的方法,都是只剩下一条线段。
公式对任意简单多面体都是正确的。
欧拉定理又一证法:
多面体,设顶点数V,面数F,棱数E。
剪掉一个面,将其余的面拉平,使它变为平面图形, 我们在两个图中求所有面的内角总和Σα。
一方面,利用面求内角总和.。
b sin A=a sin B,
(b co s A)2+(b sin A)2=(c-a co s B)2+ (a sin B)2,
∴a co s B+b co s A=c(射影定理),
a sin A =
b
sin B
(正弦定理),
b2=c2+a2-2ca co s B(余弦定理).
用向量法证明欧拉线问题
刘步松 (江苏省运河师范学校 221300)
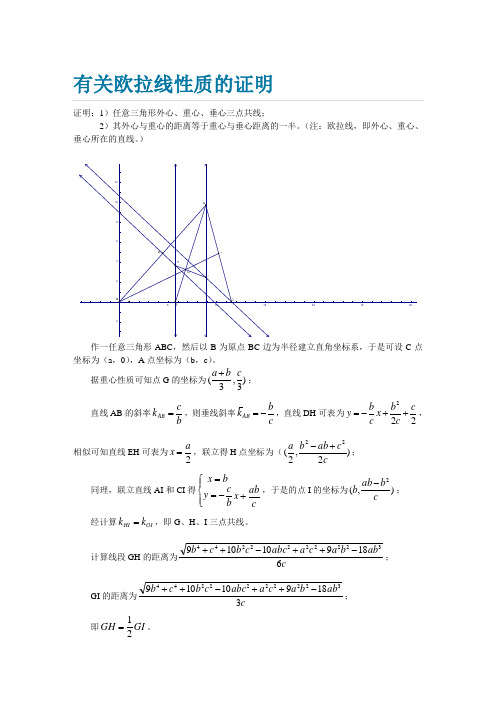
设三角形A B C外心为O,重心为W,垂心为H,则O,W,H三点共线,且 OH = 3 OW ,这便是著名的欧拉线问题.但平面几何证法较麻烦,笔者用向量坐标法去证,感觉过程较为简洁.
证 以外心O为原点,过O平行于B C 的直线为x轴,B C的中垂线为y轴,建立直角坐标系.设A D是B C上的高,并设各点坐
图1
标如下:A(a,b),B
(-c,d),C(c,d),
H(a,y),则B H=
(a+c,y-d),A C
=(c-a,d-b),因
为B H⊥A C,有B H
・A C=0,即(a+
c)(c-a)+(y-d)(d-b)=0,解之得y= -a2+c2+bd-d2
-d+b
.因为O是外心,所以 OA = OB = O C ,即a2+b2=(-c)2+ d2=c2+d2,从而a2-c2=d2-b2,代入y的表达式,求得y=b+2d,即H的坐标是(a,b+ 2d).从H及A,B,C的坐标可以发现,O H =
OA+OB+O C.又由重心定理OW=
1
3
(OA+OB+O C),从而有H,W,O共线,并
有 O H =3 OW .证毕.
构造法解竞赛题初探
胡国生 (江苏省洪泽县中学 223100)
大多数竞赛试题设计新颖,构思巧妙,综
合性强,注重对学生的思维能力的考查,因此
难度较大,不少学生无从下手.本文在用构造
法解竞赛题方面做一些粗浅探讨,希望对数
学爱好者有所启迪.
1 构造特殊图形
例1 正数a,b,c,A,B,C满足a+A=b
+B=c+C=k,求证:aB+bC+c A<k2.
(第24届前苏奥赛试题)
证明 构造正方形:从三个和数相等联
想到四边相等,a+A=b+B=c+C=b+B
=k,作边长为k的正方形,由面积关系(如图
1)知道:
aB+bC+c A<(a+A)2=k2.
图1
例2 已知五
边形A B CD E中,
∠A B C=∠A ED
=90°,A B=CD=
A E=
B C+D E=
2,求五边形
A B CD E的面积.
(江苏省第17届初中数学联赛试题)
解 如图2,构造全等三角形,延长CB
至F,使B F=D E.
易证R t△A B F≌R t△A ED,
∴A F=A D.
∵CF=CD,A C=A C,
∴R t△A CD≌R t△A CF,・
2
4
・ 中学数学月刊 2003年第10期。