当前位置：文档之家 ›  质点的角动量

质点的角动量

  • 格式：ppt
  • 大小：1.09 MB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

2-6-角动量

2-6-角动量

m1 − m2 m1 − m2 v(t ) − v(0) = ∫ gdt = gt 0 m +m m1 + m2 1 2
t
这也可以从牛顿动力学方程中得到。 这也可以从牛顿动力学方程中得到。
13
r 4.3 角动量守恒定律 r dL 合 M外 = 由质点系的角动量定理 dt r
r M外 = 0 r L合 = 常矢量
v dS | ∴ L |= mrv sinα = 2m dt
v ∆S ∴ L |= mrvsinα = 2m lim | ∆t →0 ∆t
即行星对太阳的矢径 在相等的时间内扫过 相等的面积。 相等的面积。这个结 论也叫等面积原理。
18
作
业
教材P88 2-1，3，，9，11，14，18，24，27 ， ， ， ， ， ， ， ，
11
有两个质量分别为m 的物体， 例6 有两个质量分别为 1 、m2 (m1>m2) 的物体，通 过一条不计质量的绳跨在一个质量忽略不计的、 过一条不计质量的绳跨在一个质量忽略不计的、轴处 摩擦力也不计的定滑轮上。 的加速度； 摩擦力也不计的定滑轮上。求： m1 的加速度；若t = 0 的速度为零， 上升的速度。 时 m1的速度为零，求m2上升的速度。 的速度为零 上升的速度 以轴心为原点， 解：以轴心为原点，以m1 、m2 、
2 3 0 0 L
θ
∴L = mR3/ 2 (2g sin θ )1/ 2
QL = mR2ω
2g ∴ω = ( sin θ )1/ 2 R 2g 1/ 2 0 ∴ω = ( ) 由题B点 由题 点，θ =90
R
9
质点系的角动量定理 根据质点的角动量定理：
r r r QLi = ri × mi vi
角动量与角动量定理

角动量与角动量定理

rr pr
1
L
dt 2 dt 2 dt 2
2m
2m
太阳对行星的引力总是指向太阳，因而行星对太阳
中心的角动量守恒，L为常量，所以得证。
L rmv mr2
方向 垂直于圆面
② 质点作匀速直线运动时，角 动量守恒。
L rmv sin mvd
方向始终垂直纸面向外
r L
r pr r
O
Or
r
d
pr
③ 角动量与参考点的位置有关。
r L
因而在说明一个质点的角动量
pr
时，必须指明是相对于哪一个 参考点而言的。
O
rr
θ m
锥摆 O
l
m
O
v
且在高速低速范围均适用。
例题1：
证明行星运动的开普勒第二定律：行星对太阳
的矢径在相等的时间内扫过的面积相等。
r
L
解：行星位矢扫过的面积dS
dS
1
r
r dr
sin
1
rr drr
dS r
2
2
单位时间行星位矢扫过的面积
•
drr
dS 1 rr drr 1 rr drr 1 rr vr 1
vr
y
xp z
L z
xp y
yp x
L , L , L 分别称为角动量在x、y、z轴上的分 x yz
量式，或称为对x、y、z轴的角动量。
二、力矩
1、定义
力
r F
对参考点O

rr
r F
r
M
r
rr
F
θ
Or
m
大小：
M
rF
sin
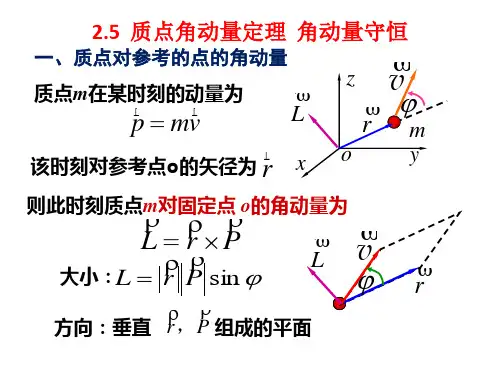
质点角动量定理 角动量守恒

质点角动量定理 角动量守恒


v2
o
v1
4)角动量守恒定律是物理学的基本定律之一。不 仅适用于宏观体系，也适用于微观系统。
2.5 质点角动量定理 角动量守恒
例1 一小球在光滑平面上作圆运动，小球被穿 过中心的线拉住 。开始时绳半径为r1 ，小球速 率为 v1 ；后来，往下拉绳子，使半径变为 r2 ， 小球速率变为 v2 ，求v2 =？
ri fi 0
i
有
dL M外 dt
质点系的角动量定理：质点系对某定点的角 动量的时间变化率等于质点系对该点的合外 力矩。
2.5 质点角动量定理 角动量守恒
结论：
1）内力对定点的力矩之和为零。 2）只有外力矩才能改变系统的总角动量。 3.质点系的对轴的角动量
L Lx i Ly j Lz k
当质点系对某点的合外力矩为零时，则质点 系对该点的角动量保持不变，称为角动量守恒定 律。
角动量守 恒例题
2.5 质点角动量定理 角动量守恒
盘状星系——角动量守恒的结果
质点系对o点的角动量
r2
o
r1
L Li ri Pi
i i
质点系对o点的角动量等于系统中各质点对 同一点角动量的矢量和。
2.5 质点角动量定理 角动量守恒
2.质点系的角动量定理
用 f i 表示第i个质点所受内力之和
用 Fi 表示第i个质点所受外力之和
三、质点的角动量定理 dP 由牛顿第二定律 F dt
dP 两边用位矢叉乘 r F r dt dp d dr r (r p) p dt d dt t
由速度定义
dr v v p 0 dt
1.质点的角动量

1.质点的角动量


应用角动量守恒定律可以证明 开普勒第二定律
行星与太阳的连线在相同时间内扫过相等的面积
动画演示表明，行星在一段时 间内从 A 点运动到B点，位矢扫过 的面积是ds1；在另一段相同的时 间间隔内从 C点运动到 D点，这 时位矢扫过的面积是 ds2 。开普 勒观测的结果是 ds1=ds2。 16世纪末至17世纪初，开普勒仔细地分析整理了 前人记录下的大量精确的有关行星运动的资料，总 结出行星运动的规律、即开普勒三定律。 只是开普勒尚不理解，他所发现的三大定律已传达 了重大的“天机”。由于角动量正比于位矢的掠面 速度，因此开普勒第二定律意味着角动量守恒。
质点角动量的增量等于作用于质点上的冲量矩。 注意： 定理中的力矩和角动量都必须是相对 于同一参考点而言的。
2.质点的角动量守恒定律
law of conservetion of Angular momentum
如果：M 0， 则： L 恒矢量
如果对于某一固定点，质点所受的合外力 矩为零，则质点对该固定点的角动量矢量保持 不变。 说明： 1）角动量守恒定律是物理学中最基本的定律之 一，和动量守恒定律一样，它不仅适用于宏观 物体的运动，而且对于牛顿第二定律不能适用 的微观粒子的运动，它也适用．
L
x
z
r
υ
θ
m
o
y
L r p r mυ 大小: L rmυ sinθ
L
υ
θ
r
方向：服从右手螺旋定则
θ 是位矢 r 和动量 mυ 之间的夹角。
L 方向的判定：右手螺旋定则
Lr p
L
L 垂直于 r 和 p 所决定的平面，
例题 一颗地球卫星，近地点181km，速率 8.0km/s，远地点327km，求该点的卫星速率。 解： 角动量守恒
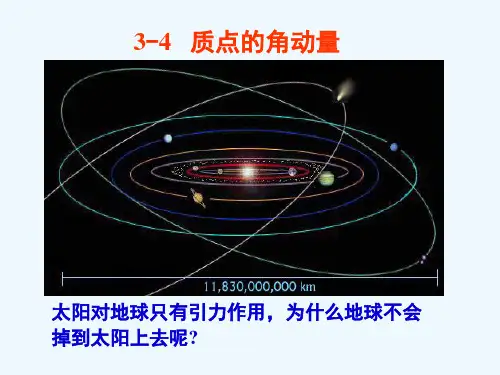
03-5质点的角动量

03-5质点的角动量


•力矩的单位
Nm
三 质点对定点的角动量定理
根据牛顿 第二定律
dp F dt
M
O d
r
P
p d r F r 与角动量有什么关系？ d t 对于O点的力矩 F r d p d L d d p r ( rp ) d t d t d t d t 0 v m v
总结：
质点角动量定 理的微分形式
Lrp dL M dt
t 2
M r F
力矩是使质点角动量发生变化的原因 质点角动量定 理的积分形式
M d t L L 2 1 t
1
作用在质点上的合力的冲量距等于质点角动量的增量 质点的角动量守恒定律 如果
M 0
L rp 恒 矢 量
1 2
太阳对地球只存在引力作用，为什么地球不会掉到太 阳上去呢? 太阳对地球的引力是有心力， 所以地球对太阳的角动量守恒
要使物体掉到太阳上去，其角
动量相对于太阳来说都要是零
只要在太阳系形成时，地球相
对于太阳具有一定的角动量， 就不会掉到太阳系上去
拉普拉斯
人造地球卫星在运行一段时间后会掉回地球上的原因 在于大气的摩擦阻力，大气摩擦力总是与卫星运动方 向相反，对地心的力矩不为零，在此力矩作用下卫星 的角动量逐渐减小，最后掉回地球
与牛顿第二定律相比，只是用力矩代替了作用在 质点上的力，用角动量代替了动量
角动量定理只适用于惯性系
质点角动量定理的积分形式
对M 两边做积分 d t d L
d t L L L 2 1 M
t 2 t 1
角动量的增量 冲量矩 作用在质点上所有力的合力在某段时间内的 冲量距等于质点在该段时间内角动量的增量
角动量守恒定律的公式

角动量守恒定律的公式

角动量守恒定律的公式
1. 角动量守恒定律公式。

- 对于质点，角动量L = r× p（其中r是质点相对于某参考点的位矢，p = mv 是质点的动量，×表示矢量叉乘）。

- 在合外力矩M = 0时，角动量守恒，即L_1 = L_2。

- 对于定轴转动的刚体，角动量L = Iω（其中I是刚体对轴的转动惯量，ω是刚体的角速度）。

当合外力矩M = 0时，I_1ω_1=I_2ω_2。

2. 相关知识点（人教版教材相关内容补充）
- 转动惯量。

- 对于离散质点系，I=∑_im_ir_i^2，其中m_i是第i个质点的质量，r_i是该质点到转轴的垂直距离。

- 对于质量连续分布的刚体，I = ∫ r^2dm。

不同形状的刚体转动惯量有不同的计算公式，例如，对于质量为m、半径为R的均匀圆盘绕通过圆心且垂直于盘面的轴转动，其转动惯量I=(1)/(2)mR^2；对于质量为m、长为l的细棒绕通过中心且垂直于棒的轴转动，I=(1)/(12)ml^2。

- 角动量定理。

- 对于质点，M=(dL)/(dt)（M是合外力矩），这表明质点所受合外力矩等于它的角动量对时间的变化率。

- 对于刚体定轴转动，M = Iα（α是角加速度），结合L = Iω也可推导出
M=(dL)/(dt)。

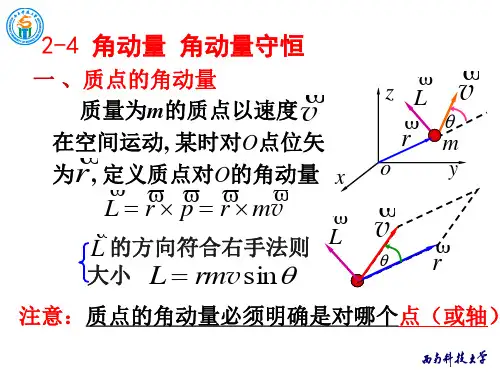
2-4 角动量 角动量守恒

2-4 角动量 角动量守恒


将角动量
Lrp
两边对时间求导
M 为合外力对同一固定点的力矩
第二项
dr p v m v 0 dt
所以
dL M dt
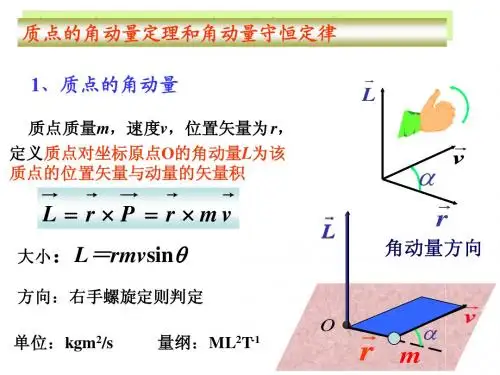
质点所受的合外力矩等于其角动量对时间 的变化率——质点的角动量定理（微分形式）。 2.质点系的角动量定理
对于由n个质点组成的质点系，系统对固 定点o的总角动量为各质点对o点角动量的矢 量和，即系统对点的总角动量为:
------质点(系)角动量守恒定律
由于角动量是矢量，角动量守恒意味着角 动量的大小和方向均保持不变。 如果力矩但对某个轴（例如z 轴）的分量为 零，则质点(系)对该轴的角动量守恒。这就是 质点(系)对轴的角动量守恒定律。
角动量守恒定律是一条普遍的规律，存在 于很多自然现象中，例如，行星受恒星引力作 用作椭圆轨道运动，引力的作用线始终通过恒 星中心，这样的力称为有心力。由于有心力对 力心的力矩恒为零，因此，受有心力作用的质 点对力心的角动量守恒。 m 掠面速度
v

r
注意：质点的角动量必须明确是对哪个点（或轴）
在直角坐标系中
Lrp
(xi yj zk ) (pxi p y j pz k )
Lx yp z zp y Lz xp y yp x
各坐标轴的分量 L zp xp y x z
开普勒第二定律
讨论：行星的掠面速度与角动量
矢径 r 在d t 时间内扫过的面积为dS。 1 m dS r vdt 2 r f 掠面速度
·
dS 1 rv dt 2
o
r
v dt
为一不变量
L r p 为一恒量，即角动量守恒
4-3角动量 角动量守恒定律

4-3角动量 角动量守恒定律

in
M L 常量
ex
角动量守恒定律是自然界的一个基本定律.
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律 电荷守恒定律 质量守恒定律 宇称守恒定律等
许多现象都可 以用角动量守恒来 说明. 花样滑冰 跳水运动员跳水
跳水运动员
茹可夫斯基凳
例3 质量很小长度为l 的均匀细杆，可 绕过其中心 O并与纸面垂直的轴在竖直平面 内转动．当细杆静止于水平位置时，有一只 小虫以速率 v 0 垂直落在距点O为 l/4 处，并背 离点O 向细杆的端点A 爬行．设小虫与细杆 的质量均为m．问：欲使细杆以恒定的角速 度转动，小虫应以多大速率向细杆端点爬行?
解 设飞船在点 A 的速度 v 0 , 月球质 量 mM ,由万有引力和 牛顿定律
vB
R
B
vA
v0
v
O h A
u
v mM m G m 2 ( R h) Rh mM g G 2 2 R R g
2 0
v0 (
Rh
)
12
1 612 m s
1
质量 m' 在 A 点和 B 点只受有心力作用 , 角动量守恒
d r mv r F dt
所以
dL M＝ dt
dL M dt

t2
t1
M dt L2 L1
冲量矩
t1
t2
M dt
对同一参考点O，质点所受的冲量矩 等于质点角动量的增量．——质点的角动 量定理
3、质点的角动量守恒定律
若质点所受的合外力矩为零，即 M=0，
4－3 角动量 角动量守恒定律
力对时间累积效应： 冲量、动量、动量定理． 力矩对时间累积效应： 冲量矩、角动量、角动量定理．
质点的角动量

质点的角动量



i
ri p i ,
对于标号为i的质点，它不仅受到来自系统外的作用力，而且 还受到系统内其它质点的作用力（内力）
fi

j
f ij ,
利用质点的角动量定理 可得
d dt
d Li dt
ri Fi f i ,

i


i
Li

i
ri ( Fi f i )
r1 , 以角速度 1旋转，然后慢慢向下拉 离为 r2时，拉力对质点所做的
v
绳，求质点离圆心距
功。

选小孔为参考点，任意 时刻质点受力矩 M r f 0 , 质点的角动量守恒，因 而有：
o r f
f
mr 1 1 mr 2 2
2 2
根据动能定理，外力做功为
v
O
rห้องสมุดไป่ตู้m
若一个质量为m的粒子在半径为r的圆周上以速 v 运动，则它的动量为 P m v ,相对于圆心的 度 位置矢量 r 与粒子运动速度 v 互相垂直 ，角 动量大小为： L m rv m r 2
是质点运动的角速度
角动量的方向由右手螺旋法则判断，垂直于物体转动 所在的平面
2
1
4、推广到质点系情形
利用牛顿第三定律，我们还可以将质点角动量定律推广到质 点系的情况，得到质点系总角动量的时间变化率与合外力 矩的简单关系，即质点系的角动量定理。 我们定义质点系对给定参考点O的总角动量为系统内所有质 点对选定参考点O的角动量的矢量和，即 ：
L

i
Li
多个外力作用于同一个质点的合力矩等于各 力的力矩的矢量和，即如果
4.0 质点的角动量 角动量定理和守恒定律

4.0 质点的角动量 角动量定理和守恒定律


定义： 质点对选取的参考点的角动量等于其 矢径 r 与其动量 mv 之矢量积。用 L 表示。
LO
LO
LO r mv
o m
mv r mv r
L
LO
o m
mv r
LO r mv
注意：1)为表示是对哪 个参考点的角动量，通 常将角动量L画在参考 点上. 2）单位：
MO
注意：
1）大小
MO r F
o m
F r
M
3）单位：牛顿米
2）方向： r F 的方向
M rF sin
F
r
M
O
4）当 F 0 时
A) r 0
有两种情况,
M 0
B）力的方向沿矢径的方向（ sin 0 ） 有心力的力矩为零.
dL 0 L 恒矢量 则： dt
合外力矩
0
角动量守恒定律：当系统所受合外力矩为零 时，质点系的角动量保持不变. 注意：1、角动量守恒定律是宇宙中普遍成立的定律，
无论在宏观上还是微观领域中都成立. 2、守恒定律 ：表明尽管自然界千变万化，变换 无穷，但决非杂乱无章，而是严格地受着某种规律的制 约，变中有不变. 这反映着自然界的和谐统一.
两式相加：
d M 1 M 10 M 2 M 20 ( L1 L2 ) 3 dt
d M 1 M 2 ( L1 L2 ) 4 dt 令：M M 1 M 2 质点所受的合外力矩
L L1 L2
F
三、角动量定理 1、角动量定理的微分形式 对一个质点：
大学物理-角动量守恒定律

大学物理-角动量守恒定律


1 dA ( r sin )ds 2
4-3 角动量
角动量守恒定律
dA 1 ds 1 ( r sin ) r sin v dt 2 dt 2 1 1 r sin mv rp 2m 2m 而行星的角动量 r p 大小恒定，所以 dA 常量 dt
一般情形下， r 和 p 都是变化的，所以 L 没 有确定的方向，但任一时刻， L 总垂直于 r 和 p 所确定的平面。在直角坐标系下，L 的三个分量
为：
3
Lx ypz zp y Ly zpx xpz Lz xp y ypx
4-3 角动量
这就是开普勒第二定律。 如果一个力的方向始终指向某一点，这力称 为有心力，这点，称为力心。有心力对力心的力 矩恒为0，因此，在有心力作用下的质点对力心 的角动量守恒。 10
4-3 角动量
角动量守恒定律
质点系角动量变化定理和角动量守恒定律 1. 质点系角动量
L l i ri 量
角动量守恒定律
3. 角动量守恒定律 如果质点系所受合外力矩 M 外 0，则
dL 0 ，L 常矢量 dt
实验表明，对于不受外界影响的粒子系统所 经历的任意过程，包括不能用牛顿力学描述的 过程，都遵守角动量守恒定律。
13
4-3 角动量
角动量守恒定律
【例1.21】光滑水平面上轻弹簧两端各系一小球， 开始弹簧处于自然长度，两小球静止。今同时 打击两个小球，让它们沿垂直于弹簧轴线方向 获得等值反向的初速度v0。如果在以后的运动过 程中弹簧的最大长度为2l0，求初速度v0。 解 系统：弹簧和小球 质心C点固定不动，相对 C点系统的角动量守恒。
必须指明是对哪个点而言的

质点的角动量角动量守恒定律

物理学
第五版
角动量概念的提出与自然界普遍存在的物体的转动 有关，大到星系，小到电子、中微子都具有转动的特征。 角动量概念在18世纪才在物理学中被定义和使用，19世 纪人们才把它看成是力学中最基本的概念之一，到20世 纪，它成为和动量、能量同样重要的物理量。角动量守 恒与空间旋转对称性相对应。因此它是自然界最基本最
普遍的规律之一。
角动量
角动量 变化率
角动量 角动量守
力矩
定理
恒定律
物理学
第五版
一、质点的角动量 质量为 的质点以
速度 在空间运动，某 时对 O 的位矢为 ，质 点对O的角动量
大小 的方向符合右手法则 角动量单位：kg·m2·s-1
物理学
第五版
质点以 作半径为 的圆运动，相对圆心
质点在一条直线上运动, 质点对 o点的角动量?
o•
m
力矩是矢量，M 的方向垂直于r和 F所决定的平面，其指向
用右手螺旋法则确定。
2 、 力矩的单位、 牛·米(N·m)
3 、力矩的计算： M 的大小、方向均与参考点的选择有关
物理学
第五版
力对固定点的力矩为零的情况：
A）
B）力的方向沿矢径的方向（
）
有心力的力矩为零.
※在直角坐标系中，其表示式为
物理学
第五版
三、质点的角动量定理 质点角动量定理的推导
物理学
第五版
作用于质点的合力对参考点 O
的力矩，等于质点对该点 O 的角动量
随时间的变化率.
冲量矩
质点的角动量定理：对同一参考点O， 质点所受的冲量矩等于质点角动量的增量.
与质点的动量定理比较:
物理学
第五版
例 一半径为 R 的 光滑圆环置于竖直平面 内. 一质量为 m 的小球 穿在圆环上, 并可在圆 环上滑动. 小球开始时 静止于圆环上的点 A (该点在通过环心 O 的 水平面上)，然后从 A 点开始下滑．设小球与圆环间的摩擦略去 不计．求小球滑到点 B 时对环心 O 的角动 量和角速度．

质点角动量定理及角动量守恒定律

我们把质点对z轴上任意一点的角动量L在z轴上的投影，叫做质点对于z轴的角动量，用Lx表示．上面已证明，Lz的数值是与参考点无关的．
在国际单位制中，角动量的单位为千克·米2／秒（kg·m2·s-1）．
例1如图3-2所示，质量为m的质点以速率v绕半径为r的圆轨道作匀速率运动．求此质点相对于圆心O点的角动量．
L=|rmvsinφ|
（3.2）
式中φ是r与mv两矢量之间的夹角．
按以上定义，角动量L含有动量mv因子，因此L与参考一点的角动量也依赖于参考点的位置．例如，在图3-1b中，参考点为O点时的角动量L与参考点为O′点时的角动量L′是不同的．
应当指出的是，虽然质点相对于任一直线（例如z轴）上的不同参考点的角动量是不相等的，但这些角动量在该直线上的投影却是相等的．如图3-1b所示，取S平面与z轴垂直，则质点对于O点及O′点的角动量分别为L与L′，L和L′分别等于以r及mv为邻边及以r′及mv为邻边的平行四边形的面积，L与L′在z轴上的投影分别是Lz=Lcosα和L′z=L′cosα′（α与α′分别是L与L′和z轴间的夹角），由图3-1b可见，Lz和L′z分别是相应的两个平行四边形在S面上的投影面积，两者是相同的，故Lz=L′z．
3．行星绕太阳的运动
作为质点角动量守恒定律的应用，我们来讨论行星绕太阳的运动．16世纪末至17世纪初，开普勒仔细地分析整理了前人记录下的大量精确的有关行星运动的资料，总结出行星运动的规律、即开普勒三定律．
应用牛顿定律的万有引力定律可以全面证明这三条由天文观察资料中总结出来的实验规律．而在本课程中，只限于讨论其中的第二条，即对任一行星，由太阳到行星的径矢在相等的时间内扫过相等的面积．根据角动量守恒定律，我们可以推导出行星运动的开普勒第二定律．
角动量守恒定律是物理学中最基本的定律之一，和动量守恒定律一样，它不仅适用于宏观物体的运动，而且对于牛顿第二定律不能适用的微观粒子的运动，它也适用．

质点的角动量

质点的角动量
一、概念解释
质点的角动量是指质点绕某一固定点旋转时所具有的动量。

在物理学中，角动量是一个基本的物理量，它与质点的旋转运动密切相关。

角动量的大小和方向决定了质点旋转运动的状态。

二、计算公式
质点的角动量可以用以下公式来计算：
L = r × p
其中，L表示角动量；r表示质点相对于某一固定点的位置矢量；p表示质点的动量。

三、单位
角动量的单位是牛·米·秒（N·m·s），也可以用焦耳·秒（J·s）表示。

四、守恒定律
在不受外力作用时，系统总角动量守恒。

这个守恒定律被称为角动量守恒定律。

这意味着系统中每个物体所拥有的角动量之和始终保持不变。

五、应用
1. 刚体转动：刚体绕固定轴线旋转时，每个质点都有自己独立的角速度和角加速度，并且每个质点都有自己独立的角动量。

2. 原子物理：原子核内部存在着粒子的旋转，这些粒子的角动量对于原子物理研究具有重要意义。

3. 天体物理：天体物理中，行星、恒星等天体绕自身轴线旋转时，它们的角动量也是非常重要的物理量。

六、总结
总之，质点的角动量是一个非常重要的物理量，它与质点旋转运动密切相关。

在计算角动量时需要考虑质点相对于某一固定点的位置矢量和质点的动量。

此外，在不受外力作用时，系统总角动量守恒。

在实际应用中，角动量被广泛应用于刚体转动、原子物理和天体物理等领域。

大学物理角动量定理


dL
dt
ri Fi
ri f内i
质点系对某一参考点的角动量随时间的变化率等于系统 所受各个外力对同一参考点力矩之矢量和。
质点或质点系的角动量守恒定律：
当系统所受外力对某参考点的力矩之矢量和始终为零 时，质点或质点系对该点的角动量保持不变。
第三章 守恒定律
4
大学 物理
3-6 角动量定理
证明开普勒第二定律：行星和太阳之间的连线在相等时间内
扫过的椭圆面积相等 。
证： dS 1 r dr 2
dS 1 r dr 1 r v dt 2 dt 2
dr
r
dS 1 r mv 1 L 有心力作用下角动量守恒
dt 2m
2m
dS 恒矢量 dt
证毕
第三章 守恒定律
5
大学 物理
3-6 角动量定理
例.在光滑的水平桌面上有一小孔0，一细绳穿过小孔，其一端
3-6 角动量定理
竖直平面内. 一质量为 m 的小球
穿在圆环上, 并可在圆环上滑动.
小球开始时静止于圆环上的点 A
(该点在通过环心 O 的水平面上)，
然后从 A点开始下滑．设小球与
圆环间的摩擦力略去不计．求小
球滑到点 B 时对环心 O 的角动量
和角速度．
解 小球受力 P 、FN 作用, FN 的力矩为零，重力矩垂直
i 1
z F1 Fi
0
ri
dpi dt
ri
Fi f内i
dL
dt
ri Fi
ri f内i
r1
ri
O
x
r2
F2
y
第三章 守恒定律
3
大学
一对力对某一固定点的力矩

讨论质点的角动量是相对于某一参考点而言的.


r
m
v
大小为L=rp，L的方向垂直于圆周轨道平面，与角速度ω的 方向相同。
p mv m r L m vr mr
2
2 L mr
三、作直线运动的质点的角动量 若质量为m的质点作直线运动，任一 时刻对o点的矢径为r，动量为p,则任 一时刻对于点o的角动量的大小为
dv dv 1.1 0的运动是什么运动？ 0的运动是什么运动？ dt dt
1.2. 在下图中标 出
讨论题
r , r , v , v
r1
o
v1
r2
i 1 i 1
由于质点系中的内力是成对出现的，每一对内力都大小相 等方向相反，作用在同一条直线上，所以内力对同一参考 点力矩的矢量和等于零。 n n n d L 令M ( ri Fi ) ( ri f i ) 0 ( ri Fi )
i 1
解：如图，行星在太阳引力作用 下沿椭圆轨道运动，Δt时间内行 星径矢扫过的面积
r
r
1 | r r | 2
S
1 S | r r | 2 dS S 1 | r r | 1 dr 面积速度: lim lim |r | dt t 0 t t 0 2 t 2 dt
y
M
F
F x F y Fz 质点角动量的改变取决于矢积 r×F ，把作 用于质点上的合外力F对参考点o的矢径r的 矢积 r 定义为力矩 ×F 单位：牛· 米（N· m） M r F
O
r

r sin
r ( F1 F2 Fn ) r F M
力矩的大小：M=rFsinθ 方向：由右手螺旋定则确定。 作用于质点上所有力矩的矢量和，等于合力的力矩。 力矩满足 M i r F1 r F2 r Fn 叠加原理

质点角动量的定义

质点的角动量是描述质点围绕某一轴旋转运动时的物理量，它衡量了质点旋转的程度和方向。

质点的角动量可以用以下公式表示：L = Iω
其中，L表示质点的角动量，I表示质点相对于旋转轴的转动惯量，ω表示质点的角速度。

转动惯量（或称为惯性矩）I是描述质点对于旋转轴的分布和构型所表现的抵抗转动的性质，它可以通过质点的质量分布和几何形状来计算。

转动惯量决定了质点在给定角速度下旋转的角动量大小。

角速度ω表示质点围绕旋转轴旋转的快慢和方向，它定义为质点围绕旋转轴的角位移与时间的比值。

质点的角动量有着保守性原理，即角动量在没有外力或力偶作用下保持不变。

这意味着如果没有外界扭矩作用于质点，其角动量将保持恒定。

需要注意的是，以上公式适用于质点的理想情况，即质点自身没有线性运动和形变，并且旋转轴通过质心。

在实际情况下，考虑到质点的线性运动和形变，角动量的计算可能需要更复杂的方法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

N P r r (t ) r (t t )
M
O
面积，称为它的掠面速度，即
位矢 r 在单位时间内扫过的
S dS lim t 0 t dt
角动量的大小与掠面速度成正比
例： 质点以角速度 作半径 为 r 的圆运动，相对圆心的 角动量
L
p
dL (M r F ) dt
即：
L r mv 恒矢量
(constant vector)
若质点所受合力对某参考点的力矩总保持为零， 则质点对该点的角动量保持不变。 质点对参考点的角动量守恒定律
• 角动量守恒定律是物理学中最基本的定律之一，和动量 守恒定律一样，它不仅适用于宏观物体的运动，而且对于牛 顿第二定律不能适用的微观粒子的运动，它也适用。
※ 角动量守恒定律
v
L

m
r
例：行星受力方向与
矢径在一条直线上 （有心力），故对心 的角动量守恒.
r
1 r r sin r L r mv mvr sin m r sin 2m 2 t t
2m
S =常数 t
开普勒第二定律：行星对恒星的矢径的掠面速度不变 .
冲量矩

t2
t1
M dt
质点角动量定理的积分形式： 对同一参考点，质点（转动物体）所受合外力 矩的冲量矩等于在这段时间内质点（转动物体）角 动量的增量。
冲量矩

t2
t1
M dt
冲量矩：反映在一段时间内力矩的时间积累作用.
说明
质点角动量定理
dL M r F dt

Lrp
例：如图, 圆锥摆. 摆球 m 对O和O’点的角动量是否守恒？ 1) 对固定点O，质点m所受合外力矩: M R (mg T ) 以逆时针为正
O’
L+ l L+ R mg o
M
L R mv
o
mgR TR sin
.
m
T
mgR TR cos 0
M mgRcos
由质点的角动量定理
dL mgR cos dt
dL mgR cos dt
dL m gRcosdt
考虑到
d dt, L mRv mR2
得
LdL m gR cosd
2 3
由题设条件积分上式

L
0
LdL m gR
2
32
3


0
cosd
(1) 角动量定理和角动量守恒定律也只是在惯性系中成立； (2) 质点在有心力场
[ F F (r )r ]中运动，其角动量守恒．
Notes:
1. 匀速直线运动质点相对任意固定点的角动量守恒 F=0 2. 匀速圆周运动质点相对圆心的角动量守恒. 3. 行星围绕太阳的椭圆运动中,相对于太阳的角动量 保持不变. 因为受到的是有心力.
例：质点作直线运动
O
d O
r
mv
对O点： L 0 大小：mvd 对O点：L 方向：
角动量的几何含义： L r p r L mvr sin m lim r sin t 0 t
1 r r sin 2m lim 2 t 0 t S 2m lim t 0 t
r0 r sin 称力臂
1、力矩定义（对O点） torque
M0 r F
力的作用效果，不仅与力的大小 magnitude 有关， 还与力的方向 direction 和力的作用点 acting point 有关。力 矩是全面考虑这三要素的一个重要的概念。
力矩与参考系的选择有关；
• 解：卫星在运行时只受地球对它的引力， 方向始终指向地心o, 力的大小只依赖于 两点距离（这种力称为有心力），对于O 点，力矩为零，
合力矩等于各分力矩的矢量和:
i 即 ： M M1 M 2 M n
M r Fi r F1 r Fn
2、质点对固定点的角动量 angular momentum
定义：任取一点o, 建立坐标系oxyz，设质点A 的质量为m，速度为 v ，矢径为 r，则质点A对o点 的角动量(或动量矩)为：
力矩和角动量须是对于惯性系中同一 固定点而言的 .
力的时间累积效应
冲量、动量、动量定理.
力矩的时间累积效应
冲量矩、角动量、角动量定理.
例: 一半径为 R 的光滑圆环置于竖直平面内.一质 量为 m 的小球穿在圆环上, 并可在圆环上滑动. 小球开始 时静止于圆环上的点 A (该点在通过环心 O 的水平面上), 然后从 A 点开始下滑.设小球与圆环间的摩擦略去不计.求 小球滑到点 B 时对环心 O 的角动量和角速度. 解 小球受重力和支持 力作用, 支持力的力矩为零, 重力矩垂直纸面向里
12
L mR
2
L mR (2 g sin )
2g 12 ( sin ) R
三、质点角动量守恒定律
law of conservation of angular momentum of particle
由角动量定理可知，
若： M 0 （条件) dL 0 dL 0 （结论） 则： 或 dt
L Rmv mvl sin
则对O 点角动量守恒(大小、方向均不变) 2) 对固定点O’，质点m 所受合外力矩:
M
o'
mgl sin 0
对O’点角动量
.
Lo ' l mv

大小 Lo’=mvl
方向随时间变化 不守恒
*合外力矩、角动量均对同一点而言
例: 如图, 圆锥摆.
由动量定理:
mg
R
v
j IT 2mvk
R IT 2mvk mg j v
例： 用细绳系一小球在光滑的水平面上作圆周运动,
圆半径 r0 , 速率 v0 . 今缓慢地拉下绳的另一端, 使圆半径逐步减小. 求圆半径缩至 r 时, 小球的 速率 v 是多大?
m 对于 o 点的角动量是否守恒? (是)
m 对于 o’ 点的角动量是否守恒? (否) (否) mA
R
O’
y
x
m 动量是否守恒?
v
o
B
质点绕行半周时间内的绳的张力冲量是多少? (A点--B点)
解: 绕行半周时间
t
R
v
绕行半周动量增量为: mvk mvk 2mvk
又 为角动量, 则:
M r F
为力矩.
质点角动量定理微分形式
M ——对某一点的合力矩
L ——对同一点的角动量
2、角动量定理 angular momentum theorem
dL M r F dt
质点角动量定理微分形式
在惯性系中，质点对某参考点的角动量对时 间的变化率等于作用于质点的合力对同一参考 点的力矩。 质点对参考点的角动量定理
把位置矢量和动量 矢量结合起来; 角动量与参考点O的 选择有关；
x
z
r
o
m y
v
L
v

r
角动量与参考系的选择有关. ※ 说明力矩和角动量时，须指明对哪一个点而言.
L 又称动量矩(moment of momentum)
SI 单位: kgm2/s or Js
• 角动量守恒定律和动量守恒定律一样，是自然 界最基本最普遍的定律之一。
§5.1 质点的角动量
一、 质点角动量(angular momentum) 的定义
1、力对固定点的力矩 torque :
M0 r F
M
F
力 F 对O点的力矩
SI单位：N m
r

o
r0
方向：由右手螺旋法则; 即：右手四指从 r 方向绕向 F 则拇指指的就是 M 的方向 大小： M 0 M 0 F r sin r0 F ——力臂乘以力
L r p r mv
方向：由右手螺旋定则确定，
right hand screw rule
z
r
x o
m y
v
大小：
L
v

L r p sin mvr sin
r
2、质点对固定点的角动量 angular momentum
L r p r mv
第五章 角动量 • 关于对称性
（Chapter 5 Angular momபைடு நூலகம்ntum & Symmetry）
本章的基本要求：
1. 理解质点及质点系角动量的物理意义 ； 2. 掌握质点、质点系的角动量定理 ；
3. 掌握角动量守恒定律 ；
4. 理解对称性的概念，了解守恒律与对称性的关系。
角动量
m
o r
大小： 方向：
L mr I
2
与角速度 的方向相同。
例：长为 l 的轻杆，其两端分别固定有质量为m和3m的物体， 3 取与杆垂直的固定轴O，重物m与O轴的距离为 l ，绕轴 4 转动的线速度为 v 。求它们对转轴的总角动量。 解：两球的角速度相等
故3m质点线速度为：
r
v0 r0
解：小球相对圆心所受力矩
零
M r F 0
L r mv C
（有心力)
所以，小球相对圆心的角动量守恒